Numerical Investigation of Nucleated Bubbles around a Heated

Square Obstacle using Thermal Hybrid Lattice Boltzmann Method

Salaheddine Channouf

, Mohammed Jami

and Ahmed Mezrhab

Mechanical and energetic laboratory, First Mohamed university, faculty of sciences, Oujda, Morocco

Keywords: Boiling phenomenon, nucleated bubbles, lattice Boltzmann method, 2-order Runge-Kutta finite difference

scheme, heat transfer, phase-change.

Abstract: The phenomenon of boiling has become one of the challenges of the LB community in recent years, as it is

frequently used in industry and deals with a complex natural phenomenon. For this purpose, we have devel-

oped a computational code that allows us to simulate this phenomenon around a square obstacle of variable

length in a rectangular cavity. We aim to study the behaviour of nucleated bubbles which appear around this

obstacle due to its heat exchange with the liquid. The pseudopotential multi-relaxation time lattice Boltzmann

method MRT-LBM proposed by (Li, 2013) is used as a solver of the fluid flows combined with the 2-order

Runge-Kutta finite difference scheme for modelling the phase change from a liquid to a vapour phase

(Zhao,2018) and the temperature field.

1 INTRODUCTION

Lattice Boltzmann method (LBM) has become a pre-

cision and efficient tool for simulating hydro-thermo-

dynamic phenomena because its simplicity of imple-

mentation and insertion of boundaries. This method

contains 2 main steps represented by a distribution

function denoted 𝑓





𝒙,𝑡



which presents a set of par-

ticles having precise velocities in a regular mesh

called lattice Boltzmann and follows their movements

in phase space. These two steps describe the collision

and streaming of particles over time on the lattice

(Meng, 2014) and allow to have a simple algorithm to

calculate the macroscopic variables as density, veloc-

ity components, temperature, etc. In this paper, the

collision and streaming steps are represented in mo-

mentum space, this space aims to shift each macro-

scopic quantity towards the equilibrium by the multi-

relaxation time (MRT) collision operator model

(Krüger, 2017) as opposed to the simple relaxation

time operator known as the BGK operator model (An-

dries, 2002) which is used to relax the distribution

function around the equilibrium distribution function.

The MRT model is used due to its reliability and high

stability. In our work, the pseudopotential MRT-

https://orcid.org/0000-0002-8538-5629

https://orcid.org/0000-0002-5356-4729

https://orcid.org/0000-0001-6013-7496

LBM approach (Shan,2014) is adopted. This is the fa-

mous model of the LB community for the simulation

of a multiphase flow thanks to its simplicity to obtain

the separation of the phases without the need to track

at each step time the interface between the phases.

This model allows to successfully simulate several

numerical problems in multiphases such as wettabil-

ity, condensation, boiling, collapsing and rising bub-

bles, etc.

In the present work, this model is combined with

the celebrate Runge-Kutta finite difference scheme

(Zhao, 2018, Zheng, 2018) to simulate the thermal be-

havior of liquid chosen at saturated temperature dur-

ing phase change around a heated obstacle with a var-

iable characteristic length 𝐷.

2 METHODOLODY

The hybrid model proposed in this work is described

by the following equation

𝑓



∗



𝒙,𝑡



𝑓





𝒙,𝑡



𝑴

𝟏

𝜦𝑴𝑓





𝒙,𝑡



𝑓







𝒙,𝑡



𝛿𝑡𝑴𝑭

(1)

Channouf, S., Jami, M. and Mezrhab, A.

Numerical Investigation of Nucleated Bubbles around a Heated Square Obstacle using Thermal Hybrid Lattice Boltzmann Method.

DOI: 10.5220/0010730400003101

In Proceedings of the 2nd International Conference on Big Data, Modelling and Machine Learning (BML 2021), pages 171-174

ISBN: 978-989-758-559-3

171

The term in the left hand represents the post-collision

distribution function which can be calculated with the

previous distribution function 𝑓





𝒙,𝑡



by subtracting

its disturbance around the equilibrium distribution

function relaxing by nine relaxation times given by

the relaxation matrix 𝜦 and by adding the forcing

term 𝑭. The parameters 𝑴 and 𝑴

𝟏

describe the

transformation matrix and its inverse from the phase

space to the momentum space.

The 2-order Runge-Kutta finite difference scheme

is used as a solver of energy equation to simulate the

liquid-vapor phase-change transformation as (Zhao,

2018, Zheng, 2018)

𝑑𝑇

𝑑𝑡

𝐯.𝛁𝑇

𝑇

𝜌𝑐





𝜕𝑃



𝜕𝑡





𝛁.𝐯 

𝜌𝑐



𝛁.𝜆𝛁𝑇

(2)

𝑃



is the pressure according to equation of state

proposed by Peng-Robinson (Yuan, 2006) which is

calculated from the pseudopotential function, 𝜆 is the

thermal conductivity and 𝑐



is the specific heat coef-

ficient 𝐯 is the macroscopic velocity of flows and 𝜌 is

the macroscopic density. These macroscopic parame-

ters can be calculated as follows

𝜌

𝑓



; 𝜌𝐮

𝑓



𝑐



(3)

𝒄

𝒊

is the lattice speed in i

direction.

3 VALIDATION MODEL

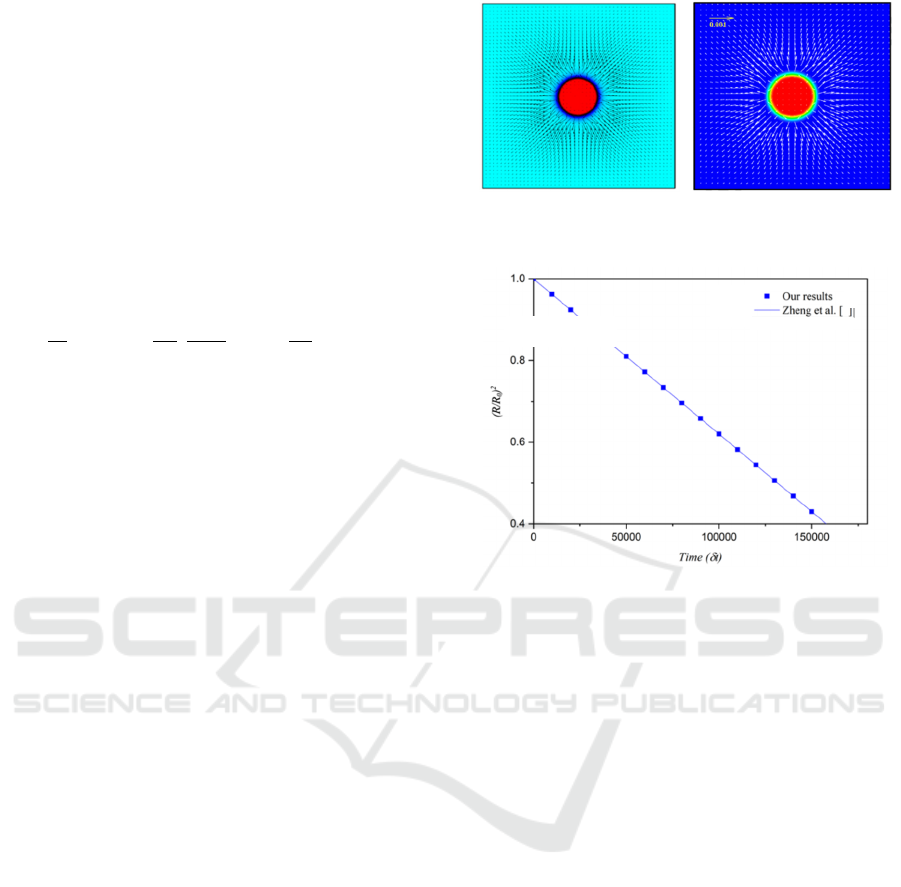
Figures 1 and 2 show the validation of our code using

the work of Zheng et al. (Zheng, 2018) to check its

accuracy and its efficiency. For this purpose, a ther-

mohydrodynamic effect is investigated to simulate

the evaporation behavior of a heated liquid droplet

placed in the center of a cavity and surrounded by a

saturated vapor by implementing the periodic bound-

ary for all cavity walls in which the thermal conduc-

tivity is set to be constant 𝜆1 which allows to ne-

glect the convective effect.

From Figure 2, the results show a reducing of ini-

tial radius of droplet over time δt, this reduction is de-

scribed by the square rate of change of the radius with

a negative slope line. However, the vector field

shown in Figure 1 shows the direction of the loss of

liquid mass caused by the transformation of the liquid

into vapor. The same remarks are made from the ref-

erence work. Therefore, our numerical results show a

strong corresponding with those reported by Zheng et

al. (Zheng, 2018).



𝑎



resul



𝑏



Zheng e

al. (Zheng, 2018)

Figure 1: Comparative results with reference (Zheng, 2018)

Figure 2: Square rate change of radius over time 𝛿𝑡 in com-

parison with reference (Zheng, 2018).

4 RESULTS AND DISCUSSIONS

4.1 Presentation of the Computational

Problem

Figure 3 shows the computational domain of a satu-

rated liquid confined in a rectangular cavity of height

𝐻 and length 𝐿 in which a heated square obstacle at

temperature 𝑇



 1.16𝑇





is placed halfway between

the vertical walls at a distance of 𝐻/6 from the bot-

tom wall. The obstacle has a height h and a variable

characteristic length D. In our simulation, the critical

temperature is set to be 𝑇





 0.07292. For the fluid

flow, the periodic boundaries are selected for both

right and left vertical walls. The bounce-back bound-

aries are adopted for the bottom wall, while the out-

flow boundary is applied on the top wall. For the ob-

stacle faces, the no-slip boundaries are selected. Their

density value is adjusted to be in a non-wetting phase.

All computational domain is set at saturated temper-

ature 𝑇



(Zheng, 2018)

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)

172

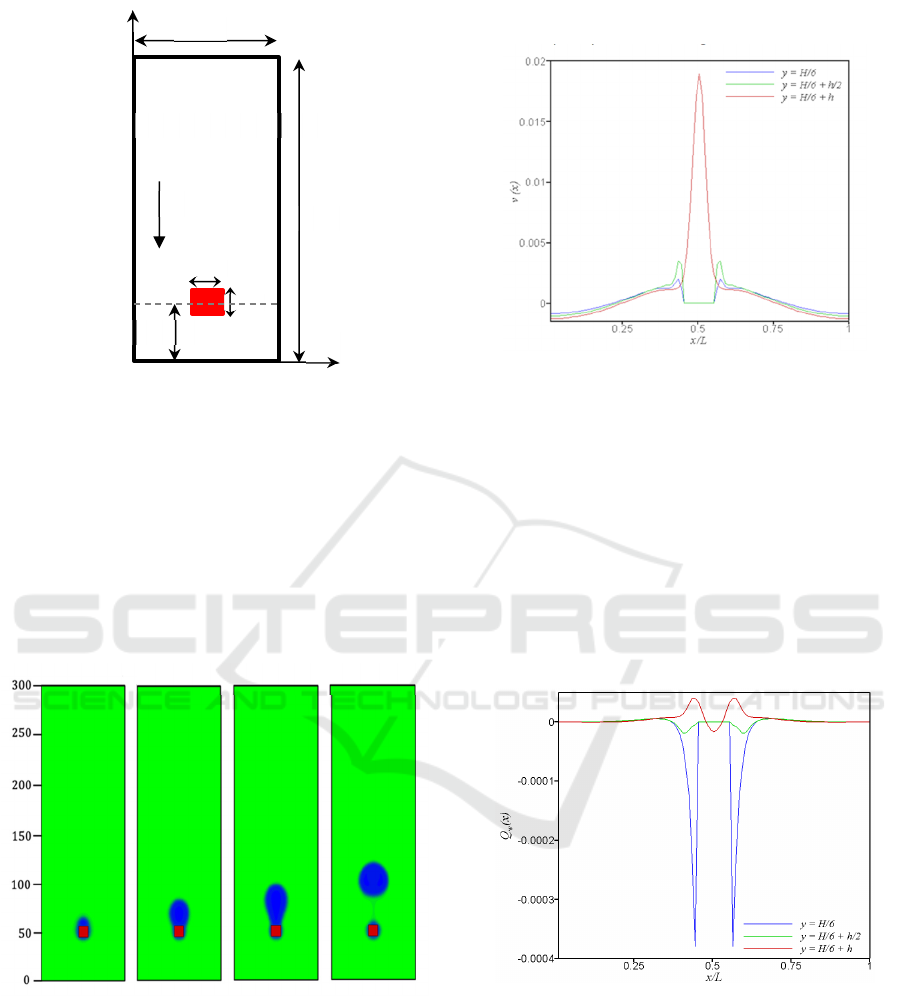
Figure 3: Illustration of the computational problem.

4.2 Formation Pattern of Nucleated

Bubble around the Obstacle

Figure 4 illustrated the density behavior of both liquid

and vapor during phase change caused by the heated

obstacle. It can be seen that the nucleated bubble

formed around the obstacle grows progressively over

time until its volume becomes important, then, it

moves upward due to the buoyant force.

Figure 4: Steps of the nucleated bubble formation around

the heated obstacle.

Figure 5 describes the velocity at three different posi-

tions near to the obstacle at time 𝑡

∗

 3.66 corre-

sponding to the final step of formation of nucleated

bubble. At 𝑦𝐻/6, the velocity is zero on the ob-

stacle and tends to increase in the surrounding area.

However, it remains weak due to friction with the

solid. At the obstacle-liquid interface 𝑦  𝐻/6 

ℎ/2, the velocity increases but it keeps the same

form. finally, at 𝑦  𝐻/6  ℎ, an intense peak due

to the buoyancy effect during nucleation is noted.

Figure 5: The velocity component in y-direction at different

positions.

The heat flux exchanged between the obstacle and the

liquid is illustrated in Figure 6 at three different posi-

tions and at 𝑡

∗

 3.66. This heat leads to the for-

mation of the nucleated bubbles. For 𝑦  𝐻/6, the

exchange flux is greater at the vertical solid-liquid in-

terfaces then it decreases to be zero when moving

away from these interfaces. At position 𝑦  𝐻/6 

ℎ/2, the exchanged flux behaves in the same way as

in the first case but it is reduced. For the last position,

a decrease in flux at the center of the curve is noted.

This is due to the flux transferred to the bubbles.

Figure 6: The exchange heat flux between liquid and heated

obstacle at different positions.

4.3 Effect of Variation of

Characteristic Length D on

Nucleation

In this part, we adjusting the characteristic length 𝐷 to

study its impact on the nucleated bubble for-mation.

The same parameters of fluid flows and temperature

field are chosen as the previous part.

𝑇



Liquid at 𝑇𝑇



𝐷

ℎ

𝐻

𝐿

𝐻/6

𝑡

∗

 0.7 𝑡

∗

 1.3

𝑡

∗

 2.45 𝑡

∗

4

Numerical Investigation of Nucleated Bubbles around a Heated Square Obstacle using Thermal Hybrid Lattice Boltzmann Method

173

(

)

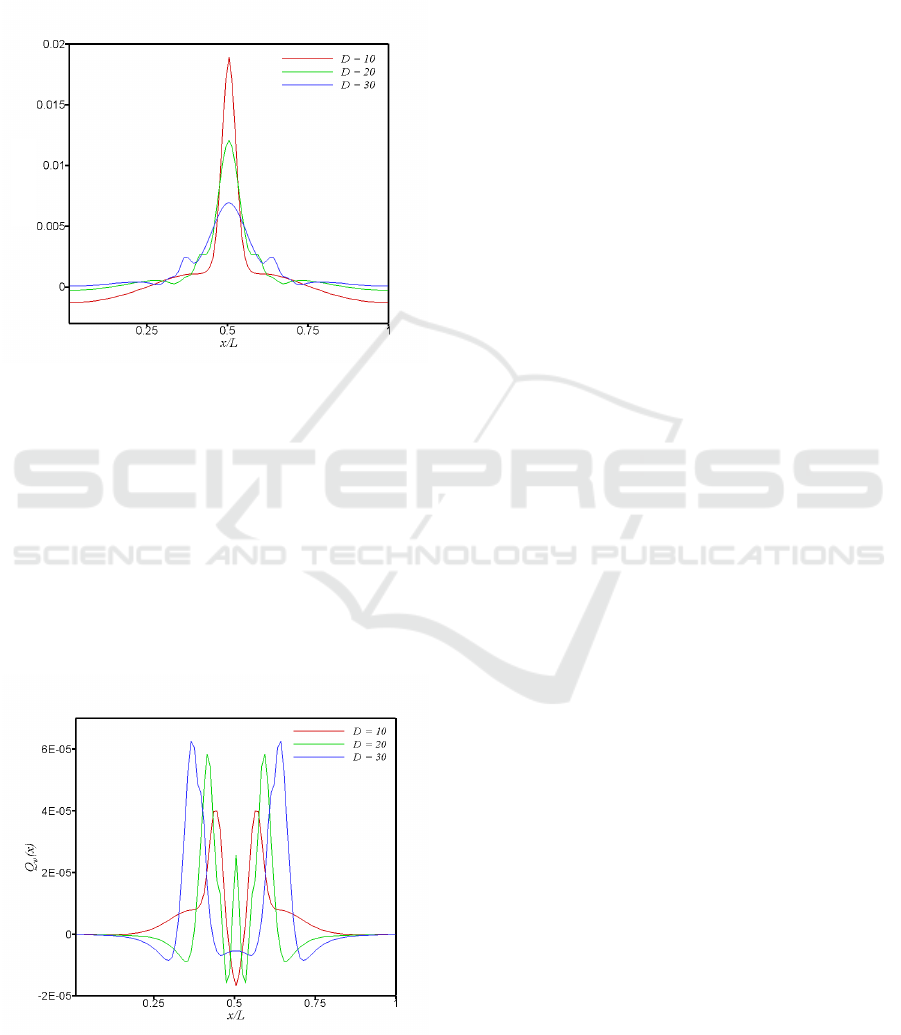
Figure 7 gives the behavior of the velocity com-

ponent in the y direction for three different values of

D and for the position 𝑦 𝐻/6ℎ. We notice that

the velocity decreases with the increase of D. Indeed,

when D increases, the number of nucleated bubbles

increases then they merge to give a large bubble

which is more slowed down by the liquid.

Figure 7: The velocity component in y-direction by varying

the length D of the obstacle at y = H/6+h.

Figure 8 shows the heat flux exchanged between the

upper face of the solid and the liquid to give more de-

tails on the formation of nucleated bubbles around the

obstacle. For this purpose, the heat flux exchanged is

studied for three different values of the characteristic

length D. The curves show that the increase in the

characteristic length leads to an increase in heat flux

at the right and left sides of the obstacle. Moreover,

in the middle of the cavity in the x direction, the heat

flux form changes with D and indicates that the heat

transferred to the liquid is important for small bubbles

than for large bubbles.

Figure 8: The exchange heat flux between liquid and heated

obstacle by varying the length D of the obstacle at y =

H/6+h.

5 CONCLUSIONS

In the light of this work, we can draw the following

conclusions:

- When the characteristic length D increases, the heat

exchange between the solid and the liquid increases

at the vertical faces of the obstacle. However, this flux

decreases in the area of nucleated bubbles.

- The large bubble formed by the nucleated bubbles

is all the more slowed down as its volume is im-

portant.

These results allow us to make the right choice of

the characteristic length D that gives a compatible

boiling shape. In future work, 3D will investigate and

validate that with experiment by applying this method

to the study of phase change materials.

REFERENCES

Li, Q., Luo, K. H., & Li, X. J. 2013. Lattice Boltzmann

modeling of multiphase flows at large density ratio with

an improved pseudopotential model. Physical Review

E, 87(5), 053301.

Zhao, W., Zhang, Y., Xu, B., Shang, W., & Jiang, S. 2018.

Pseudopotential multiple-relaxation-time lattice Boltz-

mann simulation of vapor condensation on vertical sub-

cooled walls. arXiv preprint arXiv:1808.04973.

Meng, J., & Zhang, Y. 2014. Diffuse reflection boundary

condition for high-order lattice Boltzmann models with

streaming–collision mechanism. Journal of Computa-

tional Physics, 258, 601-612.

Krüger, T., Kusumaatmaja, H., Kuzmin, A., Shardt, O.,

Silva, G., & Viggen, E. M. 2017. MRT and TRT Colli-

sion Operators. In the Lattice Boltzmann Method (pp.

407-431). Springer, Cham.

Andries, P., Aoki, K., & Perthame, B. 2002. A consistent

BGK-type model for gas mixtures. Journal of Statistical

Physics, 106(5), 993-1018.

Shan, X., & Chen, H. 1993. Lattice Boltzmann model for

simulating flows with multiple phases and components.

Physical review E, 47(3), 1815.

Zheng, S., Eimann, F., Fieback, T., Xie, G., & Gross, U.,

2018. Numerical investigation of convective dropwise

condensation flow by a hybrid thermal lattice Boltz-

mann method. Applied Thermal Engineering, 145, 590-

602.

Yuan, P., & Schaefer, L. (2006). Equations of state in a lat-

tice Boltzmann model. Physics of Fluids, 18(4),

042101.

Chen, L., Kang, Q., Mu, Y., He, Y. L., & Tao, W. Q. (2014).

A critical review of the pseudopotential multiphase lat-

tice Boltzmann model: Methods and applications. Inter-

national journal of heat and mass transfer, 76, 210-236.

BML 2021 - INTERNATIONAL CONFERENCE ON BIG DATA, MODELLING AND MACHINE LEARNING (BML’21)

174