Initializing k-means Clustering

Christian Borgelt

1,2

and Olha Yarikova

University of Konstanz, Universit

atsstraße 10, D-78457 Konstanz, Germany

Paris-Lodron-University of Salzburg, Hellbrunner Straße 34, A-5020 Salzburg, Austria

Keywords:

k-means, Cluster Initialization, Maximin, k-means++.

Abstract:

The quality of clustering results obtained with the k-means algorithm depends heavily on the initialization of

the cluster centers. Simply sampling centers uniformly at random from the data points usually yields fairly

poor and unstable results. Hence several alternatives have been suggested in the past, among which Maximin

(Hathaway et al., 2006) and k-means++ (Arthur and Vassilvitskii, 2007) are best known and most widely used.

In this paper we explore modiﬁcations of these methods that deal with cases, in which the original methods

still yield suboptimal choices of the initial cluster centers. Furthermore we present efﬁcient implementations

of our new methods.

1 INTRODUCTION

If groups of similar objects are to be found in given

data, the k-means clustering algorithm is among the

most popular approaches. However, a problem of the

k-means algorithm is that its success depends heavily

on its initialization. If the initial centers are poorly

chosen, it may get stuck in a local optimum far infe-

rior to what may be possible. This is often the case

for the na

ıve approach of choosing the initial cluster

centers uniformly at random from the data points.

Two common approaches to address this problem

are the Maximin method (Hathaway et al., 2006) and

the k-means++ procedure (Arthur and Vassilvitskii,

2007). In this paper, after a brief review of the ba-

sic k-means algorithm in Section 2, we consider in

Section 3 extensions of these two methods that aim

at reducing the chances of low quality center choices.

These variants try to avoid choosing outliers or cen-

ters that are too close together by restricting the data

points from which the next center may be chosen, ei-

ther strictly or in probability. In Section 4 we present

experimental results on several standard benchmark

data sets, evaluating both result quality and number

of distance computations. The paper closes with Sec-

tion 5, in which we draw conclusions from our exper-

iments and their results.

2 k-means CLUSTERING

The k-means algorithm ﬁnds a desired number k of

clusters in a data set x

, . . . , x

∈

. It starts by

choosing k initial centers, e.g. by sampling uniformly

at random from the data points. In the subsequent

optimization phase, two steps are executed alternat-

ingly: (1) each data point is assigned to the center that

is closest to it and (2) the centers are re-computed as

vector means of the data points assigned to them.

If ν(x) denotes the center closest to a data point x,

this update scheme can be written as

∀i;1 ≤ i ≤ k : c

t+1

∑

j=1

(ν

) = c

) · x

∑

j=1

(ν

) = c

)

The upper indices indicate the update step and (φ)

yields 1 if φ is true and 0 otherwise. ν

) represents

the assignment step, the fraction computes the mean

of the points assigned to center c

It can be shown that this update scheme must con-

verge, that is, must reach a state in which another

execution of the two steps does not change the clus-

ter centers anymore (Selim and Ismail, 1984). How-

ever, there is no guarantee that the obtained result is

optimal in the sense that it yields the smallest sum

of squared distances between the data points and the

cluster centers they are assigned to. Rather, it is very

likely that the optimization gets stuck in local opti-

mum.

260

Borgelt, C. and Yarikova, O.

Initializing k-means Clustering.

DOI: 10.5220/0009872702600267

In Proceedings of the 9th International Conference on Data Science, Technology and Applications (DATA 2020), pages 260-267

ISBN: 978-989-758-440-4

real[][] maximin (real data[][], int n, int k):

(* data: data points, n: number of data points, k: number of clusters *)

int i, j, imax; (* loop variables, array indices *)

real dsts[n], dmax, d; (* (min/max) distance to centers *)

int hcis[n]; (* highest used cluster indices *)

real ctrs[k][]; (* chosen initial cluster centers *)

ctrs[0] = data[randint(0, n-1)]; (* choose ﬁrst center randomly *)

for i = 0 to n-1: (* compute distances to ﬁrst cluster *)

dsts[i] = distance(data[i], ctrs[0]); hcis[i] = 0;

for j from 1 to k-1: (* select the remaining clusters *)

dmax = 0; imax = 0; (* init. max. distance and index *)

for i = 0 to n-1: (* traverse the data points *)

if dsts[i] <= dmax: continue; (* if less than maximum, skip point *)

while hcis[i] < j-1: (* traverse skipped clusters *)

hcis[i] += 1; (* compute distance to center *)

d = distance(ctrs[hcis[i]], data[i]);

if d < dsts[i]: (* if less than known distance, *)

dsts[i] = d; (* update the minimum distance *)

if d < dmax: break; (* if less than current maximum, skip *)

if dsts[i] > dmax: (* if larger than current maximum, *)

dmax = dsts[i]; imax = i; (* note new maximum and index *)

dsts[imax] = 0.0; (* mark the data point as selected *)

ctrs[j] = data[imax]; (* and add it to the set of centers *)

return ctrs; (* return the chosen cluster centers *)

Figure 1: Efﬁcient implementation of the Maximin cluster center initialization.

3 k-means INITIALIZATION

The quality of a k-means result depends heavily on

the initial centers. Poor choices can lead to inferior re-

sults due to a local optimum. However, improvements

over na

ıvely sampling uniformly at random from the

data points are easily found, for example the Maximin

method (Hathaway et al., 2006) (Section 3.1) and the

k-means++ procedure (Arthur and Vassilvitskii, 2007)

(Section 3.2).

3.1 Maximin and Its Variants

Standard Maximin. A simple and straightforward

method to obtain well dispersed initial centers is the

Maximin method (Hathaway et al., 2006): the ﬁrst

center is sampled uniformly at random from the data

points. All subsequent centers are chosen as those

data points that maximize the minimum distance to

the already chosen cluster centers (hence the name

“Maximin”).

A na

ıve implementation of Maximin computes,

after the ﬁrst center has been chosen, the distances

of all data points to the most recently chosen center

and updates a minimum distance to a center that is

stored for each data point. This requires

∑

k−1

i=1

(n−i) ≈

(k −1)n distance computations. However, using ideas

that are inspired by approaches like (Elkan, 2003;

Hamerly, 2010; Newling and Fleuret, 2016a) for ac-

celerating the optimization phase, the number of dis-

tance computations can be reduced (Yarikova, 2019).

The core idea is as follows: we store for each data

point a (minimum) distance to a center and the index

of this center. These distances are initialized with the

distance to the ﬁrst center and all indices are set to

zero. Any new center can obviously only reduce the

stored distances. Hence, in the search for the maxi-

mum of the minimum distances of data points to al-

ready chosen centers, any data points with a smaller

minimum distance than the current maximum can be

skipped, even if not all distances to the currently cho-

sen centers have been computed. These distances

are computed only on a need-to-know basis: if the

minimum distance stored with a data point is greater

than the current maximum, it could yield the new

maximum, and hence distances to centers that were

skipped before are determined, but only as long as

the minimum distance of the data point remains larger

than the current maximum. Thus, for data points close

to some already chosen cluster center, distance com-

putations may no longer be necessary. A formal de-

scription of this algorithm in pseudo-code (somewhat

Python-like) is shown in Figure 1.

Trimmed Maximin. A core problem of the Max-

imin method is that it tends to select outliers, that is,

data points at the very rim of the data point cloud.

Although this ensures well dispersed initial centers,

it also tends to select centers that are far away from

Initializing k-means Clustering

261

other data points and thus atypical for any clusters.

A simple solution to this problem is trimmed Max-

imin (Hathaway et al., 2006), where in each selection

step a certain number s (or fraction) of the farthest

data points are trimmed. Hence the data point with the

(s+1)-th largest minimum distance to already chosen

centers is selected.

Such an approach is easily implemented by re-

placing the single maximum distance dmax and cor-

responding index imax in the algorithm in Figure 1

by a minimum heap of size s + 1, which collects

the s + 1 data points with the largest minimum dis-

tances (Yarikova, 2019). We used a simple binary

heap in our implementation. Whenever a data point

has a larger minimum distance than the data point at

the top of the heap, the data point at the top of the

heap is replaced (unless the heap is not yet full—then

the new point is simply added) and the new point sifts

down in the heap to its proper place. After all data

points have been processed, the data point at the top

of the heap is chosen as the next center.

Sectioned Maximin. An alternative to excluding ex-

treme data points is to reduce at least the chance

that outliers are chosen by selecting the data point

with the largest maximum distance not among all

data points, but only in a (random) subset of the data

points (Yarikova, 2019).

This can be achieved with a simple modiﬁca-

tion of the algorithm shown in Figure 1: The subset

size s ≤ n is passed as an additional parameter. The

loop “for i = 0 to n-1:” is replaced by a loop

“for r = 1 to s:” (r is a new variable), while the

variable i is initialized to zero before it and updated

by “i = (i+1) mod n;” in each loop. In this way

the subsets, from which the next centers are chosen as

those data points with the largest minimum distances,

are sections of data points that are cut cyclically from

the (initially shufﬂed) data points. Note that choos-

ing s = n conveniently yields the original Maximin

behavior as a special case (Yarikova, 2019).

3.2 k-Means++ and Its Variants

Standard k-Means++. The k-means++ procedure

(Arthur and Vassilvitskii, 2007) can be seen as a ran-

domized version of the Maximin method. The data

point with the largest minimum distance from the al-

ready chosen centers is not selected absolutely, but

is merely assigned a (signiﬁcantly) higher probability

than other data points. To be more speciﬁc, the prob-

ability that a data point is chosen as the next center is

proportional to the square of the minimum distance it

has to already chosen cluster centers (sampling from

a d

-distribution). Thus data points that are far away

from all already chosen centers have a high probabil-

ity of being chosen, without the farthest one being the

only possible choice.

A standard implementation of k-means++ re-

quires, like a na

ıve implementation of the Maximin

method,

∑

k−1

i=1

(n − i) ≈ (k − 1)n distance computa-

tions. Unfortunately, this cannot be reduced so eas-

ily as for the Maximin method, because all minimum

distances to cluster centers need to be known for the

random sampling. For large data sets, the methods

suggested in (Bachem et al., 2016a; Bachem et al.,

2016b) may be useful, which yield an approxima-

tion of k-means++ with the help of a Markov Chain

Monte Carlo method. We implemented these as well,

but since their results do not differ much for standard

benchmark data sets, we do not study them here.

Trimmed k-Means++. k-means++ still suffers from

two drawbacks: in the ﬁrst place, outliers again have a

high probability of being chosen as initial cluster cen-

ters. Secondly, even though data points with a small

minimum distance to already chosen centers are as-

signed only a small probability, the number of these

data points naturally increases as more centers are be-

ing selected. Hence they collect considerable prob-

ability mass simply by their number. As a conse-

quence, the chance that centers are chosen that are

too close together may be unfavorably high.

We address these problems with a trimming ap-

proach based on quantiles (Yarikova, 2019): data

points with a minimum distance below a user-

speciﬁed lower quantile 1 − q

or above a user-

speciﬁed upper quantile 1 − q

cannot be chosen as

the next cluster center. (Note that we specify both

quantiles as 1 − q, because we want q

and q

to refer

to fractions of data points with the largest minimum

distances.)

Especially if the lower quantile is large (we rec-

ommend to choose q

< 0.5), this also enables an

efﬁcient implementation that can use (similar to the

trimmed Maximin method) a heap to ﬁnd the data

points above the lower quantile 1 − q

. That is, we

create a minimum heap of size s = bq

·nc, which col-

lects the data points having the s largest minimum dis-

tances to already chosen cluster centers. This heap is

ﬁlled in exactly the same way as the one for trimmed

Maximin. After all data points have been processed,

the top t = bq

·nc data points (that is, the t data points

with the largest minimum distances) may be trimmed

from the heap using the quickselect scheme (Hoare,

1961) for ﬁnding a quantile quickly as well as col-

lecting the values above the quantile. A formal de-

scription of this algorithm in pseudo-code (somewhat

Python-like) is shown in Figure 2 (Yarikova, 2019).

DATA 2020 - 9th International Conference on Data Science, Technology and Applications

262

real[][] kmeanspp (real data[][], int n, int k, int s, int t):

(* data: data points, n: number of data points, k: number of clusters *)

(* s, t: number of data point from lower/upper quantile to end n *)

int i, j, isel; (* loop variables, array indices *)

real dsts[n+1], dcum[], d; (* (min/cum) distances to centers *)

int hcis[n]; (* highest used cluster indices *)

int heap[s], h[]; (* heap for largest min. distances *)

real ctrs[k][]; (* chosen initial cluster centers *)

ctrs[0] = data[randint(0, n-1)]; (* choose ﬁrst center randomly *)

for i = 0 to n-1: (* compute distances to ﬁrst cluster *)

dsts[i] = distance(data[i], ctrs[0]); hcis[i] = 0;

dsts[n] = -1.0; (* set distance sentinel for heap *)

for j from 1 to k-1: (* select the remaining clusters *)

heap[0] = n; j = s; (* set heap sentinel, start index *)

for i = 0 to n-1: (* traverse the data points *)

if dsts[i] <= dsts[heap[0]]: continue; (* if less than heap data, skip point *)

while hcis[i] < k-1: (* traverse skipped clusters *)

hcis[i] += 1; (* go to the next cluster *)

d = distance(ctrs[hcis[i]], data[i]);

if d < dsts[i]: dsts[i] = d; (* if less, update minimum distance *)

if dsts[i] <= dsts[heap[0]]: (* if less than heap data, *)

continue; (* skip the data point *)

if j > 0: j -= 1 (* get (next) position in heap *)

sift(heap, j, s, i, dsts); (* let new distance sift down in heap *)

if t <= 0: h = heap; (* if all in top quantile, use heap *)

else: (* if to trim uppermost quantile *)

quantile(heap, s, t-1, dsts); (* trim off t largest distances *)

if t < s: h = heap[t:]; (* get the remaining heap *)

else: h = heap[-1:] (* or at least the last element *)

dcum = cumsum([dsts[i] for i in h]); (* form cumulative sums *)

isel = searchsorted(dcum, dcum[-1] *random());

if isel >= len(h): isel = len(h)-1; (* sample randomly from d

distrib. *)

isel = h[isel]; (* get chosen data point index *)

dsts[isel] = 0.0; (* mark the data point as selected *)

ctrs[j] = data[isel]; (* and add it to the set of centers *)

return ctrs; (* return the chosen cluster centers *)

Figure 2: Efﬁcient implementation of the trimmed k-means++ procedure. The function sift performs a standard sift down

operation for a binary heap (as a simple array), called on the heap, the number of empty elements in the heap, and the size of

the heap, the data point and its distance. The function cumsum forms the cumulative sums of the values in its parameter array;

the function searchsorted ﬁnds the index of an element in an array.

3.3 Local Outlier Factor

In order to prevent outliers from being chosen as clus-

ter centers (this is the main problem of the Maximin

approach, see above), we also tried ﬁnding (potential)

outliers ﬁrst and excluding them from the available

choices for (initial) cluster centers. That is, the de-

scribed methods for choosing initial cluster centers

were executed only on those data points that were not

labeled as outliers, while all data points were used in

the subsequent cluster optimization phase.

For detecting outliers we relied on the local out-

lier factor measure (Breunig et al., 2000) in the

SciKitLearn (Pedregosa et al., 2011) implementa-

tion, using default settings (20 neighbors, automatic

thresholding). For all used data sets, the local outlier

factors were computed and turned into outlier indica-

tors (thresholds determined as described in (Breunig

et al., 2000)), which could then be passed in a sepa-

rate ﬁle to the actual clustering program. In this way

we avoided having to re-compute the local outlier fac-

tors again for each clustering run, although execution

times were generally very low (see the last column of

Table 1 in the next section).

We also experimented with the somewhat newer

method of local outlier probability (Kriegel et al.,

2009), in the implementation that is provided by

PyNomaly

. However, the execution times were so

much longer than those of the local outlier factor

implementation of SciKitLearn that we soon aban-

doned this possibility.

4 EXPERIMENTS

For our experiments we used the data sets shown in

Table 1, most of which stem from (Fr

anti and Siera-

https://github.com/vc1492a/PyNomaly

Initializing k-means Clustering

263

noja, 2018)

, although the data sets “iris”, “wine” and

“yeast” can also be found in the UCI machine learning

repository (Dheeru and Taniskidou, 2017). The data

set “hepta” (Ultsch, 2005) is part of the Umatrix pack-

age for R.

These data sets have been used several

times in similar contexts (e.g. (Newling and Fleuret,

2016b; Fr

anti and Sieranoja, 2018)) and hence may

be viewed as standard benchmark data sets. All data

sets were z-score normalized in all dimensions, that

is, transformed in such a way that each dimension

has a mean of zero and a standard deviation of one.

After an initialization with the different methods de-

scribed above, the actual k-means optimization was

conducted with the Exponion method (Newling and

Fleuret, 2016a).

Experimental results on these data sets are shown

in Tables 2 to 6. Table 2 shows the number of dis-

tance computations needed in the initialization phase

relative to the number needed in a naive Maximim or

a standard k-means++ implementation (i.e.,

∑

k−1

i=1

(n −

i) ≈ (k − 1)n). Clearly, the optimized form of Max-

imin can reduce distance computations considerably,

often down to less than half. Trimming comes, of

course, at a price, since the restrictions on the min-

imum distances that have to be considered are less

strict. (It does not sufﬁce for a minimum distance to

be less than the current maximum to skip additional

distance computations, but it must be less than the top

x% of minimum distances.) Sectioned Maximin, es-

pecially for small section sizes, reduces the number of

distance computations the most, sometimes to as little

as a ﬁfth.

As can be seen, the k-means++ procedure clearly

proﬁts from trimming, and, not surprisingly, proﬁts

the more, the tighter the trimming: Trimming allows

similar optimizations of skipping distance computa-

tions as Maximin: what cannot enter the heap needs

no update.

Table 3 shows the clustering error, measured as

the sum of squared distances between centers and

assigned data points. All results are averages over

100 runs. Clearly, trimming very often improves the

initialization, although there are cases (wine, yeast),

where proper trimming parameters are crucial. This

is not too surprising, though, as the best parameters

depend on the level of contamination of the data set

with outliers.

If such outliers are identiﬁed before initialization

by computing a local outlier factor (see Table 4), the

percentages become somewhat worse. However, the

reason for this is that the standard Maximin method

http://cs.joensuu.ﬁ/sipu/datasets/

https://cran.r-project.org/web/packages/Umatrix/

index.html

Table 1: Used data sets and their properties: m: number

of dimensions, n: data points, k: clusters, o: outliers (local

outlier factor), “time/s”: time in seconds for outlier compu-

tation (SciKitLearn).

data set m n k o time/s

iris 4 150 3 5 <0.01

wine 14 178 3 8 <0.01

yeast 8 1484 10 44 0.04

hepta 3 212 7 0 <0.01

r15 3 600 30 48 <0.01

d31 3 3100 31 215 0.02

a1 2 3000 20 82 0.02

a2 2 5250 35 181 0.03

a3 2 7500 50 261 0.04

s1 2 5000 15 158 0.03

s2 2 5000 15 123 0.02

s3 2 5000 15 67 0.03

s4 2 5000 15 97 0.02

birch1 2 100000 100 156 0.61

birch2 2 100000 100 2731 0.67

birch3 2 100000 100 857 0.61

fares better, as it can no longer select such outliers as

cluster centers. The higher percentages thus reﬂect

the smaller base of standard Maximin rather than that

trimming works less well. Nevertheless the initializa-

tion still proﬁts considerably from trimming.

A better initialization is one thing, but does this

also improve the error of the ﬁnal result after opti-

mization? Table 5 shows that this is actually often the

case, although results depend heavily on the speciﬁc

data set. Note, however, that this table shows average

errors over 100 runs, which is not necessarily what

is relevant. In practice, clustering will be run several

times with different initializations and then the best

result gets selected. W.r.t. best results over 100 runs

(not shown) the different approaches hardly differ for

these data sets (they usually ﬁnd the global optimum

if only they are executed often enough). A lower av-

erage error can be read as a higher chance to obtain

a good or even the best clustering result in a limited

number of runs, though.

An important insight gained from Table 5 is that

k-means++, the de facto standard for k-means initial-

ization, performs worse than Maximin on many data

sets, sometimes considerably (hepta, d31). In these

cases trimming has a very beneﬁcial effect: not only

does it reduce the number of distance computations,

but it also makes k-means++ competitive with Max-

imin again.

Finally, Table 6 shows that the trimming ap-

proaches also lead to gains in the number of update

steps (iris appears to be somewhat of an exception,

but this may be acceptable given the better result qual-

ity, see Table 5). For most data sets, better results can

thus even be obtained in less time (or more runs can

be conducted in the same time, thus increasing the

DATA 2020 - 9th International Conference on Data Science, Technology and Applications

264

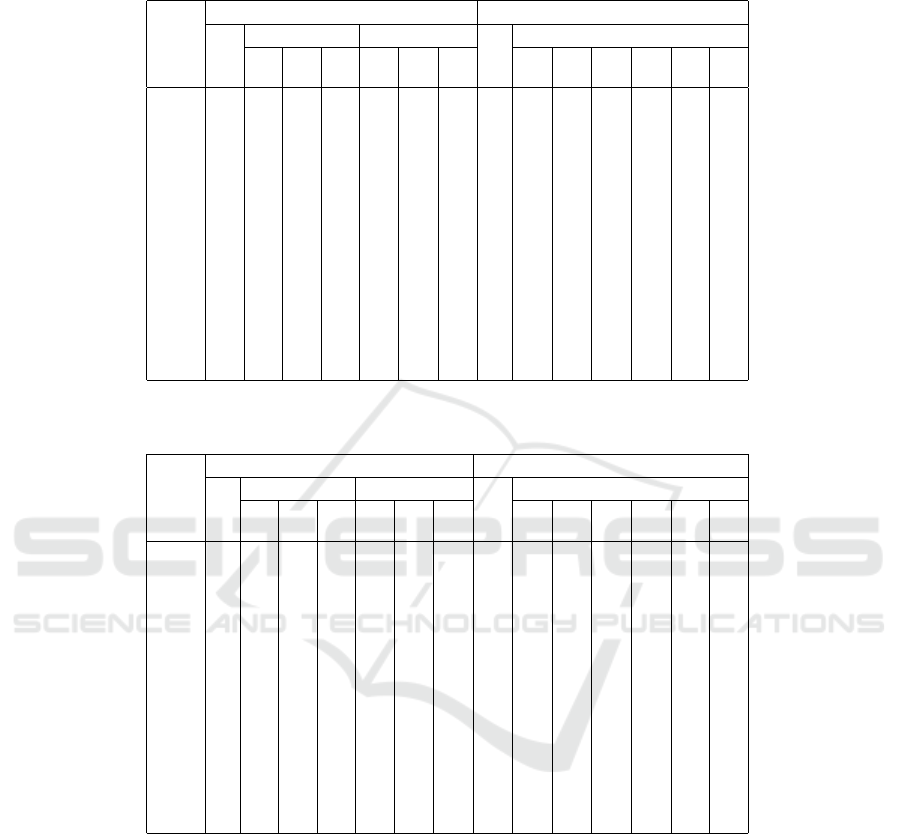
Table 2: Numbers of distance computations for different initialization methods on different data sets. All numbers are per-

centages relative to a naive computation (both Maximin or k-means++), which requires

∑

k−1

i=1

(n − i) ≈ (k − 1)n distance

computations.

maximin kmeans++

opt trimmed sectioned std trimmed

1% 2% 5% 5% 10% 20% 20% 20% 10% 10% 5% 5%

data set 0% 2% 0% 2% 0% 1%

iris 60.9 73.7 76.2 80.4 51.6 52.4 53.6 100 86.0 86.6 78.7 79.4 72.5 72.3

wine 53.7 62.5 68.7 76.0 51.4 52.0 52.4 100 84.9 85.1 75.8 76.7 68.3 68.0

yeast 14.1 67.3 63.9 64.2 13.9 14.8 15.2 100 72.3 73.0 57.2 60.0 44.5 46.7

hepta 50.0 72.7 72.2 72.4 23.3 27.6 33.7 100 81.8 82.0 74.6 74.8 68.2 68.4

r15 35.9 40.6 42.7 51.5 34.3 36.3 35.8 100 74.4 74.7 61.0 61.0 51.4 50.9

d31 46.6 56.3 58.2 62.1 32.7 40.2 44.2 100 77.0 76.9 67.8 67.8 62.1 62.0

a1 38.4 51.8 54.5 60.6 23.3 32.8 36.4 100 76.9 76.9 67.4 67.3 60.4 60.3

a2 36.5 52.6 54.6 60.0 30.2 34.3 35.6 100 76.5 76.4 66.6 66.7 60.0 60.1

a3 35.8 52.9 54.9 60.3 32.3 34.9 36.0 100 76.2 76.1 66.7 66.6 60.3 60.3

s1 40.2 56.1 58.7 63.7 20.0 30.3 36.8 100 77.9 77.9 69.3 69.6 63.3 63.9

s2 40.2 54.6 56.9 62.6 19.4 29.2 35.8 100 77.6 77.7 68.7 68.8 62.4 62.7

s3 37.5 52.9 55.0 59.0 18.8 28.3 33.9 100 77.1 77.0 67.1 66.8 60.9 59.7

s4 40.7 53.8 55.8 61.0 18.5 27.9 34.5 100 77.0 76.8 67.5 67.3 61.2 60.7

birch1 31.0 49.6 52.6 58.4 28.6 29.8 30.3 100 75.8 75.7 65.7 65.6 58.5 58.5

birch2 38.6 46.3 48.2 56.2 34.0 36.1 37.4 100 75.1 74.9 64.0 63.8 56.1 55.7

birch3 32.4 43.2 45.7 52.6 29.3 30.8 31.5 100 72.0 71.8 61.0 60.5 53.1 52.4

Table 3: Average error (sum of squared distances of data points to closest clusters, 100 runs) directly after the initialization.

All columns show percentages relative to the column “maximin:std”, which thus necessarily always shows 100%.

maximin kmeans++

std trimmed sectioned std trimmed

1% 2% 5% 5% 10% 20% 20% 20% 10% 10% 5% 5%

data set 0% 2% 0% 2% 0% 1%

iris 100 109 103 73.7 60.6 65.9 77.7 65.9 60.3 57.7 68.1 61.7 81.6 71.6

wine 100 121 108 98.6 84.1 86.0 93.8 80.3 81.9 79.4 88.9 80.9 92.9 88.9

yeast 100 114 95.5 77.4 76.1 84.8 90.8 55.9 57.5 69.8 64.2 73.9 72.2 74.4

hepta 100 91.4 90.8 80.6 107 91.0 93.5 145 93.2 93.4 86.5 84.7 91.9 88.6

r15 100 67.1 60.2 56.7 62.9 69.9 78.3 62.8 58.7 57.9 60.4 57.5 61.6 58.0

d31 100 50.3 47.6 78.3 63.9 72.2 81.7 85.5 61.1 70.8 55.0 57.7 53.7 50.8

a1 100 62.4 61.1 66.7 76.4 82.6 89.4 78.8 66.8 66.3 63.9 62.0 64.2 61.8

a2 100 60.7 61.5 66.4 77.7 83.3 90.3 84.9 66.8 69.2 64.5 64.2 64.4 62.0

a3 100 62.3 64.6 67.1 77.5 84.9 90.3 87.7 69.1 71.1 64.8 67.1 64.3 62.3

s1 100 46.9 42.0 36.9 65.2 75.3 84.0 70.5 49.9 47.7 44.1 43.2 46.8 40.0

s2 100 50.6 44.9 45.4 69.4 78.5 85.1 64.7 52.5 51.6 49.9 46.0 51.8 46.2

s3 100 64.3 59.0 55.8 81.8 87.3 92.7 67.8 60.0 56.8 61.4 55.3 63.1 57.0

s4 100 61.5 57.1 51.0 79.3 83.8 89.8 64.4 57.5 53.3 57.5 52.5 59.0 55.3

birch1 100 78.6 78.6 81.7 95.1 96.6 98.4 102 83.9 86.9 81.3 82.4 80.6 79.7

birch2 100 61.6 63.7 84.6 93.0 95.4 97.7 75.0 61.4 80.9 60.3 74.6 60.5 63.5

birch3 100 58.4 55.9 62.4 90.6 93.8 96.0 53.8 49.8 56.6 50.9 56.0 53.7 53.7

chance of obtaining a good result), not only by reduc-

ing the needed number of distance computations in

the initialization, but also by reducing the number of

update steps and thus the number of distance compu-

tations in the optimization process.

5 CONCLUSION

We developed two new initialization methods for k-

means clustering, namely sectioned Maximin and

trimmed k-means++, and provided efﬁcient im-

plementations of all Maximin versions (standard,

trimmed, sectioned) as well as of trimmed k-means++

(see also the URLs given below, from where our soft-

ware can be obtained).

As our experimental results demonstrate, these

methods can yield better clustering quality, while at

the same time reducing the number of distance com-

putations needed for the center initialization as well

as the number of update steps (and thus the distance

computations) needed until the k-means optimization

procedure converges.

Somewhat surprisingly, ﬁnding outliers ﬁrst and

excluding them from the choice of initial cluster cen-

ters did not really improve the results—likely, be-

cause trimming during initialization already handles

outliers very effectively.

Initializing k-means Clustering

265

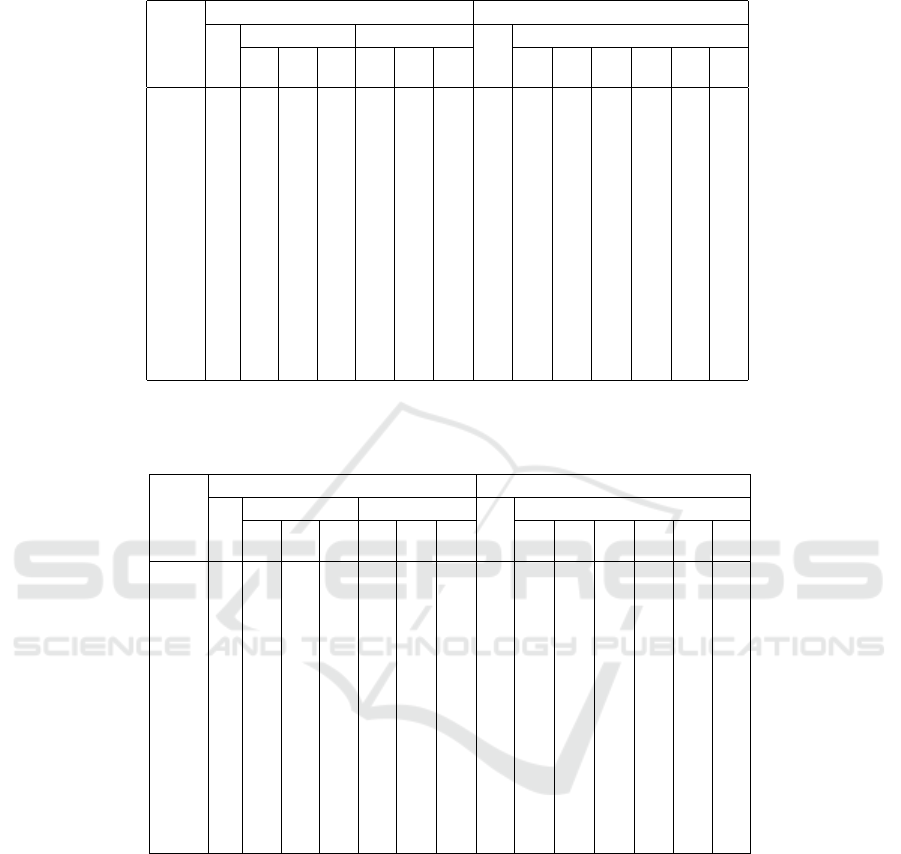
Table 4: Average error directly after the initialization (100 runs), if found outliers are ineligible as cluster centers. All columns

show percentages relative to the column “maximin:std”, which thus necessarily always shows 100%.

maximin kmeans++

std trimmed sectioned std trimmed

1% 2% 5% 5% 10% 20% 20% 20% 10% 10% 5% 5%

data set 0% 2% 0% 2% 0% 1%

iris 100 109 95.1 70.9 68.6 74.0 79.5 69.6 68.3 63.5 74.5 69.6 84.2 75.9

wine 100 97.5 101 91.2 86.5 89.7 92.9 88.9 86.1 83.9 87.2 84.2 93.4 89.8

yeast 100 103 84.1 82.3 78.6 84.5 91.3 59.5 61.3 77.9 66.6 81.3 72.3 79.5

hepta 100 91.0 91.2 80.8 102 90.1 92.3 156 91.4 95.7 86.9 84.9 91.2 87.7

r15 100 75.6 68.7 67.2 74.2 77.4 84.4 77.9 71.8 71.1 71.9 70.4 73.5 70.0

d31 100 60.3 58.2 98.0 71.4 78.4 85.9 109 74.8 81.4 67.9 70.7 63.6 62.6

a1 100 65.1 62.8 72.0 77.8 84.3 90.1 85.0 69.5 71.1 67.3 66.4 67.4 65.0

a2 100 66.3 64.3 72.2 80.0 86.1 90.5 91.7 74.5 77.2 69.9 72.0 69.6 67.9

a3 100 68.3 70.9 75.4 82.0 87.5 91.9 97.0 74.2 80.1 70.7 73.6 70.5 69.6

s1 100 55.5 48.3 43.0 72.5 79.3 88.6 78.7 56.1 57.1 52.3 50.9 51.8 45.9

s2 100 54.9 50.1 51.3 75.1 83.2 87.8 73.0 58.9 55.7 54.2 52.1 55.8 51.4

s3 100 64.1 61.0 54.9 82.1 87.2 92.7 72.0 61.2 58.4 61.9 57.0 62.6 57.7

s4 100 66.0 59.8 56.6 80.8 86.0 90.8 70.3 61.5 58.6 63.1 57.3 65.6 59.1

birch1 100 80.9 81.1 84.4 95.0 97.0 98.2 104 86.9 89.7 83.8 85.2 82.1 81.7

birch2 100 62.8 66.0 89.6 93.1 95.8 98.2 75.1 63.1 84.5 61.4 75.7 62.0 63.8

birch3 100 60.3 58.7 69.7 90.1 93.3 95.7 56.8 52.4 61.2 53.1 60.7 55.8 56.7

Table 5: Average error (sum of squared distances of data points to closest clusters, 100 runs) after k-means optimization

until convergence. All columns show percentages relative to the column “maximin:std”, which thus necessarily always shows

100%.

maximin kmeans++

std trimmed sectioned std trimmed

1% 2% 5% 5% 10% 20% 20% 20% 10% 10% 5% 5%

data set 0% 2% 0% 2% 0% 1%

iris 100 89.3 89.4 91.9 93.0 93.8 95.7 95.3 93.5 94.2 94.8 92.8 95.8 96.4

wine 100 99.2 99.2 102 99.9 101 100 99.5 100 101 99.8 101 101 101

yeast 100 94.0 105 108 96.9 97.7 99.3 98.8 94.1 109 94.8 109 96.2 107

hepta 100 100 100 100 118 100 100 178 110 110 100 100 100 100

r15 100 101 104 103 102 102 101 106 104 104 103 103 103 103

d31 100 96.5 97.9 137 97.5 97.6 98.0 153 118 130 106 112 100 103

a1 100 93.8 95.3 98.8 98.6 97.5 98.4 103 98.4 99.7 97.3 96.8 96.6 96.0

a2 100 89.5 90.7 95.5 94.3 95.7 97.1 107 96.0 98.1 92.6 93.3 92.4 91.2

a3 100 89.7 90.9 96.7 93.8 95.1 96.4 113 99.8 101 95.7 96.5 91.9 93.6

s1 100 70.4 72.0 73.1 83.9 87.4 90.2 108 88.4 88.8 80.0 81.1 79.1 72.4

s2 100 91.7 85.8 88.6 94.1 93.0 95.8 102 91.9 90.9 90.5 88.8 89.5 87.5

s3 100 101 101 101 101 101 101 103 102 101 101 101 102 102

s4 100 99.5 100 99.8 102 101 102 101 101 99.4 100 101 102 99.9

birch1 100 95.1 95.1 95.9 98.8 98.9 99.2 98.8 96.4 96.5 96.1 96.1 95.7 95.9

birch2 100 99.0 99.1 99.9 102 101 101 101 97.8 99.0 98.2 98.9 98.3 98.4

birch3 100 94.3 95.1 99.4 98.5 99.1 99.5 94.3 92.8 97.5 92.4 96.2 92.8 94.4

However, selecting an outlier as an initial clus-

ter center may not be so bad either. Since outliers

are “surrounding” the data point cloud, they may still

be reasonably good choices for initial cluster centers

that are directed to their proper places by the opti-

mization procedure. This effect may also explain why

Maximin often outperforms kmeans++. This demon-

strates that the current de facto initialization standard

may be worse than it is held to be, at least it can

be improved upon. Our trimming approaches make

kmeans++ competitive with Maximin again, though.

However, in terms of the number of needed distance

computations, Maximin still wins.

Software and Extended Results. Our implementa-

tions (Python and C, MIT License) as well as ex-

tended result tables can be obtained at http://www.

borgelt.net/cluster.html http://www.borgelt.net/docs/clsinit.

txt

ACKNOWLEDGEMENT

The ﬁrst author gratefully acknowledges the ﬁnancial

support from Land Salzburg within the WISS 2025

project IDA-Lab (20102-F1901166-KZP and 20204-

WISS/225/197-2019).

DATA 2020 - 9th International Conference on Data Science, Technology and Applications

266

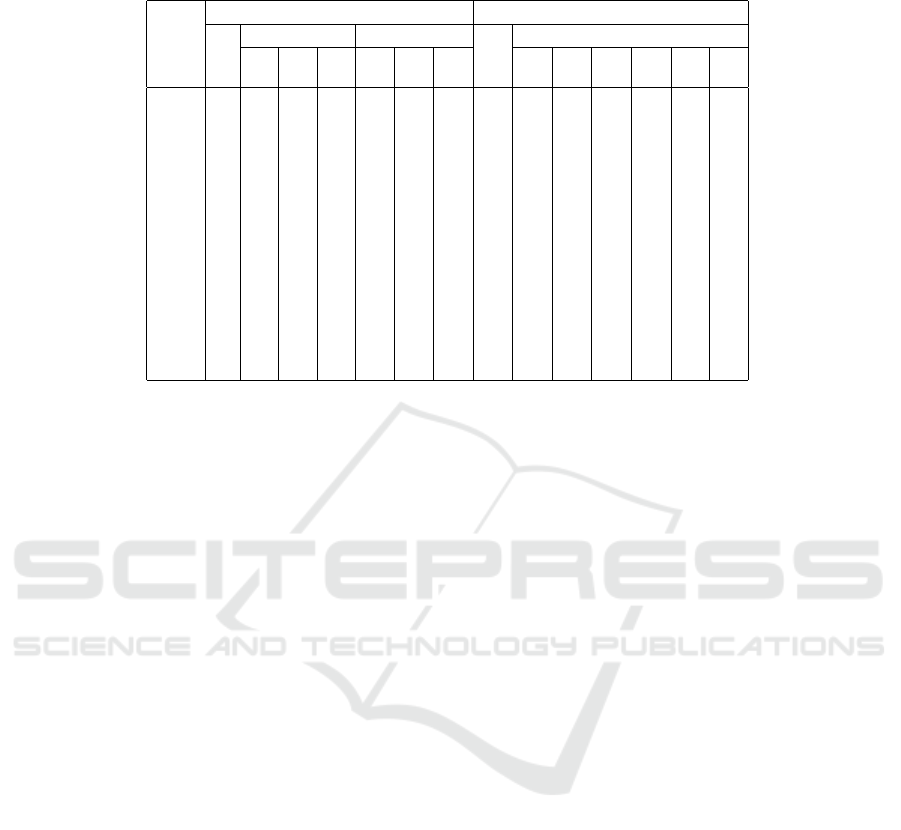
Table 6: Average number of update steps (epochs) until the k-means optimization converges (100 runs). All columns show

percentages relative to the column “maximin:std”, which thus necessarily always shows 100%.

maximin kmeans++

std trimmed sectioned std trimmed

1% 2% 5% 5% 10% 20% 20% 20% 10% 10% 5% 5%

data set 0% 2% 0% 2% 0% 1%

iris 100 112 121 99.3 108 111 106 103 105 95.7 105 104 114 105

wine 100 87.7 79.9 76.7 89.2 89.7 93.2 89.0 78.4 82.6 87.0 78.7 89.0 83.4

yeast 100 58.9 71.6 86.8 91.3 103 88.6 79.7 75.2 78.5 80.6 83.3 89.7 86.4

hepta 100 100 100 100 116 102 100 158 106 110 100 100 100 100

r15 100 95.9 113 101 94.7 92.2 94.6 99.8 93.3 97.2 96.9 95.4 90.3 93.7

d31 100 70.4 75.4 117 72.4 83.1 85.4 137 110 123 93.3 106 86.4 87.1

a1 100 57.7 66.1 73.3 79.1 82.5 87.1 72.7 67.9 69.7 68.7 67.8 70.1 67.6

a2 100 76.9 85.9 90.3 90.3 98.9 102 117 92.9 102 90.1 90.0 86.1 80.4

a3 100 70.8 69.9 87.0 80.3 80.9 87.0 100 91.4 94.1 80.2 85.2 73.4 79.7

s1 100 46.9 50.4 53.0 75.9 81.7 94.1 133 92.3 83.7 67.7 68.9 62.8 48.6

s2 100 73.8 68.1 64.8 94.1 87.1 95.7 104 84.8 88.0 71.5 75.5 68.4 67.4

s3 100 95.6 91.1 94.2 101 104 104 103 90.7 92.7 96.5 96.9 96.0 93.2

s4 100 87.0 89.9 84.1 94.4 100 100 92.4 92.6 90.0 86.1 76.9 85.9 85.9

birch1 100 72.9 72.0 77.7 87.9 91.9 99.0 96.8 79.9 81.5 73.5 75.5 72.5 77.6

birch2 100 135 138 139 113 107 109 134 135 145 132 140 121 134

birch3 100 96.8 90.6 103 95.8 99.4 97.7 102 94.9 98.8 95.6 97.4 99.4 101

REFERENCES

Arthur, D. and Vassilvitskii, S. (2007). k-means++: The

advantages of careful seeding. In Proc. 18

Annual

SIAM Symp. on Discrete Algorithms (SODA’07, New

Orleans, LA), pages 1027–1035, Philadelphia, PA,

USA. Society for Industrial and Applied Mathemat-

ics.

Bachem, O., Lucic, M., Hassani, S., and Krause, A.

(2016a). Approximate k-means++ in sublinear time.

In Proc. 30 AAAI Conf. on Artiﬁcial Intelligence

(AAAI’16, Phoenix, AZ), pages 1459–1467, Menlo

Park, CA, USA. AAAI Press.

Bachem, O., Lucic, M., Hassani, S., and Krause, A.

(2016b). Fast and provably good seedings for k-

means. In Proc. 30

Conf. on Neural Informa-

tion Processing Systems (NIPS’16, Barcelona, Spain),

pages 55–63, Red Hook, NY, USA. Curran Asso-

ciates.

Breunig, M., Kriegel, H.-P., Ng, R., and Sander, J. (2000).

Lof: Identifying density-based local outliers. SIG-

MOD Record, 29:93–104.

Dheeru, D. and Taniskidou, E. (2017). UCI Machine Learn-

ing Repository. University of California at Irvine,

Irvine, CA, USA.

Elkan, C. (2003). Using the triangle inequality to accel-

erate k-means. In Proc. 20

Int. Conf. on Machine

Learning (ICML’03, Washington, DC), pages 147–

153, Menlo Park, CA, USA. AAAI Press.

anti, P. and Sieranoja, S. (2018). k-means properties on

six clustering benchmark datasets. Applied Intelli-

gence, 48:4743–4759.

Hamerly, G. (2010). Making k-means even faster. In Proc.

SIAM Int. Conf. on Data Mining (SDM 2010, Colum-

bus, OH), pages 130–140, Philadelphia, PA, USA. So-

ciety for Industrial and Applied Mathematics.

Hathaway, R., Bezdek, J., and Huband, J. (2006). Maximin

initialization for cluster analysis. In Proc. Iberoameri-

can Cong. on Pattern Recognition (CIARP 2006, Can-

cun, Mexico), pages 14–26, Berlin/Heidelberg, Ger-

many. Springer.

Hoare, C. (1961). Algorithm 65: Find. Communications of

the ACM, 4:321–322.

Kriegel, H.-P., Kr

oger, P., Schubert, E., and Zimek, A.

(2009). Loop: Local outlier probabilities. In Proc.

ACM Int. Conf. on Information and Knowledge

Management (CIKM’09, Hong Kong, China), pages

1649–1652, New York, NY, USA. ACM Press.

Newling, J. and Fleuret, F. (2016a). Fast k-means with ac-

curate bounds. In Proc. 33

Int. Conf. on Machine

Learning (ICML’16, New York, NY), pages 936–944.

JMLR Workshop and Conference Proceedings 48.

Newling, J. and Fleuret, F. (2016b). k-medoids for k-means

seeding. In Proc. 31

Conf. on Neural Informa-

tion Processing Systems (NIPS’17, Long Beach, CA),

pages 5195–5203, Red Hook, NY, USA. Curran As-

sociates.

Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, Y.,

Thirion, B., Grisel, O., Blondel, M., Prettenhofer,

P., Weiss, R., Dubourg, V., Vanderplas, J., Passos,

A., Cournapeau, D., Brucher, M., Perrot, M., and

Duchesnay, E. (2011). Scikit-learn: Machine learn-

ing in python. Journal of Machine Learning Research,

12:2825–2830.

Selim, S. and Ismail, M. (1984). k-means-type algorithms:

A generalized convergence theorem and characteriza-

tion of local optimality. IEEE Trans. Pattern Analysis

and Machine Intelligence, 6:81–87.

Ultsch, A. (2005). U*C: Self-organized clustering with

emergent feature maps. In Lernen, Wissensentdeckung

und Adaptivit

at (LWA), pages 240–244, Saarbruecken,

Germany.

Yarikova, O. (2019). Vergleich der Initialisierungsmetho-

den f

ur den k-Means-Clustering-Algorithmus.

Initializing k-means Clustering

267