Fuzzy Fusion for Two-stream Action Recognition
Anderson Carlos Sousa e Santos
1
, Helena de Almeida Maia
1
, Marcos Roberto e Souza
1
,
Marcelo Bernardes Vieira
2
and Helio Pedrini
1
1
Institute of Computing, University of Campinas, Campinas-SP, 13083-852, Brazil
2
Federal University of Juiz de Fora, Juiz de Fora-MG, 36036-900, Brazil
Keywords:
Action Recognition, Multi-stream Neural Network, Video Representation, Fuzzy Fusion.
Abstract:
There are several aspects that may help in the characterization of an action being performed in a video, such
as scene appearance and estimated movement of the involved objects. Many works in the literature combine
different aspects to recognize the actions, which has shown to be superior than individual results. Just as
important as the definition of representative and complementary aspects is the choice of good combination
methods that exploit the strengths of each aspect. In this work, we propose a novel fusion strategy based on
two fuzzy integral methods. This strategy is capable of generalizing other common operators, besides it allows
more combinations to be evaluated by having a distinct impact in sets linearly dependent. Our experiments
show that the fuzzy fusion outperforms the most commonly-used weighted average on the challenging UCF101
and HMDB51 datasets.
1 INTRODUCTION
Nowadays, a visual inspection performed by a hu-
man operator, in order to identify events of interest
in videos, has become quite impracticable due to the
massive amount of data produced in real-world sce-
narios, especially in situations that require a real-time
response.
The automatic recognition of events in video se-
quences is a very challenging task, however, it bene-
fits several other problems, such as health monitoring,
surveillance, entertainment, and forensics (Cornejo
et al., 2015; Gori et al., 2016; Ji et al., 2013; Ryoo
and Matthies, 2016).
In this work, we are especially interested in hu-
man action recognition (Alcantara et al., 2013, 2016,
2017a,b; Concha et al., 2018; Moreira et al., 2017),
which aims to classify activities performed by human
agents from video data. Most of the approaches avail-
able in the literature can be classified into two cate-
gories: (i) traditional methods and (ii) deep learning
methods. In the first one, handcrafted features are ex-
tracted to describe regions of the video. On the other
hand, deep learning methods use neural networks that
automatically learn features from the raw data.
Recent deep learning strategies have explored in-
formation from traditional methods in order to im-
prove the convergence by (i) using expert knowledge
together with deep models and (ii) applying tech-
niques well-established for still images in a video
context. According to this trend, the majority of the
state-of-the-art approaches use multi-stream architec-
tures based on 2D CNNs, in which each stream deals
with different and ideally complementary informa-
tion.
Despite the recent advances in these approaches,
the strategy for combining the streams outputs has not
received much attention in the literature. Usually, a
simple weighted average is applied to fuse the predic-
tions. In this work, we propose a novel method for
the combination of the streams using fuzzy integral
in the late fusion. This type of fuzzy-based fusion is
capable of generalizing other common operators and
thus presents more adaptive behavior. Two types of
integral were evaluated as fusion operators for action
classification.
Experiments conducted on two well-known chal-
lenging data sets, HMDB51 (Kuehne et al., 2013) and
UCF101 (Soomro et al., 2012), show that the fuzzy
fusion surpassed the common weighted average in
the combination of classification scores from differ-
ent streams.
This paper is organized as follows. In Section 2,
we briefly describe relevant related work. In Sec-
Santos, A., Maia, H., Souza, M., Vieira, M. and Pedrini, H.
Fuzzy Fusion for Two-stream Action Recognition.
DOI: 10.5220/0008973901170123
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 5: VISAPP, pages
117-123
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
117

tion 3, we present our proposed fusion method for a
two-stream architecture. In Section 4, experimental
results achieved with the proposed method are pre-
sented and discussed. Finally, we present some con-
cluding remarks and directions for future work in Sec-
tion 5.
2 RELATED WORK
The first convolutional neural networks (CNNs) pro-
posed for action recognition used 3D convolutions
to capture spatio-temporal features (Ji et al., 2013).
Karpathy et al. (2014) trained 3D networks from
scratch using the Sports-1M, a data set with more than
1 million videos. However, it does not outperform tra-
ditional methods in terms of accuracy due to the diffi-
culty in representing motion.
To overcome this problem, Simonyan and Zisser-
man (2014) proposed a two-stream method in which
motion is represented by pre-computed optical flows,
which consists in estimating the apparent motion of
pixels between adjacent frames (Szeliski, 2010). An
RGB sample is the other stream representing the spa-
tial context. Both are separately encoded with a 2D
CNN.
Later, Wang et al. (2015) further improved the
method, especially using more recent deeper archi-
tectures for 2D CNN and taking advantage of the pre-
trained weights for the temporal stream. Many ap-
proaches still use the two-stream strategy by adding or
modifying the streams or propose new architectures
for the CNNs involved.
Wang et al. (2016) introduced the temporal seg-
ment networks that posses a new form of training
that aggregates more samples and allows to capture
longer temporal relationships. Carreira and Zisser-
man (2017) proposed a 3D CNN that is an inflated
version of a 2D CNN and also uses the pre-trained
weights, in addition to training the network with
a huge database of action and achieving significant
higher accuracy rates.
Wang et al. (2017) added a third stream that uses
a composition of the differences between consecutive
frames of the entire video. Concha et al. (2018) also
introduced a new stream that uses the whole video, the
visual rhythm that extracts a slice of each frame and
composes a new image whose texture reflects motion
patterns. Bilen et al. (2018) used dynamic images, an
image that represents the parameter of a ranking in
videos frames, as an additional stream.
Zhu et al. (2017) introduced a generative network
for computing the optical flow representation that can
be learned in an end-to-end fashion with the action
classes. Similarly, Fan et al. (2018) developed a con-
volutional network that acts as an optical flow solver,
even without training, but can be further trained to the
action-specific task.
Hommos et al. (2018) proposed an alternative for
optical flow with an Eulerian phase-based motion rep-
resentation that can also be learned in an end-to-end
scheme. Santos and Pedrini (2019) proposed a third
stream that can be learned in a end-to-end fashion and
compress the video to an image with an autoencoder
architecture.
There were also attempts to combine features of
the streams using Long Short Term Memory (LSTM)
networks (Gammulle et al., 2017; Ma et al., 2019;
Ng et al., 2015) and other encoding methods (Diba
et al., 2017). Nevertheless, the late fusion did not
encounter much change; in the original two-stream
reference (Simonyan and Zisserman, 2014), experi-
ments were performed with support vector machines
(SVM) to perform the fusion, but it did not surpass
the weighted average, being a trainable method that
requires much more computational cost and data.
To the best of our knowledge, our work is the first
to employ fuzzy fusion for the human action clas-
sification task using CNNs. It is mainly found in
image processing tasks such as enhancement (Rao,
2018) and segmentation (Santos et al., 2016). Re-
cently, fuzzy fusion has been used in conjunction with
convolutional neural networks to classify sonar im-
ages (Galusha et al., 2019).
3 PROPOSED FUSION METHOD
Our method is built over a two-stream model for
action recognition (Simonyan and Zisserman, 2014)
through the application of a novel fuzzy fusion strat-
egy to the classification scores of the spatial and tem-
poral streams. Figure 1 illustrates a diagram of the
proposed method, where its input is a video.
The spatial stream is composed of a single sam-
pled RGB image as input to the 2D CNN classifica-
tion image network. Several different architectures
have been proposed for the image recognition task. In
this work, we choose the InceptionV3 (Szegedy et al.,
2016) since it achieves good results in the ImageNet
competition. In addition, it is very compact and easy
to converge.
For the temporal stream, images generated with
the TV-L1 optical flow estimation method (Zach et al.,
2007) are used as input. The classification network
is modified to cope with the input of a stack of 20
optical flow images, 10 for each x and y direction.
The expected number of channels for input to the net-
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
118

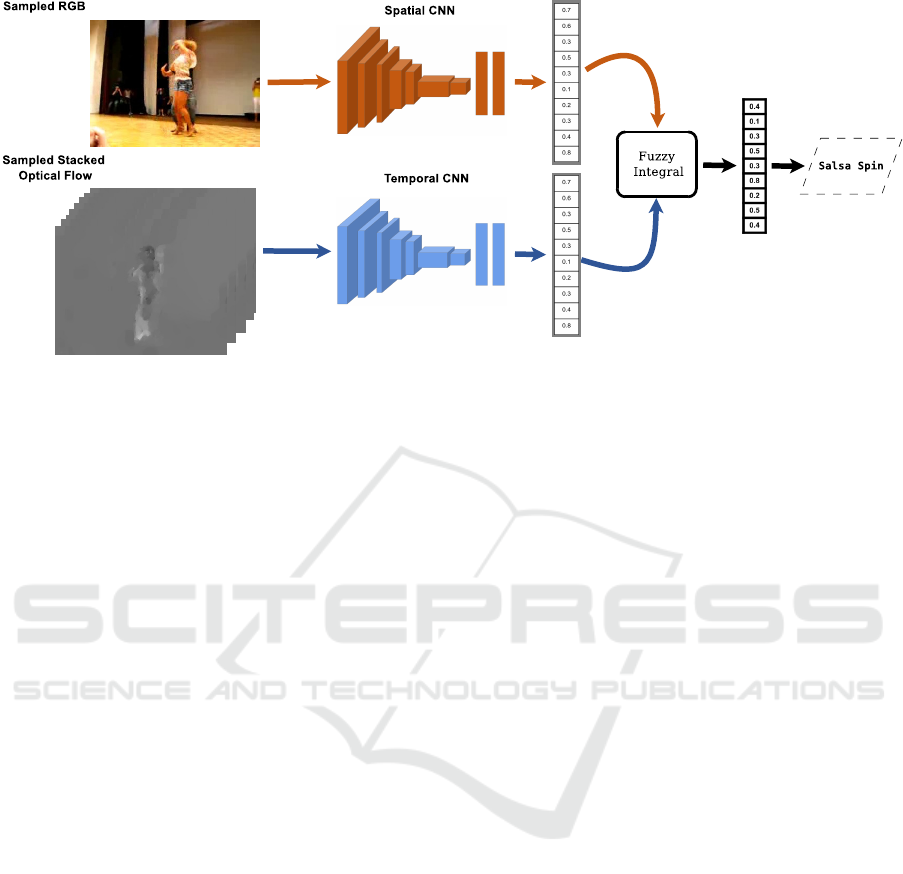
Figure 1: Fuzzy fusion strategy combined with a two-stream architecture for action recognition.
work is 3, such that it is necessary to change the input
layers in order to accept 20 images. This would be
as simple as changing one parameter, however, we
would lose the pre-trained weights between the in-
put and the first hidden layer. Following the strat-
egy described by Wang et al. (2015), the weights of
the three-channel version are averaged and copied 20
times.
Each CNN is trained separately and the streams
are combined only for the action classification test,
where they generate the predictive confidences for
each class. A weighted average usually produces a
final prediction, such that the action label is the one
with the highest confidence.
In this work, we propose the use of a novel fusion
strategy. Fuzzy integral generalizes other common
fusion operators, such as average, maximum and or-
dered weighted average. It is characterized by the use
of fuzzy membership functions (h(x
i
)) as integrands,
whereas fuzzy measures are characterized as weights
and the type of fuzzy connectives applied.
Fuzzy measures serve as a priori importance for
the integrands. They define coefficients for each
source, which are denoted as fuzzy densities and also
for the union of different sources, characterizing the
level of agreement between them. Thus, coefficients
µ(A
j
) are defined for all subsets of the set of inte-
grands (χ) in the interval [0, 1] and they must satisfy
the monotonicity condition, expressed in Equation 1.
A
j
⊂ A
k
=⇒ µ(A
j
) ≤ µ(A
k
) ∀A
j
, A
k
∈ χ (1)
There are two main fuzzy integrals that differen-
tiate on the used fuzzy connectives, which are ex-
plored in our work: Sugeno Fuzzy Integral (Equa-
tion 2) (Murofushi and Sugeno, 2000), which uses
minimum (∧) and maximum (∨), as well as Choquet
Fuzzy Integral (Equation 3) (Murofushi and Sugeno,
1989), which employs product and addition.
S
µ
[h
1
(x
i
), ..., h
n
(x
n
)] =
n
_
i=1
[h
(i)
(x
i
) ∧ µ(A
(i)
)] (2)
C
µ
[h
1
(x
i
), ..., h
n
(x
n
)] =
n
∑
i=1
h
(i)
(x
i
)[µ(A
(i)
) − µ(A
(i−1)
)] (3)
where the enclosed sub-index
(i)
refers to a previous
sorting on the integrands, h
(1)
(x
1
) is the source with
the highest value, and A
(k)
is the subset with the k
highest values, such that A
(n)
= χ.
To establish the fuzzy measures and avoid deal-
ing with the monotonicity condition and also narrow
down the search space, we explored the particular
fuzzy-λ measures (Tahani and Keller, 1990) that de-
fine the coefficients of the union of subsets based on
the individual subsets, as shown in Equation 4.
µ(A
i
∪ A
j
) =
µ(A
i
) + µ(A
j
) + λµ(A
i
)µ(A
j
)
∀A
i
, A
j
∈ χ (4)
where λ is found by considering that the fuzzy mea-
sure for the interaction of all sources is equal to 1
(µ(χ) = 1). Therefore, only three parameters corre-
sponding to the fuzzy densities of each stream need
to be defined. Algorithm 1 summarizes the main steps
of using Choquet Integral as the fusion operator.
Function get_lambda solves Equation 5 for λ.
λ + 1 =
n
∏
i=1
(1 + λ × w
i
) (5)
Fuzzy Fusion for Two-stream Action Recognition
119

Algorithm 1: Fuzzy Fusion (Choquet).
input : set of classification scores S, set of
fuzzy densities w
output: Final classification score ff
1 λ ← get_lambda(w)
// Decrease sorting
2 idx ← argReverseSort(S)
3 h ← S[idx]
4 fm ← w[idx]
// initialization of values
5 A
0
= fm
0
6 ff = h
0
× fm
0
// fuzzy integral
7 for i ∈ 1, ..., |S| − 1 do
8 A
i
= A
i−1
+ fm
i
+ λ × fm
i
× A
i−1
9 ff = ff + h
i
× (A
i
− A
i−1
)
10 A
i−1
= A
i
11 ff = ff + h
|S|−1
× (1 − A
i−1
)
12 return ff
The scores for each source of information are
sorted from higher to lower and the fuzzy densities
(weights) are reorganized to follow their respective
sources. After some initial values are defined, the
loop in the algorithm performs, at each iteration, the
union of the previous fuzzy measure with the current
fuzzy density, thus allowing to compute the fuzzy in-
tegral, as defined in Equation 3.
The steps involved in the Sugeno integral are sim-
ilar to the Choquet integral, differing only in the op-
erator used. In Algorithm 2, we present the fusion
strategy using Equation 2 to highlight the differences.
Algorithm 2: Fuzzy Fusion (Sugeno).
input : set of classification scores S, set of
fuzzy densities w
output: Final classification score ff
1 λ ← get_lambda(w)
// Decrease sorting
2 idx ← argReverseSort(S)
3 h ← S[idx]
4 fm ← w[idx]
// initialization of values
5 A
0
= f m
0
6 ff = min(h
0
, fm
0
)
// fuzzy integral
7 for i ∈ 1, ..., |S| do
8 A
i
= A
i−1
+ fm
i
+ λ × fm
i
× A
i−1
9 aux = min(h
i
, A
i
)
10 ff = max(ff, aux)
11 A
i−1
= A
i
12 return ff
A comparison of the experimental results using
both Sugeno and Choquet fuzzy integral approaches,
as well as the weighted average, is described in Sec-
tion 4.
4 EXPERIMENTS
In this section, we describe the data sets used in our
experiments, relevant implementation details, as well
as experimental results for different configurations of
our method.
4.1 Data Sets
Two challenging data sets that are benchmarks for the
human action recognition problem were used in the
experiments. The UCF101 (Soomro et al., 2012) data
set is composed of 101 classes equally distributed in
13,320 video clips. The sequences have a fixed res-
olution of 320×240 pixels, a frame rate of 25 fps
and different lengths. The HMDB51 (Kuehne et al.,
2013) data set is composed of 51 classes and 6,766
sequences extracted mostly from movies. It includes
lower quality videos with blur, noise, cuts and actions
from unusual points of views.
Both data sets provide a protocol with three splits
of the samples, where each split contains 70% of sam-
ples for training and 30% for testing for each action
class. This is a standard evaluation protocol proposed
by the authors of the data sets, which is followed
in the literature of action recognition for comparison
purposes.
4.2 Experimental Setup
The Inception V3 (Szegedy et al., 2016) network was
the 2D CNN selected in our experiments. It achieved
state-of-the-art results in the ImageNet competition,
such that we started with its trained weights in all
cases.
The two-stream approach is inspired by the prac-
tices described by Wang et al. (2015). The data aug-
mentation is the same as the used for the autoencoder,
that is, random crop and random horizontal flip. The
random crop scheme uses multi-scale crops of the
four corners and their centers.
The spatial stream uses a 0.8 dropout before the
softmax layer and 250 epochs, whereas the temporal
stream uses a 0.7 dropout and 350 epochs. In both
of them, the stochastic gradient descent optimizer is
used with decay zero, Nesterov momentum equal to
0.9. For all tests, the used batch size is 32 and the
learning rate starts at 0.0001 and drops by a factor of
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
120

0.1 – until the bottom limit of 1
−10
– if the validation
loss does not improve in more than 20 epochs.
The final classification of each testing video is an
average of the predictions for 25 frames considering
the augmented version – four corners, the center and
the horizontal flip – adding up to 10 predictions per
frame.
The method was implemented in Python 3 pro-
gramming language using Keras library. All experi-
ments were performed on a machine with an Intel
R

Core
TM
i7-3770K 3.50GHz processor, 32GB of mem-
ory, an NVIDIA GeForce R GTX 1080 GPU and
Ubuntu 16.04.
4.3 Results
In this subsection, we present the results obtained
with the fuzzy fusion methods for the action recogni-
tion problem. Initially, the individual results of each
stream are shown in Tables 1 and 2.
Table 1: Accuracy rates (%) for individual streams on the
UCF101 data set.
Stream
UCF101
Split 1 Split 2 Split 3 Average
Spatial 86.39 85.62 85.20 85.74
Temporal 86.17 88.56 87.88 87.54
The stack of optical flow images obtained the
best results compared to the RGB samples on the
HMDB51 data set (Table 2). The difference in
the accuracy values between the temporal and spa-
tial streams is substantial for the HMDB51 data set,
whereas the difference is smaller for the UCF101 data
set.
Table 2: Accuracy rates (%) for individual streams on the
HMDB51 data set.
Stream
HMDB51
Split 1 Split 2 Split 3 Average
Spatial 52.68 52.22 52.48 52.46
Temporal 57.52 59.41 59.74 58.89
To perform the fusion for the weighted average
and fuzzy integral schemes, it is necessary to define
their weights. In our work, the weights were defined
through a linear search, where the best weights were
selected considering the accuracy in the first split of
the HMDB51 data set applied to all data sets and
splits, including the UCF101. Table 3 reports the
weights used in each scenario.
Table 3: Weights for the stream fusion.
Fusion
Weights
Spatial Temporal
Weighted Average 3.00 5.00
Fuzzy (Sugeno) 0.50 1.00
Fuzzy (Choquet) 0.20 0.33
The range for the weighted average (WA) was
[1, 10] with step 1. For the fuzzy fusion, the weights
need to be in the range [0, 1], so the search range is the
same except that the weight is divided by 10. Consid-
ering the arithmetic average, the values are based on
proportions; for example, the sets of weights (0.2, 0.4)
and (0.4, 0.8) are equivalent when performing aver-
age because both indicate that a classifier has 2 times
more weight than the other. In the fuzzy fusion, these
sets of weights represent different combinations, al-
lowing more feasible weights. Thus, we performed a
second search using the same range but dividing by 2
times the sum of the weights.
Table 4 shows the comparative results between the
two types of fuzzy fusion, as well as the weighted av-
erage on the UCF101 data set.
Table 4: Accuracy rate (%) for two-stream fusion on the
UCF101 data set.
Fusion
UCF101
Split 1 Split 2 Split 3 Average
Weighted Average 92.36 92.42 92.80 92.53
Fuzzy (Sugeno) 90.77 91.30 91.31 91.13
Fuzzy (Choquet) 93.02 92.66 92.94 92.87
The results with the fuzzy fusion using the Cho-
quet integral are superior, however, the difference
from the weighted average is smaller. The Sugeno
version achieved poor results. Table 5 shows the com-
parative results on the HMDB51 data set.
Table 5: Accuracy rate (%) for two-stream fusion on the
HMDB51 data set.
Fusion
HMDB51
Split 1 Split 2 Split 3 Average
Weighted Average 64.71 66.01 63.66 64.79
Fuzzy (Sugeno) 61.63 61.96 60.85 61.48
Fuzzy (Choquet) 66.27 66.21 65.10 65.86
The accuracy rate followed the previous results
with the Sugeno fuzzy fusion, achieving the lowest
values, whereas the Choquet version obtained the best
results. However, the difference was higher, with a
Fuzzy Fusion for Two-stream Action Recognition
121

gain of more than one percentage point from the av-
erage.
5 CONCLUSIONS
This work presented and analyzed the use of fuzzy
integral as fusion operator for the action classification
in videos using a two-stream model. The fuzzy fu-
sion generalizes other operators and is more sophis-
ticated than simple averaging, since it uses ordered
weighting. Two types of integrals were investigated:
(i) Sugeno, that uses maximum and minimum opera-
tors, and (ii) Choquet, that uses product and sum op-
erators.
Two well-known and challenging data
sets, HMDB51 (Kuehne et al., 2013) and
UCF101 (Soomro et al., 2012), were used to
validate the proposed method. Using fuzzy fusion
with the Choquet integral, the experiments revealed
that the accuracy rate surpassed the weighted average,
whereas the Sugeno integral obtained worse results.
This was expected because the use of minimum
and maximum operators makes the combination
discrete, which is not suitable for classifier ensemble,
where a real-value confidence over the classes can be
generated (Soria-Frisch, 2004).
Several action classification methods include ad-
ditional streams to the two-stream framework adopted
in our work. Therefore, a straightforward direction
for future work would be to apply the proposed fuzzy
fusion to a multi-stream approach. The expected ad-
vantage of the fuzzy fusion over the weighted average
would improve with more classifiers since it consid-
ers the weighing of subsets in all combinations. As a
drawback of the method is its manual definition of the
weights, further research is intended to automatically
determine the weights in a more adaptive way.
ACKNOWLEDGMENTS
The authors are thankful to FAPESP (grants
#2017/09160-1 and #2017/12646-3), CNPq (grants
#305169/2015-7 and #309330/2018-7), CAPES and
FAPEMIG for their financial support, and NVIDIA
Corporation for the donation of a GPU as part of the
GPU Grant Program.
REFERENCES
Alcantara, M. F., Moreira, T. P., and Pedrini, H. (2013).
Motion Silhouette-based Real Time Action Recogni-
tion. In Iberoamerican Congress on Pattern Recogni-
tion, pages 471–478. Springer.
Alcantara, M. F., Moreira, T. P., and Pedrini, H. (2016).
Real-Time Action Recognition using a Multilayer De-
scriptor with Variable Size. Journal of Electronic
Imaging, 25(1):013020–013020.
Alcantara, M. F., Moreira, T. P., Pedrini, H., and Flórez-
Revuelta, F. (2017a). Action Identification using a De-
scriptor with Autonomous Fragments in a Multilevel
Prediction Scheme. Signal, Image and Video Process-
ing, 11(2):325–332.
Alcantara, M. F., Pedrini, H., and Cao, Y. (2017b). Human
Action Classification based on Silhouette Indexed In-
terest Points for Multiple Domains. International
Journal of Image and Graphics, 17(3):1750018_1–
1750018_27.
Bilen, H., Fernando, B., Gavves, E., and Vedaldi, A. (2018).
Action Recognition with Dynamic Image Networks.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 40(12):2799–2813.
Carreira, J. and Zisserman, A. (2017). Quo Vadis, Action
Recognition? A New Model and the Kinetics Dataset.
In IEEE Conference on Computer Vision and Pattern
Recognition, pages 4724–4733. IEEE.
Concha, D. T., Maia, H. D. A., Pedrini, H., Tacon, H., Brito,
A. D. S., Chaves, H. D. L., and Vieira, M. B. (2018).
Multi-stream Convolutional Neural Networks for Ac-
tion Recognition in Video Sequences Based on Adap-
tive Visual Rhythms. In 17th IEEE International Con-
ference on Machine Learning and Applications, pages
473–480. IEEE.
Cornejo, J. Y. R., Pedrini, H., and Flórez-Revuelta, F.
(2015). Facial Expression Recognition with Oc-
clusions based on Geometric Representation. In
Iberoamerican Congress on Pattern Recognition,
pages 263–270. Springer.
Diba, A., Sharma, V., and Van Gool, L. (2017). Deep Tem-
poral Linear Encoding Networks. In 2017 IEEE Con-
ference on Computer Vision and Pattern Recognition,
pages 1541–1550. IEEE.
Fan, L., Huang, W., Gan, C., Ermon, S., Gong, B., and
Huang, J. (2018). End-to-end Learning of Motion
Representation for Video Understanding. In IEEE
Conference on Computer Vision and Pattern Recog-
nition, pages 6016–6025.
Galusha, A., Dale, J., Keller, J., and Zare, A. (2019).
Deep Convolutional Neural Network Target Classifi-
cation for Underwater Synthetic Aperture Sonar Im-
agery. In Detection and Sensing of Mines, Explosive
Objects, and Obscured Targets XXIV, volume 11012,
page 1101205. International Society for Optics and
Photonics.
Gammulle, H., Denman, S., Sridharan, S., and Fookes, C.
(2017). Two Stream LSTM: A Deep Fusion Frame-
work for Human Action Recognition. In IEEE Win-
ter Conference on Applications of Computer Vision,
pages 177–186. IEEE.
Gori, I., Aggarwal, J. K., Matthies, L., and Ryoo, M. S.
(2016). Multitype Activity Recognition in Robot-
Centric Scenarios. IEEE Robotics and Automation
Letters, 1(1):593–600.
VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications
122

Hommos, O., Pintea, S. L., Mettes, P. S., and van
Gemert, J. C. (2018). Using Phase Instead of Op-
tical Flow for Action Recognition. arXiv preprint
arXiv:1809.03258.
Ji, S., Xu, W., Yang, M., and Yu, K. (2013). 3D Convo-
lutional Neural Networks for Human Action Recog-
nition. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 35(1):221–231.
Karpathy, A., Toderici, G., Shetty, S., Leung, T., Suk-
thankar, R., and Fei-Fei, L. (2014). Large-Scale Video
Classification with Convolutional Neural Networks.
In IEEE Conference on Computer Vision and Pattern
Recognition, pages 1725–1732.
Kuehne, H., Jhuang, H., Stiefelhagen, R., and Serre, T.
(2013). HMDB51: A Large Video Database for Hu-
man Motion Recognition. In High Performance Com-
puting in Science and Engineering, pages 571–582.
Springer.
Ma, C.-Y., Chen, M.-H., Kira, Z., and AlRegib, G. (2019).
TS-LSTM and Temporal-Inception: Exploiting Spa-
tiotemporal Dynamics for Activity Recognition. Sig-
nal Processing: Image Communication, 71:76–87.
Moreira, T., Menotti, D., and Pedrini, H. (2017). First-
Person Action Recognition Through Visual Rhythm
Texture Description. In IEEE International Confer-
ence on Acoustics, Speech and Signal Processing,
pages 2627–2631. IEEE.
Murofushi, T. and Sugeno, M. (1989). An Interpretation
of Fuzzy Measures and the Choquet Integral As an
Integral with Respect to a Fuzzy Measure. Fuzzy Sets
and Systems, 29(2):201–227.
Murofushi, T. and Sugeno, M. (2000). Fuzzy Measures and
Fuzzy Integrals. In Grabisch, M., Murofushi, T., and
Sugeno, M., editors, Fuzzy Measures and Integrals –
Theory and Applications, pages 3–41. Physica Verlag,
Heidelberg.
Ng, J. Y.-H., Hausknecht, M., Vijayanarasimhan, S.,
Vinyals, O., Monga, R., and Toderici, G. (2015). Be-
yond Short Snippets: Deep Networks for Video Clas-
sification. In IEEE Conference on Computer Vision
and Pattern Recognition, pages 4694–4702.
Rao, B. S. (2018). A Fuzzy Fusion Approach for Mod-
ified Contrast Enhancement Based Image Forensics
Against Attacks. Multimedia Tools and Applications,
77(5):5241–5261.
Ryoo, M. S. and Matthies, L. (2016). First-Person Ac-
tivity Recognition: Feature, Temporal Structure, and
Prediction. International Journal of Computer Vision,
119(3):307–328.
Santos, A., Paiva, J., Toledo, C., and Pedrini, H. (2016).
Improved Human Skin Segmentation Using Fuzzy Fu-
sion Based on Optimized Thresholds by Genetic Al-
gorithms. In Hybrid Soft Computing for Image Seg-
mentation, pages 185–207. Springer.
Santos, A. and Pedrini, H. (2019). Spatio-Temporal Video
Autoencoder for Human Action Recognition. In 14th
International Joint Conference on Computer Vision,
Imaging and Computer Graphics Theory and Appli-
cations, pages 114–123, Prague, Czech Republic.
Simonyan, K. and Zisserman, A. (2014). Two-Stream
Convolutional Networks for Action Recognition in
Videos. In Ghahramani, Z., Welling, M., Cortes, C.,
Lawrence, N., and Weinberger, K., editors, Advances
in Neural Information Processing Systems 27, pages
568–576. Curran Associates, Inc.
Soomro, K., Zamir, A. R., and Shah, M. (2012). UCF101:
A Dataset of 101 Human Actions Classes from Videos
in the Wild. arXiv preprint arXiv:1212.0402.
Soria-Frisch, A. (2004). Soft Data Fusion for Computer
Vision. Fraunhofer-IRB-Verlag.
Szegedy, C., Vanhoucke, V., Ioffe, S., Shlens, J., and Wojna,
Z. (2016). Rethinking the Inception Architecture for
Computer Vision. In IEEE Conference on Computer
Vision and Pattern Recognition, pages 2818–2826.
Szeliski, R. (2010). Computer Vision: Algorithms and Ap-
plications. Springer Science & Business Media.
Tahani, H. and Keller, J. M. (1990). Information Fu-
sion in Computer Vision using the Fuzzy Integral.
IEEE Transactions on Systems, Man, and Cybernet-
ics, 20(3):733–741.
Wang, L., Ge, L., Li, R., and Fang, Y. (2017). Three-Stream
CNNs for Action Recognition. Pattern Recognition
Letters, 92:33–40.
Wang, L., Xiong, Y., Wang, Z., and Qiao, Y. (2015). To-
wards Good Practices for very Deep Two-Stream Con-
vnets. arXiv preprint arXiv:1507.02159.
Wang, L., Xiong, Y., Wang, Z., Qiao, Y., Lin, D., Tang,
X., and Van Gool, L. (2016). Temporal Segment
Networks: Towards Good Practices for Deep Action
Recognition. In European Conference on Computer
Vision, pages 20–36. Springer.
Zach, C., Pock, T., and Bischof, H. (2007). A Duality
Based Approach for Realtime TV-L
1
Optical Flow.
In Joint Pattern Recognition Symposium, pages 214–
223. Springer.
Zhu, Y., Lan, Z., Newsam, S., and Hauptmann, A. G.
(2017). Hidden Two-Stream Convolutional Net-
works for Action Recognition. arXiv preprint
arXiv:1704.00389.
Fuzzy Fusion for Two-stream Action Recognition
123