Video Summarization through Total Variation, Deep Semi-supervised

Autoencoder and Clustering Algorithms

Eden Pereira da Silva

, Eliaquim Monteiro Ramos

, Leandro Tavares da Silva

1,2

, Jaime S. Cardoso

and Gilson A. Giraldi

National Laboratory for Scientiﬁc Computing, Petr

opolis, Brazil

Federal Center of Technology Education Celso Suckow da Fonseca, Petr

opolis, Brazil

INESC TEC and University of Porto, Porto, Portugal

Keywords:

Summarization, Cosine Similarity Metric, Total Variation, Autoencoder, K-means.

Abstract:

Video summarization is an important tool considering the amount of data to analyze. Techniques in this area

aim to yield synthetic and useful visual abstraction of the videos contents. Hence, in this paper we present a

new summarization algorithm, based on image features, which is composed by the following steps: (i) Query

video processing using cosine similarity metric and total variation smoothing to identify classes in the query

sequence; (ii) With this result, build a labeled training set of frames; (iii) Generate the unlabeled training set

composed by samples of the video database; (iv) Training a deep semi-supervised autoencoder; (v) Compute

the K-means for each video separately, in the encoder space, with the number of clusters set as a percentage of

the video size; (vi) Select key-frames in the K-means clusters to deﬁne the summaries. In this methodology,

the query video is used to incorporate prior knowledge in the whole process through the obtained labeled

data. The step (iii) aims to include unknown patterns useful for the summarization process. We evaluate the

methodology using some videos from OPV video database. We compare the performance of our algorithm

with the VSum. The results indicate that the pipeline was well succeed in the summarization presenting a

F-score value superior to VSum.

1 INTRODUCTION

Daily, millions of videos are posted online, and some

billions are available for public or private access,

as on YouTube, for example. This content is pro-

vided by professionals or amateurs recorders, with

many different devices as smartphones, surveillance

or trafﬁc cameras, among others. If we can provide

some video summary, where the important informa-

tion along the video is captured, it will greatly reduce

the effort to browse through the enormous amount of

content available, during a content based video re-

trieval task. Video summarization can be described as

a subset selection problem, where the subsets contain

frames, sparsely distributed in the whole sequence,

or shots (set of temporally continuous interval-based

segments). In both cases, the subset is smaller than

the original video. The ﬁrst case depends on key-

frames selection. The second case is implemented

through key shots selection.

In terms of pattern recognition tasks, two ap-

proaches are commonly applied to video summariza-

tion: unsupervised and supervised ones. The former

uses heuristics to satisfy some properties in order to

create summaries of the videos (Yuan et al., 2019; Li

et al., 2019). Supervised methods (Zhao et al., 2019;

Rochan et al., 2018) have access to raw videos and

their corresponding ground truth summaries. More-

over, they use mainly the advances on deep learn-

ing to construct summaries. Although the supervised

approaches have achieved better results than unsu-

pervised techniques, labeling data with the deﬁned

ground-truth is not easily available.

A semi-supervised approach for ﬂuid ﬂow sum-

marization, in the context of computational ﬂuid dy-

namics, is proposed in (Ramos et al., 2018), but the

authors did not present computational results. That

work suggests to use transferring learning (Hu et al.,

2016), combining labeled and unlabeled training sets

in order to allow an autoenconder (AE) to efﬁciently

learn how to encode samples in a reduced dimension

space. After the AE training, the data set is processed

by encoder and the feature vectors yielded enter into

a clustering algorithm for classiﬁcation. In this paper,

Pereira da Silva, E., Ramos, E., Tavares da Silva, L., Cardoso, J. and Giraldi, G.

Video Summarization through Total Variation, Deep Semi-supervised Autoencoder and Clustering Algorithms.

DOI: 10.5220/0008969303150322

In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 4: VISAPP, pages

315-322

ISBN: 978-989-758-402-2; ISSN: 2184-4321

315

we propose some improvements of this methodology

and its application in video summarization.

Speciﬁcally, the methodology proposed in

(Ramos et al., 2018) uses the following pipeline: (a)

build the labeled training set X

in the original space;

(b) perform a coarse temporal ﬂow segmentation

using a simple similarity measure combined with an

interval tree analysis; (c) select key numerical frames

inside each obtained segment and assemble these

frames in a training set X

; (d) a semi-supervised AE

architecture is trained using the sets X

and X

generate a metric distance (encoding function); (e)

Apply X-means (Pelleg and Moore, 2000) clustering

technique, with the metric distance, to compute

the ﬁnal partition of the frame sequence; (f) For

each obtained cluster, take a key-frame to build the

summarization sequence.

However, we have noticed that interval tree and

a simple distance metric (like Frobenius distance) do

not provide a satisfactory temporal segmentation in

the frames of videos. Futhermore, the X-means al-

gorithm tries to perform clustering without the need

to set a pre-deﬁned number K of groups. However,

in the case of video sequences, the obtained results

are not satisfactory. Besides, it is not clear the ad-

vantages of a high cost semi-supervised AE against a

simpler unsupervised one. Therefore, in our work we

propose to use total variation denoising, followed by

differentiation and thresholding instead of the interval

tree. We also replace the distance metric by a similar-

ity measure based on the data correlation. Moreover,

we perform clustering using K-means instead of X-

means. We also compare a simple AE with the semi-

supervised AE proposed in (Ramos et al., 2018) to

evaluate the encoded quality of the former against the

latter. Up to the best of our knowledge, this is the

ﬁrst work that applies a semi-supervised technique for

video summarization in a systematic procedure. The

whole methodology is the main contribution of this

paper.

The remaining text is organized as follows. Sec-

tion 2 we survey related works. In section 3 we

describe the background techniques. The proposed

methodology is presented in section 4. Next, section

5 discusses the computational experiments. Conclu-

sions and possible future works are presented in sec-

tion 6.

2 RELATED WORKS

A variety of video summarization techniques have

been proposed as seen in the literature (Yuan et al.,

2019; Zhao et al., 2019; Li et al., 2019; de Avila

et al., 2011). In this paper we focus only on the tech-

nique based on image features to construct the sum-

mary. Generally, those techniques can be classiﬁed

into unsupervised and supervised ones.

Clustering algorithms are one of the most popu-

lar unsupervised methodology. Given hand-craft fea-

tures, similar frames are grouped forming a cluster

and, from each cluster, the centers are taken to build

the summary. Also, some works in unsupervised class

use the frame histograms to learn clusters (de Avila

et al., 2011). In (Mohan and Nair, 2018) there is an

extension of this approach: the shot histograms are

compressed by a high-level feature extractor before

the clustering step. Other works construct models, as

in (Lei et al., 2019), where the video is modeled as

graph, where a graph vertex corresponds to a frame

and the edge between vertexes is weighted by the

Kullback-Leibler divergence of two frames based on

semantic probability distributions. A clustering and a

rank operation is applied on this graph method to cre-

ate the summary. Recent works in unsupervised sum-

marization have applied deep learning (Yuan et al.,

2019; Zhao et al., 2019; Jung et al., 2018), using in

general, convolutional or recurrent neural networks.

Deep learning is the principal tool in supervised

summarization approaches. In this case, the sum-

mary is modeled as a classiﬁcation problem, where

in the ground truth, frames have labels that represent

classes in the video (Jung et al., 2018). However, even

with better results in video summarization, labeling

for many video frames is tedious task that depends on

the human intervention. Moreover, overﬁtting prob-

lems can frequently occur if no sufﬁcient labeled data

is available. Therefore a semi-supervised approach,

which uses just one labeled video to summarize a set

of other videos, can mitigate these limitations being a

contribution to the area, which motivates our work.

3 TECHNICAL BACKGROUND

In mathematical terms, the total variation denoising

computes a smooth version of an input signal y ∈

by solving the optimization problem (Selesnick,

2012),

ˆx = arg min

x∈R

y − x

+ λkDxk, (1)

where x ∈ R

; λ is the smooth factor, and D is a ma-

trix (N − 1) × N described in (Selesnick, 2012).

An AE can be viewed as a special case of feed-

forward neural network that is trained to reproduce

its input at the output layer (Goodfellow et al., 2016).

The AE architecture is depicted in Figure 1. Both

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

316

encoder and decoder in this ﬁgure are implemented

through a multilayer perceptron (MLP) neural net-

works where W

(ξ)

and b

(ξ)

are the weight matrix and

bias, respectively, for the layer ξ. Given an input V ,

the corresponding output V

(ξ)

at the ξ-th layer is com-

puted as:

(ξ)

(V ) = V

(ξ)

= ϕ



(ξ)

(ξ−1)

+ b

(ξ)



, (2)

where ϕ is a non-linear activation function (sigmoid

function, for instance), which operates component-

wisely.

(1)

(2)

(M)

(M+1)

(M+2)

(2M)

Encoder

Decoder

Coded

Input

(M)

(0)

(1)

(M)

(M+1)

(M+2)

(2M)

Figure 1: Autoencoder (AE) graph representation. Com-

posed by one encoder and one decoder neural network. The

sets of weights on each AE layer are represented in matrix

form, where W

(m)

is the set of weights of the m-th layer.

On the same way, the bias for the m-th layer in represented

(m)

. Each f

(m)

represents the view of the layer as a trans-

formation. For an input x, f

(M)

(x), f

(2M)

(x) are the encoder

and decoder output respectively. The V

(M)

= f

(M)

(•) is the

output of the encoder.

The semi-supervised AE used in this work has

a loss function that incorporates the Fisher analysis,

based on the terms S

and S

, that represent the intra-

class variation and inter-class separation, respectively

(Hu et al., 2016):

(m)

∑

i=1

∑

j=1

i j

(m)

(~x

,~x

), (3)

(m)

∑

i=1

∑

j=1

i j

(m)

(~x

,~x

), (4)

where N

is the number of samples of X

, d

(m)

is the

square of the Euclidean distance, P

i j

= 1 if ~x

is one

of k

nearest neighbors of ~x

, in the same class of it,

and P

i j

= 0 otherwise. Moreover, Q

i j

= 1 if ~x

is one

of k

nearest neighbors of ~x

, belonging to a different

class, and Q

i j

= 0 otherwise.

In order to add a measure of the dispersion of

training samples, it is introduced in the loss function

the expression:

(m)

) =



∑

i=1

(m)

(~x

)−

∑

i=1

(m)

(~x

)



(5)

where N

is the number of labeled samples and N

the

number of unlabeled elements.

Besides, it is necessary to add terms related to re-

construction errors, generating the ﬁnal loss function

used in (Hu et al., 2016), given by:

min

(M)

, f

(2M)

J =α

(M)

− α

(M)

+ βD

(M)

)

+ γ

∑

m=1

(m)

+ k

(m)

)

∑

i=1

k f

(2M)

(~x

) −~x

∑

i=1

k f

(2M)

(~x

) −~x

, (6)

where α

, α

, β, are parameters deﬁning the impor-

tance of each corresponding term in the learning pro-

cess, γ is a regularization parameter, and θ

and θ

controls the inﬂuence of the reconstruction errors in

the objective function. The semi-supervised AE ap-

plied in this paper has an loss function given by ex-

pression (6) with α

= 1, α

= 1, β = 0.

For all AEs on this work, the training process uses

backpropagation to efﬁciently calculate the gradient

of expression (6) with respect to the parameters and a

gradient descent method, in our work, based on adap-

tive moment estimation (ADAM) (Goodfellow et al.,

2016).

4 PROPOSED METHOD

The video summarization approach proposed in this

paper is based in transfer learning, whose main idea is

to use the knowledge learned from a previous dataset,

to learn about a new dataset. The authors propose the

feature reduction, leaving data to a metric space using

the semi-supervised AE with loss function (6). The

summarization methodology follows the pipeline:

1. Query video processing using cosine similarity

metric and total variation smoothing to identify

classes in the query video frames;

2. With this result, user builds the labeled training

set X

of frames ;

3. Generate the unlabeled training set X

, that is

composed by samples of the video database;

4. Training the AE with X

∪ X

, to learn the metric

space;

5. Compute the K-means for each video separately,

in the encoder space, with the number of clusters

set as a percentage of the video size;

Video Summarization through Total Variation, Deep Semi-supervised Autoencoder and Clustering Algorithms

317

6. Select key-frames in the K-means clusters to de-

ﬁne the summaries;

In this methodology, the query video is used to

incorporate prior knowledge in the whole process

through the obtained labeled data. The step (3) aims

to include unknown patterns useful in the summariza-

tion process.

The utilization of cosine similarity metric in step

(1) gives an efﬁcient way to compare consecutive

frames. Given q RGB frames Q

,··· ,Q

q−1

with resolution M × N, the ﬁrst step is to convert

these images to gray scale, generating the sequence

,··· ,T

q−1

. Then, to obtain the similarity r(i) be-

tween the frames T

i+1

and T

, i ∈ {0,1,··· ,q − 1}, we

calculate:

r(i) =

∑

m=1

∑

n=1

i+1

(m,n) −

i+1

)(T

(m,n) −

)

∑

m=1

∑

n=1

i+1

(m,n) −

i+1

)

∑

m=1

∑

n=1

(m,n) −

)

−1/2

, (7)

where

M.N

∑

m=1

∑

n=1

(m,n), j ∈

{

i,i + 1

}

. On

the similarity formula, the terms in the square brack-

ets is a normalization factor. Beside that, this for-

mula is the cosine of the angle between the vectorized

forms of matrices (T

i+1

−

i+1

)and (T

−

), which

implies that r(i) ∈ [−1, 1], i ∈ {0,1,··· ,q − 1}.

On the pipeline, in steps (2)-(3), it is constructed

a training set with two different subsets, one from

frames whose labels are previously known and a sec-

ond one whose labels are unknown. Using these sets

the approach aims to improve the summarizing using

transfer learning (Hu et al., 2016), transferring what

is learned from the labeled set to the unlabeled group.

To build the labeled training set X

, we take

a video query and applied total variation (ex-

pression (1)) in the similarity vector S(q − 1) =

(r(1), r(2), ...,r(q − 1), where r is calculated through

expression (7). Next, we apply ﬁrst order differential

operation and with the absolute value of the differ-

ence, we use a threshold to determinate the segments

of frames, which represent candidate clusters, or can-

didate labels in the video. This temporal segmenta-

tion by total variation combined with differentiation

and threshold is validated, by a user, which deﬁnes

the ﬁnal frame classes. Then, the algorithm randomly

selects a percentage of frames from each segment to

construct the X

set. This process is performed be-

cause we may have segments disjoint that contains

the same visual information; for instance, a video clip

containing a scene that periodically repeats along the

time sequence. The proposed temporal segmentation

pipeline is not able to distinguish such situation.

Next, in step (3), for each video of the database

some frames are randomly selected to compose the

unlabeled training set X

. After building the sets X

and X

they are used for training the semi-supervised

AE of section 3. Considering each layer as a set of

transformation of its correspondent input, the neural

network learns a non-linear transformations set, trans-

ferring the knowledge from the labeled source do-

main to the target unlabeled domain. On this phases

the aim is to learn the metric space, whose met-

ric is d

) =



(M)

) − f

(M)

)



, where

(M)

) is the M-th layer output, the encoder output

over the input V

, as showed in Figure 1, also called

the data in metric space by (Hu et al., 2016). In our

case V

is a vectorized version of the input frame T .

Following, with the metric space learned, given

a frame sequence, it is coded by the encoder ( f

(M)

transforming each frame from the sequence on vec-

tors on the metric space. In sequence, a clustering

algorithm is applied on these data using the metric

learned. From each cluster generated by the K-means

algorithm, the centroid nearest frame is chosen as the

key-frame to build the video summarization, building

a set of representative frames from the sequence. The

number K of cluster to initialize K-means is set as a

percentage of the video size. The corresponding frac-

tion is determined having the number of classes in X

as reference.

5 EXPERIMENTS

All the experiments were executed in a computer with

Linux Ubuntu 18.04, 64 bits, 16 GB of RAM mem-

ory, 4 TB of hard-disk and Intelri7 processor. The

experiments were coded in Python, Tensorﬂow

and

Keras using Tensorﬂow as background

For the evaluation of our methodology, we use the

F-score measure, comparing the video labels

with

the labels from the clustering step. Moreover, due

to the fact that the K-means implementation initial-

izes the centroids in random way, we performed 30

realizations of the clustering and then take the mean

F-score.

Besides, we want to compare the semi-supervised

AE with the supervised one. Moreover, we need to

analyze the efﬁciency of the encoder metric space

The Python framework for Machine Learning coding.

The Python framework for Deep Learning coding.

All videos are labeled by a user.

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

318

against the original data space regarding the summa-

rization. Consequently, we have three spaces for data

representation: original, AE, and semi-supervised

AE, named DTML AE, as performed in (Hu et al.,

2016). Moreover, we compare our results with the

VSum technique, published in (de Avila et al., 2011).

5.1 Dataset

To evaluate our methodology we use videos from

Open Project Videos (OPV) dataset. This dataset

was chosen because it is free available and commonly

used to evaluate video summarization (Stavropoulos

et al., 2019; Fajtl et al., 2018; Rochan and Wang,

2018; Rochan et al., 2018). We choose ten different

videos from the dataset.

Each video sequence has between 503 and 3611

snapshots, in RGB format, each one with spatial reso-

lution of 240×320. To save computational resources,

we resize each image to 48 × 68 and converted it to

gray scale.

5.2 Query Video Processing

Once a query video is selected, it is processed by

our methodology. Hence, we compute the cross-

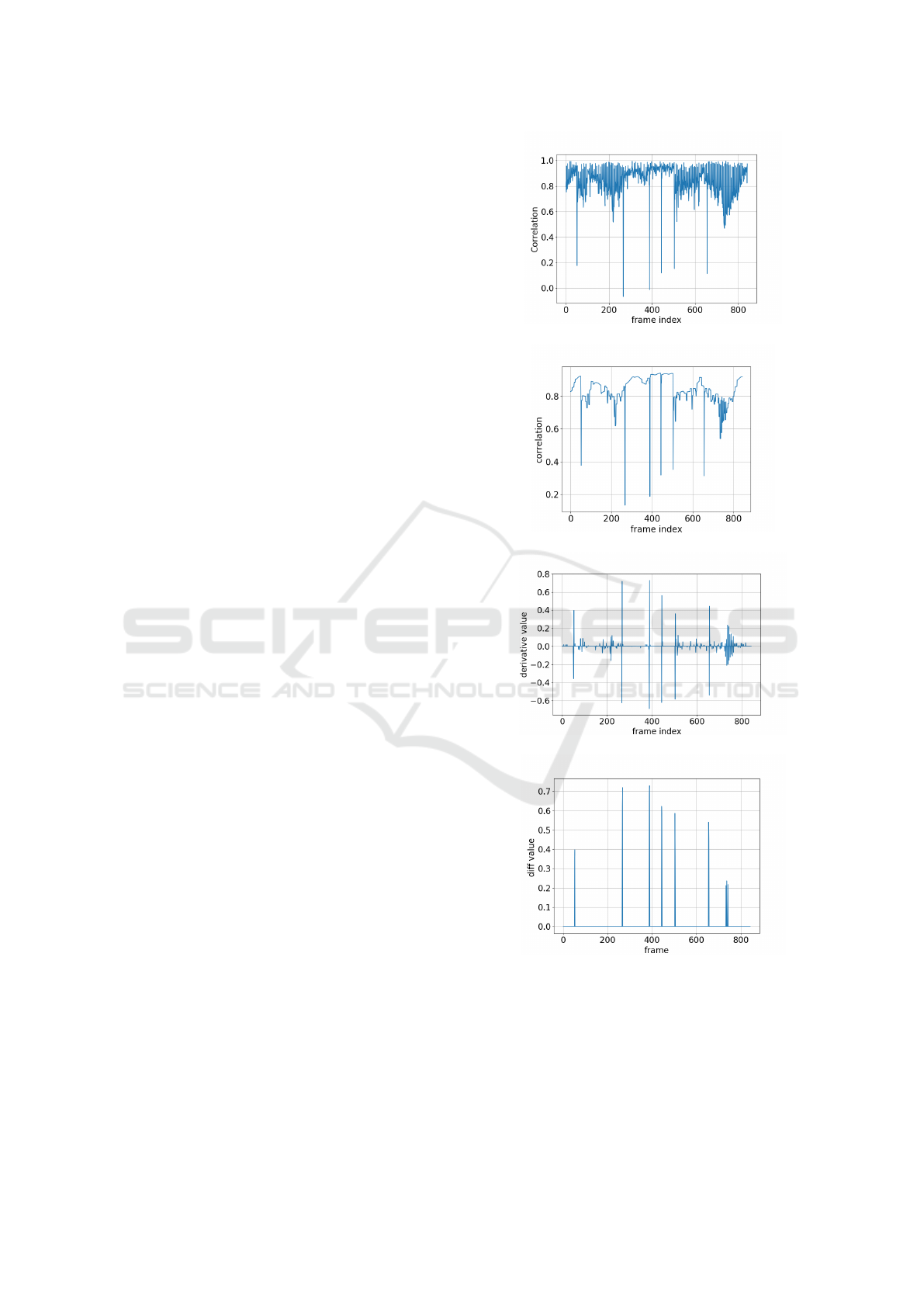
correlation through expression (7), shown in Figure

2.(a). Next, the obtained result is processed with

the total variation method (section 3), to obtain the

smoother proﬁle of Figure 2.(b). Then, the differ-

entiation operator is applied with the result shown in

Figure 2.(c). Following, a simple thresholding gives

the result of Figure 2.(d) highlighting the intervals.

In these operations, we use the following parameters

values obtained by trial and error: (1) Total varia-

tion parameters: λ = 0.2 and number of iterations

= 100; (b) Threshold for differentiation operator

result: T = 0.3 .

The bars observed in Figure 2.(d) deﬁne the be-

ginning and the end of each video segment, which

are candidates to be classes in our approach. The

user analyses these segments to identify the correct

classes and performs the labeling of the query video

images. Besides he/she selects a subset (in this case,

60% frames of each identiﬁed class) of labeled im-

ages to compose the set X

(a)

(b)

(c)

(d)

Figure 2: (a) Correlations C

i,i+1

. (b) Total variation ﬁltering

signal (T (C)

i,i+1

) obtained with λ = 0.2 and N

= 10. (c)

Visualization of the differentiation operation. (d) Intervals

obtained by thresholding with T = 0.3 the differentiation

result: [1,53], [54,267], [268,389], [390,445], [446, 505],

[506,656], and [657,844].

Video Summarization through Total Variation, Deep Semi-supervised Autoencoder and Clustering Algorithms

319

5.3 Building Unlabeled, Training and

Validation Sets

For each video of the database we randomly take 10%

of samples and assemble these frames in the unla-

beled set X

and other 5% to construct a validation

set. We then assemble the labels and unlabeled sets,

and X

, to form the training dataset.

5.4 Autoencoders

The autoencoders were build with the same conﬁg-

uration. The architecture had an input layer, ﬁve

hidden layers and one output layer, in the sequence:

[3072,1024, 800, 512, 800, 1024, 3072].

To implement the DTML AE we use Tensorﬂow

and for the common AE the code was performed in

Keras with Tensorﬂow as background. We did not

implement both in Keras, because Tensorﬂow is more

friendly to deal with the customized loss function of

DTML AE approach (expression (6)).

For learning rate µ value in Tensorﬂow DTML

AE, it was adopted µ = 0.001 and for the common

AE it was used the Keras default value.

All parameters were chosen after some experi-

ments, evaluating the reconstruction error evolution.

The conﬁguration above had have the least error in re-

construction in the evaluation. Furthermore, the num-

ber of epochs for training the network was equal to

500 to the common AE and 1000 for DTML AE.

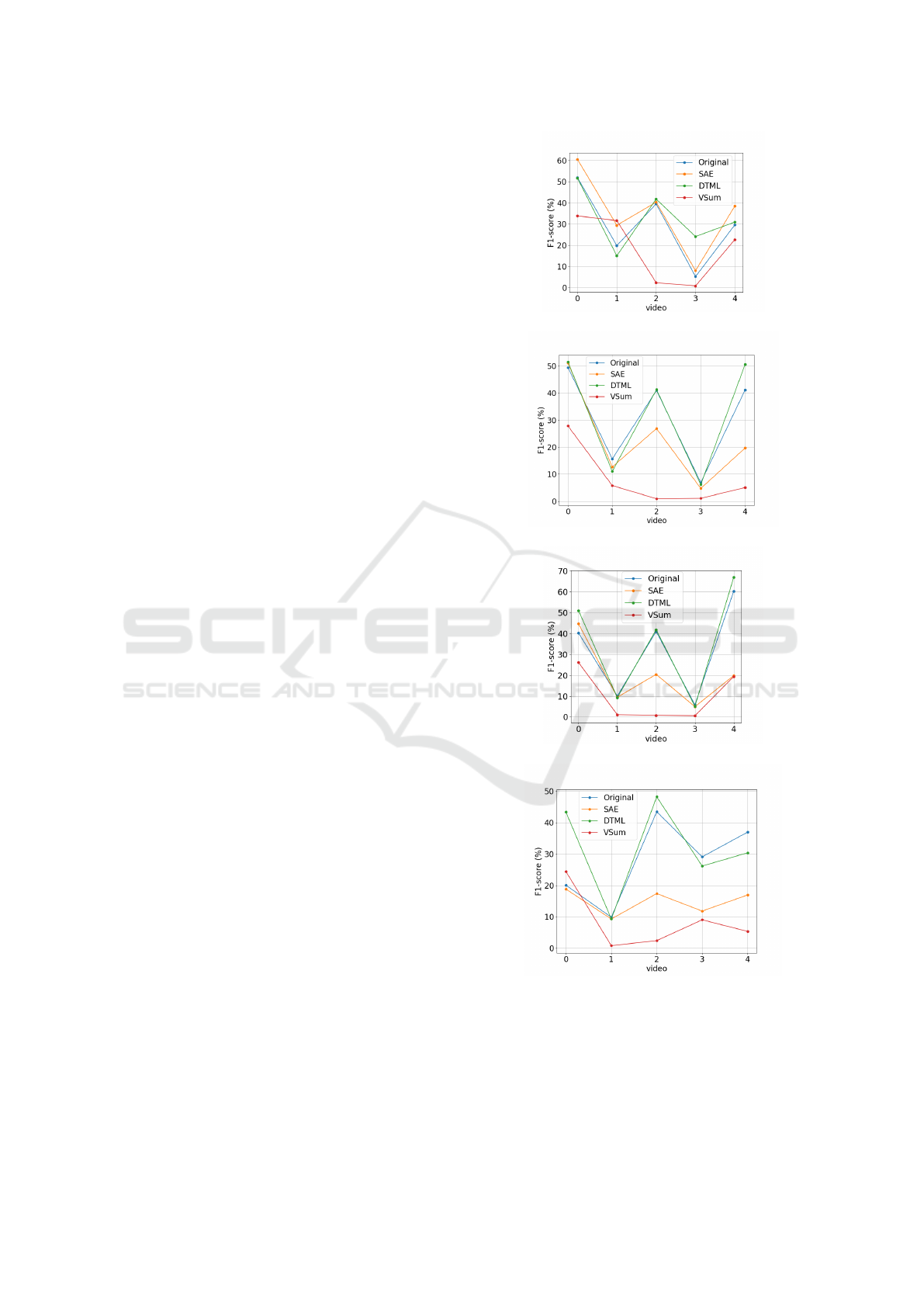
5.5 Test 1

In this test we use ﬁve videos from the database for the

ﬁnal clustering step. This videos were similar to the

query video used to make the X

set. The keyframes

were selected based in the proximity with the cluster

centers.

The query video has seven segments, as pointed

by total variation+diff+threshold (results in Figure 2)

and checked in the ground truth. Hence, we set the

number K of clusters to compute the K-means as K ∈

{5,7, 8, 10} in order to test the sensitivity of the F-

score against this parameter. The results are shown in

Figure 3.

We can observe in Figure 3 the mean F-score for

each video and for each space tested, as well as with

different cluster numbers. From this ﬁgure we can

observe that DTML AE approach had the higher per-

centile F-score in more videos than the others ap-

proaches. This result is conﬁrmed by the mean per-

centile F-score of all videos as showed in Table 1.

(a) clustering with k=5

(b) clustering with k=7

(d) clustering with k=10

Figure 3: Mean F-score for the 30 realizations of k-means

(a) Mean F-score for ﬁve test videos using k = 5 clusters;

(b) Mean F-score for ﬁve videos using k = 7 clusters; (c)

Mean F-score for ﬁve videos using k = 8 clusters (d) Mean

F-score for ﬁve videos using k = 10 clusters.

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

320

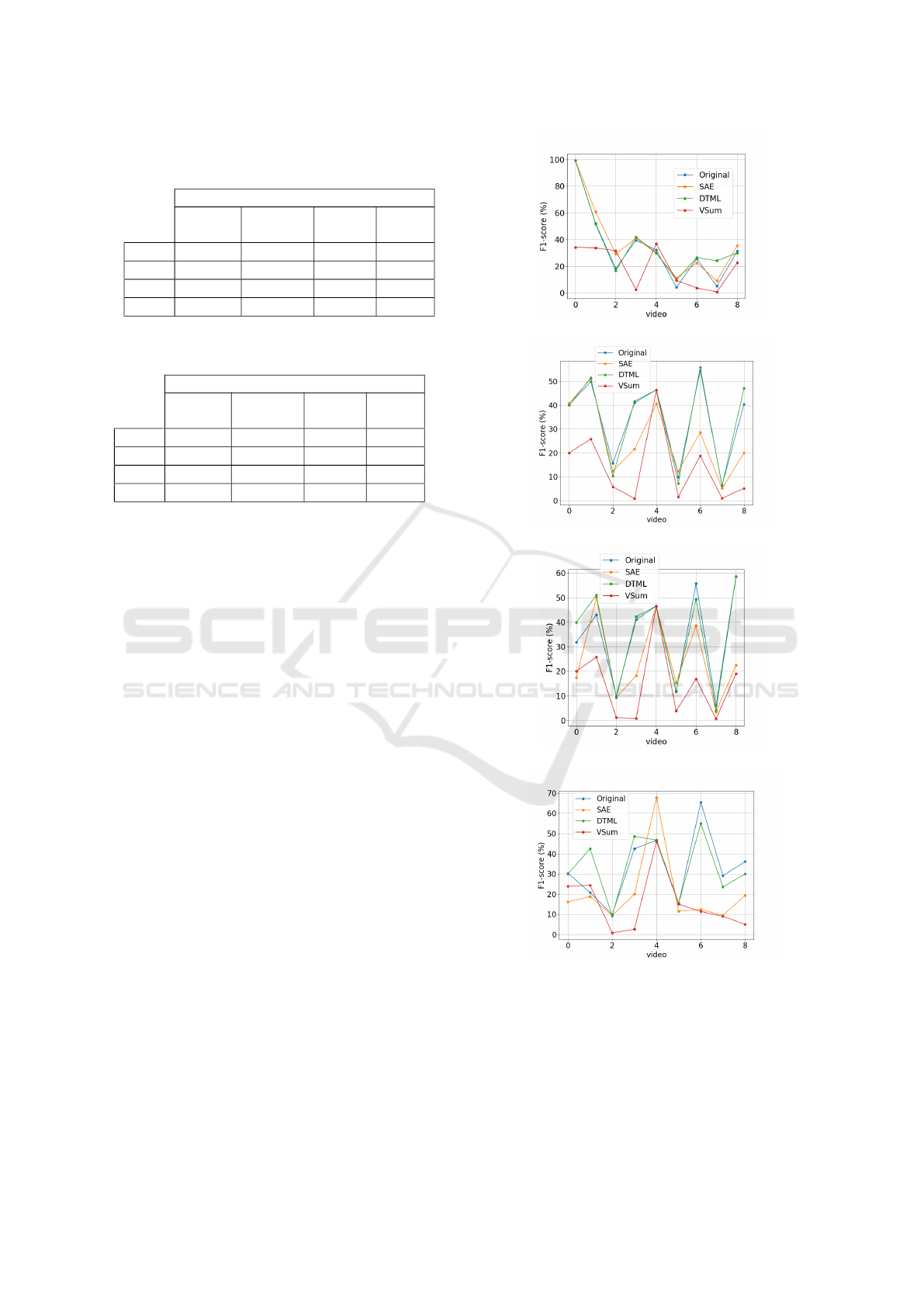
Table 1: F-score for each space varying the clusters number,

using the database with videos similar to the query.

Mean F-score for space

original

common

DTML

VSum

k = 5 0.339 0.258 0.340 0.139

k = 7 0.308 0.230 0.321 0.081

k = 8 0.315 0.199 0.348 0.096

k=10 0.279 0.148 0.315 0.084

Table 2: F-score for each space varying the clusters number.

Considering a database the entire videos.

Space

original

common

DTML

VSum

k = 5 0.342 0.376 0.366 0.195

k = 7 0.338 0.258 0.340 0.139

k = 8 0.338 0.246 0.348 0.150

k=10 0.329 0.205 0.334 0.153

5.6 Test 2

In this test we use all videos from the database for

the ﬁnal clustering step, in a total of 9 videos. This

database includes videos with different patterns re-

spect to the query video used to make the X

set.

It was used the same procedure as the test be-

fore. The results are showed in Figure 4. By the

results shown in Figure 4 we can observe again that

DTML AE approach had the higher percentile F-score

in more videos than the others approaches. This result

is conﬁrmed also by the mean percentile F-score of all

videos reported in Table 2.

6 CONCLUSIONS

In this paper we propose a pipeline to video summa-

rization based on a semi-supervised approach, where

an autoenconder is used to learn a metric space and

the summarization is performed in the encoder space.

The methodology is inspired in the work (Ramos

et al., 2018), originally proposed for ﬂuid summariza-

tion in numerical simulations without computational

experiments reported. We have adapted the method-

ology for video summarization, replacing some ele-

ments of the original pipeline to total variation (TV)

with differentiation and thresholding; cosine similar-

ity; the k-means for clustering. Also, we perform

tests using simple AE, the DTML AE proposed in

(Hu et al., 2016), and compare the methodology re-

sults with the VSum technique.

(a) clustering with k=5

(b) clustering with k=7

(d) clustering with k=10

Figure 4: Mean F-score for the 30 realizations of k-means

(a) Mean F-score for ﬁve videos using k = 5 clusters; (b)

Mean F-score (%) for ﬁve videos using k = 7 clusters; (c)

Mean F-score for ﬁve videos using k = 8 clusters (d) Mean

F-score for ﬁve videos using k = 10 clusters.

Video Summarization through Total Variation, Deep Semi-supervised Autoencoder and Clustering Algorithms

321

The results showed that the F-score for DTML AE

gives the best result in mean, when compared with

a common AE, the original data space, and VSum

methodology. This result is the same when we con-

sider videos that are similar to the query video, or

when we include videos with low similarity with the

query.

As future works we intent to improve the pipeline

by testing the methodology with convolutional au-

toencoders, using larger datasets for tests and also to

apply a more state of art transformation, as percep-

tual hashing (Monga and Evans, 2006). Moreover,

we want to explore the methodology to content visual

retrieval and to compare the results with more recent

approaches of videos summarization.

ACKNOWLEDGEMENTS

The authors thank to CNPq for support.

REFERENCES

de Avila, S. E. F., ao Lopes, A. P. B., da Luz, A., and

de Albuquerque Ara

ujo, A. (2011). Vsumm: A mech-

anism designed to produce static video summaries and

a novel evaluation method. Pattern Recognition Let-

ters, 32(1):56 – 68. Image Processing, Computer Vi-

sion and Pattern Recognition in Latin America.

Fajtl, J., Sokeh, H. S., Argyriou, V., Monekosso, D., and

Remagnino, P. (2018). Summarizing videos with at-

tention.

Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep

Learning. MIT Press.

Hu, J., Lu, J., Tan, Y.-P., and Zhou, J. (2016). Deep transfer

metric learning. Trans. Img. Proc., 25(12):5576–5588.

Jung, Y., Cho, D., Kim, D., Woo, S., and Kweon, I. S.

(2018). Discriminative feature learning for unsuper-

vised video summarization.

Lei, Z., Zhang, C., Zhang, Q., and Qiu, G. (2019). Framer-

ank: A text processing approach to video summariza-

tion.

Li, X., Li, H., and Dong, Y. (2019). Meta learning for task-

driven video summarization. IEEE Transactions on

Industrial Electronics, 2019.

Mohan, J. and Nair, M. S. (2018). Dynamic summa-

rization of videos based on descriptors in space-time

video volumes and sparse autoencoder. IEEE Access,

6:59768–59778.

Monga, V. and Evans, B. L. (2006). Perceptual image hash-

ing via feature points: Performance evaluation and

tradeoffs. Trans. Img. Proc., 15(11):3452–3465.

Pelleg, D. and Moore, A. W. (2000). X-means: Extend-

ing k-means with efﬁcient estimation of the number

of clusters. In Proc. of the Seventeenth International

Conference on Machine Learning, ICML ’00, pages

727–734, San Francisco, CA, USA.

Ramos, E., da Silva, L., Cardoso, J. S., and Giraldi, G.

(2018). Deep neural network for vector ﬁeld topology

recognition with applications to ﬂuid ﬂow summariza-

tion.

Rochan, M. and Wang, Y. (2018). Video summarization by

learning from unpaired data.

Rochan, M., Ye, L., and Wang, Y. (2018). Video summa-

rization using fully convolutional sequence networks.

Selesnick, I. (2012). Total variation denoising (an mm algo-

rithm). http://eeweb.poly.edu/iselesni/lecture notes/

TVDmm/TVDmm.pdf. Accessed: 2019-06-10.

Stavropoulos, P. P., Pereira, D., and Kee, H.-Y. (2019). Mi-

croscopic mechanism for higher-spin kitaev model.

Yuan, L., Tay, F. E., Li, P., Zhou, L., and Feng, J. (2019).

Cycle-sum: Cycle-consistent adversarial lstm net-

works for unsupervised video summarization.

Zhao, B., Li, X., and Lu, X. (2019). Hierarchical recurrent

neural network for video summarization.

VISAPP 2020 - 15th International Conference on Computer Vision Theory and Applications

322