
Visualization to Assist Interpretation of the Multilevel Paradigm in
Bipartite Graphs
Diego S. Cintra
a
, Alan Valejo
b
, Alneu A. Lopes
c
and Maria Cristina F. Oliveira
d
Instituto de Ci
ˆ
encias Matem
´
aticas e de Computac¸
˜
ao (ICMC),
University of S
˜
ao Paulo (USP), CP 688, S
˜
ao Carlos SP, 13560-970, Brazil
Keywords:
Visualization, Bipartite Graphs, Multilevel Paradigm, Graph Summarization.
Abstract:
Multilevel methods refer to a general framework for solving optimization problems in large graphs consider-
ing a hierarchy of contracted representations of the target graph. A recent extension to bipartite graphs has
been introduced and successfully employed in diverse applications, but experience suggests the method is
highly susceptible to the choice of vertex matching strategy for graph contraction and on whether the super-
vertices are relevant generalizations to the problem addressed. Although the flexibility in obtaining contracted
representations of an original graph is a potential advantage, appropriate choice and parameterization of the
contracting algorithms is challenging. Experts would benefit from solutions capable of assisting them in as-
sessing alternatives and making informed decisions. In this work we describe a visualization system that
creates an interactive graphical representation of a multilevel graph hierarchy obtained as a result of executing
a multilevel method on bipartite graphs. We provide illustrative case studies showing the proposed visualiza-
tion can support algorithm developers in inspecting and interpreting how different parameter choices in the
coarsening stage impact the resulting multilevel hierarchies.
1 INTRODUCTION
Multilevel methods provide a framework for solv-
ing optimization problems in large graphs (Walshaw,
2004). They gradually reduce a large scale graph by
coarsening it into a hierarchy of successively smaller
graphs; employ a target algorithm to solve the prob-
lem in the smallest graph instance and project the so-
lution thus obtained backwards into the hierarchy of
increasingly complex graph models, up to the original
one. An approximate solution may be thus obtained
in situations where executing the target algorithm di-
rectly on the original graph might be unfeasible. This
general framework has been instantiated in a variety
of combinatorial problems in graphs, e.g., sparse ma-
trix factorization (Gupta et al., 1997), graph partition-
ing (Padmavathi and George, 2014) and graph draw-
ing (Hachul and J
¨
unger, 2004). Solving a problem on
a small graph requires searching a reduced solution
space rather than the possibly cost-prohibitive solu-
tion space associated with the full graph. Thus, a so-
lution is computed at a reduced cost and then gener-
a
https://orcid.org/0000-0002-7278-0611
b
https://orcid.org/0000-0002-9046-9499
c
https://orcid.org/0000-0003-3112-4746
d
https://orcid.org/0000-0002-4729-5104
alized to the original graph. The quality of the final
solution depends both on the quality of the initial so-
lution and the generalization capability of the graph
contraction strategy.
Originally defined on homogeneous networks, in
which the vertices represent entities of a single type,
the multilevel approach has recently been extended to
bipartite graphs and networks (Valejo et al., 2018).
Vertices in bipartite graphs represent two types of
entities, so that the vertex set is split into two non-
overlapping subsets and edges can only connect ver-
tices in different subsets. Such graphs occur fre-
quently in data analysis scenarios, e.g., document-
word and protein-ligand networks are two illustrative
examples in connection with relevant real-world prob-
lems (Rossi et al., 2016; Jeong et al., 2000).
The framework introduced by Valejo et al. (2018)
to support the multilevel approach on bipartite graphs
is powerful, conceptually simple and highly flexible,
with potential applicability in a wide variety of data
analysis problems. Yet, successful application of mul-
tilevel strategies involves difficult choices, e.g., the
choice and parameterization of vertex matching al-
gorithm required for coarsening may strongly impact
the method’s performance and solution quality. Mak-
ing informed choices when handling novel applica-
Cintra, D., Valejo, A., Lopes, A. and Oliveira, M.
Visualization to Assist Interpretation of the Multilevel Paradigm in Bipar tite Graphs.
DOI: 10.5220/0008903501330140
In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020) - Volume 3: IVAPP, pages
133-140
ISBN: 978-989-758-402-2; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
133

tion problems is particularly challenging. This work
addresses this gap by introducing a visualization solu-
tion aimed at supporting algorithm developers in in-
specting and interpreting the graph hierarchy result-
ing from an execution of the multilevel method on bi-
partite graphs. Our solution relies on a novel graphi-
cal metaphor for depicting a multilevel bipartite graph
hierarchy, which is the key component of an interac-
tive interface implemented as a front-end to the afore-
mentioned framework.
This paper is organized as follows. The multilevel
strategy is detailed in Section 2, and related work is
briefly reviewed in Section 3. In Section 4 we de-
scribe the components of the visualization system de-
veloped and in Section 5 we present case studies illus-
trating how it can support developers interpreting the
behavior of the multilevel method and understanding
the implications of alternative choices. Concluding
remarks are presented in Section 6.
2 MULTILEVEL METHOD ON
BIPARTITE GRAPHS
A graph G = (V, E) is defined by a set of vertices V
and a set of edges E that indicate relationships be-
tween pairs of vertices. The set V in a bipartite graph
G = (V
1
, V
2
, E) is split into two disjoint subsets (lay-
ers) V
1
and V
2
, V
1
∩V
2
=
/
0, and edges connect vertices
in different layers (Bondy et al., 1976). Edges or ver-
tices may have weigths or other attributes. Vertices u
and v are neighbors (adjacent) if edge (v, u) ∈ E. The
degree of v ∈ V, d
G
(v), is equal to the total weight
of its adjacent edges. The vertex h-hop neighborhood
consists of the vertices in set Γ
h
(v) = {u| there is a
path of length h between v and u} (Valejo et al., 2018).
Figure 1 illustrates the stages of a multilevel
method applied to a bipartite graph. Initially a
coarsening algorithm creates a sequence of simplified
(coarsened) versions of the input graph at gradually
increasing contraction levels. Coarsening comprises
the steps of matching, which selects which vertices
will be collapsed; and contraction, which builds the
reduced representation, collapsing the matched ver-
tices and their incident edges into so-called super-
vertices and super-edges, respectively. A super-
vertex is called a successor of its originating ver-
tices, which are themselves called predecessors of the
super-vertex. An initial solution to the target problem
is computed on the coarsest graph instance. In the
final uncoarsening stage this initial solution is pro-
jected backwards and refined through the intermedi-
ate sequence of coarsened graphs, until obtaining the
final solution in the original input graph.
Figure 1: Multilevel method applied to a bipartite graph G
0
:
the coarsening stage computes a sequence of intermediate
coarsened graphs {G
1
, ..., G
S−1
, G
S
} from G
0
, wherein G
S
is the coarsest graph, on which an initial solution to a tar-
get problem is computed. The uncoarsening stage projects
this initial solution backwards onto the intermediate graphs
{G
S−1
, ..., G
1
} down to G
0
, yielding the final solution.
The vertex matching algorithm is a key component
of an effective multilevel solution. Inadequate match-
ings may yield poor initial solutions, or poor perfor-
mance of the target algorithm, perhaps both. For-
mally, a matching
1
M = {V
k
}
K
k=0
is a partition of V
into a set of K non-empty and disjoint subsets V
i
∈ V ,
1 ≤ |V
i
|, ∀i and i 6= j ⇒ V
i
∩V
j
= ∅. A vertex u ∈ V
i
is called matched, otherwise, if @V
i
∈ M | u ∈ V
i
, u is
called unmatched. Algorithms rely on a user-provided
function to assess vertex similarity, e.g., Common
Neighbors (Watts, 2004) considers the pair of ver-
tices with more neighbors in common as the most
similar; Adamic Adar (Adamic and Adar, 2003) re-
lies on a logarithm function to define a “relevance
factor” in assessing vertex similarity; Preferential At-
tachment (Newman, 2001) considers the adjacent ver-
tex of highest degree as the most similar.
Many matching algorithms have been developed
relying on different policies to establish how vertices
will be collapsed. We briefly review two recent al-
gorithms targeted at bipartite graphs, namely GMb
(Greedy Matching for bipartite graphs) (Valejo et al.,
2018) and MLPb (Multilevel Label Propagation for
bipartite graphs) (Valejo et al., 2019a). Both take as
input parameters the initial graph G
0
; the layers to be
coarsened, i.e., if layer V
1
, layer V
2
or both; and the
similarity function S(u, v), u, v ∈ V . Input parameters
are informed with indexes 1 or 2 to indicate they refer
respectively to layer V
1
or V
2
.
GMb matching merges vertices pairwise relying
on a priority queue of candidate pairs v and u, wherein
Γ
2
(v) = u, organized according to their similarity as
computed by the given function S
j
(u, v), j ∈ 1, 2, so
that highly similar pairs are matched first. Addi-
1
Note, in the mathematical discipline of graph theory, a
matching is defined as a set of independent edges.
IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications
134

tional inputs are the number of coarsening levels l
j
and the graph reduction factors r f
j
. For instance, set-
ting l
1
= l
2
= 3 and r f
1
= r f
2
= 0.3 creates a 3-level
graph hierarchy G
1
, G
2
, G
3
with each graph layer at a
level k having 30% of its vertices paired into super-
vertices, relative to the previous level k − 1. A max-
imum reduction factor of 50% is attained in a single
iteration. Coarsening large graphs will require many
iterations, incurring in high processing and memory
costs. Moreover, matching quality tends to degrade
towards the final iterations, as vertices considered for
matching later are less likely to find good candidate
pairs.
MLPb (Multilevel Label Propagation for bipartite
graphs) has been introduced to overcome these limita-
tions. It relies on label propagation to collapse vertex
groups, rather than pairs. Every vertex is initially as-
signed a unique label. At each iteration, each vertex
updates its label with the the most frequent label in its
neighboring vertices. Intuitively, a densely connected
group of vertices will converge to a single dominant
label, and upon convergence vertices with the same
label will be collapsed into a single super-vertex. Be-
sides G
0
and S
j
(u, v), MLPb takes as input parame-
ters the desired layer sizes in the coarsest graph, ζ
j
,
and a maximum number of iterations T . E.g., given
G
0
with |V
1
| = |V
2
| = 200, |E| = 10.000 and setting
ζ
1
= ζ
2
= 20 MLPb will attempt to execute T iter-
ations to create G
1
with |V
1
| = |V
2
| = 20. If this is
not feasible, it will coarsen G
1
to yield a new graph
G
2
and again execute up to T iterations. The pro-
cess continues until the target sizes are met, yielding
a multilevel graph hierarchy.
The bipartite multilevel framework MOb (Valejo
et al., 2018) has been developed in Python as a flex-
ible solution that admits plugging alternative match-
ing algorithms and can be instantiated to solve mul-
tiple categories of problems. It provides the back-
end to our multilevel visualization front-end, called
MObViewer. The aim is to facilitate interpretation of
the behavior and limitations of matching algorithms
and the impact of parameter choices on the outcome
of a multilevel process applied to a bipartite network.
3 RELATED WORK
Multilevel methods have been applied, for instance, to
reduce the computational cost of computing node-link
layouts (Harel and Koren, 2000; Gajer and Kobourov,
2001; Hachul and J
¨
unger, 2004), and an experimental
evaluation of their usage in association with energy-
based layout algorithms has been reported (Bartel
et al., 2011).
Wong et al. (2009) describe a visualization solu-
tion which relies on the hierarchy of coarsened graphs
displayed in interactive node-link views, which users
can browse when executing analysis tasks. Providing
graph views at varying coarsening levels addresses
the visual clutter typical of node-link layouts. In-
deed, whilst node-link representations are intuitive
to convey global topological structures (Ghoniem
et al., 2004), rendering large graphs is computa-
tionally expensive and may yield highly cluttered
views on which exploratory tasks can be severely im-
paired (Von Landesberger et al., 2011).
Visual aggregation of nodes and edges is often
employed to mitigate clutter. Edge bundling is possi-
bly the best established solution for implicit edge ag-
gregation (Lhuillier et al., 2017), whereas vertex ag-
gregation strategies are usually explicit and domain-
driven. Most solutions rely on clustering or com-
munity detection to group vertices into meta-vertices,
super-vertices, clusters or communities (Von Landes-
berger et al., 2011), resulting in a hierarchical repre-
sentation useful for visualization purposes.
Another category of related work comprises re-
cent solutions for exploratory visualization of data
modeled as large scale bipartite graphs. Several
systems employ the biclustering algorithm (Heinrich
et al., 2011) to generate vertex aggregations in this
context (Zhao et al., 2018; Xu et al., 2016; Steinbock
et al., 2018). Yet, other approaches are possible, e.g,
the system WAOW-Vis (Pezzotti et al., 2018) adopts
a hierarchical dimensionality reduction technique to
create hierarchical representations of bipartite graphs
and users may interact to expand a particular region.
The previous contributions deal with issues re-
lated to visualization of large graphs, focusing mostly
on supporting data analysis. Our contribution is dif-
ferent in two ways. First, we deal with the problem of
depicting a hierarchy of graphs resulting from coars-
ening in the context of the multilevel method. Second,
we aim at assisting developers of multilevel solutions
in assessing the effect of distinct choices of coarsen-
ing strategy. We are not aware of previous efforts of
developing interactive visualizations to improve inter-
pretation of the multilevel method or to support navi-
gation in multilevel graph hierarchies, for the case of
either homogeneous or bipartite graphs. Our goal is
to investigate to which extent a visualization of the
multilevel graph hierarchy can enhance user interpre-
tation of the graph generalization process yielded by
the multilevel method, in the particular case of bipar-
tite graphs.
Visualization to Assist Interpretation of the Multilevel Paradigm in Bipartite Graphs
135

4 MObViewer
Figure 2 shows MObViewer’s graphical metaphor for
a multilevel graph with four hierarchical levels, where
a vertex has been user selected (outlined in red). Ver-
tices and super-vertices are shown metaphor as circles
of varying sizes, with circle size proportional to the
number of predecessors of the super-vertex. The two
innermost circle rows depict the layers of the coarsest
graph, while moving outwards from the central rows,
the outer rows represent the remaining hierarchy of
intermediate levels for each layer. The two outermost
rows, rendered in gray, depict the layers of the input
graph. By convention, the hierarchy relative to layer
V
1
is displayed in the bottom area, whereas the hier-
archy relative to layer V
2
is shown at the top.
Edges are rendered on-demand, upon vertice se-
lection: once the user selects a vertex its correspond-
ing circle is outlined in red and its incident edges
are rendered. This choice has the benefit of avoiding
line clutter and overdrawing. There are two types of
edges: adjacency edges, rendered in blue as full lines,
and hierarchy edges, rendered as green dotted lines.
The first define the actual graph topology, i.e., how
vertices in layers V
1
and V
2
are connected. The second
show a vertex connections to their successor or pre-
decessor (super-)vertices in the multilevel hierarchy.
Adjacency edges are only displayed at the coarsest
graph level, i.e., between the two inner rows/layers.
Since graph layers are stacked on top/bottom of each
other, the vertices are lined-up placing all predeces-
sors of a super-vertex side-by-side, which prevents
edge crossing and allows users to easily track which
vertices have been grouped into a super-vertex. The
complete thread of edges connecting a selected vertex
to its predecessor/successor vertices is shown, with
the circles depicting vertices in the hierarchical path
outlined in green; and the circles depicting the adja-
cent vertices to the selected one outlined in blue. For
weighted graphs the weights of adjacency edges are
mapped to color intensity, so darker shades of blue
indicate heavier edges.
MObViewer has been implemented as a client-
server web application, with the back-end running
MOb and the front-end running the visualization mod-
ule. We used Javascript for implementation, with
Node.js on the server-side; Express.js, a middleware
for server-client data routing and communication;
Three.js to render the graph metaphor and D3.js (Bo-
stock et al., 2011) functions for visualization. MOb-
Viewer is available to interested readers at https:
//github.com/diego2337/MObViewer.
Figure 2: Visual metaphor depicting a multilevel graph hi-
erarchy, with a selected vertex (outlined in red) and its adja-
cency edges (blue lines) and hierarchy edges (green lines).
5 RESULTS
We illustrate how MObViewer can support developers
of multilevel solutions. The software has been exe-
cuted on a Linux Mint 18.2 with 32GB RAM, Intel
Core i7-3770 3.40 GHz and video card GeForce GTX
660. We considered scenarios of interest to develop-
ers of multilevel solutions, and report results from an
empirical investigation of the following questions rep-
resentative of issues faced by users of matching and
coarsening algorithms:
Q1 How does the choice of similarity function af-
fect preservation of the community structures in
the multilevel hierarchy?
Q2 Is it possible to identify at which point in coars-
ening community structures start to degrade, i.e.,
super-vertices are created with predecessors ver-
tices from multiple communities?
Q3 How does parameter reduction factor impact the
construction of the multilevel hierarchy?
Q4 Is the matching algorithms’ capability of preserv-
ing community structures affected by the number
of communities in the input graph?
MobViewer allows inspecting how the match-
ing algorithms behave with distinct parameter set-
tings, and thereby comparing the outcome of differ-
ent choices and assessing the convenience of adopt-
ing alternative strategies. Indeed, the ability to ‘see’
a multilevel graph hierarchy and its properties is an
important facility for developers. Here we present
illustrative scenarios of how each question could be
investigated, taking as example a particular combina-
tion of algorithm, parameter settings and input graph.
Of course, these questions are just a sample of what
might be asked and they could be further investigated
considering other settings.
In order to study the method’s behavior on graphs
with diverse properties we synthesized weighted bi-
IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications
136

partite graphs with arbitrary community structures
and topological properties using a benchmarking
tool called BNOC (Benchmarking weighted Bipar-
tite Networks with Overlapping Community struc-
ture) (Valejo et al., 2019b). Table 1 summarizes the
synthetic networks considered. Graphs SG
1
and SG
2
are sparse with an equal number of communities in
both layers, whereas graph SG
3
is denser with 3 com-
munities in layer V
1
and 5 in layer V
2
. Graphs SG
4
and SG
5
have vertex sets of the same size, but SG
4
is
denser and the graphs differ in the number of commu-
nities in each layer.
Table 1: Synthetic graphs used in case studies.
Graph Vertices Edges V
1
V
2
Communities
SG
1
100 555 50 50 [4, 4]
SG
2
1.000 6.603 500 500 [7, 7]
SG
3
1.819 23.052 542 1.277 [3, 5]
SG
4
15.000 189.254 10.000 5.000 [15, 15]
SG
5
15.000 19.102 10.000 5.000 [40, 40]
In order to answer questions Q1 and Q2 we con-
sidered three configurations of the multilevel method
using GMb matching with distinct similarity func-
tions: “Common Neighbors” in configuration C.CN,
“Adamic Adar” in C.AA and “Preferential Attach-
ment” in C.PA. In the figures, glyph colors map the
corresponding vertex communities; glyphs represent-
ing super-vertices may have multiple colors reflecting
the community distribution of their predecessors.
Figure 3 shows the hierarchy of coarsened graphs
obtained executing MOb on SG
2
with the three con-
figurations. The hierarchy yielded by configuration
C.CN, Figure 3(a), includes a few super-vertices with
predecessors from mixed communities, outlined in
red. Configuration C.PA, Figure 3(c), did not pre-
serve the community structure, which was best pre-
served with the settings of configuration C.AA, Fig-
ure 3(b). Equivalent analyses were conducted on SG
1
and SG
3
(not shown), with similar conclusions.
Addressing related question Q2, Figures 4(a)
and 4(b) show two closer views of the multilevel hier-
archies of graph SG
1
yielded by configurations C.PA
and C.CN, respectively. In the multilevel graph in
Figure 4(a) one notices vertices from distinct commu-
nities merging into a single super-vertex at the second
hierarchical level, see the zoomed-in views. However,
in the multilevel hierarchy computed with configura-
tion C.CN, shown in Figure 4(b), super-vertices with
mixed communities only appear at the final levels.
Community structure was best preserved with Com-
mon Neighbors similarity, Figure 4(b).
In order to address question Q3 we executed the
multilevel method again with the GMb matching algo-
rithm and the “Common Neighbors” similarity, with
4 distinct settings of parameters reduction factor and
number of levels (applied to both layers), informed
in Figure 5, which shows the corresponding coarsest
graphs SG
1
. The number of super-vertices is strongly
affected by the choice of r f , i.e., as reduction factors
decrease fewer super-vertices are created and they are
more imbalanced in size; notice, for instance, the
super-vertices in Figures 5(a) and (d). Figure 6 shows
an equivalent analysis on graph SG
2
considering two
extreme configurations. Unlike the coarsest graph
in (a), where most super-vertices have predecessors
originating from a single community, the graph in (b)
has just 2 super-vertices (outlined in red) with pre-
decessors from mixed communities. Small reduc-
tion factors imply in few super-vertices, very likely
formed by predecessor vertices from multiple com-
munities, impairing community preservation.
Question Q4 was investigated on SG
5
, a sparse
graph with 40 communities in each layer, again us-
ing the “Common Neighbors” similarity. We applied
two different matchings, MLPb with ζ
1
= 3.900, ζ
2
=
1.200 and T = 1, and GMb with r f
1
= r f
2
= 0.5
and l
1
= l
2
= 3 (settings chosen to obtain a coarsest
level graph with layers of equivalent sizes to MLPb).
Figure 7 shows the coarsest level graphs, which for
the most part preserved the community structures in
merging vertices. This example illustrates that both
algorithms, despite adopting very distinct strategies,
can preserve the community structures even in graphs
with many communities. Other configurations were
investigated, yielding similar results (not shown).
6 CONCLUSIONS
We introduced MObViewer, a visualization tool that
supports interpreting the outcome of executing the
multilevel method on bipartite graphs. It relies on a
visual metaphor designed to depict multilevel bipar-
tite graphs hierarchies computed with the MOb frame-
work. Illustrative case studies confirmed its capabil-
ity of conveying the behavior of a matching algorithm
applied with distinct parameter settings. Thus, devel-
opers of multilevel solutions can quickly assess alter-
native configurations in order to interpret and under-
stand the impact of choices of matching algorithm,
similarity function, and reduction factors.
Scalability is a critical issue in MObViewer. In
spite of using state-of-the-art technologies the current
implementation does not scale to graphs with roughly
over 20.000 vertices or 30.000 edges. Performance
is also hindered on multilevel hierarchies with many
intermediate coarsening levels. On-demand network
processing could be considered to overcome scalabil-
ity limitations on interactive visual data analytics sce-
Visualization to Assist Interpretation of the Multilevel Paradigm in Bipartite Graphs
137

(a) C.CN{r f
0
= r f
1
= 0.5, l
0
= l
1
= l
3
, S =Common Neighbors}
(b) C.AA{r f
0
= r f
1
= 0.5, l
0
= l
1
= l
3
, S =Adamic Adar}
(c) C.PA{r f
0
= r f
1
= 0.5, l
0
= l
1
= l
3
, S =Pref. Attachment}
Figure 3: Multilevel hierarchies resulting from coarsening SG
2
with GMb matching considering 3 distinct similarity functions
S: community structures were best preserved using the Adamic Adar and Common Neighbors functions (a, b).
(a) C.PA{r f
0
= r f
1
= 0.5, l
0
= l
1
= 3, S =Pref. Attachment}
(b) C.PA{r f
0
= r f
1
= 0.5, l
0
= l
1
= 3, S =Common Neighbors}
Figure 4: User-selected super-vertex in graph SG
1
and the thread of edges to its predecessors in 2 multilevel hierarchies
obtained with 2 distinct choices of S. (a) shows super-vertices with predecessors from mixed communities at level 2 of the
hierarchy; in (b) such vertices only appear at the coarsest level (zoomed-in views of the areas outlined in blue are shown).
IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications
138
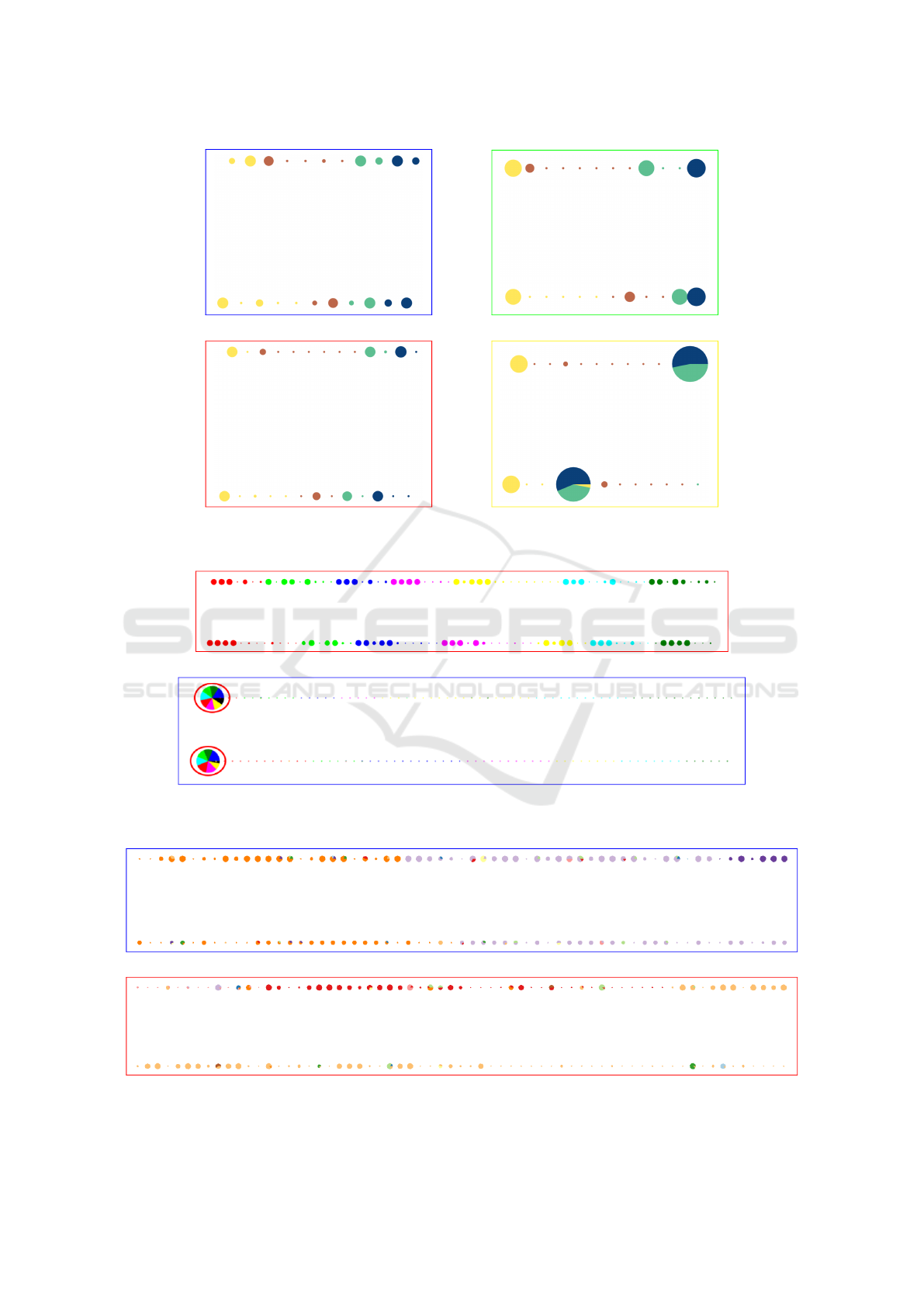
(a) C1{r f
1
= r f
2
= 0.4, l
1
= l
2
= 3} (b) C2{r f
1
= r f
2
= 0.3, l
1
= l
2
= 5}
(c) C3{r f
1
= r f
2
= 0.1, l
1
= l
2
= 16} (d) C4{r f
1
= r f
2
= 0.2, l
1
= l
2
= 7}
Figure 5: Coarsest graphs of the multilevel hierarchies computed for SG
1
with 4 distinct parameter settings in GMb.
(a) C.1{r f
1
= r f
2
= 0.4, l
1
= l
2
= 4} S =Common Neighbors.
(b) C.2{r f
1
= r f
2
= 0.1, l
1
= l
2
= 20} S =Common Neighbors.
Figure 6: Coarsest graphs of the multilevel hierarchy obtained from graph SG
2
with two settings of GMb.
(a) Coarsest graph from MLPb matching with ζ
1
= 3.900, ζ
2
= 1.200, T = 1.
(b) Coarsest graph from GMb matching with r f
1
= r f
2
= 0.5 and l
1
= l
2
= 3.
Figure 7: Coarsest level graphs after coarsening SG
5
with different matching algorithms and S =Common Neighbors.
Visualization to Assist Interpretation of the Multilevel Paradigm in Bipartite Graphs
139

narios. Rather than processing the full network in a
batch-like operation mode, the system could build and
process a sub-network reflecting a current user focus
on-the-fly, where these sub-networks satisfying a user
requirement would likely have manageable sizes. Ad-
ditional interaction facilities could be incorporated,
such as supporting interaction with selected levels of
the multilevel hierarchy. Further validation on addi-
tional scenarios is also necessary.
ACKNOWLEDGEMENTS
The authors acknowledge the financial support of
FAPESP grants 2016/25107-0 and 2017/05838-3 and
CNPq grants 134806/2016-6 and 301847/2017-7.
REFERENCES
Adamic, L. A. and Adar, E. (2003). Friends and neighbors
on the web. Social Networks, pages 211–230.
Bartel, G., Gutwenger, C., Klein, K., and Mutzel, P. (2011).
An experimental evaluation of multilevel layout meth-
ods. In Graph Drawing, pages 80–91, Berlin, Heidel-
berg. Springer.
Bondy, J. A., Murty, U. S. R., et al. (1976). Graph theory
with applications, volume 290. Elsevier Science Ltd.,
Oxford, UK.
Bostock, M., Ogievetsky, V., and Heer, J. (2011). D3:
Data-driven documents. IEEE Trans. Visualization
and Computer Graphics, 17(12):2301–2309.
Gajer, P. and Kobourov, S. G. (2001). Grip: Graph draw-
ing with intelligent placement. In Marks, J., editor,
Graph Drawing, pages 222–228, Berlin, Heidelberg.
Springer Berlin Heidelberg.
Ghoniem, M., Fekete, J. D., and Castagliola, P. (2004). A
comparison of the readability of graphs using node-
link and matrix-based representations. IEEE Symp.
Information Visualization, pages 17–24.
Gupta, A., Karypis, G., and Kumar, V. (1997). Highly scal-
able parallel algorithms for sparse matrix factoriza-
tion. IEEE Trans. Parallel and Distributed Systems,
8(5):502–520.
Hachul, S. and J
¨
unger, M. (2004). Drawing large graphs
with a potential-field-based multilevel algorithm. In
Proc. 12th Int. Conf. Graph Drawing, GD’04, pages
285–295, Berlin, Heidelberg. Springer.
Harel, D. and Koren, Y. (2000). A fast multi-scale method
for drawing large graphs. Proc. Working Conf. Ad-
vanced Visual Interfaces, pages 282–285.
Heinrich, J., Seifert, R., Burch, M., and Weiskopf, D.
(2011). Bicluster viewer: A visualization tool for
analyzing gene expression data. In Advances in Vi-
sual Computing, pages 641–652, Berlin, Heidelberg.
Springer Berlin Heidelberg.
Jeong, H., Tombor, B., Albert, R., Oltvai, Z. N., and
Barab
´
asi, A.-L. (2000). The large-scale organization
of metabolic networks. In Nature, volume 407, page
651. Nature Publishing Group.
Lhuillier, A., Hurter, C., and Telea, A. (2017). State of the
art in edge and trail bundling techniques. Computer
Graphics Forum, pages 619–645.
Newman, M. E. (2001). The structure of scientific collabo-
ration networks. Proc. National Academy of Sciences,
pages 404–409.
Padmavathi, S. and George, A. (2014). Multilevel hybrid
graph partitioning algorithm. In IEEE Int. Advance
Computing Conf., pages 85–89.
Pezzotti, N., Fekete, J.-D., H
¨
ollt, T., Lelieveldt, B., Eise-
mann, E., and Vilanova, A. (2018). Multiscale vi-
sualization and exploration of large bipartite graphs.
Computer Graphics Forum, pages 12–25.
Rossi, R. G., de Andrade Lopes, A., and Rezende, S. O.
(2016). Optimization and label propagation in bipar-
tite heterogeneous networks to improve transductive
classification of texts. Information Processing & Man-
agement, pages 217 – 257.
Steinbock, D., Groller, E., and Waldner, M. (2018). Casual
visual exploration of large bipartite graphs using hier-
archical aggregation and filtering. Int. Symp. Big Data
Visual and Immersive Analytics, pages 1–10.
Valejo, A., Faleiros, T., Oliveira, M. C. F., and Lopes, A. A.
(2019a). A coarsening method for bipartite networks
via weight-constrained label propagation. Knowledge-
Based Systems (accepted).
Valejo, A., G
´
oes, F., Romanetto, L., Oliveira, M. C. F., and
Lopes, A. A. (2019b). A benchmarking tool for the
generation of bipartite network models with overlap-
ping communities. Knowledge and Information Sys-
tems.
Valejo, A., Oliveira, M. C. F., R. Filho, G. P., and Lopes,
A. A. (2018). Multilevel approach for combinatorial
optimization in bipartite networks. Knowledge-Based
Systems, pages 45–61.
Von Landesberger, T., Kuijper, A., Schreck, T., Kohlham-
mer, J., van Wijk, J. J., Fekete, J.-D., and Fellner,
D. W. (2011). Visual analysis of large graphs: state-
of-the-art and future research challenges. Computer
Graphics Forum, pages 1719–1749.
Walshaw, C. (2004). Multilevel refinement for combina-
torial optimisation problems. Annals of Operations
Research, pages 325–372.
Watts, D. J. (2004). Small worlds: the dynamics of networks
between order and randomness, volume 9. Princeton
University Press.
Wong, P. C., Mackey, P., Cook, K. A., Rohrer, R. M., Foote,
H., and Whiting, M. A. (2009). A multi-level middle-
out cross-zooming approach for large graph analytics.
IEEE Symp. Visual Analytics Science and Technology.,
pages 147–154.
Xu, P., Cao, N., Qu, H., and Stasko, J. (2016). Interactive
visual co-cluster analysis of bipartite graphs. IEEE
Pacific Visualization Symp., pages 32–39.
Zhao, J., Sun, M., Chen, F., and Chiu, P. (2018). Bidots: Vi-
sual exploration of weighted biclusters. IEEE Trans.
Visualization and Computer Graphics, pages 195–
204.
IVAPP 2020 - 11th International Conference on Information Visualization Theory and Applications
140
