Guessing Games Experiments in Ukraine: Learning towards

Equilibrium

Oleksii P. Ignatenko

1 a

Institute of Software Systems NAS Ukraine, 40 Academician Glushkov Ave., Kyiv, 03187, Ukraine

Keywords:

Behavioral Game Theory, Guessing Game, K-Beauty Contest, Active Learning, R.

Abstract:

The paper deals with experimental game theory and data analysis. The research question, formulated in this

work, is how players learn in complex strategic situations which they never faced before. We examine data

from different games, played during lectures about game theory and present ﬁndings about players progress

in learning while competing with other players. We proposed four “pick a number” games, all with similar-

looking rules but very different properties. These games were introduced (in the body of scientiﬁc popular

lectures) to very different groups of listeners. In this paper we present data gathered during lectures and

develop tool for exploratory analysis using R language. Finally, we discuss the ﬁndings propose hypothesis to

investigate and formulate open questions for future research.

1 INTRODUCTION

Game theory is a ﬁeld of science which investigates

decision-making under uncertainty and interdepen-

dence, that is, when the actions of some players affect

the payoffs of others. Such situations arise around

us every day and we, consciously or unconsciously,

take part in them and try to succeed. The struggle to

achieve a better result (in some broad sense) is called

rationality. Every rational player must take into ac-

count the rules of the game, the interests and capabil-

ities of other participants in other words think strate-

gically. Game theory provides a tool for analyzing

such situations, which allows you to better understand

the causes of conﬂicts, learn to make decisions under

uncertainty, establish mutually beneﬁcial cooperation

and much more.

A key element of strategic thinking is to include

into consideration what other agents do. Agent here is

a person, who can make decisions and his/her actions

have inﬂuence on the outcome. Naturally, person can-

not predict with 100% what will others do, so it is im-

portant to include into model beliefs about other per-

son thinking and update them during the game. Also,

if we can’t know what other player think, we can un-

derstand what is his/her best course of action. This is

the main research topic of game theory.

All this makes decision making very interesting

https://orcid.org/0000-0001-8692-2062

problem to investigate. In this work we will ap-

ply game theory to analyze such problems. Game

theory provides mathematical base for understanding

strategic interaction of rational players. There is im-

portant note about rationality, we should make. As

Robert Aumann formulate in his famous paper (Au-

mann, 1985), game theory operates with “homo ra-

tional”, ideal decision maker, who is able to deﬁne

his/her utility as a function and capable of computing

best strategy to maximize it. This is the main setup of

game theory and one of major lines of criticism. In re-

ality, of course, people are not purely rational in game

theory sense. They often do not want to concentrate

on a given situation to search for best decision or sim-

ply do not have enough time or capabilities for this.

Sometimes they just copycat behavior of others or use

some cultural codes to make strange decisions. Also

(as we see from the experiments) it seems that some-

times homo sapiens make decisions with reasons, one

can (with some liberty in formulation) label as “try

and see what happens”, “make random move and save

thinking energy” and even “make stupid move to spoil

game for others”.

This is rich area of research, where theoretical

constructions of game theory seems to fail to work

and experimental data shows unusual patterns. How-

ever, these patterns are persistent and usually do

not depend on age, education, country and other

things. During last 25 years behavioral game the-

ory in numerous studies examines bounded rational-

156

Ignatenko, O.

Guessing Games Experiments in Ukraine. Learning towards Equilibrium.

DOI: 10.5220/0010929600003364

In Proceedings of the 1st Symposium on Advances in Educational Technology (AET 2020) - Volume 2, pages 156-168

ISBN: 978-989-758-558-6

ity (best close concept to rationality of game theory)

and heuristics people use to reason in strategic situa-

tions. For example we can note surveys of Crawford

et al.; Mauersberger and Nagel (Crawford et al., 2013;

Mauersberger and Nagel, 2018). Also there is com-

prehensive description of the ﬁeld of behavioral game

theory by Camerer (Camerer, 2011).

Also we can note work of Gill and Prowse (Gill

and Prowse, 2016), where participants were tested on

cognitive abilities and character skills before the ex-

periments. Then authors perform statistical analysis

to understand the impact of such characteristics on the

quality of making strategic decisions (using p-beauty

contest game with multiple rounds). In more recent

work of Fe et al. (Fe et al., 2019) even more elabo-

rate experiments are presented. It is interesting that in

the mentioned paper experiments are very strict and

rigorous (as close to laboratory purity as possible) in

contrast to games, played in our research. But in the

end of the day the results are not differ very much.

The guessing games are notable part of research

because of their simplicity for players and easy anal-

ysis of rules from game theoretic prospective. In

this paper we present results of games played during

2018–2020 years in series of scientiﬁc popular lec-

tures. The audience of these lectures was quite hetero-

geneous, but we can distinguish three main groups:

• kids (strong mathematical schools, ordinary

schools, alternative education schools);

• students (bachelor and master levels);

• mixed adults with almost any background;

• businessmen;

• participants of Data Science School.

We propose framework of four different games,

each presenting one idea or concept of game theory.

These games were introduced to people with no prior

knowledge (at least in vast majority) about the the-

ory. From the other hand, games have simple formu-

lation and clear winning rules, which makes them in-

tuitively understandable even for kids. This makes

these games perfect choice to test ability of strate-

gic thinking and investigate process of understanding

of complex concepts during the play, with immediate

application to the game. This dual learning, as we

can name it, shows how players try-and-learn in real

conditions and react to challenges of interaction with

other strategic players.

1.1 Game Theory Deﬁnitions

We will consider games in strategic or normal form in

non-cooperative setup. A non-cooperativeness here

does not imply that the players do not cooperate, but

it means that any cooperation must be self-enforcing

without any coordination among the players. Strict

deﬁnition is as follows.

A non-cooperative game in strategic (or normal)

form is a triplet G = {N , {S

}

i=∈N

, {u

}

i∈N

where:

• N is a ﬁnite set of players, N = {1, . . . , N};

• S

is the set of admissible strategies for player i;

• u

: S −→ R is the utility (payoff) function for

player i, with S = {S

×·· ·×S

} (Cartesian prod-

uct of the strategy sets).

A game is said to be static if the players take their

actions only once, independently of each other. In

some sense, a static game is a game without any no-

tion of time, where no player has any knowledge of

the decisions taken by the other players. Even though,

in practice, the players may have made their strate-

gic choices at different points in time, a game would

still be considered static if no player has any informa-

tion on the decisions of others. In contrast, a dynamic

game is one where the players have some (full or im-

perfect) information about each others’ choices and

can act more than once.

Summarizing, these are games where time has a

central role in the decision-making. When dealing

with dynamic games, the choices of each player are

generally dependent on some available information.

There is a difference between the notion of an action

and a strategy. To avoid confusions, we will deﬁne a

strategy as a mapping from the information available

to a player to the action set of this player.

Based on the assumption that all players are ra-

tional, the players try to maximize their payoffs

when responding to other players’ strategies. Gen-

erally speaking, ﬁnal result is determined by non-

cooperative maximization of integrated utility. In

this regard, the most accepted solution concept for a

non-cooperative game is that of a Nash equilibrium,

introduced by John F. Nash. Loosely speaking, a

Nash equilibrium is a state of a non-cooperative game

where no player can improve its utility by changing

its strategy, if the other players maintain their cur-

rent strategies. Of course players use also informa-

tion and beliefs about other players, so we can say,

that (in Nash equilibrium ) beliefs and incentives are

important to understand why players choose strategies

in real situations. Formally, when dealing with pure

strategies, i.e., deterministic choices by the players,

the Nash equilibrium is deﬁned as follows:

A pure-strategy Nash equilibrium (NE) of a non-

cooperative game G is a strategy proﬁle s

∈ S such

that for all i ∈ N we have the following inequality:

Guessing Games Experiments in Ukraine. Learning towards Equilibrium

157

, s

−i

) ≥ u

, s

−i

)

for all s

∈ S

Here s

−i

= {s

| j ∈ N , j 6= i} denotes the vector

of strategies of all players except i. In other words,

a strategy proﬁle is a pure-strategy Nash equilibrium

if no player has an incentive to unilaterally deviate to

another strategy, given that other players’ strategies

remain ﬁxed.

1.2 Guessing Games

In early 90xx Rosemary Nagel starts series of experi-

ments (Mitzkewitz and Nagel (Mitzkewitz and Nagel,

1993)) of guessing games, summarized in (Nagel,

1995). She wasn’t the ﬁrst one to invent the games,

it was used in lectures by different game theory re-

searchers (for example Moulin (Moulin, 1986)). But

her experiments were ﬁrst experimental try to inves-

tigate the hidden patterns in the guessing game. Ho

et al. (Ho et al., 1998) gave the name “p-beauty con-

test” inspired by Keynes (Keynes, 1936) comparison

of stock market instruments and newspaper beauty

contests. This is interesting quote, so lets give it here:

“To change the metaphor slightly, professional invest-

ment may be likened to those newspaper competi-

tions in which the competitors have to pick out the six

prettiest faces from a hundred photographs, the prize

being awarded to the competitor whose choice most

nearly corresponds to the average preferences of the

competitors as a whole; It is not a case of choosing

those which, to the best of one’s judgment, are really

the prettiest, nor even those which average opinion

genuinely thinks the prettiest. We have reached the

third degree where we devote our intelligence to an-

ticipating what average opinion expects the average

opinion to be. And there are some, I believe, who

practice the fourth, ﬁfth and higher degrees.” (Keynes,

1936, chapter 12.V).

The beauty contest game has become important

tool to measure “depth of reasoning” of group of peo-

ple using simple abstract rules. Now there are variety

of rules and experiments presented in papers, so lets

only mention some of them.

2 EXPERIMENTS SETUP

The setup is closer to reality then to laboratory and

this is the point of this research. All games were

played under following conditions:

1. Game were played during the lecture about the

game theory. Participants were asked not to com-

ment or discuss their choice until they submit it.

However, this rule wasn’t enforced, so usually

they have this possibility if wanted;

2. Participants were not rewarded for win. The win-

ner was announced, but no more.

3. During some early games we used pieces of pa-

per and we got some percentage of joking or trash

submission, usually very small. Later we have

switched to google forms, which is better tool

to control submission (for example only natural

numbers allowed).

4. Google forms gives possibility to make multiple

submission (with different names), since we didnt

have time for veriﬁcation, but total number of sub-

mission allows to control that.

The aim of this setup was to free participants to

explore the rules and give them ﬂexibility to make

decision in uncertain environment. We think it is

closer to real life learning without immediate rewards

then laboratory experiments. Naturally, this setup has

strong and weak sides. Lets summarize both.

The strong sides are:

1. This setup allow to measure how people make de-

cisions in “almost real” circumstances and under-

stand the (possible) difference with laboratory ex-

periments;

2. These games are part of integrated approach to

active learning, when games are mixed with ex-

planations about concepts of game theory (ratio-

nality, expected payoff, Nash equilibrium etc),

and they allow participants to combine experience

with theory;

3. Freedom and responsibility. The rules doesn’t

regulate manipulations with conditions. So this

setup allows (indirectly) to measure preferences

of players: do they prefer cheat with rules, just

choose random decision without thinking or put

efforts in solving the task.

Weak sides are:

1. Some percentage of players make “garbage” de-

cisions. For example choose obviously worse

choice just to spoil efforts for others;

2. Kids has (and often use) possibility to talk out de-

cision with the neighbors;

3. Sometimes participants (especially kids) lost con-

centration and didn’t think about the game but

made random choice or just didn’t make decisions

at all;

4. Even for simplest rules, sometimes participants

failed to understand the game ﬁrst time. We sup-

pose it is due to conditions of lecture with (usu-

ally) 30-40 persons around.

AET 2020 - Symposium on Advances in Educational Technology

158

2.1 Rules

All games have the same preamble: Participants are

asked to guess integer number in range 1 – 100, mar-

gins included. Note, that many setups, investigated

in references, use numbers starting with 0. But the

difference is small.

To provide quick choice calculation we have used

QR code with link to google.form, where participants

input their number. All answers were anonymous

(players indicate nicknames to announce the winners,

but then all records were anonymized). The winning

condition is speciﬁc for every game.

1) p-beauty contest. The winning number is the clos-

est to 2/3 of average;

2) Two equilibrium game. The winning number is

the furthest from the average;

3) Coordination with assurance. The winning num-

ber is the number, chosen by plurality. In case of

tie lower number wins;

4) No equlibrium game. The winning number is the

smallest unique.

All these games are well-known in game the-

ory. Lets brieﬂy summarize them. First game is

dominance-solvable game. Strategy “to name num-

bers bigger then 66” is (weakly) dominated, since it

is worse then any other for almost all situations and

equal in the rest. So rational player will not play it and

everybody knows that. Then second step is to elimi-

nate all numbers higher then 44 and so on. At the end

rational players should play 1 and all win. In our setup

we go further then just give players learn from obser-

vation. After ﬁrst round we explain in detail what is

Nash equilibrium and how it affect the strategies. Af-

ter this explanation all participants actually knew that

choosing 1 is the equilibrium option, when everyone

wins. We supposed, that this should help to improve

strategies in next round, but it is not.

Second game is about mixed strategies. Easy to

show that if you want to choose number smaller then

50 – best way is to choose 1, since all other choices

are dominated. And if you want to choose number

bigger then 50 – best idea is to choose 100. Also it is

meaningful to choose 50 – it almost never wins. So if

many players will choose 1 – you should choose 100

and visa versa. In this game the best way to play is

literally drop a coin and choose 1 or 100.

Third game has many equilibria, basically every

number can be winning. But to coordinate players

must ﬁnd some focal points (Schelling (Schelling,

1960)). Natural focal point (but not only one!) is the

smallest number since smaller number wins in case

of tie. This slim formulation allow nevertheless make

successful coordination in almost all experiments.

Finally last game is in a dark waters. As far as

we know there is no equilibrium or rational strategy

to play it. So sometimes very strange numbers are

winners here.

3 RESULTS AND DATA ANALYSIS

In this section we present summary of data, gathered

during the games.

3.1 First Game

Summary of results of First game is given in the ta-

ble 1.

Almost all winning numbers are fall (roughly) in

the experimental margins, obtained in Nagel (Nagel,

1995) work. With winning number no bigger then 36

and not smaller then 18 in ﬁrst round. Two excep-

tions in our experiments were Facebook on-line test

(15.32), when players can read information about the

game in, for example, Wikipedia. And other is alter-

native humanitarian school (40.1), where participants

seems didn’t got the rules from the ﬁrst time.

Using R statistical visualization tool we can an-

alyze in details how players from different types

change their decisions between ﬁrst and second round

(ﬁgure 1).

3.1.1 Metrics and Analysis

Interesting metric is the percent of “irrational

choices” – choices that can’t win in (almost) any case.

Lets explain, imagine that all players will choose 100.

It is impossible from practice but not forbidden. In

this case everybody wins, but if only one player will

deviate to smaller number – he/her will win and oth-

ers will lose. So playing numbers bigger then 66 is not

rational, unless you don’t want to win. And here we

come to important point, in all previous experiments

this metric drops in second round and usually is very

low (like less than 5%) (Ho et al., 1998). But in our

case there are experiments where this metric become

higher or changes very slightly. And initially values

are much higher then expected. So here we should in-

clude factor of special behavior, we can call it “let’s

show this lecturer how we can cheat his test!”. What

is more interesting – this behavior more clear in case

of adult then kids.

It is also interesting to see distribution of choices

for different types of groups. We can summarize

choices on the histograms (ﬁgure 2). Using models of

Guessing Games Experiments in Ukraine. Learning towards Equilibrium

159

Table 1: Summary of ﬁrst game for types of players.

Type Round Average Winning Median Count Irrationality

Adults 1 40.6 27 40 19 10.5

Adults (facebook online) 1 22.98 15.32 17 102 4.9

Alternative humanitarian 1 60.2 40.1 63 24 45.8

Alternative humanitarian 2 9.67 6.44 4 24 4.17

Alternative humanitarian 3 3.08 2.05 2 13 0

Alternative mathematical 1 41.9 27.9 42 35 17.1

Alternative mathematical 2 20.7 13.8 18 33 0

Business 1 44.4 29.6 41 65 27.7

Business 2 14.1 9.43 12 99 1.01

DS conference attendees 1 35.6 23.7 32.5 142 12.0

DS conference attendees 2 15.9 10.6 9 148 6.08

Math lyceum 1 37.7 25.1 33 148 14.2

Math lyceum 2 19.2 12.8 13 106 4.72

MS students 1 39.0 26.0 30 35 20

MS students 2 8.6 5.75 8.5 8 0

Ordinary school 1 48.7 32.5 46.5 26 23.1

Ordinary school 2 19.8 13.2 22 23 0

Tech School 1 43.4 28.9 45 51 23.5

Tech School 2 46.5 31.0 29 62 33.9

Figure 1: Graphical representation of learning between rounds.

AET 2020 - Symposium on Advances in Educational Technology

160

strategic thinking we will adopt the theory of k-levels.

According to this idea 0-level reasoning means, that

players make random choices (drawn from uniform

distribution), and k-level reasoning means that these

players use best-response for reasoning of previous

level. So 1-level reasoning is to play 33, which is best

response to belief that average will be 50, 2-level is

best response to belief that players will play 33 and

so on.

Highlighting ﬁrst 4 levels with dotted lines is a

good idea, it is showing hidden patterns in strategy

choosing of players.

As we can see from the diagram 2, some spikes

in choices are predicted very good, but it depends

on the background of players. The best prediction

is for attendees of Data Science conference, which

presumes high level of cognitive skill and computer

science background.

Next two ﬁgures show the learning process from

different angles. On ﬁgure 3 we can see points, de-

ﬁned by number of players with 0-level and “irra-

tional” (choices with big numbers) versus “too smart”

choices – choices from [1,5], which is not good for

ﬁrst round. The players, who choose small rounds

probably knew about this game or they thought that

everyone are as smart as they are. It is also possible,

that some part of them were 0-level players, who just

pick small number randomly. In any case, we can see

two distinct clusters: ﬁrst round (round dots) and sec-

ond round (triangles). The explanation about equilib-

rium concept created this transition in choices, when

choices from [50,100] decreasing, and choices from

[1,5] increasing.

Interesting hypotheses, that need to be tested in

details, can be formulated: Higher number of

choices from [50,100] in ﬁrst round leads to higher

number of choices from [1,5] in second round and

vice verse.

Another metric (G

uth et al., 2002) is how much

winning choice in second round is smaller then in

ﬁrst. Due to concept of multi-level reasoning, every

player in this game trying to its best to win but cant

do all steps to winning idea. So there are players,

who just have 0-level reasoning, they choose random

numbers. First-level players choose 33, which is best

response for players of 0-level and so on. Based on

result of ﬁrst round and, in fact, explanation about the

Nash equilibrium, players must know that it is better

to choose much lower numbers. But graph shows that

decrease is quite moderate. Only students shows good

performance in this matter. And tech school shows in-

crease in winning number in second round! (ﬁgure 4)

3.1.2 Levels of Reasoning Analysis

Another point about the process of learning in this

game is how players decision are distributed over the

space of strategies. We claim that there is distinct dif-

ference in changes between ﬁrst and second round for

different groups. To perform this analysis we apply

the idea of k-level thinking.

To ﬁnd differences we need to simplify this ap-

proach. First, we deﬁne b-level players players who

choose numbers from the range [50,100]. It is begin-

ner players, who do not understand rules (play ran-

domly) or do not expect to win or want to loose inten-

tionally (for reasons discussed above). The substanti-

ation for such range is that numbers higher then 50 did

not win in any game. Second level we call m-level, it

is for range [18,50]. It is for players with middle lev-

els of reasoning, usually ﬁrst round winning number

is in this range (and in part of second rounds also).

Third level is h-level, it is for range [5, 18]. It

is for high level reasoning and ﬁnally inf-level ([1,5]

range) is for “almost common knowledge” level of

thinking.

Calculating the number of levels for each game

we can estimate change (in percentage of number of

players) in adopting different strategy levels.

There are some limitation of this approach:

• number of players changed with rounds, since not

everyone participated (it was option, not obliga-

tion);

• limits of ranges are not deﬁned by model or data.

It can be future direction of research – how to de-

ﬁne levels in best way.

Results are presented in table 2.

What conclusions we can draw from this data?

There are no clear difference in changing, but at least

we can summarise few points:

• Usually after ﬁrst round and equilibrium concept

explanation there is decrease in b-level and m-

level;

• Symmetrically, there is increase in two other lev-

els, but sometimes it is more distributed, some-

times it is (almost) all for inf-level;

• Last situation is more likely to happen in schools,

were kids are less critical to new knowledge;

• Usually second round winning choice in the realm

of h-level, so groups with biggest increase in this

parameter are the ones with better understanding.

3.1.3 Size and Winning Choice

This game is indeed rich for investigation, let us for-

mulate last (in this paper) ﬁnding about this game.

Guessing Games Experiments in Ukraine. Learning towards Equilibrium

161

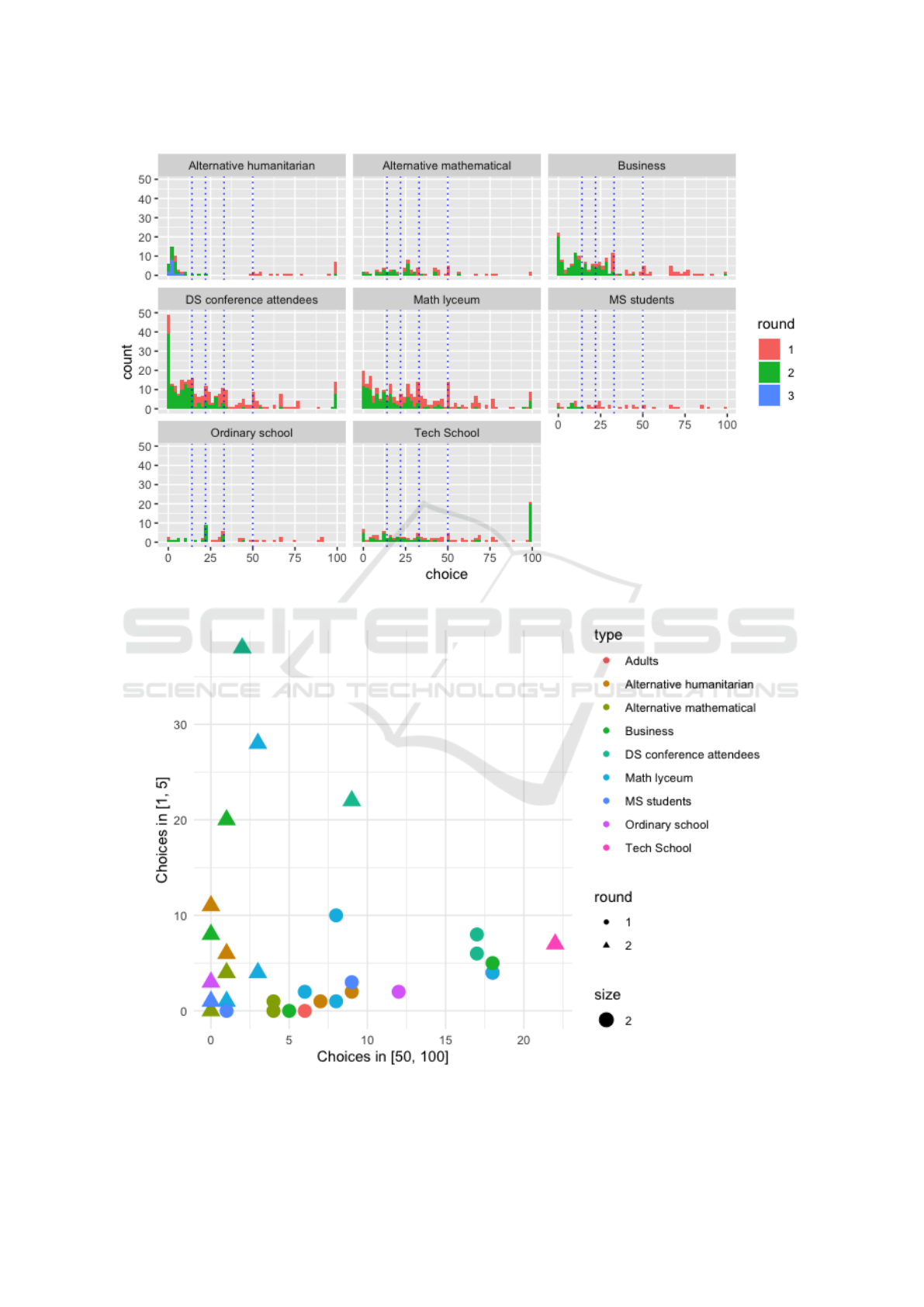
Figure 2: Histogram of choices for each round.

Figure 3: Comparing choices for different levels.

AET 2020 - Symposium on Advances in Educational Technology

162

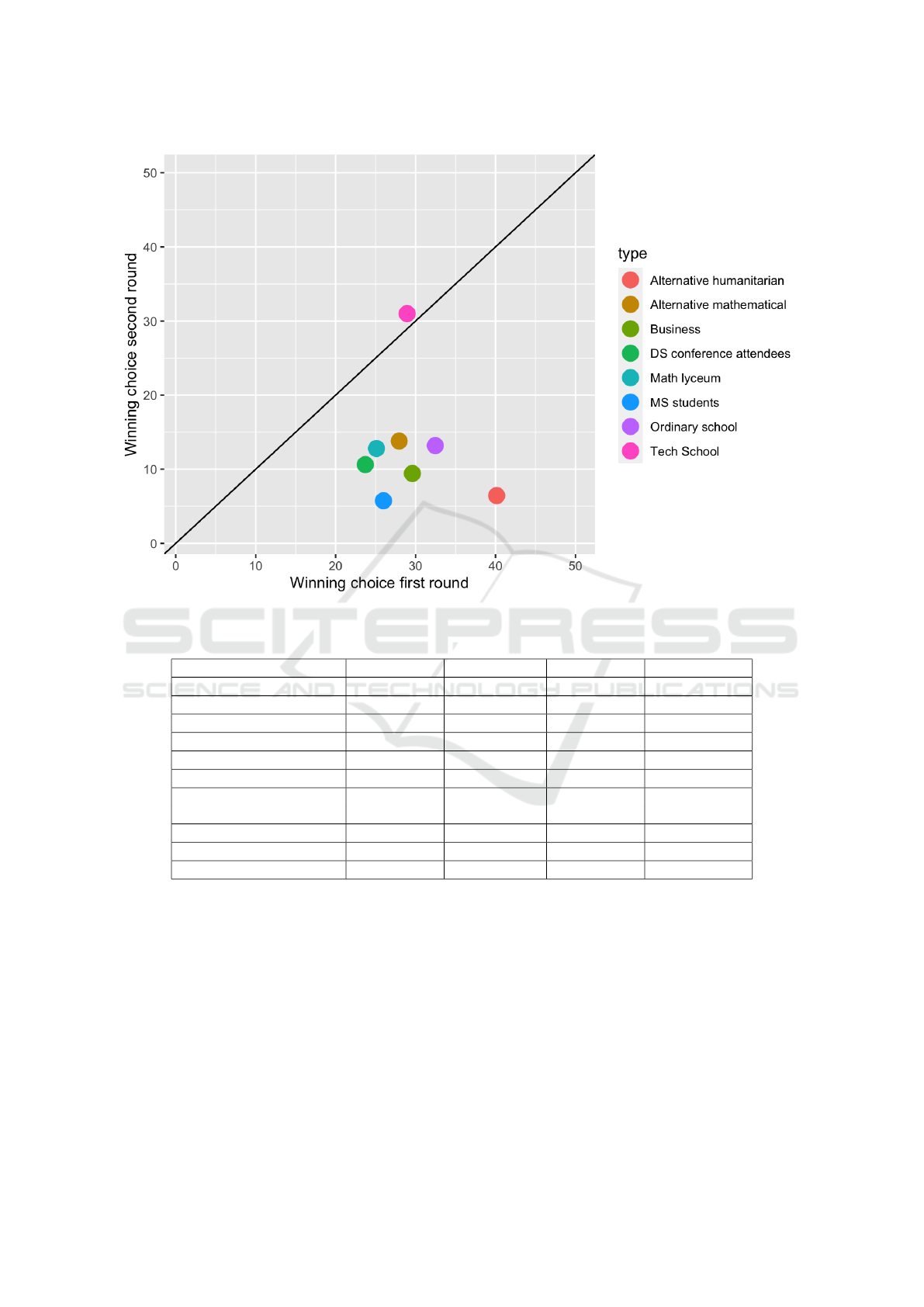
Figure 4: Change in winning number for rounds.

Table 2: Summary of change in strategy levels.

Type b-difference m-difference h-difference inf-difference

Alternative humanitarian -72 -8 0 72

Alternative mathematical -24 -6 30 -6

Alternative humanitarian -52 0 17 43

Math lyceum -9 -36 24 34

Math lyceum -10 -24 28 7

Ordinary school -49 12 20 4

DS conference attendees -14 -32 14 27

MS students -12 -50 50 12

Alternative mathematical -17 -34 23 23

DS conference attendees -17 -30 23 35

Business -32 -17 21 28

Can we in some way establish connection between

number of players and winning number (actually with

strategies, players choose during the game)? To clar-

ify our idea see at 5. It is scatter plot of two-

dimensional variable, x-axis is for number of partici-

pants in the game and y-axis is for winning choice per

round. Different color are for different types of group,

where games was played.

Summarise ﬁndings about this plot:

• First and second rounds form two separate clus-

ters. This is expected and inform us that play-

ers learned about the equilibrium concept between

rounds and apply it to practice;

• There are two visible groups inside each round –

undergraduates (schoolchildren, masters) and

adults. Inside each group there is mild tendency

that bigger group has bigger winning number.

This is yet too bold to formulate connection be-

tween size of the group and winning number, but

probably the reason is that when size of the group is

bigger, number of “irrational” players increases. It

can be due to some stable percentage of such persons

in any group or other reasons, but it is interesting con-

nection to investigate.

Guessing Games Experiments in Ukraine. Learning towards Equilibrium

163

Figure 5: Change in winning number for rounds.

3.2 Second Game

In second game the key point is to understand that

almost all strategies are dominated. The results are

presented on ﬁgure 6 and we can see that average can

be bigger or smaller then 50, and accordingly win-

ning choice will be 1 or 100. It is worth to note, that

popular nature of these experiments and freedom to

participate make the data gathering not easy. For ex-

ample many participants just didn’t take any decision

in second game. Results are summarised in the ta-

ble 3.

We reﬁne players decisions to see how many play-

ers made choices with rationalizability (Bernheim

(Bernheim, 1984)), which are best response for some

strategy proﬁle of other players. In this game there are

only two best responses possible (in pure strategies),

literally 1 and 100.

This is remarkable result, players without prior

communications choose to almost perfect mixed equi-

librium: almost the same percentage choose 1 and

100. This is even more striking taking into account

no prior knowledge about mixed strategies and mixed

equilibrium, kids play it intuitively and without any

communication. To illustrate the mixed Nash learn-

ing by groups, put dependency of percent of 1 choices

and 100 choices on plot (ﬁgure 7).

3.3 Third Game

Third game is simpler then ﬁrst two, it is coordina-

tion game where players should coordinate without

a word. And, as predicted by Schelling (Schelling,

1980), they usually do. Date presented on ﬁgure 8

shows that 1 is natural coordination point, with one

exception – Tech school (id = 1 here) decided that it

would be funny to choose number 69 (it was made

without single word). Probably, it is the age (11th

grade) here to blame. Also we can note attempt to

coordinate around 7, 50 and 100.

Interesting and paradoxical result, which is ex-

pected from general theory, that with fewer options

coordination in fact is more difﬁcult. Lets consider

(ﬁgure 9), where players decision was to choose inte-

ger from [1,10], only 10 choices. Comparing to pre-

vious game with 100 possible choices, coordination

was very tricky – two numbers got almost the same

result.

AET 2020 - Symposium on Advances in Educational Technology

164

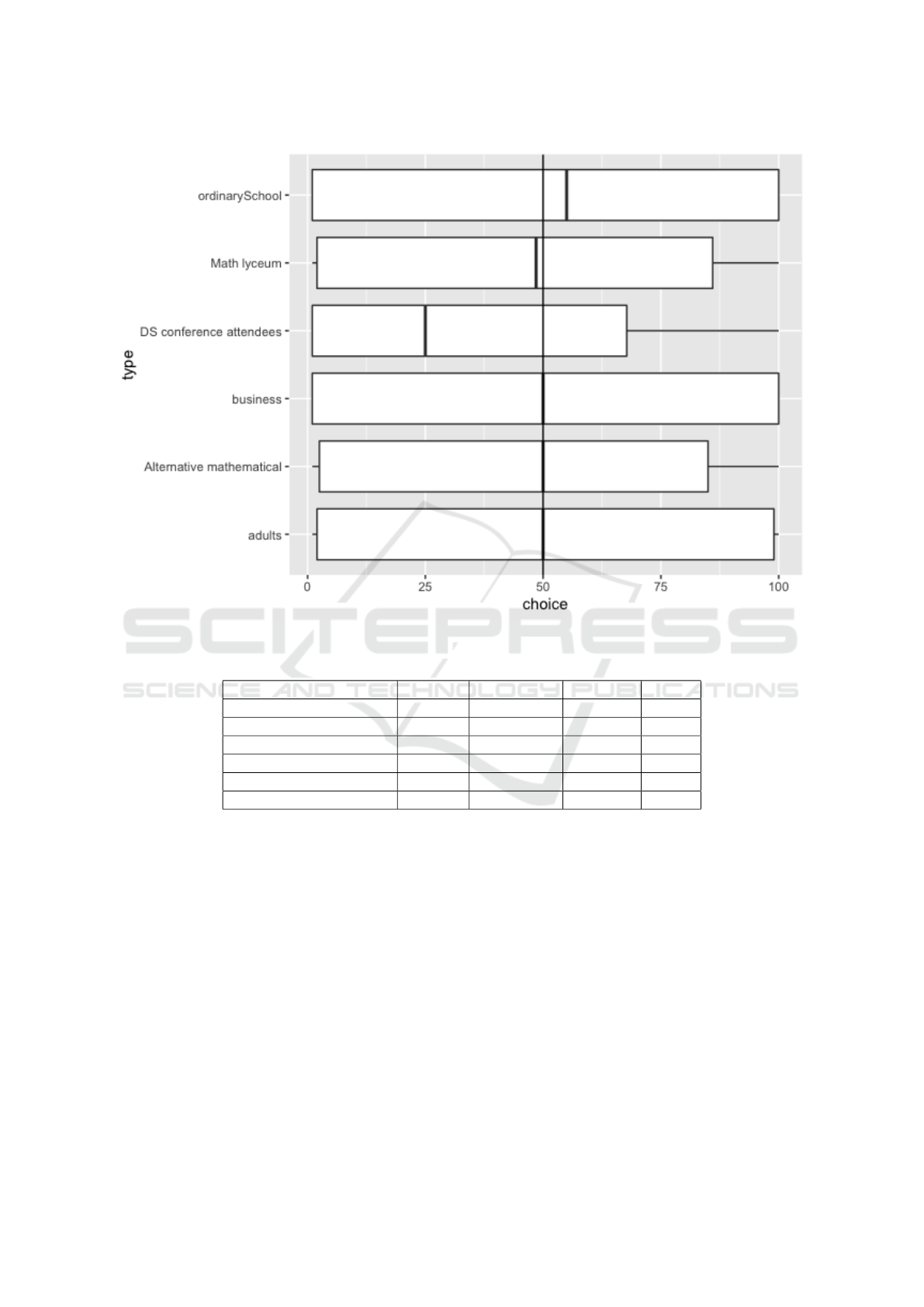
Figure 6: Statistics for choices.

Table 3: Second game. Rationalizable choices summary.

Type Average Choose 100 Choose 1 Count

Adults 46.5 24.3% 24.34% 115

Alternative mathematical 43.8 25.9% 27.9% 27

Business 50.6 29.3% 29.3% 99

DS conference attendees 37.4 15.8% 36.8% 114

Math lyceum 48.5 22.7% 24.7% 154

Ordinary school 51.2 30.4% 30.4% 23

3.4 Fourth Game

Here we just note, that the winning numbers were:

12, 2, 4, 20. Since no equilibrium here was theoreti-

cally found, we can only gather data at this stage and

formulate hypothesis to found one.

All experimental data and R ﬁle for graphs can be

accessed in open repository (Ignatenko, 2021).

4 CONCLUSIONS

In this paper we have presented approach to make ex-

perimental game theory work for learning in educa-

tional process and be a research tool at the same time.

Our result show classical pattern in decision making –

actually every group behave in almost the same way

dealing with unknown game. Some tried to deviate

for unusual actions (like choosing 100 or choosing

69), and this is interesting point of difference with

more “laboratory” setup of existing research. The

main ﬁndings of the paper are following:

1. To learn the rules you need to break them. Partic-

ipants have chosen obviously not winning moves

(> 66) partly because of new situation and trou-

ble with understanding the rules. But high percent

of such choices was present in second round also,

when players knew exactly what is going on. This

effect was especially notable in the cases of high

school and adults and almost zero in case of spe-

cial math schools and kids below 9th grade. We

can formulate hypothesis that high school is the

Guessing Games Experiments in Ukraine. Learning towards Equilibrium

165

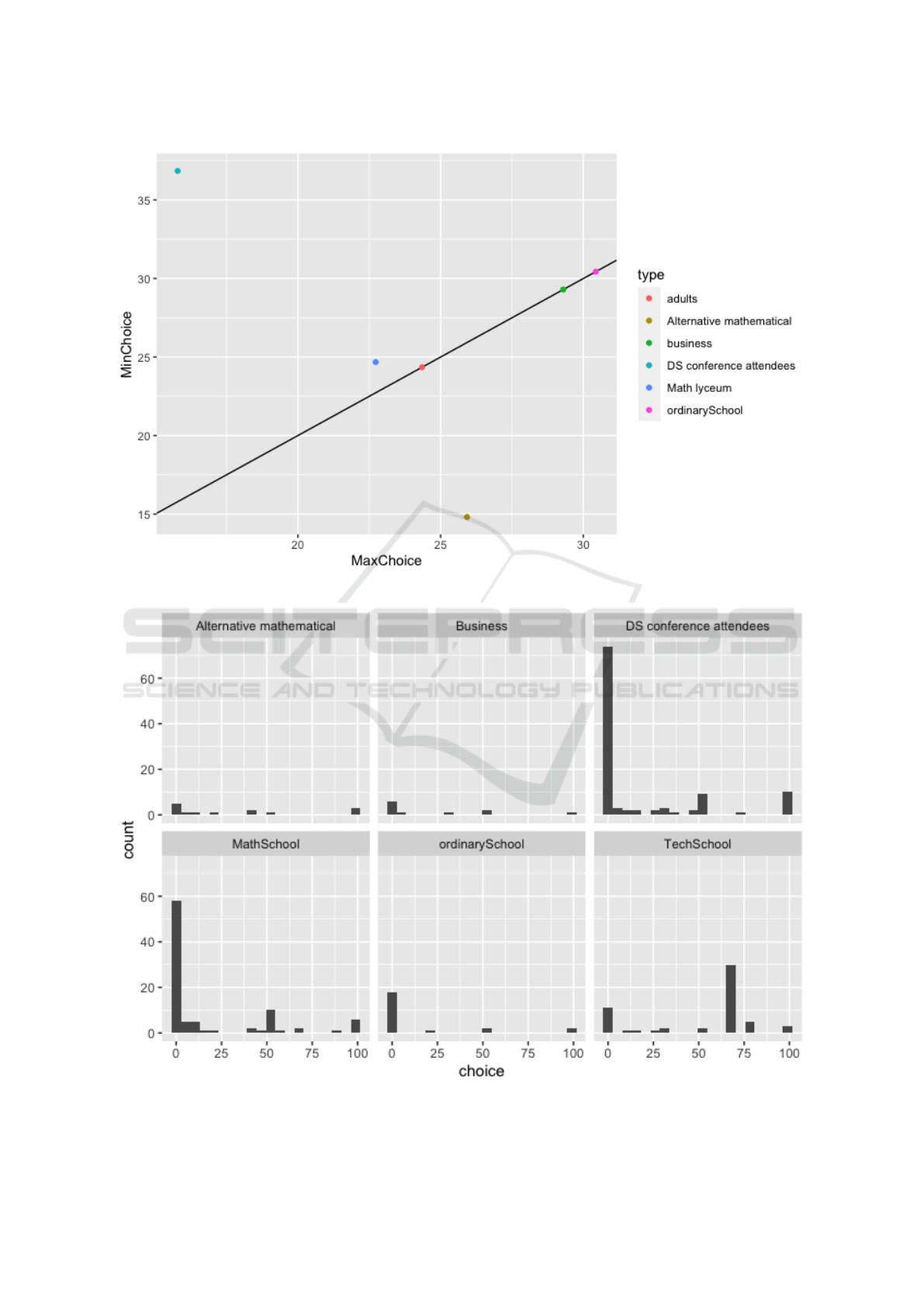
Figure 7: Difference in percent of rationalizable choices.

Figure 8: Histogram of choices.

AET 2020 - Symposium on Advances in Educational Technology

166

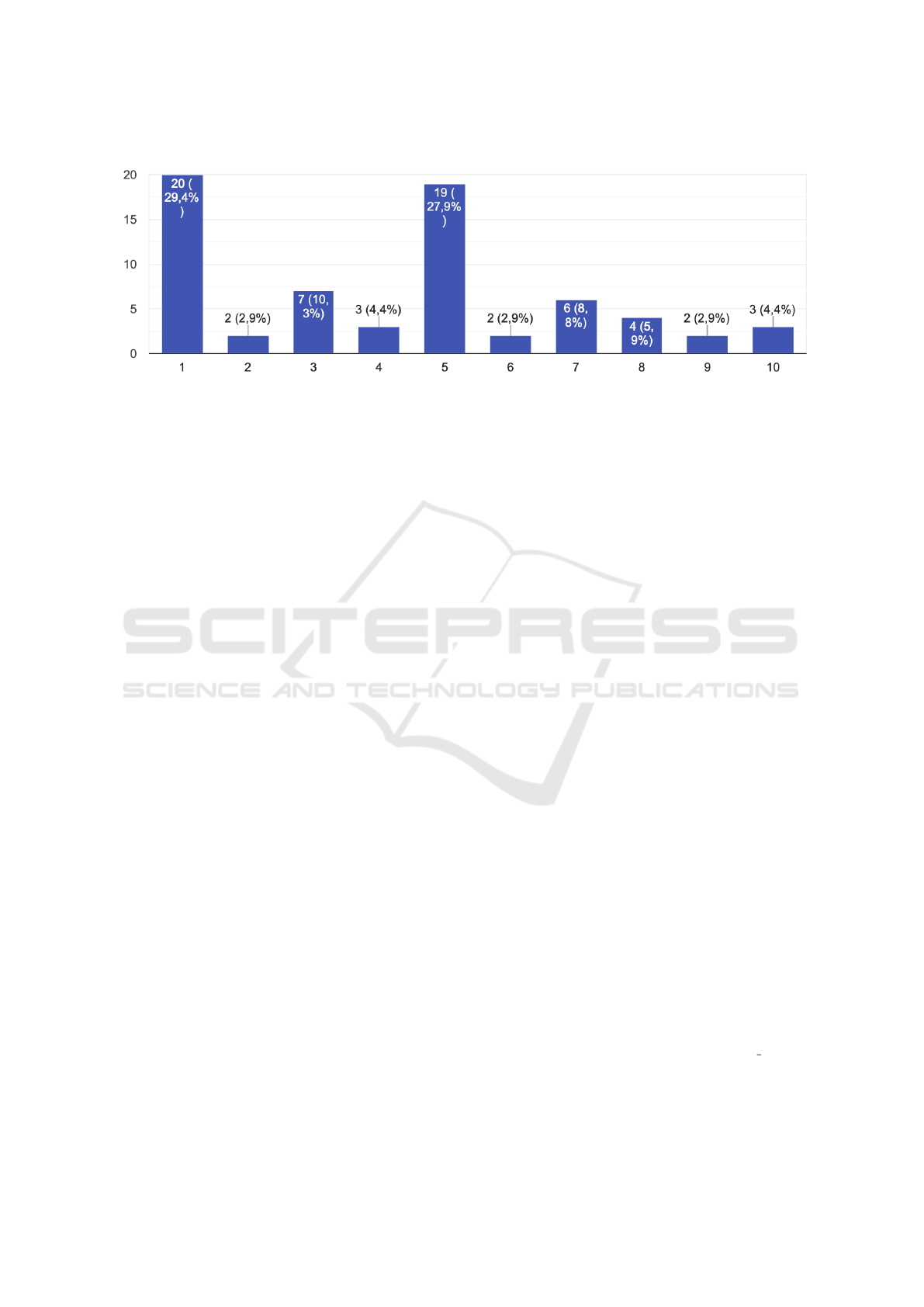
Figure 9: Histogram of choices for 1-10 game.

age of experimentation when children discover

new things and do not afraid to do so.

2. If we considered winning number as decision of

a group we can see that group learning fast and

steady. Even if some outliers choose 100, mean

still declines with every round. It seems that

there is unspoken competition between players

that leads to improvement in aggregated decision

even if no prize is on stake. Actually, it is plau-

sible scenario when all participants choose higher

numbers. But this didn’t happen in any experi-

ment. The closest case – Tech school, when bunch

of pupils (posible coordinating) switch to 100 still

only managed to keep mean on the same level.

3. In second game the surprising result is that players

use mixed strategies very well. It is known (from

experiments of Colin Camerer) that chimpanzee

can ﬁnd mixed equilibrium faster and better than

humans. It seems that concept of mixed strategies

is very intuitive and natural. But still in quite un-

familiar game players made almost equal number

of 1 and 100, so each player unconsciously ran-

domized his own choice.

4. In third game players coordinates to 1, as ex-

pected, because of condition that from numbers

with equal choices – lesser wins. Also we can

note attempts of coordination around 7, 50 and

100. What is interesting is that in practice the

condition was never applied – majority chooses

1 and that’s it. If we decrease the numbers range

to 1-10, other numbers has chance to win (5 or

7 for example). So this is unexpected result –

increasing of number of choices leads to bigger

uncertainty when players trying to ﬁnd slightest

hint what to do, and this is condition of “lesser

wins”. When players apply this condition to big

area, they probably think – “1 is perfect choice,

and other will think in that way also, this increase

chances of winning”.

The results have multiple applications:

• to provide kids with ﬁrst hand experience about

strategic interactions and explain their decisions;

• to demonstrate how game theory experiments can

be used in educational process;

• to understand difference in decision making

among groups;

• to compare results with classical experiments and

replicate them in current Ukrainian education sys-

tem.

REFERENCES

Aumann, R. J. (1985). What is game theory trying to ac-

complish? In Arrow, K. and Honkapohja, S., editors,

Frontiers of Economics, pages 5–46. Basil Blackwell,

Oxford. http://www.ma.huji.ac.il/ raumann/pdf/what

Bernheim, B. D. (1984). Rationalizable strate-

gic behavior. Econometrica, 52(4):1007–1028.

http://www.jstor.org/stable/1911196.

Camerer, C. F. (2011). Behavioral game theory: Exper-

iments in strategic interaction. Princeton University

Press.

Crawford, V. P., Costa-Gomes, M. A., and Iriberri, N.

(2013). Structural models of nonequilibrium strategic

thinking: Theory, evidence, and applications. Journal

of Economic Literature, 51(1):5–62.

Fe, E., Gill, D., and Prowse, V. L. (2019). Cognitive skills,

strategic sophistication, and life outcomes. Work-

ing Paper Series 448, The University of Warwick.

https://warwick.ac.uk/fac/soc/economics/research/

centres/cage/manage/publications/448-2019 gill.pdf.

Gill, D. and Prowse, V. (2016). Cognitive ability, charac-

ter skills, and learning to play equilibrium: A level-k

analysis. Journal of Political Economy, 124(6):1619–

1676.

Guessing Games Experiments in Ukraine. Learning towards Equilibrium

167

uth, W., Kocher, M., and Sutter, M. (2002). Experimen-

tal ‘beauty contests’ with homogeneous and heteroge-

neous players and with interior and boundary equilib-

ria. Economics Letters, 74(2):219–228.

Ho, T.-H., Camerer, C., and Weigelt, K. (1998). Iterated

dominance and iterated best response in experimental

”p-beauty contests”. The American Economic Review,

88(4):947–969. http://www.jstor.org/stable/117013.

Ignatenko, O. P. (2021). Data from experiments. https://

github.com/ignatenko/GameTheoryExperimentData.

Keynes, J. M. (1936). The General Theory of

Employment, Interest and Money. Palgrave

Macmillan. https://www.ﬁles.ethz.ch/isn/125515/

1366 KeynesTheoryofEmployment.pdf.

Mauersberger, F. and Nagel, R. (2018). Chapter 10 - lev-

els of reasoning in keynesian beauty contests: A gen-

erative framework. In Hommes, C. and LeBaron,

B., editors, Handbook of Computational Economics,

volume 4 of Handbook of Computational Economics,

pages 541–634. Elsevier.

Mitzkewitz, M. and Nagel, R. (1993). Experimental results

on ultimatum games with incomplete information. In-

ternational Journal of Game Theory, 22(2):171–198.

Moulin, H. (1986). Game theory for the social sciences.

New York Univeristy Press, New York, 2nd edition.

Nagel, R. (1995). Unraveling in guessing games: An ex-

perimental study. The American Economic Review,

85(5):1313–1326. https://www.cs.princeton.edu/

courses/archive/spr09/cos444/papers/nagel95.pdf.

Schelling, T. (1960). The Strategy of Conﬂict. Harvard Uni-

versity Press, Cambridge.

Schelling, T. C. (1980). The Strategy of Conﬂict: With a

New Preface by The Author. Harvard University Press.

AET 2020 - Symposium on Advances in Educational Technology

168