
Rough Continuity Represented by Intuitionistic Fuzzy Sets
Zolt
´
an Ern
˝
o Csajb
´
ok
a
Department of Health Informatics, Faculty of Health, University of Debrecen,
S
´
ost
´
oi
´
ut 2-4, HU-4406 Ny
´
ıregyh
´
aza, Hungary
Keywords:
Rough Set Theory, Pawlak’s Approximation Spaces, Rough Real Functions, Fuzzy Sets, Intuitionistic Fuzzy
Sets.
Abstract:
Studying rough calculus was initiated by Z. Pawlak in his many papers. He originated the concept of rough
real functions. Like the notion of continuity in classical analysis, the rough continuity is also a central notion in
rough calculus. Relying on the Pawlak’s approximation spaces on the real closed bounded intervals, first, two
intuitionistic fuzzy sets are established starting from rough functions. Then, based on them, some necessary
and sufficient conditions for the rough continuity in terms of intuitionistic fuzzy set theory will be presented.
1 INTRODUCTION
In 1965, Lotfi A. Zadeh initiated the fuzzy set theory
(Zadeh, 1965) as a new mathematical theory to man-
age uncertainty. In the early 1980s, Zdzisław Pawlak
established a new mathematical tool also to manage
uncertainty which is called the rough set theory (RST)
(Pawlak, 1982).
Let U be a nonempty reference set which is com-
monly called the universe. Any set, classical or non-
classical, is formed from the elements of the universe.
They can be represented with more or less similar
tools, called membership functions.
A classical or crisp set S can be represented,
among other things, by its characteristic function
χ
S
: U → {0,1} (Halmos, 1960; Hayden et al., 1968).
Generalizing this representation, a fuzzy set F is de-
fined by a function µ
F
: U → [0,1] which is called the
fuzzy membership function. In rough set theory, how-
ever, the definition of a similar representation tool is
somewhat more complex.
In RST, first, it is assumed that a beforehand pre-
defined family of subsets of U is given. Namely,
this set family is a partition of U generated by an
equivalence relation. Any equivalence class can be
viewed as a set of indiscernible objects characterized
by the available information (knowledge) about them.
Accordingly, in RST an equivalence relation is actu-
ally called the indiscernible relation.
The partition is called the base system, and its
elements, i.e., the equivalence classes are the base
a
https://orcid.org/0000-0002-6357-0233
sets. From the base sets the so–called definable sets
are formed with the union operation.
Next, with the help of base sets, lower and up-
per approximation sets are formed for any S ⊆ U .
The former is the union of all base sets which are in-
cluded in S, whereas the latter is the union of all base
sets which have a nonempty intersection with S. The
difference of upper and lower approximation sets is
the boundary of S. S is exact if its boundary is the
empty set, otherwise it is rough.
In RST, the rough membership function,
rm–function in short, is defined as follows. Let U be
finite. Then, the rm–function is commonly defined by
µ
S
(u) =
|JuK ∩ S|
|JuK|
,
where |·| denotes the number of elements of a set, and
JuK is the base set (equivalence class) to which u ∈
U belongs (|
/
0| = 0 by definition). This rm–function
quantifies the degree of the relative overlap between
the set S and a base set.
Both characteristic and fuzzy membership func-
tions are of a priori nature. They have a wide range of
applications, see, e.g., (Aquino et al., 2020; de Jesus
Rubio, 2009; Chiang et al., 2019; Elias et al., 2020;
Meda-Campa
˜
na, 2018; Hern
´
andez et al., 2020)
In contrast, in RST, initially some information
about the elements of the universe is necessary to have
at our disposal in order to be able to approximate a set.
Thus, the rm–function is of a posteriori nature.
Still, an rm–function can formally be viewed as a
special type of fuzzy membership function, of course,
264
Csajbók, Z.
Rough Continuity Represented by Intuitionistic Fuzzy Sets.
DOI: 10.5220/0010164302640274
In Proceedings of the 12th International Joint Conference on Computational Intelligence (IJCCI 2020), pages 264-274
ISBN: 978-989-758-475-6
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

with many constraints owing to their derived nature
(Yao and Zhang, 2000). However, the converse is not
true in general ((Biswas, 2000), Example 3.1).
It is broadly accepted that the fuzzy and rough
set theories are related but distinct and complemen-
tary to each other. Nevertheless, they can be com-
bined with each other (Dubois and Prade, 1987;
Dubois and Prade, 1992). Moreover, their common/
distinct features can be outlined based on their fuzzy/
rough membership functions (Chakraborty, 2011;
Csajb
´
ok and K
¨
odm
¨
on, 2020).
In Section 2 some basic notations are summarized
for the sake of full clarity. Then, the notion of rough
real function and its two possible representations will
be described.
Section 3 contains the material which is required
to establish the connection between the rough
continuity and intuitionistic fuzzy sets. It is the most
extensive section in the paper.
Section 4 presents the main result of the paper. It
provides a necessary and sufficient conditions for the
rough continuity in terms of intuitionistic fuzzy set
theory.
2 ROUGH REAL FUNCTIONS
In the mid 1990s, relying on rough set theory,
Pawlak originated the study of rough calculus in many
papers (Pawlak, 1994; Pawlak, 1996; Pawlak, 1997).
Its basic notion is the rough real function. In
(Csajb
´
ok, 2020), employing Pawlak’s ideas, some ad-
ditional representations of rough real functions are
given. Two of them, pointwise and blockwise rep-
resentations, will be required in the rest of this paper.
Let U,V be two nonempty sets. A function f
is denoted by f : U → V , u 7→ f (u) with domain
Dom f = U and co-domain Im f = V . In addition,
u 7→ f (u) is the assignment or mapping rule of f . For
any S ⊆ U , f (S) = { f (u) | u ∈ S} ⊆ V is the direct
image of S. V
U
denotes the set of all such functions.
If f ,g ∈ V
U
, the operation f g, ∈ {+,−, ·, /},
and the relation f g, ∈ {=, 6=,≤,<,≥,>} are
understood pointwise.
R is the set of real numbers. R
≥0
denotes the set
of nonnegative real numbers.
Let a,b ∈ R (a ≤ b). [a,b] = {x ∈ R | a ≤ x ≤ b}
and ]a,b[= {x ∈ R | a <x <b} denote the closed and
open bounded intervals, respectively. It is easy to
interpret, then, the open-closed ]a,b] and closed-open
[a,b[ intervals.
By (·,·), we mean an ordered pair.
Let [n] = {0,1,.. . , n} ⊆ N denote a finite set
of natural numbers. Accordingly, ]n] = {1, . . . ,n},
[n[= {0,1,. . . , n − 1}, and ]n[= {1,...,n − 1}.
Throughout the paper, let I be a closed bounded
interval I = [0,a] (a ∈ R
≥0
, a > 0).
The initial notion of the rough calculus is the fol-
lowing.
Definition 1. A categorization or discretization of I
is the sequence S
I
= {x
i
}
i∈[n]
⊆ R
≥0
, where n ≥ 1 and
0 = x
0
< x
1
< ··· < x
n
= a.
Let I
S
denote the equivalence relation generated
by the categorization S
I
. Let x,y ∈ I. xI
S
y if
• x = y = x
i
∈ S
I
for some i ∈ [n], or
• x,y ∈]x
i
,x
i+1
[ for some i ∈ [n[.
The partition I/I
S
generated by I
S
is the following:
I/I
S
= {{x
0
},]x
0
,x
1
[,{x
1
},... , ]x
n−1
,x
n
[,{x
n
}},
where {x
i
} = [x
i
,x
i
] (i ∈ [n]).
The block of the partition I/I
S
containing x ∈ I is
denoted by JxK
I
S
. In particular, if x ∈ S
I
, JxK
I
S
= {x}.
If x ∈ JxK
I
S
=]x
i
,x
i+1
[, then JxK
I
S
denotes the closed
interval [x
i
,x
i+1
]. When x ∈ S
I
, JxK
I
S
= JxK
I
S
= {x}.
In terms of RST terminology, I
S
is an indiscerni-
bility relation on I. The members of I/I
S
are the
base sets. Any union of base sets are referred to as
definable sets. By definition,
/
0 is definable. Their
collection is D
I/I
S
.
In RST, the domain and co–domain of the lower
and upper approximation functions are the power set
of I. In the rough calculus, however, the closed
bounded intervals of the form [0,x] (x ∈ I) will only
be approximated. Therefore, the lower and upper
approximations sets are defined by
l
S
([0,x]) = {x
0
∈I | Jx
0
K
I
S
⊆ [0,x]}
= ∪{Jx
0
K
I
S
∈I/I
S
| Jx
0
K
I
S
⊆ [0,x]};
u
S
([0,x]) = {x
0
∈I | Jx
0
K
I
S
∩ [0,x] 6=
/
0}
= ∪{Jx
0
K
I
S
∈I/I
S
| Jx
0
K
I
S
∩ [0,x] 6=
/
0}.
PAS(I) = (I, I/I
S
,D
I/I
S
,l
S
,u
S
) is called the
Pawlak approximation space.
The boundary of [0,x] is
bnd
S
([0,x]) = u
S
([0,x]) \ l
S
([0,x]).
With a slight abuse of the notations, in order to
simplify the above notations, let us define the follow-
ing numbers:
l
S
(x) = max{x
0
∈ S
I
| x
0
≤ x},
u
S
(x) = min{x
0
∈ S
I
| x
0
≥ x}.
Then, it is easy to check that
• if x ∈ S
I
, then l
S
([0,x]) = [0,l
S
(x)] = [0,x] and
u
S
([0,x]) = [0,u
S
(x)] = [0,x];
Rough Continuity Represented by Intuitionistic Fuzzy Sets
265

• if x /∈ S
I
, then l
S
([0,x]) = [0, l
S
(x)] $ [0, x], and
u
S
([0,x]) = [0,u
S
(x)[ % [0,x];
• if x ∈ S
I
, then bnd
S
([0,x]) =
/
0; if x /∈ S
I
, then
bnd
S
([0,x]) = ]l
S
(x),u
S
(x)[ 6=
/
0.
The number x ∈ I is exact with respect to PAS(I) if
l
S
(x) = u
S
(x), otherwise x is inexact or rough (Pawlak,
1996). Of course, x ∈ I is exact iff x ∈ S
I
.
In this context, the members of I/I
S
are called the
rough numbers with respect to PAS(I). In addition,
the categorization points in S
I
are called the roughly
isolated points with respect to PAS(I).
Let I = [0,a
I
] and J = [0,a
J
] be two closed
bounded intervals with a
I
, a
J
∈ R
≥0
, a
I
,a
J
> 0. Let S
I
and P
J
be the categorizations of I and J, respectively,
where S
I
= {x
i
}
i∈[n]
and P
J
= {y
j
}
j∈[m]
⊆ R
≥0
in such
a way that m, n ≥ 1, and 0 = x
0
< x
1
< ··· < x
n
= a
I
,
0 = y
0
< y
1
< · · · < y
m
= a
J
. The corresponding
Pawlak approximation spaces are PAS(I), PAS(J).
A Cartesian coordinate system whose x and y
axes equipped with PAS(I) and PAS(J) is called the
(S
I
,P
J
)–coordinate system, or rough coordinate sys-
tem in short. Any function f ∈ J
I
attached to a rough
coordinate system is called the rough real function.
In order to make the rough coordinate system
easier to handle technically, the blocks of the parti-
tion I/I
S
are enumerated as follows.
N
I
: I/I
S
→ [2n],
JxK
I
S
7→
B
2i
= 2i, if ∃i ∈ [n](JxK
I
S
= {x
i
}),
B
2i+1
= 2i + 1, if ∃i ∈ [n[(x ∈]x
i
,x
i+1
[).
The inverse of N
I
is:
N
−1
I
: [2n] → I/I
S
,
B
i
7→
(
{x
i/2
}, if i ≡ 0 (mod 2)
i
x
i−1
2
,x
i+1
2
h
, if i ≡ 1 (mod 2)
.
The equivalence classes of J/J
P
can be enumer-
ated in the same way with the help of an enumeration
function N
J
. They are referred to as C
j
’s ( j ∈ [2m]).
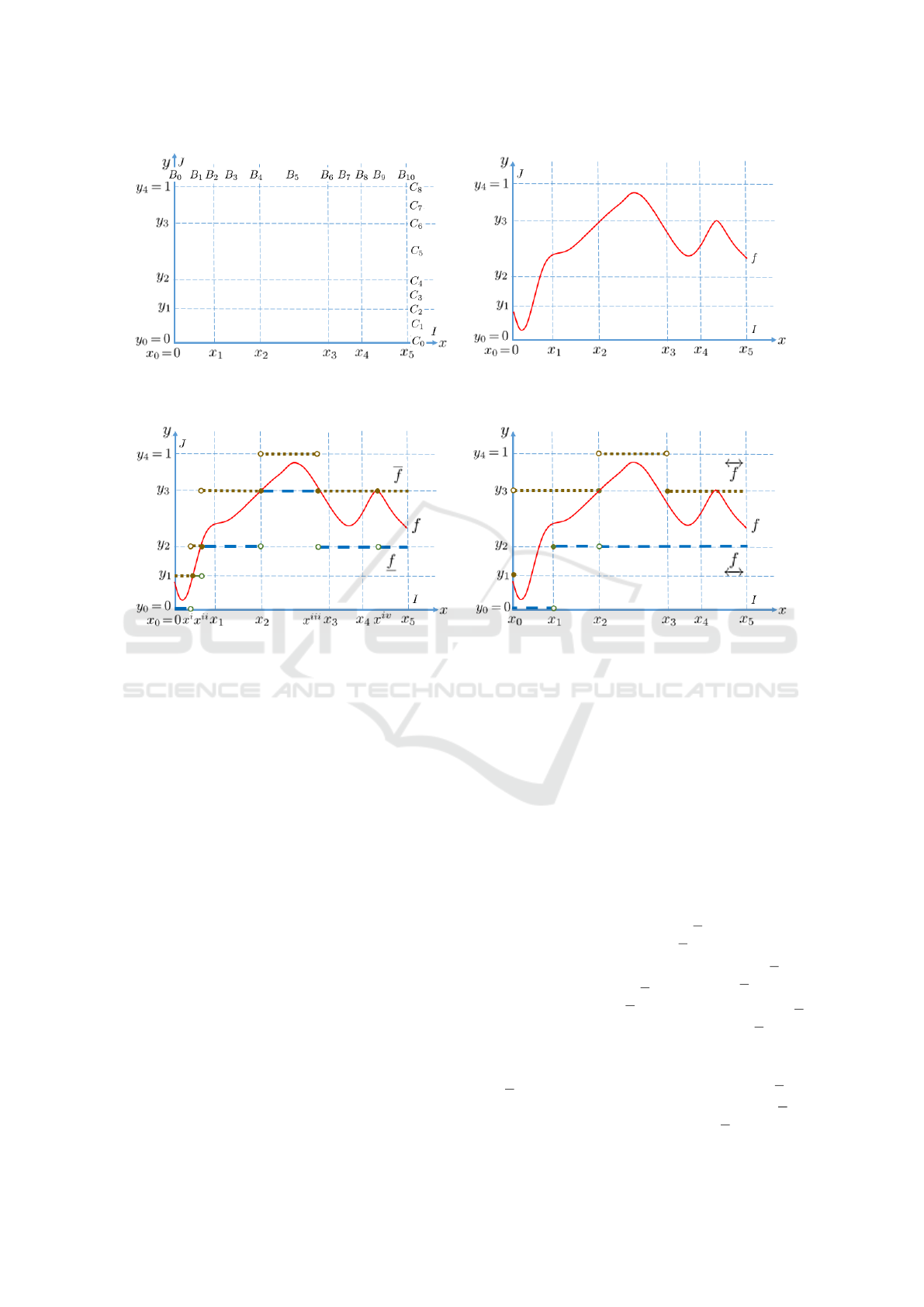
Example 1. Figure 1 (a) depicts a rough coordinate
system with S
I
= {x
0
= 0, x
1
,x
2
,x
3
,x
4
,x
5
} and P
[0,1]
=
{y
0
= 0, y
1
,y
2
,y
3
,y
4
= 1}. Figure 1 (b) presents a
rough real function attached to this rough coordinate
system.
Definition 2 ((Pawlak, 1994)). Let f ∈ J
I
. The
pointwise (S
I
,P
J
)–lower and (S
I
,P
J
)–upper approx-
imations of f are the functions
f
: I → P
J
, x 7→ l
P
( f (x)) = max{y ∈ P
J
| y ≤ f (x)},
f : I → P
J
, x 7→ u
P
( f (x))= min{y ∈ P
J
| y ≥ f (x)}.
f is pointwise exact at x if f (x) = f (x), otherwise
f is pointwise inexact or rough at x.
f is pointwise exact on I
0
⊆ I if f (x) = f (x) for all
x∈I
0
, otherwise f is pointwise inexact (rough) on I
0
.
Definition 3. Let f ∈ J
I
. The block by block,
blockwise in short, (S
I
,P
J
)–lower and (S
I
,P
J
)–upper
approximations of f are the functions
f
←→
: I → P
J
, x 7→ l
P
(inf f (JxK
I
S
)),
←→
f : I → P
J
, x 7→ u
P
(sup f (JxK
I
S
)).
The function f is blockwise exact on B
i
for some
i ∈ [2n] if f
←→
(B
i
) =
←→
f (B
i
), that is, the direct images
of B
i
with respect to f
←→
and
←→
f are equal; otherwise
f is blockwise inexact (rough) on B
i
.
The function f is blockwise exact on I if f is
blockwise exact on all B
i
∈ I/I
S
, otherwise f is block-
wise inexact (rough) on I.
Owing to the fact that inf f (JxK
I
S
) and sup f (JxK
I
S
)
are constant on every B
i
, the functions f
←→
and
←→
f are
constant on every B
i
(i ∈ [2n]). Accordingly, using the
word “blockwise” is appropriate.
Example 2. Figure 2 (a) depicts the pointwise lower
and upper approximations of f . f is pointwise exact
at x
i
,x
ii
,x
2
,x
iii
,x
iv
, and pointwise rough at all other
points.
Figure 2 (b) shows the blockwise lower and upper
approximations of f . f is blockwise exact only on
B
4
= {x
2
}, and blockwise rough on all other blocks.
It is easy to check the following simple but impor-
tant statement.
Lemma 1. Let f ∈ J
I
be a rough real function. Then,
f
←→
≤ f ≤ f ≤ f ≤
←→
f
holds on I.
3 DERIVING INTUITIONISTIC
FUZZY SETS FROM ROUGH
REAL FUNCTIONS
Let U be a nonempty set.
According to (Zadeh, 1965) a fuzzy set (FS) on U
is the function µ ∈ [0, 1]
U
; see also, (Klir and Yuan,
1995; Dubois and Prade, 2000; Zimmermann, 2001;
Ross, 2010). µ is also called the membership function.
F S (U) denotes the family of all fuzzy sets on U.
FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications
266
(a) (b)
Figure 1: A rough coordinate system and a rough real function.
(a) (b)
Figure 2: Pointwise and blockwise lower/upper approximations of f .
Let I = {[a,b] | 0 ≤ a ≤ b ≤ 1}.
Let µ
A
,ν
A
∈ F S (U) with µ
A
≤ ν
A
. An interval-
valued fuzzy set (IVFS) on U is the function
µ
IV FS
A
: U → I, u 7→ [µ
A
(u),ν
A
(u)] (Gorzałczany,
1987). µ
IV FS
A
is also denoted simply by [µ
A
,ν
A
].
Let µ
A
,ν
A
∈ F S (U) with 0 ≤ µ
A
+ ν
A
≤ 1. An
intuitionistic fuzzy set (IFS) on U is defined by
the function pair µ
IFS
A
= (µ
A
,ν
A
) (Atanassov, 1986;
Atanassov, 1999; Atanassov, 2012). µ
A
and ν
A
are the
IFS membership and IFS nonmembership functions,
respectively. π
A
= 1 − µ
A
− ν
A
∈ F S (U) is the IFS
indeterminacy function. The family of all intuitionis-
tic fuzzy sets on U is denoted by I F S (U).
Let µ
IFS
A
,µ
IFS
B
∈ I F S (U). Then,
• µ
IFS
A
= µ
IFS
B
if µ
A
= µ
B
and ν
A
= ν
B
;
• µ
IFS
A
⊆ µ
IFS
B
if µ
A
≤ µ
B
and ν
A
≥ ν
B
.
It is well known that every IVFS [µ
A
,ν
A
] cor-
responds to an IFS (µ
A
,1 − ν
A
), while every IFS
(µ
A
,ν
A
) corresponds to an IVFS [µ
A
,1 − ν
A
]
(Atanassov and Gargov, 1989; Bustince and Burillo,
1996).
There are many papers dealing with the interre-
lationship between rough set and intuitionistic fuzzy
set theory (Rizvi et al., 2002; Cornelis et al., 2003;
Zhou and Wu, 2011; Xu et al., 2014). In this paper,
the starting point is the rough real functions, i.e., real
functions managing them in rough coordinate sys-
tems. Thereafter, intuitionistic fuzzy sets are derived
from their pointwise and blockwise representations.
For the rest of this section, let PAS(I) and
PAS([0, 1]) be two Pawlak approximation spaces
defined on the intervals I and [0,1] with the catego-
rizations S
I
= {x
0
= 0, x
1
,... , x
n
} and P
[0,1]
= {y
0
= 0,
y
1
,... , y
m
= 1}. In addition, let f ∈ [0, 1]
I
be a rough
function attached to the (S
I
,P
[0,1]
)–coordinate system.
According to Definition 2 , f , f ∈ [0,1]
I
, that is,
the pointwise (S
I
,P
[0,1]
)–lower and upper approxi-
mations of f are fuzzy sets. Moreover, f ≤ f also
holds. Hence, f
IV FS
pw
= [ f , f ] forms an interval–valued
fuzzy set. Then, the function pair f
IFS
pw
= ( f ,1 − f )
forms an intuitionistic fuzzy set. (The subscript “pw”
refers to “pointwise”.)
In the intuitionistic fuzzy set theory context, f and
1 − f are the IFS membership and nonmembership
functions, respectively, and π
−
f
= 1 − f − (1 − f ) =
Rough Continuity Represented by Intuitionistic Fuzzy Sets
267

f − f is the IFS indeterminacy function.
Similarly, according to Definition 3 , f
←→
,
←→
f ∈
[0,1]
I
, that is, the blockwise (S
I
,P
[0,1]
)–lower and
upper approximations of f are also fuzzy sets, and
f
←→
≤
←→
f holds, too. Hence, f
IV FS
bw
=
f
←→
,
←→
f
forms
an interval–valued fuzzy set, and so the function pair
f
IFS
bw
=
f
←→
,1 −
←→
f
is an intuitionistic fuzzy set.
(The subscript “bw” refers to “blockwise”.)
In terms of intuitionistic fuzzy set theory, f
←→
and
1 −
←→
f are the IFS membership and nonmembership
functions, respectively, and π
←→
f
= 1 − f
←→
− (1 −
←→
f )
=
←→
f − f
←→
is the IFS indeterminacy function.
Intuitionistic fuzzy sets f
IFS
pw
and f
IFS
bw
are derived
from f with respect to a (S
I
,P
[0,1]
)–coordinate sys-
tem. They are called the pointwise and blockwise
roughly derived intuitionistic fuzzy sets.
There are many different geometric interpreta-
tions of intuitionistic fuzzy sets. For our purposes,
the so–called “unit segments” representation will be
appropriate (cf. (Atanassov, 1999), Figure 1.3.).
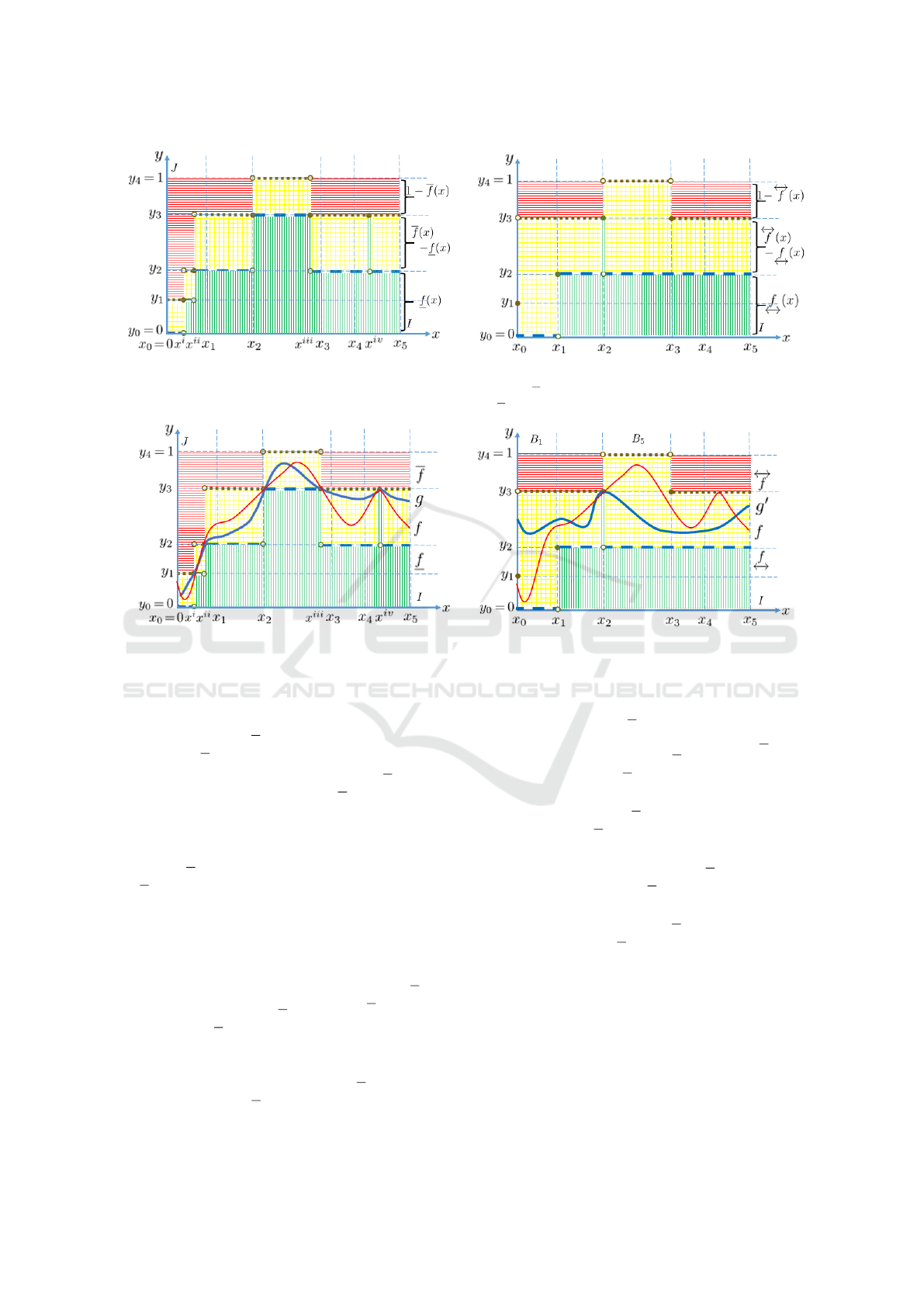
Figure 3 in this way depicts the geometric interpre-
tations of f
IFS
pw
= ( f , 1 − f ) and f
IFS
bw
= ( f
←→
,1 −
←→
f ) .
Accordingly, in Figure 3 (a), unit segments f (x),
f (x) − f (x), and 1 − f (x) are assigned to every
x ∈ I; correspondingly, in Figure 3 (b), unit segments
f
←→
(x),
←→
f (x) − f
←→
(x), and 1 −
←→
f (x) are assigned to
every x ∈ I.
Proposition 1. The both inclusion relations
f
IFS
pw
= ( f ,1 − f ) ⊆ f
IFS
bw
= ( f
←→
,1 −
←→
f ) (1)
f
IFS
bw
= ( f
←→
,1 −
←→
f ) ⊆ f
IFS
pw
= ( f ,1 − f ) (2)
fail in general.
Proof. Due to Lemma 1 , in general,
• f ≤ f
←→
fails in the case of Equation 1 , and
• 1 −
←→
f ≥ 1 − f fails in the case of Equation 2 .
Proposition 2. Let f
IFS
pw
and f
IFS
bw
be the pointwise
and blockwise roughly derived intuitionistic fuzzy
sets. Then, f
IFS
pw
(x
i
) = f
IFS
bw
(x
i
) for every x
i
∈ S
I
(i ∈ [n]) categorization point.
Proof. f
IFS
pw
= f
IFS
bw
⇔ ( f , 1 − f ) = ( f
←→
,1 −
←→
f ) ⇔
f = f
←→
and f =
←→
f . Then, the statement follows from
the fact that f (x
i
) = f
←→
(x
i
) and f (x
i
) =
←→
f (x
i
) for
every x
i
∈ S
I
(i ∈ [n]) categorization point.
Example 3. According to Figures 2 (a) and 2 (b),
• f (x
0
) = f
←→
(x
0
) = y
0
= 0, f (x
1
) = f
←→
(x
1
) = y
2
,
f (x
2
) = f
←→
(x
2
) = y
3
, f (x
3
) = f
←→
(x
3
) = y
2
,
f (x
4
) = f
←→
(x
4
) = y
2
, f (x
5
) = f
←→
(x
5
) = y
2
.
• f (x
0
) =
←→
f (x
0
) = y
1
, f (x
1
) =
←→
f (x
1
) = y
3
,
f (x
2
) =
←→
f (x
2
) = y
3
, f (x
3
) =
←→
f (x
3
) = y
3
,
f (x
4
) =
←→
f (x
4
) = y
3
, f (x
5
) =
←→
f (x
5
) = y
3
.
Linked to the indeterminacy functions π
−
f
and
π
←→
f
, pointwise and blockwise indeterminacy regions
Π
−
f
and Π
←→
f
are defined by
Π
−
f
= {(x,y) | x ∈ I, y = f (x) = f (x) or
y ∈] f (x), f (x)[ if f (x) 6= f (x)};
Π
←→
f
=
n
(x,y)
|
x ∈ I, y = f
←→
(x) =
←→
f (x) or
y ∈
i
f
←→
(x),
←→
f (x)
h
if f
←→
(x) 6=
←→
f (x)
o
Example 4. In Figures 3 (a) and 3 (b), the areas filled
with grid pattern and solid circles depict the indeter-
minacy regions Π
−
f
and Π
←→
f
, respectively.
Having defined the indeterminacy regions, let us
define two families of functions with the help of them:
G
−
f
= {g | g : I → [0, 1],(x,g(x)) ∈ Π
−
f
},
G
←→
f
= {g | g : I → [0, 1],(x,g(x)) ∈ Π
←→
f
}.
Example 5. In Figures 4 (a) and 4 (b) show a function
g from G
−
f
and a function g
0
from G
←→
f
, respectively.
Proposition 3. Let f be a rough real function. Then,
1. Π
−
f
⊆ Π
←→
f
.
2. Π
−
f
= Π
←→
f
if and only if f
IFS
pw
= f
IFS
bw
.
Proof. 1. Case x ∈ I, f (x) 6= f (x). Applying Lemma
1 , ] f (x), f (x)[ ⊆
i
f
←→
(x),
←→
f (x)
h
, and so
{(x,y) | x ∈ I, y ∈] f (x), f (x)[}
⊆
n
(x,y) | x ∈ I, y ∈
i
f
←→
(x),
←→
f (x)
ho
Case x ∈ I, f (x) = f (x). If x
0
∈ S
I
, then
f (x
0
) = f (x
0
) = f (x
0
) = f
←→
(x
0
) =
←→
f (x
0
).
Thus, (x
0
, f (x
0
)) ∈ {(x,y) | x ∈ I,y = f (x) = f (x)},
and (x
0
, f (x
0
)) ∈
n
(x,y) | x ∈ I, y = f
←→
(x) =
←→
f (x)
o
also holds.
FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications
268
(a) (b)
Figure 3: Geometric interpretations of f
IFS
pw
= ( f , 1 − f ) and f
IFS
bw
= ( f
←→
,1 −
←→
f ).
(a) (b)
Figure 4: A function g from G
−
f
, and a function g
0
from G
←→
f
.
Let x
0
/∈ S
I
. It may occur that
f (x
0
) = f (x
0
) = f (x
0
) = f
←→
(x
0
) =
←→
f (x
0
).
Then, (x
0
, f (x
0
)) ∈ {(x, y) | x ∈ I,y = f (x) = f (x)} and
(x
0
, f (x
0
)) ∈
n
(x,y) | x ∈ I,y = f
←→
(x) =
←→
f (x)
o
holds
at the same time.
If f
←→
(x
0
)6=
←→
f (x
0
), then (x
0
, f (x
0
))∈ {(x, y) | x ∈I,
y = f (x) = f (x)}, and, due to Lemma 1 , (x
0
, f (x
0
)) ∈
n
(x,y) | x ∈ I, y ∈
i
f
←→
(x),
←→
f (x)
ho
also holds.
2. (⇒) It should be proved that “Π
−
f
= Π
←→
f
implies f
IFS
pw
= f
IFS
bw
”. Instead, its contrapositive form
“ f
IFS
pw
6= f
IFS
bw
implies Π
−
f
6= Π
←→
f
” will be proved.
On one hand, f
IFS
pw
6= f
IFS
bw
⇔ ( f ,1 − f ) 6=
( f
←→
,1−
←→
f ) ⇔ f 6= f
←→
or f 6=
←→
f . On the other hand,
according to point 1. of this Proposition, Π
−
f
6= Π
←→
f
⇔ Π
←→
f
6⊆ Π
−
f
.
Let us assume that f 6= f
←→
(the case f 6=
←→
f can be
proved similarly). Then, there is an x
0
∈ I in such
a way that f
←→
(x
0
) < f
(x
0
). Hence, there is an
h ∈ G
←→
f
in such a way that f
←→
(x
0
) < h(x
0
) < f (x
0
).
If f
←→
(x
0
) < h(x
0
) < f (x
0
) < f (x
0
) ≤
←→
f (x
0
), then it
is straightforward that (x
0
,h(x
0
)) ∈
i
f
←→
(x
0
),
←→
f (x
0
)
h
,
but (x
0
,h(x
0
)) /∈] f (x
0
), f (x
0
)[. In other words,
(x
0
,h(x
0
)) ∈ Π
←→
f
, but (x
0
,h(x
0
)) /∈ Π
−
f
, i.e., Π
←→
f
6⊆ Π
−
f
satisfies.
If f
←→
(x
0
) < h(x
0
) < f (x
0
) = f (x
0
) ≤
←→
f (x
0
),
of course, (x
0
,h(x
0
)) ∈
i
f
←→
(x
0
),
←→
f (x
0
)
h
also holds.
In addition, h(x
0
) 6= f (x
0
) = f (x
0
). Therefore, in
this case, (x
0
,h(x
0
)) ∈ Π
←→
f
, but (x
0
,h(x
0
)) /∈ Π
−
f
, i.e.,
Π
←→
f
6⊆ Π
−
f
also satisfies.
(⇐) It is straightforward.
Example 6. In Figures 3 (a), (b), it can be observed
that the area of the pointwise indeterminacy region
Π
−
f
is included in the area of the blockwise indetermi-
nacy region Π
←→
f
in accordance with Proposition 3 1.
As shown in Figure 3, f
IFS
pw
6= f
IFS
bw
, in particular,
Rough Continuity Represented by Intuitionistic Fuzzy Sets
269
(a) (b)
Figure 5: Π
−
f
6= Π
←→
f
.
both f
←→
≤ f and f ≤
←→
f satisfy. It can be seen that
Π
−
f
⊆ Π
←→
f
but Π
−
f
6= Π
←→
f
in accordance with Propo-
sition 3 2.
Example 7. Figure 2 (a) shows that the graph of f in-
tersects the horizontal line segments y = y
1
at x
i
, and
y = y
2
at x
ii
. In Figure 5 (a), x
0
∈ ]x
i
,x
ii
[ in such a
way that y
0
= f
←→
(x
0
) < h(x
0
) < f (x
0
) = y
1
. Moreover,
h(x
0
) ∈
i
f
←→
(x
0
), f (x
0
)
h
= ]y
0
,y
1
[ and f (x
0
) ∈
] f (x
0
), f (x
0
)[=]y
1
,y
2
[.
In other words, the points (x
0
, f (x
0
)) and
(x
0
,h(x
0
)) are on the vertical line segment x = x
0
.
More precisely, (x
0
,h(x
0
)) is between the points
(x
0
,y
0
) and (x
0
,y
1
), and (x
0
, f (x
0
)) is between the
points (x
0
,y
1
) and (x
0
,y
2
).
Moving on for any x ∈ ]x
i
,x
ii
[ and suitable func-
tions h ∈ G
←→
f
, the points (x, h(x))’s form the rectan-
gular area ]x
i
,x
ii
[ × ]y
0
,y
1
[ .
1
This area is filled with
diagonal up pattern in Figure 5 (b). It is belongs to
Π
←→
f
but does not belong to Π
−
f
. The area filled with
diagonal down pattern can be derived similarly.
Corollary 1. Let f be a rough real function. Then,
1. G
−
f
⊆ G
←→
f
.
2. G
−
f
= G
←→
f
if and only if f
IFS
pw
= f
IFS
bw
.
Proof. These statements immediately follow from
Proposition 3 .
In Figure 4 (b), it can be observed that g
0
∈G
←→
f
, but
f
←→
6= g
0
←→
,
←→
f 6=
←→
g
0
. This is because f
←→
=y
0
< y
2
= g
0
←→
on B
1
=]x
0
,x
1
[, and
←→
f = y
4
> y
3
=
←→
g
0
on B
5
=
]x
2
,x
3
[. In other words, f
IFS
bw
6= g
0IFS
bw
. This observa-
tion motivates the following definition.
1
Here, × denotes the Cartesian product operation.
Definition 4. Let f
IFS
pw
and f
IFS
bw
be pointwise and
blockwise roughly derived IFSs.
• f
IFS
pw
is roughly strong if f
IFS
pw
= g
IFS
pw
for all
g ∈ G
f
, otherwise f
IFS
pw
is roughly weak.
• f
IFS
bw
is roughly strong if f
IFS
bw
= g
IFS
bw
for all
g ∈ G
←→
f
, otherwise f
IFS
bw
is roughly weak.
In the case of f
IFS
pw
, Figure 4 (a) suggests that f
IFS
pw
is always roughly strong. That is what the following
proposition is about.
Proposition 4. For any pointwise roughly derived
IFS f
IFS
pw
, f
IFS
pw
is roughly strong, that is, f
IFS
pw
= g
IFS
pw
for all g ∈ G
−
f
.
Proof. Let g ∈ G
−
f
. Then, (x,g(x)) ∈ Π
−
f
.
Case x ∈ I, g(x) ∈ ] f (x), f (x)[ . In this case,
g(x) ∈ ] f (x), f (x)[= ]l
P
( f (x)),u
P
( f (x))[
= ] max{y ∈ P
[0,1]
| y ≤ f (x)},
min{y∈P
[0,1]
| y ≥ f (x)}[
= ]y
j
,y
j+1
[
= ] max{y ∈ P
[0,1]
| y ≤ g(x)},
min{y∈P
[0,1]
| y ≥ g(x)}[
= ]g(x),g(x)[,
where y
j
,y
j+1
∈ P
[0,1]
for some j ∈ [m[ .
That is,
f
IFS
pw
(x) = ( f (x),1− f (x)) = (g(x),1−g(x)) = g
IFS
pw
(x)
satisfies for all such x ∈ I that f (x) 6= f (x).
Case x ∈ I, g(x) = f (x) = f (x). Then, g(x) =
f (x) = f (x) = y
j
, where y
j
∈ P
[0,1]
for some j ∈ [m].
And so g(x) = y
j
= g(x) = g(x).
That is, f
IFS
pw
(x) = g
IFS
pw
(x) also holds for all such
x ∈ I that f (x) = f (x).
FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications
270

Proposition 5. Let f
IFS
bw
be a blockwise roughly
derived IFS.
f
IFS
bw
is roughly strong if and only if f
IFS
pw
= f
IFS
bw
.
Proof. (⇒) On the contrary, let us assume that
f
IFS
pw
6= f
IFS
bw
. Then, such a function g ∈ G
←→
f
will be
constructed for which g
IFS
bw
6= f
IFS
bw
holds. However, it
contradicts the condition that f
IFS
bw
is roughly strong.
f
IFS
pw
6= f
IFS
bw
⇔ ( f , 1 − f ) 6= ( f
←→
,1 −
←→
f ) ⇔
f 6= f
←→
or f 6=
←→
f . It us assumed that f 6= f
←→
, the case
f 6=
←→
f can be proved similarly. However, due to
Proposition 2 , f (x
i
) = f
←→
(x
i
) satisfies for every x
i
∈
S
I
(i ∈ [n]) categorization point. Then, there should
be an open interval B
i
=
i
x
i−1
2
,x
i+1
2
h
∈ I/I
S
, where
i ≡ 1 (mod 2) (i ∈ [2n[) in such a way that f 6= f
←→
,
i.e., f
←→
< f on B
i
.
The case f = f on B
i
is not possible, because it
would imply that f = f = f
←→
=
←→
f on B
i
. However, it
contradicts the condition that f
←→
< f on B
i
.
When f 6= f on B
i
, let g ∈ G
←→
f
with the constraint
that g(x) ∈ ] f , f [ on B
i
. It is possible, because ] f , f [⊆
i
f
←→
,
←→
f
h
on B
i
. Then, f
←→
< f = g
←→
on B
i
, and so
f
IFS
bw
6= g
IFS
bw
which is the requested contradiction.
(⇐) According to Proposition 4 , f
IFS
pw
is roughly
strong, and so f
IFS
bw
is roughly strong as well.
4 ROUGH CONTINUITY AND
ROUGHLY DERIVED
INTUITIONISTIC FUZZY SETS
Rough continuity is a central notion in rough calculus
like the continuity in the classical real analysis.
Let I and J two real intervals with categorizations
S
I
and P
J
as they are given above.
Definition 5 ((Pawlak, 1996)). A rough real
function f ∈ J
I
is (S
I
,P
J
)–continuous or roughly
continuous at x if
f (JxK
I
S
) ⊆ J f (x)K
J
p
.
Otherwise, f is (S
I
,P
J
)–discontinuous or roughly
discontinuous at x ∈ I.
f is (S
I
,P
J
)–continuous (roughly continuous)
on I
0
⊆ I if f is (S
I
,P
J
)–continuous at every point of
I
0
. Otherwise, f is not roughly continuous on I
0
.
Proposition 6 ((Csajb
´
ok, 2019)). A rough real
function f ∈ J
I
is (S
I
,P
J
)–continuous at every x ∈ S
I
roughly isolated point.
Definition 6 ((Csajb
´
ok, 2019)). The (S
I
,P
J
)-discon-
tinuity types of f ∈ J
I
are defined as follows.
The rough discontinuity of f is called
(1) the rough jump discontinuity of the first kind if it
is derived from touching a straight line y = y
j
for
some j ∈ [m];
(2) the rough jump discontinuity of the second kind if
it is derived from intersecting a straight line y = y
j
for some j ∈]m[;
(3) any other type of discontinuity is called the rough
jump discontinuity of the third kind.
Example 8. Figure 6 (a) depicts rough jump disconti-
nuities of the first and second type.
• f has the rough jump discontinuity of the first
kind at x
vi
because it is derived from touching the
straight line y = y
3
at x
vi
:
f (Jx
vi
K
I
S
) = f ([x
4
,x
5
]) ⊆ ]y
2
,y
3
]
6⊆ {y
3
} = J f (x
vi
)K
J
p
.
• f has the rough jump discontinuities of the
second kind at x
i
, x
ii
, and x
iv
because they are
derived from intersecting the line segments y = y
1
,
y = y
2
, and y = y
3
, respectively. For instance,
f (Jx
i
K
I
S
) = f ([x
0
,x
1
]) ⊆ ]y
0
,y
3
]
6⊆ {y
1
} = J f (x
i
)K
J
p
.
The discontinuities at x
ii
and x
iv
can be showed in
similar way.
It should be noted that f touches at x
1
and in-
tersects at x
2
the line segment y = y
3
but f is still
continuous at both points. It can be seen that the
contact point is (x
1
,y
3
) and the intersection point is
(x
2
,y
3
), that is, their both coordinates are categoriza-
tions points.
In Figure 6 (b), f has rough jump discontinuities
of the third kind at x
iii
and x
v
:
f (Jx
iii
K
I
S
) = f ([x
2
,x
3
]) ⊆ ]y
2
,y
4
[
6⊆ [y
0
,y
1
] = J f (x
iii
)K
J
p
;
f (Jx
v
K
I
S
) = f ([x
3
,x
4
]) ⊆ ]y
2
,y
4
[
6⊆ [y
2
,y
3
] = J f (x
iii
)K
J
p
.
Although, f is roughly continuous at x
3
pursuant
to Proposition 6 , it may cause rough jump discontinu-
ities of the third kind in blocks ]x
2
,x
3
[ and/or ]x
3
,x
4
[,
specially, in ]x
3
,x
4
[ at x
v
.
Rough Continuity Represented by Intuitionistic Fuzzy Sets
271
(a) (b)
Figure 6: Rough discontinuities.
Proposition 7 ((Csajb
´
ok, 2019)). A rough real func-
tion f ∈ J
I
is (S
I
,P
J
)–continuous on I if and only if f
does not have rough jump discontinuity of any kind.
Proposition 8. A rough real function f ∈ J
I
is
(S
I
,P
J
)–continuous on I if and only if the blockwise
roughly derived IFS f
IFS
bw
is roughly strong.
Proof. (⇒) Since f is roughly continuous on I, then
f (JxK
I
S
) ⊆ J f (x)K
J
p
for all x ∈ I.
It is straightforward that on C
j
(∈ J/J
P
, j ∈ [2m]),
f
←→
=
←→
f = y
j/2
if j ≡ 0 (mod 2), and f
←→
= y
j−1
2
,
←→
f = y
j+1
2
if j ≡ 1 (mod 2). Thus,
• f (x) = y
j/2
on JxK
I
S
if f (JxK
I
S
) = J f (x)K
J
p
= C
j
for some j ∈ [2m], j ≡ 0 (mod 2);
• y
j−1
2
≤ f (x) ≤ y
j+1
2
on JxK
I
S
if f (JxK
I
S
) ⊆
J f (x)K
J
p
= C
j
for some j ∈ [2m], j ≡ 1 (mod 2).
It means, considering the definition of Π
←→
f
and
G
←→
f
, that for all g ∈ G
←→
f
, f
IFS
bw
= g
IFS
bw
, i.e., f
IFS
bw
is
roughly strong.
(⇐) On the the contrary, let us assume that f is
roughly discontinuous for some x ∈ I. Since f is
roughly continuous in every roughly isolated point,
see, Proposition 6 , x belongs to an open interval
B
i
= JxK
I
S
=
i
x
i−1
2
,x
i+1
2
h
∈ I/I
S
for some i ∈ [2n[,
i ≡ 1 (mod 2).
First, it can be stated that f (JxK
I
S
) ∩ J f (x)K
J
p
6=
/
0,
because x ∈ JxK
I
S
, and so f (x) ∈ f (JxK
I
S
),J f (x)K
J
p
.
Moreover, there must be an x 6= x
0
∈ JxK
I
S
in such
a way that f (x) 6= f (x
0
) and f (x
0
) ∈ f (JxK
I
S
) but
f (x
0
) /∈ J f (x)K
J
p
, otherwise f (JxK
I
S
) ⊆ J f (x)K
J
p
would
be, which contradicts the assumption that f discontin-
uous at x.
It may occur that |J f (x)K
J
p
| = 1. It happens when
f (x) = f (x) = f (x), that is when f touches or inter-
sects a horizontal line segment y = y
j
at x.
Case |J f (x)K
J
p
=1. Then, J f (x)K
J
p
= {y
j
} for
some y
j
∈ P
J
, j ∈ [m]. Moreover, let us recall that
f (x
0
) 6= f (x) = y
j
.
First, let us assume that f touches the line segment
y = y
j
at x, i.e., f (x)= f (x)= f (x)=y
j
.
Let g ∈ G
←→
f
with the constraint that g(x) = y
j
on
JxK
I
S
. Such a function g exists, because f (x) = y
j
6=
f (x
0
), and so
• f
←→
< y
j
≤
←→
f if f (x
0
) < y
j
, or
• f
←→
≤ y
j
<
←→
f if f (x
0
) > y
j
hold on JxK
I
S
.
Then, f
←→
< g
←→
= y
j
on JxK
I
S
if f (x
0
) < y
j
, while
←→
g = y
j
<
←→
f on JxK
I
S
if f (x
0
) > y
j
, i.e., f
IFS
bw
6= g
IFS
bw
which contradicts the condition that f
IFS
bw
is roughly
strong.
Secondly, let us assume that f intersects the line
segment y = y
j
at x. In this case, j ∈]m[, and f (x) =
f (x) = f (x) = y
j
. Hereinafter, the proof is similar to
the previous case.
Case |J f (x)K
J
p
|>1. Then, J f (x)K
J
p
=
h
y
i−1
2
,y
i+1
2
i
for some j ∈ [2m[, j ≡ 1 (mod 2). Moreover, let us
recall that f (x
0
) /∈
h
y
i−1
2
,y
i+1
2
i
.
First, if f (x
0
) < y
i−1
2
, let g ∈ G
←→
f
with the
constraint that g(x) = y
i−1
2
on JxK
I
S
. Such a function
g exists, because f
←→
< y
i−1
2
≤
←→
f holds on JxK
I
S
.
Then, f
←→
< g
←→
= y
i−1
2
on JxK
I
S
, i.e., f
IFS
bw
6= g
IFS
bw
,
which contradicts the condition that f
IFS
bw
is roughly
FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications
272

strong.
Secondly, if f (x
0
) > y
i+1
2
, let g ∈ G
←→
f
with the
constraint that g(x) = y
i+1
2
on JxK
I
S
. Such a function
g exists, because f
←→
≤ y
i+1
2
<
←→
f holds on JxK
I
S
.
Then, g
←→
= y
i+1
2
<
←→
f on JxK
I
S
, i.e., f
IFS
bw
6= g
IFS
bw
,
which contradicts the condition that f
IFS
bw
is roughly
strong.
Corollary 2. A rough real function f ∈ J
I
is (S
I
,P
J
)–
continuous on I if and only if Π
−
f
= Π
←→
f
.
Proof. f is roughly continuous
⇔ f
IFS
bw
is roughly strong by Proposition 8
⇔ f
IFS
pw
= f
IFS
bw
by Proposition 5
⇔ Π
−
f
= Π
←→
f
by Propositions 3 2.
Corollary 3. A rough real function f ∈ J
I
is (S
I
,P
J
)–
continuous on I if and only if G
−
f
= G
←→
f
.
Proof. f is roughly continuous
⇔ f
IFS
bw
is roughly strong by Proposition 8
⇔ f
IFS
pw
= f
IFS
bw
by Proposition 5
⇔ G
−
f
= G
←→
f
by Corollary 1 2.
5 CONCLUSION AND FUTURE
WORK
Rough continuity is a central notion in rough calculus.
This paper has characterized the rough continuity in
three different ways in terms of intuitionistic fuzzy
set theory.
This characterization establishes a connection be-
tween the two theories of uncertainty management,
the rough set theory and intuitionistic fuzzy set
theory. It may allow the application of the means of
intuitionistic fuzzy calculus in rough calculus.
In the future, the investigations can be continued
in several directions. This article has addressed only
one important concept of rough calculus, namely, the
rough continuity. First of all, rough continuity has
some additional features, such as rough discontinuity,
rough Darboux property or Intermediate Value
Property (IVP). The question is how they could also
be captured with the help of IFS tools. Moreover,
the relationships between additional notions of rough
calculus and IFS can also be studied.
Classical Pawlak’s rough set theory has many
different generalizations. The question is whether
they can be captured with IFS tools in one way or
another.
ACKNOWLEDGEMENTS
The author would like to thank the anonymous
referees for their useful comments and suggestions.
REFERENCES
Aquino, G., Rubio, J. D. J., Pacheco, J., Gutierrez, G. J.,
Ochoa, G., Balcazar, R., Cruz, D. R., Garcia, E.,
Novoa, J. F., and Zacarias, A. (2020). Novel nonlinear
hypothesis for the delta parallel robot modeling. IEEE
Access, 8:46324–46334.
Atanassov, K. and Gargov, G. (1989). Interval valued
intuitionistic fuzzy sets. Fuzzy Sets and Systems,
31(3):343–349.
Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy
Sets and Systems, 20(1):87–96.
Atanassov, K. T. (1999). Intuitionistic Fuzzy Sets: Theory
and Applications. Studies in Fuzziness and Soft Com-
puting. Physica-Verlag HD.
Atanassov, K. T. (2012). On Intuitionistic Fuzzy Sets The-
ory, volume 283 of Studies in Fuzziness and Soft Com-
puting. Springer Publishing Company, Incorporated.
Biswas, R. (2000). Rough sets are fuzzy sets. BUSEFAL,
(83):24–30.
Bustince, H. and Burillo, P. (1996). Vague sets are intuition-
istic fuzzy sets. Fuzzy Sets and Systems, 79(3):403–
405.
Chakraborty, M. (2011). On fuzzy sets and rough sets from
the perspective of indiscernibility. In Banerjee, M. and
Seth, A., editors, Logic and Its Applications. 4th In-
dian Conference, ICLA 2011 Delhi, India, January 5-
11, 2011, Proceedings, volume 6521 of LNAI, pages
22–37, Berlin Heidelberg. Springer-Verlag.
Chiang, H., Chen, M., and Huang, Y. (2019). Wavelet-
based EEG processing for epilepsy detection using
fuzzy entropy and associative Petri Net. IEEE Access,
7:103255–103262.
Cornelis, C., De Cock, M., and Kerre, E. (2003). Intuition-
istic fuzzy rough sets: at the crossroads of imperfect
knowledge. Expert Systems, 20(5):260–270.
Csajb
´
ok, Z. E. (2019). On the roughly continuous real func-
tions. In Mih
´
alyde
´
ak, T., Min, F., Wang, G., Baner-
jee, M., D
¨
untsch, I., Suraj, Z., and Ciucci, D., edi-
tors, Rough Sets, pages 52–65, Cham. Springer Inter-
national Publishing.
Csajb
´
ok, Z. E. (2020). On possible approaches to dif-
ferentiation of rough real functions. In Fazekas, I.,
Kov
´
asznai, G., and T
´
om
´
acs, T., editors, 11th Inter-
national Conference on Applied Informatics (ICAI),
number 2650 in CEUR Workshop Proceedings, pages
65–75, Aachen.
Rough Continuity Represented by Intuitionistic Fuzzy Sets
273

Csajb
´
ok, Z. E. and K
¨
odm
¨
on, J. (2020). Roughness and
Fuzziness, pages 23–34. Springer International Pub-
lishing, Cham.
de Jesus Rubio, J. (2009). Sofmls: Online self-organizing
fuzzy modified least-squares network. IEEE Transac-
tions on Fuzzy Systems, 17(6):1296–1309.
Dubois, D. and Prade, H. (1987). Rough fuzzy sets and
fuzzy rough sets. Fuzzy Sets and Systems, 23:3–18.
Dubois, D. and Prade, H. (1992). Putting rough sets and
fuzzy sets together. In Slowinski, R., editor, Intel-
ligent Decision Support - Handbook of Applications
and Advances of the Rough Set Theory, pages 203–
232. Kluwer Academic, Dordrecht.
Dubois, D. and Prade, H., editors (2000). Fundamentals
of Fuzzy Sets. The Handbooks of Fuzzy Sets Series.
Kluwer, Boston, Mass.
Elias, I., Rubio, J. d. J., Martinez, D. I., Vargas, T. M.,
Garcia, V., Mujica-Vargas, D., Meda-Campa
˜
na, J. A.,
Pacheco, J., Gutierrez, G. J., and Zacarias, A. (2020).
Genetic algorithm with radial basis mapping network
for the electricity consumption modeling. Applied Sci-
ences, 10(12):4239.
Gorzałczany, M. B. (1987). A method of inference in ap-
proximate reasoning based on interval-valued fuzzy
sets. Fuzzy Sets and Systems, 21(1):1–17.
Halmos, P. R. (1960). Naive Set Theory. D. Van Nostrand,
Inc., Princeton, N.J.
Hayden, S., Zermelo, E., Fraenkel, A., and Kennison, J.
(1968). Zermelo-Fraenkel set theory. Merrill mathe-
matics series. C. E. Merrill.
Hern
´
andez, G., Zamora, E., Sossa, H., T
´
ellez, G., and
Furl
´
an, F. (2020). Hybrid neural networks for big data
classification. Neurocomputing, 390:327–340.
Klir, G. J. and Yuan, B. (1995). Fuzzy Sets and Fuzzy Logic.
Theory and Applications. Prentice Hall, New Jersey.
Meda-Campa
˜
na, J. A. (2018). On the estimation and con-
trol of nonlinear systems with parametric uncertainties
and noisy outputs. IEEE Access, 6:31968–31973.
Pawlak, Z. (1982). Rough sets. Int. J. Comput. Inf. Sci.,
11(5):341–356.
Pawlak, Z. (1994). Rough real functions. volume 50. Insti-
tute of Computer Science Report, Warsaw University
of Technology, Warsaw.
Pawlak, Z. (1996). Rough sets, rough relations and rough
functions. Fundamenta Informaticae, 27(2/3):103–
108.
Pawlak, Z. (1997). Rough real functions and rough con-
trollers. In Lin, T. and Cercone, N., editors, Rough
Sets and Data Mining: Analysis of Imprecise Data,
pages 139–147, Boston, MA. Kluwer Academic Pub-
lishers.
Rizvi, S., Naqvi, H., and Nadeem, D. (2002). Rough intu-
itionistic fuzzy sets. volume 6, pages 101–104.
Ross, T. J. (2010). Fuzzy Logic with Engineering Applica-
tions. John Wiley & Sons, 3rd edition.
Xu, Y.-H., Wu, W.-Z., and Wang, G. (2014). On the In-
tuitionistic Fuzzy Topological Structures of Rough In-
tuitionistic Fuzzy Sets, volume 8449 of LNCS, pages
1–22. Springer.
Yao, Y. Y. and Zhang, J. P. (2000). Interpreting fuzzy
membership functions in the theory of rough sets. In
Ziarko, W. and Yao, Y. Y., editors, Rough Sets and
Current Trends in Computing, volume 2005 of LNCS,
pages 82–89. Springer.
Zadeh, L. A. (1965). Fuzzy sets. Information and Control,
8(3):338–353.
Zhou, L. and Wu, W.-Z. (2011). Characterization of rough
set approximations in Atanassov intuitionistic fuzzy
set theory. Computers & Mathematics with Applica-
tions, 62(1):282–296.
Zimmermann, H.-J. (2001). Fuzzy Set Theory–and Its Ap-
plications. Springer Netherlands. Fourth Edition.
FCTA 2020 - 12th International Conference on Fuzzy Computation Theory and Applications
274
