On Specifying and Analysing Domain Ontologies for Workflows in
“Binary Model of Knowledge"
Gerald S. Plesniewicz
1
and Valery B. Tarasov
2
1
Applied Mathematics Department, National Research University MPEI, Krasnokazarmennaya 14, Moscow, Russia
2
CIM Department, Bauman Moscow State Technical University, 2
nd
Baumanskaya 5, Moscow, Russia
Keywords: Knowledge Bases, Ontologies, Workflows, Concept Languages, Logical Inference, Analytic Tableaux.
Abstract: The main purpose of the present paper is to show how concept languages of the system “Binary Model of
Knowledge” can be used for specifying workflow ontologies. The system is under development in the
Applied Mathematics and Artificial Intelligence Department of National Research University MPEI
(Moscow). In particular, the system includes the language LTS of temporal specification. The language
includes the sentences matching the sentences of the Boolean and metric extensions of Allen’s interval
logic. For the extended logics we present the complete systems of inference rules (in style of analytic
tableaux).
1 INTRODUCTION
Workflow is a representation of a process whose
participants (agents which are humans or programs),
perform, having a common goal, some set of tasks in
accordance with certain rules and constraints (Aalst
et al., 2002).
The concept of workflow appeared in business
informatics. But at present, the workflow technique is
used in many other areas such as medical informatics,
bioinformatics (in particular, genomics), scientifique
process automation et al.An important application of
workflows is the design of web services.
An ontology is based on a conceptualization. A
conceptualization is an abstract, simplified view of
the subject world that we wish to represent. Every
knowledge base, knowledge-based system, or
knowledge-level agent is committed to some
conceptualization. An ontology is an explicit
specification of a conceptualization (Gruber, 1993).
There are logical approaches to modeling and
analysis of workflows. In such cases a workflow is
considered as an instance of a workflow scheme, and
the scheme is written as a set of sentences in
appropriate logic. Then we get the opportunity to
express properties of workflows and to verify them
using logical procedures. In particular, the co-called
Kifer’s transaction logic was applied (Davulcu, 1989),
(Mukherjee et al., 2002).Also, temporal logics was
used for analyzing workflows (Bettini, 2002).
A conceptualization Czof a workflow scheme
Sfor a real application contains many concepts and
relations between them.It is natural to define in
concept languages an ontology Othat specifies the
conceptualization Cz.
The main purpose of the present paper is to show
how concept languages of the system “Binary Model
of Knowledge” can be used for specifying workflow
ontologies. The system is under development in the
Applied Mathematics Department of National
Research University MPEI (Moscow). In particular,
the system includes the language LTS of temporal
specification. The language includes the sentences
matching the sentences of the Boolean and metric
extensions of Allen’s interval logic. For the
extended logics we present the complete systems of
inference rules (in style of analytic tableaux
(Agostino et al., 2001), (Fitting, 1996)). We show
(by examples) how to use the inference systems for
recognizing inconsistency of ontologies and for
query answering.
2 ABOUT THE SYSTEM
“BINARY MODEL OF
KNOWLEDGE”
“BinaryModel of Knowledge” is the system of
concept languages and tools for their interpretations
Plesniewicz, G. and Tarasov, V.
On Specifying and Analysing Domain Ontologies for Workflows in â
˘
AIJBinary Model of Knowledge".
DOI: 10.5220/0010134902050212
In Proceedings of the 12th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2020) - Volume 2: KEOD, pages 205-212
ISBN: 978-989-758-474-9
Copyright
c
 2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
205

(Plesniewicz, 2014). These languages have
semantics based on formal concepts.
A formal concept has the following components:
 The name C of the concept;
 The unverse U
C
of the concept – a countable
set of names denoting possble instances of the
concept. The universe also contains so-called
surrogates {object-oriented identifyiers):
Surr = {#1, #2,…} ⊆U
C
.
 The extension E
C
of the concept, i.e., the set of
names that denoteinstances of the concept,
E
C
⊆ U
C
;
 The coreferentiality relation ~
C
⊆ E
C
X E
C
.
Ifa ~
C
b then the names a and b denote the
same object of the application modelled.
Example 1. Define a formal concept as follows:
 U
Person
=String ∪
{[Surr:x,Name:y,SSN:z,works_in:u]|
y ∈String, z ∈typeSSN, x, u ∈Surr};
Here typeSSN is the attribute domain (data
type) for social security numbers (i.e., strings
of the format XXX-XX-XXXX, where X are
decimal digits);
 E
Person
= {…,#105,[Surr:#110,
Name:john,SSN:078-05-1120,
works_in:#27],…};
 {…,#105~
Person
[Surr:#105,
Name:john,SSN:078-05-1120,
works_in:#27],…}.
The concept Person has three attributes:
Name,SSN and works_in. The first two attributes
take values in the standard data type String and in
the specified data type typeSSN.The third attribute
takes the value #27 which is the surrogate
referred to some organization where John works.
The conceptPersonfrom Example 1 is static in
the sense that their extensions do not depend on
time. In general, the extension of a concept is
variable. It is natural to introduce a special attribute
Por(point of reference) whose values refer to this
variability.The attribute Por may have such
components as time (point or interval), position in
space, state of affairs, context, truth degree et al.
For any point of reference γ, we denote by E
C
γ
the extension of the concept C at the point of
reference γ. Let Γ be the set of all possible points of
reference that are considered under a given
conceptualization. Then we say that the family of
sets {E
C
γ
| γ ∈ Γ} is thetotal extension of the concept
C,
So, formally conceptualization of a given
application can be represented by a (finite) set S of
formal concepts with the same set Γ of points of
reference. An ontology Othat specifies the set S of
formal concepts is written in the concept languages
of the system BMK.
The sentences of the ontology O differ in what
components of concepts they specify. The sentences
that specify concept universes U
C
(C ∈ S), define the
structure of members of U
C
, and therefore, we call
them structural sentences. We call logical the
sentences that specify the extensions E
C
(C ∈ S). We
also call transitory the sentences that specify the
changes (E
C
γ
– E
C
δ
) ∪ (E
C
δ
– E
C
γ
) in the transition
from the point γ to the point δ.
In the system “Binary Model of Knowledge”,
there are the languages for structural, logical and
transitory specification of ontologies.
2.1 Language LSS of Structural
Specification
In the language LLS two type of concepts are
distinguished: classes and binary relations. LLS
sentences are composed of primitive sentences that
have the following forms:
C[D], C[A:D], C[A:T], (CLD), (CLD)[E],
(CLD)[A:E], (CLD)[A:T].
Here C, D, Eare names of classes, L is a name of
binary relation, A is an attribute, and T is a data type
specification. (There are some means for defining
data types in LSS.)
An arbitrary structural sentence is obtained by
joining primitive sentences. For example, the
sentence C[D, A: (String, Integer), E(*)]arises from
the primitive sentencesC[D], C[A: (String, Integer)]
and C[D, A:E(*)].
Here are some examples of structural sentences.
1) Car[Brand:String,Engine,
Dimensions:
(Length/m/:Integer,
Width/mm/:Integer,
Height/mm/:Integer,
Wheelbase/mm/:Integer)
Gearbox:String].
2) Engine[Type:Integer,
Power/hp/:Integer,
Max_speed/km/h/: Integer].
3)(Person owns Car}
[RegisterDate:Date,
DocsReg:String].
The assertion e ∈ E
C
γ
 corresponds to the fact
“e is an instance of the concept C at the point of
reference γ”, and e ∉E
C
γ
corresponds to the fact
KEOD 2020 - 12th International Conference on Knowledge Engineering and Ontology Development
206

“e is a counter-instance of the concept C at the point
of reference γ”.
In the system BMK facts are represented as
tuples of the tables whose headers are determines by
LSS sentences. For example, the second sentence
determines the following table header.
Engine
Surr Por Type Power Max_speed
Note that the language LSS is essentially a data
description language for some object-oriented
language model. In the system BMK there is an
appropriate query language.
2.2 Language LLS of Logical
Specification
There are several types of LLS sentences. Here are
some examples of LLS sentences:
1) Car ISA Car(Engine.
Max_speed/km/h/ =< 300).
(Every car has a maximum speed of not more than
300 kilometers per hour.)
2) Minivan == Car(Dimension.
Length/mm/ =< 3600;
Width/mm/ =< 1600).
3) NOT EXIST Person THAT own SOME
Car THAT has a SOME Defect.
(There is no person who owns a car with a defect.)
4) EACH Product(Brand = AAA)
Transported_bySOME Minivan.
(Each brand AAA product is transported by a
minivan owned by the company “TransVan”.)
5) EACH Product(Brand = BBB) NOT
Transported_byANYCar THAT
Belong_to “RoadTrans”.
(No BBB products are transported by cars of the
firm RoadTrans.)
2.3 Language LTS of Temporal
Specification
In workflow ontologies, the main role is played by
events, i.e. concepts whose instances exist in
temporal intervals.
If the concept E is an event then it has two
special attributes Beg(begin) and End. Thus, When
we use language LTS for specifying such
ontologies, we chose events for modelling workflow
tasks (works).
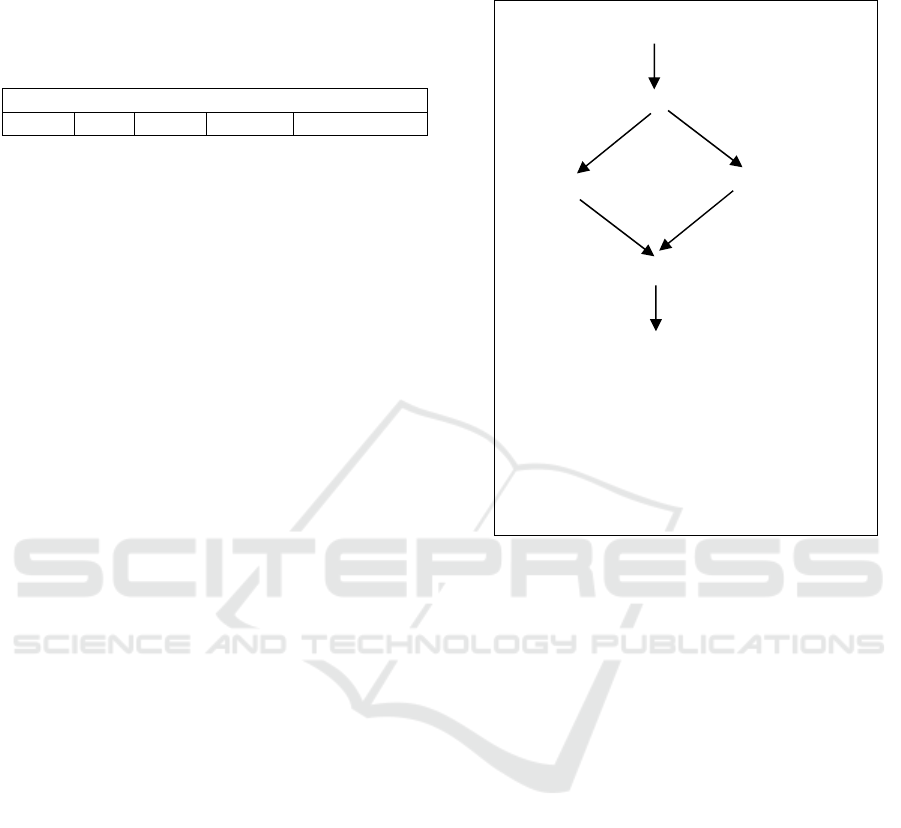
Consider a simple example of a workflow.
Example 2. The workflow represents a business
process that aims to transport goods by trucksof two
companies “TransVan” and “RoadTrans”. Figure 2
shows a diagram of tasks and relations between
them that determine their possible sequencing.
A
B
C D
E
F
Legend:
A: order processing
B: invoice registration
C: goods transportation by“TransVan”
D: goods transportation by “RoadTrans”
E: goods unloading
F: payment registration
Figure 1: Example of workflow scheme.
The business process of goods transportation
starts with an order processing (task A). Then, the
invoice is registered (task D) and the goods
transportation is carried out (tasks C and D).
Suppose, there is a condition p affecting how the
transportation is carried out. If p is satisfied then all
goods are transported by the company “TransVan”.
Otherwise, ittransports only part of the goods, and
the rest is transported by the firm “RoadTrans”; in
this case “RoadTrans” starts loading the goods a
little later and brings the goods later than
“TransVan”. After delivery, the goods are
unloaded(task E). Finely, the payment is
registered(task F).
In the language LTS, the temporal relations
between tasks can be write as following workflow
ontology:
O = {
OrderProc BEFOREInvoiceRegist.
InvoiceRegist BEFORE Transp1.
Transp1 ISA Transp.
Transp2 ISA Transp.
IF CondP THEN
Transp1 OVERLAP Transp2.
Transp BEFORE Unload.
Unload BEFORE PaymentRegist}.
On Specifying and Analysing Domain Ontologies for Workflows in â
˘
AIJBinary Model of Knowledge"
207

This ontology is written in the language LTL of
temporal specification from the system BMK, more
exactly, in the fragment of LTL consisted in the
sentences that correspond to Boolean extension of
Allen’s temporalinterval logic BAL. With the logic
BAL we can determine relations between temporal
intervals during which works are performed.
For example, the LTL sentence
IF W1 BEFORE W2 THEN (W2 START
W3)
OR (W3 START W2).
states that if it turns out that work W1 was
performed before work W2, then work W2 should
be started simultaneously with work W3.
In the ontology Othe namesBEFOREand
OVERLAP denote are the relations between events
that correspond to Allen’s relations b and obetween
temporal intervals (Allen, 1983). There are 7 Allen’s
relations and 6 inverse relations:
BEFORE(b), MEET(m),DURING(d),START(s),
OVERLAP (o), FINISH (f),EQUAL (e),
AFTER(b
–1
),MET-BY(m
–1
),CONTAIN (d
–1
),
STARTED-BY(s
–1
),OVERLAPPED-BY(o
–1
),
FINISHED-BY(b
–1
).
(v
–1
denotes the reverse relation: A v
–1
B BvA.)
The language LTS contains also the temporal
quantifiers ANYTIME and SOMETIME.
The following sentence specifies the concept
“former car owner”:
‘Former car owner’ ==Person THAT
Own (SOMETIME X) SOME Car;X
BEFORENow.
The following term defines those persons who at the
current moment (expressed by the time interval
NOW) have changed their Audi 200 car to a Toyota
Land Cruiser:
Person THAT Owns (SOMETIME X)
SOME Car (Brand=‘Audi 200’) AND
Owns (SOMETIME Y)SOME
Car(Make=‘Toyota land cruiser’);
X START NOW; NOW FINISH Y;
X MEET Y.
3 BOLEAN AND METRIC
EXTENSIONS OF ALLEN’ S
INTERVAL LOGIC
The above mention workflow ontology O can be
rewrite in Allen’s notation as
O
A
= {A b BBbC, B bD, C b E, D b E, Eb F,
p →Do F},
where the names of the intervals in O are renamed
accordingly. In general, let O
A
denote the result of
such renaming for anyLTS ontologyO.
It is clear, if the ontology O
A
is inconsistent then
the ontology O is also inconsistent. Since the
problem of logical consequence is reduced to the
problem of inconsistency, then for any sentence φ,
O|= φ takes place if O
A
|= φ
A
.
3.1 Boolean Extension of Allen’s Logic
Let Ω = {b, m, d,s, o, f, e, b
–1
, m
–1
, d
–1
, s
–1
, o
–1
, b
–1
}.
A sentence of Allen’s logic AL has the form A ω B
where A, B are temporal interval and ω is a subset
of Ω written as a word. (For example, A bdm
–1
B is
a AL sentence.This sentence is equivalent to the
disjunction A b B∨A dB∨BmA.)
Table 2: Inference rules for propositional connectives.
No Antecedent Consequents
1 +~p –p
2 –~p +p
3
+ p∧q
+p, +q
4
– p∧q
–p |–q
5
+ p∨ q
+p |+q
6
– p∨q
–p, –q
7 + p→q –p |+q
8 – p→q +p, –q
Table 3: Inference rules for Allen’s connectives.
No Antecedent Consequent
1 +А b В В
–
–A
+
≥ 1
2 –А b В A
+
–B
–
≥0
3 +А m В А
+
=В
–
4 – А m В A
+
–В
–
≥ 1 |B
–
–A
+
≥ 1
5 + А oВ B
–
–A
–
≥ 1, A
+
–B
–
≥ 1, B
+
–A
+
≥ 1
6 – А oВ A
–
–B
–
≥ 0 |B
–
–A
+
≥ 0 |A
+
–B
+
≥ 0
7 + А fВ А
–
–В
–
≥ 1, А
+
=В
+
8 – А fВ В
–
–А
–
≥ 0|А
+
–B
+
≥ 1| B
+
–A
+
≥ 1
9
+ А sВ
А
–
=В
–
, B
+
–A
+
≥ 1
10 – А sВ A
–
–B
–
≥ 1 |B
–
–A
–
≥ 1 |A
+
–B
+
≥ 0
11 + А dВ A
–
–B
–
≥ 1, B
+
–A
+
≥ 1
12 – А dВ B
–
–A
–
≥ 0| A
+
–B
+
≥ 0
13 +А eВ A
–
= B
–
, A
+
= B
+
14
– А eВ B
–
–A
–
≥ 1 |A
–
–B
–
≥ 1
B
+
–A
–
≥ 1 |A
–
–B
–
≥ 1
15 + A θ
–1
B +Bθ A
16 –А θ
–1
В –B θA
17 + А θωВ + А θ В| + А ωВ
18 –А θωВ –А θ В,–А ωВ
θ ∈Ω, ω ⊆Ω
KEOD 2020 - 12th International Conference on Knowledge Engineering and Ontology Development
208

The Boolean extension BAL of Allen’s logic AL
has Boolean combinations of AL sentences and
propositional variables as its sentences. (For
example,
(p∧~q→ ~A b B∧B sdoC) ∨ ~A f C
is a BAL sentence.)
The tables Table 1 and Table 2 contain the
inference rules by analytic tableaux method for the
logic BAL. (Note that the rules of Table 1 is usual
tableaux inference rules for signified propositional
formulas (Fitting, 1996).)
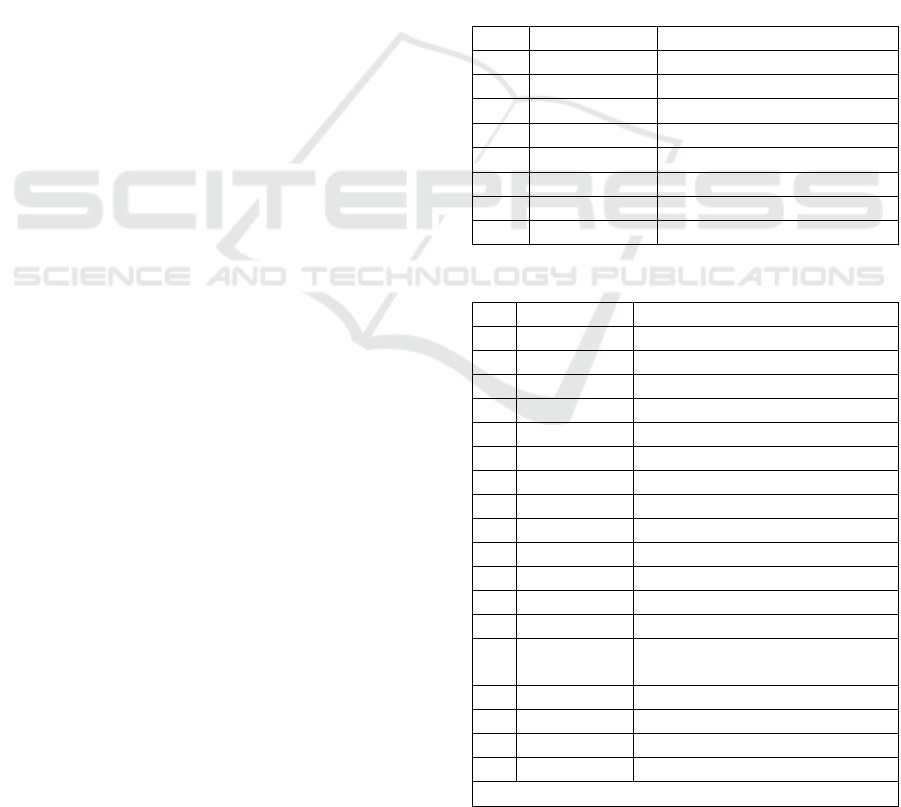
Consider an example ofan inference tree for
proving logical consequences in the logic BAL.
Example 3. Take three sentences
p → A m B, ~B bm C →q,A o D ∧ D o C
as an ontology Oin the logic BAL.
For the sentence p∧~q → B d D, let us put the
question O|= p∧~q → B d D ? (“Is it true or not
that O logically impliesp∧~q → B d D ?”)
Due the known relation between the problems of
inconsistency and logical consequence, we have
O|= p∧~q → B d D
if and only if the set O∪ {~(p∧~q →B d D)} is
inconsistent, i.e. the set
E = {p→A m B, ~B bm C→q, A o D ∧ D o C,
~(p∧~q →B d D)}
is inconsistent.
Figure 2 shows the inference tree built for
proving the inconsistency of the set E. We started
by writing formulas from E with “+” signs as the
initial branch of the inference tree. Then inference
rules are applied step by step to the BAL sentences
assigned to the vertices of the tree under
construction.
So, at step 1, the rule 3 from Table 2 is applied
to the sentence +A o D ∧ D o C. As a result of
applying the rule, two sentences +A o Dand+D o C
are obtained that are attached sequentially to the
initial branch. At step 8, the rule 7 from Table 2 is
applied to the sentence +p → A m B.As a result, two
sentences – pand +Am
Bare obtained, and the “fork”
of these sentences is attached to the current branch
of the tree.
Here we followed the standard tactics for
choosing the sentence to which an inference rule
should be applied and choosing the branches to
which the resulting consequents should be attached
(Fitting, 1996).
The sign “X” attached to the branch at step 9
signalized that it is closed in the sense that the
sentences and inequalitiesfrom the branch form an
inconsistent set (in this case, due the presence of +p
and –p). So, in the inference tree there are two
brunches marked by the sign “X”.
+p → A m B [8]
+~B bm C →q [11]
+A o D ∧ D o C [1]
+ ~p∧~q → B d D[2]
1: +A o D [6]
1: + D o C [7]
2: – ~p∧~q → B d D[3]
3: +p∧~q[4]
3: – B d D[14]
4: + p (9)
4: + ~q [5]
5: – q (12)
6: D
–
–A
–
≥ 1
6: A
+
–D
–
≥ 1
6: D
+
–A
+
≥ 1
7: C
–
–D
–
≥ 1
7: D
+
–C
–
≥ 1
7: C
+
–D
+
≥ 1
_________|_________
| |
8: – p(9) 8: +AmB[10]
9:X 10: А
+
= В
–
________|_______
| |
11 – ~BbmC[13] 11: +q(12)
13: +BbmC[15] 12: X
_____|___________
| |
14:D
–
–B
–
≥ 0 14: B
+
–D
+
≥ 0
___|_____ ______|______
| | | |
15:+BbC [16] | 15:+BbC[18] |
16:C
–
–B
+
≥1 | 18:C
–
–B
+
≥1 15:+BbC[19]
15:+BmC[17] 19:C
–
–B
+
≥1
17: В
+-
= C
–
Figure 2: Inference tree for the set E.
Let us write out inequalities from other branches:
E
1
= {D
–
–A
–
≥1, A
+
–D
–
≥1,D
+
–A
+
≥1,
C
–
–D
–
≥ 1, D
+
–C
–
≥ 1, C
+
–D
+
≥ 1,
А
+
= В
–
,D
–
–B
–
≥ 0, C
–
–B
+
≥ 1},
E
2
= {D
–
–A
–
≥1, A
+
–D
–
≥1,D
+
–A
+
≥1,
C
–
–D
–
≥ 1, D
+
–C
–
≥ 1, C
+
–D
+
≥ 1,
А
+
= В
–
, D
–
–B
–
≥ 0,В
+-
= C
–
},
E
3
= {D
–
–A
–
≥1, A
+
–D
–
≥1,D
+
–A
+
≥1,
C
–
–D
–
≥ 1, D
+
–C
–
≥ 1, C
+
–D
+
≥ 1,
А
+
= В
–
,B
+
–D
+
≥ 0,C
–
–B
+
≥ 1},
E
4
= {D
–
–A
–
≥1, A
+
–D
–
≥1,D
+
–A
+
≥1,
C
–
–D
–
≥ 1, D
+
–C
–
≥ 1, C
+
–D
+
≥ 1,
А
+
= В
–
,B
+
–D
+
≥ 0, В
+-
= C
–
}.
Let us add toevery E
i
the standard inequalities A
+
–A
–
≥ 1, B
+
–B
–
≥ 1,C
+
–C
–
≥ 1,D
+
–D
–
≥ 1,and denote E
i
*
the resulting set.
On Specifying and Analysing Domain Ontologies for Workflows in â
˘
AIJBinary Model of Knowledge"
209

It turns out that the sets E
i
* are inconsistent. In
fact, consider, for example, the set E
1
*. It contains
the inequalities А
+
= В
–
,D
–
–B
–
≥ 0, A
+
–D
–
≥1. From
here we have
В
–
–А
+
≥ 0,D
–
–B
–
≥ 0, A
+
–D
–
≥ 1.
Adding up these inequalities, we get
(В
–
–А
+
).+ (D
–
–B
–
) +(A
+
–D
–
)≥ 0 + 0 + 1,
i.e. the contradictory 0 ≥ 1. Thus, the setE
1
* is
inconsistent.
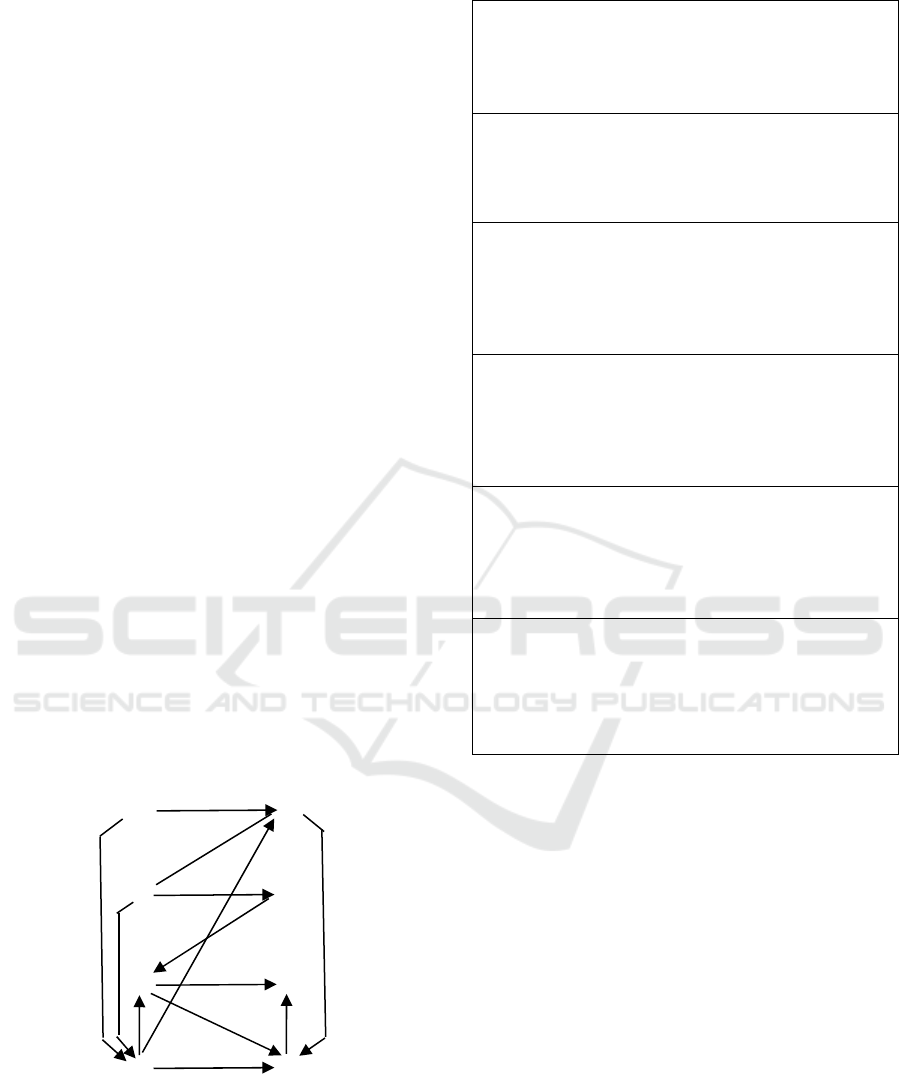
Let us associate with any setSof inequalities of
the form X
i
– X
j
≥ r (r∈ {0, 1}) the following graph
Γ(S):
• The set of Γ(S) vertices makes up of X
i
;
• The set of Γ(S) edges with labels makes up of
(X
i
, X
j
, r) such that X
i
– X
j
≥ r.
Figure 3 shows the graph Γ(E
1
*).
It easy to prove that the set of inequalities S is
inconsistent if and only if the graph Γ(S) contains a
positive cycle (i.e., the cycle having at least one
edge with the label 1).
For example, the graph Γ(E
1
*) in Figure 3 has
the positive cycle
(B
–
,D
–
,0), (D
–
, A
+
, 1), (A
+
, B
–
, 0).
Hence, the set E
1
* is inconsistent.
Thus, we can apply an algorithm for detecting
positive cycles in the graph Γ(S) to recognize the
inconsistency of the set S of inequalities.Hence, the
set E
1
* is inconsistent.
3.2 Metric Extension of Allen’s Logic
This logic MAL is an extension of the logic BAL by
inserting durations of temporal intervals and their
fragments into AL sentences.
A
–
A
+
B
–
B
+
0
C
–
C
+
D
–
D
+
Figure 3: Graph Γ(E
1
*).
The fragments of intervals entering sentences are
denoted by I, J and K. Figure 4 shows how they are
represented by the ends of temporal intervals in AL
sentences. For example, for the sentence A b Bwe
have I =A
+
– A
–
, J =B
–
–A
+
and K =B
+
–B
–
.
A bB
A
–
========= A
+
B
–
======B
+
|-------- I ---------|------ J ------|---- K ------|
I =A
+
– A
–
J =B
–
– A
+
K =B
+
– B
–
A mB
A
–
========== A
+
=B
–
=====B
+
|---------- I --------|-------K -------|
I =A
+
– A
–
K =B
+
– B
–
A d B
A
–
======= A
+
B
–
=========================B
+
|------ I ------|------ J -------|----- K ------|
I =A
–
– B
–
J =A
+
– A
–
K =B
+
– A
+
A s B
A
–
========= A
+
B
–
====================B
+
|-------- J -------|-------K --------|
J = A
+
– A
–
K =B
+
– B
–
A o B
A
–
================== A
+
B
–
====================B
+
|------ I ------|--------- J -------|------- K -------|
I = B
–
– A
–
J = A
+
– B
–
K =B
+
– A
–
A fB
A
–
========= A
+
B
–
====================B
+
|-------- I --------|--------J-------|
I =A
–
– B
–
J = A
+
– A
–
Figure 4: Intervals and their fragments for AL sentences.
sentences. For example, for the sentence A b Bwe
have I =A
+
– A
–
, J =B
–
–A
+
and K =B
+
–B
–
.
The expressions of the form
I ≥ r, J ≥ r, K ≥ r, I ≤ r, J ≤ r, J ≤ r,K ≤r
where r is an integer, are called α-estimates. Also,
α-termsare conjunctions of α-estimates where
semicolons are used as conjunction signs. For
example, the expression
I ≤2; I ≥5;J ≤–1;K ≤4; K ≥ 2
an α-term.Another type estimates is β-estimates:
X– Y ≥ r, X– Y ≥ r (X, Y ∈ A
+
, B
+
, A
–
, B
–
}, X
≠Y}. Also, β-terms are conjunctions β-estimates.
Sentences of the logic MAL are obtained by
inserting α-estimates and α into BAL sentences
For example, from the BAL sentence
A bs B ∧B d C → A foC
we can obtain the MAL sentence
A b(J ≥ 2)s B ∧B d C→A f(I ≥ 3; K ≤ 5)o C.
KEOD 2020 - 12th International Conference on Knowledge Engineering and Ontology Development
210

The inference system for the logic MAL consists
the rules entering the tables Table 1 – Table 4.
Table 4: Inference rules for the logic MAL.
No Antecedent Consequents
1 +A θ(τ)B +A θB, +θ(τ)
2 +A θ
–1
(τ)B +B θA, +θ(τ)
3 – A θ(τ)B –A θB|–θ(τ)
4 – A θ
–1
(τ)B –B θA|–θ(τ)
5 + b(τ)
+ τ{I :=A
+
– A
–
, J :=B
–
– A
+
,
K:=B
+
– B
–
}
7 + m(τ) +τ{I :=A
+
–A
–
,K :=B
+
– B
–
}
9 + d(τ)
+τ{I :=A
–
– B
–
,J := A
+
– A,
K := B
+
– A
+
}
11 +s(τ) τ{I :=A
+
– A
–
,K :=B
+
– B
–
}
9 + o(τ)
τ{ I :=A
–
– B
–
,J := A
+
– B
–
;
K :=B
+
– B
–
}
11 + f(τ) +τ{I :=A
–
– B
–
,J :=A
+
– A
–
}
12 +σ;τ +σ, +τ
13 –σ;τ –σ | –τ
Plus the rules which the same as the rules 5 – 11
but with the replacement the signs ‘+’ with ‘–‘..
Consider an example of an inference in the
logicMAL.
Example 4. Let there are three works Wa,Wb
and Wc with temporal intervals A, B, C, the lengths
of which are 4, 8, and 5, respectively. In addition,
there are conditions p and q for which the following
statements are true:
(1) if p is true, then Wa is performed during
Wb, and Wafinishes 2-4 time units before
the end of Wb;
(2) ifqis true, then action Wcfinishes with
action Wb.
Put the question: “Does action aoverlap in time
with action c, under the assumption that both
conditions p and q are satisfied? If so, then find the
best estimate for the overlap time.”
This knowledge can be represent in the language
MAL an ontology:
O ={|A| = 4, |B| = 8, |C| = 5,
p→Ad(2 ≤ K ≤4) B, q → C f B}.
The question can be written as the query to the
knowledge base O:
Q: ? max x, min y
: p ∧ q →A o(x ≤J≤y)C.
Fig.5 shows the inference tree for the set of
signed sentences +Kb∪ {–p ∧ q →A o(x ≤J≤y) C}.
The fourth branch of the graph contains the
following inequalities (β-estimates):
A
+
– A
–
≥ 4, A
–
– A
+
≥ –4, B
+
– B
–
≥ 8,B
–
– B
+
≥ –8,
C
+
– C
–
≥ 5,C
–
– C
+
≥ –5, A
–
–B
–
≥ 1, B
+
–A
+
≥ 2,
+|A| = 4 [1]
+|B| = 8 [2]
+|C| = 5 [3]
+p → A d(2 ≤ K ≤4) B [6]
+q → C f B [11]
– p ∧q → A o(x ≤ J ≤ y) C [4]
1: A
+
– A
–
≥ 4
1: A
–
– A
+
≥ –4
2: B
+
– B
–
≥ 8
2: B
–
– B
+
≥ –8
3: C
+
– C
–
≥ 5
3: C
–
– C
+
≥ –5
4: +p ∧q [5]
4: –A o(x ≤ J ≤ y) C [14]
5: +p [7]
5: +q [12]
_______|______
| |
6: –p [7] 6: +A d(2 ≤ K ≤4) B [8]
7: X 8: +A dB [9]
8: 2 ≤ K ≤4 [10]
9: A
–
–B
–
≥ 1
9: B
+
–A
+
≥ 1
10: B
+
–A
+
≥ 2
10: A
+
–B
+
≥ – 3
_______|______
| |
11: –q [12] 11: +CfB [13]
12: X 13:C
–
–В
–
≥ 1
13: C
+
=В
+
_________|___________
| |
14: –AoC 14: – x ≤ J ≤ y
________|________ |
| | | _______|___
А
–
–C
–
≥1 C
–
–A
+
≥1 А
+
–C
+
≥1 | |
C
–
–A
+
≥1– x A
–
–C
+
≥ y– 1
Figure 5: Inference tree for knowledge base in Example 4.
4 4
A
–
A
+
A
–
A
+
–4 –4
–3 2 –3 2
8 8
B
–
B
+
B
–
B
+
–8 –8
0 0
1–x 1+ y
5 5
C
–
C
+
C
–
C
+
–5 –5
Figure 6: Graphs for the fourth and the fifth branches of
the inference tree.
On Specifying and Analysing Domain Ontologies for Workflows in â
˘
AIJBinary Model of Knowledge"
211

Fig.6 shows the graph constructed from this
inequalities. It easy to see that the graph contain
cycle
A
+
, C
–
,C
+
, A
+
, which corresponds to the inequalities
C
–
– A
+
≥1– x, C
+
– C
–
≥5, B
–
– C
+
≥0, A
+
– B
–
≥–3.
Adding up these inequalities, we obtain the
inequality 0 ≥ 1 – x + 5 + 0 –3, i.e., 0 ≥ 3– x.
Therefore, this inequality is contradictory if and only
if x ≤ 2. Thus, 2 is the maximum of x when the
fourth branch is closed.
Similarly, in the fifth graph there is the cycle
A
+
, B
+
, C
+
, C
–
,A
+
with the corresponding inequalities
B
+
–A
+
≥2, C
+
–B
+
≥ 0, C
+
–C
–
≥–5, A
+
– C
–
≥y– 1.
Adding up these inequalities, we obtain the
inequality 0 ≥ 2 + 0 – 5 + 1+ y –1, i.e., 0 ≥ y– 3.
Therefore, this inequality is contradictory if and only
if y ≥ 4. Thus,4 is the minimum of y when the fifth
branch is closed.
It is easy to verify that the first 3 branches are
closed. Thus, x = 2, y = 4 is the answer to the query
Q addressed the knowledge base O.
4 CONCLUSION
We examined the possibility of using the
languagesof the system “Binary Model of
Knowledge” for describing domain workflow
ontologies. The languages have users-friendly
syntax and semantics which is based on formal
concepts. It is important for workflows to model
temporal properties. In “Binary Model of
Knowledge”, there is the language LTS of temporal
specification. We have introduced the logic that
extends Allen’s interval logic by inserting durations
of temporal intervals and their fragments.
ACKNOWLEDGEMENTS
This work was supported by Russian Foundation for
Basic Research (projects 20-07-00615, 18-29-03088,
20-57-00015 and 20-07-00770).
REFERENCES
Aalst, W.H.P van der, Hee K.M. van, 2002. Workflow
Management: Models, Methods and Systems, MIT
Press, Cambridge.
Agostino, M., Gabbay, D.,Hahnle, R., Possega, 2002.
Handbook of tableaux methods, Springer (2001).
Allen, J.F., 1983. Maintaining Knowledge about Temporal
Intervals. Communications of the ACM, 26(11).
Bettini, X. Wang, and S. Jajodia. Temporal Reasoning in
Workflow Systems. Distributed and Parallel
Databases, 11(3):269–306, 2002.
Davulcu, H., M. Kifer, M., 1998, Ramakrishnan, C.,
Ramakrishnan, I. Logic based modelling and analysis
of workflows. In ACM International Symposium on
Principles of Database Systems (PODS),
Fitting, M., 1996.First-order logic and automated theorem
proving, Springer.
Gruber, T.R., 1993. Translation approach to portable
ontology specifications. Knowledge Acquisition, 5(2).
Mukherjee, S., Davulcu, H., Kifer, M., Senkul, S., Yang,
G., 2003. Logic based approaches to workflow
modeling and verification. In J. Chomicki, R. van der
Meyden, and G. Saake, editors, Logics for Emerging
Applications of Databases. Springer Verlag.
Plesniewicz, G. S., Karabekov, B. S., 2014.
Ontologies in the “Binary Model of Knowledge”.
ProgrammnyjeProduktyiSistemy, 1 (105).
KEOD 2020 - 12th International Conference on Knowledge Engineering and Ontology Development
212