
Intensional Model for Data Integration System in Open Environment
Islam Ali and Kenneth McIsaac
Department of Electrical and Computer Engineering, Western University, Richmond Street, London, Ontario, Canada
Keywords: Data Integration, Data Integration System, Mediated-P2P, Intentional Modeling, Open Environment,
Epistemic Logic, Intensional Epistemic Logic.
Abstract: Open environment allows agents to associate and/or dissociate with the environment without affecting the
overall functionality of the system. There are several challenges to modeling data integration systems (DIS)
in open environment. This is because of the distributed, dynamic, heterogeneous, and loosely coupled nature
of open environment. It is also important to note that information systems are intensional in nature. This is
because the belief of an agent and the knowledge of an information system are intensional contexts. Open
environments are also intensional in nature. This is because, the dynamic nature of open environment
imposes no constrains on the set of participating agents or the number information systems plugged into the
system. We propose the use of Mediated P2P architecture for the architecture of data integration systems in
open environment. The DIS is formulated using Intensional Epistemic Logic (IEL). We also present an
interface and query answering semantics that are based on the IEL. The proposed model accounts for the
intensional, distributed, dynamic, and loosely-coupled characteristics of open environment.
1 INTRODUCTION
Ontology is being used, to address the issue of
heterogeneity between various data sources, in
several fields. (Gusenkov, Bukharaev, and Birialtsev
2019) applied the use of ontology to corporate data
integration. (Chen et al. 2017) used a goal driven
learning process to construct an ontology that
evolves through a learning process. Ontology has
also been applied in toxicology (Boyles et al. 2019),
air traffic management (Egami et al. 2020) and many
other fields. This is because ontologies have explicit
semantics. These semantics are maintainable and, if
maintained, are up to date. Ontology has also been
used to bridge the heterogeneity gap in open
environment (Wang 2009), (Xue 2010), and (Ali and
Ghenniwa 2014).
In open environment, however, there are several
other challenges. The dynamic nature is one of the
most challenging aspects for modeling in open
environment (Ali and Ghenniwa 2012) and (Ali and
Ghenniwa 2014). In open environment, there are no
constraints on the set of data sources or the number
of information systems plugged into the system. The
system needs to account for data sources entering
and leaving the environment at any time (Ali and
Ghenniwa 2012) and (Ali and Ghenniwa 2014).
Open environments are also distributed in nature.
Moreover, the agents that associate with the
environment can posses certain degree of autonomy.
This means, the knowledge of each agent about the
beliefs of another agent can be different. This is
because these relative beliefs will depend on what
each agent decide to share with other agents. It will
also depend on any accessibility rules and
constraints each agent sets while dealing with other
agents. This emphasises the loosely-coupled nature
of open environment (Ali and Ghenniwa 2014).
(Wang 2009) proposed a framework to address
the heterogeneous, autonomous, and distributed
characteristics of open environment. The proposed
model followed an extensional reduction
formalization (Guarino and Giaretta 1995), (Guarino
1998), and (Guarino, Oberle, and Staab 2009). The
extensional reduction model is based on the possible
world approach (Anderson 1984). There are several
formal and intuitive concerns about the use of
possible world approach to describe intensional
matters (Jubien 1988), (Bealer 1982), (Bealer 1998),
and (Bealer 1979). As shown in (Ali and Ghenniwa
2012) and (Ali and Ghenniwa 2014), this is
particularly challenging when modeling information
systems in open environment. This is also quite
evident in (Wang 2009) when the author uses a
Ali, I. and McIsaac, K.
Intensional Model for Data Integration System in Open Environment.
DOI: 10.5220/0010132201890196
In Proceedings of the 12th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2020) - Volume 2: KEOD, pages 189-196
ISBN: 978-989-758-474-9
Copyright
c
2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
189

definition for equivalence that is extensional in
nature.
(Xue 2010) presented another framework to
address the data integration in open environment.
The author attempted to address three main issues,
namely; the heterogeneity, the architecture, and the
modeling and representation of ontologies. The
author in (Xue 2010) proposed the use of ontology
and semantic matching to bridge the heterogeneity
gap between various information systems. In (Xue
2010), however, database schemas were used to
extract semantics and to generate ontologies. This
yields a set of data-driven-ontologies (DDO). The
use of DDO is a good idea when an ontology is
missing. However, relying on the schema as a source
of semantics is inadequate. This is because the
semantics embedded in the database schemas are
lost, tossed, outdated, and/or not maintainable.
Moreover, the author in (Xue 2010) employed a
frame-based language (Xue, Ghenniwa, and Shen
2010). It is known that Frame-based languages are
limited in their expressiveness and reasoning. The
semantics of Frame-based languages are also not
precisely defined (Selman and Levesque 1993). The
author in (Xue 2010) also used an extensional
reduction model. It has been shown in (Ali and
Ghenniwa 2012) and (Ali and Ghenniwa 2014) that
the extension reduction model does not address the
needs of an open environment.
And finally, a mediated architecture was adopted
by (Xue 2010). Similar architectures are also utilized
in (Ali and Ghenniwa 2014), (Calvanese et al. 2018)
and (De Giacomo et al. 2018). The mediated
architecture relaxes the requirement that each
information system behaves as a DIS on its own.
This is a constraint that P2P systems (Majkić 2009)
naturally require. On the other hand, the mediated
architecture is centralized and, as such, is not
adequate for open environment.
In this work, a framework for data integration
system is presented. The proposed framework
addresses the issues mentioned above. We will start
by shedding some light on the IEL as the IEL is
important to modeling DIS in open environment.
2 PROPOSITIONAL EPISTEMIC
LOGIC
Epistemic logic is the logic of knowledge and belief.
Even though, epistemic logic and doxastic logic
formalize the knowledge and belief, respectively, the
term epistemic logic is also commonly used to refer
to both the logic of knowledge and the logic of
belief. The main focus of epistemic logic is the
propositional knowledge. That said, an agent bears
the propositional attitude “knowing” or “believing”
towards a proposition. As such, when we say: “Joe
knows that Tom loves Merry” we are asserting that
Joe is an agent who bears the propositional attitude
“knows” towards the proposition expressed by “Tom
loves Merry”.
The syntax of the propositional epistemic logic is
simply the result of augmenting the language of
propositional logic with the unary knowledge or
belief operators K
a
or B
a
; where a is an agent, and
the operators K and B are the epistemic operators for
knowledge and belief respectively. In that sense, if P
is an arbitrary proposition, following is how these
operators are read:
K
a
P reads “Agent a knows that P”
And for the belief operator of doxastic logic:
B
a
P reads “Agent a believes that P”
3 INTENSIONAL EPISTEMIC
LOGIC
As discussed in (Fitting 2006) and (Bealer 1979)
knowledge and beliefs are intensional matters. The
same interpretation is adopted by (Ali and
Ghenniwa 2012) in the context of knowledge
engineering. IEL (Jiang 1993) offers a way to
properly handle relative intensions in nested
believes. The most distinguished feature of the
intensional epistemic logic is the use of intensional
index on the terms. The basic idea is that, given a
formula like B
a
p(b), b does not have to have to be
rigid. That means, b does not have to have the same
meaning everywhere in the formula or same
denotation in all possible worlds. And so, we need
some mean to distinguish the case when b is
evaluated inside the intensional scope of agent a,
and the case when b is evaluated outside the
intensional scope of agent a. to achieve this, a
superscripted index is attached to each term to
denote the number of the believe operator that
contains the intended meaning of the term. If a term
is not attached with an intensional index, then the
intended meaning of the term is rigid. For example;
the formula B
a
(Q B
b
Q), where Q’s intended
meaning is in the scope of B
a
, can be represented in
IEL as B
a
(Q
1
B
b
Q
1
). If the second Q in the original
formula is intended to be local to B
b
, then the
KEOD 2020 - 12th International Conference on Knowledge Engineering and Ontology Development
190
formula should be represented, in IEL, as: B
a
(Q
1
B
b
Q
2
).
As such, the language for IEL (Jiang 1993) is a
first order logic language with equality, augmented
with the believe operator B for each agent, with
superscripted terms.
4 INTENSONAL MODEL FOR
ONTOLOGY-BASED DIS
There are two major architectures for virtual data
integration; the mediated architecture, and the Peer-
to-Peer P2P architecture. While a P2P DIS allows
the flexibility of querying against any peer, the
mediator-based approach does not require every
single information system to act as a DIS on its own.
The P2P architecture, however, requires that every
information system behaves as a DIS. This is too
high of an expectation in open environment. At the
same time, the mediated architecture adopted in,
(Xue 2010) and (Ali and Ghenniwa 2014), is
centralized. This makes it inadequate for an open
environment which is distributed in nature.
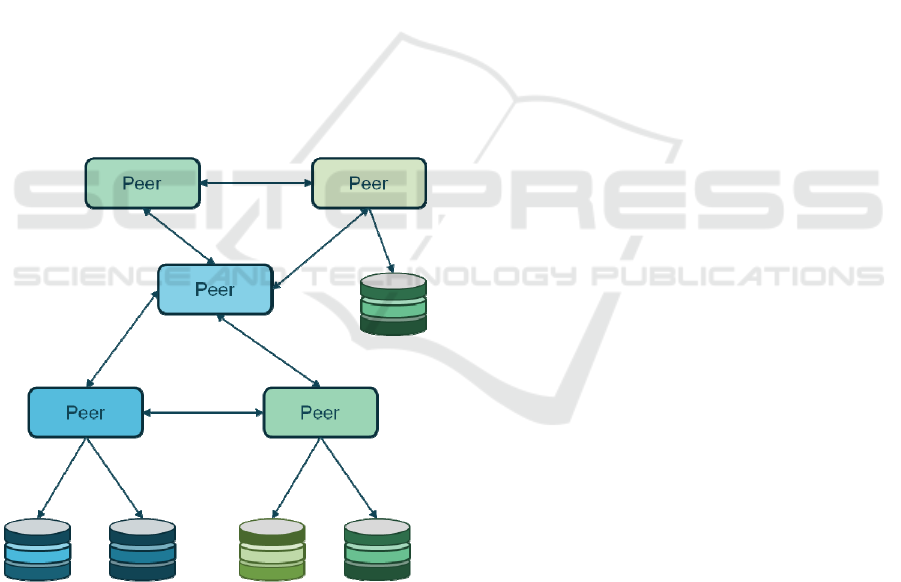
Figure 1: Mediated Peer-to-Peer Architecture.
We argue that the Mediated P2P architecture,
first proposed in (Halevy et al. 2003) and
(Lumineau, Doucet, and Gançarski 2006) is a good
compromise between the mediated and the P2P
architectures. The Mediated P2P architecture, shown
in Figure 1, is distributed but yet, it does not expect
every single information system to work as a DIS on
its own. This is the balance that can address the
needs for modeling in open environment.
The IEL is utilized for the formulation and
semantics of the Mediated P2P DIS in open
environment. Using IEL, given the formula B
a
q(x),
the query q(x) does not have to have the same
interpretation in all possible worlds. Attaching a
superscripted index to the term or the query will
indicate the number of the belief operator that will
include the intended meaning or the intended
interpretation of the term or the query. Another main
feature of the proposed model is that, the answer to a
query does not have to depend on the satisfaction of
the query in a universal model of the whole P2P
system. Instead, every mediator network will be
treated as a separate entity and the answer to the
query will be the union of all the answers coming
separately from each mediated network
In this formulation, a Mediated P2P DIS will be
modeled as a two level logic system. Each level will
be modeled as a set of IEL theories. The first level is
the P2P level which will model the interaction
between various mediators for the purpose of
answering a user query. The second level will be a
mediated level that will model the interaction inside
the local network of each peer.
The main reason why the model is divided into
two levels is to distinguish between the theory of
one peer, a mediator, and the theory of the P2P
system. This will abstract out the structure of one
mediated network and the interaction that will
happen within the mediator’s network. More
importantly, as has been discussed earlier, the open
environment is dynamic in nature. And as such, it is
important to separate the interaction between peers
from the interactions within each peer’s local
network. This way, the addition or withdrawal of a
data source are abstracted out so they do not affect
the logic theory or the interaction at the P2P level or
at the level of other peers’ local networks.
Also, from a practical point of view, a peer only
interacts with the other peers that have direct
connections to it. As such, with the exception of its
immediate neighbours, a peer cannot distinguish the
status of another peer. That said, reasoning will take
place in stages and each stage will be represented by
a separate IEL theory.
Definition: An ontology based Mediated P2P DIS of
N peers in open environment is defined as:
2 = {
|1≤≤}
(1
)
where MP
i
is a mediated peer network defined as:
=(
,
,
,
,
,
)
(2)
Intensional Model for Data Integration System in Open Environment
191

where:
OP
i
: is the private ontology that is local to the peer
MP
i
and is not accessible to other mediated peers.
OG
i
: is a global ontology for the mediated network
MP
i
that is shared with the immediate P2P
neighbours of the mediated peer MP
i.
The following relationship holds between the private
ontology and the global ontology of peer MP
i
:
⊆
(3)
The operator ⊆
in equation (3) is understood as;
any query that can be answered by ontology OG
i
can
also be answered by OP
i
.
S
i
: is a set of data sources for the mediated peer MP
i
.
R
i
: is a set of accessibility relations between the peer
MP
i
and other peers in the P2P network.
G
i
: is a set of P2P interfaces G
ij
, each of which
consists of a set of mappings between the elements
of the private ontology OP
i
of the peer MP
i
and the
global ontology OG
j
of its immediate P2P
neighbouring peer MP
j
. A concept of one ontology is
defined as a query over another ontology.
() ↝
()
(4)
The mapping above maps an ontological view over
the local ontology OP
i
to another ontological view
over the global ontology OG
j
. The ontological view
is defined as:
Definition: Ontological View: an ontological view
over an ontology is a stored query over that
ontology.
L
i
: is a set of sets of local mappings L
ik
. Each L
ik
is a
set of local mappings between the concepts of the
private ontology OP
i
of the peer MP
i
and the local
ontologies of the data source S
ik
S
i
, where S
i
is the
set of local data sources for the mediator peer MP
i
.
Traditionally, the entire DIS is represented as a
single theory. When dealing with a distributed
system, if a query is posed to the private ontology
OP
i
of a peer MP
i
, the answers to the intensionally
equivalent query that is executed against another
peers will be considered as part of the global answer
to the original user query. However, these answers
are based on the relative believes of each peer about
the knowledge of its own neighbours. As such, the
peer MP
i
can only make claims about what it beliefs
the knowledge of its own neighbour is. As such the
global answer will be expressed in terms of the
nested believes and will be calculated in stages until
the last peer is reached. This shows that the whole
network in the IEL setting may not be formulized as
a single theory. Instead, every mediated peer and its
immediate neighbours are represented by a separate
theory. At the same time, the mediated network of
each peer has its own IEL theory as well.
Definition: The ontology based Mediated P2P DIS
in open environment is formalized as a set T
GP
of N
distinguished global IEL theories, one for each
mediated network MP
i
, and a set T
LP
of N
distinguished local IEL theories, one for each
mediated network. This can be expressed as follows:
=<
,
>
(5
)
where:
={
|1 ≤ ≤ }
(6)
and,
={
|1 ≤ ≤ }
(7)
Each global, P2P, IEL theory T
GPi
is defined by:
A set of agents AGTS:
=
{
}
∪{
|
∈
(
)
}
(8)
The alphabet A
TGPi:
A
TGPi
for the IEL theory
T
GPi
is the disjoint union of the alphabets of
the private ontology OPi and the alphabets
of the global ontologies OG
j
of its
immediate P2P neighbours.
=
⨆{
|
∈
(
)
}
(9)
All the formulas of the private ontology
OP
i
, and the global ontologies OG
j
of the
immediate neighbours of MP
i
are going to
be axioms in the theory T
GPi
For every global mapping assertion in the
set G
ij
of the form:
() ↝
()
(10)
there is an axiom in T
GPi
in the form:
∀(
(
)
←
(
)
)
(11)
The assertion in equation (11) is interpreted as; if
mediated peer MP
j
believes something about the
query q
2
(x), then the neighbouring P2P mediated
peer MP
i
believes that peer MP
j
believes the same
thing about the query q
1
(x) evaluated at mediated
peer MP
j
. Here query q
1
(x) evaluated at peer MP
j
is
understood to be the result of applying the
KEOD 2020 - 12th International Conference on Knowledge Engineering and Ontology Development
192

appropriate P2P mappings to q
1
(x) to yield a query
q
2
(x) over the global ontology of mediated peer MP
j
and executing the query q
2
(x) to get the answer in an
actual interpretation at mediated peer MP
j
.
On the other hand, each local, Mediated, IEL
theory T
LPi
is defined by:
A set of agents AGTS:
=
{
}
∪
(12)
The alphabet A
TLPi
for the IEL theory T
LPi
is
the disjoint union of the alphabets of the
private ontology OP
i
and the alphabets of
the set S
i
of its local data sources.
=
⨆{
|
∈
}
(13)
All the formulas of the private ontology
OP
i
and the ontologies of all data sources
of its local mediated network are going to
be axioms in the theory T
LPi
.
For every local mapping assertion in the set
L
ik
of the form:
() ↝
()
(14)
there is an axiom in T
LPi
in the form:
∀(
(
)
←
(
)
)
(15)
The assertion in equation (15) is understood as; if
there is an assignment that makes query q
2
(x) true in
the intended interpretation of data source S
k
of
mediated network MPi, then MP
i
believes the same
thing about the intensionally equivalent global query
q
1
(x). Here query q
2
(x) is the result of applying the
appropriate local mappings L
ik
to q
1
(x).
In this setting, the system can be seen as a set of
collaborating data integration systems. Each data
integration system consists of a peer, the set of its
neighbouring peers, and the set of its local data
sources.
5 INTERFACE AND QUERY
SEMANTICS
The interface between one peer and the data sources
within its mediated network will be modelled as
Global-As-View GAV mapping (Lenzerini 2002).
This is because queries will always come from
the mediator to a data source. On the other hand,
since the query can be asked to any peer, we model
the mapping between peers in the P2P network as
GLAV model (Friedman, Levy, and Millstein 1999).
In the GLAV model, queries of one ontology are
mapped to equivalent queries over other ontologies.
This mapping requires the two queries to be
equivalent. The intensional equivalence between two
queries is expressed as follows:
q
1
(x) ≡
q
2
(x)
(16)
Another important point is that, the answer to a
query posed to a peer is expressed in terms of its
local beliefs plus the nested relative believes of the
peers that are accessible from this peer. These
neighbours are found using the accessibility function
R defined above. Using the IEL, the intensional
index will indicate the belief operator, and in turns
the domain, in which the query will be evaluated.
The intensional semantics for the Mediated P2P
data integration system in open environment is
described below.
We consider a model M for the intensional
epistemic logic ontology driven Mediated P2P data
integration network of N peers, i.e. N mediated
networks, as a structure:
M =<W, π, D, K>
(17)
where,
W: is the set of the different states or
interpretations for the Mediated P2P
network. Here we limit the set of possible
interpretations to the actual interpretations,
intended interpretation, at each peer’s
network.
π: is a set of reflexive relations on the form
(w
ik
, w
ik
) where w
ik
is a possible states for
the mediator peer MP
i
and (w
ik
W). As
such, it is enough for the query to be
satisfied in the actual world in order for the
extensionalization of the query to be an
answer.
D = {D
1
, D
2
, … D
N
} is the disjoint union of
the domains of all the mediator in the
network.
K: is a set of extensionalization functions
for the mediators. It follows that, for a
query q(x) posed to a mediator peer MP
i
,
the local answer to the query is
k
i
(q
i
(x))D
i
. The global answer includes all
the answers for the equivalent queries
k
j
(G
ij
(qi(x)))D
j
for each mediated
network MP
j
accessible to mediated
network MP
i
and so on.
1. A query q(x) is satisfied in a state w
ik
of a
peer MP
i
by the tuple of constants c,
ℳ,
⊨
(
)
if k
j
(q(x)) = c D
i
and
Intensional Model for Data Integration System in Open Environment
193
q(c) is true in interpretation w
ik
, where
k
j
(q(x)) is the extensionalization of query
q(x) in the world w
ik
of a peer MP
i
.
2. An atom of the form B
Pi
(q(x)
1
) is satisfied
in the world w
ik
of mediator peer MP
i
by
the tuple c, ℳ,
⊨
(
)
, if q(c) is
true in state w
i
of mediator peer MP
i
and
k
i
(q(x)) = c D
i
. This is equivalent to
saying that q(c) is true in all worlds w
j
where (w
i
, w
j
) π. However, π is only a
reflexive relation. This means that, the set
of possible worlds for peer MP
i
is a set of
only one member which is the actual world
w
ik
for mediator peer MP
i.
3. An atom of the form B
Pi
B
Pj
(q(x)
2
) is
satisfied in the peer MP
i
by the tuple of
constants c, ℳ,
⊨
(
)
if peer
MP
j
is accessible from MP
i
and G
ij
(q(c)) is
true in a world w
jl
of MP
j
and the
extensionalization of query G
ij
(q(x)) in the
world w
jl
of MP
j
is k
j
(G
ij
(q(x))) = c D
j
.
4. An atom of the form B
Pi
B
Pj
… B
Pm
(q(x))
with n nested modal belief operators is
satisfied in the actual world of peer MP
i
by
the tuple of constants c if B
Pj
…
B
Pm
(G
ij
(q(x)
DEC
)) is satisfied in a possible
world of mediator peer MP
j
by the tuple of
constants c D
j
. Here q(x)
DEC
is the result
of decreasing all the intensional indexes in
the formula q(x) by 1.
6 QUERY ANSWERING
Answering queries in a mediated P2P network in
open environment can be challenging. There are
several formal and practical challenges. In this work,
we will attempt to describe the query answering
semantics in light of the proposed intensional
epistemic logic model. (Yang and Garcia-Molina
2002) presented three different approaches for
finding an answer to a query in a P2P network. The
methods described in (Yang and Garcia-Molina
2002) depend on some metrics. These metrics
depend on, for example, whether satisfying the
query is more important or optimizing the execution
time is of more value. In order to describe the query
answering semantics for the proposed Mediated P2P
model, we will use the satisfiability of the query as
our metric. As such, all possible routes for an answer
will be pursued.
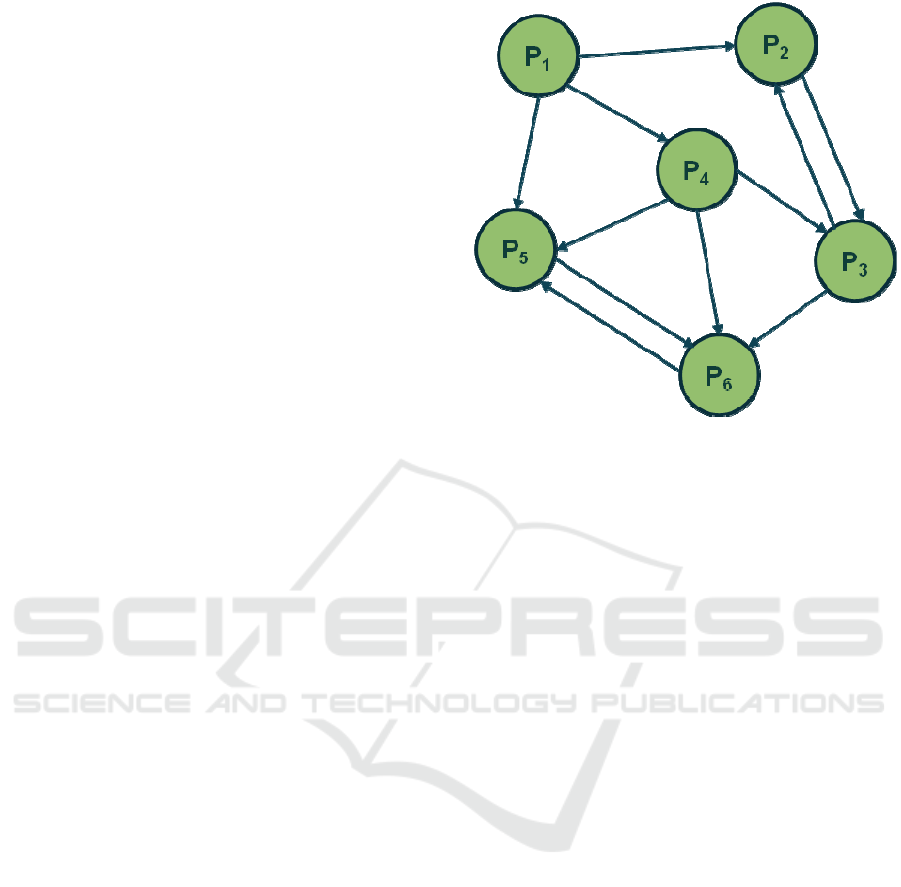
Consider the Mediated P2P network in Figure 2.
For simplicity, the mediated network is abstracted
Figure 2: P2P network with 6 peers.
out. Since the graph in Figure 2 is cyclic, the tree in
Figure 3 is formed. In Figure 3, the nodes, in the
level past the second level, are prefixed in order to
indicate the route to that node. Calculating all the
possible answers to a query posed to the peer P
1
in
Figure 2 is equivalent to calculating the answers at
all nodes of the tree in Figure 3. This assumes some
mappings exist from the root to the node at which
the query answer is calculated. The global answer to
query q(x) is expressed in term of the set of all
possible answers. If we refer to the global answer as
Ans
g
and the possible answers as Ans
p
, the global
answer for q(x) at P
i
is expressed as follows:
Ans
g
(q(x), MP
i
) = B
Pi
q(x)
1
Ans
p
(q(x),
P
i
, P
i
)
(18)
where,
B
Pi
q(x)
1
=
k
Si
k
ik
(q(x))
(19)
and,
Ans
p
(q(x), P
i
, P
i
) =
j
Children(Pi)
Ans
P
(q(x), P
i
, P
j
)
(20)
and,
Ans
p
(q(x), P
i
, P
j
) = B
Pi
B
Pj
q(x)
2
Ans
p
(G
i
j
(q(x)), P
j
, P
j
)
(21)
The global answer to the query is the set of all
possible answers in the query tree in a nested
manner. In that sense, the beliefs of a nodes about a
query affects the beliefs of all its ancestors about the
equivalent queries but not the other way around. In
order to describe the local answer to a query q
j
(x) at
KEOD 2020 - 12th International Conference on Knowledge Engineering and Ontology Development
194

Figure 3: Acyclic query answering tree.
a peer MP
j
we will consider a data source S
jk
in the
mediated network of MP
j
. We will also consider that
the query q
j
(x) is expressed over the global ontology
of peer MP
j
. The semantics of the local answer to the
query q
j
(x) is described as follows:
Ans
l
(q
j
(x), P
j
, S
jk
) = B
Pj
B
Sjk
q
j
(x)
1
=
k
jk
(q
j
(x))
(22)
Where k
jk
(q
j
(x) is the extensionalization of the
intensionally equivalent query to q
j
(x) after applying
the proper local mapping L
jk
.
As has been demonstrated, the use of intensional
epistemic logic enables us to present a model that,
not only accounts for the intensional nature of
information systems and open environment, but also
is able to describe the relative beliefs between
various agents. This allows us to address the loosely-
coupled nature of open environment. It also
facilitates the development of clear intensional
semantics for query answering in open environment.
7 CONCLUSION
An intensional model for data integration system in
open environment is proposed. The architecture used
is Mediated P2P architecture. This architecture is
distributed in nature. But it also does not require
every single information source to act as a DIS on its
own. This addresses the distributed nature of open
environment while eliminating the requirement that
every information system acts as a DIS on its own.
The DIS is formulated as a two level logic system.
Each level consists of N intensional epistemic logic
theories. This relaxes the constraint that all data
information systems share the same domain. It also
allows information systems to associate or dissociate
with the system without affecting the overall
functionality. Since information systems are
intensional in nature, using intensional logic is a
nature choice. Also, employing the intensional
epistemic logic enabled us to describe the relative
beliefs between different peers. This is particularly
useful to address the loosely-coupled nature of open
environment. This, also, is a key to specifying clear
semantics for query answering in open environment.
REFERENCES
Ali, Islam, and Hamada Ghenniwa. 2012.
“Conceptualization-A Novel Intensional-Based
Model.” In KEOD, 2:257–264. SCITEPRESS.
Ali, Islam, and Hamada Ghenniwa. 2014. “Ontology-
Driven Mediated Data Integration in Open
Environment.” In KEOD, 230–239.
Anderson, C. Anthony. 1984. “General Intensional
Logic.” In Handbook of Philosophical Logic: Volume
II: Extensions of Classical Logic, edited by D. Gabbay
and F. Guenthner, 355–85. Synthese Library.
Dordrecht: Springer Netherlands.
Bealer, George. 1979. “Theories of Properties, Relations,
and Propositions.” The Journal of Philosophy 76 (11):
634–48.
Bealer, George. 1982. Quality and Concept. Oxford
University Press. https://philarchive.org.
Bealer, George. 1998. “Intensional Entities.” In Routledge
Encyclopaedia of Philosophy, 803–7. London:
Routledge.
Boyles, R. R., A. E. Thessen, A. Waldrop, and M. A.
Haendel. 2019. “Ontology-Based Data Integration for
Advancing Toxicological Knowledge.” Current
Opinion in Toxicology, Systems Toxicology, 16
(August): 67–74.
Calvanese, Diego, Giuseppe De Giacomo, Domenico
Lembo, Maurizio Lenzerini, and Riccardo Rosati.
2018. “Ontology-Based Data Access and Integration.”
In Encyclopedia of Database Systems, edited by Ling
Liu and M. Tamer Özsu, 2590–96. New York, NY:
Springer.
Chen, Jingliang, Dmytro Dosyn, Vasyl Lytvyn, and
Anatoliy Sachenko. 2017. “Smart Data Integration by
Goal Driven Ontology Learning.” In Advances in Big
Data, edited by Plamen Angelov, Yannis
Manolopoulos, Lazaros Iliadis, Asim Roy, and Marley
Vellasco, 283–92. Advances in Intelligent Systems
and Computing. Cham: Springer International
Publishing.
De Giacomo, Giuseppe, Domenico Lembo, Maurizio
Lenzerini, Antonella Poggi, and Riccardo Rosati.
Intensional Model for Data Integration System in Open Environment
195

2018. “Using Ontologies for Semantic Data
Integration.” In A Comprehensive Guide Through the
Italian Database Research Over the Last 25 Years,
edited by Sergio Flesca, Sergio Greco, Elio Masciari,
and Domenico Saccà, 187–202. Studies in Big Data.
Cham: Springer International Publishing.
Egami, Shusaku, Xiaodong Lu, Tadashi Koga, and Yasuto
Sumiya. 2020. “Ontology-Based Data Integration for
Semantic Interoperability in Air Traffic Management.”
In 2020 IEEE 14th International Conference on
Semantic Computing (ICSC), 295–302.
Fitting, Melvin. 2006. “Intensional Logic.” In The
Stanford Encyclopedia of Philosophy, edited by
Edward N. Zalta, Spring 2020. Metaphysics Research
Lab, Stanford University.
Friedman, Marc, Alon Levy, and Todd Millstein. 1999.
“Navigational Plans for Data Integration.” In
Proceedings of the 1999 International Conference on
Intelligent Information Integration - Volume 23, 72–
78. III’99. Stockholm, Sweden: CEUR-WS.org.
Guarino, Nicola. 1998. Formal Ontology in Information
Systems: Proceedings of the First International
Conference (FOIS’98), June 6-8, Trento, Italy. Vol.
46. IOS press.
Guarino, Nicola, and Pierdaniele Giaretta. 1995.
“Ontologies and Knowledge Bases.” Towards Very
Large Knowledge Bases, 1–2.
Guarino, Nicola, Daniel Oberle, and Steffen Staab. 2009.
“What Is an Ontology?” In Handbook on Ontologies,
1–17. Springer.
Gusenkov, A., N. Bukharaev, and E. Birialtsev. 2019. “On
Ontology Based Data Integration: Problems and
Solutions.” Journal of Physics: Conference Series
1203 (April): 012059.
Halevy, A.Y., Z.G. Ives, D. Suciu, and I. Tatarinov. 2003.
“Schema Mediation in Peer Data Management
Systems.” In Proceedings 19th International
Conference on Data Engineering (Cat.
No.03CH37405), 505–16.
Jiang, Yue J. 1993. “An Intensional Epistemic Logic.”
Studia Logica: An International Journal for Symbolic
Logic 52 (2): 259–80.
Jubien, Michael. 1988. “Problems with Possible Worlds.”
In Philosophical Analysis: A Defense by Example,
edited by David F. Austin, 299–322. Philosophical
Studies Series. Dordrecht: Springer Netherlands.
Lenzerini, Maurizio. 2002. “Data Integration: A
Theoretical Perspective.” In Proceedings of the
Twenty-First ACM SIGMOD-SIGACT-SIGART
Symposium on Principles of Database Systems, 233–
246. PODS ’02. Madison, Wisconsin: Association for
Computing Machinery.
Lumineau, Nicolas, Anne Doucet, and Stéphane
Gançarski. 2006. “Thematic Schema Building for
Mediation-Based Peer-to-Peer Architecture.”
Electronic Notes in Theoretical Computer Science,
Proceedings of the International Workshop on
Database Interoperability (InterDB 2005), 150 (2): 21–
36.
Majkić, Zoran. 2009. “Intensional First-Order Logic for
P2P Database Systems.” Edited by Stefano
Spaccapietra. Journal on Data Semantics XII, Lecture
Notes in Computer Science, , 131–52.
Selman, Bart, and Hector J. Levesque. 1993. “The
Complexity of Path-Based Defeasible Inheritance.”
Artificial Intelligence 62 (2): 303–39.
Wang, Ying Daisy. 2009. “Ontology-Driven Semantic
Transformation for Cooperative Information
Systems.” University of Western Ontario.
Xue, Yunjiao. 2010. “Ontological View-Driven Semantic
Integration in Open Environments.”
Xue, Yunjiao, Hamada H. Ghenniwa, and Weiming Shen.
2010. “A Frame-Based Ontological View
Specification Language.” In The 2010 14th
International Conference on Computer Supported
Cooperative Work in Design, 228–33.
Yang, B., and H. Garcia-Molina. 2002. “Improving Search
in Peer-to-Peer Networks.” In Proceedings 22nd
International Conference on Distributed Computing
Systems, 5–14.
KEOD 2020 - 12th International Conference on Knowledge Engineering and Ontology Development
196
