Nanogrids: A Smart Way to Integrate Public Transportation Electric
Vehicles into Smart Grids
Emanuele Ferrandino
a
, Antonino Capillo
b
,
Fabio Massimo Frattale Mascioli
c
and Antonello Rizzi
d
Department of Information Engineering, Electronics and Telecommunications, University of Rome “La Sapienza”,
Via Eudossiana 18, 00184 Rome, Italy
Keywords:
Smart Grid, Electric Vehicles, Bidirectional Fast Charge, Renewable Energy Source, Vehicle-to-Grid,
Grid-to-Vehicle, Microgrid, Nanogrid, Energy Management System, Fuzzy Logic, Evolutionary Computing,
Hierarchical Genetic Algorithm.
Abstract:
The need for efficient integration of an Electric Vehicles (EVs) public transportation system into Smart Grids
(SGs), has sparked the idea to equip them with Renewable Energy Systems (RESs), in order to reduce their
impact on the SG. As a consequence, an EV can be seen as a Nanogrid (NG) whose energy flows are optimized
by an Energy Management System (EMS). In this work, an EMS for an electric boat is synthesized by a Fuzzy
Inference System-Hierarchical Genetic Algorithm (FIS-HGA). The electric boat follows cyclic routes day by
day. Thus, single day training and test sets with a very short time step are chosen, with the aim of reducing
the computational cost, without affecting accuracy. A convex optimization algorithm is applied for benchmark
tests. Results show that the EMS succesfully performs the EV energy flows optimization. It is remarkable that
the EMS achieves good performances when tested on different days than the one it has been trained on, further
reducing the computational cost.
1 INTRODUCTION
A SG consists of an energy distribution network
that allows to optimize energy exchanges between
the internal nodes and the main energy distribution
network, also considering EVs charging infrastruc-
tures and related Charging Stations (CS). The internal
nodes of a typical SG include residential buildings,
factories and industries, energy production plants
(from renewable sources or from fossil fuels) and
storage systems (Commission, 2006).
In an advanced SG, the internal nodes would also
include a public transportation system made up of
one or more fleets of EVs. Recharging energy infras-
tructures must be orchestrated in real time in order
to ensure continuity of service, thus featuring Grid-
to-Vehicle (G2V) services. On the other hand, the
Vehicle-to-Grid (V2G) paradigm allows to use the
storage system of the EV to power external devices or
to feed energy back into the SG (Deng et al., 2015).
a
https://orcid.org/0000-0001-6472-6597
b
https://orcid.org/0000-0002-6360-7737
c
https://orcid.org/0000-0002-3748-5019
d
https://orcid.org/0000-0001-8244-0015
With the hypothesis that each EV in the fleet is
capable of producing renewable energy on board in-
dependently, as well as consuming it, they potentially
become an active element of the SG with a func-
tion similar to that of a Microgrid (MG). In other
words, the EV described above can implement the
V2G paradigm with a beneficial energy impact on the
SG.
The implementation of the V2G and G2V
paradigms, i.e. of bidirectional exchanges of energy,
together with the independent RES on board the EVs
of a fleet, represents an update of the SG, thanks to the
introduction of new prosumers (or active consumers)
(Deng et al., 2015; Commission, 2007), which can be
summarized as: an increase of the storage energy ca-
pacity (the energy storage system of each EV can be
considered an extension of the main grid energy stor-
age capacity); an increase of the renewable energy
generation capacity (Commission, 2006); an expan-
sion of the SG energy distribution network through
mobile agents; a potential increase in SG flexibility
and resilience at the cost of an increase in the com-
plexity of the SG EMS, or ’tertiary control’ (Olivares
and al, 2014).
512
Ferrandino, E., Capillo, A., Mascioli, F. and Rizzi, A.
Nanogrids: A Smart Way to Integrate Public Transportation Electric Vehicles into Smart Grids.
DOI: 10.5220/0010110005120520
In Proceedings of the 12th International Joint Conference on Computational Intelligence (IJCCI 2020), pages 512-520
ISBN: 978-989-758-475-6
Copyright
c
 2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Up to now these aspects have been addressed in
the literature thanks to the integrations of MGs into
the SG (Deng et al., 2015; Arefifar et al., 2012), im-
plemented in single houses (Adika and Wang, 2014)
or in small residential agglomerations (Kumar et al.,
2017; Hijjo et al., 2016). The purpose of this pa-
per is to propose a solution to extend this approach
also to EVs. (Mahmud and al, 2020). In the follow-
ing, we focus on a specific class of EVs that is in-
troduced alongside the term Nanogrid-vehicle (NG-
vehicle). This paper deals with energy management
optimization of a single NG-vehicle and validate the
hypothesis that it is possible to obtain an adequate op-
timization of energy management for the case study
that will be presented and for similar cases even with
short but sufficiently dense data sets.
Section 2 illustrates in detail what we mean by
NG-vehicle, the network architecture, its EMS and
the objective function chosen for the optimization of
the energy flows involving the NG-vehicle. Section
3 illustrates the case study chosen to conduct the ex-
periments, the creation of the data set and the formal-
ization of a mathematical model of the NG-vehicle
useful for conducting the experiments in a simulation
environment (MATLAB). Section 4 illustrates the op-
timization method chosen to optimize the NG-vehicle
EMS, according to the FIS-HGA paradigm. Section 5
reports an alternative optimization method useful for
comparison with that is described in section 4 and
forming part of the synthesis procedure of an ade-
quate EMS. In section 6 the synthesis procedure is
illustrated and in sections 7 and 8 are reported the re-
sults of the experimentation and the conclusions, re-
spectively.
2 NANOGRID-VEHICLE: AN
ELECTRIC VEHICLE AS A
MICROGRID
We want to highlight the similarities and dissimilari-
ties between a MG, the NG-vehicle and a traditional
EV. Unlike a traditional EV, the NG-vehicle can pro-
duce energy independently and exchange energy from
and to the outside. This factor makes the NG-vehicle
a grid, which is composed of the four main nodes
characteristic of each MG: generation, load, storage
and a link with an external grid.
Unlike a MG, the NG-vehicle does not have a per-
manent link to the external grid. The Stand-Alone
configuration of an MG finds correspondence in the
NG-vehicle at all times when it is moving. Con-
versely, while it is stationary and connected to a CS,
it is in the corresponding On-Line configuration of an
MG. This peculiarity translates, as we will see below,
in the fact that the equation of the inner energy bal-
ance depends on a binary variable, which represents
the working mode (’0’: Stand-Alone, ’1’: On-Line).
The proposed EV is classified as NG, due to its
smaller physical and energy dimensions than a MG.
The NG-vehicle requires a energy flow management,
or ’secondary control’ (Olivares and al, 2014; Kumar
et al., 2017; Sabzehgar, 2015). The EMS is responsi-
ble for deciding how much energy to exchange with
the external grid, represented by a Bidirectional Fast
Charge Station (BFCS), as well as the energy flow di-
rection in order to meet the following requirements:
• Be consistent with the problem, i.e. there must be
no exchange of energy between the NG-vehicle
and the SG when the former is not On-Line;
• Ensure the completion of each route, i.e. do not
consume all the energy of the storage system be-
fore completing the route;
• Keep the storage system close to the Safety Op-
eration Area (SOA) and make sure that each day
starts and ends with a good energy level;
• When the NG-vehicle is On-Line, transfer any
surplus energy produced by the on board RES to
the SG without compromising the storage system.
We assume that any energy request from the SG is
immediately available and that the amount of energy
to be delivered can always be accepted by the SG, i.e.
the storage energy capacity of the SG is assumed infi-
nite. It is also assumed that both the energy generated
by on board renewable source system and the energy
required by the propulsion system of NG-vehicle are
hard to be predicted. For this reason we have cho-
sen to implement the EMS of the NG-vehicle as a FIS
(Santis et al., 2013; Leonori et al., 2017; Gaoua et al.,
2013; Leonori et al., 2016a; Ansari et al., 2014).
2.1 NG-vehicle Architecture
Figure 1 illustrates the grid architecture of the NG-
vehicle including the EMS and the BFCS.
The square nodes (N and S) can exchange bidirec-
tional energy flows, while the circular nodes (G and
L) can exchange unidirectional energy flows (in par-
ticular G can only produce energy and L can just con-
sume it). Each node is associated with a variable of
the type E
X
k
which represents the fraction of energy
exchanged by node X in the time-slot k that goes from
the discrete instant k to the discrete instant k + 1. It
is assumed that the fraction of energy E
X
k
evaluated
at the discrete instant k is constant during the entire
time-slot. It is also assumed that if at the time-slot
Nanogrids: A Smart Way to Integrate Public Transportation Electric Vehicles into Smart Grids
513

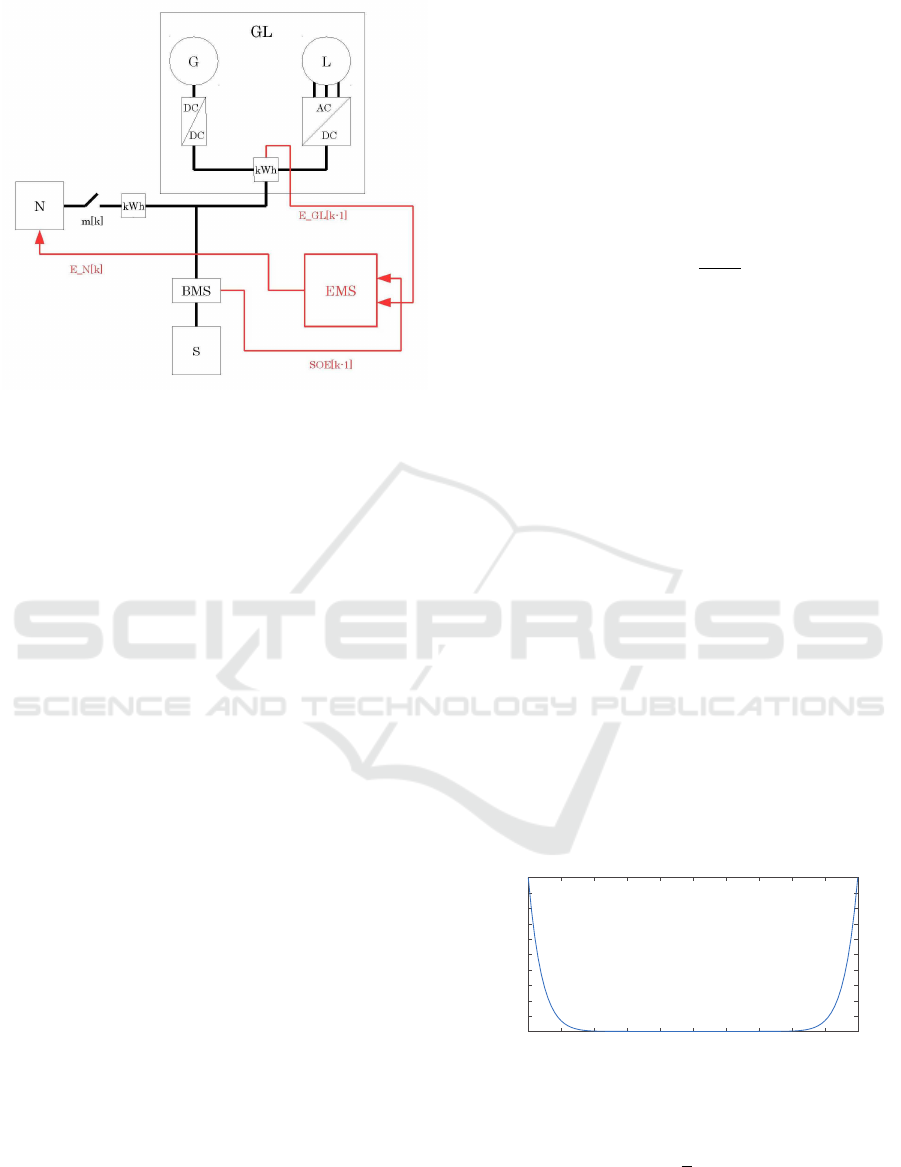
Figure 1: NG-vehicle Architecture and EMS with BFCS
link. The EMS, the input variables and the output variable
are colored red.
k the node X is producing energy then E
X
k
> 0, oth-
erwise E
X
k
< 0. It follows that E
L
k
≤ 0, E
G
k
≥ 0 and
that E
N
k
and E
S
k
can be positive, negative or null at any
time-slot k.
Aggregating the unidirectional nodes G ad L as a
unique bidirectional node allows treating it as a pro-
sumer. So, we will represent with E
GL
k
the fraction
of energy exchanged by GL node. It is possible to
readapt the grid architecture of a generic MG to this
application (Kumar et al., 2017; Hijjo et al., 2016;
Moore and Lopes, 2014; Cheddadi et al., 2015).
In Figure 1 E
GL
k−1
is the fraction of energy mea-
sured on the GL node, SOE
k−1
is the State of Energy
measured on the S node and E
N
k
is the fraction of en-
ergy that controls the N node.
Figure 1 also shows a boolean variable that selects
the NG-vehicle mode, m
k
, which acts as a gauge of
the presence of the link with N. The energy fraction
exchanged by S is determined by the energy balance
equation (1) and is limited by the actual SOE status
and maximum charge/discharge current:
E
S
k
+ E
N
k
× m
k
+ E
GL
= 0 (1)
E
S
k
≤ E
S,MaxDischarge
k
(2)
E
S
k
≥ −E
S,MaxCharge
k
(3)
E
S,MaxDischarge
k
= SOE
k
× E
S
max
(4)
E
S,MaxCharge
k
= (1 − SOE
k
) × E
S
max
(5)
E
S
max
= V
S
nom
× I
S
max
× dt (6)
where V
S
nom
is the nominal voltage of the storage sys-
tem, I
S
max
is the maximum charge/discharge current
(determined by the nominal capacity and the maxi-
mum C-Rate) and dt is the length of a time-slot ex-
pressed in hours (all energy quantities are expressed
in kWh).
The SOE is updated through the following formu-
las:
C
S
k
= C
S
k−1
− E
S
k
(7)
SOE
k
=
C
S
k
C
S
nom.
(8)
where C
S
nom.
is the nominal capacity of the storage sys-
tem.
2.2 Objective Function
The objective function is calculated as summation
of the NG-vehicle performance for each time-slot of
the simulation, for a given EMS. In order to extend
the storage system life in terms of charge/discharge
cycles, the performance is a measure of the storage
stress. The stress of the storage system is due to deep
charges and discharges, i.e. charge over 0.8 p.u. and
discharge over 0.2 p.u. These values of the SOE de-
fine the SOA. Thus, optimization translates into min-
imizing the objective function. The stress of the stor-
age system is a personalization of the ’penality func-
tion’ (Leonori et al., 2017; Storti et al., 2015; ?), il-
lustrated in Figure 2 and whose expression is set out
below:
P
S
k
= f
P
(SOE
k
) = ((SOE
k
−SOE
opt
)/SOE
opt
)
12
(9)
where SOE
opt
is 0.5 p.u. is the value in which the
SOA is centered and in which the penalty function
assumes a null value.
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
SOE [p.u.]
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Penality [p.u.]
Penality function
Figure 2: Penality function.
The objective function is calculated as follows:
OF =
1
n
n
∑
k=1
P
S
k
(10)
where n represents the length of the experiment in
terms of time-slots.
CI4EMS 2020 - Special Session on Computational Intelligence for Energy Management and Storage
514

3 CASE STUDY: THE ELECTRIC
BOAT VALENTINO III
In the context of the European project Life for Silver
Coast - LFSC (LIFE16 ENV/IT/000337), an exam-
ple of an intermodal sustainable mobility system, our
department, in collaboration with the Laboratories of
Cisterna di Latina Polo per la Mobilit
`
a Sostenibile
(POMOS), are focused on the design and engineering
of a small fleet of electric autonomously driven boats
dedicated to public transportation and environmental
monitoring (Lisena et al., 2016) in inland waters (the
Western and Levant Lagoons of Orbetello).
The boats are called Valentino III (see Figure 3),
as they represent the third generation of a class of
electric trimaran ferry boats. Each boat integrates:
an energy generation system based on a photovoltaic
plant, which forms the roof, also providing protection
to passengers from the sun’s rays; an energy storage
system based on a battery pack consisting of lithium-
ion phosphate cells; a propulsion system, which con-
sists of four paddle wheels independently driven by as
many motors located on both the sides of the boat; a
BFCS compatible interface.
Figure 3: Rendering of the Valentino III.
Every day the boat must follow four scheduled
routes: at 8:00, 10:00, 12:00 and 14:00. The dura-
tion of each route is one hour and consists of an out-
ward and a return. For both the lagoons, the piers of
Orbetello represent the starting and arrival points of
each route, as they are equipped with BFCSs. Both
routes cover approximately 6km. This implies that
the average speed that the boat must hold is 6km/h or
approximately 4kn.
During navigation, the propulsion system must be
supplied with adequate power to maintain the speed of
navigation and to face winds below ten meters of alti-
tude and surface water currents produced by the wind
itself (drift water currents). In addition, the propul-
sion effort is influenced by the weight on board, which
represents mostly passengers and crew members.
3.1 Data Set
A data set was created containing the mooring pro-
files, photovoltaic generation and consumption of the
propulsion system. Project specifications were taken
into consideration for the first profile: duration and
daily frequency of the routes. For the generation and
consumption profiles, it was necessary to obtain in
advance the speed profiles of the boat, the use of
the public transportation system by people, the pho-
tovoltaic generation, winds and surface water cur-
rents. With regard to the use of public transporta-
tion, it was considered that the weight of the boat has
a Gaussian distribution between the dry weight and
the fully loaded weight and centered in the middle of
the year (high season). An online simulation platform
was used for photovoltaic generation and wind data
(https://www.renewables.ninja/). The surface water
currents profile was created based on the wind pro-
file.
The dynamic equation of motion of the boat was
used to calculate the energy consumption data, which
uses the speed profile of the boat, the weight profile,
the wind profile and the water current profile .
It should be noted that in practice both the energy
consumed and the energy produced are unpredictable
as it is not known a prior the intensity of the wind and
water currents, the number of people on board and the
photovoltaic generation.
Finally the data set consists of two sequences
{(E
GL
k
,m
k
)}. Given the cyclical nature of the routes, a
time-slot dt equal to 1 minute was chosen, in order to
investigate deeply every operational condition of the
boat. This results is a very dense data set.
3.2 Adopted Vehicle Model
This section illustrates the formulation of a NG-
vehicle model (which also includes a simplifying
model of the BFCS). The model is used to simulate
the energy flows determined by its EMS and simu-
lation data. The NG-vehicle model also includes the
calculation of the objective function which summa-
rizes the performance of the EMS.
The EMS output is the quantity q
N
k
defined in the
real interval [0,1] which must be translated into the
energy fraction E
N
k
, as follows:
E
N
k
= f
N
(q
N
k
) = E
N
max
×(2×q
N
k
−1),q
N
k
∈ [0,1] (11)
E
N
max
= P
N
nom.
× dt (12)
where P
N
nom.
is the nominal power of the BFCS.
Nanogrids: A Smart Way to Integrate Public Transportation Electric Vehicles into Smart Grids
515

In the same way, the input variable E
GL
k
is nor-
malized in a quantity q
GL
k
∈ [0,1] defining the inverse
model of GL:
q
GL
k
= f
−1
GL
(E
GL
k
) =
(
0.49
E
L
max
× (E
L
max
− E
GL
k
),E
GL
k
< 0
(E
GL
k
+ E
G
max
) ×
0.5
E
G
max
,E
GL
k
≥ 0
(13)
E
L
max
= 4 × P
M
nom.
× dt (14)
E
G
max
= P
G
nom.
× dt (15)
where P
M
nom.
and P
G
nom.
are the rated powers of each
motor and the photovoltaic system, respectively.
The input variable SOE
k
on the other hand is al-
ready normalized as it is calculated in parts per unit.
4 FIS-HGA DESIGN
EMS synthesis and optimization was carried out by
the FIS-HGA paradigm (Santis et al., 2013; Leonori
et al., 2017; Siddique and Adeli, 2013; Shi et al.,
1999; Capillo et al., 2018; Leonori et al., 2016b), ac-
cording to which a Mamdani FIS is optimized by a
Hierarchical Genetic Algorithm (HGA) (Santis et al.,
2017; Delgado et al., 2001; Tang et al., 1998).
4.1 FIS Structure
The FIS consists of two inputs (SOE and E
GL
) and
one output (E
N
). The Term Set of each input and of
the output counts five Membership Functions (MFs),
which partially overlap (Fig. 4).
0.10
0
0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0.2
0.4
0.6
0.8
1
“Very Low” “Low” “Medium” “High” “Very High”
Degree of membership
Input
Figure 4: The Term Set for both the two inputs and the out-
put.
The rule base is set to contain all the possible rules
(25), which come from the combination between the
input MFs, as follows:
n
rules
= n
n
inputs
MFs
(16)
where n
rules
, n
MFs
and n
inputs
are the numbers of rules,
MFs and inputs, respectively. The only logical opera-
tor between antecedents is AND.
4.2 FIS Genetic Encoding
The FIS is encoded into the genes of the HGA generic
individual, as follows:
• The first 10 genes are binary and represent the
presence/absence of a MF in the two input Term
Sets (not by chance, the size of this set of genes is
the product of n
MFs
by n
inputs
);
• The next 39 genes are real and encode the vertices
abscissas of all the input and output MFs. all the
abscissas can be tuned, except the ones outside the
Universe of Discourse (Fig. 4). The number of
these genes is the product of the tunable abscissas
of each input and output Term Sets (13) by the
total number of inputs and outputs of the FIS (3);
• The next 25 real genes represent the rule weights;
• The last 25 genes are integers selecting MFs from
the output Term Sets (each rule must have only
one MF in the consequent part).
4.3 The Optimization Process
Two subsequent optimization processes are per-
formed. During the first optimization, the HGA tunes
the FIS rule base. Only the first 10 binary genes of the
generic individual evolve through generations, while
the OF is minimized. If the i-th gene is set to 0, this
means that the i-th MF in the set of the whole inputs
MFs (from the first to the last input) is deleted. As a
consequence, each rule enclosing the i-th MF as an-
tecedent is deleted from the rule set. Thus, the first
optimization aims at reducing the number of rules
by selecting the most relevant ones for the problem
at hand. It is worth mentioning that, when a MF is
deleted, the vertices abscissas of the remaining ad-
jacent MFs are modified in order to cover the entire
Universe of Discourse (Fig. 5). During the second
optimization, the rest of genes of the generic indi-
vidual evolve over generations, meaning that the FIS
parameters (MFs vertices abscissas and rule weights)
and the consequent are tuned, while the OF is mini-
mized. Only the genes related to the rule base coming
from the first optimization are tuned. In this sense, the
first binary genes are at an higher hierarchical level
than the others, making the GA hierarchical.
4.4 HGA Operators and Settings
For the first optimization, a one-point crossover is
adopted, together with a bit string mutation. For the
second optimization, the choice of the crossover op-
erator depends on the type of genes: for the genes
of the vertices abscissas, a convex crossover; for the
CI4EMS 2020 - Special Session on Computational Intelligence for Energy Management and Storage
516

0.10
0
0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0.2
0.4
0.6
0.8
1
“Very Low” “Low” “Medium” “High” “Very High”
Degree of membership
Input
Figure 5: Universe of Discourse coverage after deleting a
MF (in this case, the central one).
weights and consequent genes, a uniform crossover.
A uniform mutation is performed during the second
optimization. A tournament selection with tourna-
ment size 2 is chosen for both the first and the second
optimization.
The population consists of 100 individuals for
both the optimization processes, as well as for the
crossover fraction, set to 0.8. The stopping condition
is always the reaching of the maximum stall gener-
ations while the maximum number of generations is
set to 50 for the first optimization and to 300 for the
second optimization.
5 CONVEX OPTIMIZATION
PROBLEM
In order to know how good is the solution found by
optimization through FIS-HGA, it is necessary to find
the optimal solution. This can be exactly found by
solving a convex optimization problem.
Note that the penalty function expressed in Equa-
tion (9) is a convex function of the SOE, which is a
linear combination of the energy fractions exchanged
over time between node N and the NG-vehicle. So
the penalty function is a convex function of the EMS
output E
N
k
, that becomes the variable of the problem.
The problem is a constrained problem.
In particular: SOE
k
must belong to the real
range [0,1]; E
S
k
must belong to the real range
[−E
SMaxCharge
k
,E
SMaxDischarge
k
], in which the extremes
depend on the SOE
k−1
; the fraction of energy E
N
k
must belong to the real interval [−E
N
max
,E
N
max
].
While it is not even easy to understand whether
the problem is convex or not, it is possible in many
cases to rewrite a non-convex problem in such a form
that it is convex. Some tools can solve optimization
problems, even non-convex ones, for example solving
the dual problem if it turns out to be convex (Boyd and
Vandenberghe, 2004).
The problem can be written as follows:
min
E
N
k
OF
s.t 0 ≤ SOE
k
≤ 1
E
S
k
≤ E
SMaxDischarge
k
E
S
k
≥ −E
SMaxCharge
k
kE
N
k
k ≥ kE
N
max
k
E
S
k
= −(E
N
k
× m
k
+ E
GL
k
)
(17)
where OF is described in Equation (10).
6 SYNTHESIS PROCEDURE
The FIS synthesis is the result of the following proce-
dure:
1. Train the FIS by the HGA and solve the convex
optimization problem (17) on the Training set;
evaluation of the training errors as the Root Mean
Square Error Percent - RMSEP on SOE and on
E
N
. If the training errors are too high (greater than
10%) different solutions must be considered:
• Increase the number of iterations of the HGA;
• Change the HGA optimization process.
2. Test the HGA optimized FIS and solve the convex
optimization problem (17) on sets distinct from
the training set; evaluation of the test errors; if
the test errors are too high (greater than 10%) it
implies data overfitting. It is necessary to repeat
steps 1. and 2. until the conditions on RMSEP are
met.
The training set is sufficiently rich even lasting
only 1 day as a time-slot of 1 minute was chosen, un-
like the typical time-slot of 15 minutes, as in (Deng
et al., 2015; Olivares and al, 2014; Leonori et al.,
2016b; Santis et al., 2017), for data on MGs and SGs.
In fact, 1 day contains 1440 samples which is a good
amount of data. We are particularly interested in the
high season. In particular, for the training set we con-
sidered the day in which the highest peak of energy
generation by the photovoltaic plant was recorded (in-
dicative of the high season).
7 RESULTS
The significant reduction in the Fuzzy Rule Base, due
to the first optimization process (from 25 to 6 Fuzzy
Rules), has lead to a lower computational cost for the
FIS-EMS synthesis.
Nanogrids: A Smart Way to Integrate Public Transportation Electric Vehicles into Smart Grids
517

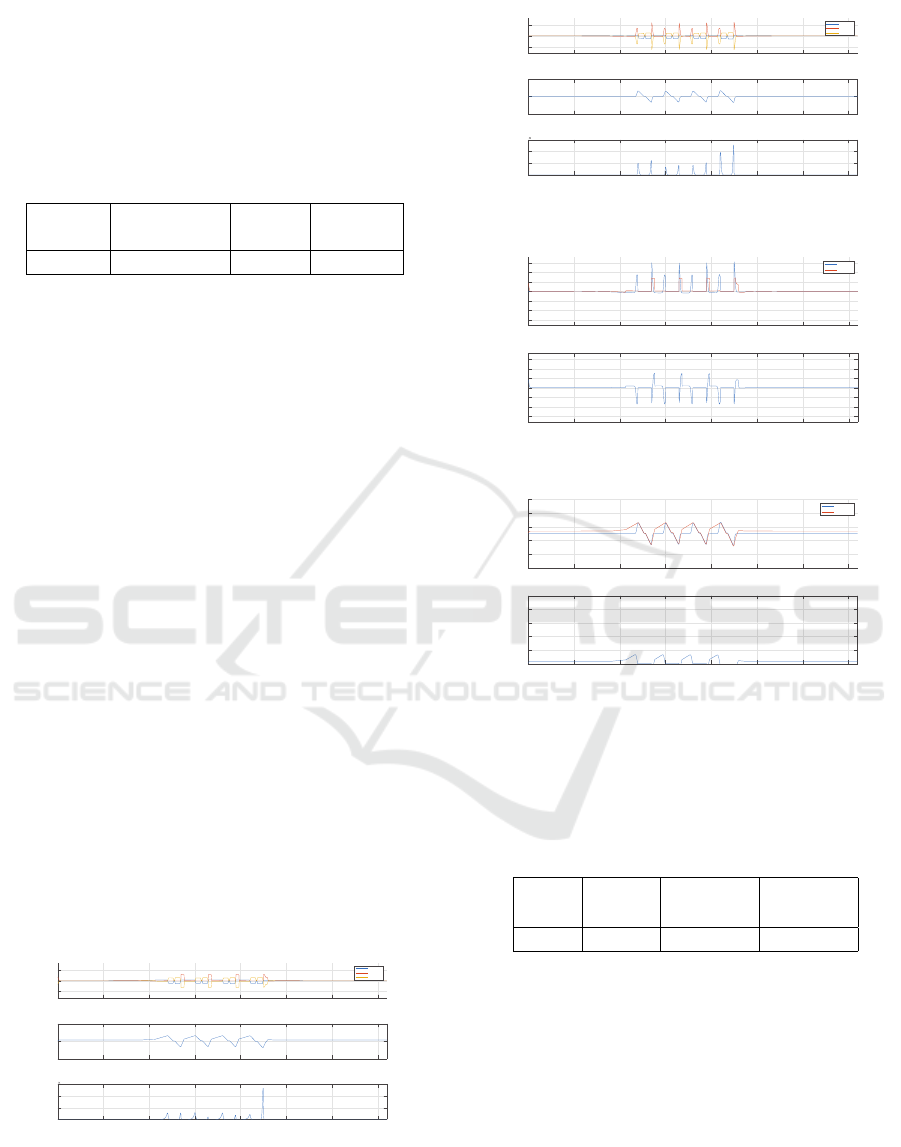
The best energy flows returned by the FIS-HGA
EMS for the Training Set and the same figures re-
turned by the optimal EMS (optimized by convex op-
timization), are shown in Figure 6 and Figure 7, re-
spectively. The OF value of the two solutions and the
training errors are listed in Table 1.
Table 1: Optimal and SubOptimal OF values, E
N
RMSEP
(E
N
err.) and SOE RMSEP (SOE err.) on Training day.
Opt.OF Sub Opt.OF E
N
err. SOE err.
p.u. p.u. % %
3.7e-08 5.8e-08 4.56 4.79
It can be seen that for both solutions the require-
ments of the EMS are met. In particular, in both the
solutions, the energy flows between the BFCS and the
NG-vehicle show a charging phase of the storage sys-
tem alternating with each scheduled route to an ex-
tent that guarantees the completion of the next route
and the containment of the SOE in the SOA limiting
the stress on the storage system. Furthermore, when
recharging does not take place, in the remaining time-
windows between two routes, the surplus energy pro-
duced by the RES is transferred to the SG, as it is not
needed to bring the storage system back to a better
SOE value.
The EMS optimized by the FIS-HGA performs
recharges of the storage system softer and longer than
the optimal one. This reduces the time-windows in
which the EMS can transfer surplus energy to the SG.
In Figure 8 are shown the E
N
RMSEP on the
Training day (in the top plot title), the E
N
profiles of
the two solutions (in the top plot) and the difference
between them (in the bottom plot). Figure 9 shows the
SOE RMSEP (in the top plot title), the SOE profiles
of the two solutions (in the top plot) and the difference
between them (in the bottom plot). Despite the differ-
ences in terms of E
N
k
, both the RMSEP are lower than
the established threshold of 10%, in particular below
5%, allowing to consider the whole synthesis proce-
dure to be effective.
200 400 600 800 1000 1200 1400
[min]
-0.5
0
0.5
[kWh]
Training on day 146:
OF = 5.8017e-08
Energy Flows
GL node
N node
S node
200 400 600 800 1000 1200 1400
[min]
0
0.5
1
[p.u.]
State of Energy
200 400 600 800 1000 1200 1400
[min]
0
2
4
6
[p.u.]
10
-6
Storage Stress
Figure 6: EMS Optimized by FIS-HGA (Training Set).
In order to have a more precise idea of the differ-
ences just shown between the EMS optimized by the
FIS-HGA and the optimal EMS, the amount of energy
200 400 600 800 1000 1200 1400
[min]
-0.5
0
0.5
[kWh]
Optimal Solution on day 146:
OF = 3.7262e-08
Energy Flows
GL node
N node
S node
200 400 600 800 1000 1200 1400
[min]
0
0.5
1
[p.u.]
State of Energy
200 400 600 800 1000 1200 1400
[min]
0
1
2
3
[p.u.]
10
-6
Storage Stress
Figure 7: Optimal EMS on Training Set.
200 400 600 800 1000 1200 1400
[min]
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
[kWh]
EN RMSEP on day 146 = 4.559696
EN
optimal
EN
FIS
200 400 600 800 1000 1200 1400
[min]
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
[kWh]
EN error
Figure 8: Training error: energy fractions at node N.
200 400 600 800 1000 1200 1400
[min]
0
0.2
0.4
0.6
0.8
1
[p.u.]
SOE RMSEP on day 146 = 4.793316
SOE
optimal
SOE
FIS
200 400 600 800 1000 1200 1400
[min]
0
0.2
0.4
0.6
0.8
1
[p.u.]
SOE error
Figure 9: Training error: State of Energy.
taken from the SG in one day, Q
N
buy
, and the amount
of energy transferred to the SG in one day, Q
N
sell
, for
the two solutions are shown in Table 2.
Table 2: Optimal and Sub-Optimal energy from and to the
SG.
Q
N
sell
Q
N
buy
Opt.Q
N
sell
Opt.Q
N
buy
kWh kWh kWh kWh
2.586 17.472 7.374 21.561
Note that the use of NG-vehicles for the implemen-
tation of a transportation system has a lower energy
impact on the SG of Q
N
sell
, compared to the use of
equivalent EV without RESs (Eq. EVs).
In Table 3 are summarized the results of the test
phase performed by simulating the EMS obtimized by
FIS-HGA and solving the convex optimization prob-
lem (17) for the eight days. The E
N
and SOE RM-
SEP values are below the 10% threshold for all tests:
the optimization of the EMS through FIS-HGA on
the Training Set has generated a solution that is valid
throughout most of the year. The worst result is that
CI4EMS 2020 - Special Session on Computational Intelligence for Energy Management and Storage
518

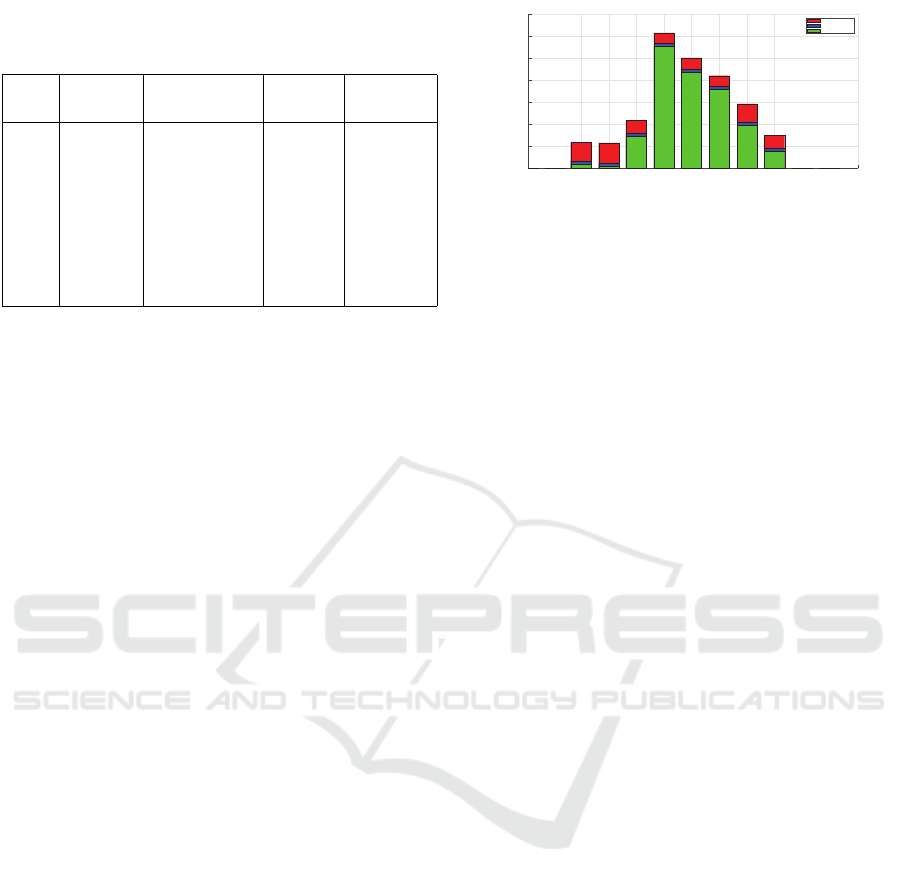
Table 3: Optimal and Sub Optimal OF values on Test days,
E
N
k
RMSEP (E
N
k
err.) and SOE RMSEP (SOE err.) on Test
days.
Test Opt.OF Sub Opt.OF E
N
err. SOE err.
day p.u. p.u. % %
59 9.7e-10 3.0e-09 2.18 4.63
90 1.0e-09 2.5e-07 2.93 6.85
120 1.8e-09 4.4e-08 3.52 5.48
151 6.0e-07 5.3e-04 6.33 8.78
181 8.4e-07 1.4e-05 5.74 5.37
212 1.3e-07 7.9e-07 5.08 4.71
243 2.2e-09 1.1e-07 3.93 5.10
273 1.1e-09 4.2e-08 2.89 5.63
related to the day 151 (high season). This is explained
by the fact that around this day the maximum weight
at full load is recorded; remember that the weight on
board, representing the people who use the transporta-
tion service offered by the single boat, strongly influ-
ences the consumption of the propulsion system.
8 CONCLUSIONS
The EMS of an NG-Vehicle has been synthesized
through a FIS-HGA algorithm, aiming at manag-
ing the bidirectional exchanges of energy fractions
with an SG through a BFCS according to the time-
windows in which the NG-vehicle is On-Line and the
completion of the scheduled routes. The EMS opti-
mization was performed aiming to minimize the stor-
age stresses possibly due to deep charges/discharges
of the NG-vehicle storage system. The synthesis
of EMS as FIS through the proposed procedure has
proved effective in avoiding data overfitting. These
choices led to a synthesis with a satisfactory perfor-
mance value for all the 8 test days, as also reported by
the RMSEP values. The synthesized EMS has satis-
fied all the proposed requirements. In particular, the
NG-vehicle transfers its energy surplus to SG, due to
the continuity of the energy production by the photo-
voltaic roof. Therefore, since the optimization aims at
minimizing the stress on the storage system, the gen-
eration system from renewable sources on board not
only supports the storage system during Stand-Alone
mode (i.e. navigation mode), as commanded by the
NG-vehicle architecture, but it reduces the energy im-
pact that the NG-vehicle has on the SG.
Figure 10 shows the energy impacts on the SG of
the Valentino III with sub-optimal EMS, the Valentino
III with the optimal EMS and the Eq.-EV (Valentino
III without RES), for each of the eight test days. Re-
sults show that the energy impact of the Valentino III
with sub-optimal EMS is closer to the energy impact
1 59 90 120 151 181 212 243 273 365
[day]
0
5
10
15
20
25
30
35
[kWh]
Energy Impact on SG
Equivalent Vehicle
NG-Vehicle
optimal NG-Vehicle
Figure 10: Energy Impact on the SG of the Valentino III
Eq-EV, the Valentino III with sub-optimal EMS and the
Valentino III with optimal EMS.
of the one with optimal EMS than to the energy im-
pact of the Eq.-EV. Future analisys will be performed
in order to increase the difference in terms of energy
impact from the worst case. To achieve this goal, one
way consists in performing an optimization with the
same FIS-HGA algorithm, while minimizing both the
stress on the storage system and the energy impact on
the SG.
We also reserve for the future the wider topic of
optimizing the energy flow management of a fleet of
NG-vehicles.
ACKNOWLEDGMENTS
The POMOS Laboratories and the DIET Department
(University of Rome “La Sapienza”) would like to
thank the EU for financial support to environmental
and climate action projects like LIFE for Silver Coast
(LIFE16 ENV/IT/000337). Such a help is crucial to
achieve natural and historical preservation of Italy, es-
pecially of touristic areas.
REFERENCES
Adika, C. and Wang, L. (2014). Autonomous appliance
scheduling for household energy management. IEEE
Transactions on Smart Grid, vol. 5, no. 2, pages 673–
682.
Ansari, M., Al-Awami, A., Abido, M., and Sortomme, E.
(2014). Optimal charging strategies for unidirectional
vehicle-to-grid using fuzzy uncertainties. IEEE PES
TD Conference and Exposition, pages 1–5.
Arefifar, S., Mohamed, Y., and El-Fouly, T. (2012). Supply-
adequacy-based optimal construction of microgrids in
smart distribution systems. IEEE Transactions on
Smart Grid, vol. 3, no. 3, pages 1491–1502.
Boyd, S. and Vandenberghe, L. (2004). Convex Optimiza-
tion. Cambridge University Press.
Capillo, A., Luzi, M., Paschero, M., Rizzi, A., and Masci-
oli, F. F. (2018). Energy transduction optimization of
a wave energy converter by evolutionary algorithms.
Nanogrids: A Smart Way to Integrate Public Transportation Electric Vehicles into Smart Grids
519

International Joint Conference on Neural Networks
(IJCNN), pages 1–8.
Cheddadi, Y., Gaga, A., Errahimi, F., and Es-Sbai, N.
(2015). Design of an energy management system for
an autonomous hybrid micro-grid based on labview
ide. 3rd International Renewable and Sustainable En-
ergy Conference (IRSEC), pages 1–6.
Commission, E. (2006). The SmartGrids European Tech-
nology Platform — SmartGrids. Luxembourg.
Commission, E. (2007). Strategic Research Agenda for Eu-
rope’s Electricity Networks of the Future. Brussel.
Delgado, M. R., Zuben, F. V., and Gomide, F. (2001). Hier-
archical genetic fuzzy systems. Information Sciences,
Vol.136, page 29 – 53.
Deng, R., Yang, Z., Chow, M., and Chen, J. (2015). A sur-
vey on demand response in smart grids: Mathematical
models and approaches. IEEE Transactions on Indus-
trial Informatics, vol. 11, no. 3, pages 570–582.
Ehsani, M., Gao, Y., and Emadi, A. (2009). Modern elec-
tric, hybrid electric, and fuel cell vehicles: fundamen-
tals, theory, and design. CRC Press.
Gaoua, Y., Caux, S., Lopez, P., and Salvany, J. (2013). On-
line hev energy management using a fuzzy logic. 12th
International Conference on Environment and Electri-
cal Engineering, EEEIC, pages 46–51.
Hijjo, M., Felgner, F., Meiers, J., and Frey, G. (2016). En-
ergy management for islanded buildings integrating
renewables and diesel generators. IEEEPES Power-
Africa, Livingstone, pages 62–66.
Kumar, A., Deng, Y., He, X., Kumar, P., and Bansal, R.
(2017). Energy management system controller for
a rural microgrid. The Journal of Engineering, vol.
2017, no. 13, pages 834–839.
Leonori, S., Paschero, M., Rizzi, A., and Mascioli, F. F.
(2016a). Optimization of a microgrid energy man-
agement system based on a fuzzy logic controller.
IECON.
Leonori, S., Paschero, M., Rizzi, A., and Mascioli, F. F.
(2017). An optimized microgrid energy management
system based on fis-mo-ga paradigm. Fuzzy Systems
(FUZZ-IEEE), pages 1–6.
Leonori, S., Santis, E. D., Rizzi, A., and Mascioli, F. F.
(2016b). Multi objective optimization of a fuzzy
logic controller for energy management in microgrids.
IEEE Congress on Evolutionary Computation (CEC),
pages 319–326.
Lisena, V., Paschero, M., Gentile, V., Amicucci, P., Rizzi,
A., and Mascioli, F. F. (2016). A new method to re-
store the water quality level through the use of electric
boats. IEEE International Smart Cities Conference
(ISC2), pages 1–4.
Mahmud, K. and al (2020). Real-time load and ancillary
support for a remote island power system using elec-
tric boats. IEEE Transactions on Industrial Informat-
ics, vol. 16, no. 3, pages 1516–1528.
Moore, R. and Lopes, J. (2014). The energy management
and optimized operation of electric vehicles based on
microgrid. IEEE Transactions on Power Delivery, vol.
29, no. 3, pages 1427–1435.
Olivares, D. and al (2014). Trends in microgrid control.
IEEE Transactions on Smart Grid, vol. 5, no. 4, pages
1905–1919.
Sabzehgar, R. (2015). A review of ac/dc microgrid-
developments, technologies, and challenges. IEEE
Green Energy and Systems Conference (IGESC),
pages 11–17.
Santis, E. D., Rizzi, A., and Sadeghian, A. (2017). Hierar-
chical genetic optimization of a fuzzy logic system for
energy flows management in microgrids. Applied Soft
Computing, vol. 60, pages 135 –149.
Santis, E. D., Rizzi, A., Sadeghiany, A., and Mascioli, F.
(2013). Genetic optimization of a fuzzy control sys-
tem for energy flow management in micro-grids. Joint
IFSA World Congress and NAFIPS Annual Meeting
(IFSA/NAFIPS), pages 418–423.
Shi, Y., Eberhart, R., and Chen, Y. (1999). Implementation
of evolutionary fuzzy systems. IEEE Transactions on
Fuzzy Systems, vol. 7, no. 2, pages 109–119.
Siddique, N. and Adeli, H. (2013). Computational Intel-
ligence: Synergies of Fuzzy Logic, Neural Networks
and Evolutionary Computing. Wiley.
Storti, G., Paschero, M., Rizzi, A., and Mascioli, F.
(2015). Comparison between time-constrained and
time-unconstrained optimization for power losses
minimization in smart grids using genetic algorithms.
Neurocomputing, vol. 170, page 353 – 367.
Tang, K., Man, K., Liu, Z., and Kwong, S. (1998). Min-
imal fuzzy memberships and rules using hierarchical
genetic algorithms. IEE Transactions on Industrial
Electronics, vol. 45, no.1, pages 162–169.
CI4EMS 2020 - Special Session on Computational Intelligence for Energy Management and Storage
520