Discrete Pigeon Inspired Simulated Annealing Algorithm and

Contract Net Algorithm based on Multi-objective Optimization for

Task Allocation of UAV Formation

Xuzan Liu

, Yu Han

2, 3

, Jian Chen

, Yi Cao

and Shubo Wang

College of Engineering, China Agricultural University, 17 Qinghua East Rd., Beijing, China

College of Water Resources & Civil Engineering, China Agricultural University, 17 Qinghua East Rd., Beijing, China

State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University,

129 Luoyu Rd., Wuhan 430079, China

Keywords: Task Allocation, Multi-objective Optimization, Multi-Unmanned Aerial Vehicles, Discrete Pigeon-inspired

Optimization-Simulated Annealing Algorithm, Contract Net Algorithm.

Abstract: In this paper, a mathematical model of multi-objective optimization under complex constraints is established

to solve the task allocation problem. Among them, the constraint indexes include UAV quantity constraint

and fuel consumption constraint; the optimization objectives include the gain, loss and fuel consumption.

Discrete Pigeon Inspired Optimization-Simulated Annealing (DPIO-SA) algorithm is proposed to solve this

problem. The experimental results show that while the total fitness reaches the optimum, the gain is the largest,

the loss and fuel consumption are the smallest. After running the algorithm 30 times. The number of times

that DPIO-SA reaches the global optimum is 15, while DPIO is 2. In addition, the average value of DPIO-SA

after stabilization is 13.5% larger than that of DPIO. Both prove that after joining SA, the algorithm is easier

to reach the global extremum. The Contract Net Algorithm (CNA) is adopted to solve the task scheduling

problem. The UAVs are divided into tenderer UAV, potential bidder UAVs, bidder UAVs and winner UAV.

After network communication, suitable bidder UAV is found to replace tenderer UAV to perform the task.

Experimental results show that the algorithm has good applicability.

1 INTRODUCTION

Multi-Unmanned Aerial Vehicles (UAVs)

cooperative task allocation is a process that multi

UAVs are divided into small-scale formation and

assigned to different tasks according to a set of

specific constraints to achieve some optimal or sub

optimal performance (Zong et al., 2017).

The mathematical model of task allocation is

mainly divided into centralized model and distributed

model. The centralized task allocation model includes

Multi-dimensional Traveling Salesman Problem,

Vehicle Routing Problem model, Multi-Dimensional

Dynamic Network Flow Optimization model, Multi-

dimensional Multi-choice Backpack Problem model

and the improvement of related models (Chen and

Qiao, 2016). Distributed task allocation includes

contract net model, auction algorithm model, et al.

Task allocation has been proved to be a NP hard

problem (Qi et al., 2019). At present, many

algorithms have been used to solve this problem,

including Particle Swarm Optimization algorithm

(PSO), Simulated Annealing (SA) algorithm, Tabu

search algorithm and so on. In recent years, various

bio-optimization algorithms have emerged, such as:

Ant Colony Optimization (ACO), Artificial Fish

Swarm algorithm (AFSA) ， Pigeon-Inspired

Optimization (PIO) and so on. ACO uses information

feedback mechanism to move towards a better

solution through the exchange of information

between individuals. But the search time is long and

sensitive to initialization values. If the initial value is

not selected properly, it is easy to fall into local

extremum (Ratanavilisagul et al., 2017). AFSA

imitates the five behaviours of the fish swarm:

selection, search, swarm, follow and bulletin. It is

helpful to solve real-time problems, but often cannot

get accurate solutions (Zainal et al., 2015). PIO

algorithm was proposed by Duan in 2014 (Duan and

Qiao, 2014). At first, it is used to solve the problem

176

Liu, X., Han, Y., Chen, J., Cao, Y. and Wang, S.

Discrete Pigeon Inspired Simulated Annealing Algorithm and Contract Net Algor ithm based on Multi-objective Optimization for Task Allocation of UAV Formation.

DOI: 10.5220/0010106401760183

In Proceedings of the 12th International Joint Conference on Computational Intelligence (IJCCI 2020), pages 176-183

ISBN: 978-989-758-475-6

of air robot path planning, and then it is applied to

image restoration and parameter optimization (Duan

and Wang, 2016; Duan and Xu, 2020). These proves

that PIO algorithm has great application potential and

good applicability. However, PIO algorithm is often

used to deal with continuous problems, and the

mining of discrete problems is not deep enough. By

deeply understanding the mechanism of PSO

algorithm, Ye(Ye et al, 2017) adopted the crossover

and replacement operations of genetic algorithm

(GA) to update the speed and position of particles,

and solves the problem of task allocation. Inspired by

him, this paper adopts the same form to update

pigeons’ state information, and realizes the discrete

processing of PIO algorithm. On the other hand, at

present, a single algorithm can no longer meet the

needs of various problems, so it has become a general

trend to merge the advantages of multiple algorithms

to make up for the shortcomings of a single algorithm.

In view of the advantage of SA algorithm which can

keep the poor solution with a certain probability and

jump out of the local extremum, this paper integrates

SA in DPIO, which not only avoids the premature

convergence of the algorithm, but also effectively

shortens the optimization time of the algorithm.

After task allocation, if a certain UAV cannot

perform the task under special circumstances, the

Contract Net Algorithm (CNA) is used for task

scheduling. CNA is one of the distributed task

allocation algorithms, which has better scalability and

robustness. It is a kind of negotiation and

coordination mechanism, which simulates the

economic behaviour of "tender-bid-win" mechanism

to schedule tasks (Qiao et al., 2016). At present, the

research of CNA has a broad basis. Chen (Chen and

Qiao, 2016) adopted the CNA to study the real-time

scheduling of the manufacturing system. Experiments

show that the method can effectively reduce the

impact of disturbance factors such as equipment

failure on the system operation. Li (Li and Zhang.,

2017) combines the task load rate index and token

ring network in the CNA, which solves the task

allocation problem of multi autonomous underwater

vehicles and reduces the irrationality of task

allocation. Because of the good real-time

performance of CNA, this algorithm is adopted to

solve the task scheduling problem.

The rest of this paper is arranged as follows: In

section 2, the task allocation model is introduced; In

section 3, the DPIO-SA algorithm is proposed to

solve the task allocation problem; In section 4, CNA

is adopted to solve the task scheduling problem; In

section 5, the experimental results and simulation are

listed; In section 6, conclusion.

There are two innovations in this paper. Firstly,

the exchange and cross operations are used to update

the state information of pigeons and realize the

discretization of PIO algorithm. Secondly, Adding

SA algorithm to DPIO algorithm makes it easier to

jump out of local extremum.

2 TASK ALLOCATION MODEL

For the convenience of analysis, the variables in this

paper are defined as shown in Table 1:

Table 1: Related variables in task allocation model.

Paramete

Meaning

Number of UAVs

_task nums

Number of tasks

(

)

Initial position of the

UAV

(

)

Initial position of the

task

Lower limit of UAVs quantity

required for

task

Upper limit of UAVs quantity

required for

task

,ti

Number of UAVs performing

task actuall

()

att uav

Attack capability of

UAV

()

def uav

Defensive capability of

UAV

()

att task

Attack capability of

task

()

def task

Defensive capability of

task

()

val uav

Importance of

UAV

()

val task

Importance of

task

max

uel

Maximum fuel that a single UAV

can carr

,ui

uel

Fuel consumption per unit

distance

1234

,,,

ωωωω

Weights of related indexes

2.1 Constraints

Using the coordinate information of the UAVs and

tasks, the distance of

UAV and

task is

calculated.

,,,,,

()()

xx yy

ij ui tj ui tj

dpppp=−+−

(1)

The relationship between the fuel consumption

and distance can be expressed by:

Discrete Pigeon Inspired Simulated Annealing Algorithm and Contract Net Algorithm based on Multi-objective Optimization for Task

Allocation of UAV Formation

177

,,iuiij

uel fuel d=⋅

(2)

When performing the task, we consider the UAV

to be at a constant speed, so

,ui

uel

is set as a constant.

Then the fuel constraint can be expressed by:

maxi

uel fuel≤

(3)

When assigning tasks to UAVs, the number of

UAVs required for each task is different, and they

need to be kept within a range. If the number is not in

this range, it may affect the interaction and

communication of UAVs. The number constraint of

UAV required for each task can be expressed by:

itii

ll l≤≤

(4)

Transforming this constraint into penalty can be

expressed as:

0 others

task nums

iti i ti

task nums

iti i ti

ll l l

pe l l l l



−>



=−<









(5)

At the same time, each task requires multi UAVs

to perform together, and a single UAV can only

perform one task. It can be expressed as:

1, 1, 2, .

task nums

allo i U





(6)

2.2 Performance Indicators

The loss index of the UAV is related to the defensive

ability of UAV and the attack ability of task.

Similarly, the damage index of the task is related to

the attack ability of UAV and the defensive ability of

task, which can be expressed as:

()/()

ij j i

los att task def uav=

(7)

()/( )

ij i j

dam att uav def task=

(8)

The loss of each UAV can be expressed as the

product of loss index of the UAV and the importance

of the UAV.

()

task nums

ij ij i

utlos allo los val uav



(9)

The cost of fuel consumption can be expressed as

the sum of fuel consumed by each UAV after running

to the designated task location.

utfuel fuel



(10)

The gain of executing tasks is defined as the

product of the damage index of the task and the

importance of the task.

()

task nums

ij ij j

utgain allo dam val task



(11)

The gain, loss, fuel consumption and penalty are

integrated in the evaluation function as the total

fitness. Then the evaluation function is combined

with the constraints to solve the following problem:

max

. . 1, 1, 2, ,

task nums

J w utgain w utlos

w utfuel w pe

t allo i U

fuel fuel

=⋅ −⋅

−⋅ −⋅

≤





(12)

3 DPIO-SA ALGORITHM

PIO is generally used to solve the continuous

problem, while the task allocation problem is a

discrete problem, so the form of solution needs to be

rewritten. In this paper, multi-dimensional integer

vector coding is adopted to represent solutions. In the

result of DPIO, the vector dimension represents the

UAV number, and the vector element represents the

task number to be executed. For example, if the

solution is 1-3-3-2-1, which means the number of

UAV executing task 1 is 1,5; the number of UAV

executing task 2 is 4; the number of UAV executing

task 3 is 2,3.

Due to the complexity of the constraints and the

large amount of calculation, the DPIO is proposed for

solving.

When pigeons are far away from their destination,

they will fly in a general direction according to the

magnetic field and the sun. Reflected in the early

stage of the algorithm, it is expressed as learning from

the global optimal individual. Through in-depth

analysis and research on the mechanism of the PIO

algorithm, it is found that the essence of the compass

operator is to use the individual's own information

and the optimal individual to update the position, so

we can reconstruct its update formula.

() () ()

{

}

iig

t c Fw FXt pt+=⊗ ⊗





(13)

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

178

where,

()

represents the positions of pigeon

group in the

iteration.

()

represents the

global extremum.

represents the inertia weight.

represents learning coefficient.

()

1 i

is the

function of the influence of pigeon's own velocity on

its position.

() ()

()

2 ig

Xt pt，

is the function that

pigeons learn from global extremum.

The position update formula consists two parts.

Let

()

be the temporary variable:

(i)

() ()

()

twFXt

Xt r w

trw

=⊗







≥





(14)

This is the inertia part of the individual, which

indicates the reference of the individual to its own

speed. Among them,

()

represents the pigeon's

speed. During speed updating, a random number

in the interval [0, 1] is generated by

()rand

. If

rw<

, genes exchange will be perform. Two random

numbers

and

are generated, and then the genes

and

positions in the solution are exchanged,

which means, the task to be performed by the

UAV is exchanged with that to be performed by the

UAV. As shown in Figure 1.

Figure 1: Schematic diagram of exchange operation.

(ii)

( ) () ()

()

() ()

()

iig

tcFtpt

tpt r c

trc

+=⊗







≥





(15)

This is the learning part of the individual, which

indicates that the pigeon adjusts its position

according to the global extremum

()

. During

learning, a random number

in the interval [0, 1] is

generated by

()rand

. If

rc<

, genes cross will be

performed. Two random numbers

and

are

generated, and then the genes between

and

positions in the solution are exchanged by global

extremum

()

, which means, the tasks performed

by the

to the

UAVs are all replaced by the tasks

performed by the

to the

UAVs in the global

extremum

()

. As shown in Figure 2.

Figure 2: Schematic diagram of cross operation.

When the pigeon group is close to the destination,

it will be closer to the population that is familiar with

the landmark information. After each iteration, the

number of pigeon population will be halved, and the

first half with better adaptability will be selected as

the current population. The center of the remaining

pigeon group is obtained by averaging the genes in

the remaining pigeon group, and the center is used as

the reference direction to update the position of each

pigeon. The operation is as follows:

()

() ()

(1)

Xt round

Xt d FX t







+=⊗ +







(16)

When the position is updated, a random number

is generated by

()rand

. If

rd<

, two random

numbers

and

are generated. Then the genes

between

and

of the current individual are replaced

by the genes of the reference center.

However, DPIO is easy to fall into local

extremum. In order to solve this problem, SA is used

to improve it. The main idea of SA is to judge whether

to accept new solution according to the Metropolis

criterion. The metropolis guidelines are as follows:

()

1 0

exp / 0T

Δ>







ΔΔ≤





，

(17)

where

() ()

itness new fitness oldΔ= −

The specific method is: after each iteration of

compass operator and landmark operator, the fitness

Discrete Pigeon Inspired Simulated Annealing Algorithm and Contract Net Algorithm based on Multi-objective Optimization for Task

Allocation of UAV Formation

179

of the new solution and the current solution is

compared. If the fitness of new solution is higher, the

new solution is accepted; Else, a random value

[

]

0,1r ∈

is generated. If

ry<

, the new solution is

accepted, otherwise the solution is not updated.

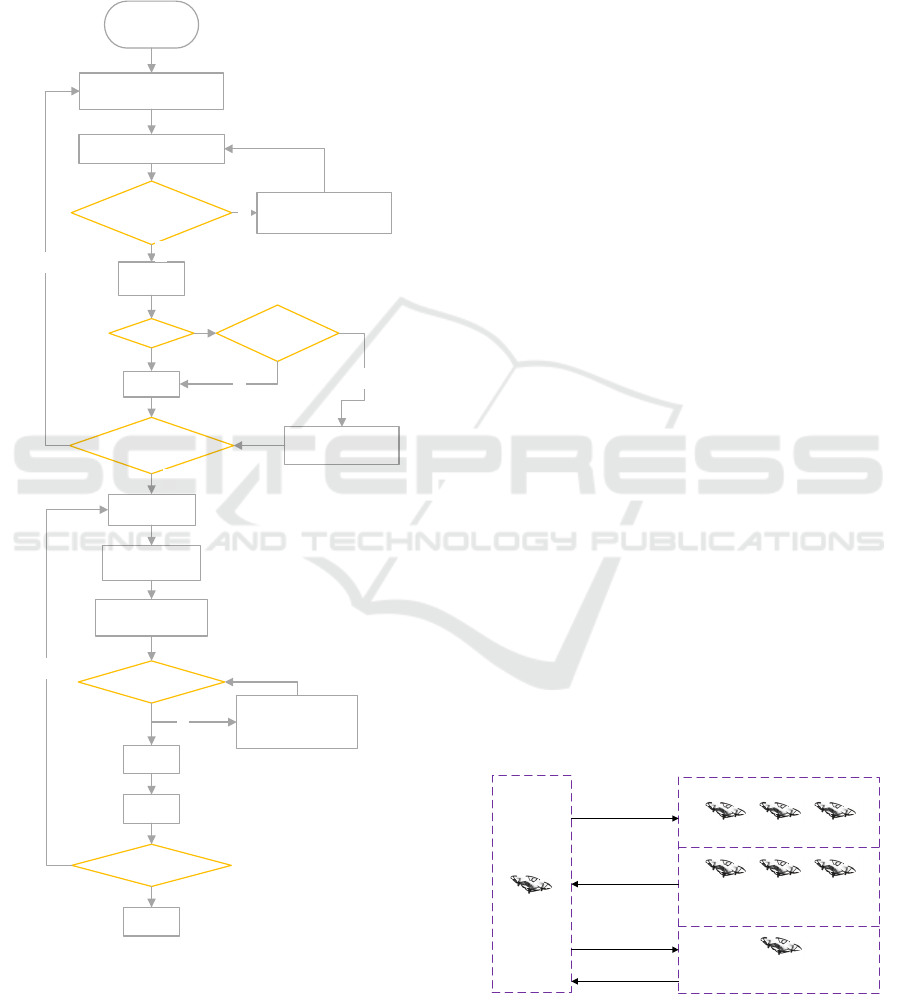
The flow chart of DPIO-SA is shown in Figure 3.

Population

initialization

Get the global

optimal particle

Update

Output

result

Genes exchange

Cross

End of compass

operators?

Sort fitness

Half the

population

Find center of

the group

Satisfy

constraints?

Replace genes

that do not meet

constraints

Satisfy

constraints?

Cross

Update

Keep original

particle

End of landmark

operator?

Keep the original

particle

exp( / )

kT<Δ

0?Δ>

Figure 3: Flow chart of DPIO-SA algorithm.

4 CONTRACT NET ALGORITHM

In the CNA, UAVs are divided into the tenderer

UAV, the potential bidder UAV, the bidder UAV and

the winner UAV. The tenderer UAV is the owner of

the task; The potential bidder UAV is the UAV that

have a communication relationship with the tenderer

UAV and the bidder UAVs are the UAVs that meet

the task constraints. The winner UAV is the UAV that

finally signs the contract with the tenderer UAV after

bidding.

When a UAV is unable to perform the current task

due to special circumstances, the CNA is used for task

scheduling. First, whether the task performed by the

UAV meet the UAV quantity constraint is judged. If

it is not satisfied, i.e.

ti i

ll<

, then the UAV will issue

tasks as the tenderer UAV. Then, the tenderer UAV

issues tasks to the UAVs that have communication

relationship with it. These UAVs are defined as

potential bidder UAVs.

Next, in the bidding stage, the potential bidder

UAV first judges whether there are redundant UAVs

in the currently executed task. If not, the UAV cannot

perform other tasks; if there are, then, it is judged

whether the UAV meets the fuel constraint from its

position to the task assembly point of the bidder's

UAV, if so, it will be marked as the bidder UAV. And

the

ain

utlos

and

utfuel

will be used as

performance indicators to calculate the overall

capacity and send it to the tenderer UAV.

21 2 3

=J w utgain w utlos w utfuel⋅−⋅−⋅

(18)

Finally, the tenderer UAV selects the bidder UAV

with the largest overall capacity according to the

returned information and sends winning information

to it. After receiving the information, the winner

UAV changes its task attributes and executes the task

assigned to the tenderer UAV. The specific

negotiation process is shown in Figure 4:

…

Potential Contractor UAVs

Contractor UAVs

Winner UAV

UAV 1

UAV 2 UAV 3

Tenderer UAV

send out the

bidding information

Send the fitness

message

Send winning

information

Send the contract

Figure 4: Task negotiation process based on CAN.

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

180

5 EXPERIMENT SIMULATIONS

In order to verify the effectiveness of the algorithm,

the simulation experiments are carried out under the

Windows 10 operating system based on Matlab2019

(a) environment.

5.1 DPIO-SA Experiment Results

After running the program, we can get the value range

of gain is [6.1235, 6.7347], the value range of loss is

[29.6690, 36.1274], and the value range of fuel

consumption is [480.5009,721.3119]. In order to

ensure that the length of the three values are the same,

let

10w =

1w =

0.025w =

. In order to ensure that

the task allocation results meet the quantity

constraints,

must be large enough, so

=1000w

The number of the number of simulated pigeons is

100n =

. The number of compass iterations is

100Dt =

The number of landmark iterations is

50Dt =

.The initial temperature of SA is

8T =

the temperature attenuation factor is

0.8k =

, The

number of SA iterations is

=30L

. The UAVs are

randomly distributed in the site of

100 100mm×

.The

number of UAVs used in the experiment is 24, and

each task target is at the quintile of the site. Due to the

excessive number of UAVs, their performance

parameters are too large, which will not be listed here.

Task performance parameters are shown in Table 2.

Table 2: Task parameters.

Task1 Task 2 Task 3 Task 4 Task 5

x 25 50 25 75 75

25 50 75 25 75

A 54 72 46 54 54

D 77 68 42 77 77

V 0.45 0.15 0.25 0.45 0.45

4 4 4 4 4

8 9 9 8 8

where (x, y) is the position of tasks, A and D are the

attack and defensive ability of the tasks, respectively.

V is the value of the tasks.

Run the program 30 times to find the average

value of each parameter. The iteration results of each

indicator of task allocation are shown in the figure 12:

(a)

Total fitness

(b)

Gain

(c)

Loss

(d)

Fuel consumption

Figure 5: Results of task allocation.

where Fig 5(a) shows the total fitness, Fig 5(b) shows

the gain. Fig 5(c) shows the loss, Fig 5(d) shows the

fuel consumption. It can be seen from the Figure 5

that the algorithm converges after 103 iterations in

average, and we can see that while ensuring the total

fitness is maximized, the gain is maximized, the loss

and the fuel consumption are minimized.

Discrete Pigeon Inspired Simulated Annealing Algorithm and Contract Net Algorithm based on Multi-objective Optimization for Task

Allocation of UAV Formation

181

The algorithms based on DPIO and DPIO-SA are

simulated. Take the average values of the algorithms

after 30 runs. The comparison is shown in Figure 6.

Figure 6: Comparison of DPIO and DPIO-SA.

As can be seen from the Figure 6, the average

convergence value of DPIO-SA is 21.9444, and

DPIO-SA is 20.5672. In order to better compare the

two algorithms, a baseline is set, here we set it as the

minimum fitness during the execution of the

algorithm. Therefore, the following formula can be

used for comparison:

fitness

DPIO

fitness base

−

(19)

where

fitness DPIO SA DPIO

fitness fitness

−

Δ= −

10.3712base =

. It can be concluded that the

convergence value of DPIO-SA is 13.5% higher than

that of DPIO. At the same time, in 30 runs, the

number of times DPIO-SA reaches the global

extremum is 15. And DPIO is 2. Both mean DPIO-

SA is easier to jump out of local extremum.

The optimal solution of the task allocation is

shown in the Table 3:

Table 3: Results of the task allocation.

Task numbe

UAV numbe

1 1-6-7-22

2 5-14-16-21

3 8-9-10-17-18

4 2-3-11-12-20

5 4-13-15-19-23-24

5.2 CNA Experiment Results

First, a UAV is randomly selected as the tenderer

UAV release the task. Assume that the tenderer UAV

is UAV6. From the task allocation result, UAV6

performs task1. The lower limit of the number of

UAVs required for task1 is

l =

, so when UAV 6

fails to perform task1, the task cannot be completed.

At this time, the CNA is used for task scheduling.

Firstly, UAV6 issues task to all UAVs in the

network. Because of the large number of UAVs, the

UAV communication diagram is represented by task

network. When there is a connection between two

tasks, it means that all UAVs between the two tasks can

communicate with each other. The task networking

diagram of this paper is shown in Figure 7:

Figure 7: The task network diagram.

It can be seen from Figure 7 that tasks associated

with task 1 include task 3, task 4, and task 5.

According to the task allocation result, all UAVs

performing task 3, task 4, and task 5 have redundant

UAVs, so all UAVs performing these three tasks will

be considered as potential bidder UAVs. According

to whether the fuel constraints between UAVs and

task1 are met, the potential bidder UAVs can be

considered as bidder UAVs. The fitness is calculated

according to the contract, as shown in Table 5. After

bidding, the winner UAV is UAV 17. The types of

UAVs in the CNA are shown in Table 4.

Table 4: Types of UAVs in the contract network.

Potential Bidde

UAVs

Bidde

UAVs

Winne

UAV

UAV2, UAV3, UAV4,

UAV8, UAV9, UAV10,

UAV11, UAV12, UAV13,

UAV15, UAV17, UAV18,

UAV19, UAV20, UAV23,

UAV24

UAV2,

UAV11,

UAV13,

UAV17,

UAV20

UAV17

Table 5: Bidder UAVs and corresponding fitness.

UAV numbe

Fitness

UAV 2 20.9041

UAV 11 21.1804

UAV 17 21.4688

UAV 13 21.093

UAV 20 21.3611

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

182

6 CONCLUSION

In this paper, aiming at the problem of multi-UAV

task allocation, a mathematical model for multi-

objective optimization under complex constraints is

established, and DPIO-SA algorithm is proposed to

solve it. Firstly, the speed and position information of

the pigeon group are changed according to the

exchange and cross operations, which solves the

difficulty of the PIO algorithm to deal with the

discrete problem. Then, after each iteration, the SA

algorithm is used to judge whether to accept the new

solution or not, which makes the algorithm easier to

jump out of the local extremum. The experimental

results show that when the overall performance index

reaches the optimum, the profit value reaches the

maximum and the loss and fuel consumption reach

the minimum. After run the algorithms 30 times, it

can be seen clearly that DPIO-SA has better

optimization ability than DPIO. Aiming at the task

scheduling problem, this paper proposes the CNA to

get the optimal task scheduling scheme through four

stages: First, the tenderer UAV sends out bid

information to potential bidder UAV. Then, the

potential bidder UAV is screened out as the bidder

UAV according to the contract requirements, and the

fitness information is sent to the tenderer UAV. Then,

the tenderer UAV selects the appropriate bidder UAV

as the winner UAV and sends the winning

information. Finally, the tenderer UAV and the

winner UAV sign the contract.

ACKNOWLEDGEMENTS

This research was supported in part by the National

Natural Science Foundation of China under grant No.

51979275, by the National Key Research and

Development Program of China under grant Nos.

2017YFD0701003 and 2018YFD0700603, by the

Jilin Province Key Research and Development Plan

Project under grant No. 20180201036SF, by the Open

Fund of Synergistic Innovation Center of Jiangsu

Modern Agricultural Equipment and Technology,

Jiangsu University, under grant No. 4091600015, by

the Open Research Fund of State Key Laboratory of

Information Engineering in Surveying, Mapping and

Remote Sensing, Wuhan University, under grant No.

19R06, by the Open Research Project of the State Key

Laboratory of Industrial Control Technology,

Zhejiang University, China, under grant No.

ICT20021, and by the Chinese Universities Scientific

Fund under grant No. 2019TC108 and 10710301.

REFERENCES

Chen, X., Qiao, Y. Z., 2016. Summary of unmanned aerial

vehicle task allocation. Journal of Shenyang Aerospace

University. 33(06):1-7.

Duan., H. B, Qiao, P. X., 2014. Pigeon-inspired

optimization: a new swarm intelligence optimizer for

air robot path planning. International Journal of

Intelligent Computing & Cybernetics. 7(1): 24-37.

Duan, H. B., Wang, X. H, 2016. Echo State Networks with

Orthogonal Pigeon-Inspired Optimization for Image

Restoration. Neural Networks and Learning Systems,

IEEE Transactions on. 27(11): 2413-2425.

Duan, H. B., Xu, X. B, et al., 2020. ADRC controller design

for UAV based on variable weighted mutant pigeon

inspired optimization. Acta Aeronautica et

Astronautica Sinica. 40(1):323490.

Huang, T. X., Tang D. B., Zhang, H. T., 2017. Research on

Realtime and Dynamic Scheduling Mechanism of

Intelligent Manufacturing System Based on Agent.

Machine Building Automation. 46(06):164-168.

Li, J., Zhang, K. Y., 2017. Heterogeneous Multi-AUV

Cooperative Task Allocation Based on Improved

Contract Net Algorithm. Journal of Unmanned

Undersea Systems. 25(5): 418-423.

Qi, X. G., Li, B., Fan, Y. S., et al. 2019. A survey of mission

planning on UAV system based on multi-constraints.

CAAI transactions on intelligent systems. 12(2):1-14.

Qiao, T. Z., Guo, X. P., Li, Y. W., 2016. Cooperative task

assignment simulation of Multi-UAVs in dynamic

environments. Journal of System Simulation.

28(09):2126-2132.

Ratanavilisagul, C., 2017. Modified Ant Colony

optimization with Pheromone Mutation for Travelling

Salesman Problem. 2017 14th International

Conference on Electrical Engineering/Electronics,

Computer, Telecommunications and Information

Technology 1(02), 411-414.

Ye, W., Zhu, A. H., Ouyang, Z. H., et al., 2010. Multi-

UCAV Cooperation Mission Assignment Based on

Hybrid Discrete Particle Swarm Optimization

Algorithm. Acta Armamentarii. 31(03):331-336.

Zainal, N., Zain, A, M., Sharif S., 2015. Overview of

Artificial Fish Swarm Algorithm and its Applications in

Industrial Problems. Applied Mechanics and Materials

815:253-257.

Zong, Q., Wang, D. D., et al., 2017. Research status and

development of multi UAV coordinated formation

flight control. Journal of Harbin Institute of

Technology. 49(03):1-14.

Discrete Pigeon Inspired Simulated Annealing Algorithm and Contract Net Algorithm based on Multi-objective Optimization for Task

Allocation of UAV Formation

183