Looking for the Hardest Hamiltonian Cycle Problem Instances

Joeri Sleegers

and Daan van den Berg

Informatics Institute, University of Amsterdam, The Netherlands

Keywords:

Hamiltonian Cycle Problem, Evolutionary Algorithms, Plant Propagation Algorithm, Instance Hardness,

NP-Complete.

Abstract:

We use two evolutionary algorithms to make hard instances of the Hamiltonian cycle problem. Hardness,

or ﬁtness, is deﬁned as the number of recursions required by Vandegriend-Culberson, the best known exact

backtracking algorithm for the problem. The hardest instances, all non-Hamiltonian, display a high degree of

regularity and scalability across graph sizes. These graphs are found multiple times through independent runs

and in both algorithms, suggestion the search space might contain monotonic paths to the global maximum.

The one-bit neighbourhoods of these instances are also analyzed, and show that these hardest instances are

separated from the easiest problem instances by just one bit of information. For Hamiltonian-bound graphs, the

hardest instances are less uniform and substantially easier than their non-Hamiltonian counterparts. Reasons

for these less-conclusive results are presented and discussed.

1 INTRODUCTION

The Hamiltonian cycle problem involves deciding

whether an undirected and unweighted graph contains

a path that visits every vertex exactly once and returns

to the ﬁrst vertex, closing the loop. In stark contrast

to the closely related Euler cycle problem, which is

easy, the Hamiltonian cycle problem is notoriously

hard, and even has an entry (number 10) on Richard

Karp’s infamous list of NP-complete problems (Karp,

1972). Under the common assumption that the classes

of P and NP are not equal, being NP-complete means

that the Hamiltonian cycle problem has no subexpo-

nential solving algorithm, but candidate solutions can

still be veriﬁed in polynomial time (Garey and John-

son, 1990)(Cook, 1971). NP-complete problems are

in some sense ‘at the summit of NP’: if a polynomial

time algorithm is found for just one of these problems,

the class of NP-complete problems disappears. Un-

fortunately, such an algorithm is not known for any of

the myriad problems in this class, which are therefore

intractable even at very small instance sizes.

But the exponential runtime increase for solving

algorithms

is not as crippling as it might appear on

https://orcid.org/0000-0003-1701-6319

https://orcid.org/0000-0001-5060-3342

Whenever we say ‘solvers’ or ‘solving algorithms’, we

always mean exact or complete algorithms, and never their

heuristic or non-deterministic counterparts.

ﬁrst sight. As it turns out, there are substantial dif-

ferences in instance hardness for many NP-complete

problems, and literature on the subject is widely

available (Cheeseman et al., 1991). One example

is graph colorability, for which Daniel Br

elaz’ algo-

rithm performs signiﬁcantly better than the problem’s

exponential upper bound on many instances (Br

elaz,

1979)(Turner, 1988). For the satisﬁability problem

(SAT), which could be considered ‘the root of all NP-

completeness’, the hardness of individual instances,

measured in computational effort required for solv-

ing, critically depends on the ratio of clauses to vari-

ables in the formula (Larrabee and Tsuji, 1993)(Sel-

man et al., 1996). Instances of SAT with many vari-

ables and relatively few clauses are generally speak-

ing easy to decide, because they have many solutions.

On the other hand, instances with few variables and

many clauses are also easy to decide, because they

can be quickly asserted to be unsolvable. But right

in the middle, around the clause-to-variable ratio of

α ≈ 4.26, where a randomly generated formula has

50 % chance of being solvable, is where the hard-

est instances occur

(Cheeseman et al., 1991)(Hutter

et al., 2014). In this sense, the clause-to-variable ra-

tio α functions as an ‘order parameter’, or ‘predictive

data analytic’, indicating where to expect the worst

For further reﬁnement on solver performance

around the phase transition in SAT, see (Coarfa et al.,

2000)(Aguirre and Vardi, 2001)

Sleegers, J. and van den Berg, D.

Looking for the Hardest Hamiltonian Cycle Problem Instances.

DOI: 10.5220/0010066900400048

In Proceedings of the 12th International Joint Conference on Computational Intelligence (IJCCI 2020), pages 40-48

ISBN: 978-989-758-475-6

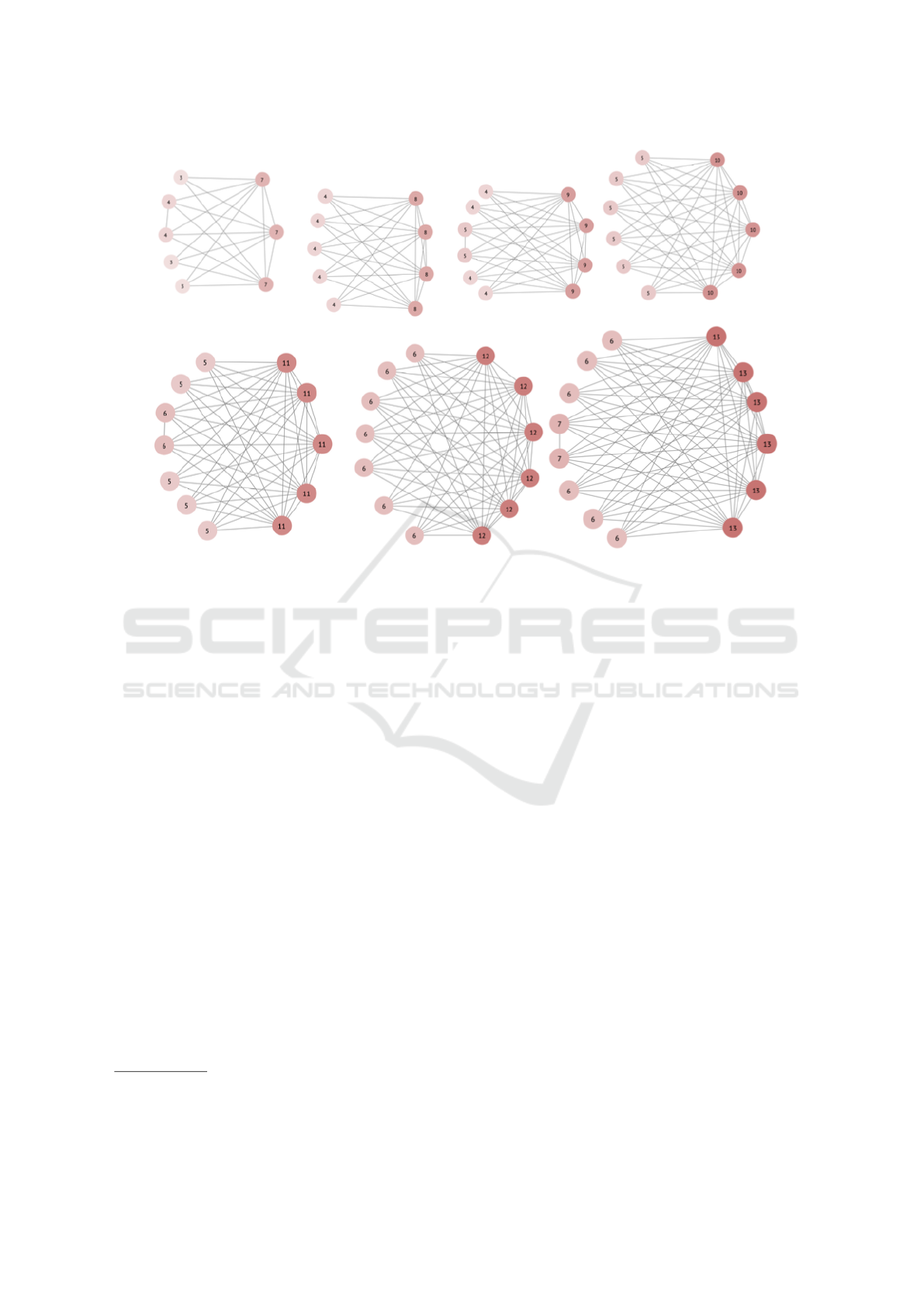
Figure 1: The hardest instances of the Hamiltonian cycle problem are all non-Hamiltonian, highly structured, and maximally

dense. Graphs were found with evolutionary algorithms, and the ﬁtness measured in recursions needed for the Vandegriend-

Culberson algorithm, the most efﬁcient backtracker available. The dominant conﬁguration of a ’wall’ (left hand side) and a

fully connected clique was reached multiple times in independent runs and in both algorithms.

runtimes when solving instances of randomly gener-

ated SAT-formulas.

For the Hamilton cycle problem, such an order pa-

rameter also exists, and it is again related to the solv-

ability of the individual instance. For any randomly

generated graph of V vertices and E edges, the prob-

ability of being Hamiltonian is given by

Hamiltonian

(V ,E) = e

−e

−2c

(1)

which is a strictly increasing function on any ﬁnite

interval, and in which c depends on E as

E =

/2 V · ln(V ) +

/2 V · ln(ln(V )) + cV (2)

following the results of J

anos Koml

os and Endre Sze-

mer

edi (Koml

os and Szemer

edi, 1983). In this equa-

tion, P

Hamiltonian

(V ,E) has its steepest derivative at

c = 0, where E =

/2 Vln(V ) +

/2 Vln(ln(V )). Al-

though this ’threshold point’ happens to be at e

−1

≈

0.368, rather than a more intuitive 0.5 like in SAT

this ‘Koml

os-Szemer

edi bound’ is considered as the

The origin of this speciﬁc value is that the threshold

function becomes ever steeper exactly around e

−1

as graph

size increases, approaching a step function as V → ∞.

central point for the hardest Hamiltonian problem in-

stances. The number of edges (or equivalently: ver-

tex degree) is consequentially proposed as its order

parameter (Cheeseman et al., 1991)(van Horn et al.,

2018). For a numerical example: randomly generated

undirected graphs of 120 vertices, the hardest Hamil-

tonian cycle problem instances would occur around

381 edges, where the probability of being Hamilto-

nian is ≈ 37%. Far more edges make for much eas-

ier problems instances, as dense graphs contain many

Hamiltonian cycles, and one is quickly found. Graphs

with far fewer edges are also easy, because they can be

qualiﬁed as unhamiltonian (i.e. not having a Hamilto-

nian cycle) relatively fast.

In an attempt to ﬁnd the absolute hardest of the

hardest problem instances, (Sleegers and van den

Berg, 2020) used evolutionary algorithms to gener-

ate graphs requiring maximum computational effort

for the best known bactracking algorithm. Starting

off from the Koml

os-Szemer

edi bound where tradi-

tionally the hardest problem instances were found,

a stochastic hillclimber and plant propagation algo-

rithm (PPA) produced graphs that required ever more

recursions for the Vandegriend-Culberson (hence-

forth ’Vacul’) algorithm, the most efﬁcient backtrack-

ing algorithm for the problem known to date (Culber-

son and Vandegriend, 2011). But NP-completeness

Looking for the Hardest Hamiltonian Cycle Problem Instances

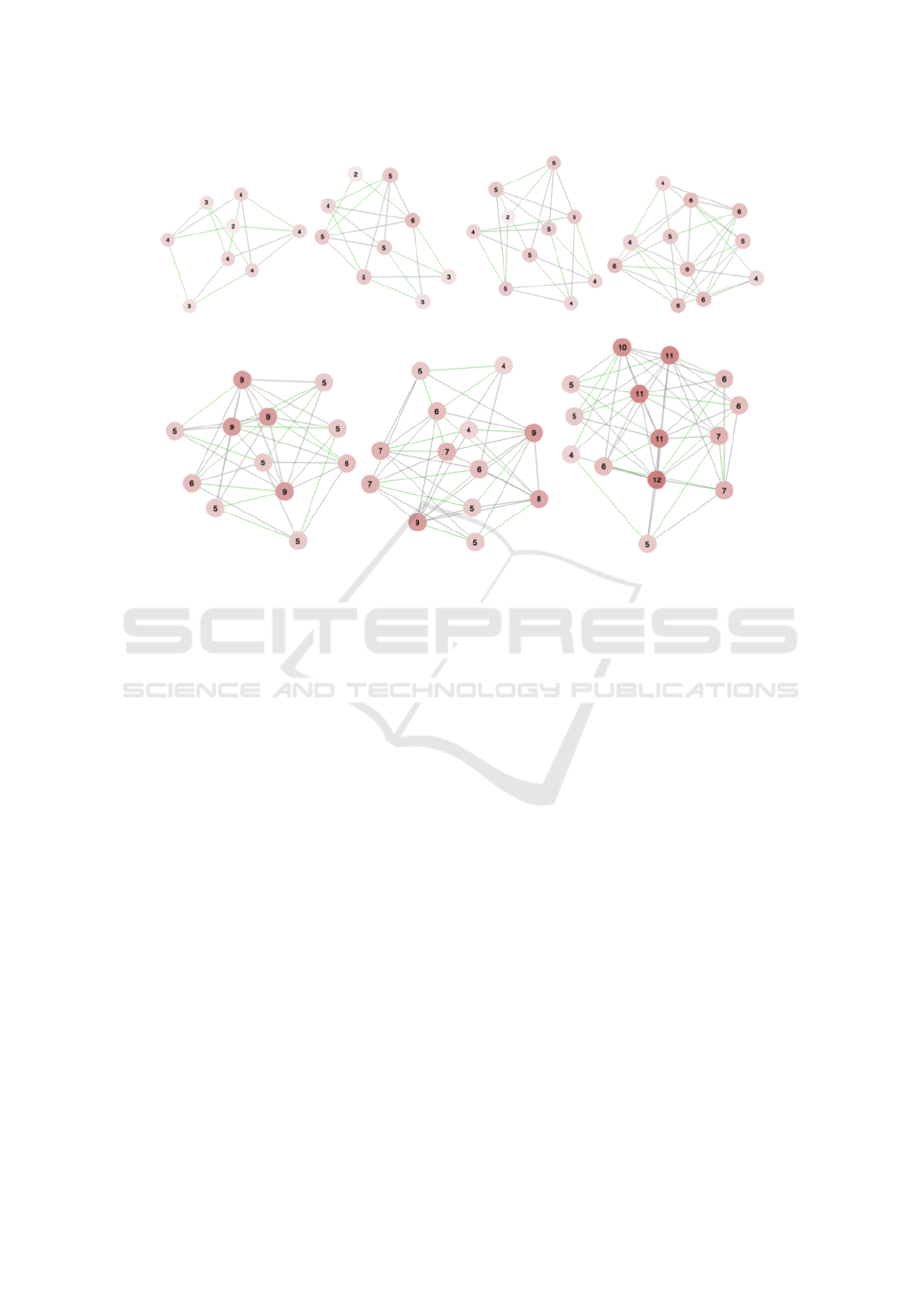
Figure 2: The hardest instances of the Hamiltonian cycle problem that do contain a Hamiltonian cycle. Structure is much less

obvious than for the non-Hamiltonian instances, although some premature tendencies towards cliquing might be discerned.

had not surrendered all of its suprises yet: the re-

sulting graphs were found nowhere near the Koml

os-

Szemer

di bound. They were much denser, and

sported a high degree of structural regularity, which

might be expressed as low Kolmogorov complexity

(Li et al., 2008). The authors hypothesized that ex-

actly for this reason, these very hard problem in-

stances had never shown up in the large randomized

ensembles of the aforementioned research endeav-

ours. But the study raised more questions than an-

swers: had the evolutionary algorithms actually con-

verged? Are these almost-regular graphs really the

hardest problem instances? And why are they all

non-Hamiltonian? What do the hardest Hamiltonian

graphs look like? And does the number of edges of

the initial graph inﬂuence the outcome?

In this study, we will answer some of these ques-

tions, and further our knowledge into the problem.

First, we will explain the algorithms involved: Vacul’s

algorithm for solving problem instances, the stochas-

tic hillclimber and the plant propagation algorithms

for evolving graphs. Then, the experiment is de-

scribed; we signiﬁcantly extend the scope of graph

sizes, runs, starting points, and evaluations. We also

conduct a ’Hamiltonian-bound’ experiment, in which

evolving graphs are forced to be Hamiltonian, to see

how hard these instances can possibly be. Hard, but

not nearly as hard as the non-Hamiltonian graphs, as

we will shortly see. The paper concludes with a dis-

cussion of the results, outlining future research direc-

tions and acknowledging the reviewers’ efforts.

2 ALGORITHMS

2.1 Hamiltonian Cycle Problem Solver

Over the last century, a great number of determinis-

tic exact solving algorithms have been developed for

the Hamiltonian cyle problem. Rooted in dynamic

programming, the Help-Karp algorithm is quite mem-

ory intensive, but by O(n

· 2

) still holds the lowest

time complexity (Held and Karp, 1962). Later al-

gorithms by Frank Rubin (1974), Martello’s ’Algo-

rithm 595’ (1983), Cheeseman’s (1991), Vandegriend

& Culberson’s (1998) and Van Horn’s (2018) are all

exact backtracking algorithms, and therefore have a

theoretical upper runtime bound of O(v!), but per-

form signiﬁcantly better on large ensembles of ran-

dom graphs due to clever optimization strategies (Ru-

bin, 1974; Martello, 1983; Cheeseman et al., 1991;

Culberson and Vandegriend, 2011; van Horn et al.,

2018). Still, the hardest graphs for all these depth-

ﬁrst based algorithms are found around the Koml

os-

Szemer

edi bound, where the probability of a random

graph being Hamiltonian goes from almost zero to al-

most one as E increases (eqs.1 and 2).

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

Interestingly enough though, all these are applied

variations and subsets of just three optimization tech-

niques: vertex degree preference, edge pruning, and

non-Hamiltonicity checks. The more the better, it

seems, as Vacul’s algorithm, containing all three tech-

niques, signiﬁcantly outperforms all the others – even

though its hardest instances are still near the Koml

os-

Szemer

edi bound (Koml

os and Szemer

edi, 1983). It

is this algorithm, the best backtracker available, that

we use for measuring the hardness of Hamiltonian cy-

cle problem instances.

Vacul’s algorithm is a depth-ﬁrst search algorithm

that uses pruning, non-Hamiltonicity checks and em-

ploys a low-degree ﬁrst ordering while recursing over

the vertices. Techniques for edge pruning and non-

Hamiltonicity checks are employed both before and

during recursion. The pruning subroutine removes

edges that cannot be in any Hamiltonian cycle, based

on ‘required edges’ that must be in a Hamilton cy-

cle, given a problem instance has one. An edge is

required if it is connected to a vertex with degree

two. The algorithm then uses two pruning methods;

the ﬁrst method seeks out vertices that have a degree

higher than two and are connected to two required

edges, rendering all other edges removable. The sec-

ond method looks for paths of required edges that do

not (yet) form a Hamilton cycle. If an edge exists that

would close such a path prematurely, it should be re-

moved.

The checks for non-Hamiltonicity examine

whether the graph cannot contain a Hamilton cycle

based on two global properties: having a vertex

with degree smaller than two, or the graph being

disconnected. Third, the algorithm checks whether

the graph is 1-connected, using Tarjan’s algorithm

(Tarjan, 1972). If any of these three conditions

are met, the graph cannot be Hamiltonian and the

recursive process can be skipped or be backtracked

upon.

2.2 Evolutionary Algorithms

The evolutionary algorithms used for making hard

problem instances are a stochastic hillclimber and

an implementation of the plant propagation algo-

rithm, adapted from an earlier application to the

traveling salesman problem (Selamo

glu and Salhi,

2016)(Geleijn et al., 2019). By applying mutations to

the edges of a graph, both algorithms try to iteratively

increase its ﬁtness, measured in number of recursions

required by the Vacul-algorithm to solve the instance.

The more recursions are required, the harder the prob-

lem instance, and the ﬁtter the graph.

The evolutionary algorithms use three mutation

types with equal probability: to insert an edge at a

random unoccupied place in the graph, to randomly

remove an existing edge from the graph, and to move

and edge, which is effectively equal to a remove mu-

tation followed by an insert mutation (on a different

unoccupied place). In the hillclimber algorithm, one

mutation is chosen at random after which the graph is

reevaluated. The mutation is reverted iff the resulting

graph is unﬁtter than its parent, and kept otherwise.

This process is repeated for a predetermined number

of evaluations (or iterations, for this algorithm).

Table 1: The number and mutability of offspring produced

by PPA’s individuals are based on its ﬁtness rank (1 =

ﬁttest).

Rank 1 2 3 4 5 6 - 10

#offspring 6 5 4 3 2 1

#mutations 1 2 5 5 10 20

The plant propagation algorithm is a population-

based algorithm that tries to balance exploration and

exploitation by letting the ﬁtter individuals in the

population produce many offspring with few mu-

tations, and unﬁtter individuals in the population

few offspring with many mutations. It can be ap-

plied to a broad spectrum of continuous, discrete

and mixed objective landscapes in scientiﬁc, indus-

trial and even artistic optimization problems (Salhi

and Fraga, 2011)(Selamo

glu and Salhi, 2016)(Geleijn

et al., 2019)(Vrielink and van den Berg, 2019)(Paauw

and Van den Berg, 2019). A most recent investigation

suggested that one version of the algorithm might be

largely parameter independent (de Jonge and van den

Berg, 2020).

The implementation of the plant propagation al-

gorithm used in this experiment is closely related to a

discrete adaptation that was earlier applied to the trav-

eling salesman problem and the university timetabling

problem (Selamo

glu and Salhi, 2016)(Geleijn et al.,

2019). Each generation, the population is sorted on

ﬁtness after which each individual produces offspring

by ﬁrst copying itself, and then applying a number of

mutations to the offspring. If any of a parent’s off-

spring is ﬁtter, it replaces the parent; if multiple off-

spring are ﬁtter, the ﬁttest replaces the parent. The

exact numbers of offspring and mutations are prede-

termined for all ranks in the sorted population (see

Table 1). In this study, the population size is 10 and

therefore the number of evaluated offspring is 25 in all

PPA-runs. These parameters are chosen intuitively, as

they abide strongly by PPA’s philosophy of balancing

the powers of exploration and exploitation, but more

efﬁcient parameter settings are ceratinly not unthink-

able. The algorithm’s source code can be accessed

Looking for the Hardest Hamiltonian Cycle Problem Instances

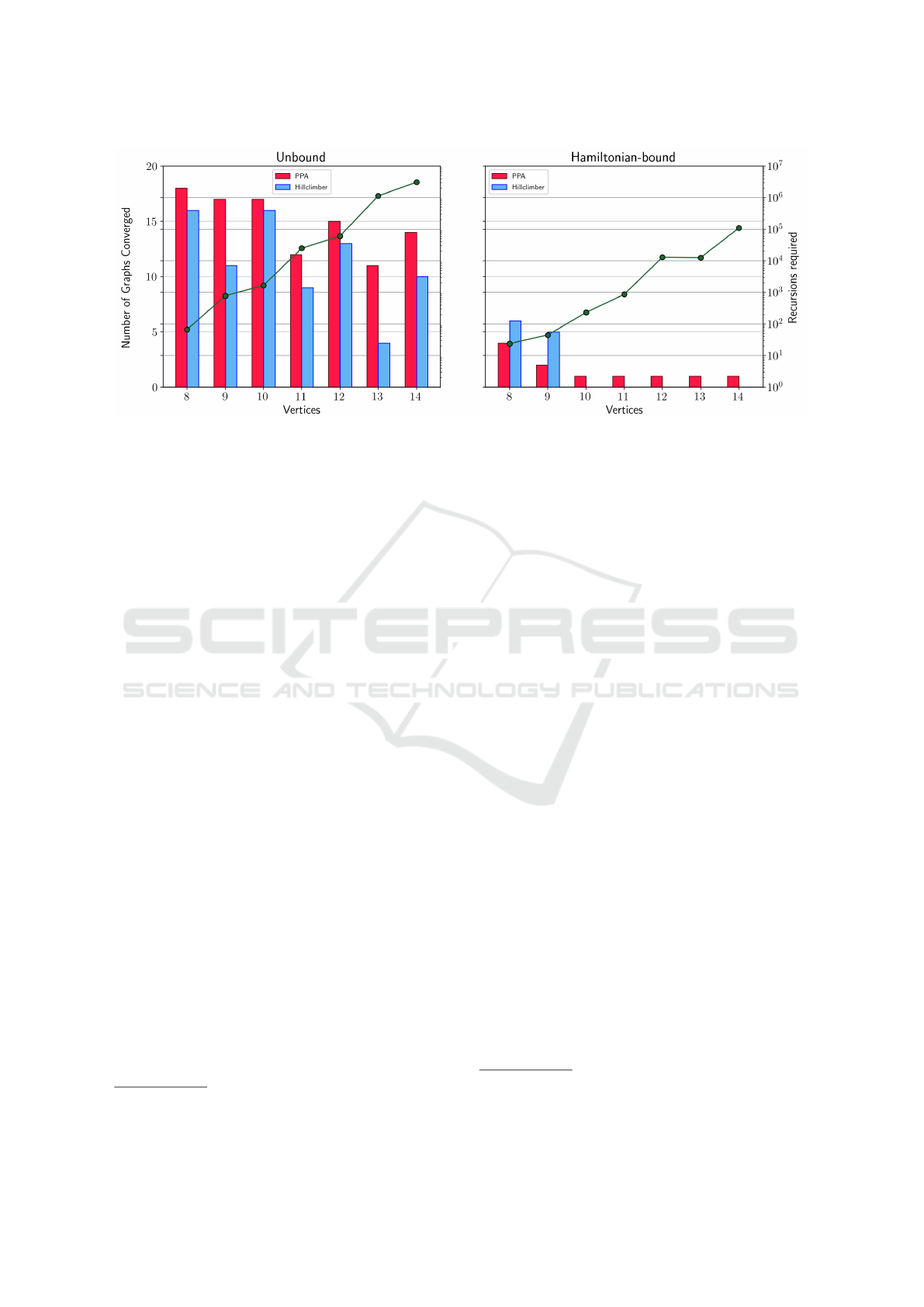
Figure 3: Recursions required for the hardest graph on the right-side vertical axis versus their corresponding graph size on

the horizontal axis. The left graph shows results of the experiment without restrictions on edge mutation, the right graph

shows the results of the experiment in which graphs forcibly retained an unmutable Hamiltonian cycle at all times. The bars

represent the number of multiple times a graph of maximum recursions was found.

through a public GitHub repository

3 EXPERIMENT

To obtain the hardest Hamiltonian cycle problem in-

stances, we evolve 560 graphs of sizes 8 ≤ V ≤ 14

in runs of 3000 evaluations. The investigation is

split in tow parts: an ’unbound’ experiment, in which

the evolutionary algorithms are free to modify all

the edges, and a ’Hamiltonian-bound’ experiment in

which the evolutionary algorithms are free to mod-

ify all the edges except the edges {(1, 2), (2, 3)...( v −

1,v), (v, 1)}, thereby enforcing the presence of a

Hamiltonian cycle in the graph at all times.

For the hillclimber runs, twenty randomly gener-

ated graphs were evenly dispersed in terms of edge

density, ranging from 0 to

/2V · (V − 1) edges, corre-

sponding to edge densities ∈ {0%,5%, 10%...100%}.

For the PPA runs, twenty initial populations were

made along the same edge density intervals, with

all graphs in one population having the same edge

density. It should be noted that these densities are

ﬁxed only upon initialization, as the evolutionary al-

gorithms are free to insert and remove edges from

graphs at every step of a run. The rationale be-

hind these choices however, is that earlier results

could have been biased from the initialization on the

Koml

os-Szemer

edi bound. Besides, this approach

would cover more of the state space, at least as seen

from the initial conditions. In the end, it didn’t make

much of a difference.

https://github.com/Joeri1324/evolving-hard-hamilton-

cycles

From these evely distributed initial positions, both

algorithms ran for 3000 function evaluations. This

means 3000 iterations for the stochastic hillclimber,

but 120 generations of PPA, which produces 25 off-

spring, and therefore performs 25 evaluations per

generation (see Table 1). These numbers might

look small, as do the numbers of vertices in the

graphs used, but the number of recursions required

for Vacul’s solving algorithm in every function eval-

uation can still easily run in the millions (see Figure

3). And as we are actively pushing towards the max-

imum, the entire unbound experiment of 280 runs (7

graph sizes with 20 starting points for two evolution-

ary algorithms) with 3000 function evaluations still

took approximately 45 days on 16 cores of the LISA

cluster computer at Amsterdam’s Science Park

. The

280 runs of 3000 evaluations for the Hamiltonian-

bound experiment took signiﬁcantly less time, possi-

bly because the Hamiltonian-bound instances require

signiﬁcantly fewer recursions to decide. Hamilto-

nian instances are easier, generally speaking. But if

you want to see for yourself, all the experiment’s re-

sources are publicly available through a repository

https://userinfo.surfsara.nl/systems/lisa

https://github.com/Joeri1324/evolving-hard-hamilton-

cycles

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

Table 2: The smallest distance between the hardest and easiest problem instances for the Hamiltonian cycle problem is just

one bit: inserting an edge on either of the two possible insertion point types makes the hardest (non-Hamiltonian) instance

trivially Hamiltonian. Removing an edge from either of the three possible types will make for a (just slightly) easier non-

Hamiltonian instance. Only ﬁve one-bit operations are possible, due to the highly structured nature of the results. Instance

hardness is measured in number of recursions required by Vacul’s algorithm.

Graph size 8 9 10 11 12 13 14

Most difﬁcult 67 785 1,673 25,061 61,051 1,139,785 3,091,141

Insert wall #1 8 9 10 11 12 13 14

Insert wall #2 8 - 10 - 12 - 14

Remove clique-clique 63 717 1,577 23,261 57,799 1,071,037 2,943,549

Remove wall-wall 49 - 1,081 - 47,655 - 2,016,877

Remove wall-clique 25 529 1,015 18,561 43,513 894,861 2,387,791

4 RESULTS

4.1 Unbound Experiment

The results of the unbound experiment clearly

show the hardest problem instances are all non-

Hamiltonian. Both evolutionary algorithms produced

structurally similar graphs consisting of a ‘clique’

and a ’wall’ for all vertex numbers (See Figure 1).

The clique is a fully connected subset consisting

of V

c(odd)

V −1

vertices in odd-sized graphs, and

c(even)

V −2

vertices in even-sized graphs. Every

graph of size V is a subgraph of size V + 1, even

though the exact addition of edges differs from odd

to even graphs. The edge number of these graphs is

consequently given by:

(V −V

) ·V

/2V

· (V

− 1) (3)

with V

= V

c(odd)

if V is odd, and

(V −V

) ·V

/2V

· (V

− 1) + 1 (4)

with V

= V

c(even)

if V is even. These quadratic

results suggest that the larger the graph, the further

away the hardest instances are from the Koml

os-

Szemer

edi bound, which only increases (double) log-

arithmically in V . It should be noted that these results

strongly contradict earlier ﬁndings that ﬁnd the hard-

est instances close to the bound (Cheeseman et al.,

1991)(Culberson and Vandegriend, 2011). This might

be due to the random nature of the test sets, but for the

related SAT-problem, two studies led by Moshe Vardi

suggest that the hardness peak itself might also move,

depending on the speciﬁc solver used in the experi-

ments (Coarfa et al., 2000)(Aguirre and Vardi, 2001).

On the lognormal scale of Figure 3, the number

of recursions roughly follows a straight line with an

inclination of 0.78, indicating that for wall-and-clique

graphs of size V , the number of recursions increases

exponentially as approximately O(c

0.78V

), in which

c > 1. The number of required recursions wobbles a

bit in V , which is possibly due to discrepancy between

odd- and even-sized graphs. In the odd-sized graphs,

there are slightly more vertices in the clique, which

results in a higher edge density, and possibly more

required recursions.

In the unbound experiment, both the plant prop-

agation algorithm and the stochastic hillclimber con-

verged multiple times to the same graph. Hillclimber

between 4 and 16 out of 20 runs for each V , aver-

aging at about 11,3 (See the bars in Figure 3, left).

In its operation, the stochastic hillclimber is prone to

get stuck in local maxima, but the plant propagation

algorithm is well equipped for navigating large non-

convex search spaces with its highly mutative off-

spring at the bottom of the population. Maybe that’s

why the algorithm did solidly better however, with

an average of 14,9 out of 20 runs converging to the

(same) wall-and-clique graph, with all values between

11 and 18. It should be noted though, that PPA only

outperforms the hillclimber only after approximately

2000 evaluations, an effect that was also witnessed

in other problems (Geleijn et al., 2019). Because of

the consistent convergence through independent runs

of both algorithms, and the insensitivity of PPA to lo-

cal maxima, it seems possible that the wall-and-clique

graphs are indeed the hardest instances of the Hamil-

tonian cycle problem for Vacul’s algorithm. More-

over, this maximum appears to be connected through

a state path of monotonically increasing ﬁtness val-

ues, but this yet awaits further veriﬁcation. A slightly

eyebrow raising observation is that both algorithms

converge somewhat better for even numbers of V .

4.2 One-bit Neighbourhood

As an added bonus, the highly structured results of

the unbound experiment allow for an exhaustive map-

ping of the one-bit neighbourhood of the most difﬁ-

Looking for the Hardest Hamiltonian Cycle Problem Instances

Table 3: The edge-independent search space increases faster than exponential in the number of vertices, but the percentage

of Hamiltonian instances increases also. This results in an ever denser volume of Hamiltonian graphs, which might explain a

possible lack of convergence in the evolutionary algorithms for the Hamiltonian-bound experiment. Numbers are rounded.

Vertices 8 9 10 11 12 13 14

Graphs 2.68 ·10

6.87 ·10

3.52 ·10

3.60 ·10

7.38 ·10

3.02 ·10

2.48 ·10

Hamiltonian 57.9% 66.5% 74.4% 81.0% 86.3% 90.4% 93.4%

cult instances. For the odd-sized graphs, there is only

one possible graph type resulting from edge insertion.

For the even-sized graphs there are two neighbouring

graph types from inserting an edge, due to the ex-

tra edge in the wall. Both these edge insertions im-

mediately make the graph Hamiltonian and decidable

within V recursions (Table 2). It is a remarkable ﬁnd-

ing, that the hardest non-Hamiltonian instances and

the easiest Hamiltonian instances are separated by just

one bit of information.

Removal of an edge can create two one-bit neigh-

bouring graph types in odd-sized graphs, either from

removal inside the clique, or removal of a wall-clique

edge. In even-sized graphs, a third removal is possi-

ble, from the single wall-wall edge. All edge removal

operations lower the number of recursions needed to

decide the graph, but the effect is much less dra-

matic than for inserting edges. Even though the num-

ber of recursions from edge removal drops between

6% and 63% for the smallest instances, the differ-

ence is only between 5% and 33% for the largest in-

stance in this study, and is expected to become ever

smaller for larger instances, simply because larger

graphs have more edges, so the removal of one could

have a smaller impact on recursion.

These neighbourhood results do show however,

that the wall-and-clique graphs are at the very least a

local maximum of instance hardness. But since both

algorithms repeatedly and independently converged

to the same graph, and PPA is not sensitive to lo-

cal maxima, it might well be that these graphs are

the hardest instances of the Hamiltonian cycle prob-

lem (for Vacul’s algorithm). These results could be

taken as a suggestion that harder problem instances

for the Vandegriend-Culberson algorithm do not ex-

ist, but more extensive testing could substantially

(dis)conﬁrm this hypothesis.

4.3 Hamiltonian-bound Experiment

For the Hamiltonian-bound experiment, results are

much less unisono than for the unbound experiment.

The hardest Hamiltonian graphs found by the evolu-

tionary algorithms are still roughly a magnitude eas-

ier than the non-Hamiltonian graphs (See Figure 3,

right), with the number of recursions increasing as ap-

proximately O(c

0.62V

), in which c > 1. Again, this

exponent is a ﬁt on only seven data points, needs fu-

ture reﬁnement, but still serves as a rough indication.

The structural resemblance between graphs of dif-

ferent sizes is also much lower (Figure 2). For graphs

of size V = 8, the maximum number of recursions

was identical in two graphs, reached in 10 out of 40

runs. For V = 9, only 7 out of 40 runs reached any of

4 graphs with maximum recursions, and for larger V ,

the hardest Hamiltonian instance was unique among

40, with just a single PPA run producing that graph.

These results suggest that the hardest possible Hamil-

tonian instances might not yet have been found, and

that harder graphs are still possible. A neighbourhood

mapping was not done for these graphs, as the lack of

structure makes it relatively cumbersome, and results

inconclusive.

5 DISCUSSION

If the problem instances found in the unbound ex-

periment are indeed global maxima, it could indi-

cate that the problem space is largely convex, since

the stochastic hillclimber acquires similar results to

the PPA. In this sense, The wall-and-clique graph

might be sitting on the top of mount hardness, with

very easy Hamiltonian instances and very hard non-

Hamiltonian instances in its immediate vicinity. For

the Hamiltonian-bound experiment, such observa-

tions are less expedient, because convergence of the

algorithms appears unlikely. So what makes these al-

gorithms perform so bad on the Hamiltonian-bound

problem instances? Surely, less freedom from ﬁx-

ing unmutable edges would make a problem easier,

right? The converse might actually be true, and the

argument is a somewhat bewildering and counterin-

tuitive numerical elaboration resulting from Koml

and Szemer

edi early results and some basic combina-

torics.

As presented in Equation 1, the probability of

a random graph being Hamiltonian sigmoidally de-

pends on the number of edges. But for a complete

edge independent search space such as ours, this prob-

ability might also be seen as a frequency. As a nu-

merical example: for V = 8 and E = 14, Koml

os and

Szemer

edi’s equations predict an approximate 61%

chance of Hamiltonicity. Equivalently, one could

say that 61% of all existable graphs with V = 8 and

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

E = 14 are Hamiltonian. Now the number of graphs

is equivalent to the number of options for placing the

E edges between V vertices:



/2 ·V · (V − 1)



(5)

which for V = 8 and E = 14, amounts to 40,116,600

graphs. Of these, approximately 61%, or 24,274,846

gaphs are Hamiltonian, the remaining 39%, or

15,841,754 graphs, are non-Hamiltonian. Summing

these results over all possible values of E for a given

V gives us the number (or percentage) of Hamiltonian

graphs in the entire edge-independent search space

(Table 3).

As it turns out, the number of Hamiltonian in-

stances ever more outweigh the number of non-

Hamiltonian instances as graphs get larger, possi-

bly making the state space harder to navigate for

our evolutionary algorithms, which have identical

numbers of evaluations for all V . This observation

might also account for the slightly deminishing re-

turns in both experiments for both algorithms as V

increases. But contrarily, these numbers do not ac-

count for graph isomorphism which might be quite

inﬂuential, but whose detection is a notorious prob-

lem in itself (McKay and Piperno, 2014). It is an

interesting and non-trivial question to see whether

other (meta)heuristic algorithms such as a properly

parameterized simulated annealing (Kirkpatrick et al.,

1983)(Dahmani et al., 2020) or genetic algorithms

ack et al., 1997) do better for this problem. It is also

plausible that metaheuristic parameter tuning and/or

control might set some serious sods to the dyke, as the

problem space clearly changes rapidly as V increases.

On a ﬁnal note, these graphs might be difﬁcult for

Vacul’s solving algorithm because its efﬁciency heav-

ily depends on pruning off edges that cannot be in

any Hamilton cycle, which only occurs when a vertex

is connected by two required edges. Because of the

compact structure of the wall-and-clique graph, this

will only happen near the full depth of the search tree,

when all but two vertices of the maximum clique are

included in a partial solution. But just the ubiquity of

pruning techniques throughout history doesn’t spell

much good for other exact algorithms either when

it comes to these graphs. The non-Hamiltonian in-

stances in this study might thereby actually be the

hardest around, but more evidence, or perhaps even

a proof, is needed to soldify this conjecture.

ACKNOWLEDGEMENTS

ECTA’s reviewers

really made an effort to under-

stand this somewhat pioneering approach to instance

hardness. A special hats off goes to Reviewer #4, who

took the time to hand-correct a host of typo’s and sup-

ply an annotated pdf along with the report. Thank you

all, you have done this paper a great favour.

REFERENCES

Aguirre, A. S. M. and Vardi, M. (2001). Random 3-sat and

bdds: The plot thickens further. In International Con-

ference on Principles and Practice of Constraint Pro-

gramming, pages 121–136. Springer.

ack, T., Fogel, D. B., and Michalewicz, Z. (1997). Hand-

book of evolutionary computation. Release, 97(1):B1.

elaz, D. (1979). New methods to color the vertices of a

graph. Communications of the ACM, 22(4):251–256.

Cheeseman, P., Kanefsky, B., and Taylor, W. M. (1991).

Where the really hard problems are. In Proceedings of

the 12th International Joint Conference on Artiﬁcial

Intelligence - Volume 1, IJCAI’91, pages 331–337,

San Francisco, CA, USA. Morgan Kaufmann Publish-

ers Inc.

Coarfa, C., Demopoulos, D. D., Aguirre, A. S. M., Sub-

ramanian, D., and Vardi, M. Y. (2000). Random 3-

sat: The plot thickens. In International Conference on

Principles and Practice of Constraint Programming,

pages 143–159. Springer.

Cook, S. A. (1971). The complexity of theorem-proving

procedures. In Proceedings of the Third Annual

ACM Symposium on Theory of Computing, STOC ’71,

pages 151–158, New York, NY, USA. ACM.

Culberson, J. C. and Vandegriend, B. (2011). The gn,m

phase transition is not hard for the hamiltonian cycle

problem. CoRR, abs/1105.5443.

Dahmani, R., Boogmans, S., Meijs, A., and van den Berg,

D. (2020). Paintings-from-polygons: simulated an-

nealing. In International Conference on Computa-

tional Creativity (ICCC’20).

de Jonge, M. and van den Berg, D. (2020). Plant propa-

gation parameterization: Offspring & population size.

Evo* 2020, page 19.

Garey, M. R. and Johnson, D. S. (1990). Computers

and Intractability; A Guide to the Theory of NP-

Completeness. W. H. Freeman & Co., New York, NY,

USA.

Geleijn, R., van der Meer, M., van der Post, Q., and van den

Berg, D. (2019). The plant propagation algorithm on

timetables: First results. EVO* 2019, page 2.

Held, M. and Karp, R. M. (1962). A dynamic program-

ming approach to sequencing problems. Journal of

the Society for Industrial and Applied mathematics,

10(1):196–210.

ECTA 2020 is part of the larger conference IJCCI 2020,

see http://www.ecta.ijcci.org/.

Looking for the Hardest Hamiltonian Cycle Problem Instances

Hutter, F., Xu, L., Hoos, H. H., and Leyton-Brown, K.

(2014). Algorithm runtime prediction: Methods &

evaluation. Artiﬁcial Intelligence, 206:79–111.

Karp, R. M. (1972). Reducibility among combinatorial

problems. In Miller, R. E., Thatcher, J. W., and

Bohlinger, J. D., editors, Complexity of Computer

Computations: Proceedings of a symposium on the

Complexity of Computer Computations, held March

20–22, 1972, at the IBM Thomas J. Watson Re-

search Center, Yorktown Heights, New York, and spon-

sored by the Ofﬁce of Naval Research, Mathemat-

ics Program, IBM World Trade Corporation, and the

IBM Research Mathematical Sciences Department,

Boston, MA. Springer US.

Kirkpatrick, S., Gelatt, C. D., and Vecchi, M. P. (1983).

Optimization by simulated annealing. science,

220(4598):671–680.

Koml

os, J. and Szemer

edi, E. (1983). Limit distribution for

the existence of hamiltonian cycles in a random graph.

Discrete Mathematics, 43(1):55–63.

Larrabee, T. and Tsuji, Y. (1993). Evidence for a satisﬁa-

bility threshold for random 3cnf formulas. Technical

report.

Li, M., Vit

anyi, P., et al. (2008). An introduction to Kol-

mogorov complexity and its applications, volume 3.

Springer.

Martello, S. (1983). Algorithm 595: An enumarative al-

gorithm for ﬁnding hamiltonian circuits in a directed

graph.

McKay, B. D. and Piperno, A. (2014). Practical graph

isomorphism, ii. Journal of Symbolic Computation,

60:94–112.

Paauw, M. and Van den Berg, D. (2019). Paintings,

polygons and plant propagation. In International

Conference on Computational Intelligence in Music,

Sound, Art and Design (Part of EvoStar), pages 84–

97. Springer.

Rubin, F. (1974). A search procedure for hamilton paths

and circuits. J. ACM, 21(4):576–580.

Salhi, A. and Fraga, E. S. (2011). Nature-inspired optimi-

sation approaches and the new plant propagation algo-

rithm.

Selamo

glu, B.

I. and Salhi, A. (2016). The plant propaga-

tion algorithm for discrete optimisation: The case of

the travelling salesman problem. In Nature-inspired

computation in engineering, pages 43–61. Springer.

Selman, B., Mitchell, D. G., and Levesque, H. J. (1996).

Generating hard satisﬁability problems. Artiﬁcial In-

telligence, 81(1):17 – 29. Frontiers in Problem Solv-

ing: Phase Transitions and Complexity.

Sleegers, J. and van den Berg, D. (2020). Plant propagation

& hard hamiltonian graphs. Evo* 2020, page 10.

Tarjan, R. (1972). Depth-ﬁrst search and linear graph algo-

rithms. SIAM journal on computing, 1(2):146–160.

Turner, J. S. (1988). Almost all k-colorable graphs are easy

to color. Journal of Algorithms, 9(1):63 – 82.

van Horn, G., Olij, R., Sleegers, J., and van den Berg, D.

(2018). A predictive data analytic for the hardness of

hamiltonian cycle problem instances. DATA ANALYT-

ICS 2018 : The Seventh International Conference on

Data Analytics.

Vrielink, W. and van den Berg, D. (2019). Fireworks algo-

rithm versus plant propagation algorithm.

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications