A Dimensionality Reduction Method for Data Visualization using

Particle Swarm Optimization

Panagiotis C. Petrantonakis

and Ioannis Kompatsiaris

Information Technologies Institute, Centre for Research and Technology - Hellas (CERTH), Thessaloniki, Greece

Keywords:

Particle Swarm Optimization, Data Visualization, Dimensionality Reduction.

Abstract:

Dimensionality reduction involves mapping of a set of high dimensional input points on a low dimensional

space. Mappings in low dimensional space are expected to preserve the pairwise distances of the high dimen-

sional inputs. In this work we present a dimensionality reduction method, called Dimensionality Reduction

based on Particle Swarm Optimization (PSO-DR), where the conversion of each input to the low dimensional

output does not depend on the rest of the inputs but, instead, it is based on a set of reference points (beacons).

The presented approach results in a simple, fast, versatile dimensionality reduction approach with good quality

of visualization and straightforward out-of-sample extension.

1 INTRODUCTION

In the era of data deluge, robust dimensionality re-

duction (DR) tools for visualization of large, high-

dimensional data have become an imperative need.

The fundamental principle of such tools is to trans-

late high dimensional data so that similar inputs are

mapped onto nearby low dimensional representations.

Ultimately, DR techniques aim at preserving as much

of the high dimensional structure either globally or lo-

cally to the low dimensional representation. A variety

of such tools for DR have been proposed the last few

decades, many of which have been reviewed by Lau-

rens van der Maaten (Van Der Maaten et al., 2009).

DR algorithms fall mainly into two categories.

The ones that preserve the distance-wise global struc-

ture of the data, such as PCA (Hotelling, 1933), Sam-

mon mapping (Sammon, 1969), and others that pre-

serve the structure of a conﬁned neighborhood (local

structure) such as, tSNE (Van Der Maaten and Hin-

ton, 2008), Isomap (Tenenbaum et al., 2000), Lapla-

cian Eigenmaps (Belkin and Niyogi, 2002; Belkin and

Niyogi, 2003), and LLE (Hadsell et al., 2006). Both

categories have been applied in a wide variety of ap-

plications with ever increasing data set sizes. Thus, it

is crucial that DR methods are both versatile and fast,

in order to cope with massive data.

In this paper we introduce a new DR technique for

https://orcid.org/0000-0001-9631-4327

https://orcid.org/0000-0001-6447-9020

data visualization based on the Particle Swarm Op-

timization algorithm (PSO) (Eberhart and Kennedy,

1995; Shi and Eberhart, 1998; Shi and Eberhart,

1999; Shi et al., 2001). The PSO-based DR ap-

proach (PSO-DR) seeks to preserve the high dimen-

sional structure by exploiting the fast and versatile na-

ture of the PSO algorithm. We provide the respective

algorithmic approach for PSO-DR and present its im-

plementation with parallel, fast computation. We test

PSO-DR on four different datasets, either real or arti-

ﬁcial, and it exhibits good performance on both cate-

gories. We compare the proposed PSO-DR approach

with the current state-of-the-art tSNE method along

with other linear and nonlinear DR algorithms. Its

performance is better or comparable with the most

of the state-of-the-art DR approaches and performs

faster than those with the best visualization quality,

especially for larger data sets. In addition, PSO-DR

allows for the mapping of new data points explic-

itly, in contrast with the majority of the nonlinear DR

techniques where approximate estimation of out-of-

sample extension leads to mapping errors of new data

points. In general, through its simplicity, versatility,

fast computation and straightforward out-of-sample

extension PSO-DR constitutes an efﬁcient, general

purpose, DR technique.

The outline of the paper is as follows. In section

2 we present the methodological approach along with

the background information, PSO-DR algorithm and

implementation issues. Section 3 describes the exper-

imental set up and presents the corresponding results.

Petrantonakis, P. and Kompatsiaris, I.

A Dimensionality Reduction Method for Data Visualization using Particle Swarm Optimization.

DOI: 10.5220/0010020601310138

In Proceedings of the 12th International Joint Conference on Computational Intelligence (IJCCI 2020), pages 131-138

ISBN: 978-989-758-475-6

131

Section 4 discusses the presented outcomes and pro-

poses future research. Finally, section 5 concludes the

paper.

2 PSO BASED DATA

VISUALIZATION

2.1 Background

The problem of DR is to ﬁnd a function that maps

the high dimensional inputs to a lower dimensional

space by preserving the intrinsic structure of the data.

Particularly, we seek to map a high dimensional data

set X ⊂ R

to a n-D data set Y ⊂ R

in a low di-

mensional space (usually n = 2 or 3, i.e., 2-D or 3-D

space). Each low dimensional point y

∈Y, i = 1, ..., M

represents the mapping of a corresponding high di-

mensional point x

∈ X , i = 1, ..., M. The approach

followed, e.g., in classical multidimensional scaling

(Torgerson, 1952) is to ﬁnd all those low dimensional

points y

, i = 1, ..., M that minimize the sum of the dif-

ferences between the pairwise distances in the high

dimensional space with the pairwise distances of the

low dimensional one, i.e., to minimize:

φ(Y ) =

∑

i j

− δ

i j

) (1)

where d

i j

is the distance (dissimilarity measure) be-

tween x

and x

whereas δ

i j

is the distance of the cor-

responding low dimensional points y

and y

In this work, instead of searching for an optimum

solution set, Y , we seek for the optimum low dimen-

sional points one by one. The key step of the proposed

approach is to deﬁne a set of high dimensional bea-

cons, X

, i.e., certain, reference points in high dimen-

sional space, and the corresponding low dimensional

ones, Y

, i.e., Y

is the low dimensional representa-

tion of X

. Then, map, e.g., a point x

to a point y

comparing the distances of x

from X

with the dis-

tances of y

from Y

. In essence, the relative position-

ing of x

with respect to X

in high-dimensional space

should be preserved in the low-dimensional space by

regulating the positioning of the y

with respect to Y

The following two subsections describe the PSO al-

gorithm and the proposed PSO-DR approach, respec-

tively.

2.2 Particle Swarm Optimization

Algorithm

PSO algorithm was introduced by Kennedy and Eber-

hart in 1995 (Eberhart and Kennedy, 1995), and it was

inspired by the social behavior of groups of, e.g., birds

in order to solve optimization problems.

PSO algorithm searches the space for optimal so-

lution based on the information shared between the

particles of a group. Each particle follows a trajec-

tory which is inﬂuenced by stochastic and determin-

istic components. In particular, each particle moves

according to its best achieved position, in terms of

the optimization problem, and the best position of the

group but with a random component. In every iter-

ation (time point t), a random particle of the group

changes its position, z

, i = 1, ..., P (P is the popula-

tion of the particles in the group) according to the new

velocity component, v

(Eberhart and Kennedy, 1995;

Koziel and Yang, 2011), i.e.:

= ωv

t−1

+ w

t−1

i, p

− z

t−1

) + w

t−1

− z

t−1

)

(2)

= z

+ v

, (3)

where z

t−1

i, p

and z

t−1

are the previous best particle

and group positions, respectively, ω, w

, w

are con-

stant weights and r

, r

are random numbers. Usually,

search space and velocity values are bounded whereas

the particles are initially distributed randomly in the

search space.

2.3 PSO-DR Algorithm

The proposed approach for DR is based on the PSO

algorithm to ﬁnd optimal positions Y that correspond

one by one to the high dimensional instances X. Thus,

for the search of an optimal solution y

, a group of

particles with positions z

, i = 1, ..., P are moving ac-

cording to the rule deﬁned by 2 and 3. The func-

tion that is minimized is the dissimilarity between

the distances of a high dimensional x

∈ X from the

high dimensional beacons x

∈ X

, j = 1, ..., J and

the distances of a low dimensional candidate solution

from the corresponding low dimensional beacons

∈ Y

, j = 1, ..., J. In particular we seek to minimize:

φ(y

) =

∑

− δ

)

(4)

where d

, j = 1, ..., J are the distances between x

and

, j = 1, ..., J, and δ

, j = 1, ..., J are the distances be-

tween y

and y

, j = 1, ..., J. In essence, the optimal

solution for Eq. 4, i.e., y

, is the mapping of the high

dimensional instance, x

, in the low dimensional space

based on the relative distances of x

and y

from the

corresponding beacon sets. Thus, as soon as the high

and low dimensional beacons are deﬁned, every high

dimensional data can be mapped onto the low dimen-

sional space by minimizing Eq. 4 using PSO.

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

132

As high dimensional beacons, X

, are used as ref-

erence points, we do not use any particular selection

criterion to deﬁne them. Instead, we randomly choose

J instances from data set X to use as the beacon set

. In order to estimate the corresponding low dimen-

sional beacons, Y

, we deﬁne as y

(associated with

the x

) a zero vector, i.e., y

= [0...0] ∈ R

. Then we

proceed with the deﬁnition of the rest of the beacons

, j = 2, ..., J as follows: y

is estimated by minimiz-

ing φ(y

) = d

− δ

where d

is the distance between

and x

, and δ

is the distance between the candi-

date y

and y

. In accordance, y

is estimated by min-

imizing φ(y

) =

∑

− δ

)

where d

, j = 1, 2 are

the respective distances between x

and x

, x

, and

, j = 1, 2 are the respective distances between the

candidate y

and y

, y

. The rest of the Y

set is esti-

mated with the same procedure. When the whole Y

set is deﬁned the rest of the X data set is mapped by

minimizing Eq. 4 with respect to the beacons Y

2.4 Implementation Issues

The PSO-DR algorithm was implemented in Mat-

lab 2019a. For the PSO algorithm the SwarmOps-

Numerical and Heuristic Optimization toolbox For

Matlab was used (toolbox available at: http://www.

hvass-labs.org/projects/swarmops/matlab/).

We ran all the experiments on a desktop PC, with

Intel Core(TM) i5-9600K at 3.70GHz, and 16 GB of

RAM.

The parameters concerning the PSO algorithm

was chosen according to the best parameters list pre-

sented in (Pedersen, 2010). In particular for the num-

ber of particles (swarm-size, P), number of iterations

of the PSO algorithm (stopping criterion), ω (iner-

tia weight), w

(particle’s-best weight), w

(swarm’s-

best weight) we used 25, 400, 0.3925, 2.5586, and

1.3358, respectively. These values were used for all

experiments conducted in this work.

For comparison reasons, other DR methods were

also used. In particular, PCA, tSNE, Isomap, Sam-

mon mapping, LLE, and Laplacian Eigenmaps were

compared with PSO-DR. For all these methods the

Matlab Toolbox for Dimensionality Reduction by

Laurens van der Maaten (Van Der Maaten et al., 2009)

was used. For each method the default values of the

parameters provided by the toolbox were used.

The number of beacons for each data set was de-

ﬁned to be a quarter of the number of instances x

in each data set X, i.e., J =

M except for the cases

where J was larger than 1000; then we set J = 1000

irrespectively of the data set size.

3 EXPERIMENTS

The experiments conducted in this work are presented

here. We ﬁrst describe the data sets used for DR and

subsequently elaborate on the experimental setup. Fi-

nally, we present the respective results.

3.1 Data Sets

Four different data sets were used to eval-

uate the performance of the PSO-DR algo-

rithm. In particular, the MNIST data set (The

MNIST data set is publicly available from

http://yann.lecun.com/exdb/mnist/index.html), the

COIL-20 data set (Nene et al., 1996), the FMNIST

data set (Xiao et al., 2017) and the Swiss Roll data

set with M = 3000.

The MNIST data set contains 60, 000, 28 × 28-

pixel (i.e., N = 784), grayscale images of hand writ-

ten digits (0, ..., 9). In this work we choose randomly

M = 6, 000 images (600 per class) to perform the

experiments. FMNIST data set has the same for-

mat as MNIST except that each class represents fash-

ion items. Again, for FMNIST we choose randomly

M = 6, 000 images (600 per class). The COIL-20 data

set, contains, 32 × 32 (i.e., N = 1, 024) images of 20

different objects which are viewed from 72 orienta-

tions, i.e., resulting in M = 1, 440 images.

3.2 Experimental Setup

For the MNIST, COIL-20, and FMNIST data sets we

use the PSO-DR, PCA, tSNE, Isomap, and Sammon

mapping techniques to transform the high dimen-

sional representations to a two-dimensional (n = 2)

map. For the Swiss Roll data set we use the PSO-DR,

PCA, Laplacian Eigenmaps, Isomap, and LLE tech-

niques to map to the 2-D space. We substituted tSNE

and Sammon mapping with Laplacian Eigenmaps and

LLE as techniques that do not employ neighborhood

graphs perform poorly on the Swiss Roll dataset (Van

Der Maaten et al., 2009).

The resulting maps in each one of the DR task

is shown as a scatter plot. The coloring in the scat-

ter plots is used to provide a way of evaluation for

the performance of the DR techniques. Moreover, for

each one of the DR methods the time needed to map

the respective data set is depicted.

For the proposed PSO-DR method, as soon as the

estimation of the beacons Y

is completed, the map-

ping of, e.g., a high dimensional input x

to the low di-

mensional space is independent of the mapping of any

other input x

, j 6= i. Thus, it is possible to map simul-

taneously multiple inputs. Hence, due to its straight-

A Dimensionality Reduction Method for Data Visualization using Particle Swarm Optimization

133

PSO-DR, 57.79 seconds

PCA, 1.17 seconds

tSNE, 432.9 seconds

Isomap, 1069.34 seconds

Sammon, 3237.79 seconds

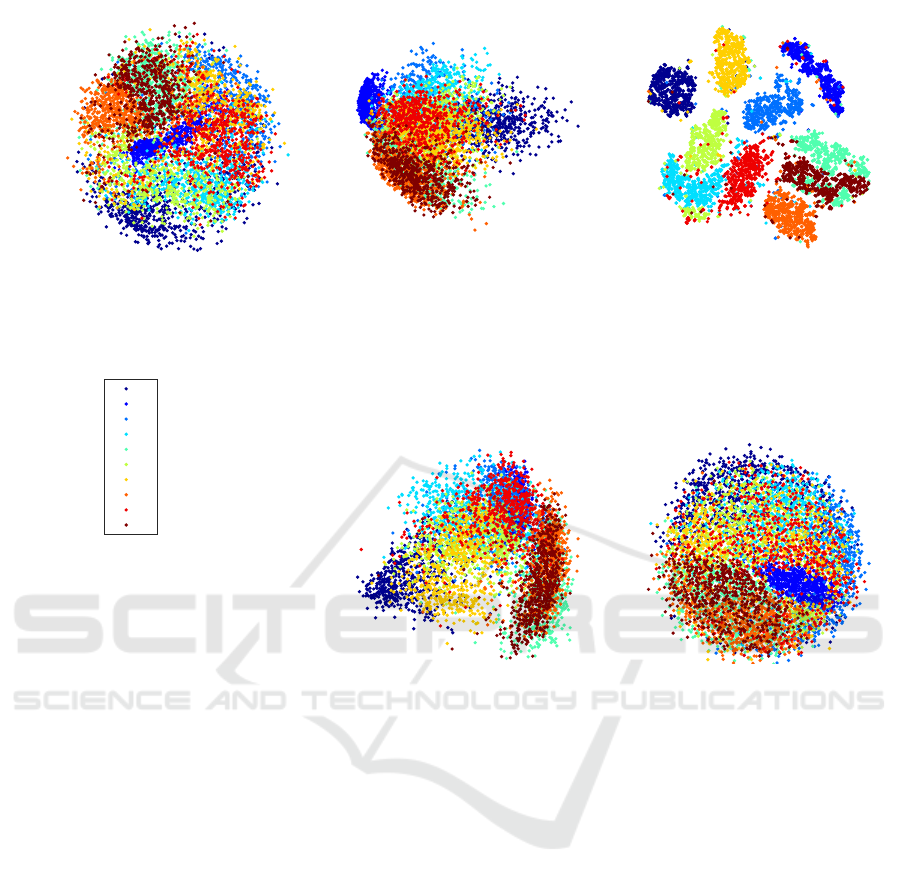
Figure 1: Visualization of the MNIST data set (6, 000 digits) using the PSO-DR, PCA, tSNE, Isomap, and Sammon mapping.

forward parallelization we used all 6 cores of the CPU

to estimate the low dimensional points y

in parallel,

accelerating that way the PSO-DR computation.

For the data sets MNIST, COIL-20, and FMINST,

and δ

measures correspond to the Euclidean dis-

tance whereas for Swiss Roll data set δ

is the

Euclidean distance whereas d

corresponds to the

geodesic distance estimated as in the Isomap method

(Tenenbaum et al., 2000).

3.3 Results

Fig. 1 shows the results of the application of PSO-

DR, PCA, tSNE, Isomap, and Sammon mapping on

the MNIST dataset. PSO-DR algorithm is much faster

than all the rest methods except for PCA. Moreover,

the visualisation quality of the proposed approach

is comparable or better that the majority of the DR

methods apart from tSNE which is currently the best

DR method for data visualization. It is noteworthy

that PSO-DR and Sammon mapping is constructing a

similar ball with PSO-DR exhibiting much faster es-

timation. The mapping of PCA and Isomap exhibit

more extensive overlap between the classes.

Fig. 2 presents the respective resutls for COIL-20

data set (labels 1-20 refer to each one of the 20 ob-

jects). Again PSO-DR is faster than tSNE and Sam-

mon mapping. Nevertheless, the time differences are

not of the same magnitude and, in addition, PSO-DR

is now slightly slower than Isomap. This is due to

the fact that COIL-20 has much fewer high dimen-

sional points. Thus, PSO-DR’s superiority in terms

of fast computation is mostly revealed in bigger data

sets. Moreover, the similarity of PSO-DR and Sam-

mon mapping is again observed. Nevertheless, Sam-

mon mapping is almost 5 times slower than the PSO-

DR approach.

Fig. 3 shows the results of the same DR methods

on FMNIST data set. Similarly, PSO-DR is signiﬁ-

cantly faster from all the other approaches, except for

PCA, with better quality of visualization from PCA

and Isomap, similar quality with Sammon mapping,

and comparable visualization quality with the tSNE

approach.

In Fig. 4 the mappings of the Swiss Roll data

set using the PSO-DR, PCA, Laplacian Eigenmap,

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

134

PSO-DR, 18.51 seconds

PCA, 0.36 seconds

tSNE, 23.9 seconds

Isomap, 16.77 seconds

Sammon, 90.25 seconds

Figure 2: Visualization of the COIL-20 data set using the PSO-DR, PCA, tSNE, Isomap, and Sammon mapping (labels 1-20

refer to each one of the 20 objects).

Isomap, and LLE methods are presented. In this im-

plementation of the PSO-DR method instead of us-

ing the Euclidean distance as a measure for d

, the

geodesic distance as estimated also in Isomap ap-

proach is used. Thus, it is revealed that PSO-DR re-

sults in almost identical representation with Isomap

whereas the rest of the state of the art approaches

have poorer performance. The PSO-DR approach,

though, is slightly slower than Isomap. Nevertheless,

this computation time corresponds to only 6 cores of

parallel computation.

It should be stressed out that if Euclidean distance

is used for the d

measure for the case of the Swiss

Roll data set, the performance of the PSO-DR ap-

proach is poorer. Nevertheless, the versatility of the

proposed approach makes it possible to easily adjust

it to the needs of the data set under consideration and

select the dissimilarity measures of the input and out-

put spaces accordingly.

4 DISCUSSION AND FUTURE

WORK

The experiments presented here demonstrate that

PSO-DR is a simple, fast and versatile algorithm for

DR for data visualization where multiple choices for

distance measures both for d

and δ

are possible in a

simple and straightforward way.

PSO-DR exhibits comparative or better visualiza-

tion quality with the majority of the state of the art

approaches that it was compared to. In essence, apart

from tSNE, PSO-DR outperforms the rest of the ap-

proaches in terms of visualization quality. Neverthe-

less, tSNE is much slower than PSO-DR especially

for large data sets and it performs poorly on certain

datasets like the Swiss Roll dataset. Moreover, for

tSNE, as for many other non-linear DR approaches,

out-of-sample extension is not straightforward (Van

Der Maaten et al., 2009). On the contrary, the out-of-

sample extension in PSO-DR is inherent in its func-

tionality, as any new input can be mapped directly

A Dimensionality Reduction Method for Data Visualization using Particle Swarm Optimization

135

PSO-DR, 54.99 seconds

PCA, 0.09 seconds

tSNE, 419.99 seconds

Isomap, 1077.21 seconds

Sammon, 2259.41 seconds

Figure 3: Visualization of the FMNIST data set (6, 000 fashion items) using the PSO-DR, PCA, tSNE, Isomap, and Sammon

mapping. (labeling was used for convenience, Labels 0 to 9 correspond to the 10 different fashion items).

by comparing it with a ﬁxed set of reference beacon-

points.

In addition, the independence of the mapping of

each high dimensional input from other inputs can fa-

vor the straightforward parallel implementation of the

algorithm. Thus, its computation time depends on and

scales in inverse proportion with the number of paral-

lel computation units (cores). Furthermore, the design

of the PSO-DR algorithm makes it a good choice for

ever increasing data sets, even with live streamed data

points as it uses a speciﬁed set of beacons to compare

the new data points and map them in the low dimen-

sional space. Nevertheless, in this work, we did not

investigated the functionality of the PSO-DR method

in such cases and we will consider evaluating it in fu-

ture research.

In essence, the only part of the PSO-DR algorithm

where the mapping of an input depends on the previ-

ous inputs is the deﬁnition of the beacon set Y

. As

soon as this step is completed, PSO-DR mapping can

be performed independently with regard to the differ-

ent inputs. The alternative approach where all map-

pings depend on the previous inputs, thus, no bea-

cons are deﬁned but all x

in X are mapped depend-

ing on the distance from all the previous inputs would

result in slower computation without better visualiza-

tion quality. Fig. 5 shows the low dimensional map-

ping of MNIST data set based on such an approach.

The result is comparable with the one shown in Fig. 1

whereas the time needed is multiple times larger that

the one needed with the beacons approach.

5 CONCLUSIONS

In this paper a new approach for DR for data vi-

sualization is presented. The PSO-DR algorithm is

based on the PSO optimization for mapping high di-

mensional inputs to low dimensional spaces with fast

and versatile way with good data visualization qual-

ity. Despite the promising performance of the pro-

posed approach future research will focus on testing

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

136

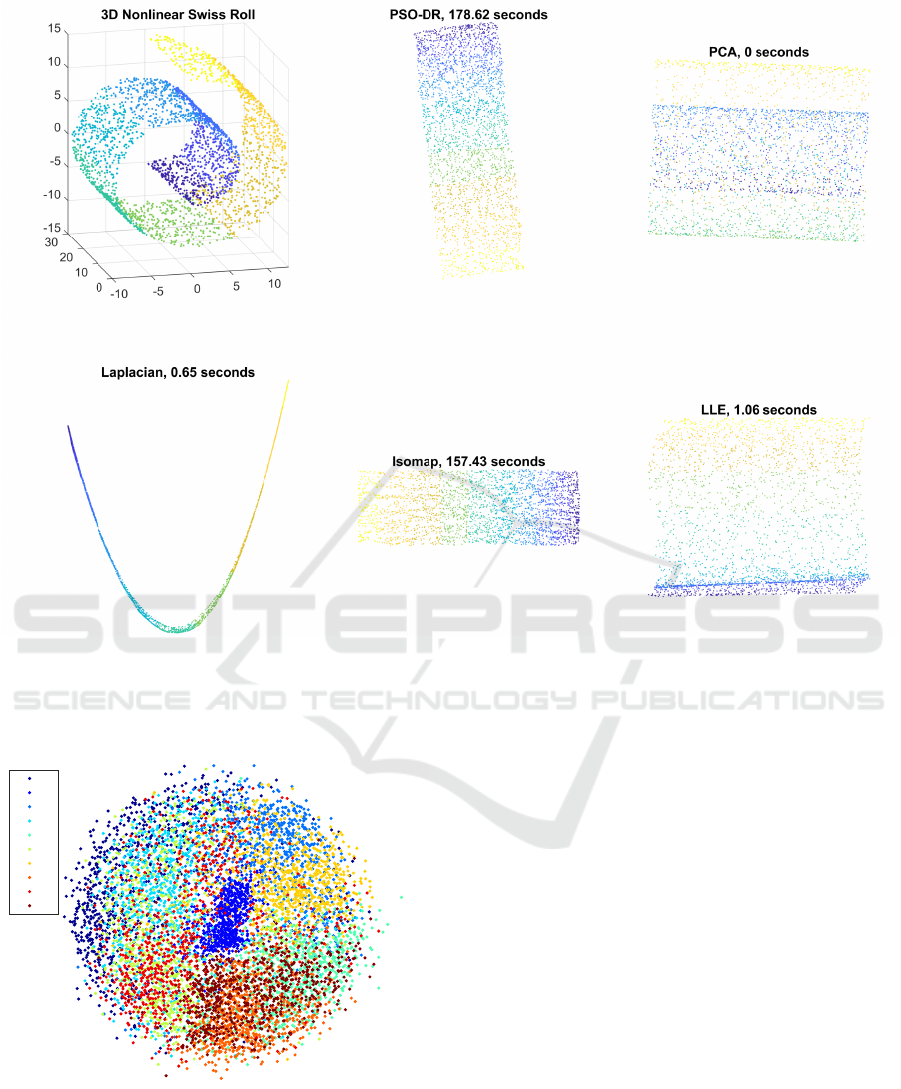
Figure 4: Visualization of the nonlinear Swiss Roll data set in 3D space and by using the PSO-DR, PCA, Laplacian Eigenmaps,

Isomap, and LLE.

PSO-DR, 187.47 seconds

Figure 5: Visualization of the MNIST data set using the

PSO-DR without beacon-points.

with more data sets and especially with live streamed

input points.

ACKNOWLEDGEMENTS

This work was supported by the European Union’s

Horizon 2020 Research and Innovation Program

through the project SUITCEYES under Grant

780814.

REFERENCES

Belkin, M. and Niyogi, P. (2002). Laplacian eigenmaps and

spectral techniques for embedding and clustering. In

Advances in neural information processing systems,

pages 585–591.

Belkin, M. and Niyogi, P. (2003). Laplacian eigenmaps

for dimensionality reduction and data representation.

Neural computation, 15(6):1373–1396.

Eberhart, R. and Kennedy, J. (1995). Particle swarm

optimization. In Proceedings of the IEEE inter-

national conference on neural networks, volume 4,

pages 1942–1948. Citeseer.

Hadsell, R., Chopra, S., and LeCun, Y. (2006). Dimen-

sionality reduction by learning an invariant mapping.

A Dimensionality Reduction Method for Data Visualization using Particle Swarm Optimization

137

In 2006 IEEE Computer Society Conference on Com-

puter Vision and Pattern Recognition (CVPR’06), vol-

ume 2, pages 1735–1742. IEEE.

Hotelling, H. (1933). Analysis of a complex of statistical

variables into principal components. Journal of edu-

cational psychology, 24(6):417.

Koziel, S. and Yang, X.-S. (2011). Computational optimiza-

tion, methods and algorithms, volume 356. Springer.

Nene, S. A., Nayar, S. K., Murase, H., et al. (1996).

Columbia object image library (coil-20).

Pedersen, M. E. H. (2010). Good parameters for particle

swarm optimization. Hvass Lab., Copenhagen, Den-

mark, Tech. Rep. HL1001, pages 1551–3203.

Sammon, J. W. (1969). A nonlinear mapping for data

structure analysis. IEEE Transactions on computers,

100(5):401–409.

Shi, Y. and Eberhart, R. C. (1998). Parameter selection in

particle swarm optimization. In International confer-

ence on evolutionary programming, pages 591–600.

Springer.

Shi, Y. and Eberhart, R. C. (1999). Empirical study of par-

ticle swarm optimization. In Proceedings of the 1999

Congress on Evolutionary Computation-CEC99 (Cat.

No. 99TH8406), volume 3, pages 1945–1950. IEEE.

Shi, Y. et al. (2001). Particle swarm optimization: develop-

ments, applications and resources. In Proceedings of

the 2001 congress on evolutionary computation (IEEE

Cat. No. 01TH8546), volume 1, pages 81–86. IEEE.

Tenenbaum, J. B., De Silva, V., and Langford, J. C. (2000).

A global geometric framework for nonlinear dimen-

sionality reduction. Science, 290(5500):2319–2323.

Torgerson, W. S. (1952). Multidimensional scaling: I. the-

ory and method. Psychometrika, 17(4):401–419.

Van Der Maaten, L. and Hinton, G. (2008). Visualizing data

using t-sne. Journal of machine learning research,

9(Nov):2579–2605.

Van Der Maaten, L., Postma, E., and Van den Herik, J.

(2009). Dimensionality reduction: a comparative re-

view. J Mach Learn Res, 10(66-71):13.

Xiao, H., Rasul, K., and Vollgraf, R. (2017). Fashion-

mnist: a novel image dataset for benchmark-

ing machine learning algorithms. arXiv preprint

arXiv:1708.07747.

ECTA 2020 - 12th International Conference on Evolutionary Computation Theory and Applications

138