
Modeling Concept Drift in the Context of Discrete Bayesian Networks
Hatim Alsuwat, Emad Alsuwat, Marco Valtorta, John Rose and Csilla Farkas
Department of Computer Science and Engineering, University of South Carolina, Columbia, SC, U.S.A.
Keywords:
Concept Drift, Concept Drift Detection, Nonstationary Environments, Bayesian Networks, Latent Variables.
Abstract:
Concept drift is a significant challenge that greatly influences the accuracy and reliability of machine learning
models. There is, therefore, a need to detect concept drift in order to ensure the validity of learned models.
In this research, we study the issue of concept drift in the context of discrete Bayesian networks. We propose
a probabilistic graphical model framework to explicitly detect the presence of concept drift using latent vari-
ables. We employ latent variables to model real concept drift and uncertainty drift over time. For modeling
real concept drift, we propose to monitor the mean of the distribution of the latent variable over time. For
modeling uncertainty drift, we suggest to monitor the change in beliefs of the latent variable over time, i.e.,
we monitor the maximum value that the probability density function of the distribution takes over time. We
implement our proposed framework and present our empirical results using two of the most commonly used
Bayesian networks in Bayesian experiments, namely the Burglary-Earthquake Network and the Chest Clinic
network.
1 INTRODUCTION
In recent years, machine learning models are increas-
ingly used in many real-world applications. A com-
mon challenge for machine learning systems is to
model environments wherein data evolves over time,
a phenomenon that is commonly known as concept
drift (Gama et al., 2014).
Detecting concept drift is crucial and active re-
search in machine learning systems. Concept drift
influences the accuracy and reliability of machine
learning models. Current approaches to detect con-
cept drift use latent variables (Borchani et al., 2015;
Caba
˜
nas et al., 2018). Latent variables (a.k.a. unob-
served variables) are variables that are not immedi-
ately observed but instead they are inferred from dif-
ferent variables that are observed and directly mea-
sured. An advantage of concept drift detection tech-
niques that are based on using latent variables is that
they tend to estimate the desired effects on the ma-
chine learning models more reliably than traditional
detection techniques. A large number of observable
variables can be aggregated in a model to represent
an underlying concept, making it easier to understand
the data and detect concept drift over time. However,
current efforts for detecting concept drift using latent
variables either limited to contentious Bayesian net-
works (Borchani et al., 2015) or not directly appli-
cable to discrete Bayesian networks (Caba
˜
nas et al.,
2018). In addition, previous efforts for detecting con-
cept drift using latent variables (Borchani et al., 2015;
Caba
˜
nas et al., 2018) are limited to naive Bayes clas-
sifiers and therefore cannot be used to model concept
drift that involves concepts span over multiple vari-
ables.
In this paper, we propose a technique for detecting
concept drift in the context of discrete Bayesian net-
works using latent variables. Our technique extends
Borchani et al. (Borchani et al., 2015) approach such
that it is directly applicable to discrete Bayesian net-
works. Borchani et al. represent concept drift using
unobserved variables in continuous domains, namely
in conditional linear Gaussian models. In addition to
modeling posterior probability distribution drift, we
propose a new method for modeling uncertainty drift.
The main contributions of this paper are as fol-
lows. We propose a framework for detecting the
presence of concept drift in the context of discrete
Bayesian networks using latent variables. Unlike pre-
viously proposed approaches (Borchani et al., 2015;
Caba
˜
nas et al., 2018) which are limited to naive Bayes
classifiers, our framework is applicable to general
Bayesian network models. We use latent variables
to model two types of drifts over time: (1) Posterior
Distribution Drift, and (2) Uncertainty Drift. We de-
velop a modeling technique using latent variables that
is able to detect posterior distribution drift. We pro-
vide a new method for modeling and detecting con-
214
Alsuwat, H., Alsuwat, E., Valtorta, M., Rose, J. and Farkas, C.
Modeling Concept Drift in the Context of Discrete Bayesian Networks.
DOI: 10.5220/0008384702140224
In Proceedings of the 11th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2019), pages 214-224
ISBN: 978-989-758-382-7
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

cept drift via modeling uncertainty over time, i.e., the
amount of belief that changes over time.
We have implemented our approach and presented
our empirical results. Our results indicate that our
modeling framework not only is sensitive to changes
in both real concept drift and uncertainty drift but also
can quickly detect the presence of drifts.
The rest of the paper is organized as follows. In
section 2, we present the problem setting. In sec-
tion 3, we present our framework for detecting con-
cept drift using latent variables in discrete Bayesian
networks. In section 4, we extend our modeling
framework into higher dimensions. In section 5 we
present our empirical results. In section 6, we give an
overview of related work. In section 7, we conclude
and briefly discuss ongoing work.
2 PROBLEM SETTING
We focus on modeling concept drift in the context of
discrete Bayesian networks. In a nonstationary en-
vironment, we assume that at each time point t (for
t = 1, 2, . . . ) data arrives in a batch (a.k.a. a window),
which is a collection of cases. Let Batch [A
1
, . . . , A
m
]
be the schema of the incoming batch with attributes
A
1
, . . . , A
m
. We assume without loss of generality that
the incoming batches have equal sizes, i.e., each batch
contains n cases. Let Batch t = {case
t
1
, . . . , case
t
n
} be
a collection of cases (a.k.a. observations or findings)
that arrives at time t.
case
1
1
, case
1
2
, . . . , case
1
n
| {z }
Batch 1, t = 1
, case
2
1
, case
2
2
, . . . , case
2
n
| {z }
Batch 2, t = 2
, . . .
Each finding, denoted as case, is over attributes
A
1
, . . . , A
m
and of the form case = < A
1
=
v
1
, . . . , A
m
= v
m
> (or simply can be written as
case = < v
1
, . . . , v
m
>), such that v
k
is the value
of attribute A
k
(1 ≤ k ≤ m). When a new batch
Batch t + 1 arrives at time point t + 1, the Bayesian
network model can simply be updated using Bayes’
theorem.
To detect the presence of concept drift between two
time points t = i and t = i + 1, we consider two types
of drifts as follows: (1) Posterior Distribution Drift,
and (2) Uncertainty Drift.
(Posterior Distribution Drift; a.k.a. Real Concept
Drift): Posterior distribution drift occurs when the
conditional probability changes on the target variable
whereas the input variables remain unchanged (Gama
et al., 2014). That is, the value of the posterior prob-
ability at time t = i, P
t
i
(y | A), is not equal to the
value of the posterior probability at time t = i + 1,
P
t
i+1
(y | A).
In Bayesian statistics, Bayes’ theorem can be writ-
ten in a useful form for Bayesian network update
and inference as follows: The posterior probabil-
ity is proportional to the product of the prior prob-
ability and the likelihood (Posterior probability ∝
Prior probability × Likelihood (Lynch, 2007)). Hav-
ing a prior that is conjugate for the likelihood func-
tion will make it mathematically convenient to cal-
culate the posterior distribution since the posterior
distribution will be from the same family of dis-
tribution as the prior (Raiffa and Schlaifer, 1961).
For instance, multiplying a beta-distributed prior,
Beta(α, β), with a binomial-distributed likelihood
function, Binomial(n, θ), yields a beta-distributed
posterior distribution, Beta(q + α, n − q + β), where
n is the total number of cases, and q is the count of
successes (Alsuwat et al., 2018).
In what follows, we consider detecting the pres-
ence of posterior distribution drift in the context of
discrete Bayesian networks with respect to a random
variable X
X
X that is beta-distributed, which we denote
as X
X
X ∼ Beta(α, β). We capture the existence of pos-
terior distribution drift by monitoring the mean of the
beta distribution at every time point t = i, denoted as
µ
i
, i.e., the expected value of X
X
X at every time point
t = i, E
E
E(
(
(X
X
X)
)
), as follows:
µ
i
= E
E
E(
(
(X
X
X)
)
) =
q
i
+ α
α + n
i
+ β
(1)
where n
i
and q
i
are the total number of cases and the
count of successes at time t = i, respectively, and hy-
perparameters α, β are greater than or equal to 1.
(Uncertainty Drift): Measuring the amount of un-
certainty in input data is defined as entropy (Shannon,
2001). Uncertainty drift is a variable that reflects the
change in beliefs over time. That is, for a random vari-
able X
X
X, the maximum value that a probability density
function f
i
(x;α, β) takes at time t = i is not equal to
the maximum value that a probability density func-
tion f
i+1
(x;α, β) takes at time t = i + 1. This kind of
drift is mainly caused by the change in the total num-
ber of observed cases. It is important to point out that
modeling uncertainty drift in the context of Bayesian
networks is powerful as it is a sensitive diagnostic for
detecting real concept drift.
Herein, we consider detecting the presence of un-
certainty drift in the context of discrete Bayesian net-
works with respect to a random variable X
X
X is beta-
distributed, X
X
X ∼ Beta(α, β). We capture the existence
of uncertainty drift by monitoring the maximum value
that the probability density function of the beta distri-
bution takes at every time point t = i, which we denote
Modeling Concept Drift in the Context of Discrete Bayesian Networks
215

Table 1: Notations.
Notation Description
B
B
Ba
a
at
t
tc
c
ch
h
h [
[
[A
A
A
1
1
1
,
,
, .
.
..
.
..
.
.,
,
, A
A
A
m
m
m
]
]
] The schema of incoming batch with attributes A
1
, ..., A
m
B
B
Ba
a
at
t
tc
c
ch
h
h i
i
i A collection of cases that arrives at time i
c
c
ca
a
as
s
se
e
e
i
i
i
j
j
j
The j
th
observation of Batch i
µ
µ
µ
i
i
i
The mean of the posterior probability at time i
ψ
ψ
ψ
i
The maximum value that the PDF takes at time i
X
X
X A random variable
X
X
X ∼ Beta(α, β) A random variable that is beta-distributed
X
X
X ∼ Dir(α
1
, . . . , α
r
) A random variable that is Dirichlet-distributed
as ψ
i
, as follows:
ψ
i
= max
X=x
f
i
(x;α, β, n
i
, q
i
)
= f
i
(
q
i
+ α − 1
α + n
i
+ β − 2
;α, β, n
i
, q
i
)
(2)
where n
i
and q
i
are the total number of cases and the
count of successes at time t = i, respectively, x is the
mode of the beta distribution (0 ≤ x ≤ 1), and hyper-
parameters α, β are greater than or equal to 1.
In our setting, we iterate over time steps (t =
1, 2, . . . ). At each time point t = i, we use the incom-
ing batch, Batch i, to update the current Bayesian net-
work model. We then use our approaches to detect the
existence of model drift. we assume that the distribu-
tion of the data does not change inside the batch, i.e.,
we capture the presence of model drift across time
steps (t = 1, 2, . . . ) and not within the set of observa-
tions arrives at a particular time point. If the variations
in the values of µ
i
and ψ
i
are important, we conclude
that our Bayesian network model has drifted.
We summarize the notations we use in this paper in
Table 1.
3 MODELING CONCEPT DRIFT
USING LATENT VARIABLES
In this section, we present a modeling technique for
detecting concept drift in discrete Bayesian networks.
We explicitly model concept drift using latent vari-
ables. To avoid unnecessary complication, we assume
that only posterior distribution and uncertainty drift
over time, i.e., for each edge A → B in a Bayesian
network model BN
1
, we detect the existence of con-
cept drift by monitoring the posterior distribution drift
and uncertainty drift of A → B over time.
Our modeling technique for detecting the presence
of concept drift in discrete Bayesian networks is de-
scribed using plate notation as shown in Figure 1. The
fundamental idea of our modeling approach is to add
a latent node for each edge A → B in a given Bayesian
network model BN
1
. We call this latent node U
t
AB
. It
is important to point out that for each collection of
observation j of time t, the unobserved node U
t
AB
is
added as the child of the observed nodes A
t
j
and B
t
j
.
The latent variable U
t
AB
captures the posterior drift
and the uncertainty drift for each collection of obser-
vations j of time t. It is essential to point to the fact
that both values of observed variables A
t
j
and B
t
j
con-
tribute to the drift of the latent variable U
t
AB
as fol-
lows:
(Posterior Distribution Drift): In our modeling
technique presented in Figure 1, the posterior distri-
bution drift of the latent variable U
t
AB
that is monitored
at each time point t = i is as follows:
µ
i
= P
t
i
(U
t
AB
| A
t
, B
t
)
=
q
i
+ α
u
α
u
+ n
i
+ β
u
where n
i
and q
i
are the total number of cases and the
count of successes at time t = i, respectively, and
hyperparameters α
u
, β
u
are greater than or equal to 1.
(Uncertainty Drift:) In our modeling technique
shown in Figure 1, to capture the uncertainty drift
of the latent variable U
t
AB
over time, we monitor the
maximum value that a probability density function
f
i
(x;α
u
, β
u
) of the latent variable takes at each time
point t = i as follows:
ψ
i
= max
X=x
f
i
(x;α
u
, β
u
, n
i
, q
i
)
= f
i
(
q
i
+ α
u
− 1
α
i
+ n
i
+ β
u
− 2
;α
u
, β
u
, n
i
, q
i
)
where n
i
and q
i
are the total number of cases and the
count of successes at time t = i, respectively, x is the
mode of the beta distribution (0 ≤ x ≤ 1), and hyper-
parameters α
u
, β
u
are greater than or equal to 1.
It is important to emphasize that our modeling
technique, at each time point t = i, receives j obser-
vations where j = 1 to n. These observations are used
to update the Bayesian network model. The latent
variable U
t
AB
is then used to capture the presence of
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
216
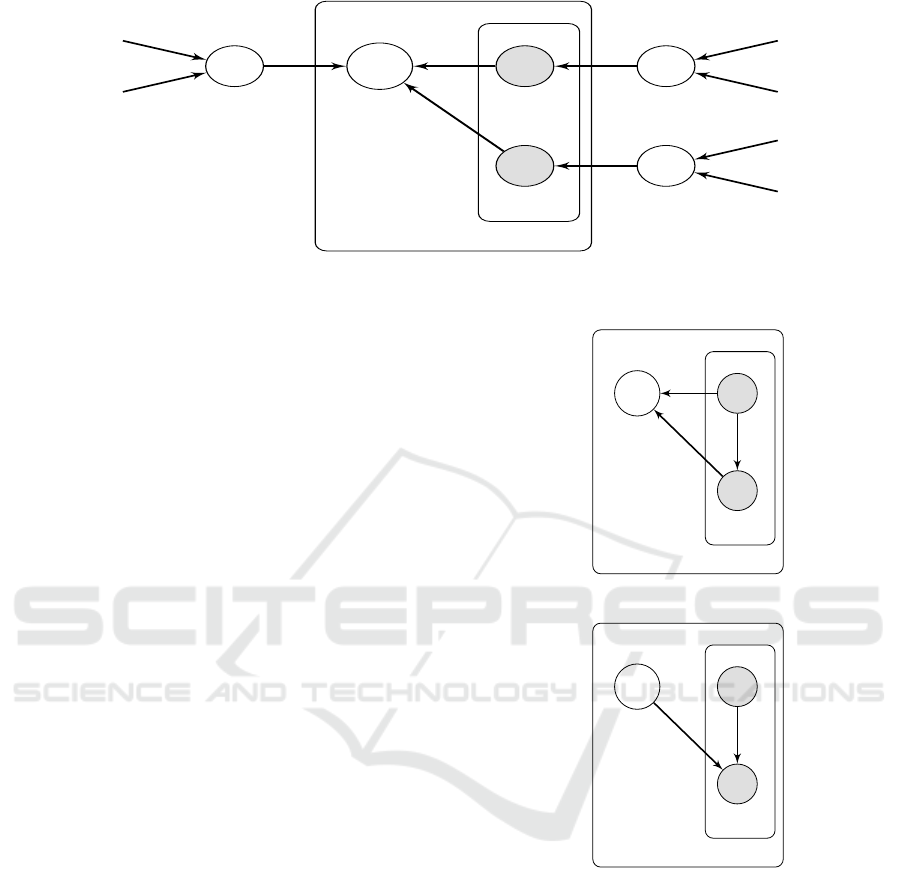
θ
u
U
t
AB
α
u
β
u
A
t
j
θ
a
α
a
β
a
B
t
j
θ
b
α
b
β
b
j
t
Figure 1: Modeling concept drift with latent variables in discrete Bayesian networks. A
t
j
and B
t
j
are observed nodes. U
t
AB
is a
latent (unobserved) node. θ
a
, θ
b
, and θ
u
are model parameters. α
a
, β
a
, α
b
, β
b
, α
u
, and β
u
are model hyperparameters.
posterior drift (i.e., drift in the value of µ
i
) and uncer-
tainty drift (i.e., drift in the value of ψ
i
). If the values
of µ
i
and ψ
i
vary significantly, we conclude that our
Bayesian network model has drifted.
The a priori expected values of concept and uncer-
tainty drifts can be expressed via the prior distribution
for the latent node U
t
AB
. We use hyperparameters α
u
and β
u
to express the prior knowledge that we may
have about concept and uncertainty drifts at a partic-
ular time point.
An important point to be made concerning the de-
velopment of our modeling technique for detecting
concept drift (presented in Figure 1) is that it contains
no causal interpretation. We do not place any causal
assumption on the interaction between the observed
variables and the latent variable. Despite the fact that
it is mathematically feasible to build causal and non-
causal modeling techniques (as shown in Figure 2) to
detect the presence of concept drift, it is not neces-
sary to consider causal effects between variables as
these effects are not the main focus of our modeling
approach. For this reason, we tolerate that the inter-
pretation of our modeling approach of concept drift is
merely statistical, i.e., associational.
4 GENERALIZATION OF OUR
FRAMEWORK INTO HIGHER
DIMENSIONS
To expand our modeling framework for variables
with more than two states, we can use the Dirich-
let distribution, which is a continuous multivari-
ate probability distribution. In Bayesian statis-
tics, Dirichlet distribution, which is denoted as
Dir(α
1
, . . . , α
r
), is parameterized by r hyperparam-
eters α
1
, . . . , α
r
such that α
i
(1 ≤ i ≤ r) is integer
and α
i
≥ 1 (Neapolitan et al., 2004). This dis-
tribution is the generalization of the beta distribu-
U
t
AB
A
t
j
B
t
j
j
t
(a) Non-causal.
U
t
AB
A
t
j
B
t
j
j
t
(b) Causal.
Figure 2: Options for building a modeling approach for de-
tecting concept drift.
tion for r > 2, i.e., beta is a special case when r =
2. A Dirichlet distributed prior is conjugate for the
likelihood function that is multinomial distributed.
That is, multiplying a Dirichlet-distributed prior,
Dir(α
1
, . . . , α
r
), with a multinomial-distributed likeli-
hood function, Multi(w
1
, . . . , w
r
;c
1
, . . . , c
r
), yields a
Dirichlet-distributed posterior distribution, Dir(α
1
+
c
1
, . . . , α
r
+ c
r
), where α
1
, . . . , α
r
are Dirichlet distri-
bution hyperparameters, w
1
, . . . , w
r
are Dirichlet dis-
tributed random variables, and c
1
, . . . , c
r
are the num-
ber of occurrences of each category.
Modeling Concept Drift in the Context of Discrete Bayesian Networks
217

We focus on detecting the presence of posterior
distribution drift in the context of discrete Bayesian
networks with respect to a random variable X
X
X =
=
=
[
[
[X
X
X
1
1
1
,
,
, .
.
..
.
..
.
.,
,
, X
X
X
r
r
r
]
]
] that is Dirichlet-distributed, which we
denote as X
X
X ∼ Dir(α
1
, . . . , α
r
). We capture the exis-
tence of posterior distribution drift by monitoring the
mean of the Dirichlet distribution at every time point
t = i, denoted as µ
i
, i.e., the expected value of X
X
X
j
j
j
at
every time point t = i, E
E
E(
(
(X
X
X
j
j
j
)
)
), as follows:
µ
i
= E
E
E(
(
(X
X
X
j
j
j
)
)
)
=
α
j
+ c
j
α
all
where α
all
=
∑
r
s=1
α
s
+ c
s
and c
j
is the number of oc-
currences of X
X
X
j
j
j
.
In addition to detecting the posterior drift, we con-
sider detecting the presence of uncertainty drift in the
context of discrete Bayesian networks with respect to
a random variable X
X
X is Dirichlet-distributed as de-
scribed above. We capture the existence of uncer-
tainty drift by monitoring the maximum value of X
X
X
j
j
j
that the probability density function of the Dirichlet
distribution takes at every time point t = i, which we
denote as ψ
i
, as follows:
ψ
i
= max
X
j
=x
f
i
(x;α, β, α
all
, c
j
)
= f
i
(
α
j
+ c
j
− 1
α
all
− r
;α, β, α
all
, c
j
)
where
α
j
+c
j
−1
α
all
−r
is the mode of the Dirichlet distribu-
tion.
5 EMPIRICAL RESULTS
We have implemented our modeling framework and
tested our approach using two of the most commonly
used example networks in Bayesian experiments,
Burglary-Earthquake Network and Chest Clinic net-
work.
5.1 Burglary-Earthquake Network
The Burglary-Earthquake Network was created by
Pearl (Pearl, 2014) and is a commonly used exam-
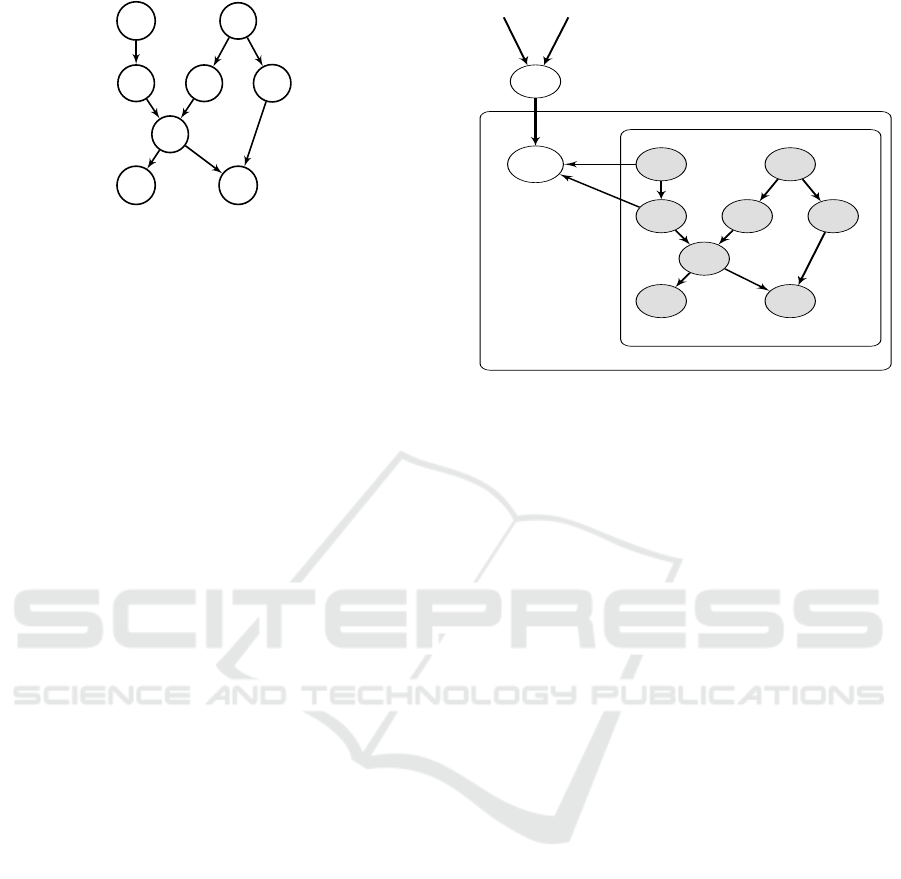
ple in Bayesian networks. As shown in Figure 3,
the Burglary-Earthquake Network is a fictitious net-
work that could be used to model an alarm system in
a house. The network consists of five nodes and four
edges. The nodes are as follows: (1) Node B shows
if there is a burglary, (2) Node E shows whether there
is an earthquake, (3) Node A shows if the alarm goes
off, (4) Node M shows if Mary calls, and (5) Node J
shows if John calls. The causal relations between the
nodes in this network is expressed by directed edges.
For instance, the edge B → A means that burglary may
cause the alarm to be activated and so on. We refer
the readers to (Pearl, 2014) for a full description of
this network.
M
E
A
J
B
Figure 3: The original Burglary-Earthquake Network.
We apply our approach for detecting the pres-
ence of concept drift in discrete domains over time
to the Burglary-Earthquake Network. To set up our
experiment, we have implemented this network us-
ing Hugin
TM
Research 8.4. Hugin
TM
case genera-
tor (Madsen et al., 2005; Olesen et al., 1992) is then
used to generate 15 simulated datasets of 1, 000 cases
each. These datasets are named Batch 1 through
Batch 15. During the simulation process of some
datasets, the posterior probabilities are changed in or-
der to simulate the existence of concept drift as fol-
lows: (1) The edge B → A: (i) the posterior prob-
abilities, P(A = F | B = F) and P(A = T | B = F),
are changed during the simulation process of datasets
Batch 3, Batch 7, and Batch 12. (ii) the posterior
probabilities, P(A = T | B = F) and P(A = T | B =
T ), are changed during the simulation process of the
dataset Batch 3. (2) The edge E → A: the poste-
rior probabilities, P(A = F | E = F) and P(A = T |
E = F), are changed during the simulation process
of the dataset Batch 4. (3) The edge A → J: the
posterior probabilities, P(J = F | A = T ), is changed
during the simulation process of the dataset Batch 7.
(4) The edge A → M: the posterior probabilities,
P(M = F | A = F) and P(M = T | A = T ), are changed
during the simulation process of the dataset Batch 7.
In our experiment, we assume that at each time point
t (t = 1, . . . , 15), we receive Batch t which has j in-
stances (we set j = 1, 000 cases).
To implement our framework, we added a latent
node for each edge in the Burglary-Earthquake Net-
work. That is, we added latent nodes U
t
BA
, U
t
EA
, U
t
AJ
,
and U
t
AM
to detect the presence of real concept drift
and uncertainty drift for the edges B → A, E → A,
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
218
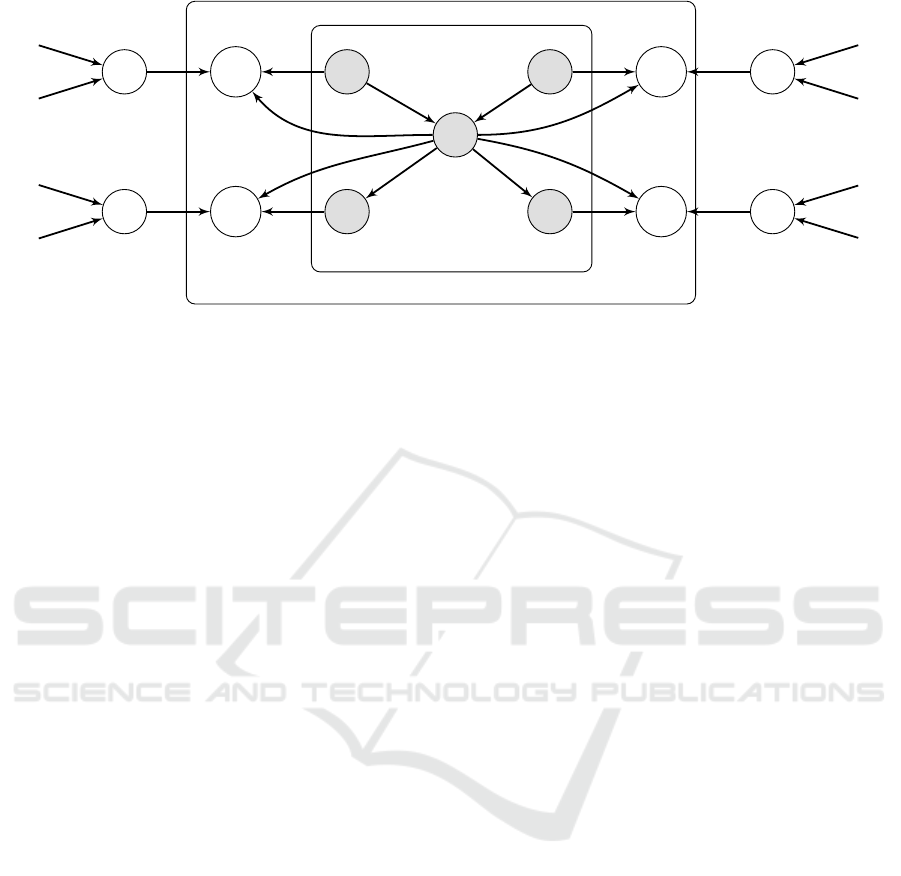
θ
ba
U
t
BA
α
ba
β
ba
B
t
j
A
t
j
E
t
j
J
t
j
M
t
j
U
t
AJ
θ
a j
α
a j
β
a j
U
t
EA
θ
ea
α
ea
β
ea
U
t
AM
θ
am
α
am
β
am
j
t
Figure 4: Our proposed framework for modeling concept drift with latent variables in the Burglary-Earthquake Network.
A → J, and A → M, respectively, as shown in Fig-
ure 4. We assume that we have no prior knowledge
about concept drift. That is, we assume that all hyper-
parameters of the latent variables, α(.) and β(.), are
equal to 1.
The results of using our framework to detect the
presence of real concept drift and uncertainty drift are
summarized in Table 2 and Table 3, respectively. Note
that values shown in bold in Table 2 and Table 3 indi-
cate the presence of drift. Our framework succeeded
in detecting the existence of real concept drift and un-
certainty drift. We observe that a change in the pos-
terior probability and the uncertainty is reflected by a
variation in the evolution of the corresponding latent
variable. For instance, we observe drifts in the pos-
terior probabilities and the uncertainties of the latent
variable U
t
BA
, namely when U = u | B = F, A = F and
U = u | B = F, A = T , at time points 3, 7, and 12.
We also observe that the posterior and the uncertainty
of the latent variable U
t
BA
drift at time point 3 namely
when U = u | B = T, A = F and U = u | B = T, A = T .
We observe that our framework is sensitive to
changes in the underlying distribution of data that
newly incoming batches may cause. That is, if the
number of observations in the newly incoming Batch t
at time t is less than the expected number of obser-
vations, then the framework shall report a drop in
the posterior and the uncertainty at time t and vice
versa. For instance, for the edge B → A, namely when
U = u | B = F, A = F, our framework captured a drop
in the posterior and uncertainty drifts in the incom-
ing batch at time point t = 3, Batch 3. This drop is
due to that fact that the number of observed cases in
Batch 3 was less than the expected number of cases.
It should be noted that after each drift, the values
of the posterior and uncertainty will be smoothly re-
increasing/re-decreasing attempting to recover from
the drift. It is also important to point out that if the
number of cases in the newly incoming batch is as ex-
pected, our framework concludes that there is no drift
to anticipate, and thus no action needs to be taken.
Explanations of the other experiments for other edges
trivially follow the explanation of the edge B → A.
All in all, we have shown that our framework
that is based on using latent variables to detect the
presence of concept drift is effective and sensitive to
changes in the underlying distribution of data in non-
stationary environments over time. Our framework
was successfully able to detect the existence of both
real concept drift and uncertainty drift. Our new pro-
posed approach for capturing uncertainty drift is sen-
sitive and useful as it can ensure the occurrence of real
concept drift.
5.2 Chest Clinic Network
The Chest Clinic network, a.k.a. the Visit to Asia
network, was created by Lauritzen and Spielgelhal-
ter (Lauritzen and Spiegelhalter, 1988) and is widely
used in Bayesian network experiments. This network
is a simple, fictitious medical network which could be
employed in a medical facility to diagnose patients as
shown in Figure 5. The Chest Clinic network consists
of eight nodes, which represent random variables, and
eight edges, which indicate the causal relations be-
tween the nodes. A complete description of this med-
ical Bayesian network model is as follows (Lauritzen
and Spiegelhalter, 1988):
Shortness-of-breath (dyspnoea) may be due
to tuberculosis, lung cancer, or bronchitis, or
none of them, or more than one of them. A
recent visit to Asia increases the chances of
tuberculosis, while smoking is known to be a
risk factor for both lung cancer and bronchitis.
The results of a single chest X-ray do not dis-
criminate between lung cancer and tuberculo-
sis, as neither does the presence or absence of
dyspnoea.
Modeling Concept Drift in the Context of Discrete Bayesian Networks
219

Table 2: Results of using our framework to detect the presence of real concept drift in the Burglary-Earthquake Network.
(a) The result of using the latent variable U
t
BA
to detect the presence of real concept drift for the edge B → A.
Posterior of 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
U
t
B=F,A=F
0.98 0.98 0.94 0.95 0.96 0.96 0.94 0.95 0.96 0.96 0.96 0.94 0.95 0.95 0.96
U
t
B=F,A=T
0.006 0.006 0.04 0.032 0.027 0.024 0.04 0.032 0.029 0.027 0.026 0.04 0.032 0.031 0.029
U
t
B=T,A=F
0.0005 0.0005 0.003 0.002 0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.001 0.001
U
t
B=T,A=T
0.01 0.01 0.02 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01
(b) The result of using the latent variable U
t
EA
to detect the presence of real concept drift for the edge E → A.
Posterior of 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
U
t
E=F,A=F
0.96 0.96 0.96 0.92 0.93 0.93 0.94 0.94 0.94 0.95 0.95 0.95 0.95 0.95 0.95
U
t
E=F,A=T
0.01 0.01 0.01 0.06 0.05 0.04 0.04 0.03 0.03 0.03 0.03 0.03 0.02 0.02 0.02
U
t
E=T,A=F
0.016 0.015 0.013 0.013 0.013 0.013 0.013 0.013 0.013 0.013 0.013 0.013 0.013 0.013 0.013
U
t
E=T,A=T
0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01
(c) The result of using the latent variable U
t
AJ
to detect the presence of real concept drift for the edge A → J.
Posterior of 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
U
t
A=F,J=F
0.93 0.93 0.93 0.93 0.93 0.93 0.93 0.93 0.93 0.93 0.93 0.93 0.93 0.93 0.93
U
t
A=F,J=T
0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05 0.05
U
t
A=T,J=F
0.002 0.002 0.002 0.002 0.002 0.002 0.005 0.005 0.005 0.004 0.004 0.004 0.004 0.004 0.003
U
t
A=T,J=T
0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01
(d) The result of using the latent variable U
t
AM
to detect the presence of real concept drift for the edge A → M.
Posterior of 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
U
t
A=F,M=F
0.97 0.97 0.97 0.97 0.97 0.97 0.95 0.95 0.96 0.96 0.96 0.96 0.96 0.96 0.96
U
t
A=F,M=T
0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01
U
t
A=T,M=F
0.0059 0.0055 0.0053 0.0052 0.0053 0.0054 0.0055 0.0054 0.0054 0.0054 0.0056 0.0058 0.0059 0.0062 0.0063
U
t
A=T,M=T
0.012 0.011 0.011 0.011 0.011 0.010 0.031 0.029 0.027 0.025 0.024 0.023 0.022 0.021 0.020
Table 3: Results of using our framework to detect the presence of uncertainty drift in the Burglary-Earthquake Network.
(a) The result of using the latent variable U
t
BA
to detect the presence of uncertainty drift for the edge B → A.
Uncertainty of 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
U
t
B=F,A=F
100.12 141.89 92.23 117.43 139.34 160.91 149.16 165.48 181.69 196.20 210.32 200.34 213.09 225.98 238.56
U
t
B=F,A=T
176.08 239.53 110.58 143.84 173.97 203.90 179.13 200.81 223.02 243.46 262.87 238.04 255.17 271.71 288.88
U
t
B=T,A=F
368.79 736.67 419.45 559.04 659.50 791.25 876.52 1001.63 1075.17 1100.22 1210.16 1272.71 1332.53 1434.97 1489.15
U
t
B=T,A=T
120.16 174.42 172.15 209.05 239.86 269.18 270.64 293.38 315.84 335.86 354.83 371.80 389.11 408.88 425.84
(b) The result of using the latent variable U
t
EA
to detect the presence of uncertainty drift for the edge E → A.
Uncertainty of 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
U
t
E=F,A=F
65.90 93.85 118.30 93.13 110.12 125.49 139.30 152.34 165.06 177.75 189.38 200.50 211.33 222.22 232.59
U
t
E=F,A=T
110.77 160.13 203.07 109.76 133.27 156.12 177.12 197.56 217.20 236.51 256.01 274.14 291.73 310.17 327.28
U
t
E=T,A=F
103.32 148.89 192.56 224.58 252.62 272.56 291.30 310.42 327.11 348.07 361.79 379.68 396.79 413.21 429.03
U
t
E=T,A=T
125.87 174.43 212.23 241.51 270.10 295.95 319.71 339.92 362.59 385.71 407.63 425.18 443.61 461.32 479.88
(c) The result of using the latent variable U
t
AJ
to detect the presence of uncertainty drift for the edge A → J.
Uncertainty of 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
U
t
A=F,J=F
50.10 70.86 86.79 99.88 111.89 123.16 132.71 142.09 150.68 158.79 166.51 173.99 181.16 188.05 195.24
U
t
A=F,J=T
57.31 81.07 98.99 113.62 127.27 139.17 153.76 164.29 174.01 183.21 191.80 200.35 208.54 215.99 223.75
U
t
A=T,J=F
271.21 391.32 482.51 559.05 626.30 687.01 459.35 511.28 560.94 608.57 647.27 684.19 726.51 774.78 822.20
U
t
A=T,J=T
103.32 146.44 181.48 210.82 236.56 267.54 294.44 313.32 329.78 345.52 364.22 379.68 393.45 408.88 425.84
(d) The result of using the latent variable U
t
AM
to detect the presence of uncertainty drift for the edge A → M.
Uncertainty of 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
U
t
A=F,M=F
77.67 111.99 136.36 157.73 176.53 194.16 156.79 173.49 187.71 200.94 213.50 225.03 236.74 246.86 257.27
U
t
A=F,M=T
120.16 178.65 215.57 247.11 280.35 305.22 330.48 360.53 380.07 394.85 412.89 428.49 445.26 459.79 473.95
U
t
A=T,M=F
176.08 250.97 308.18 356.32 391.04 423.24 453.32 487.13 518.79 543.58 562.72 577.34 592.19 603.58 615.41
U
t
A=T,M=T
120.16 170.49 209.04 244.26 272.56 305.22 190.01 212.59 232.98 253.50 272.82 291.47 310.56 327.51 345.56
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
220
A S
T L B
E
X D
Figure 5: The original Chest Clinic network.
We apply our approach for detecting the pres-
ence of concept drift in discrete domains to the Chest
Clinic network. To avoid unnecessary computations,
we use our framework to detect the presence of con-
cept drift of the weakest edge in the Chest Clinic net-
work. Using Alsuwat et al.’s link strength measure,
the edge from A → T is the weakest edge in this net-
work (Alsuwat et al., 2019). Therefore, we employ
our framework to detect the existence of concept and
uncertainty drifts of the edge A → T .
To set up our experiment, we have implemented
this network using Hugin
TM
Research 8.4. Hugin
TM
case generator (Madsen et al., 2005; Olesen et al.,
1992) is then used to generate 15 simulated datasets of
2, 000 cases each. These datasets are named Batch 1
through Batch 15. To simulate the presence of con-
cept drift, we change the posterior probabilities dur-
ing the simulation process as follows: (1) the poste-
rior probability P(T = no | A = no) is changed dur-
ing the simulation process of datasets Batch 4 and
Batch 11. (2) the posterior probability P(T = yes |
A = no) is changed during the simulation process of
dataset Batch 4. (3) the posterior probability P(T =
no | A = yes) is changed during the simulation pro-
cess of dataset Batch 11. (4) the posterior probabil-
ity P(T = yes | A = yes) is changed during the sim-
ulation process of datasets Batch 2 and Batch 10. In
this experiment, we assume that at each time point t
(t = 1, . . . ,15), our framework receives Batch t which
has j observations ( j is set at 2, 000 cases).
To implement our framework, we added a latent
node for the weakest edge in the Chest Clinic net-
work. That is, we added the latent node U
t
AT
to detect
the presence of real concept drift and uncertainty drift
for the edges A → T as shown in Figure 6. We assume
that we have no prior knowledge about concept drift,
i.e., we assume that the hyperparameters of the latent
variable U
t
AT
, α
at
and β
at
, are equal to 1.
The results of applying our framework to detect
the existence of real concept drift and uncertainty drift
of the weakest edge in the Chest Clinic network are
summarized in Table 4 and Table 5, respectively. Note
that values shown in bold in Tables 4 and 5 indicate
A S
T L B
E
X D
U
t
AT
θ
at
α
at
β
at
j
t
Figure 6: Our proposed framework for modeling concept
drift of the weakest edge in the Chest Clinic network using
a latent variable.
the presence of drift. Our framework was success-
fully able to detect the presence of real concept drift
and uncertainty drift. We observe that a change in the
posterior probability and the uncertainty is reflected
by a variation in the evolution of the latent variable
U
t
AT
. For example, we observe drifts in the posterior
probabilities and the uncertainties of the latent vari-
able U
t
AT
as follows: (1) when U = u | A = no, T = no,
the posterior and the uncertainty drift at time points
4 and 11, (2) when U = u | A = yes, T = no, the
posterior and the uncertainty drift at time point 4,
(3) when U = u | A = no, T = yes, the posterior and
the uncertainty drift at time point 11, and (4) when
U = u | A = yes, T = yes, the posterior and the uncer-
tainty drift at time points 2 and 10.
We observe that our framework is sensitive to
changes in the underlying distribution of incoming
data. Moreover, our framework is able to quickly de-
tect the existence of drifts. Another important obser-
vation is that receiving more observations that belong
to the cell with the highest test statistics value will
reflect a higher variation of the evolution of the cor-
responding latent variable and thus will reflect a drift
in the posterior and the uncertainty. Overall, we have
shown that our framework that is based on using latent
variables to model concept drift in nonstationary en-
vironments is efficient to detect posterior and uncer-
tainty drifts of the weakest edge in a given Bayesian
network model.
Modeling Concept Drift in the Context of Discrete Bayesian Networks
221
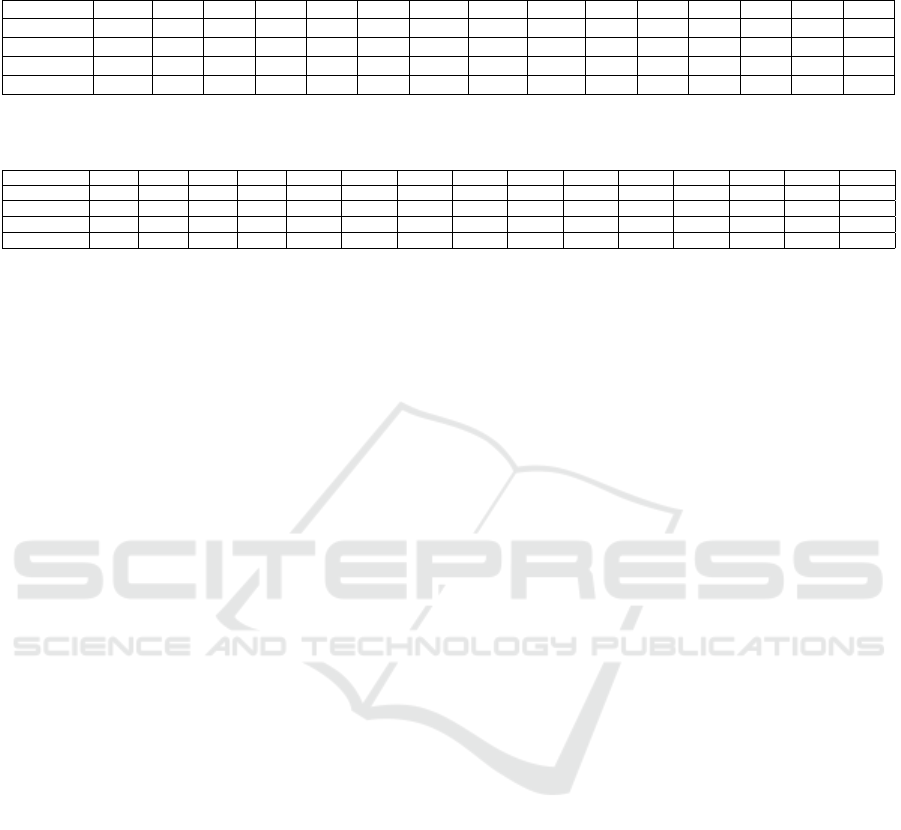
Table 4: Results of using our framework to detect the presence of real concept drift of the weakest edge in the Chest Clinic
network.
Posterior of 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
U
t
A=no,T =no
0.98 0.98 0.98 0.96 0.96 0.97 0.97 0.97 0.97 0.97 0.95 0.96 0.96 0.96 0.96
U
t
A=yes,T =no
0.008 0.008 0.008 0.02 0.02 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01
U
t
A=no,T =yes
0.009 0.009 0.009 0.009 0.009 0.009 0.009 0.009 0.009 0.009 0.02 0.02 0.02 0.02 0.02
U
t
A=yes,T =yes
0.0009 0.002 0.001 0.001 0.001 0.001 0.0009 0.0009 0.0009 0.001 0.001 0.001 0.001 0.001 0.001
Table 5: Results of using our framework to detect the presence of uncertainty drift of the weakest edge in the Chest Clinic
network.
Uncertainty of 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
U
t
A=no,T =no
137.74 184.65 228.18 197.55 231.22 262.59 290.81 317.06 340.94 361.32 298.71 318.90 338.57 357.81 376.66
U
t
A=yes,T =no
205.74 287.02 346.34 236.70 282.12 324.22 363.55 400.53 434.71 468.68 501.12 530.61 558.87 587.62 615.37
U
t
A=no,T =yes
183.30 263.10 326.76 374.87 419.77 462.42 499.52 534.05 564.76 595.52 374.68 402.07 429.08 455.05 480.74
U
t
A=yes,T =yes
736.31 527.74 751.41 955.80 1144.48 1373.21 1539.98 1696.67 1844.71 1591.53 1716.84 1838.06 1955.52 2069.48 2180.19
6 RELATED WORK
In this section, we will give a brief overview of con-
cept drift, concept drift classification, and concept
drift detection methods.
Concept Drift Overview: Applications are increas-
ingly critically dependent on concept schemes for the
semantic interoperability of their data (Wang et al.,
2010). As data evolves over time, real-time data an-
alytics are undermined as the models built to fos-
ter this learning becomes obsolete (
ˇ
Zliobait
˙
e et al.,
2016). In machine learning, concept drift is a non-
stationary learning problem that develops over time,
often because the training and data application mis-
match in real life scenarios (Moreno-Torres et al.,
2012; Gama et al., 2014). Therefore, concept drift is
associated with a greater probability for prediction in-
accuracies due to misalignment driven by changes in
the statistical properties of the target variable. Most
real-world applications confront some form and de-
gree of shift, which renders this topic highly rele-
vant to the existing and emerging machine learning
community (Moreno-Torres et al., 2012). Concept
drift thus plays a key role in machine learning and
predictive analytics optimization, as adequately ac-
counting for this phenomenon strengthens the over-
all integrity, utility, and functionality of the machine
learning model. Recent surveys on concept drift can
be found in (Iwashita and Papa, 2019; Gama et al.,
2014).
Concept Drift Classification: In contemporary sci-
entific literature, several research has been proposed
to characterize types of concept drift (Webb et al.,
2016; Gama et al., 2014; Iwashita and Papa, 2019).
Webb et al. (Webb et al., 2016) categorized types of
concept drift based on (i) Drift subject, which indi-
cates what aspects of the joint probability drifts over
a period of time, (ii) Drift frequency, which shows
how often concept drift happens during a particular
time, (iii) Drift transition, which indicates the means
wherein the process of changing from one concept to
another occurs, (iv) Drift reoccurrence, which shows
whether or not the occurring concept drift has previ-
ously appeared, and (v) Drift magnitude, which points
out the degree of drift between two time points.
Drift subject is mathematically defined as a
change in the joint probability between two time
points t
0
and t
1
as follows: P
t
0
(X, y) 6= P
t
1
(X, y),
where X is the input variables and y is the target vari-
able (Gama et al., 2014). Drift subject is divided
into two types (Gama et al., 2014): (1) real con-
cept drift, and (2) virtual concept drift. Real concept
drift occurs when the conditional probability changes
on the target variable y whereas the input variables
X remain unchanged, i.e., the posterior probability
changes between two time points t
0
and t
1
as fol-
lows: P
t
0
(y | X) 6= P
t
1
(y | X). Virtual concept drift
occurs when the prior distribution changes between
two time points t
0
and t
1
while the posterior prob-
ability remains unchanged (Tsymbal, 2004; Widmer
and Kubat, 1996), i.e., P
t
0
(X) 6= P
t
1
(X). Real concept
drift is the most important aspect in the category of
drift subject since changes in real concept drift will
degrade the accuracy of the machine learning model
and thus require an update of the model (Kelly et al.,
1999). Therefore, the discussion of this paper is re-
lated to the notion of real concept drift which we refer
to as concept drift.
Concept Drift Detection: One of the challenging
tasks in the context of concept drift is to rapidly de-
tect concept drift and provide a practical measure of
drift magnitude. A variety of concept drift detec-
tion methods have been recently developed. Gama
et al. (Gama et al., 2014) categorized such meth-
ods into four general groups as follows: (1) meth-
ods based on sequential analysis (members of this
group include the Cumulative Sum (CUSUM) and the
Page-Hinkley (PH) (Page, 1954)), (2) methods based
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
222

on statistical process control (members of this group
include the Drift Detection Method (DDM) (Gama
et al., 2004), the Early Drift Detection Method
(EDDM) (Baena-Garcıa et al., 2006), and the Expo-
nentially Weighted Moving Average (EWMA) (Ross
et al., 2012)), (3) methods based on contextual ap-
proaches (a member of this group includes the Splice
system (Harries et al., 1998)), and (4) methods based
on Monitoring distributions on two different time-
windows (members of this group include the Adap-
tive sliding Window (ADWIN) (Bifet and Gavalda,
2007), the Adaptive Cumulative Windows Model
(ACWM) (Sebasti
˜
ao et al., 2017), and SEED Drift
Detector (SEED) (Huang et al., 2014)).
The contribution of this work belongs to the last
one of the four groups. Methods based on monitoring
distributions on two different time-windows are tech-
niques that use statistical tests to compare the distribu-
tions of a fixed reference window on the previous data
and a sliding window on the most recent data (Gama
et al., 2014). Kifer et al. were first to propose compar-
ing two detection window distributions in relation to
data streams (Kifer et al., 2004). The team’s presented
algorithms assessed samples taken from two proba-
bility distributions to identify key differences in the
distributions. Another example of such methods was
proposed by (Gama et al., 2006) is the VFDTc sys-
tem, which is an algorithm for mining in nonstation-
ary environments with the ability to detect and adapt
to concept drift. The VFDTc system is used in con-
cept drift resolution through ongoing monitoring of
observed differences between two class-distributions,
including evaluation of: 1) class-distribution when
a node was a leaf, and 2) weighted sum of class-
distributions in the node’s leaf-descendants (Gama
et al., 2006).
Other more recent concept drift detection methods
based on monitoring distributions on two different
time-windows were proposed in (Borchani et al.,
2015) and (Caba
˜
nas et al., 2018). In this work, we
study concept drift detection via comparing distribu-
tions on two different time-windows. We aim to use
latent variables to model and detect concept drift in
the context of discrete Bayesian networks. Borchani
et al. proposed a modeling technique with conditional
linear Gaussian (CLG) that used latent variables to
detect concept drift (Borchani et al., 2015). Their
model is applicable to continuous Bayesian networks
and was applied to continuous domains. Cabanas et
al. proposed a method for detecting concept drift in
discrete streaming data (Caba
˜
nas et al., 2018). Their
proposed preprocessing algorithm transferred discrete
data into continuous data before applying Borchani at
el. model to detect concept drift. However, Cabanas
et al.’s technique is susceptible to data loss and results
in increased processing overhead when used in incre-
mental learning domains.
7 CONCLUSION AND FUTURE
WORK
Detecting changes in the underlying distribution of in-
coming data, a.k.a. concept drift detection, is a vital
and active research area in machine learning systems.
In this paper, we studied the presence of concept drift
in the context of discrete Bayesian networks in non-
stationary environments. We have proposed a frame-
work for modeling concept drift using latent variables
in discrete Bayesian networks. Our modeling tech-
nique using latent variables is capable of detecting
real concept drift and uncertainty drift over time. We
have applied our framework for detecting the pres-
ence of concept drift in discrete domains over time
to the Burglary-Earthquake Network and the Chest
Clinic Network, which are the most widely used net-
works in Bayesian experiments. Our results indicate
that our framework is not only sensitive to changes in
the underlying distribution of incoming data but also
can easily detect the real concept drift and uncertainty
drift over time. Our ongoing work extends these re-
sults to find explanations for the changes of the mod-
els. Such explanations will improve our understating
of the evolution of the concept drift. This indeed may
permit to distinguish malicious attacks from natural
model shift. In addition, we aim to acquire an authen-
tic dataset for further experiments and compare our
approach with other approaches that model concept
drift using latent variables.
REFERENCES
Alsuwat, E., Alsuwat, H., Valtorta, M., and Farkas, C.
(2019). Adversarial data poisoning attacks against the
pc learning algorithm. International Journal of Gen-
eral Systems, pages 1–29.
Alsuwat, E., Valtorta, M., and Farkas, C. (2018). How to
generate the network you want with the pc learning
algorithm. In Proceedings of the 11th Workshop on
Uncertainty Processing (WUPES’18), pages 1 – 12.
Baena-Garcıa, M., del Campo-
´
Avila, J., Fidalgo, R., Bifet,
A., Gavalda, R., and Morales-Bueno, R. (2006). Early
drift detection method. In Fourth international work-
shop on knowledge discovery from data streams, vol-
ume 6, pages 77–86.
Bifet, A. and Gavalda, R. (2007). Learning from time-
changing data with adaptive windowing. In Proceed-
Modeling Concept Drift in the Context of Discrete Bayesian Networks
223

ings of the 2007 SIAM international conference on
data mining, pages 443–448. SIAM.
Borchani, H., Mart
´
ınez, A. M., Masegosa, A. R., Langseth,
H., Nielsen, T. D., Salmer
´
on, A., Fern
´
andez, A., Mad-
sen, A. L., and S
´
aez, R. (2015). Modeling concept
drift: A probabilistic graphical model based approach.
In International Symposium on Intelligent Data Anal-
ysis, pages 72–83. Springer.
Caba
˜
nas, R., Cano, A., G
´
omez-Olmedo, M., Masegosa,
A. R., and Moral, S. (2018). Virtual subconcept drift
detection in discrete data using probabilistic graphi-
cal models. In International Conference on Informa-
tion Processing and Management of Uncertainty in
Knowledge-Based Systems, pages 616–628. Springer.
Gama, J., Fernandes, R., and Rocha, R. (2006). Decision
trees for mining data streams. Intelligent Data Analy-
sis, 10(1):23–45.
Gama, J., Medas, P., Castillo, G., and Rodrigues, P. (2004).
Learning with drift detection. In Brazilian symposium
on artificial intelligence, pages 286–295. Springer.
Gama, J.,
ˇ
Zliobait
˙
e, I., Bifet, A., Pechenizkiy, M., and
Bouchachia, A. (2014). A survey on concept
drift adaptation. ACM computing surveys (CSUR),
46(4):44.
Harries, M. B., Sammut, C., and Horn, K. (1998). Extract-
ing hidden context. Machine learning, 32(2):101–
126.
Huang, D. T. J., Koh, Y. S., Dobbie, G., and Pears, R.
(2014). Detecting volatility shift in data streams. In
2014 IEEE International Conference on Data Mining,
pages 863–868. IEEE.
Iwashita, A. S. and Papa, J. P. (2019). An overview on con-
cept drift learning. IEEE Access, 7:1532–1547.
Kelly, M. G., Hand, D. J., and Adams, N. M. (1999). The
impact of changing populations on classifier perfor-
mance. In Proceedings of the fifth ACM SIGKDD in-
ternational conference on Knowledge discovery and
data mining, pages 367–371. Citeseer.
Kifer, D., Ben-David, S., and Gehrke, J. (2004). Detecting
change in data streams. In Proceedings of the Thirti-
eth international conference on Very large data bases-
Volume 30, pages 180–191. VLDB Endowment.
Lauritzen, S. L. and Spiegelhalter, D. J. (1988). Local
computations with probabilities on graphical struc-
tures and their application to expert systems. Journal
of the Royal Statistical Society. Series B (Methodolog-
ical), pages 157–224.
Lynch, S. M. (2007). Introduction to applied Bayesian
statistics and estimation for social scientists. Springer
Science & Business Media.
Madsen, A. L., Jensen, F., Kjaerulff, U. B., and Lang, M.
(2005). The hugin tool for probabilistic graphical
models. International Journal on Artificial Intelli-
gence Tools, 14(03):507–543.
Moreno-Torres, J. G., Raeder, T., Alaiz-Rodr
´
ıGuez, R.,
Chawla, N. V., and Herrera, F. (2012). A unifying
view on dataset shift in classification. Pattern Recog-
nition, 45(1):521–530.
Neapolitan, R. E. et al. (2004). Learning bayesian networks,
volume 38. Pearson Prentice Hall Upper Saddle River,
NJ.
Olesen, K. G., Lauritzen, S. L., and Jensen, F. V. (1992).
ahugin: A system creating adaptive causal probabilis-
tic networks. In Uncertainty in Artificial Intelligence,
1992, pages 223–229. Elsevier.
Page, E. S. (1954). Continuous inspection schemes.
Biometrika, 41(1/2):100–115.
Pearl, J. (2014). Probabilistic reasoning in intelligent sys-
tems: networks of plausible inference. Elsevier.
Raiffa, H. and Schlaifer, R. (1961). Applied statistical de-
cision theory. Div. of Research, Graduate School of
Business Administration, Harvard Univ.
Ross, G. J., Adams, N. M., Tasoulis, D. K., and Hand,
D. J. (2012). Exponentially weighted moving average
charts for detecting concept drift. Pattern recognition
letters, 33(2):191–198.
Sebasti
˜
ao, R., Gama, J., and Mendonc¸a, T. (2017). Fad-
ing histograms in detecting distribution and concept
changes. International Journal of Data Science and
Analytics, 3(3):183–212.
Shannon, C. E. (2001). A mathematical theory of commu-
nication. ACM SIGMOBILE mobile computing and
communications review, 5(1):3–55.
Tsymbal, A. (2004). The problem of concept drift: defi-
nitions and related work. Computer Science Depart-
ment, Trinity College Dublin, 106(2):58.
Wang, S., Schlobach, S., and Klein, M. (2010). What is
concept drift and how to measure it? In International
Conference on Knowledge Engineering and Knowl-
edge Management, pages 241–256. Springer.
Webb, G. I., Hyde, R., Cao, H., Nguyen, H. L., and Petit-
jean, F. (2016). Characterizing concept drift. Data
Mining and Knowledge Discovery, 30(4):964–994.
Widmer, G. and Kubat, M. (1996). Learning in the pres-
ence of concept drift and hidden contexts. Machine
learning, 23(1):69–101.
ˇ
Zliobait
˙
e, I., Pechenizkiy, M., and Gama, J. (2016). An
overview of concept drift applications. In Big data
analysis: new algorithms for a new society, pages 91–
114. Springer.
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
224
