Information Retrieval in a Concept Lattice by using Uncertain Logical
Gates
Guillaume Petiot
CERES, Catholic Institute of Toulouse, 31 rue de la Fonderie, Toulouse, France
Keywords:
Data Mining, Formal Concept Analysis, Possibility Theory, Uncertain Logical Gates.
Abstract:
Formal Concept Analysis (FCA) is an approach of data mining which consists in extracting formal concepts
in order to provide a hierarchy of concepts also called a concept lattice. It is useful for understanding data. A
formal concept is a set of objects which share the same properties. When the number of formal concepts is too
high, it is difficult to explore all formal concepts in order to look for information. The use of a query to extract
relevant information is a solution to this problem. A logical combination of Boolean criteria, which can be
represented by a logical circuit, can serve as the condition of the query. In the uncertain formal context, we
are not sure if the objects own a property. As a consequence, we must take into account uncertainties in the
computation of formal concepts and in queries. We propose in this paper to use possibility theory to handle
these uncertainties. As a result, we compute a necessity degree for each formal concept. We can use a query
in which the condition can be computed by using possibilistic networks and uncertain logical gates. Finally,
we illustrate our approach by the analysis of a satisfaction questionnaire for a course in bachelor.
1 INTRODUCTION
Formal Concept Analysis (FCA) was presented by
Rudolf Wille as a mathematical theory (Wille, 1982).
This method of data analysis consists in extracting
formal concepts in a formal context. The latter can
be obtained from human investigation such as mea-
sures, questionnaire, etc. It is often represented as a
table. The formal context can be defined as a triplet
composed of a set of objects, a set of properties, and
a binary relation which provides the properties owned
by the objects.
All formal concepts can be compared by using a
partial order operator. As a result, we can build a con-
cept lattice from which we can extract knowledge or
rules. Another advantage of FCA is to avoid the loss
of information as in statistics summaries. The for-
mal concepts are very easy to interpret by a person
who is not an expert, thus avoiding wrong interpre-
tation. They highlight the common properties for a
set of objects, this is useful for analysing information.
Nevertheless, the number of formal concepts grows
exponentially when the size of the formal context in-
creases. As a consequence, the task of knowledge dis-
covering is more and more complex. So we can use
a query to extract formal concepts according to the
user’s expectations.
Another problem is how to deal with uncertainties
when the formal context is uncertain. Several studies
have been performed by using fuzzy set theory, accu-
racy degree, probability theory, or possibility theory
(Dubois and Prade, 2015; Yang and Qin, 1507). We
will focus our interest on possibility theory. We can
define an uncertain formal context by using a pair of
necessity measures as in (Dubois et al., 2007; Dubois
and Prade, 2009; Dubois and Prade, 2015) and pro-
pose to extract uncertain formal concepts. The cer-
tainty of all formal concepts can be computed.
Nevertheless, if there are too many formal con-
cepts, we can extract information by using a query,
but we must take into account uncertainties. In fact,
the condition of a query can be a logical combination
of criteria. Moreover, the criteria may be imprecise
and uncertain. As in Boolean logic, we propose to
represent the condition of the query by a logical cir-
cuit composed of gates AND, OR and NOT. Then,
in order to take into account imprecisions and un-
certainties, we propose to use uncertain logical gates
of possibility theory. The latter were proposed by
the authors of (Dubois et al., 2015) as an analogy of
noisy gates in probability theory. Uncertain logical
gates allow us to compute automatically the condi-
tional possibility tables of the possibilistic networks
and to avoid eliciting all conditional possibilities of
Petiot, G.
Information Retrieval in a Concept Lattice by using Uncertain Logical Gates.
DOI: 10.5220/0008065902890296
In Proceedings of the 11th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2019), pages 289-296
ISBN: 978-989-758-382-7
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
289

the table. For example, if a variable has 2 modalities
and 7 parents with 2 modalities, we have 2
8
= 256
parameters to elicit. The uncertain logical gates also
allow us to represent uncertainty and missing knowl-
edge in the models.
The goal of our experimentation is to use FCA
for the analysis of a satisfaction questionnaire for
a course of professionalization in bachelor. In this
questionnaire, there is one open question and several
closed questions. Whereas the students answer the
open question with their own words, closed questions
provide a set of possible answers. The main difficulty
is the processing of answers to the open question.
To do this, we propose to present in a first part
possibility theory, which will be used in the next parts
dealing with formal concept analysis and uncertain
logical gates. In the last part, we propose to perform a
natural language processing of the answers in order to
classify them. As the classification generates uncer-
tainties, we must propagate them in the computation
of formal concepts. Then, we must use a query to ex-
tract uncertain formal concepts and show the results
in a graph which highlights uncertainties.
2 POSSIBILITY THEORY
Possibility theory was invented by L. A. Zadeh
(Zadeh, 1978) in 1978. This theory allows us to rep-
resent the imprecision of knowledge and uncertainty.
Authors in (Dubois and Prade, 1988) define a pos-
sibility distribution π as a state of knowledge. For
example, if Ω is the universe and π
x
a possibility dis-
tribution of a variable x defined from Ω in [0,1], then
if π
x
(u) = 0 then x = u is impossible, else if π
x
(u) = 1
then x = u is possible. We can define the possibility
measure Π and the necessity measure N from the set
of subsets of Ω (noted P(Ω)) in [0,1]:
∀A ∈ P(Ω),Π(A) = sup
x∈A
π(x). (1)
∀A ∈ P(Ω),N(A) = 1 − Π(¬A) = in f
x /∈A
1 − π(x). (2)
Possibility theory is not additive but maxitive:
∀A,B ∈ P(Ω),Π(A ∪ B) = max(Π(A),Π(B)). (3)
3 FORMAL CONCEPT ANALYSIS
FCA, introduced by R. Wille (Wille, 1982), is built on
mathematical lattice theory. It organizes formal con-
cepts, which are the sets of objects, and their shared
properties into a concept lattice. Formal concepts are
defined by the intent and the extent. The intent is the
definition of the concept or the set of properties and
the extent denotes the elements to which the proper-
ties apply.
The structured data which must be provided as in-
put in formal concept analysis are called a formal con-
text. The latter is presented as a table where the lines
are the objects and the columns are the properties also
called attributes.
In fact, the formal context is a triple (O,P,ℜ)
where O =
{
o
1
,..., o
n
}
is the set of objects, P =
{
p
1
,..., p
m
}
is the set of properties, and ℜ is a rela-
tion such as ℜ ⊆ O × P. If (o, p) ∈ ℜ, then the object
o has the property p. In this case, the value of the
table is 1 or else 0.
A formal concept of (O,P,ℜ) is a pair (X,Y) such
that X ∈ O and Y ∈ P where Y is the set of properties
shared by all objects of X. For example, in the fol-
lowing formal context, we obtain 6 formal concepts.
Table 1: Example of a formal context.
ℜ
1
p
1
p
2
p
3
o
1
0 1 0
o
2
0 1 1
o
3
0 0 1
o
4
1 1 0
o
5
1 1 1
The formal concepts are ({o
2
,o
5
},{p
2
, p
3
}),
({o
4
,o
5
},{p
1
, p
2
}),({o
5
},{p
1
, p
2
, p
3
}),
({o
1
,o
2
,o
4
,o
5
},{p
2
}), ({o
2
,o
3
,o
5
},{p
3
}) and
({o
1
,o
2
,o
3
,o
4
,o
5
},{}).
The set of all formal concepts of (O,P,ℜ) is
noted β(U,V,ℜ). To compare the formal con-
cepts we can define a partial order ≤ such that
for (X
1
,Y
1
),(X
2
,Y
2
) ∈ β(U,V,ℜ), then (X
1
,Y
1
) ≤
(X
2
,Y
2
) if X
1
⊆ X
2
or Y
2
⊆ Y
1
. The lattice concept
can be defined by using this partial order and visual-
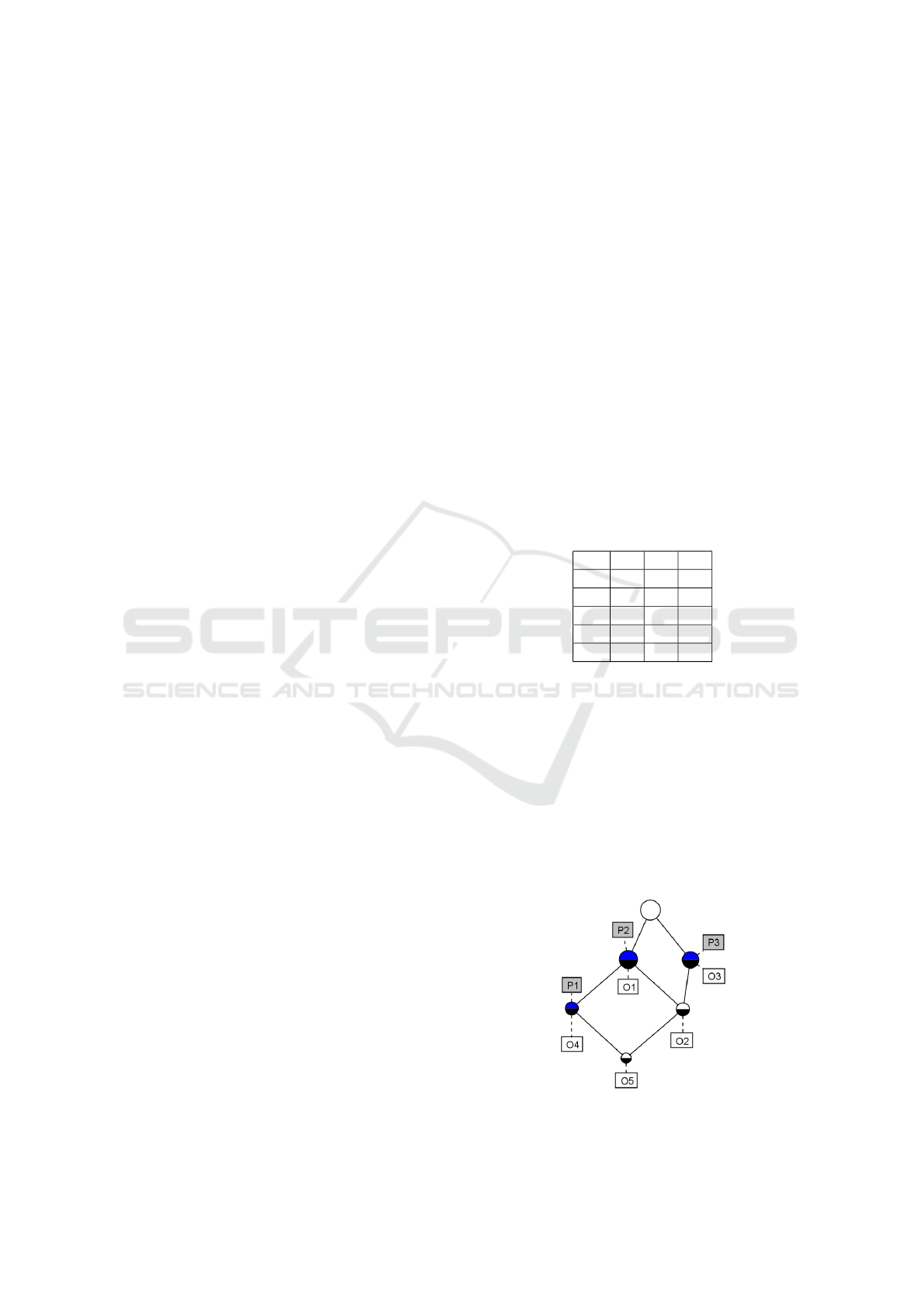
ized by using a Hasse diagram. The following figure
shows the concept lattice of the previous example:
Figure 1: Concept lattice of the example.
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
290

When the properties are many-valued, we must
perform a transformation of the context into a binary
formal context. We can take as an example the fol-
lowing many-valued context:
Table 2: Example of a many-valued context.
ℜ
2
Measure Quality
o
1
0 low
o
2
4 medium
o
3
7 medium
o
4
8 high
o
5
9 low
We can see that the measure is numerical with a
range in [0,10], so we must propose a categorization
of the values by defining for example three classes.
The first one is low for the values in [0,3], the second
is medium for the values in [4,6], and the last class
is high for the values in [7,10]. It can be transformed
into the following binary formal context:
Table 3: The transformation of the many-valued context
into a binary formal context.
ℜ
3
M
low
M
medium
M
high
Q
low
Q
medium
Q
high
o
1
1 0 0 1 0 0
o
2
0 1 0 0 1 0
o
3
0 0 1 0 1 0
o
4
0 0 1 0 0 1
o
5
0 0 1 1 0 0
So far, the properties were certain but if the prop-
erties are uncertain, the computation of the formal
concepts must take into account these uncertainties.
The authors in (Dubois et al., 2007) propose to use
possibility theory (Zadeh, 1978) and to define a pos-
sibility distribution π
o
p
(u) with u ∈ Ω, which is the
possibility that the property p of the object o is u. This
possibility distribution must be normalized. Certainty
is the necessity measure in possibility theory. The
authors in (Dubois and Prade, 2015) propose to use
a pair of necessity measures (α(o, p),β(o, p)) with
α(o, p) = N((o, p) ∈ ℜ) and β(o, p) = N((o, p) /∈ ℜ)
which represents the certainty that the object has or
does not have the property. We can define the uncer-
tain formal context in the following formula:
ℜ
0
=
{
(α(o, p), β(o, p))|o ∈ O, p ∈ P
}
(4)
Moreover, we must satisfy the property of pos-
sibility theory min(N((o, p) ∈ ℜ), N((o, p) /∈ ℜ)) =
0. The advantage of this solution is to provide a
theoretical frame to represent ignorance, which can
be partial or full. Indeed, if the pair is (1,0) or
(0,1) in the uncertain formal context, we are sure
that the object has the property or not. Otherwise,
we have two cases to describe. In the first case if
1 > max(α(o, p), β(o, p)) > 0, ignorance is partial. In
the second case, if we have (0,0), ignorance is total.
For our first experimentation, we will trans-
form the uncertain context by replacing the values
(α(o, p), 0) by 1 and (0,β(o, p)) by 0. Thus, we
obtain a new formal context for which we can eas-
ily compute the formal concepts. Once the formal
concepts are extracted, we can compute the neces-
sity measure (the certainty) of a formal concept C =
(X,Y ) by using the following formula:
N(C) = min
o∈X,p∈Y
N((o, p) ∈ ℜ) (5)
To illustrate this computation, we provide the fol-
lowing example:
Table 4: Example of an uncertain formal context.
ℜ
0
p
1
p
2
p
3
o
1
(0,1) (1,0) (0.2,0)
o
2
(0,0.5) (1,0) (1,0)
o
3
(0.5,0) (1,0) (0,0.9)
o
4
(1,0) (1,0) (0.8,0)
o
5
(1,0) (1,0) (1,0)
If we perform for this uncertain formal context the
transformation of the uncertain values into sure ones,
we obtain:
Table 5: Transformation of the uncertain formal context into
a binary formal context.
ℜ
4
p
1
p
2
p
3
o
1
0 1 1
o
2
0 1 1
o
3
1 1 0
o
4
1 1 1
o
5
1 1 1
In this example, we can see that
({o
1
,o
2
,o
4
,o
5
},{p
2
, p
3
}), ({o
3
,o
4
,o
5
},{p
1
, p
2
}),
({o
4
,o
5
},{p
1
, p
2
, p
3
}) and ({o
1
,o
2
,o
3
,o
4
,o
5
},{p
2
})
are formal concepts of this formal context. We can
now compute the certainty of these formal concepts:
Table 6: Computation of the formal concept certainties.
Formal concepts Certainty
({o
1
,o
2
,o
4
,o
5
},{p
2
, p
3
}) 0.2
({o
3
,o
4
,o
5
},{p
1
, p
2
}) 0.5
({o
4
,o
5
},{p
1
, p
2
, p
3
}) 0.8
({o
1
,o
2
,o
3
,o
4
,o
5
},{p
2
}) 1
In our experimentation, among the existing algo-
rithms described in (Kuznetsov and Obiedkov, 2003),
we have chosen Ganter Algorithm Next Closure (Gan-
ter, 1987) to find all intents or extents of the formal
concepts.
Information Retrieval in a Concept Lattice by using Uncertain Logical Gates
291

4 UNCERTAIN LOGICAL GATES
Possibilistic networks (Benferhat et al., 1999; Borgelt
et al., 2000; Dubois et al., 2015) are based on
d-separation, conditional independence (Amor and
Benferhat, 2005), and factoring property. The fac-
toring property can be defined from the joint possi-
bility distribution Π(V ) for a directed acyclic graph
G = (V,E) where V is the set of variables and E the
set of edges between the variables. Π(V ) can be fac-
torized as following:
Π(X
1
,..., X
n
) =
n
O
i=1
Π(X
i
/Pa(X
i
)). (6)
With Pa the parents of the node X
i
. The function
used for
N
is the minimum.
If we have a set of causal variables X
1
,..., X
n
which influence another variable Y called effect vari-
able, we can introduce intermediate variables Z
i
s be-
tween each X
i
s and Y. These variables represent un-
certainty in the causal influence of X
i
s on Y . For ex-
ample, even if a cause is met, it is possible that an
inhibitor will not produce Y. The Independence of
Causal Influence (D
`
ıez and Drudzel, 2007) can be de-
fined as the independence of the variables Z
i
s given
X
1
,..., X
n
. A causal mechanism is independent of all
other causal mechanisms of the model.
In probability theory, the ICI model gives birth to
the noisy model. In this model, there is a deterministic
function f which combines the individual influences
of the variables Z
i
s. The equation of the combina-
tion is the following: Y = f (Z
1
,..., Z
n
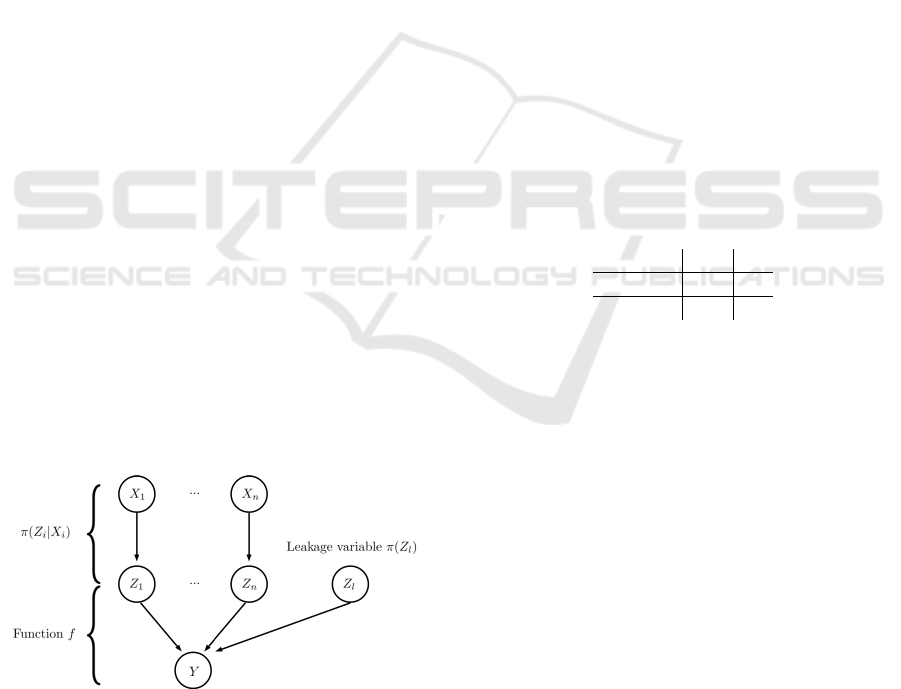
). The leaky
ICI model is derived from the noisy model by adding
a leakage variable Z
l
which represents the unknown
knowledge in the model. By analogy, we propose the
same reasoning for possibility theory and we can de-
fine a possibilistic model with the ICI. This possibilis-
tic model is presented in the following graph:
Figure 2: Possibilistic model with ICI.
We propose to calculate π(Y |X
1
,..., X
n
) by
marginalizing the variables Z
i
s as following:
π(y|x
1
,...,x
n
) =
M
z
1
,...,z
n
π(y|z
1
,...,z
n
)⊗π(z
1
,...,z
n
|x
1
,...,x
n
) (7)
The ⊗ is the minimum and the ⊕ is the maximum in
possibility theory.
π(y|x
1
,...,x
n
) =
M
z
1
,...,z
n
π(y|z
1
,...,z
n
) ⊗
n
O
i=1
π(z
i
|x
i
) (8)
where π(y|z
1
,...,z
n
) =

1 if y = f (z
1
,...,z
n
)
0 else
(9)
As a result, we obtain:
π(y|x
1
,..., x
n
) =
M
z
1
,...,z
n
:y= f (z
1
,...,z
n
)
n
O
i=1
π(z
i
|x
i
) (10)
If we add a leakage variable Z
l
in the previous
model, we obtain the following equation:
π(y|x
1
,...,x
n
) =
M
z
1
,...,z
n
,z
l
:y= f (z
1
,...,z
n
,z
l
)
n
O
i=1
π(z
i
|x
i
) ⊗ π(z
l
) (11)
Authors in (D
`
ıez and Drudzel, 2007) provide several
examples for probability theory. They are also appli-
cable to possibility theory. The functions f can be
AND, OR, NOT, INV, XOR, MAX, MIN, MEAN,
and linear combination. The Conditional Possibil-
ity Table (CPT) is obtained by the calculation of the
above formula. For Boolean variables, the possibility
table between the variables X
i
and Z
i
is as follows:
Table 7: Possibility table for Boolean variables.
π(Z
i
|X
i
) ¬x
i
x
i
¬z
i
1 κ
i
z
i
0 1
In the above table, the κ
i
parameter can be inter-
preted as the possibility that an inhibitor exists if the
cause is met. The value 0 in the table means that it
is impossible to have an effect if the cause is not met.
The possibility of the variable Z
L
is π(z
L
) = κ
L
. It cor-
responds to an external event which causes Y without
any influence of the variables X
i
. Several uncertain
logical gate connectors AND, OR, MIN and MAX
were described in (Dubois et al., 2015). A mathe-
matical simplification has been performed leading to
optimized connectors. The connectors AND, OR and
NOT allow us to build and evaluate uncertain logical
circuit. In other words, it can be used for the condi-
tion of a query on formal concepts. To do this, we
must provide the function f for the connectors AND
and OR by taking into account the leakage variables
Z
l
. The first one is the function f for the uncertain
leaky AND which is f =
V
n
i=1
Z
i
W
Z
L
. The second
one is the function f for the uncertain leaky OR which
is f =
W
n
i=1
Z
i
W
Z
L
. For example, from the equation
11 we compute the following conditional tables of the
uncertain leaky AND for two causal variables:
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
292

Table 8: Conditional tables for uncertain leaky AND.
π(¬y|X
1
,X
2
) ¬x
1
x
1
¬x
2
1 1
x
2
1 κ
1
⊕ κ
2
π(y|X
1
,X
2
) ¬x
1
x
1
¬x
2
κ
L
κ
L
x
2
κ
L
1
We provide below the same example for the con-
nector uncertain leaky OR:
Table 9: Conditional tables for uncertain leaky OR.
π(¬y|X
1
,X
2
) ¬x
1
x
1
¬x
2
1 κ
1
x
2
κ
2
κ
1
⊗ κ
2
π(y|X
1
,X
2
) ¬x
1
x
1
¬x
2
κ
L
1
x
2
1 1
This example can be generalized to the case of n
causal variables as in (Dubois et al., 2015). We can
also propose the table of the NOT connector which
has only one variable:
Table 10: Conditional table for NOT connector.
π(Y |X ) ¬x x
¬y 0 1
y 1 0
5 EXPERIMENTATION
The experimentation consists in the analysis of course
satisfaction questionnaire in bachelor. In this ques-
tionnaire realized in the Learning Management Sys-
tem Moodle, there is one open question and 32 many-
valued closed questions. 144 students answered the
questionnaire. We proposed to perform a supervised
classification of the answers to the open question by
a neural network in 8 classes. For the learning phase,
we constructed sets of samples by gathering a text de-
scription of the classes and samples for all classes.
We chose 16% of all answers for the samples. Then,
we performed a preprocessing of all sets of samples
and answers in order to obtain a Document Term Ma-
trix (DTM) for samples and answers. We present the
processing in the following graph:
In order to take into account the spelling mistake
in the answers, we proposed to use a measure of re-
semblance between the words during the computation
of the DTM and during the classification. We decided
Figure 3: Processing of the corpus.
to use a measure in [0,1]. Several string metrics ex-
ist to measure the resemblance of two strings (Chris-
ten, 2006; Jaro, 1989). The most famous are the dis-
tance of Levenshtein, Jaccard, Damerau-Levenshtein,
Hamming, the longest common subsequence, Smith-
Waterman and Jaro-Winkler (Winkler, 1999). We
chose the distance of Jaro-Winkler.
This distance is computed by using the Jaro dis-
tance between the words w
1
and w
2
:
d
J
(w
1
,w
2
) =
1
3
(
χ
|
w
1
|
+
χ
|
w
2
|
+
χ − τ
χ
) (12)
With
|
w
i
|
the size of the word i, χ the number of
matching character (the number of characters which
are in the two words with a distance smaller or equal
to
j
max(
|
w
1
|
,
|
w
2
|
)
2
k
− 1). τ is the number of transposi-
tion (the number of characters inverted). The Jaro-
Winkler distance is:
d
JW
(w
1
,w
2
) = d
J
(w
1
,w
2
) + αβ(1 − d
J
(w
1
,w
2
)) (13)
With α the size of the common prefix of the two
words with a maximum of 4 characters and β a coef-
ficient often equal to 0.1. So if d
JW
(w
1
,w
2
) < η, then
the word w
1
is different from the word w
2
. The next
step is the construction of the DTM. For example, for
the students’ answers the result is the following:
Table 11: Example of a DTM for the students’ answers.
X
X
X
X
X
X
X
X
X
X
Students
Words
intelligences gardner questionnaire proust cv ...
student 1 0.0 0.0 0.0 0.0 0.0 ...
student 2 1.0 0.96 0.0 0.0 0.0 ...
student 3 0.0 0.0 0.0 0.0 0.0 ...
... ... ... ... ... ... ...
student N 0.0 0.0 0.0 0.0 0.0 ...
When the DTM is computed for the students’ an-
swers and the samples of the classes, we can perform
the classification of the students’ answers by the neu-
ral network. The learning of the coefficient of the neu-
ral network is performed by using a backpropagation
Information Retrieval in a Concept Lattice by using Uncertain Logical Gates
293

of the gradient. The confusion matrix of the classifi-
cation is the following:
Table 12: Confusion matrix.
X
X
X
X
X
X
X
X
Actual
Predicted
C
1
C
2
C
3
C
4
C
5
C
6
C
7
C
8
C
1
35 0 0 0 0 0 0 0
C
2
0 29 0 0 0 0 0 0
C
3
0 0 25 0 0 0 0 0
C
4
0 0 0 20 2 0 0 0
C
5
0 0 0 0 11 0 0 0
C
6
0 0 0 0 1 7 0 0
C
7
0 0 0 0 0 0 4 0
C
8
0 0 0 0 2 0 0 8
The membership degree of all classes is trans-
formed in order to compute a possibility measure and
a pair of necessity measures. The next phase is the
computation of the formal concepts. We have trans-
formed the many-valued questions in order to obtain
a binary formal context. Then, we have integrated
in this formal context the pair of necessity measures
of the classification by inserting one column for all
classes. As a result, we have an uncertain formal
context where the columns are possible answers (the
properties of FCA) noted P
i
and the lines the answers
of the students (the objects of FCA). The first 8 prop-
erties concern the classes C
i
of the open question. We
present below a part of the uncertain formal context:
Table 13: A part of the uncertain formal context.
ℜ
0
P
1
(C
1
) P
2
(C
2
) P
3
(C
3
) P
4
(C
4
) P
5
(C
5
) ...
Student 1 (0,1) (0,1) (0,1) (0,1) (0.49,0) ...
Student 2 (0.99,0) (0,1) (0,1) (0,1) (0,1) ...
Student 3 (0,1) (0,1) (0,1) (0,1) (0.99,0) ...
Student 4 (0.1,0) (0,1) (0,1) (0,1) (0,1) ...
Student 5 (0,1) (0,1) (0,1) (0,1) (0.91,0) ...
... ... ... ... ... ... ...
Student 144 (0,1) (0,1) (0,1) (0,1) (0.99, 0) ...
If we look for formal concepts which fit best with
the student’s answers, we can define a score. For ex-
ample, if (X,Y ) is a formal concept with X the extent
and Y the intent, then we can propose the following
score:
S =
|X| + |Y|
max
(u,v)∈β(U,V,ℜ)
|u| + |v|
(14)
As there is often a very large number of formal
concepts, it is necessary to filter these formal concepts
in order to visualize only those which are relevant. To
do this, we have performed two processing operations
on the formal concepts. The first one is the use of a
query to extract formal concepts. The query is a log-
ical combination of criteria which can be evaluated
by using a possibilistic network which uses uncertain
logical gates. The second one is the visualization of
the result by using a directed graph. The orientation
of the edge of the graph is defined by using the par-
tial order. The size of the nodes is proportional to the
score of relevance and the color of the node is pro-
portional to the certainty of the formal concept. We
chose to use the Gephi tool for visualization. The re-
sult of the query is generated in csv files before being
imported in Gephi. For example, we present below a
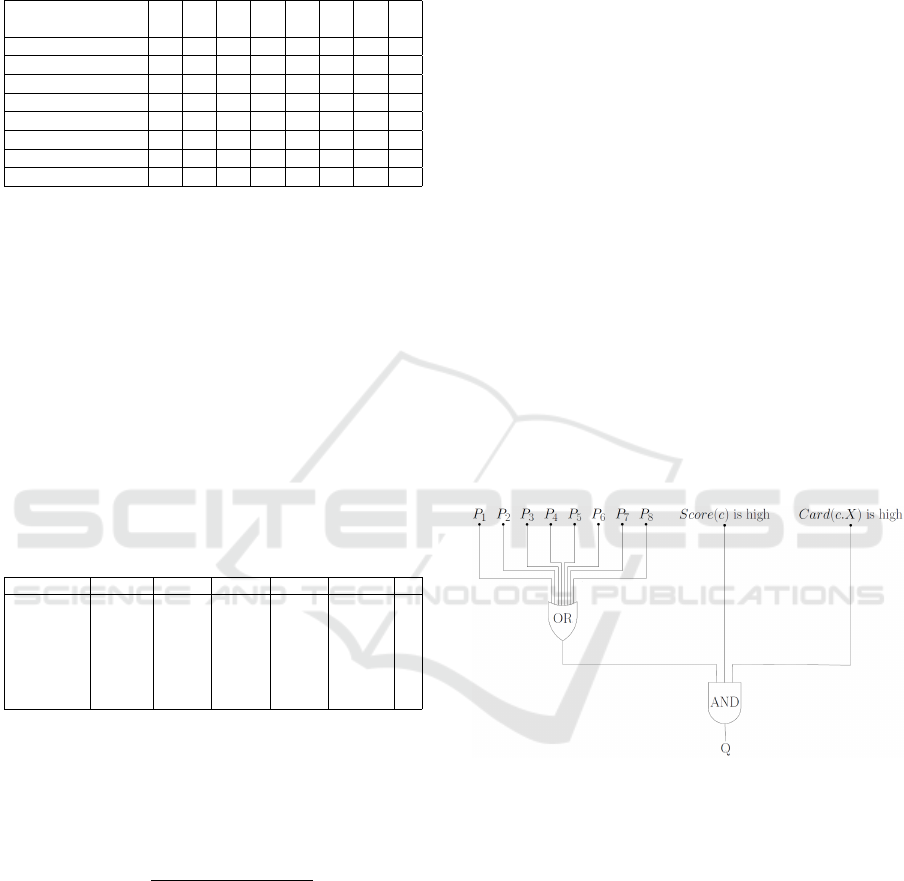
query :
Q
∗
=SELECT c FROM β(U,V,ℜ)
WHERE
((c.P
1
is true OR c.P
2
is true OR c.P
3
is true OR
c.P
4
is true OR c.P
5
is true OR c.P
6
is true OR
c.P
7
is true OR c.P
8
is true)
AND
Score(c) is high
AND
Card(c.X) is high)
With c = (X,Y ) a formal concept of β(U,V,ℜ),
Card the number of properties or objects in the formal
concept. Then, c.P
i
is true if the formal concept has
the property else c.P
i
is false. Finally, c.P
i
is true,
Score(c) is high, and Card(c.X) is high are possibility
distributions which take into account the imprecision
of knowledge. The condition of the query Q
∗
can be
represented as a logical circuit as follows:
Figure 4: Logical circuit of the condition of query Q
∗
.
The logical circuit can be transformed in a possi-
bilistic network with uncertain logical gates. The do-
main of all the variables is ( f alse,true). To evaluate
the condition, we must perform several processing op-
erations. At first, we compute the CPTs of uncertain
logical gates. Then, we compute the evidences by us-
ing the possibility distributions associated to all states
of the variables. Finally, we propagate the evidence
in the possibilistic network by using the algorithm
of message passing in a junction tree (Lauritzen and
Spiegelhalter, 1988) of Bayesian networks adapted to
possibilistic networks. The junction tree is composed
of cliques and separators. The cliques are computed
by transforming the initial graph into a moral graph
and triangulated graph (Kjaerulff, 1994). Then we
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
294

apply the Kruskal algorithm (Kruskal, 1956). To re-
sume, the propagation algorithm has three steps. The
initialization with the injection of evidence, then the
collect with the propagation of evidence from leaf to
root and the distribution with the propagation of evi-
dence from root to leaf. We propose for the example
of our query the following possibility distributions in
order to compute evidence:
(a) c.P
i
(b) Score(c) is high
(c) Card(c.X) is high
Figure 5: Possibility distributions.
We apply this computation to all formal concepts.
As a result, we obtain for the variable Q of the logi-
cal circuit a possibility measure and a necessity mea-
sure for all states. We can deduce the formal concepts
which answer the query where N(Q = true) > 0. As
in a web query in a search engine, where the result is
a ranking of the web pages, the certainty N(Q = true)
can be considered as a score of relevance which al-
lows us to perform a ranking of the formal concept
from the more certain to the less certain. For our ap-
plication, we propose the following result where the
labels are only displayed every 10 formal concepts for
more visibility:
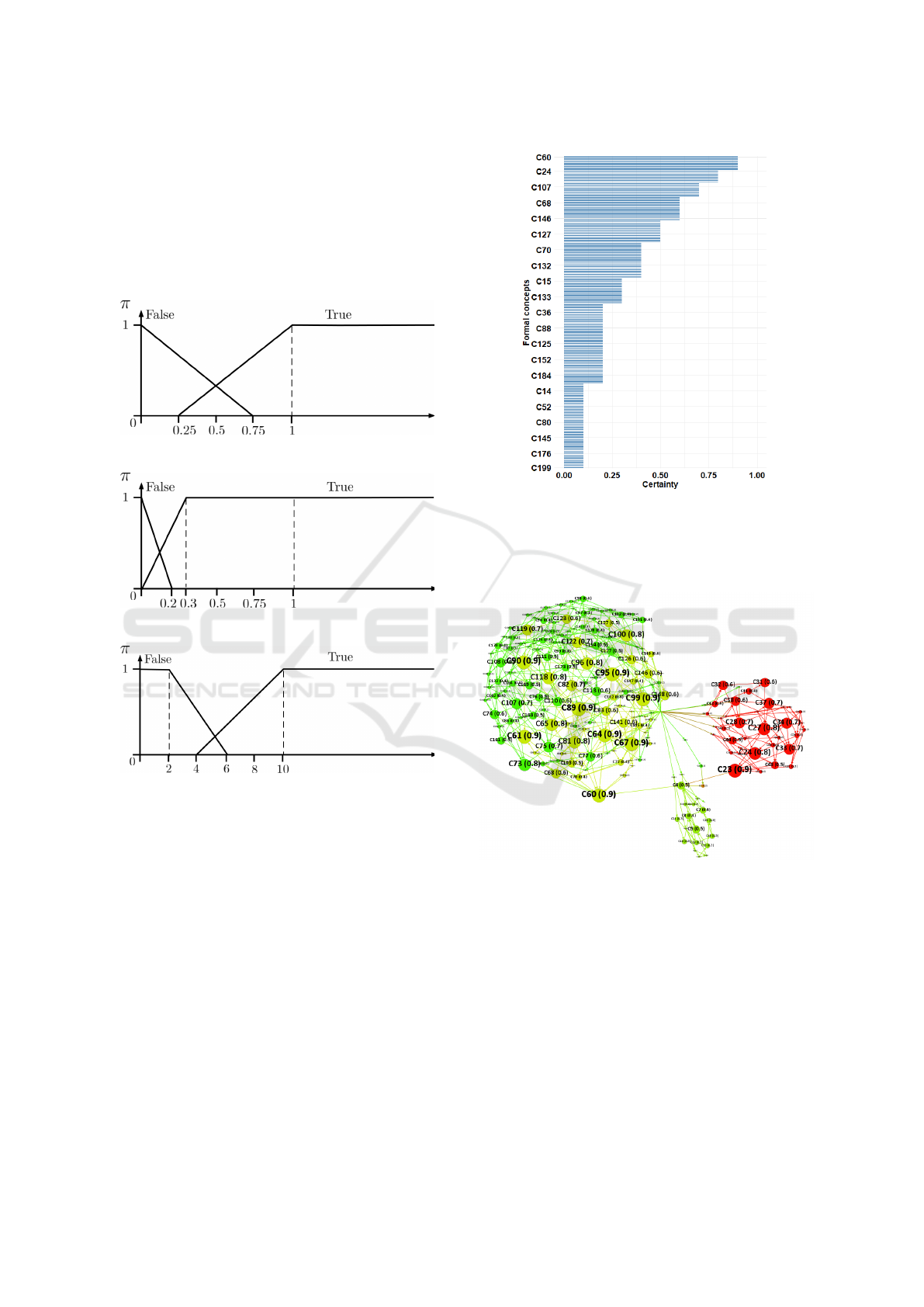
Figure 6: Score of relevance (N(Q = true)).
We can see that the formal concepts can be sorted
as expected. Then we can propose to visualize the
result of the query Q
∗
with the following diagram:
Figure 7: Example of a query result.
In this figure, we can see the certainty of the for-
mal concepts but also their score of relevance for the
query. The scores of relevance of the formal concepts
are given in brackets in the labels of the nodes in the
diagram. If we consider the example of the formal
concept C60, we can see that the size of the node is
one of the most important. The score of relevance is
equal to 0.9 for this formal concept. The knowledge
that we can extract from this formal concept is that
the students have appreciated the part of the course
concerning the theory of multiple intelligences of H.
Gardner.
Information Retrieval in a Concept Lattice by using Uncertain Logical Gates
295

6 CONCLUSIONS
In this paper, we present an experimentation of for-
mal concept analysis which allows us to take into ac-
count uncertainties. We have proposed to compute
a certainty degree for all formal concepts by using
possibility theory. We have used queries in order to
extract formal concepts in the concept lattice. The
condition of the queries can be a logical combina-
tion of criteria leading to a logical circuit. All cri-
teria are transformed into a possibility distribution in
order to take into account the imprecision and un-
certainty of knowledge. This logical circuit can be
transformed into a possibilistic network with uncer-
tain logical gates. As a result, we computed a score
of relevance for all formal concepts which allow us to
present a ranking of the formal concepts. Then, we
presented a visualization of the results in a diagram
with a colour shading proportional to the certainty of
the formal concept and a node size proportional to the
score of relevance. For our future works, we would
like to generalize this approach to variables with more
than two states in order to extend the possible crite-
ria. We would like to improve the performance of the
computation of the formal concepts and optimize the
inference of the possibilistic networks. We would like
to propose further evaluation in order to better evalu-
ate how uncertainties can be useful in applications.
Finally, we have to develop an HMI with a query as-
sistant which would allow a graphical expression of
queries and a code generation to improve the usabil-
ity of our tool.
REFERENCES
Amor, N. B. and Benferhat, S. (2005). Graphoid properties
of qualitative possiblistic independance relations. In
International Journal of Uncertainty, Fuzzyness and
Knowledge Based Systems, volume 5, pages 59–96.
Benferhat, S., Dubois, D., Garcia, L., and Prade, H. (1999).
Possibilistic logic bases and possibilistic graphs. In
In Proc. of the Conference on Uncertainty in Artificial
Intelligence, pages 57–64.
Borgelt, C., Gebhardt, J., and Kruse, R. (2000). Possibilistic
graphical models. In Computational Intelligence in
Data Mining, volume 26, pages 51–68. Springer.
Christen, P. (2006). A comparison of personal name match-
ing: Techniques and practical issues. In Proceedings
of the Sixth IEEE International Conference on Data
Mining - Workshops, ICDMW ’06, pages 290–294,
Washington, DC, USA. IEEE Computer Society.
D
`
ıez, F. and Drudzel, M. (2007). Canonical probabilistic
models for knowledge engineering. Technical report,
UNED, Technical Report CISIAD-06-01.
Dubois, D., de Saint-Cyr, F. D., and Prade, H. (2007). A
possibility-theoretic view of formal concept analysis.
In Fundam. Inf., volume 75, pages 195–213, Amster-
dam, The Netherlands. IOS Press.
Dubois, D., Fusco, G., Prade, H., and Tettamanzi, A. G. B.
(2015). Uncertain logical gates in possibilistic net-
works. an application to human geography. In Scal-
able Uncertainty Management 2015, pages 249–263.
Springer.
Dubois, D. and Prade, H. (1988). Possibility theory: An
Approach to Computerized Processing of Uncertainty.
Plenum Press, New York.
Dubois, D. and Prade, H. (2009). Possibility theory and
formal concept analysis in information systems. In
IFSA-EUSFLAT, pages 1021–1026.
Dubois, D. and Prade, H. (2015). Formal concept analysis
from the standpoint of possibility theory. In Baixeries,
J., Sacarea, C., and Ojeda-Aciego, M., editors, Formal
Concept Analysis, pages 21–38, Cham. Springer Inter-
national Publishing.
Ganter, B. (1987). Algorithmen zur formalen begriffsanal-
yse. In In B. Ganter, R. Wille, K. Wolf, (eds.), Beitrage
zur Begriffsanalyse, Wissenschaftsverlag, Mannheim,
pages 241–255.
Jaro, M. A. (1989). Advances in record linking methodol-
ogy as applied to the 1985 census of tampa florida.
In Journal of the American Statistical Society, vol-
ume 84, pages 414–420.
Kjaerulff, U. (1994). Reduction of computational complex-
ity in bayesian networks through removal of week de-
pendences. In Proceeding of the 10th Conference on
Uncertainty in Artificial Intelligence, pages 374–382.
Morgan Kaufmann.
Kruskal, J. B. (1956). On the shortest spanning subtree
of a graph and the travelling salesman problem. In
Proceedings of the American Mathematical Society,
pages 48–50.
Kuznetsov, S. O. and Obiedkov, S. A. (2003). Comparing
performance of algorithms for generating concept lat-
tices. In Journal Experimental & Theoretical Artificial
Intelligence, volume 14, pages 189–216.
Lauritzen, S. and Spiegelhalter, D. (1988). Local compu-
tation with probabilities on graphical structures and
their application to expert systems. In Journal of the
Royal Statistical Society, volume 50, pages 157–224.
Wille, R. (1982). Restructuring lattice theory: An approach
based on hierarchies of concepts. In Rival, I., edi-
tor, Ordered Sets, pages 445–470, Dordrecht. Springer
Netherlands.
Winkler, W. E. (1999). The state of record linkage and cur-
rent research problems. Technical report, Statistical
Research Division, U.S. Bureau of the Census.
Yang, J. and Qin, K. (2015/07). Uncertain concepts in a
formal context. In 2015 International Conference on
Artificial Intelligence and Industrial Engineering. At-
lantis Press.
Zadeh, L. A. (1978). Fuzzy sets as a basis for a theory
of possibility. In Fuzzy Sets and Systems, volume 1,
pages 3–28.
KDIR 2019 - 11th International Conference on Knowledge Discovery and Information Retrieval
296