New Designs of -means Clustering and Crossover Operator for

Solving Traveling Salesman Problems using Evolutionary Algorithms

Ismail M. Ali

, Daryl Essam

and Kathryn Kasmarik

School of Engineering and Information Technology, University of New South Wales, Canberra, Australia

Keywords: Traveling Salesman Problem, Genetic Algorithm, Differential Evolution, Clustering Method, Evolutionary

Algorithms.

Abstract: The traveling salesman problem is a well-known combinatorial optimization problem with permutation-based

variables, which has been proven to be an NP-complete problem. Over the last few decades, many

evolutionary algorithms have been developed for solving it. In this study, a new design that uses the -means

clustering method, is proposed to be used as a repairing method for the individuals in the initial population.

In addition, a new crossover operator is introduced to improve the evolving process of an evolutionary

algorithm and hence its performance. To investigate the performance of the proposed mechanism, two popular

evolutionary algorithms (genetic algorithm and differential evolution) have been implemented for solving 18

instances of traveling salesman problems and the results have been compared with those obtained from

standard versions of GA and DE, and 3 other state-of-the-art algorithms. Results show that the proposed

components can significantly improve the performance of EAs while solving TSPs with small, medium and

large-sized problems.

1 INTRODUCTION

The traveling salesman problem (TSP) is a prevalent

mathematics problem that requests the shortest

possible distance to visit a set of cities. Despite the

simplicity of its definition, TSP is one of the most

challenging combinatorial optimization problems

(COPs) in real world. Its practical importance is

shown in many fields, such as operational research,

algorithms design and artificial intelligence, and also

in many engineering applications, like design of

hardware devices and radio electronic systems, and

computer networks (Evans, 2017). So, it attracted the

attention of several researches for many years to find

the best way for optimally solving TSPs in a

reasonable computational time.

Many exact algorithms, which can accurately find

the optimum solution, have been introduced for

solving TSPs (Miller and Pekny, 1991). However,

they have been considered inapplicable for solving

many instances of TSPs, which were proven to be an

NP-hard COP (Jünger et al., 1995). In recent years,

https://orcid.org/0000-0001-5925-1988

https://orcid.org/0000-0002-6923-7079

https://orcid.org/0000-0001-7187-0474

several heuristics methods, which can find near

optimum solution, have been developed for TSPs and

they achieved better results than exact ones in terms

of computational time. Among these methods,

evolutionary algorithms (EAs), which demonstrate a

very promising direction for TSPs. EAs are inspired

by the biological model of evolution and natural

selection, and they have a long history of successfully

solving optimization problems (Bäck et al., 2018).

Many EAs-based approaches have been

introduced for solving TSPs. Some of them were

integrating local searches (Mavrovouniotis et al.,

2017), and these studies showed that incorporation of

local search operators can significantly improve the

performance of EAs. Other EAs, such as genetic

algorithms (GAs) and differential evolution (DE)

algorithms have also been developed for TSPs.

Recently, GA, with two local operators, called branch

and bound, and cross elimination, was used for

solving multiple TSPs (Lo et al., 2018). A new initial

population strategy, based on  -means algorithm,

was also proposed to improve the performance of GA

Ali, I., Essam, D. and Kasmarik, K.

New Designs of k-means Clustering and Crossover Operator for Solving Traveling Salesman Problems using Evolutionar y Algorithms.

DOI: 10.5220/0007940001230130

In Proceedings of the 11th International Joint Conference on Computational Intelligence (IJCCI 2019), pages 123-130

ISBN: 978-989-758-384-1

123

(Deng et al., 2015). Although the algorithm achieved

better error values than the random generation, the

obtained error values are still away from the optimal

solutions. Moreover, many DE algorithms have been

introduced for TSPs (Wei et al., 2016, Wang and Xu,

2011). However, many of the studies have been tested

on small and medium TSPs.

Seeking to improve the performance of EAs and

overcome some limitations that presented in the

previous research works, such as slow convergence,

increased computational time, and poor quality of

solutions, the following contributions are proposed in

this paper: 1) a new design of -means clustering to

be used as a repairing method for the generated

individuals in the initial population, which can

increase the convergence speed of an EA and increase

the possibility of getting the optimal solution in a

lower computational time; 2) a new crossover

operator, which is designed based on the

characteristics of TSPs to increase the population

diversity and improve the evolving processes of an

EAs. Finally, the proposed components have been

implemented using GA and DE for solving different

instances of TSP and the results were compared with

those from state-of-the-art algorithms and standard

versions of GA and DE.

The rest of this paper is organized as follows.

Section 2 presents the objective function of TSPs and

the original structures of GA and DE. Section 3

represents the proposed components. Section 4

discusses the experimental results and comparisons.

Finally, conclusion drawn from this study and future

work are provided in Section 5.

2 BACKGROUND

In this section, the definition and objective function

of TSPs, and the standard versions of GA and DE are

introduced.

2.1 Traveling Salesman Problem

The traveling salesman problem (TSP) is a well-

known COP with discrete decision variables. In 1930,

TSP was formulated as a mathematical problem for

the first time. In traditional TSP, a person has a task

of visiting  numbers of cities. He needs to visit

every city only once in any order starting from any

city and returning back to the home city from where

he started. Given the distances between each city, the

person needs to minimize the total travelled distance

during his trip. The objective is to find the shortest

tour that visits each city exactly ones, and then return

to the starting city. Mathematically, the objective

function of TSP can be described as minimization of

the total distances between visited cities, in addition

to the distance of returning to start city, as follows:

Minimize: , where

  



  







(1)

where  is the total distance of the trip,  is the

number of cities to be visited,  = 1, 2, …, . 



the return distance from the last city () to the first

one, and 



is the distance between two

consecutive cities  and  .

2.2 Standard Versions of Genetic

Algorithm and Differential

Evolution

Both GA and DE belong to EAs (Bäck et al., 2018).

They solve a problem by iteratively improving the

candidate solutions through three evolving operators,

namely: mutation, crossover and selection. These

operators are applied to guide the search to find

optimal solutions. The first basic difference between

GA and DE is the order of evolving operators’

execution, as GA applies selection then crossover and

finally mutation, whereas DE considers mutation

first, then crossover and selection. The second major

difference is that GA performs an additional process

called elitism, which ensures that the best individual

from the current generation is carried over to the next

without any modifications. This process guarantees

that the quality of the solutions is not decreased from

one generation to another. GA and DE are considered

powerful tools for solving optimization problems in

both continuous and discrete spaces. Basically, an

initial population with a pre-determined size () is

generated and then each individual ( 



), which

consists of  variables, is evolved using the three

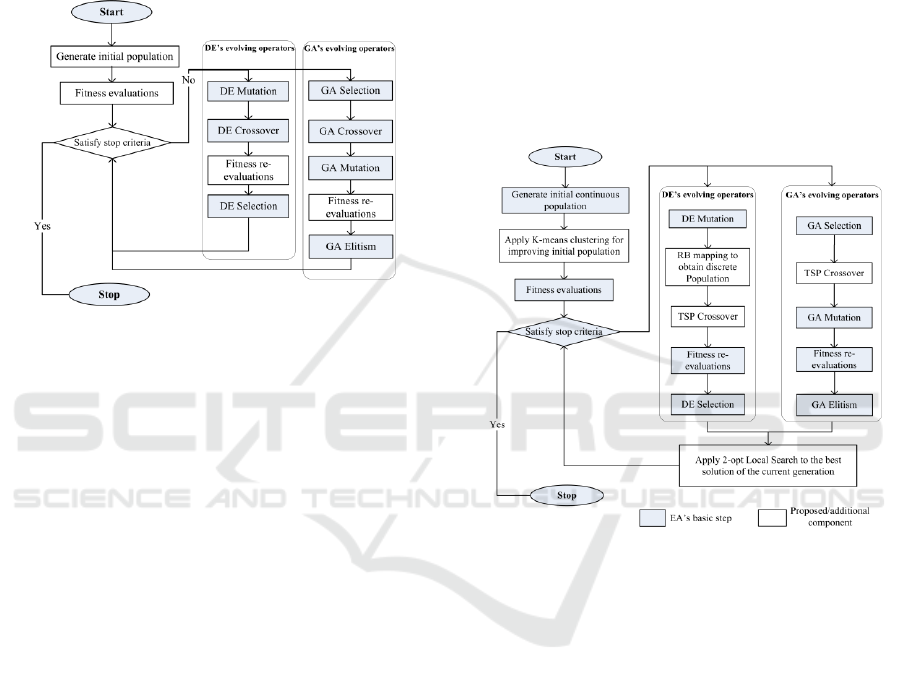
evolutionary operators. Figure 1 shows the basic

outlines of the standard versions of GA and DE and

the order of their three evolving operators.

2.2.1 Mutation Operator

In DE, a mutant vector is generated for each target

vector (



), using this simplest mutation form:













   



























 

(2)

where  is the weighting factor, that controls the

amplification of the differential variation between the

ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications

124

two vectors 







and 







, and generally lies within

the range of [0, 2]. 















 







are three

randomly chosen vectors, which are not equal to each

other or to the target vector (



). In GA, mutation

modifies one or more gene values in an individual by

swapping them with other genes or flip their values

from the initial state, and hence the individual may

change entirely from the previous one.

Figure 1: Structure of standard GA and DE.

2.2.2 Crossover Operator

In DE, new vectors (trial vectors) are generated by

combining target (individuals from last generation)

and mutant vectors according to a pre-defined

possibility. Binomial and exponential are the two

most well-known types of crossover for DE. In GA,

the new offspring is produced by exchanging

different parts of two randomly selected parents,

where if the first part of the offspring came from first

parent, the second part must come from second

parent, etc. This is called one-point crossover (Ali et

al., 2015), where a random point is generated to

divide both parents into two parts.

2.2.3 Selection Operator

In DE, a comparison of each trial vector and its

corresponding target vector is used to determine

whether trail or target vectors should survive to the

next generation. The greedy strategy is an example of

DE selection operator. In GA, a tournament method

is adopted to select an individual by running several

competitions, based on the fitness values and the

feasibility of the solutions, among a few individuals

selected randomly from the population.

In both GA and DE, the processes of the

evolutionary operations remain as long as a time or a

generation limit is reached, or the number of calling

the fitness evaluation function is greater than a pre-

defined number of calling.

3 PROPOSED EVOLUTIONARY

ALGORITHM

In this paper, two main components have been

developed and implemented in order to improve the

performance of EAs for solving TSPs. In this section,

the basic steps of EAs and the two proposed

components are briefly discussed. Figure 2 shows the

proposed components when adopting with both GA

and DE algorithms as examples of EAs.

Figure 2: Structure of proposed GA and DE.

3.1 Initial Population

The first step in most EA is to generate an initial

population of solutions. So, a population of 

solutions is randomly generated. In our algorithm,

every solution can be represented by a discrete vector,

where the length of each vector equals the number of

cities to be visited ().

3.2 -means Clustering as a Repairing

Method

As TSPs are a complex COP, we noticed that the

evolutionary process may take longer to make the

solutions in the initial population converge towards

the optimal solution. So, a new design of -means

clustering method is applied, according to a pre-

defined probability (), to the solutions in

the initial population as a repairing method to

New Designs of k-means Clustering and Crossover Operator for Solving Traveling Salesman Problems using Evolutionary Algorithms

125

improve their qualities within the initial phase, and as

a result, the optimal solution is likely to be found after

a few EA’s generations.

In -means clustering, several locations () are

generated over the geometric problem space

according to Equation 3. A number of groups, equal

to , are formed with those points as the centroids.

Each group attracts the close cities (by their

coordinates) from its centroid.

  



  

(3)

After assigning all the cities in groups, each group

is solved as a sub-TSP by finding the shortest sub-

tour between the cities in each group. In order to form

the complete tour of TSP, the distances between the

centroid points () are calculated and the two groups

with the smallest distance between their centroids are

selected to be merged and form a larger group. The

merge between groups is done by connecting two

cities of a group with their closest two cities of the

other group after breaking their local connections.

After that, the centroid point of the new formed group

is calculated and the distances between all the

centroid points (    ) of existing groups are

remeasured. This process is repeated until only one

group (  ) that contains all the cities is formed.

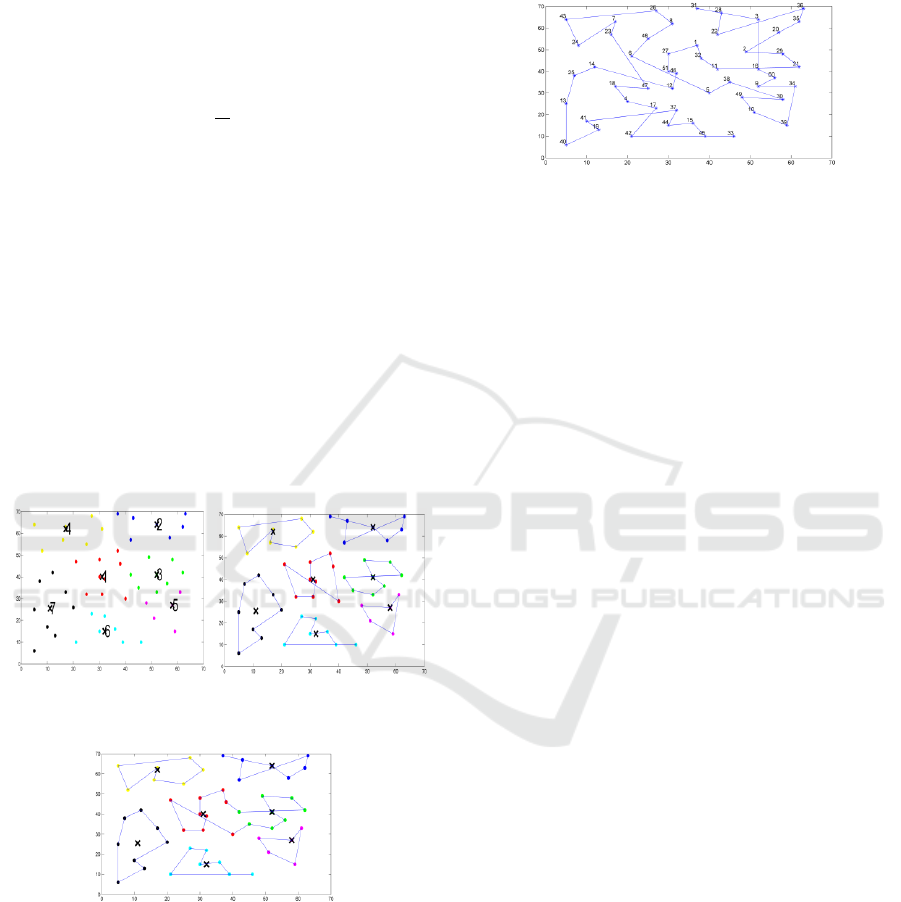
(a) Distribution of

centroid points over

geometric space.

(b) Calculate the

shortest paths in each group

Figure 3: Steps of k-means clustering repairing method.

In Figure 3, the basic steps of -means clustering

repairing method are illustrated. It shows the steps of

the proposed repairing method, for a TSP instance

called eil51 with 51 cities to be visited, as follows: (a)

gives the distribution of the  locations over the

search space of the problem; (b) shows the shortest

path in each formed group; (c) displays the generation

of the first group produced from merging group 1

with 3. This last step is repeated until one large group

including all the cities is formed with the shortest path

between them, as the example shown in Figure 4.

Figure 4: Final tour after applying  -means clustering

repairing method.

3.3 Fitness Evaluations

After the initial population is generated and repaired,

the fitness value of each individual is measured

seeking to rank them according to their qualities. The

fitness function shown on Equation 1 is used to

calculate the quality of each solution, and then the

solutions are ranked where the fittest one shown first

and the worst last.

3.4 Evolving Operators

3.4.1 Proposed Crossover for TSP

In this paper, a new design of a crossover, which uses

the characteristics of the TSP (TSP-Xover) is given.

In TSP-Xover, the one-point crossover procedure is

followed, where a random cut point () in the range

[1,  ] is chosen and two parents are randomly

selected to generate a new offspring. The first part of

the offspring [ ] is copied from one of the

parents, and the second part is completed from the

other. In order to do that, starting from the last city in

the first part of the offspring (), the next city ( 

) is selected based on its distance from . So, if the

next city is the closest one to the  city and has not

been taken before in the offspring (not in the range

[  ]), then next city will be added in offspring at

(  ) order. The pseudo-code for the proposed

crossover (TSP-Xover) is provided in Algorithm 1.

3.4.2 Mutation Operator

The standard mutation operators of GA and DE were

implemented in the proposed framework. For DE and

GA, the DE\rand\1 mutation strategy (Equation 2)

and the swap mutation (Bäck et al., 2018) were

adopted, respectively.

ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications

126

Algorithm 1: Pseudo-code of TSP-Xover.

for  form 1 to  do

if random-number <=  then

Parent1  random individual

Parent2another random individual

 random point in range   

  Distance between all cities

Offspring=Parent1(1 to )

    

while    do

 city from Parent2

with ( (Parent1(   ) and

Parent2(1 to )))

if  is not existed in

Offspring(1 to   ), then

Offspring()  

    

else

 next closest city

from Parent2

end if

end while

end if

end for

3.5 Fitness Re-evaluations and

Selection

After obtaining the new population, a selection

operator is applied to decide which solution can

survive to the next generation. The greedy selection

strategy and the tournament method are applied to DE

and GA, respectively. The solutions in the new

selected population are ranked based on their fitness

values, where the best solution located first.

For comparisons purposes, 2-Opt local search

(Savelsbergh, 1985) is used and applied to the best

solution found in each generation for all standard and

proposed versions of GA and DE.

3.6 Termination Condition

In this study, the number of calling the fitness

function is counted and if this counter exceeds the

predefined allowed number of objective function

evaluations, the algorithm is terminated.

4 EXPERIMENTAL RESULTS

To judge the effect of the proposed components on

the performance of EAs, computational simulations

were carried out using GA and DE (as popular

examples of EAs) for solving 18 instances of TSPs

with small, medium and large dimensions. The

instances were selected from the well-known TSP

library (TSPLIB), which is described in (Reinelt,

1991). Both GA and DE were coded in MATLAB

R2017b, and were performed on a PC with an i7

Processor and 16 GB memory. In our experiments,

each TSP instance was independently executed 30

times with 1,000, 5,000 and 50,000 fitness

evaluations in each run for comparison. The quality

of each algorithm is assessed by calculating the

average error of each problem, which is the error

between the best obtained solution by an algorithm

and the optimal solution of the same problem as

shown in Equation 4.

  

  



  

(4)

4.1 Parameters Settings and Tuning

In this sub-section, the parameters setup of both GA

and DE and the parameter analyses of the two

proposed components are presented.

4.1.1 Parameter Settings

Based on extensive experiments using 18 instances of

TSPs, the final parameters setup of GA and DE are

shown in Table 1.

Table 1: GA and DE parameters setup.

Parameter

Symbol

Value

Number of runs

Population size



Crossover rate



0.7

Mutation rate



0.2

Number of individuals to be

repaired in the initial population



0.1 (10%)

Maximum fitness evaluations

1000, 5000, and 50,000

4.1.2 Parameters Tuning

Two sets of experiments were designed to analyse

effects of the two proposed components’ parameters

 and , while the other parameters’ values

were fixed as shown in Table I. Both , and

, were run with different values for 10 runs for each

value and 5000 fitness evaluations for each run using

GA and DE for solving 18 TSPs. Figures 5 and 6

present the average value of errors of solved TSPs

from their optimal solutions (on bars) and standard

deviations (on vertical small bars) using DE and GA,

respectively. In the figures, DE and GA run with

 set to different values of 0, 10, 30, 50, 70,

90 and 100 (%) of . The results show that repairing

New Designs of k-means Clustering and Crossover Operator for Solving Traveling Salesman Problems using Evolutionary Algorithms

127

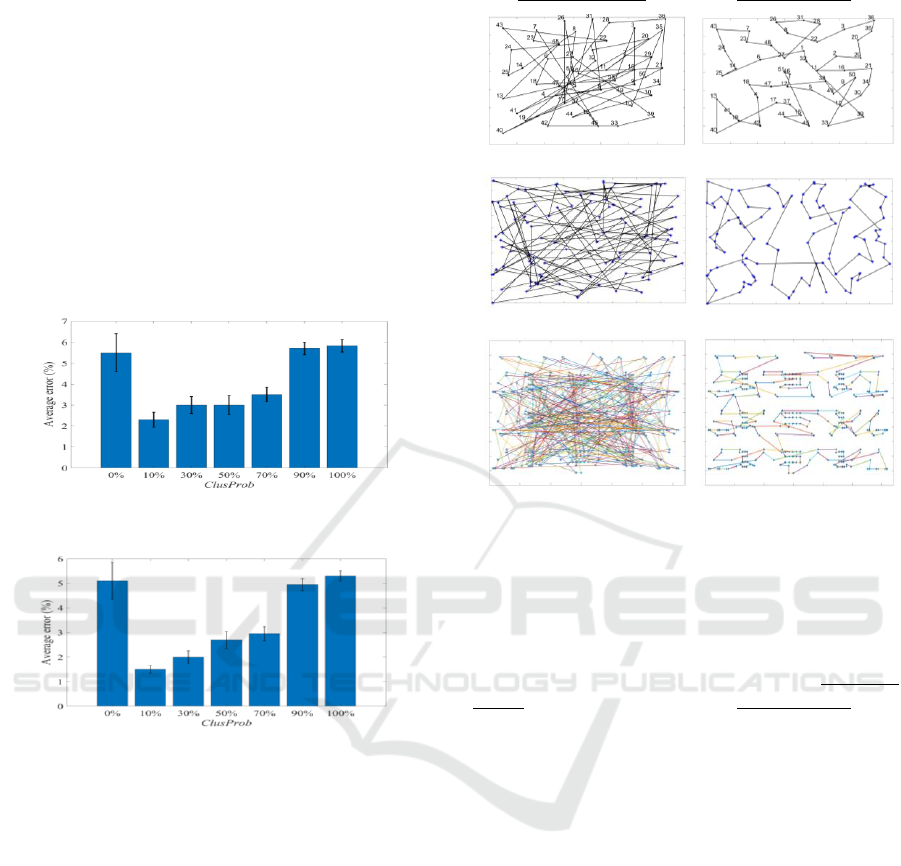
10% of the individuals in the initial population can

enhance the average error by 47.98% and 61.21%

compared with the average of other parameter values

in DE and GA, respectively. Also, we noticed that

with higher values of , the average error is

increased because of the lack of diversity in the

population. On the other hand,  =0%,

achieved worse average error than =10%,

which confirms the importance of the proposed

repairing method. Another experiment run for

analysing  parameter by setting it to different

values of 0.1, 0.3, 0.5, 0.7 and 0.9. Based on the

results, it was found that =0.7 achieved the best

average error compared with other values.

Figure 5: Analysis of  parameter with standard

deviation error bar using DE.

Figure 6: Analysis of  parameter with standard

deviation error bar using GA.

4.2 Effect of k-means Clustering

Repairing Method

This sub-section discusses the effect of applying the

proposed repairing method on performance of an EA.

In order to do that, all TSPs have been solved with

and without applying -means method. Results show

that the proposed method can enhance the quality of

solutions by 76.6% on average. To graphically

present the effect of the proposed method, the best

individuals of 3 TSPs were presented before and after

adopting the proposed method in Figure 7.

Before -means

After -means

eil51 = 1494

eil51 = 588

kroC100 = 149393

kroC100 = 29827

lin318 = 557091

lin318 = 58941

Figure 7: Graphical paths of 3 TSPs before and after

applying the proposed repairing method with the total

distance of each.

For comparison, Figure 7 shows the paths of the

same individual of each problem produced directly

after generation of the initial population (Before -

means) and after being repaired (After -means). The

figure also provides the total distances of each

individual to show differences in their qualities. From

Figure 7, it can be noticed that -means clustering

repairing method can enhance the solutions in the

initial population for TSPs “eil51”, “kroC100”, and

“lin318” by 60.64%, 80%, 89.41%, respectively. The

results demonstrate efficiency of the proposed

repairing method, especially for large TSP instances.

4.3 Comparison with Standard

Versions of GA and DE

In order to judge the effect of the proposed

components on the overall performance of EAs, in

this sub-section the performances of GA and DE will

be compared, with and without, incorporating the

proposed components. In order to do that, the best and

mean values of the average errors produced from i)

standard GA, ii) standard DE, iii) GA + -means and

TSP-Xover, and iv) DE + -means and TSP-Xover

are presented in Table 2.

ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications

128

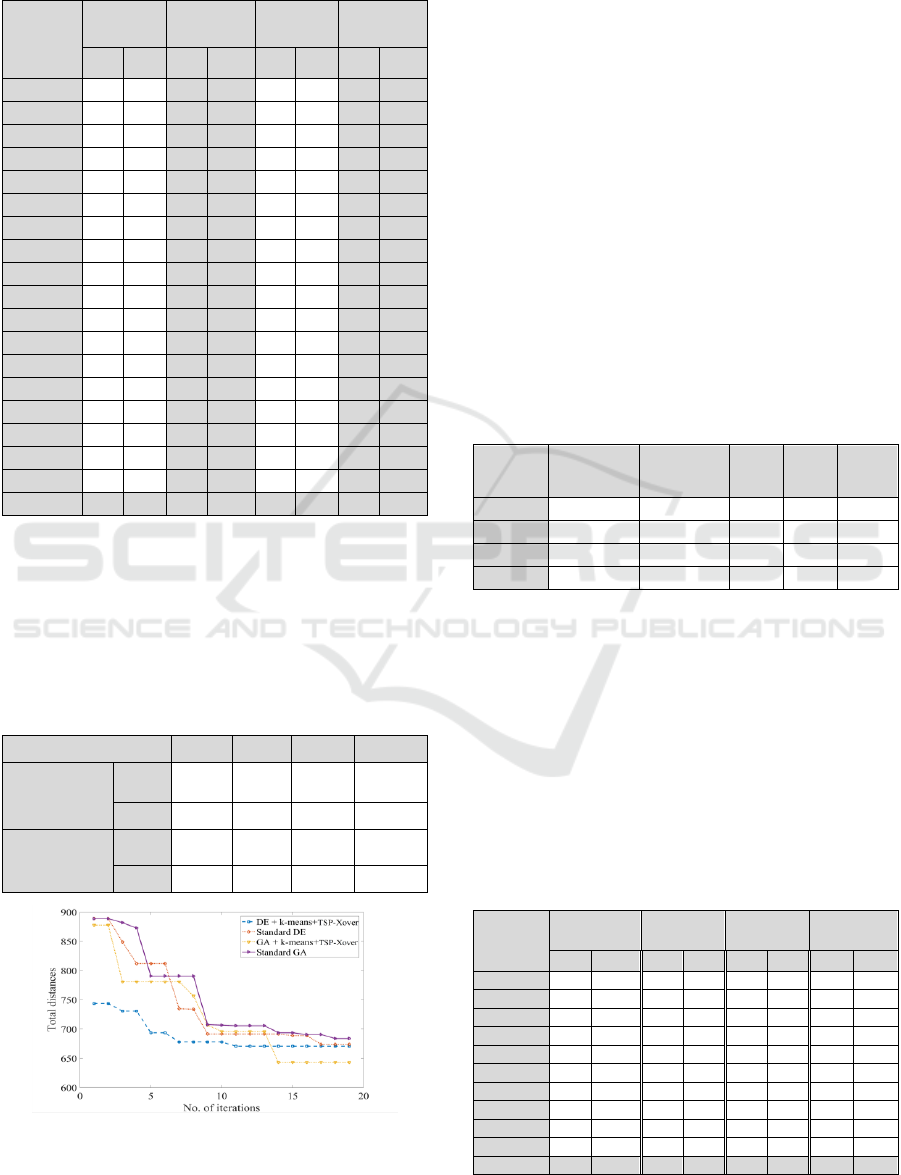
Table 2: Best (B) and mean (M) average errors for 18

instances of TSPs obtained from improved and standard

versions of GA and DE.

Probs

Standard

GA +  -

means and

TSP-Xover

Standard

DE +  -

means and

TSP-Xover

eil51

0.0

2.0

0.0

0.8

0.5

1.7

0.2

1.2

berlin52

0.3

2.0

0.0

0.1

0.0

2.2

0.0

0.6

st70

0.2

2.7

0.0

0.6

1.2

2.0

0.3

1.5

eil76

0.2

2.7

0.7

2.5

2.0

4.0

1.9

3.6

pr76

1.6

2.0

0.0

0.5

0.0

1.3

0.0

1.2

kroA100

0.2

1.0

0.0

3.9

0.8

1.9

0.8

2.1

kroC100

0.5

1.7

0.0

3.9

1.0

2.8

1.0

2.7

kroD100

1.1

2.4

0.0

3.9

1.8

3.2

1.6

3.2

eil101

2.7

4.1

0.0

2.5

3.3

5.2

3.0

5.3

lin105

0.4

4.0

0.0

1.0

0.6

1.8

0.2

1.5

pr144

0.1

1.7

0.1

0.5

0.1

0.4

0.1

0.5

ch150

2.9

4.6

0.0

5.1

3.2

4.8

2.8

4.7

kroA150

2.0

4.0

0.1

5.1

2.5

4.2

1.3

4.3

kroB150

2.1

3.6

1.0

5.5

2.3

3.8

2.0

3.9

pr152

0.5

2.1

0.2

3.6

1.2

2.2

1.1

2.3

lin318

4.0

5.7

0.9

7.0

3.8

5.5

3.9

5.5

pcb442

5.8

7.5

0.1

8.1

6.2

7.9

6.0

7.6

d493

4.5

6.3

0.8

7.2

5.2

6.2

5.0

6.3

Avg.

1.6

3.3

0.2

3.4

2.0

3.4

1.7

3.2

A nonparametric statistical test (Woolson, 2007),

which is usually used to assess whether the

population mean ranks of two related samples differ,

is applied to show the significant differences between

the proposed versions of GA and DE and their

standard versions. The outcome is listed in Table 3.

Table 3: Nonparametric Wilcoxon test based on the best

and mean errors from the optimal solution.

Better

Equal

Worse

P.Value

GA + -means

and TSP-Xover

VS. Standard

Best

0.001

Mean

0.931

DE + -means

and TSP-Xover

VS. Standard

Best

0.002

Mean

0.338

Figure 8: Convergence plot of eil101 TSP with 20 iterations

(1000 fitness evaluations).

From results in Table 2 and 3, the versions with

the added proposed components can significantly

enhance the performances of the standard GA and DE

by 86.52% and 12.13% in terms of the best errors

from the optimal solutions of 18 TSPs.

To graphically represent the performance of each

algorithm, the convergence plot of one TSP, namely:

eil101 is shown in Figure 8.

4.4 Comparison with State-of-the-Art

Algorithms

In this sub-section, the performance of the proposed

algorithm is compared with three algorithms from the

state-of-the-art algorithms: 1) improved bat algorithm

(IBA) (Osaba et al., 2016); 2) Discrete firefly

algorithm (DFA) (Osaba et al., 2016); and 3) a

discrete imperialist competitive algorithm (DICA)

(Osaba et al., 2016), as shown in Table 4.

Table 4: Total distances obtained from the proposed

versions of GA and DE and 3 state-of-the-art algorithms.

Probs

GA +  -

means and

TSP-Xover

DE +  -

means and

TSP-Xover

IBA

DFA

DICA

eil51

426

427

426

berlin52

7542

st70

675

676

675

eil76

539

540

539

543

544

Table 4 shows the competitive performance of the

proposed components with GA and DE compared

with other evolutionary algorithms. However, the

results didn’t show any differences between the

comparative algorithms.

In order to further assess the performance of the

proposed components, the proposed GA is compared

with other three algorithms: 1) GA, 2) PSO, and 3)

hybrid GA-PSO, which were recently proposed in

(Gupta et al., 2019).

Table 5: Average error % (E) and average time in seconds

(T) obtained from the proposed GA and other 3 algorithms.

Probs.

PSO

GA-

PSO

Proposed

ATT48

2.4

0.5

2.8

0.4

0.3

0.4

0.5

EIL51

2.6

0.6

3.1

0.4

1.2

0.5

1.2

0.5

ST70

4.2

0.9

4.9

0.6

0.8

0.7

0.1

0.7

PR76

2.2

1.2

2.6

0.8

0.7

1.0

0.4

1.6

RD100

4.5

1.8

5.3

1.3

1.6

1.5

0.0

1.5

KROA100

4.0

1.8

4.8

1.3

1.0

1.5

0.1

1.5

KROB100

3.1

1.8

3.7

1.2

1.8

1.5

0.1

1.3

PR107

3.2

2.1

3.8

1.5

1.2

1.7

0.0

1.8

PR124

2.0

2.4

1.6

0.3

2.1

0.0

2.3

GIL262

6.3

10.0

7.5

7.1

3.0

8.6

0.0

7.3

Average

3.4

2.3

4.1

1.6

1.2

2.0

0.3

1.9

New Designs of k-means Clustering and Crossover Operator for Solving Traveling Salesman Problems using Evolutionary Algorithms

129

Table 5 showed that the GA version with the

proposed components can achieve a higher average

error from the optimal solution than other

comparative algorithms for the first three (small)

TSPs. However, starting from the fourth problem, the

proposed GA achieved the best average error

compared with others. This indicates that the

proposed components are more suitable to solve TSPs

with large sizes. The average values showed that the

proposed GA can achieve better average errors by

92.55%, 93.70%, and 78.18% than GA, PSO, and

hybrid GA-PSO, respectively.

Moreover, the detailed results of the proposed GA

and other comparative algorithms are shown in Table

1 in the Appendix, which can be accessed from

https://github.com/IsmailMAli/TSP-Results. In

Table 1, the results of 10 TSPs with different number

of cities, mean values, average error (%), and average

computational time in seconds, are given.

5 CONCLUSION AND FUTURE

WORK

In this paper, a new design that uses the -means

clustering as a repairing method for the initial

population of an EA, and a new crossover strategy for

TSPs, are proposed. The  -means clustering

repairing method is applied directly after the initial

population is generated to enhance the quality of the

solutions. The crossover is designed to generate

offspring from the current individuals taking in

account the characteristics of the TSP. The

experimental results showed that these proposed

components can significantly improve the

performance of EAs, while solving TSPs and are very

promising especially when dealing with large TSPs.

In the future, more complex discrete problems,

such as resource constrained project scheduling

problems (RCPSPs) and traveling thief problems

(TTPs), will be used to test the effectiveness of the

proposed components while solving such problems.

REFERENCES

Ali, IM, Elsayed, SM, Ray, T & Sarker, RA. Memetic

algorithm for solving resource constrained project

scheduling problems. Evolutionary Computation

(CEC), 2015 IEEE Congress on, 2015. IEEE, 2761-

2767.

Bäck, T, Fogel, DB & Michalewicz, Z 2018. Evolutionary

computation 1: Basic algorithms and operators, CRC

press.

Deng, Y, Liu, Y & Zhou, D 2015. An improved genetic

algorithm with initial population strategy for symmetric

TSP. Mathematical Problems in Engineering, 2015.

Evans, J 2017. Optimization algorithms for networks and

graphs, Routledge.

Gupta, IK, Shakil, S & Shakil, S. A Hybrid GA-PSO

Algorithm to Solve Traveling Salesman Problem. 2019

Singapore. Springer Singapore, 453-462.

Jünger, M, Reinelt, G & Rinaldi, G 1995. The traveling

salesman problem. Handbooks in operations research

and management science, 7, 225-330.

Lo, K-M, Yi, W-Y, Wong, P-K, Leung, K-S, Leung, Y &

Mak, S-T 2018. A genetic algorithm with new local

operators for multiple traveling salesman problems.

International Journal of Computational Intelligence

Systems, 11, 1, 692-705.

Mavrovouniotis, M, Müller, FM & Yang, S 2017. Ant

colony optimization with local search for dynamic

traveling salesman problems. IEEE transactions on

cybernetics, 47, 7, 1743-1756.

Miller, DL & Pekny, JF 1991. Exact solution of large

asymmetric traveling salesman problems. Science, 251,

4995, 754-761.

Osaba, E, Yang, X-S, Diaz, F, Lopez-Garcia, P &

Carballedo, R 2016. An improved discrete bat

algorithm for symmetric and asymmetric traveling

salesman problems. Engineering Applications of

Artificial Intelligence, 48, 59-71.

Reinelt, G 1991. TSPLIB—A traveling salesman problem

library. ORSA journal on computing, 3, 4, 376-384.

Savelsbergh, MW 1985. Local search in routing problems

with time windows. Annals of Operations research, 4,

1, 285-305.

Wang, X & Xu, G 2011. Hybrid differential evolution

algorithm for traveling salesman problem. Procedia

Engineering, 15, 2716-2720.

Wei, H, Hao, Z, Huang, H, Li, G & Chen, Q. A Real

Adjacency Matrix-Coded Differential Evolution

Algorithm for Traveling Salesman Problems. Bio-

Inspired Computing-Theories and Applications, 2016.

Springer, 135-140.

Woolson, R 2007. Wilcoxon signed ‐ rank test. Wiley

encyclopedia of clinical trials, 1-3.

ECTA 2019 - 11th International Conference on Evolutionary Computation Theory and Applications

130