
Efficient Secure Floating-point Arithmetic using Shamir Secret Sharing
Octavian Catrina
a
University Politehnica of Bucharest, Bucharest, Romania
Keywords:
Secure Multiparty Computation, Secure Floating-point Arithmetic, Secret Sharing.
Abstract:
Successful deployment of privacy preserving collaborative applications, like statistical analysis, benchmark-
ing, and optimizations, requires more efficient secure computation with real numbers. We present a complete
family of protocols for secure floating-point arithmetic, constructed using a small set of building blocks that
preserve data privacy using well known primitives based on Shamir secret sharing and related cryptographic
techniques. Using new building blocks and optimizations and simpler secure fixed-point arithmetic, we obtain
floating-point protocols with substantially improved efficiency.
1 INTRODUCTION
Secure computation enables groups of parties to run
collaborative applications without having to reveal
their private inputs: data privacy is preserved through-
out the computation by cryptographic protocols. Var-
ious applications that require secure arithmetic with
real numbers have been studied and implemented
(Aliasgari et al., 2017; Bogdanov et al., 2018; Kamm
and Willemson, 2015; Catrina and de Hoogh, 2010b).
However, the performance penalty caused by crypto-
graphic protocols remains an important deterrent for
the deployment of these applications and motivates
further research on improving current solutions (Dim-
itrov et al., 2016; Krips and Willemson, 2014).
Two frameworks based on secret sharing offer
comprehensive support for multiparty secure com-
putation with real numbers. The first framework
(Catrina and de Hoogh, 2010a; Catrina and Saxena,
2010) provides a solid foundation for secure fixed-
point computation, demonstrated by solving linear
programming problems with private data (Catrina and
de Hoogh, 2010b). Privacy is protected using well
known primitives based on Shamir secret sharing and
related techniques (Cramer et al., 2015; Cramer et al.,
2005). Follow-up work added protocols for secure
floating-point computation (Aliasgari et al., 2013) and
related applications (Aliasgari et al., 2017). The other
framework, Sharemind, was developed in parallel and
relies on additive secret sharing. Its protocols for
computing with real numbers have been gradually op-
timized (Krips and Willemson, 2014) and used in var-
ious applications (Bogdanov et al., 2018; Kamm and
Willemson, 2015). These frameworks offer similar
a
https://orcid.org/0000-0002-7498-9881
security and performance for passive adversary (ex-
tension to active adversary is still expensive).
An initial goal of our project was to extend the
first framework with building blocks and optimiza-
tions that offer better support for secure computation
with real numbers. In this paper, we show how these
extensions are used to obtain important performance
gains for secure floating-point arithmetic.
The protocols provide the basic functionality and
accuracy expected by typical applications, for prac-
tical range and precision settings. We focus on im-
proving protocol performance and enabling trade-offs
between performance and precision based on appli-
cation requirements, rather than replicating the for-
mat and features specified in the IEEE Standard for
Floating-Point Arithmetic (IEEE 754). Also, we aim
at simplifying the protocols, by using a small set of
components and constructions. We selected solutions
that offer better trade-offs for the entire protocol fam-
ily, rather than optimizing particular tasks. The pa-
per is structured as follows. Section 2 is an overview
of the secure computation framework, data encod-
ing, and main building blocks. Section 3 presents
the new family of protocols for secure floating-point
arithmetic: addition and subtraction, multiplication,
division, square root, and comparison. We summa-
rize the main results in Section 4.
2 PRELIMINARIES
Secure Computation Model. The protocols pre-
sented in this paper use the secure computation frame-
work described in (Catrina and de Hoogh, 2010a),
which is based on standard primitives for secure com-
Catrina, O.
Efficient Secure Floating-point Arithmetic using Shamir Secret Sharing.
DOI: 10.5220/0007834100490060
In Proceedings of the 16th International Joint Conference on e-Business and Telecommunications (ICETE 2019), pages 49-60
ISBN: 978-989-758-378-0
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
49

putation using secret sharing (Cramer et al., 2015)
and various optimizations presented in the literature
(Cramer et al., 2005; Damg
˚
ard et al., 2006; Damg
˚
ard
and Thorbek, 2007; Reistad and Toft, 2009). We start
with an overview of this framework.
Suppose that n > 2 parties, P
1
,P
2
,...,P
n
, commu-
nicate on secure channels and want to perform a joint
computation where party P
i
has private input x
i
and
expects output y
i
. The parties use a linear secret-
sharing scheme to create a distributed state of the
computation where each party has a random share of
each secret variable. Then, they compute with these
shared variables to obtain the desired outputs, by run-
ning secure computation protocols.
Assuming perfectly secure channels and random
number generators, these protocols offer perfect or
statistical privacy: the views of protocol executions
(all values seen by an adversary) can be simulated
such that the distributions of real and simulated views
are perfectly or statistically indistinguishable, respec-
tively. Let X and Y be distributions with finite sample
spaces V and W . The statistical distance between X
and Y is ∆(X,Y ) =
1
2
∑
v∈V
S
W
|Pr(X = v) −Pr(Y =
v)|. The distributions are perfectly indistinguish-
able if ∆(X,Y ) = 0 and statistically indistinguish-
able if ∆(X,Y ) is negligible in some security parame-
ter. With real-life secure channels and pseudo-random
numbers, the protocols offer computational security.
The core primitives use Shamir secret sharing over
a finite field F. These primitives provide secure arith-
metic in F with perfect privacy against a passive
threshold adversary able to corrupt t out of n par-
ties. In this model, the parties do not deviate from
the protocol and any t + 1 parties can reconstruct a
secret, while t or less parties cannot distinguish it
from random values in F. We assume |F| > n, to en-
able Shamir sharing, and n > 2t, for multiplication of
secret-shared values. Support for stronger adversary
models can be added using various techniques, albeit
with substantial performance degradation.
In this paper, we focus on protocols that use the
field of integers modulo a prime q, denoted Z
q
. How-
ever, binary computations can be optimized by work-
ing in a small field F
2
8
(Catrina and de Hoogh, 2010a;
Catrina and Saxena, 2010). The parties locally com-
pute addition/subtraction of shared field elements by
adding/subtracting their own shares. Tasks that in-
volve multiplication of shared values require interac-
tion and are computed by dedicated protocols.
The protocols overcome the limitations of secure
arithmetic with shared field elements, by combining
secret sharing with additive or multiplicative hiding:
for a shared variable JxK the parties jointly generate a
secret random value JrK, compute JyK = JxK + JrK or
Table 1: Complexity of core protocols (selection).
Protocol Rounds Int. Op.
JaK ← Share(a) 1 1
a ← Reveal(JaK) 1 1
JcK ← JaK + JbK 0 0
JcK ← a + JbK 0 0
JcK ← aJbK 0 0
JcK ← JaKJbK 1 1
JyK = JxK ·JrK and reveal y; this is similar to one-time
pad encryption of x with key r. For secret x ∈Z
q
and
random uniform r ∈Z
q
we obtain ∆(x +r mod q, r) =
0 and ∆(xr mod q,r) = 0, hence perfect privacy. For
x ∈ [0,2
k
−1], random uniform r ∈ [0, 2
k+κ
−1], and
q > 2
k+κ+1
we obtain ∆(x + r mod q,r) < 2
−κ
, hence
statistical privacy with security parameter κ. So-
lutions with statistical privacy substantially simplify
the protocols by avoiding wraparound modulo q, al-
though they require larger q for a given data range.
We evaluate the protocols using complexity met-
rics that focus on interaction between parties. Com-
munication complexity measures the amount of data
sent by each party. For our protocols, a suitable met-
ric is the number of invocations of 3 primitives dur-
ing which every party sends a share to the others: in-
put sharing, multiplication, and secret reconstruction.
Round complexity is the number of sequential invo-
cations and is relevant for network latency. Table 1
shows the complexity of the core primitives.
The protocols offer best performance for imple-
mentations that apply the following basic optimiza-
tions. Interactive operations that do not depend on
each other are executed in parallel, in a single round.
In particular, all shared random values can be precom-
puted in parallel. We use Pseudo-random Replicated
Secret Sharing (PRSS) (Cramer et al., 2005) and its
integer variant (RISS) (Damg
˚
ard and Thorbek, 2007)
to generate without interaction shared random field el-
ements and integers, and random sharings of 0. Some
shared random values cannot be generated without in-
teraction (e.g., random bits shared in Z
q
). We indicate
separately the communication complexity of the pre-
computation round.
Data Types and Data Encoding. We consider se-
cure computation with the following data types: bi-
nary values, signed integers, fixed-point numbers, and
floating-point numbers. For secure computation, they
are encoded in a finite field F. We distinguish differ-
ent representations of a number as follows: we denote
˜x a fixed-point number, ¯x the integer value encoding
˜x, x the field element that encodes ¯x, and JxK a sharing
of x; a floating-point number is denoted ˆx. The no-
SECRYPT 2019 - 16th International Conference on Security and Cryptography
50

tation x = (condition)? a : b means that x is assigned
the value a when condition = true and b otherwise.
Logical values f alse,true and bit values 0, 1 are
encoded as 0
F
and 1
F
, respectively. F can be either
Z
q
or a small binary field F
2
m
. This encoding allows
efficient secure evaluation of Boolean functions using
secure arithmetic in F (Catrina and de Hoogh, 2010a).
We denote JaK ∧JbK = JaKJbK = Ja∧bK (AND) , JaK ∨
JbK = JaK + JbK −JaKJbK = Ja ∨bK (OR) and JaK ⊕
JbK = JaK + JbK −2JaKJbK = Ja ⊕bK (XOR).
Signed integer types are defined as Z
hki
= {¯x ∈
Z | ¯x ∈ [−2
k−1
,2
k−1
−1]}. They are encoded in Z
q
by the function fld : Z
hki
7→ Z
q
, fld( ¯x) = ¯x mod q, for
a prime q > 2
k+κ
, where κ is the security parameter
(similar to two’s complement encoding). This method
enables efficient secure integer arithmetic using se-
cure arithmetic in Z
q
: for any ¯x
1
, ¯x
2
∈ Z
hki
and ∈
{+,−, ·}, we have ¯x
1
¯x
2
= fld
−1
(fld( ¯x
1
) fld( ¯x
2
));
also, if ¯x
2
| ¯x
1
then ¯x
1
/ ¯x
2
= fld
−1
(fld( ¯x
1
) ·fld( ¯x
2
)
−1
).
Signed fixed-point types are sets of rational num-
bers defined as Q
FX
hk, f i
= {˜x ∈ Q| ˜x = ¯x2
−f
, ¯x ∈ Z
hki
},
for f < k. They are obtained by sampling at 2
−f
in-
tervals the range of real numbers [−2
k−f −1
,2
k−f −1
−
2
−f
]. The value 2
−f
is the resolution of the fixed-
point type. Q
FX
hk, f i
is mapped to Z
hki
by the function
int : Q
FX
hk, f i
7→ Z
hki
, ¯x = int
f
( ˜x) = ˜x2
f
and encoded in
Z
q
as described above. Secure multiplication and di-
vision of fixed-point numbers require q > 2
2k+κ
.
Floating-point numbers ˆx ∈ Q
FL
hl,gi
are tuples
h¯v, ¯p,s,zi, where ¯v ∈ [2
`−1
,2
`
−1] ∪{0} is the un-
signed, normalized significand, ¯p ∈ Z
hgi
is the signed
exponent, s = ( ˆx < 0)? 1 : 0, and z = ( ˆx = 0)? 1 : 0.
The value of the number is ˆx = (1−2s)· ¯v ·2
¯p
. If ˆx = 0
then z = 1, ¯v = 0, and ¯p = −2
g−1
. This encoding of
ˆx = 0 simplifies secure addition with minimal nega-
tive effects on other operations. The integer signifi-
cand and exponent are encoded as described above.
The parameters k, f , ` and g are not secret. The
protocols work for any setting of these parameters that
satisfies the type definitions. The applications usually
need k ∈[32,128], k = 2 f , ` ∈ [24,64] and g ∈[8,15],
depending on range and accuracy requirements.
The floating-point protocols are constructed using
a subset of the building blocks introduced in (Cat-
rina and de Hoogh, 2010a; Catrina and Saxena, 2010),
enhanced by optimizations added in (Catrina, 2018).
All building blocks rely on the secure computation
model described above for their own security and se-
cure composition. We summarize in the following
their functionality and the optimizations
1
. Table 2
lists their online and precomputation complexity.
1
Further details are available in the Appendix.
Multiplication and Inner Product. Standard mul-
tiplication of Shamir-shared field elements requires an
interaction. However, this interaction can be avoided
in some cases. Denote JxK
u,i
the share of x owned by
P
i
, for a random polynomial of degree u; the default
value of the degree is t. The multiplication proto-
col computes JcK ← JaKJbK as follows (Cramer et al.,
2015): for all i ∈ [1, n], P
i
locally computes JaK
i
JbK
i
;
the result is JcK
2t,i
, a share of c for a non-random poly-
nomial of degree 2t (product of the polynomials used
to share a and b); then, P
i
shares the value JcK
2t,i
by
sending to the others JJcK
2t,i
K
j
, for j ∈ [1, n], j 6= i; fi-
nally, P
i
computes its own share JcK
i
from the received
shares, by Lagrange interpolation.
A first optimization applies to multiplications fol-
lowed by additive hiding: d ← Reveal(JaKJbK + JrK).
With standard protocols, this computation needs 2
rounds. We can avoid the first round by locally ran-
domizing the share products: for all i ∈ [1,n], party i
computes JcK
2t,i
←JaK
i
JbK
i
+ J0K
2t,i
, where J0K
2t,i
are
pseudo-random shares of 0 generated with PRZS(2t)
(Cramer et al., 2005). We denote JaK ∗JbK this local
operation. The computation can now be completed
with a single interaction: d ← RevealD(JaK ∗JbK +
JrK), where RevealD is the secret reconstruction pro-
tocol for polynomials of degree 2t.
This situation occurs very often. In particular,
many of the protocols discussed below use additive
hiding of the input. We add variants of these protocols
for input shared with a random polynomial of degree
2t, and distinguish them by the suffix ’D’. The differ-
ence is that they use RevealD instead of Reveal.
Another optimization is used to compute the in-
ner product of two vectors, JcK ←
∑
m
k=1
Ja
k
KJb
k
K, in
the protocol InnerProd: the parties locally compute
the inner product of their own shares and re-share the
result. Thus, InnerProd needs a single interaction (in-
stead of m interactions). If InnerProd is followed by
additive hiding of its output, we can also use the pre-
vious optimization. We call InnerProdD a variant that
locally computes JcK
2t,i
←
∑
m
k=1
Ja
k
K
i
Jb
k
K
i
+ J0K
2t,i
.
Multiplication and Division by 2
m
. The floating-
point arithmetic protocols are built using a small set
of related protocols that efficiently compute
¯
b = ¯a ·2
m
and ¯c ≈ ¯a/2
m
, for secret ¯a,
¯
b, ¯c ∈ Z
hki
and public or
secret integer m ∈[0,k −1].
If m is public we compute ¯a ·2
m
without interac-
tion. To compute ¯a/2
m
, we use the protocols Div2m
and Div2mP, introduced in (Catrina and de Hoogh,
2010a; Catrina and Saxena, 2010). Div2m rounds
to −∞ and Div2mP rounds probabilistically to the
nearest integer. We denote their outputs b¯a/2
m
c
and b¯a/2
m
e, respectively. Div2mP computes ¯c =
Efficient Secure Floating-point Arithmetic using Shamir Secret Sharing
51

Table 2: Complexity of the main building blocks used in this paper, for inputs ¯a, ¯x ∈ Z
hki
.
Protocol Task Rounds Inter. op. Precomp.
Div2m(JaK,k,m) b¯a/2
m
c 3 m + 2 3m
Div2mP(JaK,k,m) b¯a/2
m
e 1 1 m
Div2(JaK,k) b¯a/2c 1 1 1
LTZ(JaK,k) ( ¯a < 0)? 1 : 0 3 k + 1 3k
EQZ(JaK,k) ( ¯a = 0)? 1 : 0 3 logk + 2 k + 3log k
SufOr({Ja
i
K}
k
i=1
) {
W
k
j=i
a
j
}
k
i=1
2 2k −1 3k
SufMul({Ja
i
K}
k
i=1
) {
∏
k
j=i
a
j
}
k
i=1
1 k 2k −1
PreDiv2m(JaK,k,m) {b¯a/2
i
c}
m
i=1
3 2m + 1 4m
PreDiv2mP(JaK,k,m) {b¯a/2
i
e}
m
i=1
1 1 m
Int2MaskG(JxK,k, m) {( ¯x = i)? 1 : 0}
k−1
i=0
5 k + m + 2 2k + 6m
b¯a/2
m
c+u, where u = 1 with probability p =
¯a mod 2
m
2
m
(e.g., if ¯a = 46 and m = 3 then ¯a/2
m
= 5.75; the out-
put is ¯c = 6 with probability p = 0.75 or ¯c = 5 with
probability 1 − p = 0.25). For both protocols, the
rounding error is |δ| < 1 and the output is exact if
2
m
divides ¯a. Div2mP is much more efficient (Ta-
ble 2) and its output is likely more accurate. Div2
is a more efficient solution for b¯a/2c. Finally, the
comparison protocol LTZ uses Div2m to compute
s = ( ¯a < 0)? 1 : 0 = −b¯a/2
k−1
c.
If m is secret we have to extend the collection of
building blocks in (Catrina and de Hoogh, 2010a).
The goal is to use the following constructions. We
start by computing the secret bits {x
i
}
k−1
i=0
, x
i
= (m =
i)? 1 : 0. This allows us to locally compute 2
m
=
∑
k−1
i=0
x
i
2
i
and then ¯a ·2
m
. Moreover, we can use a sim-
ilar method for ¯a/2
m
: compute the secret integers
¯
d
i
=
{b¯a/2
i
c}
k−1
i=0
and the inner product ¯a/2
m
=
∑
k−1
i=0
x
i
¯
d
i
.
The protocol PreDiv2m, suggested in (Catrina,
2018), is a generalization of Div2m that efficiently
computes {b¯a/2
i
c}
m
i=1
with secret inputs and outputs.
Surprisingly, it performs a much more complex task
than Div2m in the same number of rounds, with a
modest increase of the communication complexity
(Table 2). PreDiv2mP is a generalization of Div2mP
that computes {b¯a/2
i
e}
m
i=1
with probabilistic round-
ing to nearest, with the same complexity as Div2mP.
Protocol 1, Int2MaskG, is a generic construction
for computing {x
i
}
k−1
i=0
, x
i
= ( ¯x = i)? 1 : 0, using La-
grange polynomial interpolation in Z
q
, q > k, adapted
to our tasks. Given a secret ¯x ∈ [0,2
m−1
−1] and pub-
lic k ≤ 2
m−1
, it returns the secret bits {x
i
}
k−1
i=0
such
that x
i
= 1 if ¯x < k and i = ¯x, otherwise x
i
= 0.
Steps 1-2 map ¯x to ¯x
0
= ( ¯x < k)? ¯x : k, ¯x
0
∈ [0,k].
Let α = ¯x
0
+ 1. We compute {x
i
}
k−1
i=0
by evaluating
the functions f
i
: [1, k + 1] → {0,1}, f
i
(α) = (α =
i + 1)? 1 : 0, for i ∈ [0,k −1], using their interpolation
polynomials f
i
(α) =
∑
k
j=0
a
i, j
α
j
. The coefficients a
i, j
are pre-computed from public information (the points
that define {f
i
}
k−1
i=0
). Steps 3-4 compute {α
i
}
k
i=1
using
PreMul and then x
i
= f
i
(α), for i ∈ [0,k −1] (we set
α = ¯x
0
+ 1 because PreMul requires non-zero inputs).
The online complexity is 5 rounds and k + m + 2 in-
teractive operations.
P 1: Int2MaskG(JxK,k,m).
JdK ← LTZ(JxK −k,m + 1);1
Jx
0
K ← JdKJxK+ (1 −JdK)k;2
{Jy
j
K}
k
j=1
← PreMul({Jx
0
K + 1}
k
i=1
);
3
foreach i ∈ [0,k −1] do4
Jx
i
K ← a
i,0
+
∑
k
j=1
a
i, j
Jy
j
K;
5
return {Jx
i
K}
k−1
i=0
;6
3 SECURE FLOATING-POINT
ARITHMETIC
We present a family of floating-point arithmetic pro-
tocols for addition, subtraction, multiplication, divi-
sion, square root, and comparison. We focus on so-
lutions that offer the best tradeoffs for the entire fam-
ily and a broader range of applications. All protocols
are constructed using the techniques discussed in Sec-
tion 2, that support secure protocol composition. The
same security arguments apply to the entire family, so
we do not repeat them for each protocol.
Converting Fixed-point Numbers to Floating-
point Numbers. Given a fixed-point number ˜a ∈
Q
FX
hk, f i
, Protocol 2, FX2FL, computes h¯v, ¯p,s, zi so that
ˆa = (1 −2s)¯v2
¯p
∈Q
FL
h`,gi
, ˆa ≈ ˜a and z = ( ˆa = 0)? 1 : 0,
with secret input and output. In particular, for f = 0,
the input is an integer ¯a ∈ Z
hki
and the output is
ˆa ∈ Q
FL
h`,gi
so that ˆa ≈ ¯a. FX2FL is also used for nor-
malizing the output of floating-point arithmetic proto-
cols.
SECRYPT 2019 - 16th International Conference on Security and Cryptography
52

The computation can be summarized as follows.
Let ¯a = ˜a2
f
. Recall that ¯a ∈ [−(2
k−1
−1),2
k−1
−1]
and ¯v ∈ [2
`−1
,2
`
−1] ∪{0}. If ¯a = 0 we set ¯v = 0
and ¯p = −2
g−1
. Otherwise, |¯a| ∈ [2
m−1
,2
m
−1] for
some secret m ∈ [1,k −1] and we have to compute
¯v = |¯a|2
`−m
and ¯p = −f −` + m. When k −1 > ` we
have 2 cases: if m ≤ ` then ¯v = |¯a|2
`−m
; if m > ` then
¯v = b|¯a|/2
−`+m
c. If k −1 ≤ ` then m ≤ ` and hence
¯v = |¯a|2
`−m
. Therefore, if m ≤ ` the output is ˆa = ˜a,
otherwise ˆa ≈ ˜a, with relative error ε < 2
−`
, due to
the truncation of ¯a.
Steps 1-6 compute s = ( ¯a < 0)? 1 : 0 and z =
( ¯a = 0)? 1 : 0, together with data used in steps 6-
10 for computing ¯v and ¯p: {
¯
b
i
}
k−2
i=0
= {b|¯a|/2
i
c}
k−2
i=0
,
{a
i
}
k−2
i=0
, the binary encoding of |¯a|, and {c
i
}
k−2
i=0
=
{
W
k−2
j=i
a
j
}
k−2
i=0
. Note that
¯
b
0
= ¯a(1 −2s) = |¯a| and
c
0
=
W
k−2
j=0
a
j
= 1 −z. By using PreDiv2mD instead
of PreDiv2m, the multiplication JaK(1−2JsK) is com-
puted without interaction, saving one round.
P 2: FX2FL(JaK,k, f ,`, g).
JsK ← LTZ(JaK,k); Js
0
K ← 1 −2JsK;1
{Jb
i
K}
k−2
i=0
← PreDiv2mD(JaK ∗Js
0
K,k, k −2);2
Ja
k−2
K ← Jb
k−2
K;3
foreach i ∈ [0,k −3] do Ja
i
K ← Jb
i
K −2Jb
i+1
K;4
{Jc
i
K}
k−2
i=0
← SufOr({Ja
i
K}
k−2
i=0
);5
JzK ← 1 −Jc
0
K;6
foreach i ∈ [0,k −3] do Jd
i
K ← Jc
i
K −Jc
i+1
K;7
Jd
k−2
K ← Jc
k−2
K;8
if k −1 > ` then JvK ← Jb
0
K
∑
`−1
i=0
2
`−i−1
Jd
i
K+9
∑
k−`−2
i=0
Jd
`+i
KJb
i+1
K;
else JvK ← 2
`−k+1
Jb
0
K
∑
k−2
i=0
2
k−i−2
Jd
i
K;10
JpK ← (−f −`)(1 −JzK) +
∑
k−2
i=0
Jc
i
K −JzK2
g−1
;11
return (JvK,JpK,JsK,JzK);12
Steps 7-10 compute ¯v. We start by computing d
i
=
(i = m −1)? 1 : 0, for i ∈ [0,k −2]. If k −1 > ` we
have to compute ¯v
1
= |¯a|2
`−m
, if m ∈ [1, `], and ¯v
2
=
b|¯a|/2
−`+m
c, if m ∈[`+1, k −1]. At least one of these
values is 0, so step 9 obliviously handles both cases
by computing ¯v
1
=
¯
b
0
∑
`−1
i=0
2
`−i−1
d
i
= |¯a|2
`−m
, ¯v
2
=
∑
k−`−2
i=0
d
`+i
¯
b
i+1
=
¯
b
m−`
= b|¯a|/2
−`+m
c and ¯v = ¯v
1
+
¯v
2
. If k ≤ ` + 1 then m ≤` and ¯v = |¯a|2
`−m
. This case
is computed in step 10: ¯v = 2
`−k+1
¯
b
0
∑
k−2
i=0
2
k−i−2
d
i
=
2
`−k+1
|¯a|2
k−m−1
= |¯a|2
`−m
.
Step 11 computes ¯p. If ¯a 6= 0 then
∑
k−2
i=0
c
i
= m,
since c
i
= 1 for i ∈[0,m −1] and c
i
= 0 for i ∈[m,k −
2]; otherwise,
∑
k−2
i=0
c
i
= 0. Therefore, if ¯a 6= 0 then
z = 0 and ¯p = −f −` + m, otherwise z = 1 and ¯p =
−2
g−1
, as required.
The online complexity is 9 rounds and 5k + 3 in-
teractive operations. If the sign is not secret, we can
skip step 1 and the complexity becomes 6 rounds
and 4k + 2 operations. FX2FL is simpler and more
efficient than the protocol given in (Aliasgari et al.,
2013), which needs log k + 12 rounds and more than
(logk + 3)k operations. The improvement is due to
more efficient solutions enabled by PreDiv2m for
computing the secret index m and the multiplication
and division by secret 2
|l−m|
.
We also need FX2FLE, a general tool for normal-
izing the output of floating-point arithmetic protocols.
FX2FLE is a variant of FX2FL that takes a secret in-
teger ¯x as additional input and returns h¯v, ¯p, s, zi so
that ˆa = (1 −2s) ¯v2
¯p
∈ Q
FL
h`,gi
and ˆa ≈ 2
¯x
˜a. The differ-
ence is that step 11 computes JpK ←(JxK +JmK − f −
`)(1−JzK)−JzK2
g−1
, in parallel with the computation
of ¯v (the round complexity is the same).
Floating-point Addition and Subtraction. Proto-
col 3, AddFL, computes ˆa = ˆa
1
+ ˆa
2
, for secret
ˆa
1
, ˆa
2
, ˆa ∈ Q
FL
h`,gi
, ˆa
1
= (1 − 2s
1
) ¯v
1
2
¯p
1
, ˆa
2
= (1 −
2s
2
) ¯v
2
2
¯p
2
, and ˆa = (1−2s) ¯v2
¯p
. AddFL can also com-
pute ˆa = ˆa
1
− ˆa
2
by setting s
2
= 1 −s
2
.
The basic idea is to align the inputs’ radix point,
add the significands and normalize the result using
FX2FLE. To simplify the notation, suppose ˆa
1
≥ 0,
ˆa
2
≥ 0, and ¯p
1
≥ ¯p
2
. We want ¯v and ¯p so that
¯v2
¯p
≈ ¯v
1
2
¯p
1
+ ¯v
2
2
¯p
2
. We can align to the larger ex-
ponent, by setting ¯p = ¯p
1
and ¯v = ¯v
1
+ b¯v
2
/2
¯p
1
− ¯p
2
c,
or to the smaller exponent, by setting ¯p = ¯p
2
and ¯v =
¯v
1
2
¯p
1
− ¯p
2
+ ¯v
2
. Which method is better? Multiplica-
tion by secret 2
¯p
1
− ¯p
2
is simpler than division, but here
it is inefficient, since the result can be huge. One so-
lution is to combine the methods: use the first method
when ¯p
1
− ¯p
2
≥ `, because b¯v
2
/2
¯p
1
− ¯p
2
c = 0; other-
wise, use the second method, because ¯v
1
2
¯p
1
− ¯p
2
< 2
2`
.
AddFL uses the first method, which can be imple-
mented more efficiently with the new building blocks.
Steps 1-3 swap the inputs if ¯p
1
< ¯p
2
: ( ¯v
0
1
, ¯p
0
1
) =
( ¯p
1
< ¯p
2
)? ((1 − 2s
2
) ¯v
2
, ¯p
2
) : ((1 −2s
1
) ¯v
1
, ¯p
1
) and
( ¯v
0
2
, ¯p
0
2
) = ( ¯p
1
< ¯p
2
)? ((1 − 2s
1
) ¯v
1
, ¯p
1
) : ((1 −
2s
2
) ¯v
2
, ¯p
2
). Swap computes (c = 1)? (y,x) : (x, y)
with secret inputs and outputs. Since we encode ˆa = 0
as ¯v = 0 and ¯p = −2
g−1
(smallest value), null operands
are not special cases: if ˆa
2
= 0 then ¯p
1
≥ ¯p
2
and
¯v
2
= 0, so the protocol sets ¯p = ¯p
1
and ¯v = ¯v
1
; if
ˆa
1
= 0, ¯p
1
< ¯p
2
and the operands are swapped.
Let ∆ = ¯p
0
1
− ¯p
0
2
≥0. Steps 4-6 compute {x
i
}
`−1
i=0
=
{(∆ = i)? 1 : 0}
`−1
i=0
and {
¯
d
i
}
`−1
i=0
= {b¯v
0
2
/2
i
c}
`−1
i=0
(in
parallel), then step 7 computes ¯v
0
3
= ¯v
0
1
+
∑
`−1
i=0
x
i
¯
d
i
=
¯v
0
1
+ b¯v
0
2
/2
∆
e. Step 8 normalizes the result. If s
1
6= s
2
and ∆ = 1, |¯v
1
− ¯v
2
/2| can be close to the rounding
error, compromising the accuracy. This is avoided by
setting ¯v
0
1
= 2 ¯v
1
, ¯v
0
2
= 2 ¯v
2
, so that the division is exact,
Efficient Secure Floating-point Arithmetic using Shamir Secret Sharing
53

and invoking FX2FLE with k = `+ 3 and ¯p
0
1
= ¯p
0
1
−1.
P 3: AddFL({Jv
i
K,Jp
i
K,Js
i
K}
2
i=1
).
JcK ← LTZ(Jp
1
K −Jp
2
K,g + 1);1
Jv
1
K ← Jv
1
K(1 −2Js
1
K); Jv
2
K ← Jv
2
K(1 −2Js
2
K);2
{Jv
0
i
K,Jp
0
i
K}
2
i=1
← Swap(Jc
0
K,{Jv
i
K,Jp
i
K}
2
i=1
);3
{Jx
i
K}
`−1
i=0
← Int2MaskG(Jp
0
1
K −Jp
0
2
K,`, g + 1);4
Jd
0
K ← Jv
0
2
K;5
{Jd
i
K}
`−1
i=1
← PreDiv2mP(Jv
0
2
K,` + 1,` −1);6
Jv
0
3
K ← Jv
0
1
K +
∑
`−1
i=0
Jx
i
KJd
i
K;7
(JvK,JpK,JsK,JzK) ←8
FX2FLE(Jv
0
3
K,Jp
0
1
K,` + 2,0,`,g);
return (JvK,JpK,JsK,JzK);9
The online complexity AddFL is 19 rounds and
6`+2g +26 interactive operations. For operands with
the same, known sign the complexity is 16 rounds and
5` + 2g + 10 operations (due to simpler normaliza-
tion). With minor changes, AddFL also works when
one operand is public, with roughly the same com-
plexity. The protocol proposed in (Aliasgari et al.,
2013) needs log ` + 30 rounds and more than (log ` +
14)` + 9g operations. The improvement is due to
more efficient building blocks and the simpler algo-
rithm enabled by PreDiv2mP and Int2MaskG.
Floating-point multiplication. Protocol 4, MulFL,
computes ˆa ≈ ˆa
1
ˆa
2
, for secret ˆa
1
, ˆa
2
, ˆa ∈ Q
FL
h`,gi
, ˆa
1
=
(1 −2s
1
) ¯v
1
2
¯p
1
, ˆa
2
= (1 −2s
2
) ¯v
2
2
¯p
2
, ˆa = (1 −2s) ¯v2
¯p
.
The protocol computes ¯v
3
= ¯v
1
¯v
2
and ¯p
3
= ¯p
1
+ ¯p
2
and normalizes the result. Since ¯v
3
∈ [2
2`−2
,2
2`
−
2
`+1
+ 1] ∪{0}, normalization is easy: if ¯v
3
< 2
2`−1
then ¯v = b¯v
3
/2
`−1
c and ¯p = ¯p
3
+ ` − 1, otherwise
¯v = b¯v
3
/2
`
c and ¯p = ¯p
3
+`. Also, we efficiently com-
pute s = s
1
⊕s
2
, z = z
1
∨z
2
, and ¯p = ¯p(1−z)−z2
g−1
.
We can reduce the communication complexity by
modifying the algorithm as follows: compute ¯v
3
=
b¯v
1
¯v
2
/2
`−1
c ∈ [2
`−1
,2
`+1
−2
2
] ∪{0} and ¯p
3
= ¯p
1
+
¯p
2
+`−1; if ¯v
3
< 2
`
then set ¯v = ¯v
3
and ¯p = ¯p
3
; other-
wise, set ¯v = b¯v
3
/2cand ¯p = ¯p
3
+1. A similar method
is used in (Aliasgari et al., 2013). Our protocol is an
optimized variant.
Steps 1-3 compute h¯v
3
, ¯p
3
,s,zi as explained above
and step 4 normalizes the result using Protocol 5,
NormFLS. We use fast truncation with Div2mP, be-
cause ¯v
3
is in the range [2
`−1
,2
`+1
−1]∪{0} required
for simple normalization regardless of the rounding
method (actually, we use Div2mPD, so that the mul-
tiplication Jv
1
KJv
2
K is computed without interaction).
NormFLS normalizes ¯v ∈ [2
`−1
,2
`+1
− 1] ∪{0}
using the algorithm described above: it computes (in
parallel) b = ( ¯v < 2
`
)? 1 : 0 and ¯v
00
= b¯v/2c, then
¯v
0
= (b = 1)? ¯v : ¯v
00
and ¯p
0
= (b = 1)? ¯p(1 −z) :
( ¯p + 1)(1 −z), ¯p
0
= ¯p
0
−z2
g−1
.
The online complexity of MulFL is 5 rounds and
` + 9 interactive operations (instead of 11 rounds and
8`+10 operations reported in (Aliasgari et al., 2013)).
MulFL also works when one of the operands is public,
with minor changes and slightly lower complexity.
P 4: MulFL({Jv
i
K,Jp
i
K,Js
i
K,Jz
i
K}
2
i=1
).
Jv
3
K ← Div2mPD(Jv
1
K ∗Jv
2
K,2`,` −1);1
JsK ← Js
1
K ⊕Js
2
K; JzK ← Jz
1
K ∨Jz
2
K;2
Jp
3
K ← Jp
1
K + Jp
2
K + ` −1;3
(JvK,JpK) ← NormFLS(Jv
3
K,Jp
3
K,JzK,` + 1,g);4
return (JvK,JpK,JsK,JzK);5
P 5: NormFLS(JvK,JpK,JzK, `, g).
JbK ← LTZ(JvK −2
`
,` + 1);1
Jv
00
K ← Div2(JvK,` + 1);2
Jv
0
K ← JbKJvK + (1 −JbK)Jv
00
K;3
Jp
0
K ← (JpK + 1 −JbK)(1 −JzK) −JzK2
g−1
;4
return (Jv
0
K,Jp
0
K);5
Floating-point Division. Protocol 6, DivFL, com-
putes ˆa ≈ ˆa
1
/ ˆa
2
, for secret ˆa
1
, ˆa
2
, ˆa ∈ Q
FL
h`,gi
, ˆa
1
=
(1 −2s
1
) ¯v
1
2
¯p
1
, ˆa
2
= (1 −2s
2
) ¯v
2
2
¯p
2
, ˆa
2
6= 0, and ˆa =
(1 −2s)¯v2
¯p
. DivFL divides the significands using se-
cure fixed-point arithmetic and normalizes the result.
Let ˜v
1
= ¯v
1
2
−`
, ˜v
2
= ¯v
2
2
−`
and ˜v
3
= ˜v
1
/ ˜v
2
. Observe
that ˜v
1
, ˜v
2
∈ [0.5,1) ∪{0}, ˜v
2
6= 0 and ˜v
3
∈ (0.5,2) ∪
{0}. Step 1 computes ˜v
3
using Protocol 7, DivGS, and
steps 2-3 compute ¯p
3
= ¯p
1
− ¯p
2
−` and s = s
1
⊕s
2
(z = z
1
). DivGS returns ¯v
3
∈[2
`−1
,2
`+1
−1]∪{0} and
¯v
3
= ˜v
3
2
`
, so we can use NormFLS for normalization.
The protocol DivGS is based on a variant of Gold-
schmidt’s division algorithm (Markstein, 2004). Let
a,b ∈ R, b 6= 0. The algorithm starts with an initial
approximation w
0
≈ 1/b, with relative error ε
0
< 1,
and computes a/b iteratively, as follows: c
0
= aw
0
,
d
0
= ε
0
= 1 −bw
0
; for i > 0 do c
i
= c
i−1
(1 + d
i−1
),
d
i
= d
2
i−1
. After i iterations it obtains c
i
≈ a/b with
relative error ε
2
i
0
. If b ∈ [0.5, 1), we can start with
w
0
= 2.9142 − 2b, a linear approximation of 1/b
with relative error ε
0
< 0.08578 (Ercegovac and Lang,
2003). It provides about 3.5 exact bits, so for `-bit in-
puts the algorithm needs θ = dlog
`
3.5
e iterations.
DivGS uses this algorithm to compute ˜v
3
≈ ˜v
1
/ ˜v
2
with absolute error δ < 2
−`
, for ˜v
1
, ˜v
2
∈[0.5,1) ∪{0},
˜v
2
6= 0, and ˜v
3
∈ [0.5, 2) ∪{0}. The inputs and the
output are fixed-point numbers with resolution 2
−`
,
encoded as ¯v
1
, ¯v
2
∈ [2
`−1
,2
`
−1] ∪{0}, ¯v
2
6= 0, and
¯v
3
∈[2
`−1
,2
`+1
−1]∪{0}. Fixed-point multiplication
with resolution 2
−`
is computed as double-precision
integer multiplication followed by truncation that cuts
SECRYPT 2019 - 16th International Conference on Security and Cryptography
54

off the least significant ` bits. The rounding error due
to truncation is δ
t
< 2
−`
.
P 6: DivFL({Jv
i
K,Jp
i
K,Js
i
K,Jz
i
K}
2
i=1
).
Jv
3
K ← DivGS(Jv
1
K,Jv
2
K,`);1
JsK ← Js
1
K ⊕Js
2
K;2
Jp
3
K ← Jp
1
K −Jp
2
K −`;3
(JvK,JpK) ← NormFLS(Jv
3
K,Jp
3
K,Jz
1
K,`, g);4
return (JvK,JpK,JsK,Jz
1
K);5
P 7: DivGS(Jv
1
K,Jv
2
K,`).
θ ← dlog
`
3.5
e; m = 4; k ← ` + m;
1
Jv
1
K ← 2
m
Jv
1
K; Jv
2
K ← 2
m
Jv
2
K;2
JwK ← fld(int
k
(2.9142)) −2Jv
2
K;3
JcK ← Div2mPD(Jv
1
K ∗JwK, 2k + 1,k);4
JdK ← Div2mPD(Jv
2
K ∗JwK, 2k + 1,k);5
JdK ← fld(int
k
(1.0)) −JdK;6
foreach i ∈ [1,θ −1] do7
JcK ← JcK + Div2mPD(JcK ∗JdK, 2k + 1, k);8
Jd
0
K ← Div2mPD(JdK∗JdK,2k + 1,k);9
JdK ← Jd
0
K;
Jv
3
K ← JcK + Div2mPD(JcK ∗JdK, 2k + 1, k + m);10
return Jv
3
K;11
We prefer this algorithm to other variants (e.g.,
Newton-Raphson) because the two multiplications of
an iteration can be computed in parallel. On the
other hand, its iterations are not self-correcting, so
rounding errors accumulate, reducing the accuracy
of the result. Moreover, if the error before the last
truncation is |δ| ≥ 2
−`
, ¯v
3
may be outside the range
[2
`−1
,2
`+1
−1] ∪{0} required by fast normalization
with NormFLS. For instance, if ¯v
1
= 2
`−1
and ¯v
2
=
2
`
−1 the output can be ¯v
3
< 2
`−1
( ˜v
1
= 0.5, ˜v
2
≈ 1,
˜v
3
≈0.5); also, if ¯v
1
= 2
`
−1 and ¯v
2
= 2
`−1
, the output
can be ¯v
3
> 2
`+1
−1 ( ˜v
1
≈ 1, ˜v
2
= 0.5, ˜v
3
≈ 2).
Let ∆ be the accumulated error before the last
truncation and suppose ∆ < γ ·2
−`
for variables with
`-bit fractional part. The error can be reduced by
terminating the algorithm with a modified Newton-
Raphson iteration (Markstein, 2004); this requires ad-
ditional rounds. DivGS reduces the error to ∆ < 2
−`
by increasing the fractional part to ` + m bits, with
m = dlogγe. For our initial approximation, error anal-
ysis shows that we need m = 3 for ` ∈ [8,14] (θ = 2)
and m = 4 for ` ∈[15, 112] (θ ∈[3, 5]). For simplicity,
we set m = 4 in the pseudocode
2
.
DivGS computes Goldschmidt’s iterations for se-
cret inputs and outputs. Steps 1-3 initialize the algo-
rithm: compute θ, m, and k = `+m; set ¯v
1
= ¯v
1
2
m
and
¯v
2
= ¯v
2
2
m
to obtain fixed-point numbers with frac-
2
The error bound is computed starting from c
θ
= c
0
(1 +
d
0
)(1 + d
1
). .. (1 + d
θ−1
) and assuming δ
t
= 2
−`
for every
multiplication, including c
0
= aw
0
and d
0
= 1 −bw
0
.
tional part of ` + m bits; compute ¯w =
¯
β −2 ¯v
2
, the
initial approximation of 1/ ˜v
2
. Steps 4-6 compute in
parallel the initial values for the iteration variables:
¯c = ¯v
1
¯w/2
k
and
¯
d = (1 − ¯v
2
) ¯w/2
k
. Steps 7-10 are the
θ iterations of the algorithm. An iteration computes in
parallel ¯c = ¯c + b( ¯c
¯
d)/2
k
e and
¯
d
0
←b
¯
d
2
/2
k
e and then
sets
¯
d =
¯
d
0
. The result is in the interval required for
fast normalization regardless of the rounding method
of the last truncation, so we can use Div2mP.
The online complexity of DivFL is 5 + θ rounds
and ` + 2θ + 7 interactive operations (e.g., 9 rounds
and ` + 16 operations for ` ∈ [29,56]). DivFL is more
accurate and more efficient than the protocol given
in (Aliasgari et al., 2013), which does not address
the critical accuracy issues discussed above and needs
2log` + 7 rounds and 2(` + 2)log ` + 3` + 8 opera-
tions. The complexity improvement is due to better
initial approximation (less iterations) and more effi-
cient secure fixed-point arithmetic.
An alternative approach to floating-point division
with secret inputs and output, suggested in related
work, is to first compute the reciprocal ˆa
0
2
= 1/ ˆa
2
and then ˆa
3
= ˆa
1
· ˆa
0
2
. However, DivFL has the same
complexity as a protocol that computes 1/ ˆa
2
and
avoids the additional secure floating-point multiplica-
tion. Also, with minor changes, DivFL can compute
ˆa
3
= ˆa
1
/ ˆa
2
for public ˆa
1
and secret ˆa
2
and ˆa
3
, with
slightly lower complexity. Finally, for public ˆa
2
and
secret ˆa
1
and ˆa
3
, division consists of secure multipli-
cation between ˆa
1
and public 1/ ˆa
2
.
Square Root. Protocol 8, SqrtFL, computes ˆa ≈
p
|ˆa
1
|, for secret ˆa
1
, ˆa ∈ Q
FL
h`,gi
, |ˆa
1
| = ¯v
1
2
¯p
1
and ˆa =
¯v2
¯p
. SqrtFL is similar to DivFL and surprisingly ef-
ficient. The computation is based on the following
remark. Let ˜v
1
= ¯v
1
2
−`
∈ [0.5, 1) ∪{0}, encoded as
˜v
1
∈ Q
FX
h`,`i
. Also, let ¯p
0
1
= ¯p
1
+ `, u = ¯p
0
1
mod 2, and
¯p
2
= b ¯p
0
1
/2c. Observe that
p
|ˆa
1
| =
p
˜v
1
2
¯p
1
+`
, so
if u = 0 then
p
|ˆa
1
| =
√
˜v
1
2
¯p
2
, otherwise
p
|ˆa
1
| =
√
2 ˜v
1
2
¯p
2
=
√
2
2
√
˜v
1
2
¯p
2
+1
.
SqrtFL computes
√
˜v
1
using Protocol 9, SqrtGS,
based on Goldschmidt’s square root algorithm (Mark-
stein, 2004). Let a ∈ R, a > 0, and w
0
≈
1
√
a
such that
aw
2
0
∈ [
1
2
,
3
2
]. The algorithm computes both
√
a and
1
2
√
a
iteratively, as follows: b
0
= aw
0
, c
0
= w
0
/2; for
i > 0 do d
i−1
= 0.5 −b
i−1
c
i−1
, b
i
= b
i−1
(1 + d
i−1
),
c
i
= c
i−1
(1 + d
i−1
). After i iterations it obtains b
i
≈
√
a and c
i
≈
1
2
√
a
with relative error ε
2
i
0
. If a ∈[0.5, 1),
we can take w
0
= 1.7877−0.81a, a linear approxima-
tion of
1
√
a
with relative error ε
0
< 0.0223. Since w
0
provides almost 5.5 exact bits, the algorithm needs
θ = dlog
`
5.5
e iterations for an `-bit input.
Efficient Secure Floating-point Arithmetic using Shamir Secret Sharing
55

SqrtGS computes
˜
b ≈
√
˜v for ˜v ∈[0.5, 1)∪{0}and
˜
b ∈ [
√
2
2
,1) ∪{0} using secure fixed-point arithmetic.
Rounding errors are handled like in DivGS, by ex-
tending the fractional part to k = ` +m bits. Steps 2-3
compute ˜w = 1.7877 −0.81 ˜v, the linear approxima-
tion of
1
√
˜v
. Steps 4-5 compute (in parallel) the initial
values of the variables,
¯
b = b¯v ¯w/2
k
e and ¯c = b¯v/2c.
The steps 6-11 are the θ iterations of the algorithm.
An iteration computes
¯
d = int
k
(0.5) −b
¯
b ¯c/2
k
e and
then
¯
b =
¯
b + b
¯
b
¯
d/2
k
e and ¯c = ¯c + b¯c
¯
d/2
k
e (steps 8-
9 in parallel). The output preserves the higher preci-
sion, so that SqrtFL can accurately compute
√
2
2
√
˜v.
P 8: SqrtFL(Jv
1
K,Jp
1
K,Jz
1
K).
m = 4; k ← ` + m;1
Jv
2
K ← SqrtGS(2
m
Jv
1
K,`, k);2
Jv
0
2
K ← Div2mP(fld(int
k
(
√
2/2))Jv
2
K,2k, k + m);3
Jv
2
K ← Div2mP(Jv
2
K,k + m,m);4
Jp
0
1
K ← Jp
1
K + `; Jp
2
K ← Div2(Jp
0
1
K,g + 1);5
JuK ← Jp
0
1
K −2Jp
2
K;6
JvK ← (1 −JuK)Jv
2
K + JuKJv
0
2
K;7
JpK ← (Jp
2
K −` + JuK)(1 −Jz
1
K) −2
g−1
Jz
1
K;8
return (JvK,JpK,Jz
1
K);9
P 9: SqrtGS(JvK,`,k).
θ ← dlog
`
5.5
e; α ← fld(int
k
(0.5));
1
JwK ← Div2mP(fld(int
k
(0.81))JvK,2k,k);2
JwK ← fld(int
k
(1.7877)) −JwK;3
JbK ← Div2mPD(JvK ∗JwK,2k + 1,k );4
JcK ← Div2(JwK,k + 1);5
foreach i ∈ [1,θ −1] do6
JdK ← α −Div2mPD(JbK ∗JcK,2k + 1,k);7
JbK ← JbK + Div2mPD(JbK ∗JdK, 2k + 1, k);8
JcK ← JcK + Div2mPD(JcK ∗JdK, 2k + 1, k);9
JdK ← α −Div2mPD(JbK ∗JcK,2k + 1,k);10
JbK ← JbK + Div2mPD(JbK ∗JdK, 2k + 1, k);11
return JbK;12
SqrtFL computes the square root of |ˆa
1
| as fol-
lows. Let ˜v
2
≈
√
˜v
1
∈ [
√
2
2
,1) ∪{0} and ˜v
0
2
≈
√
2
2
˜v
2
∈
[0.5,
√
2
2
) ∪{0}, encoded as ˜v
2
, ˜v
0
2
∈ Q
FX
hk,ki
. Steps 2-4
compute ¯v
2
and ¯v
0
2
using SqrtGS, and steps 5-6 com-
pute ¯p
0
1
, ¯p
2
, and u. If u = 0 then
p
|ˆa
1
| = ˜v
2
2
¯p
2
,
so we set ¯v = b¯v
2
/2
m
e and ¯p = ¯p
2
−`. Otherwise,
p
|ˆa
1
|= ˜v
0
2
2
¯p
2
+1
; we compute ¯µ = int
k
(
√
2
2
) and ¯v
0
2
=
(¯µ ¯v
2
)/2
k
and set ¯v = b¯v
0
2
/2
m
e and ¯p = ¯p
2
−` + 1.
The two cases are obliviously computed in steps 7-
8: ¯v = (1 −u) ¯v
2
+ u ¯v
0
2
and ¯p = ¯p
2
−` + u. The result
is already normalized.
The online complexity of SqrtFL is 4 + 2θ rounds
and, surprisingly, only 3θ + 7 interactive operations
(e.g., θ = 3 for ` ∈ [24,45]). SqrtFL is much more ef-
ficient than the protocol suggested in (Aliasgari et al.,
2013), that computes Goldschmidt’s iterations using
floating-point protocols.
Floating-point comparison. Protocol 10, LTFL,
computes c = ( ˆa
1
< ˆa
2
)? 1 : 0 for ˆa
1
, ˆa
2
∈ Q
FL
h`,gi
,
ˆa
1
= (1−s
1
) ¯v
1
2
¯p
1
and ˆa
2
= (1−s
2
) ¯v
2
2
¯p
2
, with secret
inputs and output. The protocol is based on the fol-
lowing idea. Let ¯v
0
1
= (1 −s
1
) ¯v
1
, ¯v
0
2
= (1 −s
2
) ¯v
2
and
ˆ
d = ˆa
1
− ˆa
2
= 2
¯p
2
( ¯v
0
1
2
¯p
1
− ¯p
2
− ¯v
0
2
). We want to com-
pute c = (
ˆ
d < 0)? 1 : 0. Also, let z
p
= ( ¯p
1
= ¯p
2
)? 1 : 0,
c
−
p
= ( ¯p
1
< ¯p
2
)? 1 : 0, c
+
p
= ( ¯p
1
> ¯p
2
)? 1 : 0 and
c
−
v
= ( ¯v
0
1
< ¯v
0
2
)? 1 : 0. Observe that
ˆ
d < 0 if and
only if one of the following mutually exclusive con-
ditions holds: ¯p
1
= ¯p
2
and ¯v
1
< ¯v
2
; ¯p
1
< ¯p
2
and
s
2
= 0; ¯p
1
> ¯p
2
and s
1
= 1. Therefore, the output
is c = z
p
c
−
v
+ c
−
p
(1 −s
2
) + c
+
p
s
1
(inner product).
We could compute c
−
p
and z
p
, using the protocols
LTZ and EQZ (Catrina and de Hoogh, 2010a), and
then c
+
p
= (1 − c
−
p
)(1 −z
p
). Instead, we introduce
Protocol 11, CmpZ, that computes more efficiently
the triple comparison. Thus, we obtain a simpler and
more efficient solution for LTFL: steps 1-2 compute
c
−
v
using LTZD, step 3 computes c
−
p
, c
+
p
and z
p
using
CmpZ, and step 4 computes the output.
P 10: LTFL({Jv
i
K,Jp
i
K,Js
i
K}
2
i=1
).
JdK
2t
← (1 −2Js
1
K) ∗Jv
1
K −(1 −2Js
2
K) ∗Jv
2
K;1
Jc
−
v
K ← LTZD(JdK
2t
,` + 1);2
Jc
−
p
K,Jc
+
p
K,Jz
p
K ← CmpZ(Jp
1
K −Jp
2
K,g + 1);
3
JcK ← Jz
p
KJc
−
v
K + Jc
−
p
K(1 −Js
2
K) + Jc
+
p
KJs
1
K;
4
return JcK;5
P 11: CmpZ(JaK,k).
(Jr
00
K,Jr
0
K,{Jr
0
i
K}
k−1
i=1
) ← PRandM(k,k −1);1
b ← Reveal(2
k−1
+ JaK + 2
k−1
Jr
00
K + Jr
0
K);2
b
0
← b mod 2
k−1
;3
(Ju
1
K,Ju
2
K) ← BitCmp(b
0
,{Jr
0
i
K}
k−1
i=1
);4
Jc
1
K ← −((JaK −(b
0
−Jr
0
K))2
−(k−1)
−Ju
1
K);5
Jc
2
K ← (1 −Jc
1
K)(1 −Ju
2
K);6
Jc
3
K ← (1 −Jc
1
K)Ju
2
K;7
return (Jc
1
K,Jc
2
K,Jc
3
K);8
Given a secret integer ¯a ∈ Z
hki
, CmpZ returns the
secret bits c
1
= ( ¯a < 0)? 1 : 0, c
2
= ( ¯a > 0)? 1 : 0, and
c
3
= ( ¯a = 0)? 1 : 0. CmpZ uses Protocol 12, BitCmp,
with input a public integer ¯a =
∑
k
i=1
2
i−1
a
i
and a
bitwise-shared integer
¯
b =
∑
k
i=1
2
i−1
b
i
, and output the
secret bits u
1
= ( ¯a <
¯
b)? 1 : 0 and u
2
= ( ¯a =
¯
b)? 1 : 0.
CmpZ extends the protocol LTZ to compute the
bits c
2
and c
3
, besides c
1
. Steps 1-5 compute c
1
=
SECRYPT 2019 - 16th International Conference on Security and Cryptography
56

−b¯a/2
k−1
c exactly like LTZ, except that BitLT is re-
placed by BitCmp in step 4. Steps 1-3 compute and
reveal b = 2
k−1
+ ¯a +r, where r = 2
k−1
r
00
+r
0
is a ran-
dom secret integer that hides ¯a with statistical secrecy
and r
0
=
∑
k−1
i=1
2
i−1
r
i
, with {r
0
i
}
k−1
i=1
uniformly random
secret bits. Let b
0
= b mod 2
k−1
and a
0
= ¯a mod 2
k−1
.
Step 4 computes u
1
= (b
0
< r
0
)? 1 : 0 and u
2
= (b
0
=
r
0
)? 1 : 0. Observe that b
0
= a
0
+ r
0
− 2
k−1
u
1
, so
b¯a/2
k−1
c = ( ¯a −(b
0
−r
0
))2
−(k−1)
−u
1
. Also, u
2
= 1
if ¯a = 0 or ¯a = −2
k−1
, so c
2
= (1 −c
1
)(1 −u
2
) and
c
3
= (1 −c
1
)u
2
(steps 6-7, in parallel).
P 12: BitCmp(a,{Jb
i
K}
k
i=1
).
foreach i ∈ [1,k] do Jd
i
K ← a
i
⊕Jb
i
K;1
foreach i ∈ [1,k] do c
i
← 1 −a
i
;2
{Jp
i
K}
k
i=1
← SufMul({Jd
i
+ 1K}
k
i=1
);3
Js
1
K ← c
k
Jd
k
K +
∑
k−1
i=1
c
i
(Jp
i
K −Jp
i+1
K);4
Ju
1
K ← Mod2(Js
1
K,k);5
Ju
2
K ← Mod2(Jp
1
K,k);6
return (Ju
1
K,Ju
2
K);7
BitCmp is similar to the protocol BitLT given in
(Catrina and de Hoogh, 2010a). Steps 1-5 compute
u
1
exactly like BitLT, so we explain only the compu-
tation of u
2
. Step 3 computes p
i
=
∏
k
j=i
(d
j
+ 1), for
i ∈ [1, k], where d
j
= a
j
⊕b
j
. If a = b then p
1
= 1,
else p
1
is a power of 2, so u
2
= p
1
mod 2. Steps 5-6
run in parallel, so we obtain u
2
almost for free.
LTFL can also be used to compute the other com-
parison operators, by observing that c = ( ˆa
1
< ˆa
2
)? 1 :
0 = ( ˆa
2
> ˆa
1
)? 1 : 0 and 1 −c = ( ˆa
1
≥ ˆa
2
)? 1 : 0 =
( ˆa
2
≤ ˆa
1
)? 1 : 0. Moreover, it also works when an
operand is public, with the same complexity.
The online complexity of BitCmp is 2 rounds and
k + 2 interactive operations (1 operation more than
BitLT) and CmpZ needs 4 rounds and k + 5 interac-
tive operations. Therefore, the online complexity of
LTFL is 5 rounds and ` + g + 7 interactive operations
(steps 2-3 in parallel). This is similar to comparison
in Q
FX
hk, f i
using LTZ (LTFL adds 2 rounds, but usually
`+g < k, so the communication complexity is lower).
Equality of secret ˆa
1
, ˆa
2
∈ Q
FL
h`,gi
with secret out-
put can be tested as efficiently as for fixed-point num-
bers, based on the following remark. Let ˆa
1
= (1 −
s
1
) ¯v
1
2
¯p
1
, ˆa
2
= (1 −s
2
) ¯v
2
2
¯p
2
, and c = ( ˆa
1
= ˆa
2
)? 1 : 0.
Also, let ∆ = 2
`+1
( ¯p
1
− ¯p
2
)+2
`
( ¯s
1
− ¯s
2
)+( ¯v
1
− ¯v
2
) =
2
`+1
¯
d
p
+ 2
`
¯
d
s
+
¯
d
v
. Observe that
¯
d
s
∈ {−1, 0, 1} and
|
¯
d
v
| < 2
`
. If
¯
d
s
6= 0 and
¯
d
p
6= 0 then 0 < |2
`
¯
d
s
+
¯
d
v
| <
|2
`+1
¯
d
p
|, hence ∆ 6= 0. Thus, ∆ = 0 if and only if
¯
d
p
= 0,
¯
d
s
= 0, and
¯
d
v
= 0, hence c = (∆ = 0)? 1 : 0.
Protocol 13, EQFL, computes c = ( ˆa
1
= ˆa
2
)? 1 : 0
as described above. Its online complexity is 3 rounds
and log(`+ g +2)+2 interactive operations, the same
as for inputs in Q
FX
hk, f i
with k > ` + g.
P 13: EQFL({Jv
i
K,Jp
i
K,Js
i
K}
2
i=1
).
Jb
1
K ← 2
`+1
Jp
1
K + 2
`
Js
1
K + Jv
1
K;1
Jb
2
K ← 2
`+1
Jp
2
K + 2
`
Js
2
K + Jv
2
K;2
JcK ← EQZ(Jb
1
K −Jb
2
K,` + g + 2);3
return JcK;4
4 CONCLUSIONS
A broad range of privacy preserving collaborative ap-
plications require efficient secure computation with
real numbers (statistical analysis, benchmarking, data
mining, and optimizations). Starting from the frame-
work introduced in (Catrina and de Hoogh, 2010a;
Catrina and Saxena, 2010), we add building blocks
and optimizations that alleviate the performance bot-
tlenecks of the previous protocols. We show that
secure floating-point arithmetic is substantially im-
proved using a small set of powerful and efficient
building blocks (Table 2) and protocol constructions.
The online and precomputation complexity of the
floating-point protocols is summarized in Table 3
(with θ
1
,θ
2
∈[3,4] for ` ∈ [24,56]). All protocols are
specified for secret operands and secret result, in the
same security model. However, they can be adapted to
also work when one of the operands is public. In some
cases, the complexity is significantly lower when part
of the input information is not secret, e.g., FX2FL for
input with known sign, AddFL for operands with the
same sign, DivFL with public divisor.
A challenge for secure arithmetic is to find the best
complexity trade-offs, taking into account a complete
protocol family and typical applications
3
. We ana-
lyzed several variants of floating-point encoding and
building blocks. The selection presented in the pa-
per offers better tradeoffs for the round and commu-
nication complexity of the entire protocol family. The
additional building blocks (PreDiv2m, PreDiv2mP,
Int2MaskG, and non-interactive multiplication) im-
prove the performance of the underlying integer and
fixed-point arithmetic protocols and allow us to use
simpler algorithms in the floating-point protocols.
We focused on performance, accuracy and flexi-
bility, rather than trying to replicate the format and
features specified in the IEEE Standard for Floating-
Point Arithmetic (IEEE 754). The parameters ` and
3
Sign and magnitude encoding of the significand of-
fers better tradeoffs. A compact encoding h¯v, ¯pi, ˆa = ¯v2
¯p
,
¯v ∈ [2
`−2
,2
`−1
−1] ∪[−2
`−1
,−2
`−2
−1] ∪{0} simplifies
FX2FL and AddFL, but complicates the other operations.
Also, if we remove z and ignore ¯p when ¯v = 0, we have to
compute z and ¯p = (1 −z) ¯p −z2
g−1
in AddFL (4 rounds).
Efficient Secure Floating-point Arithmetic using Shamir Secret Sharing
57
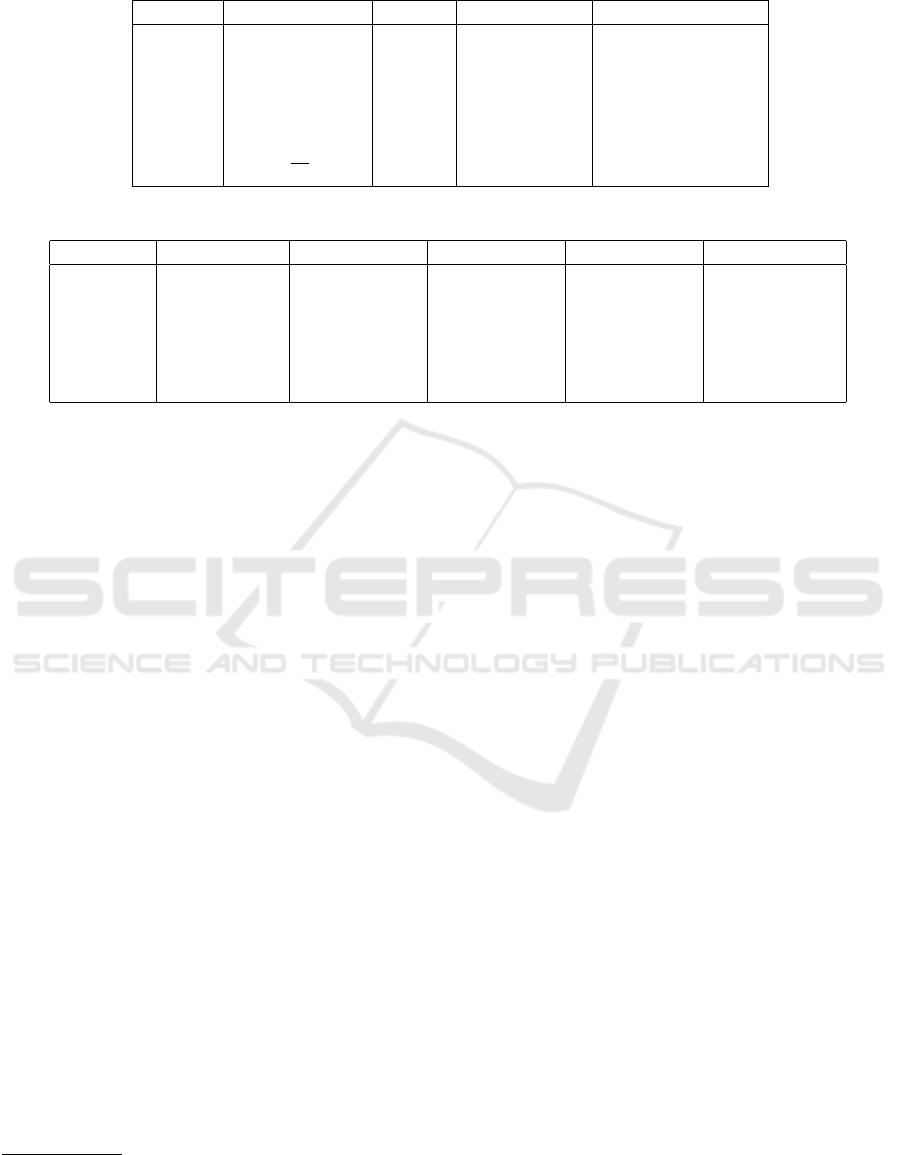
Table 3: Complexity of floating-point protocols for ˆa, ˆa
i
∈ Q
FL
h`,gi
, ˜a ∈ Q
FX
hk, f i
.
Protocol Task Rounds Inter. op. Prec.
LTFL ( ˆa
1
< ˆa
2
)? 1 : 0 5 ` + g + 7 3(` + g)
EQFL ( ˆa
1
= ˆa
2
)? 1 : 0 3 log(` + g) +2 ` + g + 3 log(` + g)
FX2FL ˆa ← ˜a 9 5k + 3 10k −11
AddFL ˆa ← ˆa
1
+ ˆa
2
19 6` + 2g + 26 ≈ 13` + 9g
MulFL ˆa ← ˆa
1
ˆa
2
5 ` + 9 4` + 6
DivFL ˆa ← ˆa
1
/ ˆa
2
5 + θ
1
` + 2θ
1
+ 6 ≈ (2θ
1
+ 4)`
SqrtFL ˆa ←
√
ˆa
1
4 + 2θ
2
3θ
2
+ 7 ≈ (3θ
2
+ 3)`
Table 4: Running time of floating-point protocols (milliseconds/operation).
Batch size 1 Prec. 10 Prec. 20 Prec. 50 Prec. 100 Prec.
LTFL 1.88 1.83 0.46 1.08 0.39 1.10 0.30 1.04 0.27 1.04
EQFL 0.94 1.35 0.17 0.71 0.13 0.70 0.09 0.64 0.08 0.63
MulFL 1.89 1.20 0.42 1.19 0.32 1.18 0.24 1.12 0.22 1.11
DivFL 3.09 4.47 0.53 3.56 0.42 3.63 0.32 3.57 0.32 3.59
SqrtFL 3.28 4.28 0.45 3.64 0.32 3.72 0.24 3.64 0.22 3.67
AddFL 7.98 5.60 2.66 4.39 2.37 4.38 2.14 4.23 1.96 4.18
g determine the range and precision of the floating
numbers, as well as the protocols’ communication
and computation complexity (the size of the field and
the number of interactive operations). All protocols
take ` and g as (implicit) parameters and work accu-
rately, with relative error 2
−(`−1)
, for the entire range
of practically relevant values (including standard sim-
ple and double precision). Thus, they can offer the
best tradeoff between accuracy and performance, ac-
cording to application requirements.
The protocols were tested using our Java imple-
mentation of the secure computation framework dis-
cussed in Section 2. Table 4 shows preliminary per-
formance measurements for 3 parties, ` = 32, g =
10, and dlogqe = 128. The protocols ran on com-
puters with 3.6 GHz CPU, connected to a 1 Gbps
LAN. The results show the baseline performance for
low-latency and high-bandwidth networks and single-
threaded code. Large batches of primitives can be
processed faster by splitting the load among CPU
cores. The single-thread code used only a small frac-
tion of the bandwidth
4
. On the other hand, longer
network latency means longer interaction rounds. A
more comprehensive performance assessment, with
broader scope, will be included in future work.
The tests ran the protocols for up to 100 parallel
operations. The table lists online and precomputation
time per operation. The results of the measurements
are well correlated with the complexity, but we expect
heavier performance penalty for protocols with larger
round complexity in networks with longer transfer de-
4
The load of the quad-core CPU (Intel i7-7700) was
20% and the data rate was 35-50 Mbps. Tests in a 100 Mbps
LAN showed modest performance degradation.
lays. The online time is clearly much shorter when
operations are part of larger batches, so the applica-
tions that use algorithms with high parallelism will
see important performance improvements.
Floating-point arithmetic protocols are inherently
more complex than fixed-point arithmetic protocols.
This complexity is partially compensated by more
compact data encoding: the protocols run more com-
plex algorithms with smaller integers encoded in
smaller fields. Multiplication and comparison proto-
cols have similar performance for floating-point and
fixed-point numbers, while floating-point division is
faster. On the other hand, secure floating-point addi-
tion remains complex and relatively slow.
On-going work, being finalized, shows important
performance gains for more complex tasks, like eval-
uating sums and polynomials, by using dedicated pro-
tocols, instead of generic constructions. However,
these optimized protocols are slower than the fixed-
point versions, since adding secret-shared fixed-point
numbers is just a local addition of field elements.
This suggests combining secure fixed-point and
floating-point arithmetic according to application re-
quirements, an approach we are currently studying.
REFERENCES
Aliasgari, M., Blanton, M., and Bayatbabolghani, F. (2017).
Secure Computation of Hidden Markov Models and
Secure Floating-point Arithmetic in the Malicious
Model. International Journal of Information Security,
16(6):577–601.
Aliasgari, M., Blanton, M., Zhang, Y., and Steele, A.
(2013). Secure Computation on Floating Point Num-
SECRYPT 2019 - 16th International Conference on Security and Cryptography
58

bers. In 20th Annual Network and Distributed System
Security Symposium (NDSS’13).
Bogdanov, D., Kamm, L., Laur, S., and Sokk, V. (2018).
Rmind: A Tool for Cryptographically Secure Statisti-
cal Analysis. IEEE Transactions On Dependable And
Secure Computing, 15(3):481–495.
Catrina, O. (2018). Round-Efficient Protocols for Se-
cure Multiparty Fixed-Point Arithmetic. In 12th In-
ternational Conference on Communications (COMM
2018), pages 431–436. IEEE.
Catrina, O. and de Hoogh, S. (2010a). Improved Primitives
for Secure Multiparty Integer Computation. In Secu-
rity and Cryptography for Networks, volume 6280 of
LNCS, pages 182–199. Springer.
Catrina, O. and de Hoogh, S. (2010b). Secure Multiparty
Linear Programming Using Fixed-Point Arithmetic.
In Computer Security - ESORICS 2010, volume 6345
of LNCS, pages 134–150. Springer.
Catrina, O. and Saxena, A. (2010). Secure Computation
With Fixed-Point Numbers. In Financial Cryptogra-
phy and Data Security, volume 6052 of LNCS, pages
35–50. Springer.
Cramer, R., Damg
˚
ard, I., and Ishai, Y. (2005). Share Con-
version, Pseudorandom Secret-sharing and Applica-
tions to Secure Computation. In Theory of Cryptogra-
phy (TCC’05), volume 3378 of LNCS, pages 342–362,
Berlin, Heidelberg. Springer.
Cramer, R., Damg
˚
ard, I., and Nielsen, J. B. (2015). Secure
Multiparty Computation and Secret Sharing. Cam-
bridge University Press, UK.
Damg
˚
ard, I., Fitzi, M., Kiltz, E., Nielsen, J. B., and
Toft, T. (2006). Unconditionally secure constant-
rounds multi-party computation for equality, compar-
ison, bits and exponentiation. In Theory of Cryptogra-
phy (TCC 2006), volume 3876 of LNCS, pages 285–
304. Springer.
Damg
˚
ard, I. and Thorbek, R. (2007). Non-interactive Proofs
for Integer Multiplication. In EUROCRYPT 2007, vol-
ume 4515 of LNCS, pages 412–429. Springer.
Dimitrov, V., Kerik, L., Krips, T., Randmets, J., and
Willemson, J. (2016). Alternative Implementations of
Secure Real Numbers. In 23rd ACM Conference on
Computer and Communications Security (CCS’16),
pages 553–564. ACM.
Ercegovac, M. D. and Lang, T. (2003). Digital Arithmetic.
Morgan Kaufmann.
Kamm, L. and Willemson, J. (2015). Secure Floating
Point Arithmetic and Private Satellite Collision Anal-
ysis. International Journal of Information Security,
14(6):531–548.
Krips, T. and Willemson, J. (2014). Hybrid Model of Fixed
and Floating Point Numbers in Secure Multiparty
Computations. In Information Security (ISC 2014),
volume 8783 of LNCS, pages 179–197. Springer.
Markstein, P. (2004). Software Division and Square Root
Using Goldschmidt’s Algorithms. In 6th Conference
on Real Numbers and Computers, pages 146–157.
Reistad, T. I. and Toft, T. (2009). Linear, Constant-Rounds
Bit-Decomposition. In International Conference on
Information Security and Cryptology, volume 3329 of
LNCS, pages 245–257. Springer.
APPENDIX
This appendix provides (for convenience) pseudocode
and further details for building blocks presented in
previous work and used in this paper.
Given a secret signed integer ¯a ∈ Z
hki
and a pub-
lic integer m ∈ [1,k −1], Protocol 14, Div2mP, re-
turns secret ¯a/2
m
with probabilistic rounding to near-
est (Catrina and de Hoogh, 2010a).
Div2mP computes ¯c = b¯a/2
m
c+ u, for u ∈{0, 1}.
Let
¯
d = 2
k−1
+ ¯a and ¯a
0
= ¯a mod 2
m
. Observe that
¯
d ≥ 0 and
¯
d mod 2
m
= ¯a
0
for any m ∈ [1, k −1]. The
protocol reveals b = d + r, where r = 2
m
r
00
+ r
0
is a
random secret integer that hides d with statistical se-
crecy and r
0
=
∑
m
i=1
2
i
r
i
, with {r
0
i
}
m
i=1
uniformly ran-
dom secret bits. Observe that b
0
= (d + r) mod 2
m
=
a
0
+ r
0
−2
m
u, where u = ((b
0
< r
0
)? 1 : 0). Therefore,
¯c = ( ¯a − ¯a
0
+ 2
m
u)2
−m
= b¯a/2
m
c+ u.
P 14: Div2mP(JaK,k,m).
(Jr
00
K,Jr
0
K,{Jr
0
i
K}
m
i=1
) ← PRandM(k,m);1
b ← Reveal(2
k−1
+ JaK + 2
m
Jr
00
K + Jr
0
K);2
b
0
← b mod 2
m
;3
JcK ← (JaK −(b
0
−Jr
0
K))2
−m
;4
return JcK;5
P 15: Div2m(JaK,k,m).
(Jr
00
K,Jr
0
K,{Jr
0
i
K}
m
i=1
) ← PRandM(k,m);1
b ← Reveal(2
k−1
+ JaK + 2
m
Jr
00
K + Jr
0
K);2
b
0
← b mod 2
m
;3
JuK ← BitLT(b
0
,{Jr
0
i
K}
m
i=1
);4
JcK ← (JaK −(b
0
−Jr
0
K))2
−m
−JuK;5
return JcK;6
P 16: Div2(JaK,k).
(Jr
00
K,Jr
0
K,Jr
0
1
K) ← PRandM(k,1);1
b ← Reveal(2
k−1
+ JaK + 2Jr
00
K + Jr
0
1
K);2
Ja
1
K ← b
1
+ Jr
0
1
K −2b
1
Jr
0
1
K;3
JcK ← (JaK −Ja
1
K)2
−1
;4
return JcK;5
Protocol 15, Div2m, is a variant that computes
¯a/2
m
with deterministic rounding to −∞ (Catrina and
de Hoogh, 2010a). This is achieved by computing the
bit u using the protocol BitLT. The online complex-
ity of Div2m is 3 rounds and m + 2 interactive opera-
tions. Div2mP needs a single online interaction, so it
is much more efficient. However, certain applications
require deterministic rounding. Protocol 16, Div2, is
a variant of Div2m optimized for m = 1, that needs a
single interactive operation.
Protocol 17, PreDiv2mP, is a generalization of
Div2mP that computes {¯a
0
i
}
m
i=1
= {b¯a/2
i
e}
m
i=1
with
Efficient Secure Floating-point Arithmetic using Shamir Secret Sharing
59

probabilistic rounding to nearest. Similarly, Proto-
col 18, PreDiv2m, computes {¯a
0
i
}
m
i=1
= {b¯a/2
i
c}
m
i=1
with deterministic rounding to −∞. PreDiv2m uses
the protocol PreBitLT, a generalization of BitLT, to
efficiently compute {u
i
}
m
i=1
= {(b
i
< r
0
i
)? 1 : 0}
m
i=1
.
P 17: PreDiv2mP(JaK,k,m).
(Jr
00
K,Jr
0
K,{Jr
0
i
K}
m
i=1
) ← PRandM(k,m);1
b ← Reveal(2
k−1
+ JaK + 2
m
Jr
00
K + Jr
0
K);2
foreach i ∈ [1,m] do3
b
i
← b mod 2
i
; Js
i
K ←
∑
i−1
j=0
2
j
Jr
0
j
K;
4
Ja
0
i
K ← (JaK −(b
i
−Js
i
K))2
−i
;5
return {Ja
0
i
K}
m
i=1
;6
P 18: PreDiv2m(JaK,k,m).
(Jr
00
K,Jr
0
K,{Jr
0
i
K}
m
i=1
) ← PRandM(k,m);1
b ← Reveal(2
k−1
+ JaK + 2
m
Jr
00
K + Jr
0
K);2
foreach i ∈ [1,m] do3
b
i
← b mod 2
i
; Js
i
K ←
∑
i−1
j=0
2
j
Jr
0
j
K;
4
{Ju
i
K}
m
i=1
← PreBitLT(b, {Jr
0
i
K}
m
i=1
);5
foreach i ∈ [1,m] do6
Ja
0
i
K ← (JaK −(b
i
−Js
i
K))2
−i
−Ju
i
K;7
return {Ja
0
i
K}
m
i=1
;8
The complexity of PreDiv2m is 3 rounds and
2m + 1 interactive operations, so it performs a much
more complex task then Div2m with the same round
complexity and slightly higher communication com-
plexity. PreDiv2mP needs a single online interaction,
so we use it instead of PreDiv2m whenever possible.
The efficient solutions described above are based
on Protocol 19, BitLT (“bitwise less than”) (Cat-
rina and de Hoogh, 2010a), and its generalization
PreBitLT (Catrina, 2018).
BitLT computes the secret bit u = (a < b)? 1 : 0
for a non-secret integer a =
∑
k
i=1
2
i−1
a
i
and a bitwise-
shared integer b =
∑
k
i=1
2
i−1
b
i
. Steps 1-2 compute
d
i
= a
i
⊕b
i
and the products p
i
=
∏
k
j=i
(d
j
+ 1), for
i ∈ [1, k]; SufMul is the protocol PreMul in (Catrina
and de Hoogh, 2010a), with inputs and outputs in
inverse order. Observe that d
j
+ 1 = 2
d
j
, so p
i
=
∏
k
j=i
2
d
j
= 2
∑
k
j=i
d
j
. Step 3 computes s = (1 −a
k
)d
k
+
∑
k−1
i=1
(1 −a
i
)(p
i
− p
i+1
). Since p
i
− p
i+1
= d
i
p
i+1
, it
follows that s = (1 −a
k
)d
k
+
∑
k−1
i=1
(1 −a
i
)d
i
2
∑
k
j=i+1
d
j
.
Assume a 6= b and let m ≤ k be the secret in-
dex of the most significant different bit. The ex-
pected result is u = 1 −a
m
. If m < k, d
m
= 1 and
d
i
= 0 for all i ∈ [m + 1, k], so s = 1 −a
m
+ 2(1 −
a
m−1
)d
m−1
+2
∑
m−2
i=1
(1−a
i
)d
i
2
∑
m−1
j=i+1
d
j
. The output is
u = s mod 2 = 1 −a
m
. If m = k, then d
k
= 1 and s =
1 −a
k
+ 2(1 −a
k−1
)d
k−1
+ 2
∑
k−2
i=1
(1 −a
i
)d
i
2
∑
k−1
j=i+1
d
j
.
The output is u = s mod 2 = 1 −a
k
. Finally, if a = b,
the expected result is u = 0. In this case, d
i
= 0 for all
i ∈ [1,k], so s = 0 and the output is u = 0.
P 19: BitLT(a,{Jb
i
K}
k
i=1
).
foreach i ∈ [1,k] do Jd
i
K ← a
i
+ Jb
i
K −2a
i
Jb
i
K;1
{Jp
i
K}
k
i=1
← SufMul({Jd
i
+ 1K}
k
i=1
);2
JsK ←(1−a
k
)Jd
k
K+
∑
k−1
i=1
(1−a
i
)(Jp
i
K−Jp
i+1
K);3
JuK ← Mod2(JsK,k);4
return JuK;5
Protocol 20, PreBitLT, is an efficient gener-
alization of BitLT: given a non-secret integer
a =
∑
k
i=1
2
i−1
a
i
and a bitwise shared integer b =
∑
k
i=1
2
i−1
b
i
, it computes the secret bits {u
i
}
k
i=1
=
{(a
0
i
< b
0
i
)? 1 : 0}
k
i=1
, where a
0
i
=
∑
i
j=1
2
j−1
a
j
and
b
0
i
=
∑
i
j=1
2
j−1
b
j
(Catrina, 2018).
P 20: PreBitLT(a,{Jb
i
K}
k
i=1
).
foreach i ∈ [1,k] do Jd
i
K ← a
i
+ Jb
i
K −2a
i
Jb
i
K;1
({Jp
i
K,Jp
0
i
K}
k
i=1
) ← SufMulInv({Jd
i
K + 1}
k
i=1
);2
Js
1
K ← (1 −a
1
)(Jp
1
K −Jp
2
K);3
foreach i ∈ [2,k −1] do4
Js
i
K ← Js
i−1
K + (1 −a
i
)(Jp
i
K −Jp
i+1
K);5
Js
k
K ← Js
k−1
K + (1 −a
k
)Jd
k
K;6
foreach i ∈ [1,k −1] do7
Ju
i
K ← Mod2D(Js
i
K ∗Jp
0
i+1
K,k);
8
Ju
k
K ← Mod2(Js
k
K,k);9
return {Ju
i
K}
k
i=1
;10
For u
k
= (a
0
k
< b
0
k
)? 1 : 0, PreBitLT works exactly
like BitLT: it computes s
k
= (1 −a
k
)d
k
+
∑
k−1
i=1
(1 −
a
i
)(p
i
−p
i+1
) and then u
k
= s
k
mod 2.
For u
`
= (a
0
`
< b
0
`
)? 1 : 0, with ` ∈ [1, k − 1],
PreBitLT computes s
`
=
∑
`
i=1
(1 − a
i
)(p
i
− p
i+1
).
Since s
`
=
∑
`
i=1
(1 − a
i
)d
i
2
∑
k
j=i+1
d
j
and p
`+1
=
2
∑
k
j=`+1
d
j
, it follows that s
`
= p
`+1
((1 − a
`
)d
`
+
∑
`−1
i=1
(1 −a
i
)d
i
2
∑
`
j=i+1
d
j
). Therefore, we can compute
u
`
= (s
`
/p
`+1
) mod 2 (like in BitLT). Since p
`+1
| s
`
,
the integer division can be computed in Z
q
, as s
`
p
−1
`+1
.
SufMulInv computes {p
i
}
k
i=1
= {
∏
k
j=i
a
j
}
k
i=1
and
{p
−1
i
}
k
i=1
= {
∏
k
j=i
a
−1
j
}
k
i=1
. It extends the protocol
PreMul and has the same complexity.
The online complexity of BitLT is 2 rounds and
k + 1 interactive operations. PreBitLT needs 2 rounds
and 2k interactive operations.
SECRYPT 2019 - 16th International Conference on Security and Cryptography
60
