
Incremental Principal Component Analysis:
Exact Implementation and Continuity Corrections
Vittorio Lippi
1
and Giacomo Ceccarelli
2
1
Fachgebiet Regelungssysteme Sekretariat EN11, Technische Universit
¨
at Berlin, Einsteinufer 17, Berlin, Germany
2
Dipartimento di Fisica, Universit
`
a di Pisa, Largo Bruno Pontecorvo 2, I-56127 Pisa, Italy
Keywords: PCA, On-line, Incremental, Dimensionality Reduction.
Abstract:
This paper describes some applications of an incremental implementation of the principal component analysis
(PCA). The algorithm updates the transformation coefficients matrix on-line for each new sample, without
the need to keep all the samples in memory. The algorithm is formally equivalent to the usual batch version,
in the sense that given a sample set the transformation coefficients at the end of the process are the same.
The implications of applying the PCA in real time are discussed with the help of data analysis examples. In
particular we focus on the problem of the continuity of the PCs during an on-line analysis.
1 INTRODUCTION
1.1 Incremental PCA
Principal Component Analysis (PCA) is a widely
used technique and a well-studied subject in the lit-
erature. PCA is a technique to reduce data dimen-
sionality of a set of correlated variables. Several natu-
ral phenomena and industrial processes are described
by a large number of variables and hence their study
can benefit from the dimensionality reduction PCA
has been invented for. As such PCA naturally ap-
plies to statistical data analysis. This means that such
technique is traditionally implemented as an offline
batch operation. Nevertheless, PCA can be useful
when applied to data that are available incrementally,
e.g. in the context of process monitoring (Dunia et al.,
1996) or gesture recognition (Lippi et al., 2009). The
PCA can be applied to a data-flow after defining the
transformation on a representative off-line training set
set using the batch algorithm (Lippi and Ceccarelli,
2011). This approach can be used in pattern recog-
nition problems for data pre-processing (Lippi et al.,
2009). Nevertheless one can imagine an on-line im-
plementation of the algorithm. An on-line implemen-
tation is more efficient in terms of memory usage than
a batch one. This can be particularly relevant for
memory consuming data-sets such as image collec-
tions; in fact in the field of visual processing some
techniques to implement incremental PCA have been
proposed, see for example (Arta
ˇ
c et al., 2002). PCA
consists of a linear transformation to be applied to the
data-set. Dimensionality reduction is performed by
selecting a subset of the transformed variables that
are considered more relevant in the sense that they
exhibit a larger variance compared to the others. Usu-
ally the transformation is calculated and computed on
the Z-score, and hence the averages and the variances
of the dataset are taken into account. Depending on
the applications the algorithm has been extended in
different ways, adding samples on-line as presented
in (Arta
ˇ
c et al., 2002) or incrementally increasing the
dimension of the reduced variable subset as seen in
(Neto and Nehmzow, 2005). A technique to dynam-
ically merge and split the variable subsets has been
presented in (Hall et al., 2000) Several approximate
incremental algorithms have been proposed for PCA,
e.g. see (Shamir, 2015) and (Boutsidis et al., 2015),
as well as for singular value decomposition (Sarwar
et al., 2002). An implementation for on-line PCA
has been proposed, for example, for the R language
(Degrasand and Cardot, 2015). In some cases the in-
cremental process is designed to preserve some spe-
cific information; for example in (Hall et al., 1998)
the average of the samples is updated with new obser-
vations.
Currently, to the best of our knowledge, there is
no available description of an exact incremental im-
plementation of PCA, where exact means that the
transformation obtained given n samples is exactly the
same as would have been produced by the batch algo-
Lippi, V. and Ceccarelli, G.
Incremental Principal Component Analysis: Exact Implementation and Continuity Corrections.
DOI: 10.5220/0007743604730480
In Proceedings of the 16th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2019), pages 473-480
ISBN: 978-989-758-380-3
Copyright
c
2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
473

rithm, including the z-score normalization, a step that
is not included in previous works presenting a simi-
lar approach like(Arta
ˇ
c et al., 2002). We decided in
light of this to describe the algorithm in detail in this
paper. The incremental techniques cited above (Hall
et al., 1998; Arta
ˇ
c et al., 2002; Hall et al., 2000) are
designed to update the reduced set of variables and
change its dimensionality when it is convenient for
data representation. In the present work, no indica-
tion is provided for which subset of variables should
be used , i.e. how many principal components to con-
sider. All the components are used during the algo-
rithm to ensure the exact solution. After describing
the exact algorithm some implication of using this in-
cremental analysis are discussed. In particular, we
provide an intuitive definition of continuity for the ob-
tained transformation and then we propose a modified
version designed to avoid discontinuities.
The concept of continuity is strictly related to the
incremental nature of the proposed algorithm: in stan-
dard PCA the batch analysis implies that the notion of
time does not exist, e.g. the order of the elements in
the sample set is not relevant for the batch algorithm.
In our treatment we instead want to follow the time
evolution of variances and eigenvectors. We are thus
lead to consider a dynamical evolution.
The paper is organized as follows. In the remain-
ing part of the Introduction we recall the PCA algo-
rithm and we introduce the notation used. In Section
2.1 we give a detailed account of the incremental al-
gorithm for an on-line use of PCA. In Section 2.2 we
address the problems related to the data reconstruc-
tion, in particular those connected with the signal con-
tinuity. In Sections 3, 4 we then present the results of
some applications to an industrial data set and draw
our conclusions.
1.2 The Principal Component Analysis
The computation for the PCA starts considering a set
of observed data. We suppose we have m sensors
which sample some physical observables at constant
rate. After n observations we can construct the matrix
X
n
=
x
1
x
2
.
.
.
x
n
(1)
where x
i
is a row vector of length m representing the
measurements of the i
th
time step so that X
n
is a n × m
real matrix whose columns represent all the values of
a given observable.
The next step is to define the sample means ¯x
n
and
standard deviations σ
n
with respect to the columns
(i.e. for the observables) in the usual way as
¯x
n( j)
=
1
n
n
∑
i=1
X
n(i j)
(2)
σ
n( j)
=
s
1
n − 1
n
∑
i=1
X
n(i j)
− ¯x
n( j)
2
(3)
where in parentheses we write the matrix and vector
indices explicitly. In this way we can define the stan-
dardized matrix for the data as
Z
n
=
x
1
− ¯x
n
x
2
− ¯x
n
.
.
.
x
n
− ¯x
n
Σ
−1
n
(4)
where Σ
n
≡ diag(σ
n
) is a m × m matrix. The covari-
ance matrix Q
n
of the data matrix X
n
is then defined
as
Q
n
=
1
n − 1
Z
T
n
Z
n
. (5)
We see that Q
n
is for any n a symmetric m× m matrix
and it is positive definite.
Finally we make a standard diagonalization so that
we can write
Q
n
= C
−1
n
λ
1
λ
2
.
.
.
λ
m
C
n
(6)
where the (positive) eigenvalues λ
i
are in descending
order: λ
i
> λ
i+1
. The transformation matrix C
n
is the
eigenvectors matrix and it is orthogonal, C
−1
n
= C
T
n
.
Its rows are the principal components of the matrix Q
n
and the value of λ
i
represents the variance associated
to the i
th
principal component. Setting P
n
= Z
n
C
n
, we
have a time evolution for the values of the PCs until
time step n.
We recall that the diagonalization procedure is not
uniquely defined: once the order of the eigenvalues is
chosen, one can still choose the “sign” of the eigen-
vector for one-dimensional eigenspaces and a suitable
orthonormal basis for degenerate ones (in Section 2.2
we will see some consequences of this fact). We stress
that, since only the eigenspace structure is an intrinsic
property of the data, the PCs are quantity useful for
their interpretation but they are not uniquely defined.
2 ON-LINE ANALYSIS
2.1 Incremental Algorithm
The aim of the algorithm is to construct the covari-
ance matrix Q
n+1
starting from the old matrix Q
n
and
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
474

the new observed data x
n+1
. To do this, at the be-
ginning of step (n + 1), we consider the sums of the
observables and their squares after step n:
a
n( j)
=
n
∑
i=1
X
n(i j)
(7)
b
n( j)
=
n
∑
i=1
X
2
n(i j)
(8)
These sums are updated on-line at every step.
From these quantities we can recover the starting
means and standard deviations: ¯x
n
= a
n
/n and (n −
1)σ
2
n
= b
n
− na
2
n
. Similarly the current means and
standard deviations are also simply obtained.
The key observation to get an incremental algo-
rithm is the following identity:
Z
n+1
=
Z
n
Σ
n
+ ∆
y
Σ
−1
n+1
(9)
where y = x
n+1
− ¯x
n+1
is a row vector and ∆ is a
n × m matrix built repeating n times the row vector
δ = ¯x
n
− ¯x
n+1
. By definition nQ
n+1
= Z
T
n+1
Z
n+1
and,
expanding the preceding identity, we get
nQ
n+1
=Σ
−1
n+1
Σ
n
Z
T
n
Z
n
Σ
n
Σ
−1
n+1
+
Σ
−1
n+1
Σ
n
(Z
T
n
∆)Σ
−1
n+1
+
Σ
−1
n+1
(∆
T
Z
n
)Σ
n
Σ
−1
n+1
+
Σ
−1
n+1
∆
T
∆Σ
−1
n+1
+
z
T
z (10)
where z = yΣ
−1
n+1
and we used the fact that the Σs are
diagonal.
Recalling that by hypothesis all the columns of the
matrix Z
n
have zero mean and that the columns of the
matrix ∆ have the same number, we see that terms in
parentheses are zero. Thus
nQ
n+1
=Σ
−1
n+1
Σ
n
Q
n
Σ
n
Σ
−1
n+1
+
nΣ
−1
n+1
δ
T
δΣ
−1
n+1
+ z
T
z (11)
where δ
T
δ, z
T
z and Q
n
are three m × m matrices. We
now see that we can compute Q
n+1
by making opera-
tions only on m× m matrices and with the sole knowl-
edge of Q
n
and x
n+1
.
The computational advantage of this strategy is
that we do not need to save in the memory all the
sampled data X
n+1
and moreover we do not need to
perform the explicit matrix product in eq. (5), which
would require a great amount of memory and time
for n ≈ 10
5/6
. Consequently this algorithm can be
fruitfully applied in situations where the sensors num-
ber m is small (e.g. of the order of tens) but the data
stream is expected to grow quickly.
The meaning of the normalization procedure de-
pends on the process under analysis and the meaning
that is associated to the data within the current study:
both centering around the empirical mean and divid-
ing by the empirical variance can be avoided by re-
spectively setting ∆ = 0 or Σ = I.
In practice, one keeps n
start
observations and com-
pute Q as given by eq. (5) and the relative C (and
hence P
start
). Then the updated Qs are used, step by
step, to compute the n
th
values for the evolving PCs
in the standard way as p
n
= z
n
C
n
. In this way the last
sample is equal for any n to the one that would result
from a batch analysis until time step n. Instead the
whole sequence of the p
n
values with n
start
< n < n
final
would not coincide with those from P
final
, since the
Qs matrices change every time a sample is added, and
likewise for the Cs matrices. The most relevant im-
plications of this fact will be considered in the next
subsection.
The library for the present implementation of the
algorithm is available on the Mathworks website un-
der the name incremental PCA.
2.2 Continuity Issues
We now consider the problem of the continuity for the
PCs during the on-line analysis. In a batch analysis,
one computes the PCs using all the data at the end of
the sampling, obtaining the matrix C
final
, and then, by
applying this transformation and its inverse, one can
pass from the original data set to the set PCs values.
Of course, since we are considering sampled data, we
cannot speak of continuity in a strict sense. As pre-
viously stated, the temporal evolution of the data is
not something relevant for the batch PCA. Regardless,
we may intuitively expect to use a sampling rate of at
least two times the signal bandwidth (for the sampling
theorem) usually even more, i.e. ten times. We hence
expect a limited difference between two samples in
proportion to the overall signal amplitude. For sam-
pled data we can then define continuity in a intuitive
sense as a condition where the difference between two
consecutive samples is smaller than a given thresh-
old. A discontinuity in the original samples may be
reflected in the principal components depending on
the transformation coefficients, in detail
p
n
− p
n−1
= z
n
C
n
− z
n−1
C
n−1
(12)
that is equal to
p
n
− p
n−1
= (z
n
− z
n−1
)C
n
+ z
n−1
(C
n
− C
n−1
) (13)
The first term would be the same for the batch pro-
cedure (in that case with constant C) and the second
term shows how p is changing due to the change in
Incremental Principal Component Analysis: Exact Implementation and Continuity Corrections
475

Samples
50 100 150 200 250
Value
0
200
400
600
800
1000
1200
PC
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
Var
0
10
20
30
40
50
60
70
80
90
100
PC var
Cumulative Var
Figure 1: Top, data-set used in the example. Bottom, variances associated to the PCs of the system.
coefficients C. We can regard this term as the source
of discontinuities due to the incremental algorithm.
To understand the problems that could arise, from
the point of view of the continuity of the PCs values,
let us consider the on-line procedure more closely.
We start with some the matrices Q
start
and C
start
.
At a numerical level the eigenvalues are all differ-
ent (since the machine precision is at least of or-
der 10
−15
), so that we have a set of formally one-
dimensional eigenspaces, from which the eigenvec-
tors are taken. Going on in the time sampling, we
naturally create m different time series of eigenvec-
tors.
We could expect that the difference of two subse-
quent eigenvectors of a given series be slowly varying
(in the sense of the standard euclidean norm), since
they come from different Cs that are obtained from
different Qs which differ only slightly (i.e. for the
last x
n+1
). But this is not fully justified, since the PCs
are not uniquely defined and in some case two subse-
quent vectors of p
n
and p
n+1
can differ considerably,
as shown in the exaple in Figure 4. There are three
ways in which one or more eigenvector series could
exhibit a discontinuity (in the general sense discussed
above).
• Consider the case of a given eigenvalue associ-
ated with two eigenspaces at two subsequent time
steps, spanned by the vectors c
n
and c
n+1
. They
belong by hypothesis to two close “lines” but the
algorithm can choose c
n+1
in the “wrong” direc-
tion. In this case, to preserve the on-line continu-
ity as much as possible, we take the new PC to
be −c
n+1
, i.e. minus the eigenvector given by the
diagonalization process at step n + 1. The “right”
orientation can be identified with simple consid-
erations on the scalar product of c
n
with c
n+1
. Re-
calling the considerations at the end of Section
1.2, this substitution does not change the meaning
of our analysis.
• Consider the case where the differences of a group
of ν contiguous eigenvalues are much smaller than
the others: we can say that these eigenvalues cor-
respond in fact to a degenerate eigenspace. In this
case we can choose an infinite number of ν or-
thonormal vectors that can be legitimately con-
sidered our PCs, but the incremental algorithm
can choose, at subsequent time steps, two basis
which considerably differ. To overcome this prob-
lem, we must apply to the new transformation a
change of basis in such a way not to modify the
eigenspaces structure and to “minimize” the dis-
tance with the old basis. Although the case of a
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
476
proper degenerated space on real data is virtually
impossible, as the difference between two or more
eigenvalues of Q is approaching zero, the numer-
ical values of the associated PCs can become dis-
continuous in a real time analysis. This by itself
does not represent an error in an absolute sense
in computing C
n
, as the specific C
n
is the same as
that which would be computed off-line.
• In the two previous cases the discontinuity was
due to an ambiguity of the diagonalization matrix.
A third source of discontinuity can consist into the
temporal evolution of the eigenvalues. Consider
two one-dimensional eigenspaces associated, one
with a variance that is increasing in time, the other
with a variance that is decreasing: there will be a
time step ¯n the two eigenspaces are degenerate.
This is called a “level crossing” and corresponds
in the algorithm to an effective swap in the “ cor-
rect” order of the eigenvectors. To restore conti-
nuity, the two components must me swapped.
3 EXAMPLES AND RESULTS
A publicly available data-set was used for this ex-
ample: it consists of snapshot measurements on 27
variables from a distillation column, with a sampling
rate of one every three days, measured over 2.5 years.
Sampling rate and time in general are not relevant per
se for PCA. Nevertheless, as we discussed the con-
tinuity issue it is interesting to see how the algorithm
behaves on physical variables representing the contin-
uous evolution of a physical system.
Variables represent temperatures, pressures, flows
and other kind of measures (the database is of indus-
trial origin and the exact meaning of all the variables
is not specified). Details are available on-line (Dunn,
2011).
This kind of data set includes variables that are
strongly correlated amongst each other, variables with
a large variance and variables almost constant during
a time of several samples. In Figure 1 we display the
time evolution of the variables and the standard batch
PCA. In Figure 3 the evolution of the covariance ma-
trix Q and the incremental PCs are shown. Notice that
the values p
n
are obviously not equal to the ones com-
puted with the batch method until the last sample. The
matrix Q almost constantly converges to the covari-
ance matrix computed with the batch method. Note
that at the beginning the Frobenius norm of the differ-
ence between the two matrices sometimes grows with
the addition of some samples, the number of samples
needed for Q to settle to the final value depends on the
regularity of the data and the variations in Q may rep-
resent an interesting description of the analyzed pro-
cess. This is expected for the estimator of the covari-
ance matrix until m & n. While the sample covariance
matrix is an unbiased estimator for n → ∞, it is known
to converge inefficiently (Smith, 2005).
In order to quantify the efficiency of the algorithm
the computational of the proposed incremental solu-
tion has been compared with the batch implementa-
tion provided by the Matlab built-in function PCA on
a Intel Core i7-7700HQ CPU running at 2.81 GHz,
with windows 10 operative system. The results are
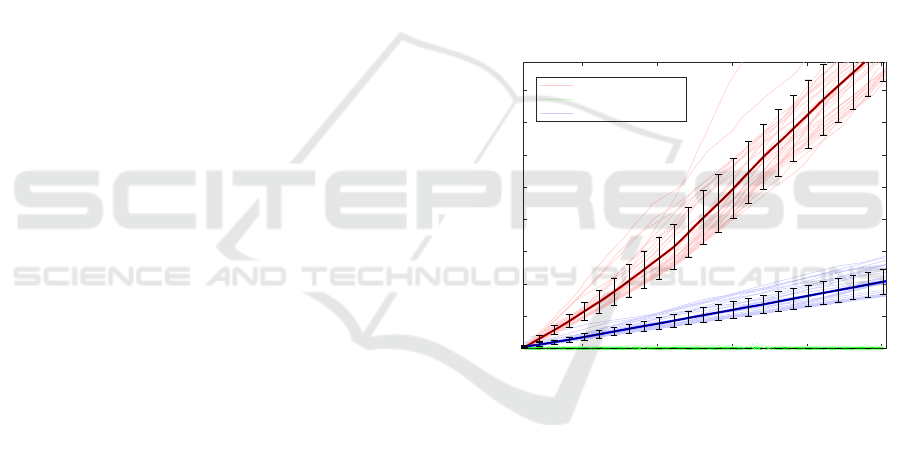
shown in Figure 2. The time required to execute the
incremental algorithm grows linearly with the number
of samples while the batch presents an increase of the
execution time associated with the size of the dataset.
As reasonably expected, the batch implementation is
more efficient than the incremental one when the PCA
is computed on the whole dataset, while the incremen-
tal implementation is more efficient when samples are
added incrementally.
50 100 150 200 250
Samples
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
Time [s]
Batch (cumulative)
Batch(single case)
Incremental(cumulative)
Figure 2: Time required to execute the incremental PCA
and the batch implementation as function of the number of
samples. For the batch algorithm both the time required
to compute the PCA on the given number of samples (sin-
gle case) and the cumulative time required to perform the
PCA with each additional sample (cumulative) are shown.
The computational time is measured empirically and can
be affected by small fluctuations due to the activity of the
operative system: in order to take this in account the aver-
age times (darker lines) and their standard deviations (error
bars) are computed on 33 trials. The batch implementation
is more efficient than the incremental one when the PCA
is computed on the whole dataset, while the incremental
implementation is more efficient when samples are added
incrementally.
In Figure 5 the variance of the whole incremental
PCA is shown. Comparing it with Figure 1 (bottom),
it is evident that the incremental PCs that are not lin-
early independent over the whole sampling time have
a slightly different distribution of the variance com-
Incremental Principal Component Analysis: Exact Implementation and Continuity Corrections
477

50 100 150 200 250
Score
-10
0
10
50 100 150 200 250
Score
-10
0
10
50 100 150 200 250
||COV-wCOV||
2
6
10
samples
50 100 150 200 250
0
5
10
15
Figure 3: Application of the incremental algorithm to the sample data-set. The uppermost picture shows the 27 principal
components computed with the batch algorithm, the second from top the incremental PCA computed without continuity
check, the third picture from top represents the Frobenius norm of the difference between the covariance matrix computed
through the incremental algorithm and a given sample and the one computed on the whole sample-set. The lowermost picture
represents the variances associated to the PCs (eigenvalues of covariance matrix). The covariance matrix and the variable
values are the same for the batch algorithm and the on-line implementation when they are provided with the same samples.
The differences in the pictures are due to the fact that same transformation computed with the batch algorithm is applied to
the whole set, while the one computed online changes with every sample.
pared to the PCs computed with the batch algorithm.
Nevertheless they are a good approximation in that
they are still ordered by variance and most of the vari-
ance is in the first components (i.e. more than 90% is
in the first 5 PCs).
4 DISCUSSION AND
CONCLUSIONS
The continuity issues arise for principal components
with similar variances. When working with real data
this issue often affects the components with smaller
variance which are usually dropped and hence it can
be reasonable to execute the algorithm without taking
measures to preserve the continuity.
Nevertheless it should be noticed that, in some
process analysis, the components with a smaller vari-
ance identify the stable part of the analyzed data, and
hence the one identifying the process, e.g. the con-
trolled variables in a human movement (Lippi et al.,
2011) or the response of a dynamic system known
through the input-output samples (Huang, 2001).
In Figure 4 the effects of discontinuities are
shown: two discontinuities present into the values of
one of the principal components are fixed according
to Section 2.2. In case the continuity is imposed the
phenomenon is limited, but this comes at the price
of modifying the exact computation of the eigenvec-
tors for Q at a given step, in case of a degenerate
eigenspace. Anyway the error introduced on the Q
eigenvectors depends on the threshold used to estab-
lish that two slightly different eigenvalues are degen-
erate and so we can still consider the transformation
to be “exact”, but not at machine precision. In the
reported example, the two big discontinuities high-
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
478
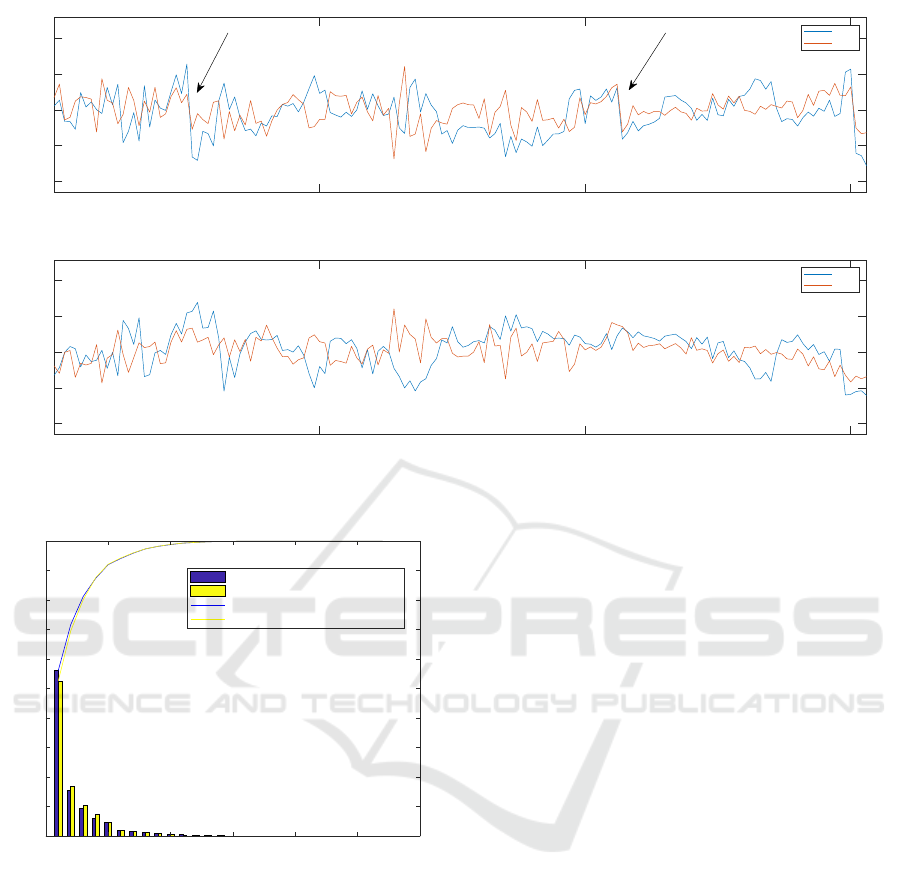
100 150 200 250
-2
-1
0
1
2
Score
Without Continuity Constraint
PC 9
PC 10
100 150 200 250
Samples
-2
-1
0
1
2
Score
With Continuity Constraint
PC 9
PC 10
Figure 4: The figure shows the 9
th
and the 10
th
PCs computed without (top) and with (bottom) continuity constraints. Note
the discontinuity addressed by the arrows.
0 5 10 15 20 25 30
PC
0
10
20
30
40
50
60
70
80
90
100
Var[%]
On-line PCA with continuity correction
Batch PCA
cumulative Var. On-line
cumulative Var. Batch
Figure 5: Variances and cumulative variance of the PCs
computed with the on-line algorithm including the continu-
ity correction (blue) and the ones computed with the batch
algorithm (yellow).The order of the on-line computed PCs
is the one produced by the transformation.. The difference
between the two set of PCs’ variances are due to the conti-
nuity correction and the fact that the variance of the on-line
series is computed on the whole set of data.
lighted by arrows disappear when the continuity is
imposed. Notice that the two PCs have different val-
ues in the corrected version also before the two big
discontinuities because of previous corrections on Q.
The choice as to whether or not the continuity is im-
posed depends on the application, on the data-set and
on the meaning associated with the analysis.
4.1 Software
The MATLAB software implementing
the function and the examples shown
in the figures is available at the URL:
https://it.mathworks.com/matlabcentral/fileexchange/
69844-incremental-principal-component-analysis
ACKNOWLEDGMENTS
The authors thank Prof. Thomas Mergner for the
support to this work.
The financial support from the European project H
2
R
(http://www.h2rproject.eu/) is appreciated.
We gratefully acknowledge financial support for the
project MTI-engAge (16SV7109) by BMBF
G.C. has been supported by I.N.F.N.
REFERENCES
Arta
ˇ
c, M., Jogan, M., and Leonardis, A. (2002). Incremen-
tal PCA for on-line visual learning and recognition.
In Pattern Recognition, 2002. Proceedings. 16th In-
ternational Conference on, volume 3, pages 781–784.
IEEE.
Boutsidis, C., Garber, D., Karnin, Z., and Liberty, E. (2015).
Online principal components analysis. In Proceedings
of the Twenty-Sixth Annual ACM-SIAM Symposium on
Discrete Algorithms, pages 887–901. SIAM.
Incremental Principal Component Analysis: Exact Implementation and Continuity Corrections
479

Degrasand, D. and Cardot, H. (2015). onlinePCA: Online
Principal Component Analysis.
Dunia, R., Qin, S. J., Edgar, T. F., and McAvoy, T. J. (1996).
Identification of faulty sensors using principal compo-
nent analysis. AIChE Journal, 42(10):2797–2812.
Dunn, K. (2011). http://openmv.net/info/distillation-tower.
Hall, P., Marshall, D., and Martin, R. (2000). Merging and
splitting eigenspace models. Pattern analysis and ma-
chine intelligence, IEEE transactions on, 22(9):1042–
1049.
Hall, P. M., Marshall, A. D., and Martin, R. R. (1998). In-
cremental eigenanalysis for classification. In BMVC,
volume 98, pages 286–295.
Huang, B. (2001). Process identification based on last prin-
cipal component analysis. Journal of Process Control,
11(1):19–33.
Lippi, V. and Ceccarelli, G. (2011). Can principal com-
ponent analysis be applied in real time to reduce the
dimension of human motion signals? In BIO Web of
Conferences, volume 1, page 00055. EDP Sciences.
Lippi, V., Ruffaldi., E., Avizzano, C. A., and Bergamasco,
M. (2009). Recognition of hand gestures tracked by a
dataglove: Exploiting hidden markov models discrim-
inative training and environment description to im-
prove recognition performance. In 5th International
Workshop on Artificial Neural Networks and Intelli-
gent Information Processing.
Lippi, V., Ruffaldi, E., Zelic, G., Lagarde, J., Tripicchio, P.,
and Avizzano, C. A. (2011). Uncontrolled manifold
and juggling: Retrieving a set of controlled variables
from data. In BIO Web of Conferences, volume 1, page
00056. EDP Sciences.
Neto, H. V. and Nehmzow, U. (2005). Incremental PCA: An
alternative approach for novelty detection. Towards
Autonomous Robotic Systems.
Sarwar, B., Karypis, G., Konstan, J., and Riedl, J. (2002).
Incremental singular value decomposition algorithms
for highly scalable recommender systems. In Fifth In-
ternational Conference on Computer and Information
Science, pages 27–28.
Shamir, O. (2015). Convergence of stochastic gradient de-
scent for pca. arXiv preprint arXiv:1509.09002.
Smith, S. T. (2005). Covariance, subspace, and intrinsic
crame r-rao bounds. Signal Processing, IEEE Trans-
actions on, 53(5):1610–1630.
ICINCO 2019 - 16th International Conference on Informatics in Control, Automation and Robotics
480
