Flight Radius Algorithms

Assia Kamal Idrissi

1,2

, Arnaud Malapert

2

and R

´

emi Jolin

1

Milanamos, 1047 route des Dolines, Sophia Antipolis, France

2

Universit

´

e C

ˆ

ote d’Azur, CNRS, I3S, France

Keywords:

Flight Radius Problem, Time-independent Model, Graph Database, Shortest Path Algorithms.

Abstract:

In this article, we present the ﬂight radius problem (FRP) on the condensed ﬂight network (CFN). Then, giv-

ing a speciﬁc ﬂight that is deﬁned by an origin and destination (OD) pair, the problem consists in ﬁnding

routes that connect the OD pair and satisfy a regret constraint on time, distance or cost. The found routes help

airline manager to ﬁnd business opportunities. This problem arises in the real world, for instance in some air

transportation companies. The FRP is formulated as ﬁnding a maximal subgraph of nodes belonging to routes

satisfying a regret constraint. Such routes can be found using shortest paths algorithms (SPA). The CFN is

generated using a time-independent approach and stored in the graph database Neo4j. Implementing SPA in

Neo4j is challenging since the graph database stores the weights of the graph in a separate data structure. In

this paper, we propose four methods to solve the FRP: these methods combine parallel and sequential process-

ing with more optimization to overcome time and memory costs. The experimental evaluation demonstrates

that the best algorithm is the extended Dijkstra algorithm which meets the real-time constraints of the targeted

industrial application.

1 INTRODUCTION

The growth of air passenger needs has forced air-

lines to improve their quality of service. The air-

lines should offer ﬂights that match with preferences

of passengers. For this reason, most airlines are in-

terested in the quality of service models called QSI.

This is a market share model used by airlines to esti-

mate their part of the market. The model determines

the probability a traveler selects a speciﬁc itinerary

connecting an airport pair based on a list of criteria

(Jacobs et al., 2012). Then, let us suppose an air-

line network, where nodes are the airports and arcs

represent ﬂights. Each arc is associated with a time,

distance, and cost. The question is to decide if it is

interesting to add a ﬂight between a pair of airports

(OD) in that network. More precisely, adding a new

arc would allow passengers to make itineraries which

are a little bit longer but cheaper than going directly

to their destination? For this, the ﬂight radius prob-

lem (FRP) consists in ﬁnding routes that pass by a

potential arc and satisfy a regret constraint. This con-

straint aims to model passengers preferences. Practi-

cally, there are many criteria to be considered but the

three considered in this study are time, distance, and

cost. The FRP is derived from PlanetOptim appli-

cation developed by the company Milanamos which

is a startup specialized in air transportation. This ap-

plication is a decision tool for airline managers to an-

alyze and simulate a new market using QSI models.

Then, given a speciﬁc ﬂight that is deﬁned by an OD

pair, the process in the application starts by ﬁnding

relevant airports with respect to the speciﬁc ﬂight and

then estimates market share for each route connecting

the origin to the destination. Following this, the air-

line manager makes a decision about adding the new

ﬂight.

Motivating Example. Let us consider this example

for which a new route will be created between NCE

and BKK airports (see Figure 1). This new route

allows passengers coming forward NCE to reach other

airports via BKK. Taking the new ﬂight can be a little

bit longer but cheaper, than going directly to the ﬁnal

destination. The choice depends on the passengers

since they have different preferences. Actually, the

application returns some uninteresting airports. For

instance, going from CDG to DXB via BKK is not a

realistic itinerary for a passenger. The itinerary is too

long and expensive than going directly. Then, the

idea of the FRP is to ﬁlter the routes that do not match

over preferences. For this reason, these preferences

should be integrated into this problem.

370

Kamal Idrissi, A., Malapert, A. and Jolin, R.

Flight Radius Algorithms.

DOI: 10.5220/0007388503700377

In Proceedings of the 8th International Conference on Operations Research and Enterprise Systems (ICORES 2019), pages 370-377

ISBN: 978-989-758-352-0

Copyright

c

Figure 1: Screen-shot of PlanetOptim application. CDG:

Paris, DXB:Dubai, NCE:Nice, BKK:Bangkok, dashed air-

ports represent uninteresting airports.

The FRP is formulated as ﬁnding a maximal sub-

graph such that for each node there exists a path that

satisﬁes the regret constraint. The regret is deﬁned

for each criterion. Such paths can be retrieved using

shortest paths algorithms. We simply begin by work-

ing on the CFN, which is stored in a graph database

Neo4j. This database uses a graph structure and its

graphical interface visualizes easily the airline net-

work. However, Neo4j stores each node’s and arc’s

properties separately: accessing those properties is

relatively slow. Then, implementing the SPA in a

graph database like Neo4j is challenging.

In this paper, we propose four methods to solve the

FRP on the CFN. The ﬁrst two are algorithms that de-

compose the FRP in shortest path problems and solve

them in parallel using as shortest path algorithm: Di-

jkstra and Bellman. The third one extends the Dijkstra

algorithm. However, the last one uses a Bellman al-

gorithm that computes at once all shortest paths from

both origin and destination for all criteria. We use par-

allel processing and sequential with more optimiza-

tion to overcome time and memory costs.

The paper is organized as follows. Section 2 in-

troduces some deﬁnitions of graph theory and some

shortest path algorithms. In Section 3, we describe

the CFN modelling and the graph database structure.

Section 4 gives the formulation of the FRP and its

properties. Section 5 describes the four algorithms.

Section 6 is dedicated to experiments.

2 PRELIMINARIES

This section gives deﬁnitions of graph theory (Ahuja

et al., 1993). Then, it states some shortest path algo-

rithms.

2.1 Graph Theory

A graph G is a couple G = (V, E) consisting of a ﬁnite

set V of nodes and a set E ⊆ V × V of arcs which

are ordered pairs (u, v) if the graph is directed. Each

arc (u, v) ∈ E has an associated non-negative weight

w(u,v). We deﬁne |V | = n, the order of the graph as

the number of nodes meanwhile |E| = m its size.

A graph G

0

= (V

0

,E

0

) is a subgraph of G if

V

0

⊆ V and E

0

⊆ E. A path is a sequence of nodes

{v

1

,v

2

,...,v

k

} such that for each 1 ≤ i < k,(v

i

,v

i+1

) ∈

E holds. If additionally v

1

= v

k

, then the path is a

cycle. The length of a path P is the sum of its arc

weights along the path and is denoted by:

l(P) :=

k−1

∑

i=1

w(v

i

,v

i+1

).

We deﬁne l

?

(s,t) for a given pair of nodes s and t, the

length of the shortest path starting at s and ending at t.

A graph G is connected if there exists a path joining

any two nodes. A transportation network should be a

connected graph.

2.2 Shortest Path Algorithms

There are two categories of shortest path algorithms:

setting algorithms and correcting algorithms. The two

types of algorithms are based on the labeling method

and differ in the strategy of selecting labeled nodes to

be scanned (Cherkassky et al., 1996).

Labeling Method. The labeled method is deﬁned

as follows. For each node u, the method maintains

a distance label d(u), which is an upper bound on

the shortest path length to the node u, parents p(u),

and status S(u). We have three status: unreached,

labeled, and scanned. Initially for each node u,

d(u) = in f , p(u) = nil, and S(u) = unreached. For

a start node, the method sets d(s) = 0 and S(s) =

labeled. Then, the method starts by scanning labeled

nodes until such node does not exist here. The SCAN

operation of a labeled node consists in checking for

all outgoing arcs (u, v) ∈ E, if d(u) + w(u,v) < d(v)

(see Function 1). Then, if it is, d(v) is updated, S(v)

become labeled, and S(u) is scanned. If there are no

negative cycles, the arcs (p(u),u) form a tree rooted

at s. When the algorithm stops, the tree rooted at s is

the shortest path tree.

Function 1: SCAN(u).

foreach (u, v) ∈ E do

if d(u) + w(u, v) < d(v) then

d(v) ← d(u) + w(u,v);

S(v) ← labeled;

p(v) ← u;

end

S(u) ← scanned;

Flight Radius Algorithms

371

Setting Algorithms. The Dijkstra algorithm (Di-

jkstra, 1959) is the most known setting algorithm that

works with positive weight arcs. In this algorithm,

the principle is to select a node with the minimum

weight at each iteration. It scans each node at most

once. That leads to a complexity of O(n

2

) as time

bound in the worst case (Ahuja et al., 1993) where n

is the number of nodes. Two sets are maintained: a

permanently set that represents selected nodes and a

temporary set that designates nodes not yet selected.

The algorithm performs the node selections operation

n times. Each operation requires that it scans each

temporarily labeled node which leads to O(n

2

). Be-

sides, the algorithm performs the distance updates op-

eration for all outgoing arcs of a node v. Overall,

the algorithm requires O (m) since each operation re-

quires, a constant time, O(1). In the end, Dijkstra’s

algorithm solves the shortest path problem in O(n

2

).

There are many versions of Dijkstra’s

algorithm with the aim of improving this time

bound by trying different data structures and several

implementations of the algorithm. In some applica-

tions of the shortest path problem, we want uniquely

to determine the shortest path between two nodes.

Bidirectional Dijkstra’s algorithm solves

the problem of ﬁnding the shortest path between two

nodes faster since it eliminates some unnecessary

computations by reducing the number of visited

vertices in practice. Besides, the A* search is an

acceleration of Dijkstra’s algorithm in the sense

that it preferably settles nodes that are closer to the

destination when ﬁnding the shortest path between

two nodes.

Correcting Algorithms. The Bellman algorithm

achieves the best currently known bound of time with

negative weight arcs O(nm). The algorithm main-

tains the set of labeled nodes in a FIFO queue and al-

lows detecting a negative cycle in a weighted directed

graph. In Bellman, the next node to be scanned is

removed from the head of the queue; a node that be-

comes labeled is added to the tail of the queue. The

algorithm performs at most n−1 passes through arcs.

Since each pass requires O (1) computations for each

arc, this implies O(nm) time bound for the algorithm.

Bellman is qualiﬁed as a robust algorithm since there

is no priority queue. Some heuristics have been in-

troduced to improve the practical performance of the

algorithm. For instance, (Cherkassky et al., 1996) in-

troduce a parent checking heuristic that scans a

node only if its parent is not in a decrease.

3 CONDENSED FLIGHT

NETWORK

3.1 Modelling

The condensed ﬂight network (CFN) is generated

from the ﬂight timetable using the time-independent

model. Nodes represent airports meanwhile the pres-

ence of an arc indicates that there exists at least one

elementary connection between two airports. Time,

distance, and cost labels are associated with each arc

of the CFN. In our study, we omit time scheduling

and keep only the transfer time represented by an arc

in the graph. This technique is often used to model the

information about the transfer since it is important in

computing shortest paths (Delling et al., 2009).

The model consists in creating two nodes for each

airport node: one to model ﬂight departures and an

other to represent ﬂight arrivals. Then, we introduce

three different types of arcs. board at is inserted

from an airport to departure node, alight at is in-

serted from an arrival node to the airport, and ﬁnally a

connect to to model the transfer time between an ar-

rival node and departure node of the same airport with

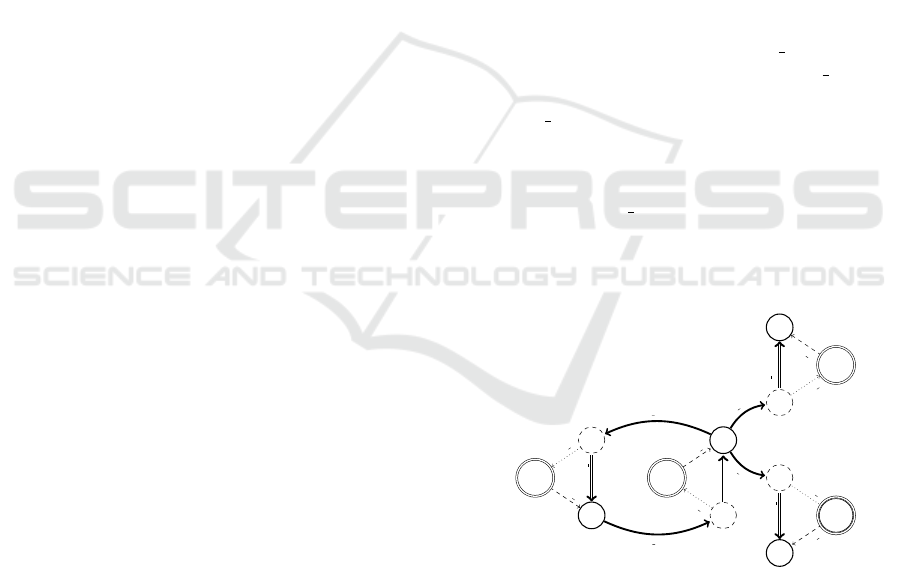
a transfer time. In Figure 2, the graph contains four

airports: NCE, BKK, PEK, ICN and four ﬂight arcs

referenced by year month. Nodes in thin style repre-

sent departures, dashed nodes for arrival nodes. Dou-

ble arcs are transferring time. Besides, dotted arcs for

arrivals and dashed arcs for departures.

NCE

d

1

o

1

BKK

o

2

d

2

P EK

o

3

d

3

ICN

o

4

d

4

year month

connect to

alight at

board at

alight at

board at

year month

connect to

year month

board at

alight at

connect to

Figure 2: The CFN of the motivating example.

3.2 Graph Database

The CFN is stored in Neo4j graph database (Neo

Technology, 2017). Neo4j is used for many appli-

cations, typically recommendation systems and com-

plex networks like transportation network. Neo4j

graph database follows the property graph model to

store and manage its data. In Neo4j, data are repre-

sented in nodes, relationships, and properties or at-

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

372

tributes. Both nodes and relationships contain proper-

ties (Robinson et al., 2015). A relationship connects

a pair of nodes: start & end, it has a direction and a

type. Neo4j proposed APOC (Awesome Procedures

on Cypher) as stored procedures that regroup a list of

procedures (Neo Technology, 2017). In addition, the

graph database offers the possibility to implement al-

gorithms as user deﬁned procedures. It simpliﬁes the

querying process.

Shortest Path Algorithms in a Graph Database.

The Neo4j graph database is proved suited for the

shortest path calculation for transport purposes (Miler

et al., 2014). The authors compare the performance of

Dijkstra implemented on Neo4j and PostgreSQL.

Results show that Neo4j outperforms the relational

database. It comes from the structure of the graph

database, the nodes and relationships are stored in

a very compact, quick-to-access format. Once a

node or relationship is retrieved, getting the adja-

cent relationships or nodes is very fast. However,

it stores each node’s (and relationship’s) properties

separately, meaning that looking through properties

is relatively slow. Then, accessing to properties ﬁle

are costly which leads to extra IO. This is the im-

portant difference between the graph theory and the

graph database.

Existing Database. The CFN, stored in the graph

database, is generated from a real-world database

which is a NoSQL database. This database uses a

MongoDB that stores data in a disconnected way and

does not use a graph structure. In MongoDB, data are

collected and queried monthly. Then it makes sense

to create a relationship per period which is a month

of the year. The relationship represents ﬂight infor-

mation (see Figure 2). We dispose of historical data

about the last ﬁfteen years. The CFN is generated for

two years and has 13,732 nodes and 1,148,303 rela-

tionships.

4 PROBLEM FORMULATION

This section gives the formulation of the ﬂight radius

problem and also some of its properties.

4.1 Formulation

The ﬂight radius problem consists in retrieving only

relevant routes regarding a speciﬁc ﬂight, and satisfy-

ing the regret constraint. The considered ﬂight is de-

ﬁned by and OD pair and represented by an arc (o, d)

in the CFN where o, d ∈ V . Then, traveling from

o

1

∈ V to d

1

∈ V by passing through the arc (o,d)

is interesting if and only if the path {o

1

,..,o,d,..,d

1

}

between o

1

and d

1

satisﬁes the regret constraint. The

satisfaction of the constraint depends on the shortest

path between o

1

and d

1

. Let R be a Boolean regret

constraint deﬁned on paths of the graph G. Therefore,

the problem consists in ﬁnding a maximal subgraph,

in terms of nodes, such that each node supports a path

that satisﬁes the regret constraint R. It means that

there exists a path connecting nodes of this subgraph

passing through the arc (o,d) and satisfying one of

the criteria. Such paths are called valid paths. The

problem is formulated as follows:

Input: a graph G = (V, E), an arc (o, d), and a re-

gret constraint R

Output: a maximal subgraph G

0

= (V

0

,E

0

) of G

that each node belongs to a path passing through

the arc (o,d) and satisfying the regret constraint.

The regret constraint R is deﬁned as follows: let

w(i, j) be the weight of the arc (i, j), l

?

(i, j) the length

of the shortest path from i to j, and l(i, j) the length

of a path passing through the arc (o, d). Then, let con-

sider the following regret constraint which is deﬁned

for each criterion:

R

od

(i, j) = l(i, j) ≤ l

?

(i, j) + K (1)

Where K ≥ 0. Each node in the maximal subgraph

G

0

must support at least a valid path satisfying at least

one criterion. The deﬁnition of the regret constraint

can appear similar to the notion of upper tolerance

(Shier and Witzgall, 1980). However, it is not the case

since our regret function depends on the given regret

parameter K.

4.2 Properties

The following property is similar to the one saying

that a subpath of the shortest path is also a shortest

path (Ahuja et al., 1993).

Property. The subpath of a valid path is also a valid

path.

l(i, j) ≥ l

?

(i,o) + w(o,d) + l

?

(d, j) (2)

The shortest path satisﬁes the triangle inequality prop-

erty: following the shortest path from i to o, passing

by the arc (o,d), and then following the shortest path

from d to j, is always a valid path if one exists.

Flight Radius Algorithms

373

Proof.

l

?

(i,o)+w(o,d) + l

?

(d, j) ≤ l

?

(i, j) + K



l

?

(i,o)+w(o,d) + l

?

(d, j) ≤



l

?

(i,o)+l

?

(o, j) + K

w(o,d) + l

?

(d, j) ≤ l

?

(o, j) + K

−→

R

od

( j) = l(o, j) ≤ l

?

(o, j) + K (3)

Where

−→

R refers to outgoing direction. Following

to the inequality 4.2, the subpath from o to j of a valid

path is also valid. In addition, the subpath from i to

d is valid. The proof of the property for incoming

direction

←−

R is symmetric.

Finally, the search can be restricted to the valid

shortest paths starting from o or ending at d. Note

that when K = 0, the set of valid paths represents all

the shortest paths passing by the arc (o,d).

Lemma 1. Any shortest path passing through the arc

(o,d) is also a valid path. Therefore, all its nodes are

supported.

5 ALGORITHMS

In this section, we propose four algorithms. First two

algorithms decompose the FRP in shortest path prob-

lems and solved them in parallel using either the Di-

jkstra or the Bellman algorithm. The third algorithm

extends the Dijkstra algorithm to avoid useless com-

putations. The fourth algorithm extends the Bellman

algorithm to compute all shortest paths for all crite-

ria at once. This last algorithm increases memory re-

quirement since processors access the same memory.

Thus, we propose to combine between sequential and

parallel processing to optimize the runtime and mem-

ory consumption. These algorithms perform parallel

computations when it is possible.

input : a CFN G = (V, E), an arc (o,d), the

criteria C

output: the set of supported nodes S

For sake of simplicity, the algorithm returns the

set of supported nodes and worries about storing the

parents of the supported nodes. In practice, the algo-

rithm also returns the union of the supported trees for

each direction and for each criterion. Based on the

regret functions, let’s deﬁne:

R(i,dir) =

(

−→

R

od

(i), if (dir = out)

←−

R

od

(i), if (dir = in)

5.1 Shortest Path Decomposition

The shortest path decomposition solves the FRP

problem by using two shortest path problems, one

from the origin o and the other from the destination

d, for each direction and for each criterion in parallel.

Then supported nodes are computed by checking the

regret constraint.

Algorithm 1: SP Decomposition.

foreach dir ∈ {in, out} in parallel

foreach c ∈ C in parallel

ShortestPaths(o,c,dir);

ShortestPaths(d, c, dir);

foreach i ∈ V do

if R(i,dir) then

S ← S ∪ {i} ;

end

return S

The shortest path subroutine is either Dijkstra or

Bellman algorithm. The computation of the short-

est paths from the origin and from the destination

is sequential for simplifying the search of supported

nodes.

5.2 Flight Radius Algorithms

Here, we design variants of Dijkstra and Bellman al-

gorithm tailored for solving the ﬂight radius problem.

5.2.1 Dijkstra FR Algorithm

We present an algorithm that computes the shortest

path from o, and then computes lazily the shortest

path from d by skipping unsupported nodes (see al-

gorithm 2). Here, the criteria are processed sequen-

tially. At each iteration, the algorithm scans the node

with the minimum weight and then relaxes its neigh-

bors. So, we check if the node satisﬁes the regret

function otherwise we skip the node. Therefore, we

skip non supported nodes that cannot be extended into

valid paths. The algorithm ends if the queue becomes

empty or all shortest paths to the supported nodes are

found. Function SCAN(i,c,dir) calls the function

presented in 2.2 for each criterion and direction.

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

374

Algorithm 2: Dijkstra FR Algorithm.

foreach dir ∈ {in, out} in parallel

foreach c ∈ C do

Dijkstra(o,c,dir);

enqueue(Q,d);

while Q 6=

/

0 and isNotClosed() do

i ← argmin

j∈Q

(d[ j]);

dequeue(Q,i);

if R(i,dir) then

S ← S ∪ {i} ;

SCAN (i,c,dir);

end

return S

5.2.2 Bellman FR Algorithm

We propose a variant of Bellman algorithm (algorithm

3) that computes at once all shortest paths from the

origin and from destination for all criteria. Then,

more nodes are added to the queue. Here, the SCAN

function updates all paths from the origin and from

the destination for all criteria.

Algorithm 3: Bellman FR Algorithm.

foreach dir ∈ {in, out} in parallel

enqueue (Q,o);

enqueue (Q,d);

while (Q 6=

/

0) do

i ← dequeue(Q);

SCAN (i,C, dir);

end

foreach i ∈ V do

if R(i,dir) then

S ← S ∪ {i} ;

end

return S

6 EXPERIMENTS

In this section, we evaluate the algorithms to solve

the FRP on real-world datasets. The SP decomposi-

tion algorithms used massive parallelism. However,

the FRP algorithms used more optimization than par-

allelism. In other words, we are especially interested

in comparing the runtime of the algorithms which im-

pacts the user experience of PlanetOptim. Besides,

the number of scanned nodes by the algorithm. This

metric is very important since it determines the ac-

cessed property values (criteria) of a relation. Those

properties are accessed incurs extra IO the ﬁrst time.

The reason is that properties reside in a separate store

ﬁle from the relationships (after that, however, they

are cached) (Robinson et al., 2015). Our experimen-

tal protocol aims to answer the following questions:

Which algorithm is the fastest and, will, therefore pro-

vide the best user experience? Is it worthwhile to de-

sign algorithms for ﬂight radius problem compared to

the decomposition into shortest path problems? Does

reduction of the number of scanned nodes lead to a

reduction of the runtime? How does the performance

evolve with the number of criteria? First, we present

how the benchmarks instances have been generated.

Second, runtime of the algorithms are compared, and

then, the relation between the runtime and the num-

ber of scanned nodes is studied. Last, we analyze the

ratio of the ﬂight radius algorithms over shortest path

decompositions depending on the number of criteria.

All the experiments were led on a computer running

on Ubuntu 16.04.5 with 32 GB of RAM and one In-

tel Core i7-3930K 3.20GHz processor (6 cores). The

implementation is based on Neo4j and APOC version

3.2.0. All algorithms are implemented in Java 8.

6.1 Instances Generation

The CFN contains historical data for the years 2016

and 2017 (24 year-months). Each year-month corre-

sponds to a different graph. The condensed ﬂight net-

work contains 13,732 nodes and 1,148,303 arcs. A

benchmark instance must specify the year-month, the

OD-pair (o,d), the number of criteria, and their re-

grets.

The number of criteria is one (time), two (time, dis-

tance), or three (time, distance, cost). For each crite-

rion, two values are considered for its regret K: 0 and

the median (over all relations and year-months). The

value 0 means that only shortest paths passing through

the arc (o, d) are valid, whereas many other paths are

valid with the median. For instance, the median dura-

tion of a ﬂight is approximately two hours. So a path

between i and j passing through the arc (o, d) is valid

if it does not exceed the duration of the shortest path

between i and j by four hours (the median duration

plus the minimum connection time).

For each year-month, each number of criteria, and

each combination of criteria values, a few pairs of

origin and destination (o, d) are drawn randomly. At

the end, more than ten thousand instances have been

tested.

Flight Radius Algorithms

375

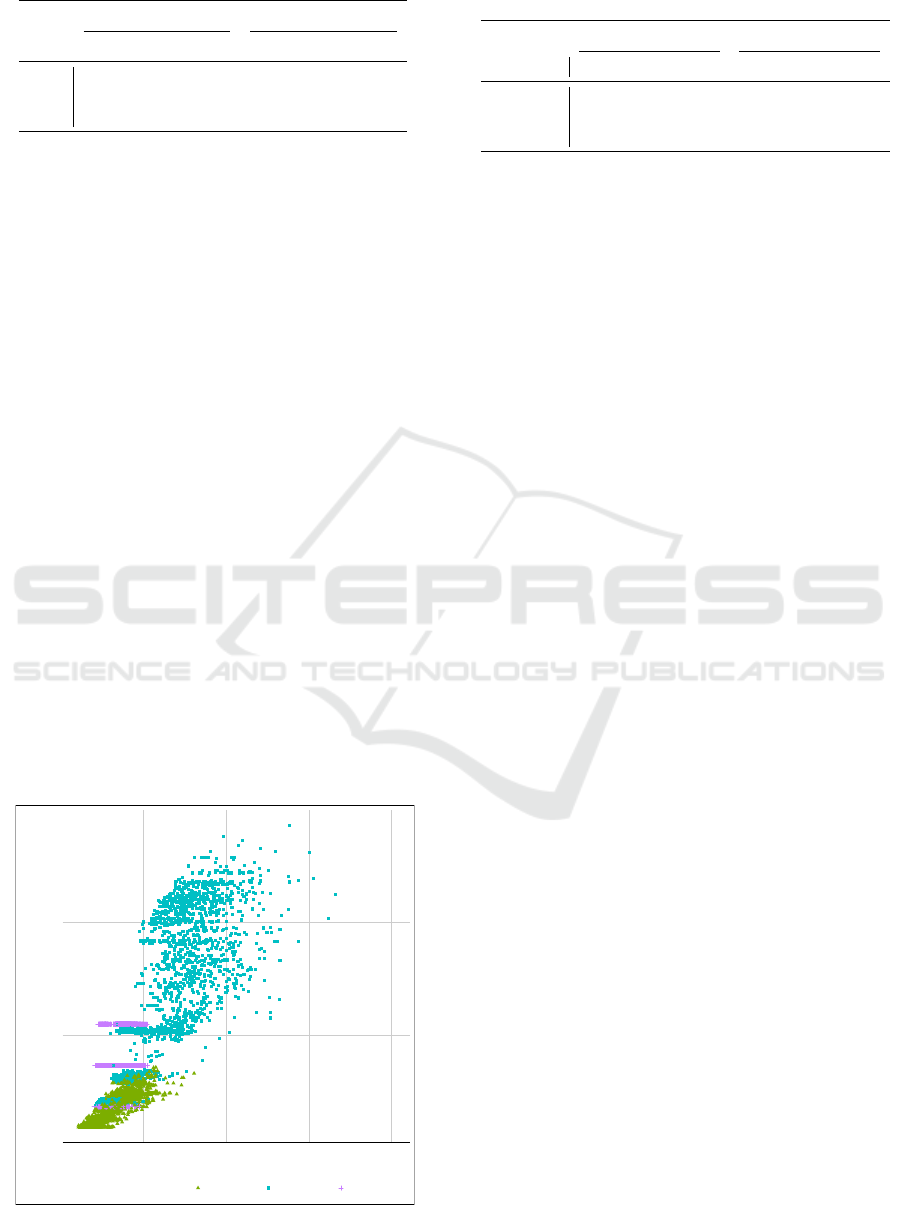
Table 1: Distribution of runtimes in milliseconds.

SP Decomposition FR Algorithm

Dijkstra Bellman Dijkstra Bellman

avg 266 500 231 604

std 60 198 90 282

max 418 1328 644 1612

6.2 Algorithms Comparison

Table 1 gives the average, standard deviation, and

maximum runtime in milliseconds of the shortest path

decompositions and of the ﬂight radius algorithms us-

ing Bellman or Dijkstra. The Dijkstra variants are ap-

proximately two times faster and have a lower stan-

dard deviation than their Bellman counterparts. The

algorithm based on Dijkstra is slightly faster than the

decomposition whereas it is not the case for Bellman.

Figure 3 analyzes the relation between the run-

time and the number of scanned nodes for each al-

gorithm. Each point represents one instance and its

x-coordinate is the runtime in milliseconds, whereas

its y-coordinate is the number of scanned nodes. The

color of a point indicates which algorithm solved the

instance. The ﬂight radius algorithm based on Bell-

man scans fewer nodes than the shortest path decom-

position based on Bellman (red points are below the

blue ones), but without reducing the runtimes (blue

points are on the left of the red ones).

It means that the additional time spent to read all

properties is not compensated by the decrease in the

number of scanned nodes. For Dijkstra, the number

of scanned nodes for the decomposition only depends

on the number of criteria whereas it is not the case

●

● ●

●

●●

●

1e+05

2e+05

400 800 1200 1600

Runtime

ScanCount

Algorithm

●

FR Bellman FR Dijkstra SP Bellman SP Dijkstra

Figure 3: Analysis of the runtimes and scan counts.

Table 2: Improvements of the FR algorithms over the SP

decompositions.

Dijkstra Bellman

#Criteria Runtime #Scans Runtime #Scans

1 0.69 0.57 1.04 0.81

2 0.79 0.41 1.15 0.57

3 1.09 0.43 1.37 0.49

for the ﬂight radius algorithm. In this case, a lower

number of scanned nodes implies a reduction of the

runtime because the number of red properties is also

reduced (green points are on the left and below purple

points). As expected, Dijkstra based algorithms scan

fewer nodes than those based on Bellman.

Last, Table 2 gives the geometric mean of the im-

provements provided by FR algorithms over the SP

decompositions in terms of runtimes and number of

scanned nodes. The improvement is the ratio of the

runtime of FR algorithm over the SP decomposition

for Bellman or Dijkstra. The improvement is lower

than 1 if the FR algorithm is better than the SP de-

composition and greater than 1 otherwise. Both FR

algorithms based on Dijkstra or Bellman reduce the

number of scanned nodes and the reduction increases

with the number of criteria. The runtimes are not re-

duced for Bellman, but are also reduced for Dijkstra

when the number of criteria is one or two. When there

are three criteria, the reduction of scanned nodes does

not compensate for the additional parallelization of

the decomposition.

To conclude, FR algorithm based on Dijkstra is

the most efﬁcient, and satisﬁes the real-time con-

straint of PlanetOptim. Besides, the runtimes of

the algorithms increase with the number of criteria in

spite of the parallelization. When there are three cri-

teria, the reduction of the number of scanned nodes

does not help to reduce the runtimes of FR algorithm

based on Dijkstra, a perspective is to parallelize along

the criteria.

7 CONCLUSION

This work presents some algorithms for solving the

FRP on the CFN. The problem was formulated as

ﬁnding a maximal subgraph, in terms of nodes, such

that each node supports a path satisfying a regret con-

straint. This constraint is used to model passengers

preferences: time, cost, or distance. We propose four

algorithms based on SPA to solve the FRP. These al-

gorithms combine sequential and parallel processing

to overcome time and memory costs. We are working

on an industrial context: the CFN is generated from

ICORES 2019 - 8th International Conference on Operations Research and Enterprise Systems

376

a Milanamos database and stored in a graph database.

Implementing SPA in graph databases is challenging

since accessing to properties ﬁles, where criteria in-

formation are stored, is costly. This is the important

difference between graph theory and graph database.

Then, two metrics are used to evaluate algorithm’s

performances: runtime and number of scanned nodes.

The last one metric evaluates the number of properties

ﬁle access. Experiments show that the FR algorithm

based on Dijkstra is the most efﬁcient, and satisﬁes

the real-time constraint of PlanetOptim. The next

step of the study is to include QSI models to speed up

computations. Latter, our solution will be integrated

in the industrial application PlanetOptim.

ACKNOWLEDGMENTS

We would like to thank Carine F

´

ed

`

ele for her insight-

ful comments on the paper, as these comments led us

to an improvement of the work.

REFERENCES

Ahuja, R. K., Magnanti, T. L., and Orlin, J. B. (1993).

Network ﬂows: theory, algorithms, and applications.

Prentice hall.

Cherkassky, B. V., Goldberg, A. V., and Radzik, T. (1996).

Shortest paths algorithms: Theory and experimental

evaluation. Mathematical programming, 73(2):129–

174.

Delling, D., Pajor, T., Wagner, D., and Zaroliagis, C. (2009).

Efﬁcient Route Planning in Flight Networks. ATMOS,

12.

Dijkstra, E. W. (1959). A note on two problems in connex-

ion with graphs. Numer. Math., 1(1):269–271.

Jacobs, T. L., Garrow, L. A., Lohatepanont, M., Koppel-

man, F. S., Coldren, G. M., and Purnomo, H. (2012).

Airline planning and schedule development. In Quan-

titative Problem Solving Methods in the Airline Indus-

try, pages 35–99. Springer.

Miler, M., Medak, D., and Odoba

ˇ

si

´

c, D. (2014). The short-

est path algorithm performance comparison in graph

and relational database on a transportation network.

Promet-Trafﬁc&Transportation, 26(1):75–82.

Neo Technology (2017). Neo4j. https://www.neo4j.

com.

Robinson, I., Webber, J., and Eifrem, E. (2015). Graph

databases: new opportunities for connected data. ”

O’Reilly Media, Inc.”.

Shier, D. R. and Witzgall, C. (1980). Arc tolerances in

shortest path and network ﬂow problems. Networks,

10(4):277–291.

Flight Radius Algorithms

377