Magneto-division of Vesicle: Theory and Possible Experiments
Yao-Gen Shu
∗
and Zhong-Can Ou-Yang
CAS Key Laboratory of Theoretical Physics, Institute of Theoretical Physics,
Chinese Academy of Sciences, Beijing 100190, China
Keywords:
Nanoreactor, Division, Deformation Theory, Diamagnetic Amphiphilic Block-copolymers, Magnetic Manip-
ulation.
Abstract:
Our theory has revealed the possibility that the vesicle, which isself-assembled by the diamagnetic amphiphilic
block-copolymers, can be manipulated into division by external magnetic field. For the case of the constraint
of constant surface area, the passive division can successively take place for 10 times in the situation of
∆p = −15 mV; and only 4.5% solution that is contained by the original vesicle with a radius of 4 µm can been
retained by 512 vesicles that each contains about 2.31×10
7
nm
3
. Thus, if the water channels are embedded in
the membrane of vesicle, this method can not only concentrate the solution, but also produce a large number
of nanoreactors, which is beneficial to yield an ensemble conclusion of chemical reaction in a very short
times. Another case of the constraint of constant volume can also be easy realized by enough supply of the
diamagnetic amphiphilic block-copolymers in the progress of division. The latter case is also important for
reaction statistics because the original solution can be in equal volume divided into hundreds nanoreactors.
This nanoreactor can be used to mimic the reaction of some organelles in vitro. We hope experimenters will
try them in future experiments.
1 INTRODUCTION
In recent years, chemists and biologist have worked
to understand how fundamental chemical princi-
ples change when systems are confined to spaces
with nanoscale dimensions or sub-microliter vol-
umes. Nanoreactors offer a means of creating unique
nanoscale chemical environments partitioned from
the surrounding bulk space to explore chemistry in
a variety of different types of nanoreactors such as
nanopores and nanoholes, hollow nanoparticles and
porous architectures, and tubular nanostructures, as
well as those that are native to biological structures,
such as protein pores, channels and organelles. Such
systems enable the number of molecules under study
to be controlled in ways not possible with bulk sys-
tems. The different behaves of the same molecules
between nanoreactors and bulk systems are possible
to be revealed. Thus, nanoreactors can be exploited
to gain new fundamental understanding of a chemi-
cal system or process or to develop an analytical tool
based upon this insight(Petrosko et al., 2016). How-
ever, the lack of material with large spontaneous cur-
vature has been blocking the development of nanore-
actors.
The diamagnetic amphiphilic block-copolymers
plays more and more important role in self-assembly
of vesicle due to its highly anisotropic magnetic sus-
ceptibility. It has been used to assemble an infolded
bowl-shaped vesicle(van Rhee et al., 2014; Hickey
et al., 2011), which is called a stomatocyte, so that
the mouth of the polymeric self-assembly can be re-
versibly opened and closed by varying an external ho-
mogeneous magnetic field. Thus, the artificial mouth
functions as a magneto-valve, and the whole artificial
stomatocyte has a great potential for the application
of targeted release of drug.
The spontaneous curvature model of the equilib-
rium shapes and deformations of lipid bilayer vesi-
cles(Helfrich, 1973), which was proposed by Hel-
frich for more than four decades, has been engaged
by us to reveal the mechanism of reversible opening
and closing of mouth and give out the relation be-
tween the size of mouth and the external magnetic
field(Deng et al., 2018). In this paper, we try to pro-
pose the model of magneto-division of vesicle which
is assembled by the diamagnetic amphiphilic block-
copolymers with a highly anisotropic magnetic sus-
ceptibility. We hope this model will inspire experi-
menter to realize it and meet the needs of nanoreac-
tors.
Shu, Y. and Ou-Yang, Z.
Magneto-division of Vesicle: Theory and Possible Experiments.
DOI: 10.5220/0007347001490153
In Proceedings of the 12th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2019), pages 149-153
ISBN: 978-989-758-353-7
Copyright
c
 2019 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
149

2 THE DEFORMATION THEORY
OF A SPHERICAL VESICLE
Here, we consider an infinitesimal deformation of
a spherical vesicle of radius r in a spatially uni-
form magnetic field intensity H (= B/µ, where B
is magnetic induction and µ is magnetic permeabil-
ity.) by minimizing the sum of bending energy (cur-
vature elastic energy: F
c
=
1
2
k
c
H
(c
1
+ c
2
−c
0
)
2
dA)
and the free energies contributed by osmotic pressure
(∆p
R
dV), the tension of membrane (λ
H
dA) and the
interaction between the magnetic field and the con-
stituent molecules (F
B
= −
1
2
∆χtµ
H
(H ·n)
2
dA), that
is(Iwamoto and Ou-Yang, 2013; Ou-Yang and Hel-
frich, 1987; Chandrasekhar, 1992),
F =
κ
c
2
I
(2H + c
0
)
2
dA+ ∆p
Z
dV + λ
I
dA
−
1
2
∆χtµ
I
(H ·n)
2
dA, (1)
where κ
c
is the bend modulus, c
1
and c
2
are the prin-
cipal curvatures, while H = −(c
1
+ c
2
)/2 is the mean
curvature, c
0
is the spontaneous curvature, ∆p ≡
p
out
− p
in
is the difference pressure of the transmem-
brane, λ is the Lagrange multiplier of the membrane
tension to ensure a constant area, t is the thickness
of membrane, n is the outward unit normal and ∆χ ≡
χ
k
−χ
⊥
, in which χ is the diamagnetic susceptibility,
while χ
k
and χ
⊥
are diamagnetic susceptibility paral-
lel and perpendicular to n respectively.
To obtain a description of the deformation of a
sphere of radius r, we have to solve the variational
equation:
δF = δF
1
+ δF
B
= 0, (2)
where F
1
≡ F
c
+ ∆p
R
dV + λ
H
dA. The equilibrium
vesicle surface is specified by the position vector
r(u,v) where u and v are surface parameters. We as-
sume that the radius of sphere is r
0
at H = 0 and will
be slightly distorted into
r ≡r
0
+ ψ(u,v)n (3)
due to any H perturbation, where ψ(u,v) is a smooth
infinitesimal function.
At first, we only consider the case of H = 0, then,
δ
(1)
F
1
=
κ
c
2
I
h
(2H + c
0
)
2
δ
(1)
(dA)
+4(2H + c
0
)δ
(1)
HdA
i
+∆p
Z
δ
(1)
(dV) + λ
I
δ
(1)
dA
=
I

∆p−κ
c
(2H + c
0
)(2H
2
−c
0
H −2K)
+2κ
c
∇
2
H −2λH

ψ
√
gdudv
= 0,
which leads to(Ou-Yang and Helfrich, 1987):
∆p−κ
c
(2H + c
0
)(2H
2
−c
0
H −2K)
+2κ
c
∇
2
H −2λH = 0, (4)
where K ≡ c
1
c
2
is a Gaussian curvature, the
Laplace-Beltrami operator ∇
2
is defined as ∇
2
≡
(1/
√
g)∂
i
(g
ij
√
g∂
j
) (i, j = u, v), in which g
ij
≡ ∂
i
r ·
∂
j
r, g
ij
≡(g
ij
)
−1
and g ≡det(g
ij
) are the coefficients
of the first fundamental form of the surface.
For a convex surface, such as the outside spher-
ical vesicle as shown in Fig.2 a, the curvature H =
−1/r. Its radius r
0
(at H = 0) then can be determined
by(Ou-Yang and Helfrich, 1987)
∆pr
3
0
+ 2λr
2
0
−κ
c
r
0
c
0
(2−c
0
r
0
) = 0. (5)
If H 6= 0 (H is along with z in a spherical coordi-
nate system ), Eq.(2) will become
δF = δ
(1)∗
F
1
+ δ
(1)
F
B
= 0
where δ
(1)∗
F
1
is different from δ
(1)
F
1
by considering
λ → λ + δλ due to H 6= 0. Then,
δ
(1)∗
F
1
=
I
[κ
c
(2δH)(2H
2
0
−c
0
H
0
−2K
0
)
+ κ
c
(2H
0
+ c
0
)(4HδH −c
0
δH −2δK)
+ 2κ
c
(δ∇
2
)H
0
+ 2κ
c
∇
2
0
δHλH
−2δλH
0
−2λδH]ψdA
=
I

2
r
0
δλ+
∑
κ
c
r
4
0

4c
0
r
0
−
2λr
2
0
κ
c
−c
2
0
r
2
0
− 2l(l + 1)]

1−
l(l + 1)
2

a
l
Y
l

ψdA, (6)
where H
0
= −1/r
0
and H = −1/r(Ou-Yang et al.,
1999).
On the other hand,
δ
(1)
F
B
= −
1
2
∆χtµ

I
(n·H )
2
δ
(1)
(dA)
+2
I
(n·H )H ·δ
(1)
ndA

= ∆χtµ
I

(H ·n)
2
Hψ+ (H ·n)H ·∇ψ

dA
= ∆χtµ
I

H(H ·n)
2
+ ∇·[H (H ·n)]

ψdA
=
I

t∆χ
µ

B
2
cos
2
θ
r
0
−
B
2
sin
2
θ
r
0

ψdA
≡ −
I
(g
0
Y
0
+ g
2
Y
2
)ψdA, (7)
where g
0
= t∆χB
2
√
4π/(3r
0
µ), g
2
= 4g
0
/
√
5. In the
derivation of Eq.(7), we have engaged the formulas:
I
(H ·n)H ·∇ψdA =
I

∇·[ψ(H ·n)H ]
− ψ∇·[H (H ·n)]

dA,
I
∇·[ψ(H ·n)H ]dA =
I

−2(H ·n)
2
Hψ

dA,
BIODEVICES 2019 - 12th International Conference on Biomedical Electronics and Devices
150

δdA = −2HψdA and δn = −∇ψ = −g
ij
r
i
∂
j
ψ (r
i
=
∂
i
r)(Weatherburn, 1927; Ou-Yang et al., 1999).
In a spherical coordinate system, u = θ, v = φ,
r
0
= r
0
(cosφsinθ,sinφsinθ,cosθ) and n = r
0
/r
0
.
Thus, the weak deformation of the radius at (θ,φ) is
r = r
0
+ ψ(θ,φ) with
ψ(θ,φ) =
∑
l,m
a
l,m
Y
l,m
(θ,φ)
=
∞
∑
l=0
a
l
Y
l
(8)
where Y
l
is a spherical harmonic function.
Now, we consider the constraint of the constant
surface area of the vesicle during deformation,
δA =
I
−2Hψr
2
0
sinθdθdφ
=
I
−2r
0
ψ(a
0
Y
0
+ a
2
Y
2
)sinθdθdφ
= 4
√
πr
0
a
0
= 0, (9)
which leads to a
0
= 0. Combining Eqs.(6), (7) with
(9), we get:
δλ =
t∆χB
2
6µ
,
a
2
=
r
4π
5
−
4
3
t∆χB
2
r
3
0
2κ
c
µ

2λ
κ
c
r
2
0
+ c
2
0
r
2
0
−4c
0
r
0
+ 12

.
Then,
ψ =
∞
∑
l=0
a
l
Y
l
= a
2
Y
2
= −
4
3
t∆χB
2
r
3
0
P
2
(cosθ)
2κ
c
µ

2λ
κ
c
r
2
0
+ c
2
0
r
2
0
−4c
0
r
0
+ 12

,(10)
where P
2
is a Legendre function.
The deformation equation of a spherical vesicle
determined by Eq.(2) in the case of H 6= 0 can be
described by
r
B
(θ) = r
0
"
1−
2t∆χ
3κ
c
µ
B
2
r
2
0
P
2
(cosθ)
2λ
κ
c
r
2
0
+ c
2
0
r
2
0
−4c
0
r
0
+ 12
#
≡ r
0

1+
qB
2
r
2
0
(3cos
2
θ−1)
ξr
2
0
−4c
0
r
0
+ 12

(11)
where q ≡−t∆χ/(3κ
c
µ), ξ ≡2λ/κ
c
+ c
2
0
.
3 RESULTS
Eq.(11) implies that the “division” of the vesicle oc-
curs most likely at θ = π/2. The magnitude of the
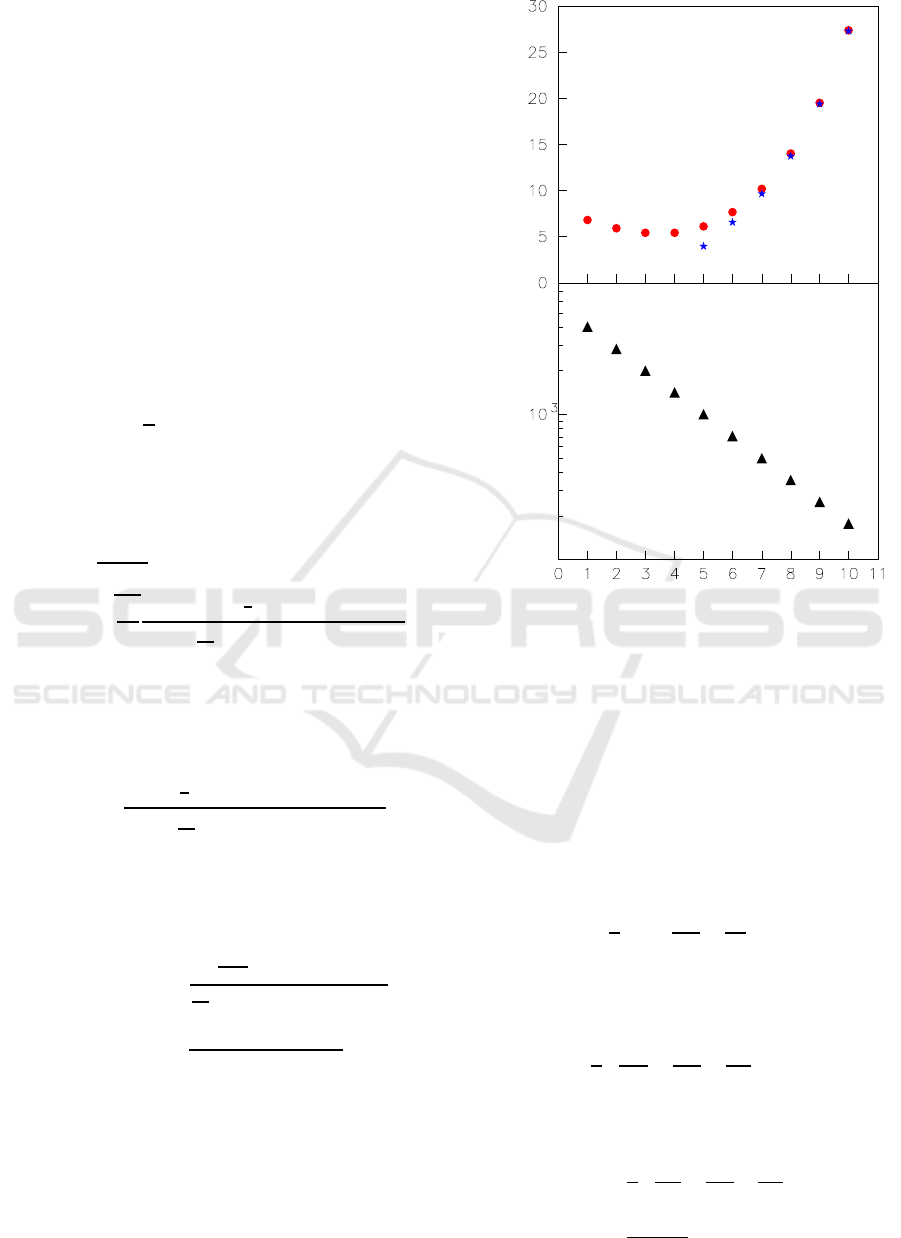
●: ∆p=-15 mv
★: ∆p=15 mv
B
d,i
(T)
a
r
0,i
(nm)
i (the number of division)
b
Figure 1: a. The relation between the magnitude of the
manipulated magnetic field and i
th
division according to
Eq.(14), where red dot indicates the situation of ∆p = −15
mV, while blue star does the one of ∆p = 15 mV. There is
a minimum manipulated magnetic field near r = 2000 nm
for the situation of ∆p = −15 mV. b. The radius varies
for each division according to Eq.(15). c
0
= −10
−3
nm
−1
with r
0,1
= 4×10
3
nm, t = 26 nm(van Rhee et al., 2014),
κ
c
= 2.6 ×10
−21
J(Manyuhina et al., 2007), ∆χ ≈ −2.0×
10
−7
(van Rhee et al., 2014; Sutter and Flygare, 1969), and
µ
water
≈1.26×10
−6
N·A
−2
.
manipulated magnetic field has to satisfy:
B
2
d
=
1
q

ξ−
4c
0
r
0
+
12
r
2
0

. (12)
Combining with Eq.(5), we get the magnitude of the
external magnetic field for the first “division”
B
2
d,1
=
1
q
"
12
r
2
0,1
−
2c
0
r
0,1
−
∆p
κ
c
r
0,1
#
, (13)
so that for the i
th
passive division
B
2
d,i
=
1
q
"
12
r
2
0,i
−
2c
0
r
0,i
−
∆p
κ
c
r
0,i
#
, (14)
r
0,i
=
r
0,1
2
(i−1)/2
, (15)
Magneto-division of Vesicle: Theory and Possible Experiments
151

because of the constraint of constant surface area.
The results of Eqs.(14) and (15) have been indicated
in Fig.1 a and b respectively. For the situation of
∆p = −15 mV, B
d,i
rises no longer monotonically
with decreasing of radius of the vesicle. It may be
related with the combination of parameters such as
c
0
, r
0
, ∆p, κ
c
, t, ∆χ and λ. Thus, there is a optimal
combination of magnetic manipulated division near
r
0
≈2000 nm, at which B
d,i
achieves minimum value.
The deformation of vesical due to magnetic ma-
nipulation before i
th
division can be described as:
r
B,i
(θ) = r
0,i
"
1+

B
B
d,i

2
(3cos
2
θ−1)
#
. (16)
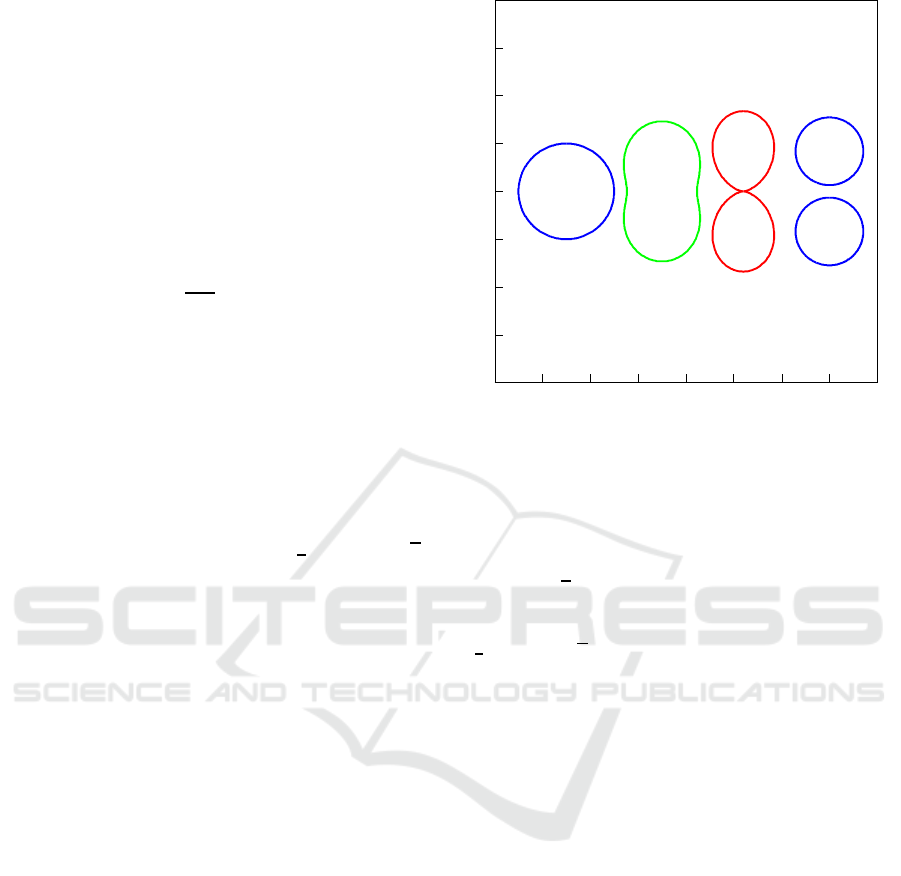
Fig.2 shows three different states during deformation
due to the varying of the manipulated magnetic field.
a and d (blue line) correspond the state of B = 0, then,
the vesicle is spherical. c corresponds the critical state
of division at B
di
, the vesicle displays a pair of pearls
which stick each other. b is the middle state between
B = 0 and B = B
di
, and looks like a dumb-bell. The
sum of the surface area in the progress of each divi-
sion is constant, however, the volume of solution that
is contained by the vesicles will lost
4
3
πr
3
i
(1−1/
√
2)
for each division.
4 CONCLUSIONS AND
DISCUSSION
Nanoreactor has a great potential for the application
of medical, such as targeted transporting of drug via
blood capillary, and digital PCR etc.. However, the
manufacture of nanovesicles with uniform volume is
still a challenge due to the lack of material with large
spontaneous curvature. Our model has revealed the
possibility that the vesicle, which is self-assembled by
the diamagnetic amphiphilic block-copolymers, can
be manipulated into division by external magnetic
field. The passive division can successively take place
for 10 times in the situation of ∆p = −15 mV. The
vesicle with radius of 4000 nm (about 2.68×10
−7
µL
solution contained) will be divided into 512 vesicles
with radius of 177 nm (about 2.31 × 10
−11
µL so-
lution contained). Because of the constraint of con-
stant surface area, the total volume of solution that
is contained by the original vesicle will lost about
2.56 ×10
−7
µL, that is, only 1.2 ×10
−8
µL solution
(about 4.5%) has been retained by 512 vesicles that
each contains about 2.31×10
7
nm
3
. Thus, if the wa-
ter channels are embedded in the membrane of vesi-
cle, this method can not only concentrate the solu-
tion, but also produce a large number of nanoreactors,
i i
B
d,i
0.5B
d,i
i+1
i+1
B=0 B=0
a b c d
Figure 2: Schematic division of vesicle. The polymer-
some is assembled from diamagnetic amphiphilic block-
copolymers with a highly anisotropic magnetic susceptibil-
ity (χ < 0). Its deformation can be manipulated by vary-
ing a external homogeneous magnetic field (B) according
to Eq.(16). a: A spherical vesicle with a radius of r
i
at i
th
division. b: The middle state of the deformation
(0 < B < B
d,i
). c: The passive division takes place at B
d,i
(see fig.1 a). d: Two spherical vesicles with a radius of
r
i+1
= r
i
/
√
2 have been produced. The sum of the surface
area is constant through the whole progress. However, the
volume of solution that is contained by the vesicles will lost
4
3
πr
3
i
(1−1/
√
2) for each division.
which is beneficial to yield an ensemble conclusion in
a short times. This nanoreactor can be used to mimic
the reaction of some organelles in vitro.
We must point that Eq.(11) is precise just for the
situation of small deformation such as B < 0.5B
d,i
,
so that the quantitatively prediction of Eq.(14) is no
longer precise. However, the possibility of passive
division does exist as long as the manipulated mag-
netic field is high enough. Here, we have just dis-
cussed the case of the constraint of constant surface
area. Another case of the constraint of constant vol-
ume should be worth trying, in which experimenter
can easily realize it by enough supply of the diamag-
netic amphiphilicblock-copolymersin the progress of
division. The latter case is also important for the re-
action statistics because the original solution can be
in equal volume divided into hundreds nanoreactors.
We hope experimenters will try them in future exper-
iments.
BIODEVICES 2019 - 12th International Conference on Biomedical Electronics and Devices
152

ACKNOWLEDGEMENTS
The authors thank the financial support by the Key
Research Program of Frontier Sciences of CAS
(No. Y7Y1472Y61), the National Natural Science
Foundation of China (No. 11574329, 11774358,
11747601, 11675017), the Joint NSFC-ISF Re-
search Program(No. 51561145002), the CAS Bio-
physics Interdisciplinary Innovation Team Project
(No. 2060299), CAS Strategic Priority Research
Program (No. XDA17010504) and the Fundamen-
tal Research Funds for the Central Universities (No.
2017EYT24).
REFERENCES
Chandrasekhar, S. (1992). Liquid Crystals. Cambridge Uni-
versity, Cambridge.
Deng, Y.-X., Liu, Y., Shu, Y.-G., and Ou-Yang, Z.-
C. (2018). Deformation theory of polymersome
magneto-valves. EPL, 123:68002.
Helfrich, W. (1973). Elastic properties of lipid bilayers:
theory and possible experiments. Z. Naturforsch,
C28:693.
Hickey, R. J., Haynes, A. S., Kikkawa, J. M., and Park,
S.-J. (2011). Controlling the self-assembly struc-
ture of magnetic nanoparticles and amphiphilic block-
copolymers: From micelles to vesicles. J. Am. Chem.
Soc., 133:1517.
Iwamoto, M. and Ou-Yang, Z.-C. (2013). Anharmonic
magnetic deformation of spherical vesicle: Field-
induced tension and swelling effects. Chem. Phys.
Lett., 590:183.
Manyuhina, O., Shklyarevskiy, I. O., Jonkheijm, P., Chris-
tianen, P. C. M., Fasolino, A., Katsnelson, M. I.,
Schenning, A. P. H. J., Meijer, E., Henze, O., Kil-
binger, A. F. M., Feast, W. J., and Maan, J. C. (2007).
Anharmonic magnetic deformation of self-assembled
molecular nanocapsules. Phys. Rev. Lett., 98:146101.
Ou-Yang, Z.-C. and Helfrich, W. (1987). Instability and
deformation of a spherical vesicle by pressure. Phys.
Rev. Lett., 59:2486.
Ou-Yang, Z.-C., Liu, J.-X., and Xie, Y.-Z. (1999). Geomet-
ric Methods in the Elastic Theory of Membranes in
Liquid Crystal Phases. World Scientific, Singapore.
Petrosko, S. H., Johnson, R., White, H., and Mirkin, C. A.
(2016). Nanoreactors: Small spaces, big implications
in chemistry. J. Am. Chem. Soc., 138:7743.
Sutter, D. H. and Flygare, W. J. (1969). Molecular g values,
magnetic susceptibility anisotropies, second moment
of the charge distribution, and molecular quadrupole
moments in furan and thiophene. J. Am. Chem. Soc.,
91:4063.
van Rhee, P. G., Rikken, R. S. M., Abdelmohsen, L. K.
E. A., Maan, J. C., Nolte, R. J. M., van Hest, J. C. M.,
Christianen, P. C. M., and Wilson, D. A. (2014). Insta-
bility and deformation of a spherical vesicle by pres-
sure. Nat. Commun., 5:5010.
Weatherburn, C. E. (1927). Differential Geometry of Three
Dimensions. Cambridge Univ. Press, Cambridge.
Magneto-division of Vesicle: Theory and Possible Experiments
153