
Optimal Control of Exogenous Reinfection Prevention and Treatment
on a Tuberculosis Model
Zainullah Zuhri
1
, Abdulloh Hamid
1
, Subchan
2
and Imam Rofiki
3
1
Department of Mathematics, Universitas Islam Negeri Sunan Ampel, Surabaya, Indonesia
2
Departement of Mathematics, Institute Teknologi Sepuluh Nopember, Surabaya, Indonesia
3
Department of Mathematics Education, Universitas Islam Negeri Maulana Malik Ibrahim, Surabaya, Indonesia
Keywords: Optimal control, exogenous reinfection, tuberculosis model, Pontryagin’s maximum principle, Forward-
Backward Sweep Method
Abstract: We apply optimal control for a system of ordinary differential equations in modelling tuberculosis disease
with exogenous reinfection. Reducing the contact between exposed and infectious tuberculosis people and
increasing the population of the medication compartment can be done to overcome the spreading of
tuberculosis disease. We use control strategy of the tuberculosis disease to represent the prevention of
exogenous reinfection and optimal treatment. Using Pontryagin’s maximum principle, we have discussed
optimal control of the tuberculosis disease. We use Forward-Backward Sweep Method to gain optimal system
numerically. Numerical results show that the performance of 2-control model is highly effective for reducing
the number of infected individuals in the Tuberculosis model by considering the simulation results from
Susceptible, Exposed, Infectious and Treated population satisfying from each expected condition.
1 INTRODUCTION
Tuberculosis (TBC) is a disease caused by bacteria
and one-third of the human population becomes
infected with TBC. Of all patients (TB), there are only
10% of the active patients (Bloom, 1993) (Miller,
1993). Most individuals are considered capable for
increasing the immune response to bacteria in their
body because the individual has been an active TB
patient. In other words, the body will adjust immune
to the previous condition so that it will not be infected
again (Feng, Capurro and Castillo, 2000). On the
other hand, individuals who are infected with latent
clinical infection will be able to transmit TB. Infected
individuals may remain in this latent stage for long
and uncertain periods, but the reality in the field
shows that many individuals die without having to
suffer active TB (Miller, 1993).
Most people who previously have been infected
have a declining immune capability when they are
old, and they may also be at risk of developing active
TB in two ways: exogenous reinfection (acquiring
new infections from other infections) or endogenous
latent bacilli reactivity (reactivation of inactive and
pre-existing infection) (Styblo, 1991 (Smith, 1994).
In the disease spreading, exogenous reinfection plays
a key role in the transmission of tuberculosis in areas
with the highest incidence, especially in Africa
(where HIV cases are very high) and in developed
countries.
Prevention on individuals infected with inactive
tuberculosis disease may be performed with
chemoprophylaxis by administering Isoniazid Anti-
tuberculosis Drugs. In order to cope with individuals
who are already infected with active tuberculosis,
WHO has recommended to administer anti-
tuberculosis drugs that are isoniazid, rifampicin,
pyrazinamide, ethambutol, and streptomycin
throughout health care units in the world (Crofton,
Horne and Miller, 2002).
Zhilan Feng, Carlos Castillo-Chavez and Angel F.
Capurro have incorporated exogenous reinfection
into the epidemiological model for the dynamics of
tuberculosis transmission and have addressed the
Zuhri, Z., Hamid, A., Subchan, . and Rofiki, I.
Optimal Control of Exogenous Reinfection Prevention and Treatment on a Tuberculosis Model.
DOI: 10.5220/0008904700002481
In Proceedings of the Built Environment, Science and Technology International Conference (BEST ICON 2018), pages 235-239
ISBN: 978-989-758-414-5
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
235

control of this disease by looking at the transmission
parameter role of the disease at the reduction of R 0
and the prevalence of disease (Feng, Capurro and
Castillo, 2000).
In this paper, we add into the model two optimal
controls related to the prevention of reinfection to see
the effect of the exogenous reinfection to become as
minimal as possible and the optimal treatment control
within efforts to reduce the number of infected
compartment individuals and increase the number of
individual treatment compartments.
2 MODEL OF TUBERCULOSIS
DEVELOPMENT
In this section, we describe the model of Tuberculosis
with reinfection exogenous, consisting of four
population groups namely susceptible S(t), exposed
E(t), infectious I(t), and treated T(t). Susceptible S(t)
is a healthy human population but likely to be infected
TB bacteria, exposed E(t) is a population of infected
humans but the symptoms of the disease are still not
seen, infectious I(t) is an infected human population
in which the symptoms of the disease is already
visible and can transmit to other susceptible
individuals and treated T(t) is the population of the
human being who is being treated or in the healing
period. We assume that individuals infected with TB
bacteria are only individuals who are in contact with
other infected individuals.
The model of the spread of TB disease can be
expressed as a system of nonlinear differential
equations as follows:
Λ
(1)
(2)
(3)
(4)
with the addition of control variables and
, 1 represents a preventive attempt
against exogenous reinfection and 11 is
the treatment effort against the individual infections
(Hattaf, Rachik, Saadi, Tabit and Yousfi, 2009)
(Nainggolan, 2017), the new model is as follows:
Λ
(5)
1
(6)
1
(7)
(8)
The initial conditions of the above equation
system are given by:
0
,
0
,
0
,
0
The parameters used in the TB model in this paper
can be seen in the table below (Hattaf, Rachik, Saadi,
Tabit and Yousfi, 2009):
Table 1: This caption has one line so it is centered.
Parameter Definition and value
Λ
Birth, 192
Dead, 0.016
Death due to Tb, 0.1
Average number of
unexpected individuals,
13
,01
The average number of
individuals treated for
infection, 0.9
Human interaction, 1
Progress is Infected,
0.005
Treatment, 2
Total population, 12000
Exogenously Infected
level, 0,4
2.1 Prevention Control of Reinfection
and Optimal Treatment on
Tuberculosis Transmission
The objective function J relating to the problem of
this equation is to reduce the number of I (t) or
actively infected individuals, so it is obtained:
,
(9)
This problem is solved by minimizing (9). In this
discussion, the numerical approach Forward
Backward Sweep Method is used. The procedure of
completion is further described as follows.
Step 1: Form the Hamiltonian function to get the
optimal solution (Workman and Lenhart, 2007)
(Subchan and Zbikowski, 2009)
Λ
1
BEST ICON 2018 - Built Environment, Science and Technology International Conference 2018
236
1
1
1
(10)
Step 2: Find that and
that are optimal.
Using
0 , we get
0 2
2
∗
(11)
Step 3: Determine the costate of that is not yet
optimal.
0 2
∗
(12)
with the boundary conditions
0
,
0
,
0
,
0
0,
0
0,
0
0,
0
0,
0
3 RESULTS AND ANALYSIS
In this chapter, we discussed the simulation of the
Tuberculosis model using the Forward-Backward
Sweep Method numerical approach to see how the
effect of one-control administration on exogenous
reprevention and 2-control administration on
exogenous reprevention and treatment.
The simulation results in the untreated TB model.
The TB model given 1 control and the TB model
given 2 controls using matlab software can be seen as
follows and after the simulation process was done
using MATLAB software, the result of comparison of
the TB model without controls and TB model with the
controls (controlling individual contact against
infectious and controlling the treatment) can be seen
as follows:
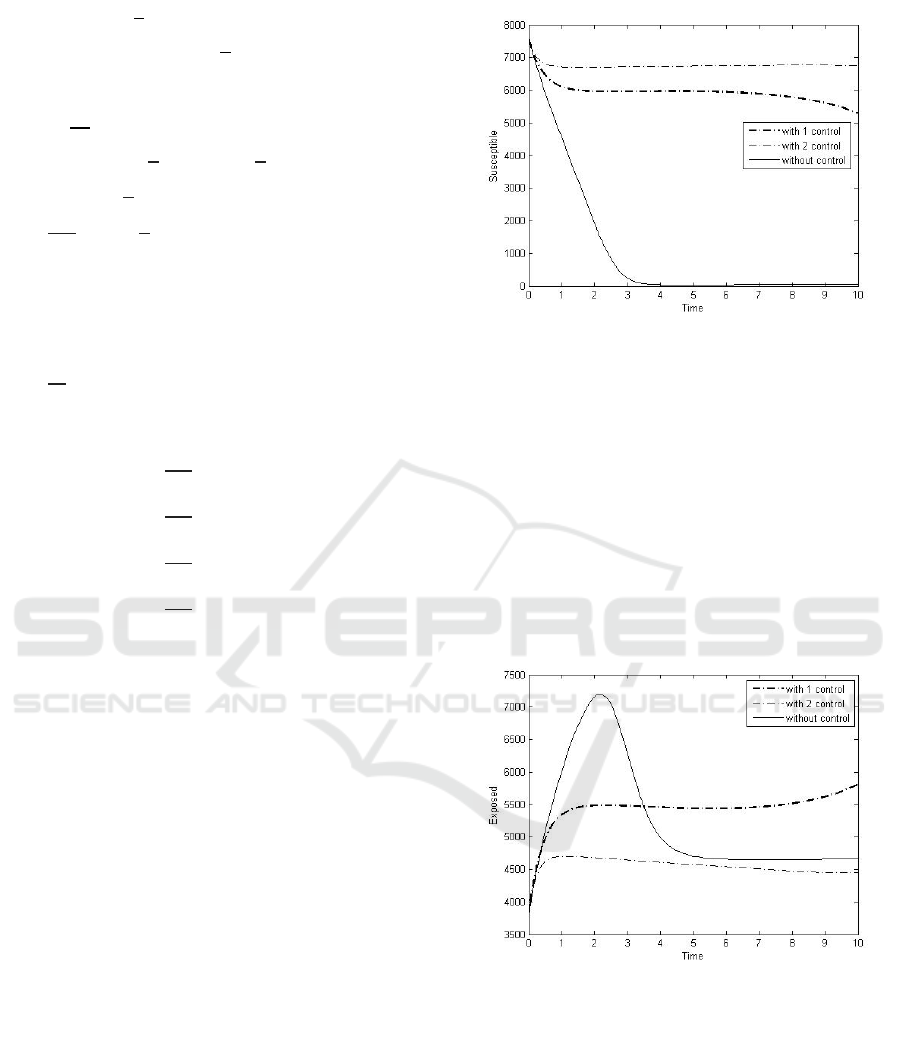
Figure 1: Suscebtible
From Figure 1, it is clear that with the use of 1
control on model, the population of susceptible
increased. This is because the contact between the
susceptible population and Exposed population
was safer, since the exposed population decreased
and minimized the chance of Susceptible to be
infected or reinfected from the Exposed
population. The use of 2 controls further increased
the susceptible population. Because of the same
reason, Exposed population was diminishing. The
treatment subjects were controlled in infectious
populations.
Figure 2: Exposed
From Figure 2, it is seen that with the use of 1
control on the model, the population of Exposed
decreased, it caused the decrease of frequency
contact between the Exposed population and the
Infectious population, so the Exposed population
could get healthy again and move on to the
susceptible population. However, in Figure 2, it is
clear that by using 1 control, initially, the Exposed
population decreased over a period of time
(approximately at 3 to 4) and increased again and
Optimal Control of Exogenous Reinfection Prevention and Treatment on a Tuberculosis Model
237
became more than the uncontrolled model. It is
contrast to the inclusion of 2 controls on the model
so that it looked better and stable with fewer
populations than uncontrolled models and models
with 1 control. In other words, the addition of
medication control successfully suppressed the
growing Infectious population and infecting
Exposed population.
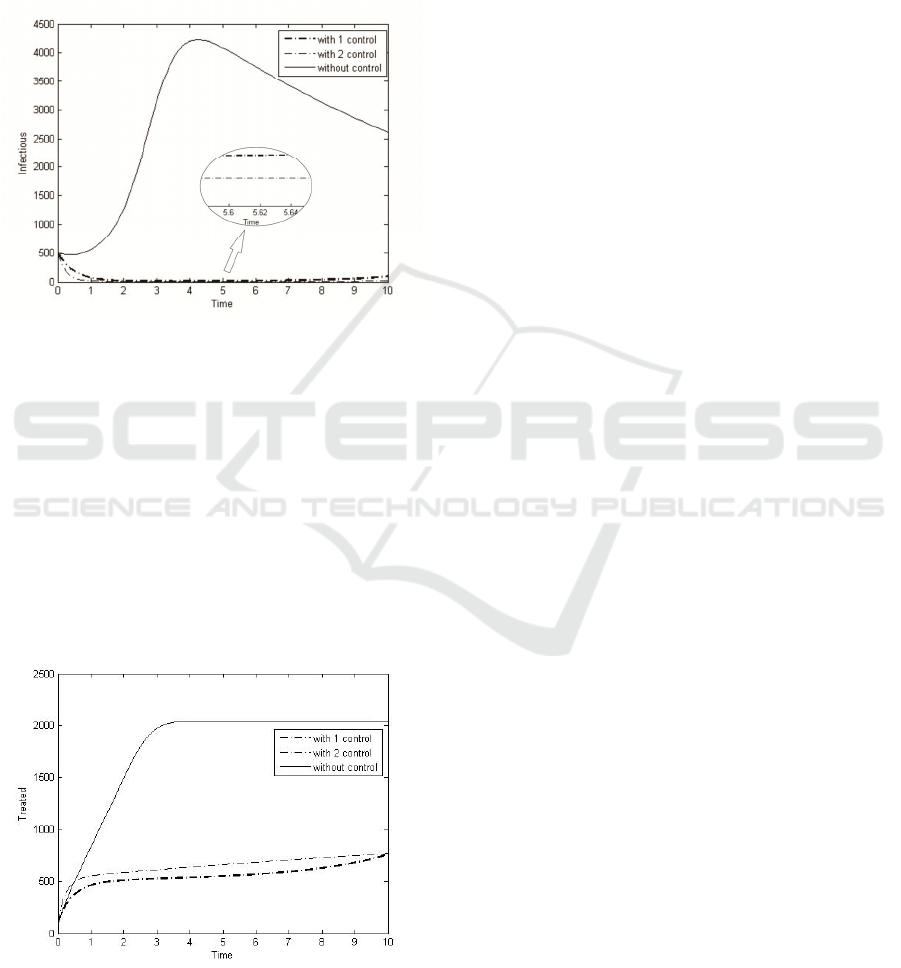
Figure 3: Infectious
From Figure 3, it can be seen that with 1
control in the reduction of the frequency of
contacts in the model, the Infectious population
tended to decrease, but at certain intervals, at t=9
from Figure 3, the Infectious population would
increase again. It was different with the model
subjected to 2 controls. The addition of optimal
treatment control was faster to reduce Infectious
populations. The results were better than models
with 1 control and without control because
Infectious stable populations did not increase
again.
Figure 4: Treated
Figure 4 shows the same thing that with the
implementation of 1 control on the model, the
Treated population decreased, illustrating that
many individuals have returned to good health
after receiving treatment, but the decrease was
temporary because the Treated population
increased again sometimes. We see in the model
subjected 2 controls, at first, it appears that
Treated population number was more than
Treated population number in the model with 1
control. It does not mean a model with 1 control
was better because in the end, the model with 2
controls had fewer populations than the model
with 1 control and without control. At the
beginning of time, the model with 2 controls had
more population than the model with 1 control due
to the addition of medication controls to the
Infectious population so that infectious
populations were treated and the Treated
population increased. Thus, the Treated
population would decrease optimally because the
Infectious population also decreased significantly.
4 CONCLUSIONS
From the exposure of the model of TB disease that
has been given 1 control in the form of reduction of
contact with the infectious individual population, then
it can be drawn outline that the controls were applied
well. However, there are some conditions that
describe those controls but need to be refined, such as
when the declining population of Susceptible,
population of Exposed, Infectious and Treated wetr
increasing. With the application of 2 controls, i.e., the
addition of optimal treatment control, then the
weakness of the model with 1 control can be resolved.
This 2-control model (5)(6)(7)(8) is highly
effective for reducing the number of infected
individuals in the Tuberculosis model by considering
the simulation results from Susceptible, Exposed,
Infectious and Treated population satisfying from
each expected condition.
REFERENCES
B. Miller., 1993. Preventive therapy for tuberculosis, Med.
Clin. North Am.
B. R. Bloom., 1994. Tuberculosis: Pathogenesis,
Protection, and Control, ASM Press, Washington, D.C.
Castillo-Chavez, C. and Feng, Z., 1997. To Treat or Not to
Treat: The Case of Tuberculosis J. Math. Biol.
Crofton, S.J., Horne, M., and Miller, F., 2002. Clinical
Tuberculosis, MacMilan Education Ltd, London.
BEST ICON 2018 - Built Environment, Science and Technology International Conference 2018
238

Hattaf, K., Rachik, M., S, Saadi, Tabit, Y., and Yousfi, N.,
2009. Optimal control of Tuberculosis with Exogenous
Reinfection, Applied Mathematical Sciences, Vol. 3, ,
no. 5, 231 - 240
John T. Workman and Suzanne Lenhart., 2007 Optimal
control applied to bio- logical models, Chapman &
Hall/CRC.
K. Styblo., 1991. Epidemiology of Tuberculosis, VEB
Gustav Fischer Verlag Jena, The Hague.
Nainggolan. J., 2017. Kontrol Pengobatan Optimal pada
Model Penyebaran Tuberkolosis Tipe SEIT, E-Jurnal
Matematika .
P. G. Smith, A. R. Moss, 1994. Epidemiology of
tuberculosis, in Tuberculosis: Pathogenesis,
Protection, and Control, B. R. Bloom, Eds., ASM
Press, Washington,
S Subchan and R Zbikowski,, 2009.Computational Optimal
Control Tools and Practice, John Wiley & Sons, Ltd.
Z. Feng, C. Castillo-Chavez and A.F., 2000 .Capurro, A
model for tuberculosis with exogenous reinfection,
Theor. Pop. Biol.
Optimal Control of Exogenous Reinfection Prevention and Treatment on a Tuberculosis Model
239
