The Approximation of Nonlinear Function using Daubechies and
Symlets Wavelets
Syamsul Bahri, Lailia Awalushaumi and Marliadi Susanto
Dept. of Mathematics, Mataram University, Majapahit Street No.62, Mataram, NTB, Indonesia
Keywords: Function approximation, Nonlinear Function, Wavelet, Daubechies, Symlets.
Abstract: The phenomena and real world problems usually can be formulated as a representation of the problem of
function approximation, which is to estimate the value of a function f(x), based on the relationship or pattern
of the input-output data, that is sequences of
( ).
ii
y f x=
In practice, some applications related to the
approximation of functions such as the problems of pattern classification, regression analysis, reconstruction
signals, and identification systems. The purpose of this research is to compare the performance of
Daubechies and Symlets wavelet types to estimate nonlinear functions. The characteristics of the
Daubechies and Symlets wavelet functions are smooth, regular, have a compact of the support and lengthy
of the filters, and an explicit the formula so it's good to handle smooth curves, reconstruct of signals, longer
filtering processes, easy and fast on computing process. The advantages of the Daubechies and Symlets
wavelet characteristics will be used as the basis for approximating non-linear functions. Numerically, based
on the means square error (MSE) indicator, the results of this research provide an overview of the accuracy
of wavelet-based approximation by Daubechies and Symlets wavelets type for the approximation of the
nonlinear function which is approximated is very significant.
1 INTRODUCTION
Some of the phenomena or real problems can be
formulated as a representation of the problem of
function approximation. In general, sample data
from observation or a result study usually in the
form of input-output ordered pairs set. Zainuddin
and Pauline (2011) stated that the main problem
related to the function approximation is to estimate
the value of a function based on the relationship that
exists in the input-output data set represented by the
pattern. Obviously, the function approximation can
be interpreted as an attempt to estimate a function
value based on a relationship or pattern that is
formed in the representation of the relationship
between the input-output values in the sample data.
In general, some practical applications regarding
function approximations are problems with pattern
classification, data mining, signal reconstruction,
and identification systems.
Wavelet analysis and wavelet transformation are
branches of mathematical studies that have been
applied to various fields of science. Early in its
development, wavelets were initiated as a
combination of pure mathematical ideas (harmonic
analysis, functional analysis, approximation theory,
fractal geometry) and applied mathematics (signal
processing, and mathematical physics). Various
studies have been carried out related to this topic.
Some publications related to wavelet applications
and wavelet transformation include forecasting and
prediction problems (Matsumoto et al., 2007),
problems of filtering data (Ahamada et al., 2010),
adaptive data and singularity problems (Bruzda,
2004), trend analysis issues( Alexsandrov et al.,
2008), stationary and non-stationary data problems
(Lineesh, 2010), inflation and price index issues
(Ysusi, 2009), multiresolution issues (Alves et al
2002), growth problems and cycles of agricultural
products (Chen, 2002 ), and variance and data
correlation issues (Gallegati et al, 2005).
The wavelet function consists of several types
such as Haar, Daubechies, Morlet, Mexican, and B-
spline wavelets. Each type of wavelet has
advantages and disadvantages, especially related to
the form of a function as a wavelet representation,
the form of wavelet curves, support areas, and so on.
At the application level, there is a certain type of
wavelet which because of its superiority and some
properties it has become the reason researchers use it
as a tool or base of analysis in the object of research
300
Bahri, S., Awalushaumi, L. and Susanto, M.
The Approximation of Nonlinear Function using Daubechies and Symlets Wavelets.
DOI: 10.5220/0008521103000306
In Proceedings of the International Conference on Mathematics and Islam (ICMIs 2018), pages 300-306
ISBN: 978-989-758-407-7
Copyright
c
 2020 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

such as Haar wavelet, Daubechies, Symlet, or
wavelet B-spline.
Liu and Din (2016) revealed that Daubechies
wavelets have the advantage of having orthogonality
and compact support. These two properties can
numerically improve the analysis performance in
terms of accuracy and ensure stability in the
computation process, and the existence of the
wavelet scaling function on [0, + ∞] used as the
basis functions for approximations. On the other
hand, Symlets constitute a family of almost
symmetric wavelets proposed by Daubechies by
modifying the construction of the dbN. Therefore,
apart from the symmetry, the other properties of the
two families are similar. The fundamental
difference is only in nature where the Daubechies
wavelet is asymmetrical and the Symlet wavelet is
almost symmetric, with the higher the order the
higher the level of symmetry. On the application
side, wavelet Symlet has vanishing moments at most
if given wide support to be one of the reasons
researchers using the wavelet Symlets as a tool in its
research analysis.
Yadav and Mehra (2016) revealed that the
superiority of Daubechies and Symlet wavelets
could improve accuracy based on the MSE indicator
in the denoising ECG signal process.
Comprehensively, the advantages of the properties
of these two-family wavelets are summarized by
Misiti et al. (2007: 92) such as regular arbitrary,
orthogonal with compact support, the arbitrary
numbers of zero moments, the existence of scaling
function, orthogonal analysis, exact reconstruction,
continuous and discrete transformation formulas,
and fast algorithm.
Therefore, based on the data characteristic of
observation/ research which is generally non-linear,
the extent of the application of wavelet/wavelet
transformation in various application fields, as well
as the superiority of wavelet characteristics of
Daubechies and Symlets, then wavelet Daubechies
and Symlets are selected and used as the basis for
approximating nonlinear functions.
2 WAVELET APPROXIMATION
2.1 Representation of The
Approximation Function
Many phenomena from various application domains
are representations of the approximation of functions
problems. The results of observations from research
or real problem usually can be represented as a set of
input-output ordered pairs. In this respect, the
problem of approximating the function is to estimate
or estimate the value based on the pattern of the
relationship between the input-output present in the
sample data.
Furthermore, in general, the representation of
real phenomena can be formulated using a
continuous function. To simplify the problems, let us
assume that the function space is assumed to be
finite. In this case, one representative function space
is Hilbert space. Let the function be
1
( ) ( )
N
ii
i
f x wh x
=
=

(1)
where
i
w
indicates weight parameter to be updated
and
()
i
hx
indicates the basis of the selected function.
Some candidate of base functions such as
polynomial, trigonometric, exponential, and
orthogonal functions. One of the functional types
that have recently been used as a base function is the
wavelet function (Zainuddin and Pauline, 2011).
In Hilbert space, the approximation using the
wavelet function is defined as follows.
1
( ) ( ( ))
N
i i i
i
f x w a x b

=
=−

(2)
where
i
a
and
i
b
respectively states the dilated and
translational coefficients of the function of the
mother wavelet
.

2.2 Wavelet and Wavelets
Transformation
Wavelets are a class of functions used to localize a
given task in two ways, i.e., position (time) and scale
(frequency). This ability that causes wavelets to
have advantages over Fourier transforms that are
widely applied in data processing such as signal
processing and time series analysis(Bahri,2016a, b).
Wavelet is defined as a shortwave that
concentrates its energy in space and time or a limited
or localized wave (Figure 1). Unlike the wave
which is a function of periodic space and time.
(i) (ii)
Figure 1: Graph of (i) wave and (ii) wavelet.
The Approximation of Nonlinear Function using Daubechies and Symlets Wavelets
301

Mathematically, the wavelet is a family of
functions constructed from the translation and
dilation of a role, defined as follows (Debnath, 2002;
Daubechies, 1992):
1
( ) , , dan 0,
,
2
tb
t a a b a
ab
a

−

−
=  


(3)
where a mother wavelet
,

a represents the scaling
(dilation) parameter that determines the degree of
compression or scale, and b represents the
translation parameter that specifies the time location
of the wavelet. The function

on (3) is called the
mother wavelet, if it verifies the following
admissibility conditions:
(i)
( ) 0,t dt


=

−
(ii)
2
( ) 1,t dt


=

−
(iii)
2
.
w
C dw
w



−
=  

−
2.1.1 The Types of Wavelet Transform
Wavelet transformation can be distinguished into
two types: continuous wavelet transformation and
discrete wavelet transformation (Boggess and
Narcowich, 2001: 184; Mohlenkamp, 2008: 31;
Daubechies 1992: 7-8 and Burrus, 1998: 7-9).
If the scaling parameter a and the translation
parameter b are continuous variables on the field,
with
0a 
on (3), we defined a continuous wavelet
transform type which is given by the following
equation:
1
( , ) ( )
2
tb
wav
T f a b a f t dt
a


−

−

=





−
.
If the scaling parameter a and the translation
parameter b are discrete numbers on (3), we have the
distinct wavelet transform type,
/2
( ) ( [ ])
, 0 0
m m m
t a a t nb a
m n o o

−−
=−
where
0
,
m
aa=
0
1a 
00
m
b nb a=
and for some
0
0b 
and integer n.
2.1.2 Haar, Daubechies, and Symlets
Wavelets
Wavelet Haar is the simplest type of wavelet that
Alfred Haar proposed in 1909 as a function. The
Haar function is given by Equation (4).
( )
1, 0 1/ 2,
1
1, 1,
2
0, others,
x
xx





= −  




(4)
with graphs as in Figure 2.
Figure 2: Graph of Haar wavelet.
Daubechies wavelet is one type of orthogonal
wavelet that is very popular for digital signal
processing. Ingrid Daubechies developed this
wavelet type in 1990. Unlike the Haar wavelet,
Daubechies wavelets have several variations which
are characterized as an order of Daubechies
wavelets, known as Daubechies wavelets with an N-
th order (DbN), for some natural number N.
Especially for N = 1 or Db1, Daubechies wavelet is
Haar wavelet. Wavelet Daubechies order
2,N 
has
2N vanishing moment and has small support an
interval [0, 2N-1]. The N-th order of Daubechies
wavelets is related to the Daubechies polynomial
order.
Daubechies polynomial order N-1 is defined as
follows:
( ) ( )
1
21
1
1
1
0
N
N
Nk
k
P y y y
N
k
k
−
−

−−
=−


−

=
(5)
Graphically the Daubechies were scaling, and
wavelet functions built by Daubechies polynomial
N-th order, N = 2, 3, 4, ..., eight are given by
Figure 3.
Symlet Wavelet is a modification of Daubechies
wavelet which has almost symmetrical
characteristics, with the higher character, the higher
the symmetry quality. As a result of the change of
Daubechies wavelets, Symlet and Daubechies
wavelets have similar symptoms.
ICMIs 2018 - International Conference on Mathematics and Islam
302

Figure 3: The graph variation of types of Daubechies
wavelet wi
th
order,
2,3, ,8i =
Figurer 4: The graph variation of the kinds of Symlet
wavelet 𝑖
th
order
2,3, ,8i =
.
The graphs from the Symlet wavelet for some i-th
order are given in Figure 4. Like the Daubechies
wavelet, the Symlet order 1 (Sym1) wavelet is also
the Haar wavelet.
2.3 Wavelets and Approximation of
Function
Suppose
2
[ , ]f L a b
,
and
( )
 
2
,
.
ab
f t dt 

The
wavelet representation of a function f is given by
2
0 , ,
01
,
j
j k j k
jk
f c f 

=
=+

,
where a
0
c
constant is
1
( )
0
0
c f t dt


=



and
1
, ( ) ( ) ,
,,
,
0
f f t t dt
j k j k
jk
  
==

with orthonormal base functions
,jk

, associated
with scale
2
j−
and position
2.
j
k
−
Functions
,jk

are called wavelets of scale
2
j−
and position
2.
j
k
−
3 RESULTS AND DISCUSSION
The use of wavelets to estimate nonlinear functions
is a relatively new method. In this study, two types
of wavelets Daubechies and Symlets are used to
show the advantages of wavelets in approximating
nonlinear functions applied to three sample data as
nonlinear function representation such as dynamical
system data, chaotic Mackey-Glass data, and
hydrological data.
3.1 Dynamical System Data
In this example, the data used are dynamically
generated system data based on the iteration
equation (Banakar and Azeem, 2006):
( )
5 ( )
1 0,5 ( ) 0,5 ( 1) 0,5 ( 2),
2
1 ( )
xn
x n x n x n x n
xn
+ = − − − + −
+
(6)
with the initial state
(0) 0.2,x =
(1) 0.3,x =
and
(2) 1.x =
The approximation of nonlinear iteration
function (6) uses wavelet approximation based on
Daubechies and Symlets type wavelets in various
orders (1-st, 2-and, 3-rd, 4-Th, and 8-the order) level
3-rd respectively given by Figure 5 and Figure 6.
Figure 5: Original data (dynamical system example)
versus approximated data using wavelet denoised with
several orders of Daubechies wavelet.
Based on Figure 5 and 6, the approximation of the
nonlinear function represented by Equation (6)
using several orders of the Daubechies wavelet
level 3-rd gives the result that the order 1-set of the
Daubechies has the smallest MSE, that is 0.401 and
the 8-the order of the Daubechies has the largest
MSE that is 0.63856. For the same case, then the
best approximation by Symlets wavelet type is
given by the 1-st order with a value of MSE is
The Approximation of Nonlinear Function using Daubechies and Symlets Wavelets
303

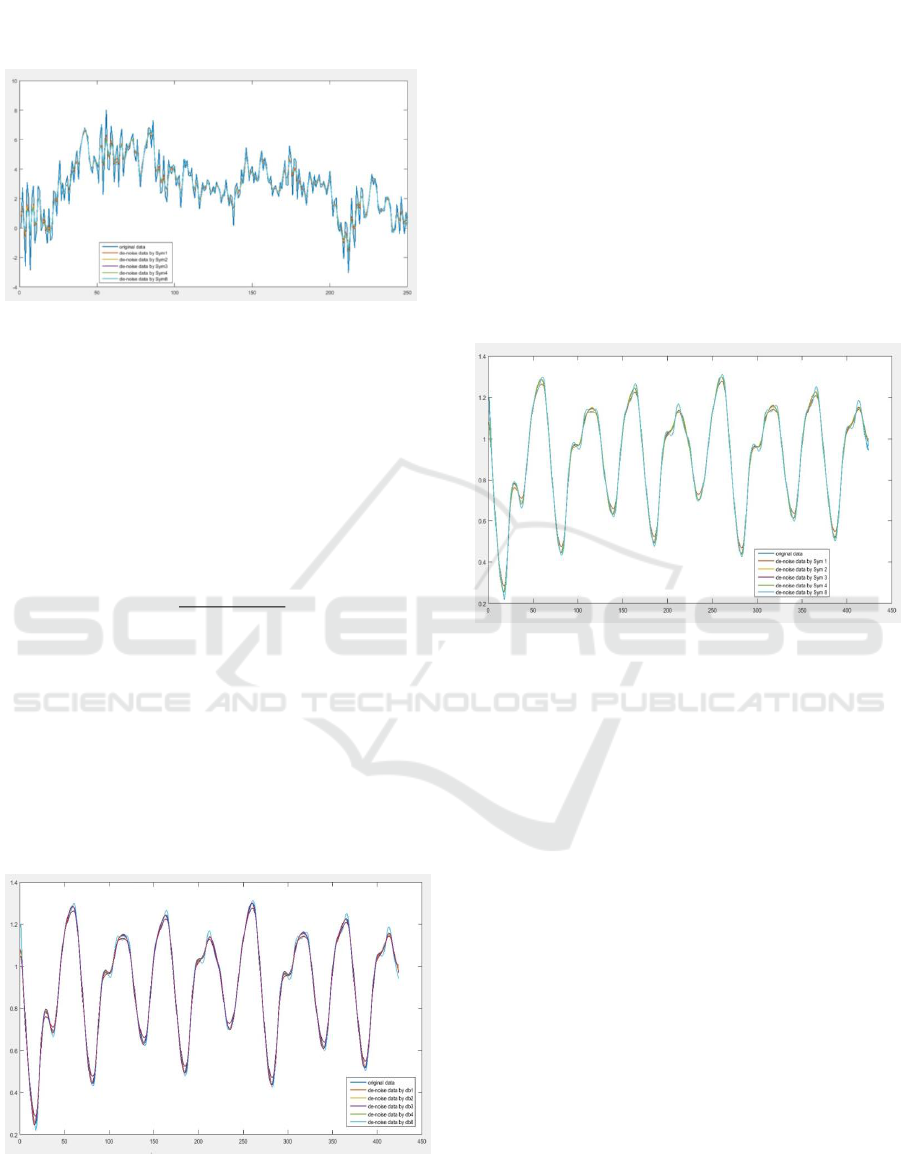
0.401 and the worst approximation is given by the
8-th order with a value of MSE is 0.62875.
Figure 6: Original data (dynamical system example)
versus approximated data using wavelet denoised with
several orders of Symlets wavelet.
3.2 Chaotic Mackey-Glass Data
In this example, the data used is data generated
based on the Mackey-Glass differential delay
equation given by the Equation (7) (Banakar and
Azeem, 2006).
( )
0,2 ( )
1 0,1 ( )
10
1 ( )
xt
x n x t
xt


•
−
+ = −
+−
(7)
with the initial state
(0) 1.2,x =
17,

=
and
( ) 0,xt =
for
0.t 
The approximation of nonlinear differential
delay Equation (7) uses wavelet approximation
based on Daubechies and Symlet type wavelets in
various orders (1-st, 2-and, 3-rd, 4-the and 8-the
order) level 3-rd respectively given by Figure 7 and
8.
Figure 7: Original data (chaotic Mackey Glass) versus
approximated data using denoised wavelet with several
orders of Daubechies wavelet.
Figure 7 and 8 establish for the Chaotic Mackey-
Glass case that the approximation of nonlinear
functions using Daubechies and Symes wavelets
provides excellent results based on the MSE
indicator. The approximation using Daubechies and
Symlets wavelets type with several orders
1,2,3,4, and 8j =
gives the effect that the best
approximation is obtained in the 2-nd order with
the value of MSE is
4
2.8566 10 .
−

For the same
case, the value of MSE of the worst approximator
using by Daubechies wavelet type is
4
4.2149 10
−

from 8-th order and
4
4.2058 10
−

using by Symlets
wavelet type from 1-st order.
Figure 8: Original data (chaotic Mackey Glass) versus
approximated data using denoised wavelet with several
orders of Symlets wavelet.
3.3 Hydrological Data
In this case, the data used is the data (daily) of water
discharge of Sungai Ancar Mataram Region,
Lombok NTB period 2014-2016 (Source: Balai
Nusa Tenggara I River Region). The approximation
of the nonlinear function represented by debit of the
Ancar River data using the wavelet approximation
based on Daubechies and Symlet types in various
orders (1-st, 2-nd, 3-rd, 4-th and 8-th order) level 3-
rd respectively is given by Figure9 and 10.
Based on three case examples, the performance
of approximation functions based on Daubechies
and Symlets type wavelet functions on actual
nonlinear functions (specific functions) or nonlinear
function representations based on data on each given
case sample based on variations in Daubechies and
Symlet wavelet orders is provided by Table 1.
For the daily hydrological data, Figure 9 and 10
show that the approximation of nonlinear functions
using Daubechies and Symles wavelets type
provides a good result based on MSE value
indicators. The best estimate of the nonlinear
function for this case give the value of MSE is
ICMIs 2018 - International Conference on Mathematics and Islam
304

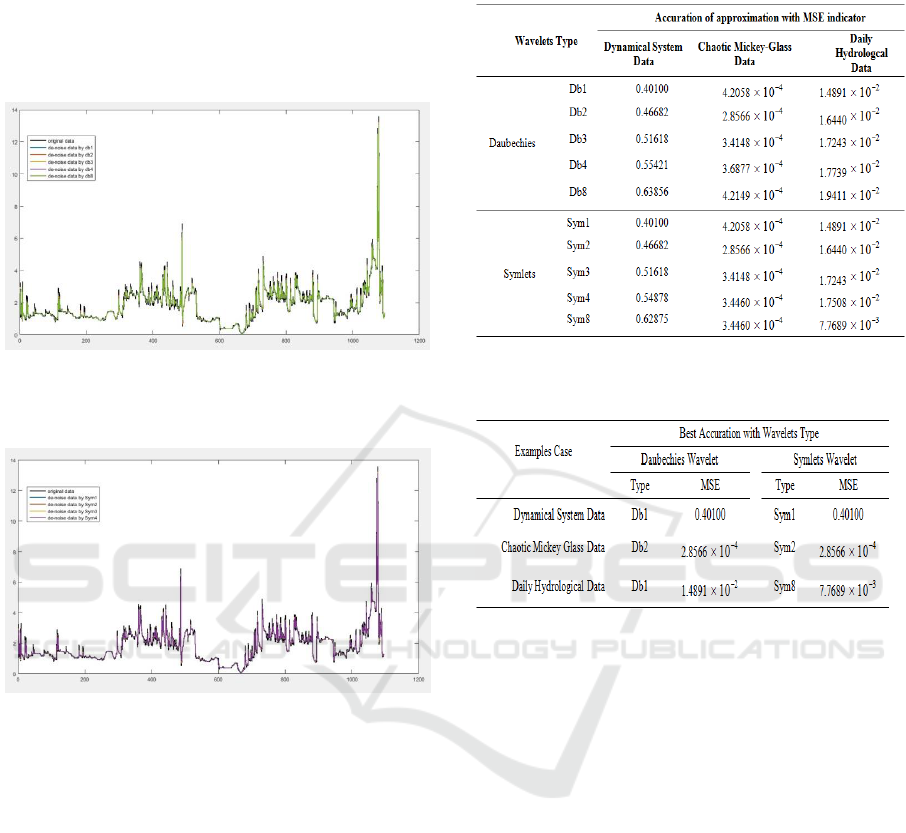
2
1.4891 10
−

for Daubechies wavelet type from Db1
and
3
7.7689 10
−

Symlets wavelet type from Sym8.
But, for the worst approximators, Daubechies
wavelets type given by Db8 with MSE values equal
to
2
1.9411 10
−

and Symlets wavelet type given by
Sym4 with the value of MSE like
2
1.7508 10 .
−

Figure 9: Original data (daily hydrology data) versus
approximated data using wavelet denoised with several
orders of Daubechies wavelet.
Figure 10: Original data (daily hydrological data) versus
approximated data using wavelet denoised with several
orders of Symlets wavelet.
Furthermore, based on Table 2 for the three case
samples observed, the first two examples of
dynamical system data and chaotic Mackey-Glass
data obtained the same results. For dynamical
system data, the best accuracy is given by the same
order of the two types of wavelets, namely Db1 and
Sym1 with the same level of skill, which is equal to
MSE = 0.401. Similar to the chaotic Mackey-Glass
data, the best accuracy is given by the same order,
i.e. Db2 and Sym2 with the same level of skill,
which is equal to MSE = 2.8566
4
10 .
−

With the daily hydrological data, the best
accuracy for the Daubechies wavelet type is
generated by the first order Daubechies wavelet (db1
or Haar wavelet) with accuracy (MSE) of 1.4891
2
10
−

. For Symlets wavelet type, the best efficiency
is given by the Symlet 8-the order wavelet with an
accuracy of 7.7689
3
10
−

.
Table 1: The value of mean square error (MSE) of data
with various orders of Daubechies and Symlets wavelet.
Table 2: Best accuration of the approximation with
Daubechies and Symlets wavelets.
4 CONCLUSIONS
The simulation results of the approximation of the
nonlinear function using the Daubechies and
Symlets wavelet type provide a reasonably good
accuracy based on the mean square error (MSE)
indicator. The performance of two wavelets base for
the first two cases, the dynamical system, and
chaotic Mackey-Glass data, shows that the two
wavelet bases with the same order provide the same
level of accuracy. But, for the case of the nonlinear
function represented by real data, the debit of Ancar
River data, the approximation function based on
Daubechies wavelet is given by 1-st order (Db1),
while for Symlets wavelet type is given by 8-th
order (sym8).
ACKNOWLEDGMENTS
We would like to thank all parties, in particular, we
wish to thank the Dean of Faculty Mathematics and
The Approximation of Nonlinear Function using Daubechies and Symlets Wavelets
305

Natural Sciences, Mataram University has provided
the opportunities and financing for this research. Our
gratitude also goes to the anonymous reviewer who
has given to the improvement of this paper.
REFERENCES
Ahamada, I., and Jolivaldt, P., 2010.Classical vs wavelet-
based filters Comparative study and application to
business cycle.Document de Travail du Centre
d'Economie de la Sorbonne - 2010.
Alexsandrov, T., Bianconcini, S., Dagum, E.B., Maass, P.,
and McElroy, T., 2008.A Review of Some Modern
Approaches to the Problem of Trend
Extraction.Research Report Series Report Issued:
March 28, 2008.
Alves, M.A., P. Cruz, A. Mendes, F.D. Magalhaes, F.T.
Pinho, and P.J. Oliveira, 2002. Adaptive
multiresolution approach for the solution of hyperbolic
PDEs.Comput. Methods Appl. Mech. Engrg., 191, p.
3909 – 3928.
Bahri, S., Widodo, dan Subanar, 2016a. Applied
Multiresolution B-Spline Wavelet to Neural Network
Model and Its Application to Predict some Economics
Data.International Journal of Applied Mathematics
and Statistics, Vol. 54; Issue No. 1, p. 92-103.
Bahri, S., Widodo, dan Subanar, 2016b. Optimization of
Wavelet Neural Networks Model by Setting the
Weighted Value of Output through Fuzzy Rules
Takagi-Sugeno-Kang (TSK) TypeAs a Fixed-
Parameter.Global Journal of Pure and Applied
Mathematics, Volume 12, Number 3, p. 2591–2603.
Bruzda, J., 2004.Wavelet vs. Spectral Analysis of an
Economic Process.Dynamic Econometric Models.
Vol. 6 – Nicolaus Copernicus University – Toruń –
2004.
Chen, P., 2002. Understanding Economic Complexity and
Coherence: Market Crash, Excess Capacity, and
Technology Wavelets.The paper which Presented at
Shanghai International Symposium on Complexity
Science.
Daubechies, Ingrid, 1992.Ten Lectures on Wavelets.
Philadelphia.Society for Industrial and Applied
Mathematics (SIAM).
Gallegati, M. and M. Gallegati, 2005. Wavelet variance
and correlation analyses of output in G7 countries.
JEL codes: C01, E31, E32. Online Paper (Accessed
onFebruary 14, 2011).
Lineesh, M. C., Minu, K.K., and John, C.J., 2010.
Analysis of Nonstationary Nonlinear Economic Time
series of Gold Price a Comparative Study.
International Mathematical Forum, 5, 2010, no. 34, p.
1673 – 1683.
Liu, Y. and Din, K., 2016. Research Article: A Numerical
Method Based on Daubechies Wavelet Basis and B-
Spline Patches for Elasticity Problems. Hindawi
Publishing Corporation, Mathematical Problems in
Engineering, Volume 2016, Article ID 2549213,
http://dx.doi.org/10.1155/2016/2549213.
Matsumoto, Y. and J. Watada, 2007.Wavelet Approach to
Chaotic Forecasting of Stock Movement.Asia Pacific
Journal of Finance and Banking Research Vol. 1. No.
1, pp. 34-44.
Misiti, Michael, Yves Misiti, G. Oppenheim, and JM.
Poggi, 2007.Wavelets and their Applications, USA:
ISTE Ltd.
Yadav, T. and Mehra, R., 2016. Denoising ECG Signal
Using Daubechies and Symlet Wavelet Transform
Techniques.International Journal of Advanced
Research in Computer and Communication
Engineering, Vol. 5, Issue 9, p. 438-443.
Ysusi, C., 2009. Analysis of the Dynamics of Mexican
Inflation Using Wavelets, Working Paper.
Zainuddin, Z. and Pauline, O., 2011. Modified wavelet
neural network in function approximation and its
application in prediction of time-series pollution
data.Applied Soft Computing, vol. 11, p. 4866–4874.
ICMIs 2018 - International Conference on Mathematics and Islam
306