A Cascading Chi-shapes based Decoder for Constraint-handling in

Distributed Energy Management

Joerg Bremer

and Sebastian Lehnhoff

Department of Computing Science, University of Oldenburg, Uhlhornsweg, Oldenburg, Germany

R&D Division Energy, OFFIS – Institute for Information Technology, Escherweg, Oldenburg, Germany

Keywords:

χ-shapes, Decoder, Flexibility Modeling, CMA-ES, Constraint-handling.

Abstract:

A steadily rising share of small, distributed, and volatile energy units like wind energy converters solar panels,

co-generation plants, or similar assigns new tasks and challenges to the smart grid regarding operation and

control. The growing complexity of the grid also imposes a growing complexity of constraints that restrict

the validity of solutions for operation schedules, resource capacity utilization or grid compliance. Using

surrogate models as an abstraction layer has recently become a promising approach for constructing algorithms

independently from any knowledge about the actual device or operation restricting constraints. So called

decoders as a special constraint handling technique allow for systematically generating feasible solutions

directly from a learned surrogate model. Some decoder approaches based on support vector machines have

already been implemented, but suffer from performance issues and a sensible parametrization. We propose

a new type of decoder based on a cascade of χ-shapes to overcome these problems. The applicability is

demonstrated with a simulation study using different types of ﬂexible energy units.

1 INTRODUCTION

Electrical power supply is currently undergoing a

transition towards a decentralized provision by renew-

able resources. Political decisions target a change

from traditional control schemes with rather few,

large power plants to a power grid operated by nu-

merous small (volatile and hardly predictable) renew-

able energy resources (DER). Grid control by decen-

tralized and individually conﬁgured units leads to a

need for new algorithms in order to cope with grow-

ing (constraint) complexity. If a huge number of small

devices is responsible for control operations, they will

have to situationally group together to jointly gain po-

tential and ﬂexibility like in virtual power plants (Son-

nenschein et al., 2014).

Individual search spaces of different units – rep-

resenting the individual capabilities within a group

– have to be integrated to a model for the operation

planning at runtime. Each individually operated unit

has its own set of distinct schedules to offer for a

scheduling algorithm. Such ﬂexibility depends on the

current, individual conﬁguration, several (technical)

constraints for operation, current operational state,

and if applicable, on state and requirements of cou-

pled units – e. g. on the thermal demand of a house

in case of a co-generation plant (Bremer et al., 2010).

Thus, a static model is not targeted as it had to be

continuously adapted and corrected.

If a simulation model of an energy unit is regarded

as a characteristic function able to indicate whether

an arbitrary, given schedule is operable by the DER

or not, it can be converted to another model that al-

lows for a standardized access to feasibility informa-

tion. The characteristic function that indicates oper-

ability of schedules may be captured e. g. by machine

learning approaches. Built on top, a so called de-

coder provides a mapping function to turn any given

schedule into a similar feasible one (with respect to

the energy unit model that has been used for train-

ing). As constraint-handling technique such decoder

may be used for solution repair or for guiding any al-

gorithm where to look for feasible solutions (Koziel

and Michalewicz, 1999).

In (Bremer and Sonnenschein, 2013) a decoder

has been proposed based on a 1-class support vector

machine (SVM). This decoder works ﬁne on a wide

range of energy unit types but has drawbacks regard-

ing training time and parametrization for precision in

high-dimensional cases. The works of (Fröhlinger,

2017; Neugebauer et al., 2016) improved precision

by extending the high-dimensional SVM approach to

184

Bremer, J. and Lehnhoff, S.

A Cascading Chi-shapes based Decoder for Constraint-handling in Distributed Energy Management.

DOI: 10.5220/0006926101840191

In Proceedings of the 10th International Joint Conference on Computational Intelligence (IJCCI 2018), pages 184-191

ISBN: 978-989-758-327-8

a cascade of classiﬁers for the ﬂexibility model. But,

for this cascading approach no cascading decoder is

known so far.

We present a new approach for ﬂexibility model-

ing and decoder based on χ-shapes that constitute a

concave hull as model for the feasible region of an en-

ergy unit. With this approach performance as well as

precision can be improved by integrating the cascade

architecture. In addition, as the χ-shape model works

directly in data space as oppose to SVM approaches

that model in reproducing kernel Hilbert spaces, new

applications regarding intersection or union of ﬂexi-

bilities from different energy units become possible.

The rest of the paper is organized as follows. We

start with an introduction to ﬂexibility modeling and

recap concave hull techniques. A description of the

new approach based on χ-shapes is complemented by

a hybridization with evolution strategies for demon-

strating integration into optimization. Finally, a sim-

ulation study with evaluation results concludes.

2 RELATED WORK

2.1 Constraints and Flexibility

Modeling

In order to understand, the concept of ﬂexibility sur-

rogate models and derived decoders for constraint-

handling, we ﬁrst have to look at the constraints and

the representation of schedules.

Usually, a DER might achieve the main task it has

been built for in different alternative ways. For ex-

ample, a CHP (combined heat and power plant) is

supposed to supply the heat for varying demand in a

household at every moment in time. But, heat usage is

often decoupled from heat production by using a ther-

mal buffer store. Thus, different production proﬁles

may be used for generating the heat. This leads, in

turn, to different respective electric load proﬁles that

may be offered as choice to a scheduling controller.

A schedule is a data vector x

x P R

, with number

of periods d. For each period the i-th element of

x describes the respective amount of electric energy

produced or consumed in this period or respectively

the mean active power output or input during this pe-

riod. The term operable denotes that a schedule does

not violate any constraint. The term constraint com-

prises hard (usually technically rooted) and soft (of-

ten economically or ecologically rooted or subject to

personal preferences) as well as often non-linear con-

straints resulting from system embedding.

Real world problems often face nonlinear and/ or

: load in period 1 (% max. load)

: load in period 2 (% max. load)

Figure 1: Simpliﬁed 2-dimensional example for the scope

of action of a modulating co-generation plant with the su-

perposition of three constraints (cf. (Bremer et al., 2010)).

combined constraints. The set of constraints deﬁnes

the shape of a region within the search space (the hy-

percube deﬁned by operation parameter limits) that

contains only feasible solutions. This feasible region

might be arbitrary shaped and discontinuous. It is this

region that deﬁnes feasibility and ﬂexibility and that

has to be modeled to allow distinguishing operable

and not operable schedules.

As the feasible region is a sub-vector space, con-

straints can be interpreted geometrically. Without any

constraint, the whole hypercube r0, 1s

(active power

between 0 and 100%) would be a model for the region

of feasible schedules. When applying constraints, dif-

ferent parts (sub-regions) of the hypercube drop off

the feasible region, because the respective schedules

are not operable. Only the remaining region (hyper-

cube minus superposition of all regions prohibited by

constraints) is the feasible region of the DER. Fig-

ure 1 shows a simpliﬁed, linear, 2-dimensional exam-

ple for a modulating CHP (power may vary between

min. and max. power: constraints C

) with a con-

nected thermal buffer store (state of charge prohibits

region C

); instantaneous changes in production level

are prohibited by inertia (constraints C

and C

The remaining white region is the feasible region F .

We denote with F

the feasible region that is speciﬁc

to an energy unit u. Examples from a productive sys-

tem would usually comprise 96 dimensions and many

more constraints, heavy non linearity and discontinu-

ity.

A ﬂexibility model is a surrogate model that sub-

stitutes a simulation model and checks whether a

given schedule is operable under current circum-

stances or not. These models are classiﬁers to tell

feasible and infeasible schedules apart (with regard

to a speciﬁc unit and a speciﬁc initial operation state)

without needing to simulate.

A decoder is a constraint-handling technique

that imposes a relationship between feasibility and

A Cascading Chi-shapes based Decoder for Constraint-handling in Distributed Energy Management

185

decoder solutions. For example, (Koziel and

Michalewicz, 1999) proposed a homomorphous map-

ping between an n-dimensional hypercube and the

feasible region in order to transform the problem into

an topological equivalent one that is easier to handle,

although with a need for extra parameters that have to

be ﬁt empirically and with a need for explicitly given

constraint formulations. Earlier approaches e.g. used

Riemannien mapping (Kim, 1998).

An example for the smart grid domain is given

in (Bremer et al., 2010). There, a ﬂexibility model

based on a one-class support vector data description

(SVDD) (Tax and Duin, 2004) was proposed. The

goal of building such a model is to learn the feasi-

ble region of the schedules of a DER by learning the

enclosing boundary around the set of operable sched-

ules. This task is achieved by determining a mapping

Φ : X Ă R

Ñ H , x

x ÞÑ Φpx

xq such that all data from a

given region X is mapped to a minimal hypersphere

in some high- or indeﬁnite-dimensional Hilbert space

H . The images enclosing ball is used as an abstract

model.

A support vector decoder can harness this rela-

tionship by mapping an arbitrary (infeasible) sched-

ule into this high-dimensional space and moving the

mapped image towards the center of the ball until it

touches the surface. This translated image can then

be mapped back to a now feasible schedule at the bor-

der of the feasible region. In the same way also a

proportional move into the ball is possible to harness

the whole feasible region.

2.2 χ-Shapes

Another general approach for modeling the enclos-

ing envelope around a point cloud is using a con-

cave hull. A concave hull constitutes a polygon that

represents the characteristic shape of a set of input

points (Duckham et al., 2008). One approach to rep-

resenting characteristic shapes of point clouds was

introduced in (Edelsbrunner et al., 2006), where α-

shapes were used. In (Melkemi and Djebali, 2000) A-

shapes where introduced. Both approaches are based

on Delaunay triangulation and Voronoi diagrams and

quickly become intractable with growing number and

dimension of points. Different approaches are based

on putting a lattice on the plane and deﬁning the union

of cells containing points as shape. An improvement

to these so called s-shapes are r-shapes that are consti-

tuted by a union of discs around points from the given

point cloud. In the 2-dimensional plane these shapes

can be calculated in linear time but require a preced-

ing step of ﬁnding suitable parameters which cannot

be determined in a closed form. More geographical

information systems related approaches can e. g. be

found in (Park and Oh, 2012; Moreira and Santos,

2007). In (Braune et al., 2016) a multi shape approach

has been developed for clustering. In (Duckham et al.,

2008) so called χ-shapes are proposed that are easy to

calculate and calculation can be done in Opn ¨ log nq.

χ-shapes are deﬁned for ﬁnite sets of at least 3

points in R

. χ-shapes model the spatial distribution

of point sets and constitute simple polygons contain-

ing all points and bounding an area inside (or equal

to) the convex hull (Duckham et al., 2008). The poly-

gon is generated based on a convex Delaunay trian-

gulation that is iteratively shrunk to a concave hull by

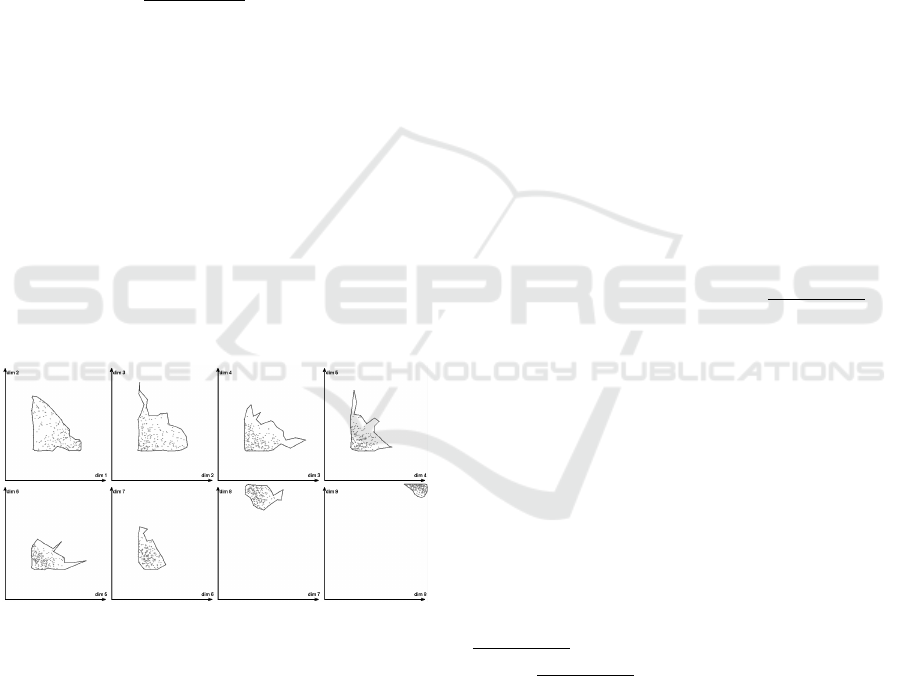
removing outer edges (Rosen et al., 2014). Figure 2

gives some examples of concave hulls around point

clouds.

So far, none of these methods had been used for

ﬂexibility modeling due to their disability to scale

well with dimensionality. In (Hörding, 2017), a ﬁrst

attempt was made to combine ideas from (Fröhlinger,

2017; Neugebauer et al., 2016) – where high dimen-

sional training sets have been disintegrated into a set

of lower dimensional ones by using a cascade of clas-

siﬁers for ﬂexibility modeling – and concave hulls and

χ-shapes as base model from (Duckham et al., 2008).

3 ALGORITHM

3.1 Model and Decoder

Here, we propose a novel method of generating a

decoder for energy management algorithms that are

based on χ-shape models of the feasible region of

possible operation of an energy unit. The approach

is based on the cascading χ-shape model from (Hörd-

ing, 2017) that also predicted the possible extension

to a fully-ﬂedged decoder method.

In general, the approach works as follows. In a

ﬁrst step, a training set is generated from an energy

units’ simulation model that serves as a stencil for the

feasible region as in the approach from (Bremer et al.,

2010; Bremer and Sonnenschein, 2013). This train-

ing set contains instances of feasible schedules with a

dimension that covers the whole planning horizon. In

day-ahead scheduling a schedule usually has a dimen-

sion of 96 of 15-minute intervals for 24 hours. This

training set is subdivided into a set of training sets

with schedules of dimension two. With this, we fol-

low the cascading approach for better classiﬁcation as

proposed in (Fröhlinger, 2017). All sub training sets

are overlapping in one neighboring dimension. In a

second step we calculate a χ-shape for each of these

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

186

sub training sets after (Duckham et al., 2008; Hörd-

ing, 2017). Finally, a decoder is derived. The task

of a decoder is to map points from the exterior of the

concave hull onto a point inside the hull.

Let x

x “ pp

,... , p

q P r0,1s

be a schedule for an

energy unit for d time intervals. The elements of x

x de-

note generated or consumed real power in p.u. (per-

centage of rated power) during the respective time in-

terval. Let X “ tx

,. .. ,x

u be a training set with in-

stances x

of random, feasible schedules.

Let x

x be an infeasible schedule (point) from the

exterior. We start by mapping the ﬁrst dimension of

x. This has to be done by line search. The ﬁrst point

along the x-axis x

that guarantees an intersection of

the line segment px

,0qpx

,1q with the ﬁrst χ-shape

polygon is taken as an anchor for the mapping.

Let X

p jq

“ tpp

, p

j`1

with j P t1, .. ., du Ď N

be a 2-dimensional training set comprising only an in-

tersection plane of the original training set along axis

j and j ` 1. We now break down the original high-

dimensional training set X into a set of 2-dimensional

training sets tX

p1q

p2q

,. .. ,X

pd´1q

For each of these 2-dimensional planes a χ-shape

p jq

q is constructed enclosing the values of feasi-

ble power for 2 succeeding time intervals j and j ` 1

in the schedule. The χ-shape consists of a set of line

segments t`

iPN

deﬁning a closed polygon enclos-

ing points of feasible power projected onto the respec-

tive plane.

Figure 2: χ-shape model of the 9-dimensional ﬂexibility of

a co-generation plant with hourly resolution.

For a simple polygon like S

it can be easily

checked whether a given point lies inside (or on the

boundary) or outside, e. g. with the ray-casting al-

gorithm (Shimrat, 1962). We denote with x

p jq

“

, p

j`1

q Ď S

that dimensions j and j ` 1 of x

x are

contained in (lie inside) S

or lie on the boundary.

Now we can deﬁne a model for the feasible region:

Let M px

xq be a general indicator function

M px

xq “

true if x

x P F

false else

. (1)

M can be deﬁned with the help of the χ-shape set

jPt1,...,d´1u

xq “

true if x

p jq

Ď S

@ j P t1, .. ., d ´ 1u

false else

(2)

A schedule is classiﬁed feasible iff in every inter-

section plane the respective 2-dimensional intersec-

tion of the schedule lies inside or on the polygon de-

ﬁned by the respective χ-shape. Figure 2 gives an ex-

ample for 9-dimensional schedules of a co-generation

plant on an hourly basis. The feasible region is mod-

eled by 8 intersection planes each modeling two di-

mensions with an overlap of one.

Based on this ﬂexibility model we can now deﬁne

a decoder. Let z

z “ pp

,. .. , p

q be an infeasible sched-

ule. For simple solution repair one could harness the

shortest path to the feasible region deﬁned by the set

of χ-shapes. For each intersection plane j one just

had to determine the point on the polygon S

with the

shortes distance to z

p jq

For a more sophisticated space mapping decoder

we propose the following approach: For a single, 2-

dimensional intersection plane the following holds.

Let z

p jq

“ pz

j`1

q be a point in R

with the ﬁrst

coordinate ﬁxed and inside the χ-shape S

. Then z

p jq

can be moved along the line segment pz

,0qpz

,1q (re-

member all values are scaled to r0,1s) until z

p jq

lies

inside S

. Let ˜z

denote the repaired coordinate of z

As neighboring intersections overlap by 1, the sec-

ond coordinate z

j`1

is identical with the ﬁrst coor-

dinate of the succeeding intersection. Therefore, the

ﬁrst coordinate there is now ﬁxed (i. e. z

i`1

“ ˜z

) and

the second can be moved inside. This process may

continue until the last coordinate of the schedule has

been pushed inside the feasible region. Only for the

ﬁrst coordinate in the ﬁrst plane a coordinate inside

has to be chosen by line search as an anchor as there

is no predecessor. All other coordinates can be deter-

mined systematically.

Coordinate mapping is done by moving along

,0qpz

,1q. To do this we determine the intersec-

tions of pz

,0qpz

,1q and S

. In case there is just a sin-

gle intersection point ι

ι P r0, 1s

between the χ-shape

and the line trajectory, the second coordinate of the

intersection is directly taken: z

j`1

“ ι

In case of multiple intersections

tι

,ι

,. .. ,ι

u, m ą 2 we rank them according

to distance δrι

,p˜z

j´1

j`1

qs and direction. Let ι

denote the nearest intersection, ι

the second nearest

in the same direction as ι

and ι

the nearest in

the opposite direction. Now we determine

j`1

by translating P “ p˜z

j´1

j`1

q proportionately in

A Cascading Chi-shapes based Decoder for Constraint-handling in Distributed Energy Management

187

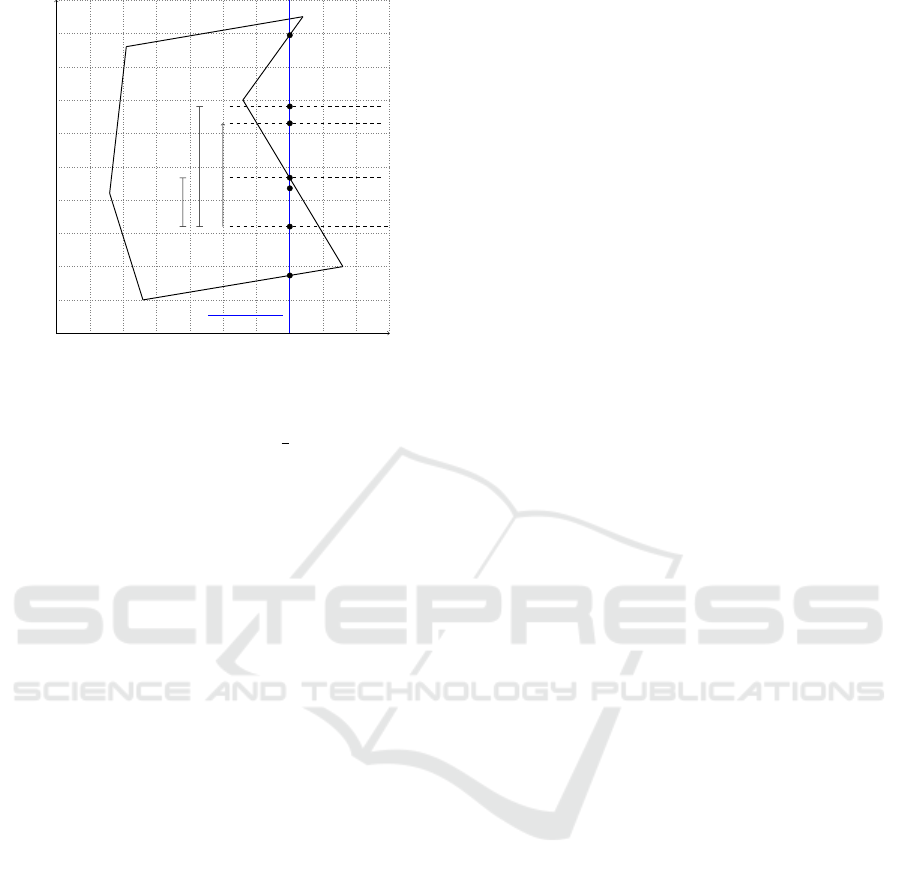
dim j

dim j ` 1

trajectory line p˜z

j´1

,0qp˜z

j´1

,1q

P “ p˜z

j´1

j`1

∆x

Figure 3: Basic scheme for mapping an infeasible coordi-

nate proportionally into the feasible region.

between ι

and ι

: P

“ O `

∆x. Figure 3

illustrates the idea. The center O between ι

and ι

and O

between ι

and ι

is determined (outer dashed

lines). The aim is to map the region in between P

and midway to ι

onto the ﬁrst half of the nearest

inner part. The length ratio between a “ O

´ O

and b “ ι

A,2

´ O

is used to scale ∆x accordingly for

determining P

“ p˜z

j´1

, ˜z

p j`1q

overlap

“ p˜z

, ˜z

j`1

In case of only 2 intersections, p˜z

j´1

,0q or

p˜z

j´1

,1q is taken as ι

depending on the direction of

. To wrap it up, a decoder function

dec

: r0, 1s

Ñ M

« F

(3)

is deﬁned by (1) line searching an anchor for the ﬁrst

coordinate and (2) mapping the second and all suc-

ceeding coordinate in every intersection plane propor-

tionally into the nearest part of the respective χ-shape

along a trajectory with ﬁxed ﬁrst coordinate.

In this way, the complete exterior of the feasible

region F inside r0, 1s

is mapped onto F . Prior to

mapping, we ﬁrst check with the help of the χ-shape

model M

. whether a questionable schedule z

z is fea-

sible and thus is already inside F . If this is the case, z

is used directly and the mapping step can be omitted.

On the other hand, at least in case of modeling en-

ergy units, studies have shown for the example of co-

generation plants a feasible portion of less than 10

´23

;

so mapping is the more frequent case (Bremer et al.,

2010).

3.2 Hybridizing with Evolution

Strategies

For evaluation, we need to hybridize the decoder with

an optimization algorithm. The covariance matrix

adaption evolution strategy (Ostermeier et al., 1994;

Hansen, 2006) (CMA-ES) is an evolution strategy

well-known for it’s good performance on multi modal

black box problems (Hansen, 2011).

A good introduction can for example be found in

(Hansen, 2011). CMA-ES is initially not designed

for integrated constraint handling in constrained op-

timization. Nevertheless, some approaches for in-

tegrating constraint handling have been proposed.

In (Kramer et al., 2009) a CMA-ES is introduced

that learns constraint function models and rotates

mutation distributions accordingly. In (Arnold and

Hansen, 2012) an approximation of the directions of

the local normal vectors of the constraint boundaries

is built by accumulating steps that violate the respec-

tive constraints. Then, the variances of these direc-

tions are reduced for mutation.

CMA-ES can be hybridized with decoders as fol-

lows (Bremer and Lehnhoff, 2017; Bremer and Lehn-

hoff, 2018). In every iteration g of CMA-ES a multi-

variate distribution is sampled to generate a new off-

spring solution population:

pg`1q

„ m

pgq

` σ

pgq

N p0,C

pgq

q, k “ 1,. .. ,λ. (4)

pgq

P R

nˆn

deﬁnes the covariance matrix of the

search distribution at generation (iteration) g with

overall standard deviation σ

pgq

which can also be in-

terpreted in terms of an adaptive step size. The mean

of the multivariate distribution is denoted by m

pgq

λ ě 2 denotes the population size.

The new mean m

pg`1q

for generating the sample

of the next generation in CMA-ES is calculated as

weighted average

pg`1q

“

i“1

pg`1q

i:λ

“ 1, w

ą 0, (5)

of the best (in terms of objective function evaluation)

individuals form the current sample x

pgq

,. .. ,x

pgq

. In

order to introduce the decoder into CMA-ES, ranking

is done with the help of the decoder mapping χ

dec

and

objective function f :

pg`1q

1:λ

,. .. ,x

pg`1q

λ:λ

“ f pχ

dec

pgq

,. .. ,χ

dec

pgq

qq (6)

to deﬁne x

pg`1q

i:λ

as the new ith ranked best individual.

For scheduling of energy units, x

x as solution candi-

date is the concatenation of schedules

x “ x

.. .x

“ pp

,. .. , p

, p

,. .. , p

(7)

with x

,. .. ,x

denoting schedules for the energy

units. Finally, the covariance matrix is updated as

usual, but also based on the decoder based ranking

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

188

Eq. 6:

pg`1q

“

i“1

pg`1q

i:λ

´ m

pgq

¯´

pg`1q

i:λ

´ m

pgq

(8)

CMA-ES has a set of parameters that can be

tweaked to some degree for a problem speciﬁc adap-

tion. Nevertheless, default values that are applicable

for a wide range of problems are usually available.

This also constituted its suitability for use cases in au-

tomation. For our experiments, we used default set-

tings after (Hansen, 2011).

4 EVALUATION

For evaluation, we used simulations with models of

several different energy units. Among them where co-

generations plants with attached thermal buffer stores

(of different size) for heating a detached house, PV

solar panels, ventilation systems, and heat pumps.

Table 1: Comparison of ﬂexibility models using support

vector data description and χ-shapes; npv: negative predic-

tion value; ccr: correct classiﬁcation rate.

indicator SV χ-shapes

fallout 0.0300 ˘ 0.0018 0.0061 ˘ 0.0003

precision 0.4106 ˘ 0.0095 0.7256 ˘ 0.0097

npv 0.9881 ˘ 0.0005 0.9835 ˘ 0.0006

recall 0.6415 ˘ 0.0143 0.4902 ˘ 0.0163

miss rate 0.3585 ˘ 0.0143 0.5098 ˘ 0.0163

speciﬁty 0.9700 ˘ 0.0018 0.9939 ˘ 0.0003

ccr 0.9597 ˘ 0.0013 0.9780 ˘ 0.0005

For comparison with the χ-shape decoder (XSD),

we used the support vector decoder (SVD) and the

related ﬂexibility model as proposed in (Bremer et al.,

2011; Bremer and Sonnenschein, 2013). In a ﬁrst test,

we compared the ﬂexibility models.

Table 1 shows the results. As both ﬂexibility mod-

els are basically classiﬁers, standard indicators for

classiﬁer evaluation can be used. The comparison

is done using a co-generation plant. Due to the tiny

share of feasible schedules for co-generation plants

(Bremer et al., 2010), it is only possible to calcu-

late the confusion matrix for rather small dimensional

cases. Thus, the experiment has been conducted using

8-dimensional schedules in order to generate a sufﬁ-

cient number of true positive instances. The confu-

sion matrix was calculated for both ﬂexibility models

with the help of the simulation models for comparing

classiﬁcation results respectively. The results show an

almost equally good performance for both ﬂexibility

models types. The χ-shapes model shows some im-

provement regarding the speciﬁty which denotes the

share of correctly classiﬁed infeasible schedules and a

better precision but classiﬁes a larger share of actually

feasible schedules falsely as infeasible.

0.5

1.5

2.5

¨10

0.5

0.6

0.7

0.8

0.9

no. of instances

Jaccard index

SVD

XSD

Figure 4: Quality of reproduces ﬂexibilities with different

training set sizes based on Jaccard index; a value of 1 de-

notes perfect accordance.

As a ﬁrst test for evaluating the decoders we gen-

erated training sets from different energy units and

respectively trained a support vector and a χ-shape

decoder. We then generated 10000 random sched-

ules (power for each time interval „ Up0, 1q) and

mapped each random schedule with both decoders.

The mapped schedules where tested regarding feasi-

bility using the original simulation model. Table 2

shows the result for 96-dimensional schedules. We

used two differently parameterized (regarding shady

phases) PV models and a ventilation system. All three

are perfectly reconstructed by both decoders with the

meaning that all schedules generated by the decoders

were feasible. Nevertheless, the χ-shape decoder per-

forms a little better here with regard to generating also

schedules from the outer regions of the feasible re-

gion. This can better be seen with the speciﬁty in Ta-

ble 1. Nevertheless, for the co-generation plant, the

support vector decoder shows a better performance.

This is rooted in the fact that for the co-generation

plant with thermal buffer store each feasible amount

of energy in a period relays on schedule decisions

from preceding time periods (e. g. early charging of

the buffer reduces options for later operation). Be-

cause the χ-shape decoder has only an overlap of one

(two succeeding time periods), it has trouble encoding

relations over larger chains of time periods. Thus, the

result for the high-dimensional schedules is degrades.

For shorter time frames the performance is still suf-

ﬁcient. Reducing the time dependability by using a

larger thermal store (CHP 2) reduces this effect.

Next, we evaluated the similarity between the re-

produced set of feasible schedules with the actual

feasible region as it is determined by the simulation

model. A comparison is given in Figure 4. We used

the Jaccard index for evaluating similarity between

A Cascading Chi-shapes based Decoder for Constraint-handling in Distributed Energy Management

189

Table 2: Comparison of the share of correctly reproduced

feasible schedules for SVD and XSD for 96-dimensional

schedules.

DER SVD XSD

PV 1 1.0000 ˘ 0.0000 1.0000 ˘ 0.0000

PV 2 0.9998 ˘ 0.0001 1.0000 ˘ 0.0000

ventilation 1.0000 ˘ 0.0000 1.0000 ˘ 0.0000

CHP 1 0.9434 ˘ 0.1265 0.3422 ˘ 0.0173

CHP 2 0.7521 ˘ 0.2267 0.7453 ˘ 0.0087

500

1,000

no. of instances

time / ms

SVD

XSD

Figure 5: Comparison of training time of SVD and XSD for

different training set size.

the region that is covered by two point clouds. Thus,

we can compare the similarity between a set of sched-

ules generated by the simulation model and a set of

random schedules that has been mapped by a decoder.

As Figure 4 shows, the χ-shape approach needs a

larger training set than the support vector approach

but then outperforms the SVD in terms of similarity

of the reproduced region to the original one.

Needing larger training sets is always an issue re-

garding performance of the approach. Hence, we

compared the computation times of SVD and XSD

for both training and usage. From analytics it is al-

ready known that training can be done in average case

for the SVD in Opn

q with training set size n, if ap-

proximated and for the XSD in Opd ¨ n ¨ log nq with n

schedules of dimension d (Duckham et al., 2008; Bre-

mer et al., 2011). The impact in practical applications

200 400

600

800 1,000

100

150

200

no. of instances

time / ms

SVD

XSD

Figure 6: Comparison of mapping performance of SVD and

XSD for different training set size (and resulting number of

support vectors and polygon lines).

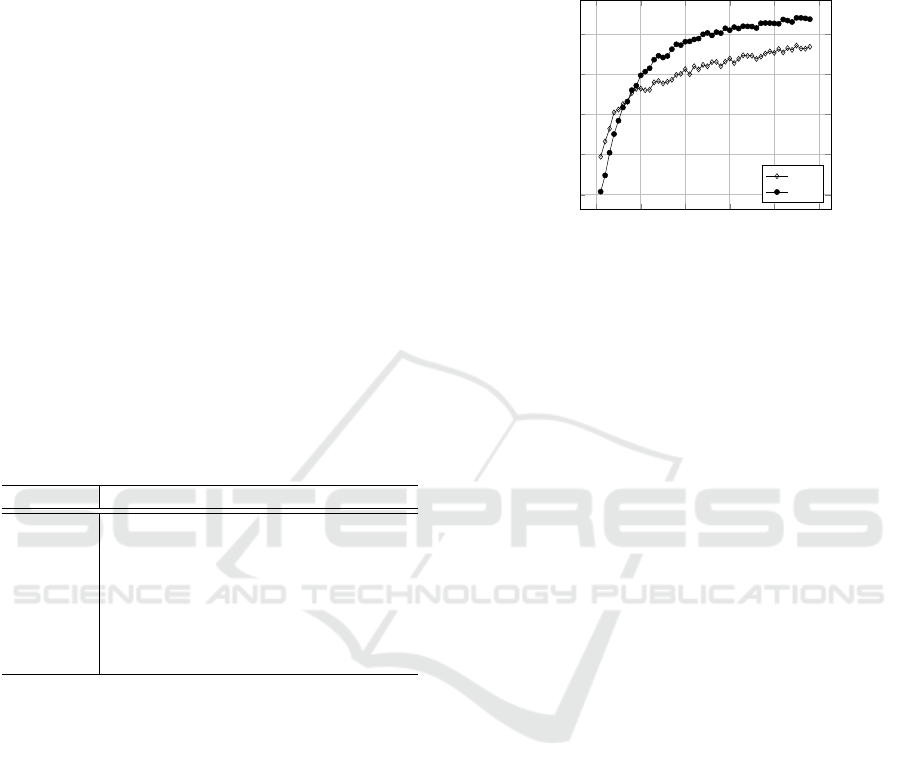
Figure 7: Example result for planning 750 co-generation

plants with residual error.

can be seen in Figure 5. For usage, the performance

of the SVD is determined by some matrix operations

with a matrix size of n

ăă n; and thus by the num-

ber of support vectors n

. The XSD approach needs

a calculation of the intersection d ´ 1 times and thus

depends on the number of edges of the set of poly-

gons. In practice, XSD is only slightly slower than

SVD. Especially for larger training set sizes when the

approximated boundary becomes smoother and thus

fewer line segments have to be intersected; cf. Figure

6. Nevertheless, there is still room for improvement

with concepts e. g. from ray-tracing.

Finally, we tested the XSD in some practical op-

timization problems. Figure 7 shows an exemplary

result for the predictive scheduling problem with 750

co-generation plants. In predictive scheduling for

each unit in a set of energy units, a schedule has to

be found such that a desired target load proﬁle is re-

sembled as close as possible for a given time frame

(Sonnenschein et al., 2014). Because all individual

schedules have to be taken from the individual fea-

sible region of the respective energy units, the opti-

mization algorithm has to use decoders for generating

candidate solutions. More formal, we want to min-

imize the distance δ (e. g. Euclidean) between target

load proﬁle ζ and the sum of individual schedules for

units u: δp

uPU

,ζq Ñ min. For solving this problem

we use the CMA-ES approach as described before.

The upper chart shows the desired target load pro-

ﬁle (artiﬁcially chosen such that a residual error of

zero is theoretically possible) and as result the ag-

gregated load proﬁle of the co-generation plants; the

lower shows the residual error. The mean absolute

percentage error for the experiment was 0.00451 ˘

0.00479.

5 CONCLUSION

The task of ﬂexibility modelling is an important pre-

requisite to many planning and control tasks in the

smart grid. We presented a novel model and decoder

IJCCI 2018 - 10th International Joint Conference on Computational Intelligence

190

approach that well suits a niche of energy resources

where it outperformed the established SVD.

All in all, the XSD has several advantages regard-

ing performance in scenarios where a frequent train-

ing is necessary and it produces a set of schedules for

optimization that better resembles the original feasi-

ble region especially at the boundary. Thus the ﬂex-

ibility of the energy unit is better harnessed. Nev-

ertheless, it has some problems capturing the opera-

tional interdependencies over time with some devices

like an electric vehicle charging station, where a set

of functionals has to be captured by the decoder that

all produce a given value for the integral over the

planning horizon. So, the χ-shape decoder may not

completely replace the support vector decoder but is

a good extension beside it with advantages for many

types of energy units.

REFERENCES

Arnold, D. V. and Hansen, N. (2012). A (1+1)-cma-es

for constrained optimisation. In Proceedings of the

14th Annual Conference on Genetic and Evolution-

ary Computation, GECCO ’12, pages 297–304, New

York, NY, USA. ACM.

Braune, C., Dankel, M., and Kruse, R. (2016). Obtaining

shape descriptors from a concave hull-based cluster-

ing algorithm. In Boström, H., Knobbe, A., Soares,

C., and Papapetrou, P., editors, Advances in Intelli-

gent Data Analysis XV, pages 61–72, Cham. Springer

International Publishing.

Bremer, J. and Lehnhoff, S. (2017). Hybrid Multi-ensemble

Scheduling, pages 342–358. Springer International

Publishing, Cham.

Bremer, J. and Lehnhoff, S. (2018). Phase-space sampling

of energy ensembles with CMA-ES. In EvoApplica-

tions, volume 10784 of Lecture Notes in Computer

Science, pages 222–230. Springer.

Bremer, J., Rapp, B., and Sonnenschein, M. (2010). Sup-

port vector based encoding of distributed energy re-

sources’ feasible load spaces. In IEEE PES Confer-

ence on Innovative Smart Grid Technologies Europe,

Chalmers Lindholmen, Gothenburg, Sweden.

Bremer, J., Rapp, B., and Sonnenschein, M. (2011). Encod-

ing distributed search spaces for virtual power plants.

In IEEE Symposium Series on Computational Intelli-

gence 2011 (SSCI 2011), Paris, France.

Bremer, J. and Sonnenschein, M. (2013). Constraint-

handling for optimization with support vector surro-

gate models – a novel decoder approach. In Fil-

ipe, J. and Fred, A., editors, Proceedings of the

5th International Conference on Agents and Artiﬁ-

cial Intelligence (2), pages 91–105, Barcelona, Spain.

SciTePress.

Duckham, M., Kulik, L., Worboys, M., and Galton, A.

(2008). Efﬁcient generation of simple polygons for

characterizing the shape of a set of points in the plane.

Pattern Recognition, 41(10):3224 – 3236.

Edelsbrunner, H., Kirkpatrick, D., and Seidel, R. (2006).

On the shape of a set of points in the plane. IEEE

Trans. Inf. Theor., 29(4):551–559.

Fröhlinger, J. (2017). Abstract Flexibility Description for

Virtual Power Plant Scheduling. phd thesis, Carl von

Ossietzly Universität, Oldenburg.

Hansen, N. (2006). The CMA evolution strategy: a compar-

ing review. In Lozano, J., Larranaga, P., Inza, I., and

Bengoetxea, E., editors, Towards a new evolutionary

computation. Advances on estimation of distribution

algorithms, pages 75–102. Springer.

Hansen, N. (2011). The CMA Evolution Strategy: A Tuto-

rial. Technical report.

Hörding, J. P. (2017). Umsetzung eines Dekoders für

kaskadierende χ-Shape Modelle verteilter Energiean-

lagen. Bachelorthesis, Department of Energyinfor-

matics, University of Oldenburg, Oldenburg, Ger-

many.

Kim, D. G. (1998). Riemann mapping based constraint han-

dling for evolutionary search. In SAC, pages 379–385.

Koziel, S. and Michalewicz, Z. (1999). Evolutionary al-

gorithms, homomorphous mappings, and constrained

parameter optimization. Evol. Comput., 7:19–44.

Kramer, O., Barthelmes, A., and Rudolph, G. (2009). Sur-

rogate constraint functions for cma evolution strate-

gies. In Proceedings of the 32Nd Annual German

Conference on Advances in Artiﬁcial Intelligence,

KI’09, pages 169–176, Berlin, Heidelberg. Springer-

Verlag.

Melkemi, M. and Djebali, M. (2000). Computing the shape

of a planar points set. Pattern Recognition, 33(9):1423

– 1436.

Moreira, A. and Santos, M. Y. (2007). Concave hull: A

k-nearest neighbours approach for the computation of

the region occupied by a set of points. Proceedings

of the Second International Conference on Computer

Graphics Theory and Applications.

Neugebauer, J., Bremer, J., Hinrichs, C., Kramer, O., and

Sonnenschein, M. (2016). Generalized cascade classi-

ﬁcation model with customized transformation based

ensembles. In IJCNN.

Ostermeier, A., Gawelczyk, A., and Hansen, N. (1994). A

derandomized approach to self-adaptation of evolu-

tion strategies. Evolutionary Computation, 2(4):369–

380.

Park, J.-S. and Oh, S.-J. (2012). A new concave hull al-

gorithm and concaveness measure for n-dimensional

datasets. Journal of Information science and engi-

neering, 28(3):587–600.

Rosen, E., Jansson, E., and Brundin, M. (2014). Implemen-

tation of a fast and efﬁcient concave hull algorithm.

Technical report, Uppsala Univ, Finland.

Shimrat, M. (1962). Algorithm 112: Position of point rela-

tive to polygon. Commun. ACM, 5(8):434–.

Sonnenschein, M., Lünsdorf, O., Bremer, J., and Tröschel,

M. (2014). Decentralized control of units in smart

grids for the support of renewable energy supply. En-

vironmental Impact Assessment Review, (0):–.

Tax, D. M. J. and Duin, R. P. W. (2004). Support vector data

description. Mach. Learn., 54(1):45–66.

A Cascading Chi-shapes based Decoder for Constraint-handling in Distributed Energy Management

191