New Error Measures for Evaluating Algorithms that Estimate the

Motion of a Range Camera

Boris Bogaerts

, Rudi Penne

1,2

, Bart Ribbens

1,3

, Seppe Sels

and Steve Vanlanduit

Faculty of Applied Engineering, University of Antwerp, Groenenborgerlaan 171, B-2020 Antwerp, Belgium

Department of Mathematics, University of Antwerp, Middelheimlaan 1, B-2020, Antwerp, Belgium

Multimedia and Communication Technology, Karel de Grote University College,

Salesianenlaan 90, B-2660 Antwerp, Belgium

Keywords:

Range Camera, Extrinsic Calibration, Motion Estimation, Conjugacy Invariants.

Abstract:

We compare the classical point-based algorithms for the extrinsic calibration of a range camera to the recent

plane-based method. This method does not require any feature detection, and appears to perform well using

a small number of planes (minimally 3). In order to evaluate the accuracy of the computed rigid motion

we propose two new error metrics that get direct access to the ground truth provided by a mechanism with

reliable motion control. Furthermore, these error metrics do not depend on an additional hand-eye calibration

between the mechanism and the sensor. By means of our objective measures, we demonstrate that the plane-

based method outperforms the point-based methods that operate on 3-D or 2-D point correspondences. In our

experiments we used two types of TOF cameras attached to a robot arm, but our evaluation tool applies to

other sensors and moving systems.

1 INTRODUCTION

The resolution of most Time-of-Flight (TOF) cameras

remains low compared to the resolution of common

RGB cameras (Hansard et al., 2012). This drawback

is an obstacle in the detection of point features, which

is a bottleneck in many procedures for intrinsic and

extrinsic calibration. On the other hand, range cam-

eras provide spatial reconstruction without the need

to detect point features. Recent publications demon-

strate the advantage of using planes instead of points

in the observed scene (Teichman et al., 2013; Penne

et al., 2015b; Penne et al., 2015a; Fern

andez-Moral

et al., 2014). Indeed, planes can be segmented easier

than corners can be detected (Fern

andez-Moral et al.,

2014; Penne et al., 2013; Pathak et al., 2010) and they

can be reconstructed using robust plane ﬁtters (Torr

and Zisserman, 2000).

In this paper we focus on the qualitity of algo-

rithms for the extrinsic calibration of range cameras,

that is, for estimating the rigid transformation be-

tween two camera poses given the images of a com-

mon scene that are taken from these two poses. We

compare three esentially different strategies for ob-

taining this extrinsic calibration. In the ﬁrst place,

because we use a range sensor, a 3-D point cloud is

given in the reference system of both camera poses.

If in addition to the detection of the points in both im-

ages also the correspondence between these point im-

ages is established, the rigid transformation between

these poses can be computed by standard methods as

reported in (Eggert et al., 1997) for instance. If the

3-D point clouds in the two camera reference systems

are given without correspondences, an iterative clos-

est point algorithm can be applied (as coined in (Besl

and McKay, 1992)), at the cost of accuracy (Bellekens

et al., 2015). On the other hand, a TOF camera (the

range sensor that is used in our experiments) also pro-

vides a 2-D intensity image. If planar calibration pat-

terns such as checker boards are viewed by both cam-

era poses, the transformation of these boards relative

to each camera pose can be computed by classical

calibration procedures (Zhang, 2000; Zhang, 1989).

Consequently, this yields the relative rigid transfor-

mation between both camera poses. Last but not least,

the arguments listed in the previous paragraph suggest

to use ﬂat objects (planes) rather than points. As a

matter of fact, this option is preferred in several pub-

lications, e.g. in the extrinsic calibration procedure

of (Fern

andez-Moral et al., 2014) or in the registra-

tion algorithm of (Pathak et al., 2010). In Section 2.3,

we describe and explain this plane-based method via

508

Bogaerts, B., Penne, R., Ribbens, B., Sels, S. and Vanlanduit, S.

New Error Measures for Evaluating Algorithms that Estimate the Motion of a Range Camera.

DOI: 10.5220/0006510005080515

In Proceedings of the 13th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2018) - Volume 5: VISAPP, pages

508-515

ISBN: 978-989-758-290-5

an elementary route, using the dual projective trans-

formation (in the same spirit as (Vasconcelos et al.,

2012; Raposo et al., 2013)). Other remarkable meth-

ods for extrinsic calibration that offer alternatives to

point measurements can be found in (Guan et al.,

2015) (for RGB-cameras, by means of spheres) or in

(Sabata and Aggarwal, 1991) (for range sensors, us-

ing lines or surfaces). But for reasons listed above,

we prefer a motion-from-planes approach.

The ﬁrst contribution of this paper is to prove

that the computation of the rigid motion between two

poses of a TOF camera is more acurate and more ro-

bust when the range data is used, rather than the lumi-

nance data. Although this conclusion could have been

predicted, it is comforting to conﬁrm it by a scientiﬁc

procedure, because the sources and the propagation

of errors are not the same for the 2D-sensor as for

the range sensor. In addition, we will conclude that

the estimated motion computed by the plane-based

method is more accurate than the point-based method

(Section 5), even when only a few planes are available

in the common view area (three, at most four). For

this comparative study we used an implementation of

the SVD algorithm of (Arun et al., 1987) for the 3-

D point-based method, an implementation of (Zhang,

1989) for the 2-D point-based method and in essence

the algorithm of (Fern

andez-Moral et al., 2014) for

the 3-D plane-based method.

The second (and to our opinion the most impor-

tant) contribution of this paper is the proposal of a

new type of error measures that directly referr to an

absolute ground truth for the estimated rigid motion.

So far, research articles evaluated the computed ex-

trinsic calibration indirectly because the ground truth

for camera motion seemed inaccessible. Common

performance measures for extrinsic calibration in the

absence of ground truth are the triangulation error, the

projection error or the reprojection error (Guan et al.,

2015). Unfortunately, these error measures need data

consisting of points and hence are not suitable to val-

idate a plane-based method. Futhermore, they im-

plicitely evaluate the intrinsic calibration of the used

camera(s) as well. Sometimes, the rigid transfor-

mation supplied by a state-of-the-art method such as

(Tsai, 1992) is used as ground truth, e.g. in (Guan

et al., 2016), which cannot be considered as absolute

reference either. In our experiments, the TOF camera

was rigidly attached to a robot manipulator (Fig. 1).

The motion of the robot’s end effector can be consid-

ered as a very accurate ground truth.

However, it is a challenge to have access to this

ground truth data, because of the famous hand-eye

calibration problem (Shah et al., 2012). This prob-

lem is caused by the fact that the relative motion be-

Figure 1: We controlled the motion of a TOF camera by

attaching it to an articulated robotarm.

tween two positions of the camera is known in the

robot basis instead of the camera basis. The trans-

formation matrix between both reference frames, one

at the camera center and the other at the robot tool

center, is an obstacle to get access to the ground truth

provided by the robot motion. We can solve for this

transformation matrix by doing the hand-eye calibra-

tion (Mao et al., 2010; Shah et al., 2012), but this is

based on the availability of a reliable camera transfor-

mation. Therefore, using the hand-eye calibration for

evaluating the extrinsic calibration (camera motion)

gives rise to a conceptual loop, and hence is not de-

sirable. Therefore, we propose to use algebraic con-

jugacy invariants, and introduce two new error met-

rics. A major drawback of our approach is the lack

of physical interpretation of these error measures be-

cause they have an algebraic rather than a geometric

nature. However, they provide a correct scale to com-

pare different methods. As a matter of fact, it can be

used to compare all algorithms for extrinsic calibra-

tion, as long as the involved sensor can be attached to

mechanism with precisely controllable motions. The

reason why we develop more than one error metric

is the fact that there does not exist a standard proce-

dure yet to validate camera motion by means of robot

motion. Fortunately, the results by both metrics cor-

relate, providing convincing proof for the ranking of

the three considered methods.

The paper is organized as follows. In Section 2

we give an overview of the three methods that we

will evaluate for estimating the rigid motion of a TOF

camera. In Section 3 we explain our error metrics for

validating the computed camera motion by means of

the given robot motions, taking into account that the

hand-eye transformation X is unknown to us. Sec-

tion 4 describes the details of the setup of the experi-

ments. Section 5 contains the results of the evaluation

of the three compared methods, for two types of TOF

cameras, by means of the proposed error metrics.

New Error Measures for Evaluating Algorithms that Estimate the Motion of a Range Camera

509

2 RIGID CAMERA MOTION:

DESCRIPTION OF THREE

METHODS

A common way to describe mathematically the rigid

motion of a TOF camera or any other 3-D object is by

means of the coordinate transformation between the

two positions of a rigidly attached reference frame

before and after the motion. The rotational part of

the rigid motion is represented by a 3 × 3 orthonor-

mal matrix R (R

−1

= R

), and the translation part by

a 3 × 1 vector t. If p and p

are the 3 × 1 coordi-

nate vectors of a given spatial point w.r.t. the rigidly

attached reference frame before and after the motion

respectively, then

p = R · p

+t. (1)

Often, it is convenient to represent this transformation

by one matrix multiplication p = B · p

, using homo-

geneous coordinates p = (p

,1)

with weight 1, and

a 4 × 4 transformation matrix

B =



R t



(2)

with 0 the 3 × 1 zero vector.

In this section we exhibit three essentially differ-

ent methods for estimating the rigid motion of a TOF

camera.

2.1 2-D Extrinsic Calibration

In the ﬁrst method we do not use the depth measure-

ments of the involved range sensor, but only its lumi-

nance image (2-D intensity image). Estimating the

motion between two camera positions is equivalent

to a stereo calibration from two 2-D-images, and can

be done by proven procedures, e.g. as described in

(Zhang, 1989). In our experiments, we carefully ac-

complished a lateral calibration of the TOF camera,

that is, we determined the intrinsic pinhole parame-

ters and removed non-linear lens distortion in a pre-

processing step.

Next, for each camera position we computed the

4 × 4 rigid transformation matrix H with respect to a

ﬁxed calibration checkerboard with known size (Sec-

tion 4). Finally, the extrinsic transformations H

and

of both camera positions relative to the ﬁxed cal-

ibration pattern yield the rigid transformation B =

−1

· H

of the camera.

2.2 3-D Point Measurements

Given a set of corresponding 3-D points,

,..., p

←→ p

,..., p

(3)

there are several methods to estimate the rigid trans-

formation (R,t) mapping the ﬁrst set to the second. A

comparison between different methods is presented in

the review paper (Eggert et al., 1997). The determi-

nation of the most likely translation t and rotation R

comes down to ﬁnding the least-squares solution of a

system of 3N linear equations caused by N pairs of

corresponding 3-D points, where each pair yields 3

equations as given by Eqn. 1. Equivalently, the mo-

tion pair (R,t) is determined by minimizing the sum

of squares error:

SSE =

∑

i=1

||p

− Rp

−t||

(4)

subject to the constraint that R has to be orthonormal.

In our experiments we followed the method of (Arun

et al., 1987), that computes the rotation and transla-

tion separately. As a ﬁrst step this centroid is calcu-

lated both before and after transformation, p

and p

such that both point clouds can be presented relative

to their centroid: p

= p

− p

and p

= p

− p

. In

(Arun et al., 1987) it is proved that the rotation matrix

R that minimizes SSE is given by

R = VU

, (5)

where the matrices V and U are found by the singular

value decomposition H = UΛV

H =

∑

i=1

. (6)

Finally, the translation part is estimated by means of

both centroids: t = p

− p

2.3 3-D Plane Measurements

If the rigid transformation of a depth camera is rep-

resented by a 4 by 4 transformation matrix B acting

on homogeneous coordinates of 3-D points as given

by Eqn. 2, then the corresponding dual transformation

acting on plane coordinates (a, b,c,d)

is represented

by B

−T

(Pottmann and Wallner, 2001):













∼ B

−T













⇔













∼ B













(7)

Because the homogeneous plane coordinates

(a,b,c,d)

are determined up to a scale factor,

it is convenient to normalize the plane normals

n = (a,b,c)

to length 1. This leaves us with one

more ambiguity, due to the two opposite directions

for n. This can be resolved by some additional

constraint, e.g. requiring that all plane normals point

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

510

towards the 3D sensor. With these conventions the

proportional similarity of Eqn. 7 can be replaced by

an equality. Consequently, the rigid motion (R,t) of

the camera transforms the plane coordinates (n

,d)

for k considered planes as follows:



··· n

... d







··· n

... d





··· R

· n

+ d

... t

· n

+ d



(8)

These equations can be decoupled into a system for R

and a system of t. Furthermore, the equations for R

make only use of the plane normals:

... n

) = R

... n

)

... d

) = t

... n

) + (d

... d

)

(9)

So, the rotational part of the desired rigid motion can

be estimated by minimizing

SSE =

∑

i=1

||n

− Rn

(10)

in the same spirit of (Arun et al., 1987). This is equiv-

alent to maximizing trace(RH), where H is the 3 × 3

matrix deﬁned by

H =

∑

i=1

, (11)

which is accomplished once again by the SVD H =

UΛV

and putting R = VU

. On the other hand, the

translational part t can be estimated by a least squares

solution for the equations containing t in the system

of Eqn. 9.

3 ERROR METRICS

3.1 The Charpoly Error Metric

In our experiments we have used two error metrics in

order to evaluate the accuracy of different methods for

estimating the rigid camera motion. The validation is

done by means of the known motion of an articulated

robot arm where the camera was rigidly attached to

(Fig. 1). Therefore, we introduce error metrics that

leverage the fact that the camera motion is conjugated

to the known robot motion. This means that the mo-

tion is the same, but expressed in different bases. If

the 4 × 4 transformation matrix A denotes the motion

of the robot, and if B represents the camera motion

matrix, then this conjugacy is algebraically expressed

by similarity of matrices (Hoffman and Kunze, 1971):

A = XBX

−1

(12)

In the literature this issue is also known as the AX =

XB calibration problem (Mao et al., 2010). This 4 × 4

matrix X is the so-called hand-eye calibration be-

tween robot and camera. In general, the transforma-

tion X between the robot coordinate frame and the

camera frame is not a priori known. In our validation

experiments, the robot transformation A is accurately

known and considered as ground truth, while the esti-

mation of B using different algorithms has to be vali-

dated.

In order to validate B by means of A we can use

conjugacy invariants. It is a fundamental algebraic

property that similar matrices have the same charac-

teristic polynomial (Hoffman and Kunze, 1971):

p(λ) = det(A − I

λ) = det(B − I

λ) (13)

Each coefﬁcient of this characteristic polynomials can

serve to evaluate camera motion matrices against the

known robotic motion matrices. In theory these coef-

ﬁcients are identical. A 4 × 4 transformation matrix

has a characteristic polynomial of degree 4 with ﬁve

coefﬁcients:

p(λ) =λ

+ (tr(R) − 1)λ

− (tr(R) + k)λ

+ (k − det (R))λ + det(R)

(14)

Analyzing the calculation of the characteristic equa-

tion of a rigid transformation matrix reveals that two

parameters determine all the coefﬁcients. The ﬁrst

parameter is the trace of the rotational part R of the

transformation matrix. The second parameter (k) is a

bit more complicated:

k = r

+ r

(15)

This parameter k and the trace of the rotational part

are the two components that compose the ﬁrst error

metric that we suggest, the charpoly error metric. No-

tice that this error metric only provides a quality eval-

uation for the rotational part of the calculated trans-

formation matrix.

CPE

= tr(R

) − tr(R

) (16)

CPE

= k

− k

(17)

These two parameters will be kept separate because

it is not immediately obvious how to combine them

into one parameter that describes the global similarity

between matrices A and B.

3.2 The Hand-eye Error Metric

The second error metric that we propose is less

straightforward. In this metric different measure-

ments associated with several camera transformations

New Error Measures for Evaluating Algorithms that Estimate the Motion of a Range Camera

511

will be combined in a system of equations that could

be used to compute the hand-eye calibration X:

AX −XB = 0 (18)

These matrices are all 4 × 4 transformation matrices

and can be expressed as block matrices:













(19)

Or, after performing the matrix multiplications:









(20)

Using the tensor product ⊗ of matrices and the vec-

torizationvec(Q) denotes of matrix Q, we obtain a

system of 12 linear equations in the 9 unknowns

(vec(R

)

) (Petersen and Pedersen, 2012):



⊗ R

− R

⊗ I

− R



| {z }



vec(R

)







| {z }

(21)

Eqn. 21 was mentioned in the review paper (Shah

et al., 2012) on hand-eye calibration. In order to de-

termine (R

) we need to know the robot motion A

and the corresponding measured camera transforma-

tion B. To actually solve this system, at least three

given transformation pairs (A,B) are necessary. In

practice, coping with noisy measurements, we com-

bine Eqn. 21 for multiple transformation pairs (n ≥ 3)

as follows:















vec(R

)















(22)

Now we introduce our second error metric, as a qual-

ity measure of the system in Eqn. 22. It is the mean

residue for the least squares solution to the transfor-

mation X:

HEE =

||s − M(M

−1

s||

/(12n) (23)

with M = (M

,...,M

)

and s = (s

,...,s

)

. We

refer to this error metric with the acronym HEE

(hand-eye-error). The error metric provided by Eqn.

23 is motivated by the following arguments:

• The robot transformation A is known accurately.

• The transformation matrix X necessarily exists

and is ﬁxed for a given robot-sensor system.

Therefore HEE would be 0 if the rigid motion B

of the depth sensor was computed correctly (as-

suming zero noise for A).

• HEE is able to assess the validity of a method

over multiple measurements, yielding a growing

system of equations (Eqn. 22). Therefore, it also

evaluates the stability of a proposed method.

4 EXPERIMENTAL SETUP

The objective of our experiments is to evaluate the ac-

curacy of three different methods for computing the

rigid motion of a TOF camera. All the tests have

been repeated for two common Time-of-Flight cam-

eras: Kinect V2 and Mesa SR4000. In order to com-

pare the computed motion to a reliable ground truth,

the Time-of-Flight sensors are mounted rigidly on an

articulated robotarm (KUKA KR16, with a repeatibil-

ity error less than 0.1mm). See Fig. 1. In each single

test we consider TOF images for a pair of robot posi-

tions, in which the attached camera observes a classi-

cal calibration checkerboard. During the whole exper-

iment we arranged 6 distinct positions of this checker-

board, that could be viewed from 20 pre-programmed

robot conﬁgurations, providing a supply of 6 ×





test pairs for each camera.

The detection of the checker corners is performed

in the luminance images of the TOF cameras. For

the 2-D extrinsic calibration we used an implemen-

tation of (Zhang, 2000), combined with a nonlinear

optimization to minimize the reprojection error.

For the second and third method we needed a

set of 3-D points, generated by both used types of

TOF sensors, directly provided in (X,Y, Z) coordi-

nates with respect to the camera frame. This means

that we assumed a priori calibrated TOF cameras. The

3-D point-based method makes use of pairs of corre-

sponding points in both range sensors. Because TOF

cameras deliver poor depth measurement accuracy at

the detected checker corners due to the black-white

transitions (Pattinson, 2011; Fuchs and May, 2008),

we preferred to reconstruct the centers of the white

checkerboard. These centers can be found by inter-

secting the diagonals of the checker squares. Note

however that these square centers (nor the checker

corners) are likely to coincide with a pixel, causing

additional round off errors for the depth measure-

ments.

The third method, based on plane measurements,

is by far the most user friendly one. Here there is no

need for performing feature detection and ﬁnd point

correspondences. We only reconstruct points on the

plane supporting the checker board. To this end we

automatically selected the pixels in the white check-

ers and on the larger panel that the calibration board

had been attached to. The 3-D measurements are di-

rectly available in these pixels, avoiding depth inter-

polation. Furthermore, depth measurements for white

pixels are known to be more accurate than for black

pixels (Pattinson, 2011; Fuchs and May, 2008). Next,

we compute the best-ﬁtting plane supporting the re-

constructed 3-D points in each of both given range im-

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

512

ages of a ﬁxed calibration board. Working with these

plane coordinates ﬂattens error ﬂuctuations for the 3-

D point measurements, and moreover avoids the task

to detect features and to establish correspondences.

This best-ﬁtting plane can be computed by principal

component analysis, but we prefer a more robust es-

timate based on Ransac (Fischler and Bolles, 1981).

More precisely, we applied an implementation of the

algorithm of (Torr and Zisserman, 2000).

5 RESULTS

For the sake of validation, random transformations are

sampled from our dataset. This dataset consists of

measurements from 20 different robot positions (Sec-

tion 4). In each such position, 6 images have been

taken by a TOF sensor that was rigidly attached to

the articulated robot arm. These TOF images con-

tain both 2-D intensity images and depth measure-

ments of the 6 ﬁxed spatial positions of a calibration

checkerboard. Finally, all these measurements have

been repeated for two different commonly used Time-

of-Flight cameras: Kinect V2 and Mesa SR4000. For

the three methods that we intend to evaluate, the rigid

camera motion is estimated for some randomly se-

lected pairs of robot positions. The three algorithms

always operate on the same pairs of robot positions

for the sake of comparison.

1. For the ﬁrst method, the extrinsic calibration

based on the 2-D luminance images, we use one

randomly selected calibration plane image, the

same for both robot positions. The checker cor-

ners are detected at subpixel level, the correspon-

dence is established in the pair of 2-D images, and

the relative transformation between both camera

poses is estimated via two extrinsic calibrations

relative to the calibration plane position.

2. If the rigid transformation is estimated by means

of 3-D point correspondences, the same calibra-

tion plane is used. The depth images enable spa-

tial recoveries of the white square midpoints (in-

tersection of the diagonals), providing a corre-

sponding pair of 3-D point sets.

3. In case we compute the rigid camera motion (R,t)

by means of planes as a solution of the system

given by Eqn. 9, some ﬁxed number of planes are

randomly selected from the 6 available calibration

boards. A solution of the system given by Eqn. 9

is determined if at least three planes with linearly

independent normals are available.

5.1 Evaluation by Means of the

Charpoly Error Metric

In our experiment a large amount of transformations

are sampled from the total set of possible transforma-

tions in the constructed dataset. The calculated trans-

formations are compared to the ground truth robot

motion. To accomplish this goal we can use the al-

gebraic conjugacy invariants of Section 3.1. The ab-

solute difference between both traces of the rotational

part and the deﬁned k value are stored. To evaluate

the quality of the rotational part of the obtained trans-

formation the distributions of the charpoly error met-

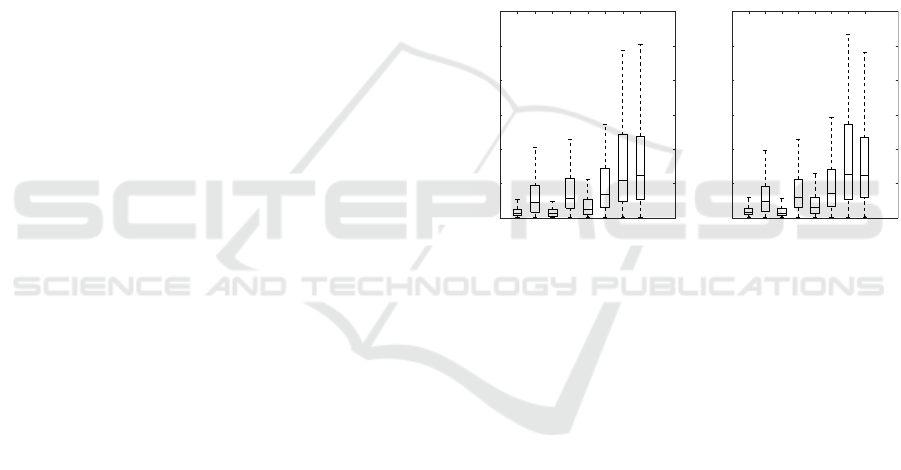
ric are visualized using boxplots (Fig. 2). For both

cameras we observe that the two conjugacy invari-

ants constituting the charpoly error metric (trace and

k) agree in their evaluation.

M K M K M K M K

0.02

0.04

0.06

0.08

0.1

0.12

absolute difference of trace

Trace

M K M K M K M K

0.05

0.1

0.15

0.2

0.25

0.3

absolute difference of k

planes (4)

planes (3) 3D-points

luminance

planes (4)

planes (3)

3D-points

luminance

Figure 2: The quality of the rotation between two positions

of TOF camera is compared for the three described meth-

ods. The plane-based method was done for 3 and for 4

planes. The two parameters of the charpoly error metric

are evaluated for the Kinect V2 (K) and the Mesa SR4000

(M).

The quality of the estimated rotation as obtained

by the plane-based method is similar to the rotation

as obtained by 3-D points, as far as the charpoly error

metric is concerned (Fig. 2). Next, it is striking that

the 3-D methods (operating on range data) compute

the camera rotation with a lower median error value

and smaller spread than the 2-D method (operating

on luminance images). So, it appears that the 2-D

method for extrinsic calibration of a 3-D sensor is less

accurate and less robust.

We also observe that the plane method performs

very well even when using the required minimum of

3 planes, and only slighty better when using 4 planes.

Our experiments demonstrate that using more redun-

dancy (5 or 6 planes) does not imply a better quality of

the estimated transformation. The empirical fact that

estimating a camera motion by means of 3 or 4 planes

is at least as good as by means of 20 correspondence

pairs of 3-D points, and deﬁnitely better than by 2-D

extrinsic calibration, can be explained by the fact that

New Error Measures for Evaluating Algorithms that Estimate the Motion of a Range Camera

513

the involved plane normals are very reliable. They are

obtained by a robust plane ﬁtter, averaging out occur-

ing depth noise.

5.2 Evaluation by Means of the

Hand-eye Error Metric

In this validation a ﬁxed number of transformations

(pairs of robot positions) were sampled for each hand-

eye calibration system size.

M K M K M K M K

HEE

luminance

3D-points

planes (3)

planes (4)

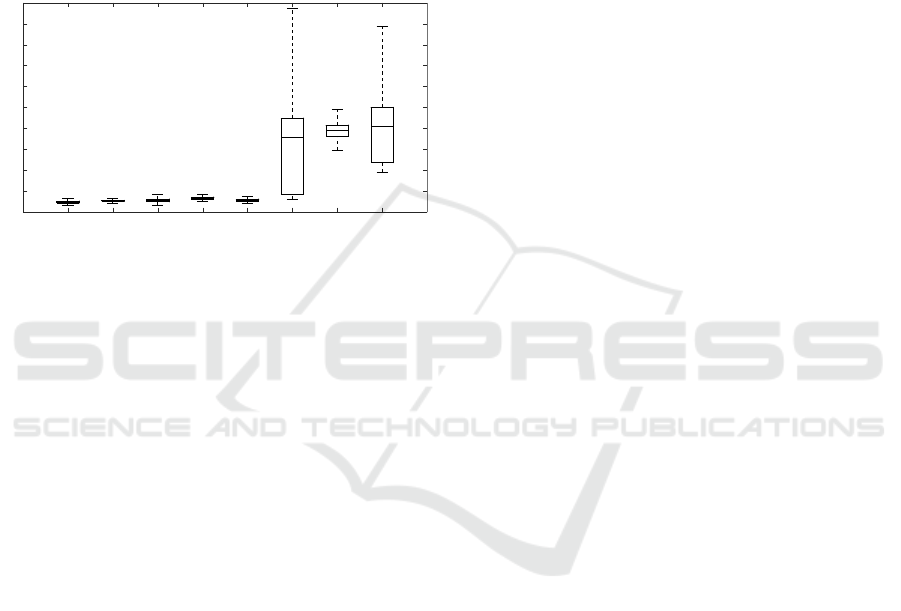
Figure 3: A boxplot visualizing the distribution of the hand-

eye error for the evaluated methods, for the Mesa SR4000

(M) and for the Kinect V2 (K). Methods with a very broad

distribution are unstable and thus unreliable.

During the experiment it turned out that the mag-

nitude of the hand-eye error strongly depends on

the selected transformation. However, this ‘instabil-

ity problem’ was not observed for the plane-based

method, for none of the used cameras (Fig. 3). The

evaluation by the hand-eye error metric implies that

the point-based methods are inherently too incon-

sistent to compute the hand-eye calibration between

robot and camera, while the plane-based method ap-

pears to be able to estimate a hand-eye transforma-

tion in a consistent way, independent of the consid-

ered robot conﬁgurations. The inferior result of the

3-D point method for the Kinect camera can be ex-

plained by its larger ﬁeld of view compared to that

of the Mesa camera. Consequently, the working dis-

tance of the Kinect is larger, and therefore the image

size of the checkerboard is smaller than observed by

the Mesa. This results in a bigger round of error in

the point matching. This inherent drawback for the

3-D point method is circumvented by the 3-D plane

method.

6 CONCLUSIONS

We investigated the quality of several methods for

computating of the rigid motion of a TOF camera. We

evaluated the classical 2-D stereovision approach, us-

ing only the luminance images of the TOF camera,

and two 3-D methods that take beneﬁt from the range

data. The 3-D points method needs corner detection

and point correspondences, while for the 3-D planes

method we only have to randomly select pixels in a

segmented region. In our experiments we considered

the motion of a computer driven robot arm as ground

truth. In order to have access to this ground truth and

to get around the unknown hand-eye transformation,

we designed two error metrics, being algebraic con-

jugacy invariants. We believe that our evaluation for

extrinsic calibration methods is more appropriate than

other perfomance measures such as triangulation er-

ror or reprojection error, because we do not depend on

feature detection nor correspondence determination.

Furthermore, the ground truth provided by a robot

manipulator is more absolute and reliable compared

to a reference obtained from a state-of-the-art algo-

rithm. All our experiments, for both types of cameras

and for both proposed error measures, agreed on the

same conclusions:

• The 3-D methods for estimating the motion of a

range camera deﬁnitely outperform 2-D methods.

• The 3-D planes method appears to be more robust

and accurate than the 3-D points method.

• it appears that only a small number of planes (3

or 4) are needed to guarantee the reported for the

plane-based method.

ACKNOWLEDGEMENTS

The ﬁrst author holds a PhD grant from the research

Fund-Flanders (FWO Vlaanderen).

REFERENCES

Arun, K. S., Huang, T. S., and Blostein, S. D. (1987). Least-

squares ﬁtting of two 3-d point sets. 9(5):698–700.

Bellekens, B., Spruyt, V., Berkvens, R., Penne, R., and

Weyn, M. (2015). A benchmark survey of rigid 3d

point cloud registration algorithms. Int. J. Adv. Int.

Systems, 8(1 & 2):118–127.

Besl, P. J. and McKay, N. D. (1992). A method for registra-

tion of 3-d shapes. IEEE Trans. Pattern Anal. Mach.

Intell., 14(2):239–256.

Eggert, D., Lorusso, A., and Fisher, R. (1997). Estimating

3-d rigid body transformations: a comparison of four

major algorithms. Machine Vision and Applications,

9(5):272–290.

Fern

andez-Moral, E., Gonz

alez-Jim

enez, J., Rives, P., and

evalo, V. (2014). Extrinsic calibration of a set of

VISAPP 2018 - International Conference on Computer Vision Theory and Applications

514

range cameras in 5 seconds without pattern. In In-

ternational Conference on Intelligent Robots and Sys-

tems. IEEE/RSJ.

Fischler, M. and Bolles, R. (1981). Random sampling con-

sensus: A paradigm for model ﬁtting with applications

to image analysis and automated cartography. Com-

munications of the ACM, 24:381–385.

Fuchs, S. and May, S. (2008). Calibration and registra-

tion for precise surface reconstruction with time of

ﬂight cameras. Int. J. Intell. Syst. Technol. Appl.,

5(3/4):274–284.

Guan, J., Deboeverie, F., Slembrouck, M., van Haeren-

borgh, D., van Cauwelaert, D., Veelaert, P., and

Philips, W. (2015). Extrinsic calibration of cam-

era networks using a sphere. Sensors, 15(8):18985–

19005.

Guan, J., Deboeverie, F., Slembrouck, M., Van Haeren-

borgh, D., Van Cauwelaert, D., Veelaert, P., and

Philips, W. (2016). Extrinsic calibration of camera

networks based on pedestrians. Sensors, 16(5).

Hansard, M., Lee, S., Choi, O., and Horaud, R. (2012). Time

of Flight Cameras: Principles, Methods, and Applica-

tions. SpringerBriefs in Computer Science. Springer.

Hoffman, K. and Kunze, R. (1971). Linear algebra.

Prentice-Hall mathematics series. Prentice-Hall.

Mao, J., Huang, X., and Jiang, L. (2010). A ﬂexible solu-

tion to ax=xb for robot hand-eye calibration. In Pro-

ceedings of the 10th WSEAS International Conference

on Robotics, Control and Manufacturing Technology,

ROCOM’10, pages 118–122, Stevens Point, Wiscon-

sin, USA. World Scientiﬁc and Engineering Academy

and Society (WSEAS).

Pathak, K., Birk, A., Va

skevi

cius, N., and Poppinga, J.

(2010). Fast registration based on noisy planes with

unknown correspondences for 3-d mapping. Trans.

Rob., 26(3):424–441.

Pattinson, T. (2011). Quantiﬁcation and Description of Dis-

tance Measurement Errors of a Time-of-Flight Cam-

era. PhD thesis, University of Stuttgard.

Penne, R., Mertens, L., and Ribbens, B. (2013). Planar

segmentation by time-of-ﬂight cameras. In Advanced

Concepts for Intelligent Vision Systems, volume 8192

of Lecture Notes in Computer Science, pages 286–

297.

Penne, R., Raposo, C., Mertens, L., Ribbens, B., and

Araujo, H. (2015a). Investigating new calibration

methods without feature detection for tof cameras. Im-

age and Vision Computing, 43:5062.

Penne, R., Ribbens, B., and Mertens, L. (2015b). An incre-

mental procedure for the lateral calibration of a time-

of-ﬂight camera by one image of a ﬂat surface. Inter-

national Journal of Computer Vision, 113(2):81–91.

Petersen, K. B. and Pedersen, M. S. (2012). The Matrix

Cookbook. Technical University of Denmark. Version

20121115.

Pottmann, H. and Wallner, J. (2001). Computational Line

Geometry. Springer-Verlag New York, Inc., Secaucus,

NJ, USA.

Raposo, C., Barreto, J., and Nunes, U. (2013). Fast and ac-

curate calibration of a kinect sensor. In International

Conference on 3D Vision. IEEE.

Sabata, B. and Aggarwal, J. (1991). Estimation of motion

from a pair of range images: A review. CVGIP: Image

Understanding, 54(3):309 – 324.

Shah, M., Eastman, R. D., and Hong, T. (2012). An

overview of robot-sensor calibration methods for eval-

uation of perception systems. In Proceedings of the

Workshop on Performance Metrics for Intelligent Sys-

tems, PerMIS ’12, pages 15–20, New York, NY, USA.

ACM.

Teichman, A., Miller, S., and Thrun, S. (2013). Unsuper-

vised intrinsic calibration of depth sensors via SLAM.

In Robotics: Science and Systems.

Torr, P. and Zisserman, A. (2000). Mlesac: A new robust

estimator with application to estimating image geom-

etry. Comput. Vis. Image Underst., 78(1):138–156.

Tsai, R. Y. (1992). Radiometry. chapter A Versatile Cam-

era Calibration Technique for High-accuracy 3D Ma-

chine Vision Metrology Using Off-the-shelf TV Cam-

eras and Lenses, pages 221–244. Jones and Bartlett

Publishers, Inc., USA.

Vasconcelos, F., Barreto, J., and Nunes, U. (2012). A min-

imal solution for the extrinsic calibration of a cam-

era and a laser-rangeﬁnder. IEEE Trans Pattern Anal

Mach Intell., 34(11):2097–2107.

Zhang, Z. (1989). Motion and structure from two perspec-

tive views: algorithms, error analysis, and error esti-

mation. 11(5):451–476.

Zhang, Z. (2000). A ﬂexible new technique for camera cal-

ibration. 22(11):1330–1334.

New Error Measures for Evaluating Algorithms that Estimate the Motion of a Range Camera

515