Search-and-Fetch with 2 Robots on a Disk

Wireless and Face-to-Face Communication Models

Konstantinos Georgiou

1,∗

, George Karakostas

2,∗

and Evangelos Kranakis

3,∗

Department of Mathematics, Ryerson University, 350 Victoria St., Toronto, ON, M5B 2K3, Canada

Dept. of Computing & Software, McMaster University, 1280 Main St. West, Hamilton, Ontario L8S 4K1, Canada

School of Computer Science, Carleton University, 1125 Col. By Dr., Ottawa, ON K1S 5B6, Canada

Keywords:

Search & Fetch, Distributed Algorithm, Rendevouz, Exploration, Face-to-Face Model, Wireless Model.

Abstract:

We introduce and study treasure-evacuation with 2 robots, a new problem on distributed searching and fetch-

ing related to well studied problems in searching, rendezvous and exploration. The problem is motivated by

real-life search-and-rescue operations in areas of a disaster, where unmanned vehicles (robots) search for a

victim (treasure) and subsequently bring (fetch) her to safety (the exit). One of the critical components in

such operations is the communication protocol between the robots. We provide search algorithms and contrast

two standard models, the face-to-face and the wireless model. Our main technical contribution pertains to

the face-to-face model. More speciﬁcally, we demonstrate how robots can take advantage of some minimal

information of the topology (i.e., the disk) in order to allow for information exchange without meeting. The

result is a highly efﬁcient distributed treasure-evacuation protocol which is minimally affected by the lack of

distant communication.

1 INTRODUCTION

We introduce the study of a new distributed problem

on searching and fetching called treasure evacuation.

Two robots are placed at the center of a unit disk,

while an exit and a treasure lie at unknown positions

on the perimeter of the disk. Robots search with max-

imum speed 1, and they detect an interesting point

(either the treasure or the exit) only if they pass over

it. The exit is immobile, while the treasure can be car-

ried by any of the robots. The goal of the search is for

at least one of the robots to bring (fetch) the treasure

to the exit, i.e. evacuate the treasure, in the minimum

possible completion time. The robots do not have to

evacuate, rather they only need to co-operate, possi-

bly by sharing information, so as to learn the locations

of the interesting points and bring the treasure to the

exit. Contrary to previous work, this is the ﬁrst time

an explicit ordering on the tasks to be performed is

imposed (ﬁrst the treasure, then the exit). This makes

the problem inherently different in nature and more

difﬁcult than similarly looking results.

Finding an optimal algorithm turns out to be a

challenging task even when the robots have some

knowledge, e.g., the arc-distance α between the exit

∗

Research supported in part by NSERC.

and the treasure. We propose treasure-evacuation pro-

tocols in two communication models. In the wireless

model robots exchange information instantaneously

and at will, while in the face-to-face model informa-

tion can be exchanged only if the robots meet. We aim

at incorporating this knowledge into our algorithm de-

signs. We offer algorithmic techniques such as plan-

ning ahead, timing according to the explicit task or-

dering, and retrieval of unknown information through

inference and not communication.

Part of our contribution is that we demonstrate

how robots can utilize the knowledge of the arc-

distance α between the interesting points. We pro-

pose protocols that induce worst case evacuation time

1 + π − α/2 + 3sin(α/2) for the wireless model and

1+π−α+4 sin(α/2) for the face-to-face model. The

upper bound in the face-to-face model, which is our

main contribution, is the result of a non-intuitive evac-

uation protocol that allows robots to exchange infor-

mation about the topology without meeting, effec-

tively bypassing their inability to communicate from

distance. Finally, we complement our results above

by showing that any algorithm in the face-to-face

model needs time at least 1+π/3+4sin (α/2), if α ∈

[0,2π/3] and at least 1+ π/3 +2 sin(α) +2sin (α/2),

if α ∈ [2π/3,π].

Georgiou K., Karakostas G. and Kranakis E.

Search-and-Fetch with 2 Robots on a Disk - Wireless and Face-to-Face Communication Models.

DOI: 10.5220/0006091600150026

In Proceedings of the 6th International Conference on Operations Research and Enterprise Systems (ICORES 2017), pages 15-26

ISBN: 978-989-758-218-9

1.1 Contributions

Rendezvous, treasure hunting and exploration have

been subjects of extensive research in the broad area

of distributed and online computing (see related work

below). Challenges in each of these fundamental

tasks arise from different computation, communica-

tion or knowledge limitations, with admittedly nu-

merous variations. The novel distributed problem of

treasure-evacuation that we introduce and study in

this work combines in a complex way challenges from

all these fundamental tasks. As such, progress to-

wards solving generic treasure-evacuation-like prob-

lems will unavoidably touch on state-of-the-art tech-

niques of achieving these tasks.

In treasure-evacuation, two stationary targets (a

treasure and an exit that we call interesting points)

are hidden on a speciﬁc domain. At ﬁrst, robots need

to (a) perform treasure hunting in this online envi-

ronment. Interestingly, the knowledge of the loca-

tion of one of these targets may or may not reveal

the location of the other. In particular, the task of the

robots does not end when both interesting points are

located, rather, only when the treasure-holder learns

(and ﬁnds) the location of the exit as well. Given

communication limitations, the latter can be accom-

plished efﬁciently only if (b) a sufﬁcient portion of the

environment is explored before both interesting points

are found, or (c) if information can be exchanged be-

tween robots. In case (b), robots “invest” in domain

exploration in an attempt to expedite treasure evacua-

tion once the interesting points are found. In case (c),

robots may need to attempt to rendezvous (not very

late in the time horizon) so that the distributed sys-

tem becomes cognitive of the environment and con-

sequently completes the given task. Clearly, in order

for a distributed system to accomplish treasure evac-

uation efﬁciently, robots need to perform and balance

all tasks (a),(b),(c) above, i.e to perform treasure hunt-

ing, while learning the environment either by explo-

ration or by rendezvous. A unique feature of treasure-

evacuation is that only the treasure has to be brought

to the exit.

The last observation gives some ﬁrst evidence

of the difﬁculty of solving treasure-evacuation, even

when the domain is a disk. Can a robot choose a tra-

jectory (maybe staying far from the exit) to help the

treasure-holder expedite evacuation? If a robot dis-

covers the treasure, is it a good strategy to become

the treasure holder and greedily search for the exit?

Should robots learn the environment by investing on

exploration or on rendezvous and hence on message

exchange? Finally, is it possible in a non-wireless en-

vironment for robots to exchange information without

meeting? An efﬁcient algorithm should somehow ad-

dress all these questions.

From the discussion above, it is not a surprise that

plain vanilla algorithms cannot be efﬁcient. Indeed,

our algorithms (for both the wireless and face-to-face

models) adapt their strategies, among others, with re-

spect to the distance of the interesting points. On

one hand, there are conﬁgurations where the evac-

uation protocols are simple and greedy-like. How-

ever, the reader can verify from our analyses that, had

we followed such simplistic approach for all conﬁg-

urations, the evacuation time would have been much

worse than our upper bounds. The simplest example

of this kind will be transparent even in the analysis of

the wireless model, in which robots can exchange in-

formation at will. To achieve our upper bound, robots

choose different trajectories (still greedy-like) for var-

ious distances of the interesting points. Nevertheless,

the analysis in this case is relatively simple.

Our main technical contribution pertains to the

face-to-face model where robots can exchange infor-

mation only if they meet. In particular, we explic-

itly exhibit distributed strategies that allow robots to

exchange information even from distance. At a high

level, and given that interesting points are located by

robots at some (carefully deﬁned) critical intervals in

the time horizon, robots choose (occasionally) highly

non-intuitive trajectories, not in order to locate the re-

maining interesting points, rather to potentially meet

their fellow robots. The trajectories are carefully cho-

sen so that a robot may deduce information, using

an involved protocol, as to what the other robot has

found, and hence learn the environment regardless of

whether the rendezvous is realized or not. For the

treasure-holder, this would result in learning the loca-

tion of the exit. For the other robot(s), this would be

an altruistic attempt to help the fellow treasure-holder.

In particular, that could result in that the non treasure-

holder never ﬁnds the exit, still expediting the treasure

evacuation time. We note that once the trajectories

are determined (which is the heart of our contribu-

tion) correctness and performance analysis is a matter

of an exhaustive and technical case analysis. Inter-

estingly, the efﬁciency of our algorithm for the face-

to-face model is only slightly worse than the solution

for the wireless case (but signiﬁcantly better than the

naive solution for the face-to-face model), indicating

that lack of communication can be compensated by

clever algorithms.

Finally, we complement our results by proving

some lower bounds for treasure evacuation with 2

robots for the face-to-face model. That concludes the

ﬁrst attempt to study distributed problems of this kind,

i.e. optimization treasure hunting problems where the

distributed systems learn the online environment by a

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

combination of exploration and rendezvous, a feature

which, to the best of our knowledge, is also novel.

1.2 Related Work

Traditional search is concerned with ﬁnding an ob-

ject with speciﬁed properties within a search space.

Searching in the context of computational prob-

lems is usually more challenging especially when

the environment is unknown to the searcher(s) (see

(Ahlswede and Wegener, 1987; Alpern and Gal,

2003; Stone, 1975)). This is particularly evident in

the context of robotics whereby exploration is taking

place within a given geometric domain by a group

of autonomous but communicating robots. The ulti-

mate goal is to design an algorithm so as to accom-

plish the requirements of the search (usually locat-

ing a target of unknown a priori position) while at

the same time obeying the computational and geo-

graphical constraints. The input robot conﬁguration

must also accomplish the task in the minimum possi-

ble amount of time (Berman, 1998).

Search has a long history. There is extensive and

varied research and several models have been pro-

posed and investigated in the mathematical and theo-

retical computer science literature with particular em-

phasis on probabilistic search (Stone, 1975), game

theoretic applications (Alpern and Gal, 2003), cops

and robbers (Bonato and Nowakowski, 2011), classi-

cal pursuit and evasion (Nahin, 2012), search prob-

lems as related to group testing (Ahlswede and We-

gener, 1987), searching a graph (Koutsoupias et al.,

1996), and many more. A survey of related search

and pursuit evasion problems can be found in (Chung

et al., 2011). In pursuit-evasion, pursuers want to

capture evaders who try to avoid capture. Examples

include Cops and Robbers (whereby the cops try to

capture the robbers by moving along the vertices of

a graph), Lion and Man (a geometric version of cops

and robbers where a lion is to capture a man in ei-

ther continuous or discrete time), etc. Searching for

a motionless point target has some similarities with

the lost at sea problem, (Gluss, 1961; Isbell, 1967),

the cow-path problem (Beck, 1964; Bellman, 1963),

and with the plane searching problem (Baeza-Yates

and Schott, 1995). This last paper also introduced the

“instantaneous contact model”, which is referred to as

wireless model in our paper. When the mobile robots

do not know the geometric environment in advance

then researchers are concerned with exploring (Al-

bers and Henzinger, 2000; Albers et al., 2002; Deng

et al., 1991; Hoffmann et al., 2001). Coordinating the

exploration of a team of robots is a main theme in

the robotics community (Burgard et al., 2005; Thrun,

2001; Yamauchi, 1998) and often this is combined

with the mapping of the terrain and the position of

the robots within it (Kleinberg, 1994; Papadimitriou

and Yannakakis, 1989).

Evacuation for grid polygons has been studied in

(Fekete et al., 2010) from the perspective of con-

structing centralized evacuation plans, resulting in the

fastest possible evacuation from the rectilinear envi-

ronment. There are certain similarities of our prob-

lem to the well-known evacuation problem on an in-

ﬁnite line (see (Baeza Yates et al., 1993) and the re-

cent (Chrobak et al., 2015)) in that the search is for

an unknown target. However, in this work the adver-

sary has limited possibilities since search is on a line.

Additional research and variants on this problem can

be found in (Demaine et al., 2006) (on searching with

turn costs), (Kao et al., 1996) (randomized algorithm

for the cow-path problem), (Kao et al., 1998) (hybrid

algorithms), and many more.

A setting similar to ours is presented in the re-

cent works (Czyzowicz et al., 2014; Czyzowicz et al.,

2016; Czyzowicz et al., 2015a; Czyzowicz et al.,

2015b) where algorithms are presented in the wire-

less and non-wireless (or face-to-face) communica-

tion models for the evacuation of a team of robots.

The “search domain” in (Czyzowicz et al., 2014; Czy-

zowicz et al., 2016; Czyzowicz et al., 2015a) is a

unit circle (while in (Czyzowicz et al., 2015b) the

search domain is a triangle or square), however, un-

like our search problem, in these papers all the robots

are required to evacuate from an unknown exit on the

perimeter. Moreover, in none of these papers is there

a treasure to be fetched to the exit.

Our work is also an attempt to analyze theoreti-

cally search-and-fetch problems that have been stud-

ied by the robotics community since the 90’s, e.g.

see (Jennings et al., 1997). A scenario similar to

ours (but only for 1 robot) has been introduced by

Alpern in (Alpern, 2011), where the domain was dis-

crete (a tree) and the approach/analysis resembled that

of standard search-type problems (Alpern and Gal,

2003). In contrast, our problem is of distributed na-

ture, and our focus is to demonstrate how robots’

communication affects efﬁciency.

1.3 Problem and Model Motivation

Our problem is motivated by real-life surveillance and

search-and-rescue operations where unmanned vehi-

cles, e.g. drones, search for victims in areas of a disas-

ter. Indeed, consider a group of rescuer-mobile-agents

(robots), initially located strategically in a central po-

sition of a domain. When alarm is triggered and a

distress signal is received, robots need to locate a vic-

Search-and-Fetch with 2 Robots on a Disk - Wireless and Face-to-Face Communication Models

tim (the treasure) and bring her to safety (the exit).

Our problem shares similarities also with classic and

well-studied cops-and-robbers games; robots rest at a

central position of a domain (say, in the centre of a

disk as in our setup) till an alarm is triggered by some

“robber” (the treasure in our case). Then, robots need

to locate the stationary robber and subsequently bring

him to jail (the exit). Interestingly, search-and-fetch

type problems resemble also situations that abound

in fauna, where animals hunt for prey which is then

brought to some designated area, e.g. back to the

lair. As such, further investigation of similar problems

will have applications to real-life rescue operations, as

well as to the understanding of animal behavior, as it

is common in all search problems.

From a technical perspective, our communication

models are inspired by the recent works on evac-

uation problems (Czyzowicz et al., 2014; Czyzow-

icz et al., 2015a; Czyzowicz et al., 2015b). No-

tably, the associated search problems are inherently

different than our problem which is closer in nature

to search-type, treasure-hunt, and exploration prob-

lems. Also, our mathematical model features (a)

a distributed setting (b) with objective to minimize

time, and (c) where different communication mod-

els are contrasted. None among (a),(b),(c) are well

understood for search games, and, to the best of our

knowledge, they have not been studied before in this

combination.

Speciﬁc to the problem we study are the number

of robots (2 and not arbitrarily many - though our

results easily extend to swarms of robots), the do-

main (disk), and the fact the robots have some knowl-

edge about the interesting points. Although extend-

ing our results to more generic situations is interest-

ing in its own right, the nature of the resulting prob-

lems would require a signiﬁcantly different algorith-

mic approach. Indeed, our main goal is to study how

limitations in communication affect efﬁciency, which

is best demonstrated when the available number of

robots, and hence computation power, is as small as

possible, i.e. for two robots. In fact, it is easy to ex-

tend our algorithms for the n-robot case.

Notably, search-and-fetch problems are challeng-

ing even for 1 robot as demonstrated in (Georgiou

et al., 2016b). In particular, the work of (Georgiou

et al., 2016b) implies that establishing provably op-

timal evacuation protocols for 2-robots is a difﬁcult

task, even when the domain is the disk. Nevertheless,

we view the domain that we study as natural. Indeed,

a basic setup in search-and-rescue operations is that

rescuer-robots inhabit in a base-station, and they stay

inactive till they receive a distress signal. As it is com-

mon in real-life situations, the signal may only reveal

partial information about the location of a victim, e.g.

its distance from the base-station, along with the dis-

tance between the points. When there are more than

one interesting points to be located, this kind of infor-

mation suggests that the points lie anywhere on co-

centric circles. When the points are equidistant from

the base-station, robots need only consider a disk, as

it is the case in our problem. We believe that with

enough technical and tedious work, our results can

also extend to non-equidistant points, however the al-

gorithmic signiﬁcance of the proposed distributed so-

lutions may be lost in the technicalities.

In order to demonstrate that robots with primitive

communication capabilities are in fact not much less

powerful than in the wireless model, it is essential to

assume that robots have some knowledge of the dis-

tance between the interesting points. The reader may

also view this piece of advice as an algorithmic chal-

lenge in order to bypass the uncertainty regarding the

locations of the interesting points. Notably, our algo-

rithms adapt strategies as a function of the distance of

the interesting points, trying to follow protocols that

would allow them to detect the actual positions of the

points without necessarily visiting them. As an easy

example, note that if a robot has explored already a

contiguous arc of length α+ ε, the discovery of an in-

teresting point reveals the location of the other α-arc

distant away interesting point (our algorithm makes

use of distance α in a much more sophisticated way).

As a result, had we assumed that distances are un-

known, robots may not be able to deduce such im-

portant information about the topology using partial

exploration, and the problem would require an inher-

ently different algorithmic approach. Apart from that,

partial knowledge of the input is also interesting due

to the efﬁciency-information tradeoffs that are natu-

rally induced by the problem, which is also a standard

theme in competitive analysis, e.g. see (Hipke et al.,

1999) and (Georgiou et al., 2016b).

Admittedly, the model we introduce is simple but

natural, general, and complex enough to require non-

standard algorithmic solutions. Most importantly, our

model allows us to demonstrate in a relatively clean

way a couple of novel algorithmic techniques for at-

tacking challenging and newly introduced types of

distributed problems. We anticipate that the ideas in-

troduced in this work will initiate new research direc-

tions towards solving a family of problems that are

not yet understood from a theoretical perspective.

1.4 Notation & Organization

A treasure and an exit are located at unknown posi-

tions on the perimeter of a unit-disk and at arc dis-

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

tance α (in what follows all distances will be arc-

distances, unless speciﬁed otherwise). Robots start

from the center of the disk, and can move anywhere

on the disk at constant speed 1. Each of the robots

detects the treasure or the exit only if its trajectory

passes over that point on the disk. Once detected, the

treasure can be carried by a robot at the same speed.

We refer to the task of bringing the treasure to the

exit as treasure-evacuation. We use the abbreviations

T,E for the treasure and the exit, respectively. For

convenience, in the sequel we will refer to the loca-

tions of the exit and the treasure as interesting points.

For an interesting point I on the perimeter of the disk,

we also write I = E (I = T ) to indicate that the exit

(treasure) lies in point I. For a point B, we also write

B = null to denote the event that neither the treasure

nor the exit is placed on B.

We focus on the following online variations of

treasure-evacuation with 2 robots, where the exact

distance α between T,E is known, but not their po-

sitions. In 2-TE

(Section 2), information between

robots is shared continuously in the time horizon,

i.e. messages between them are exchanged instanta-

neously and at will with no restrictions and no addi-

tional cost or delays. In 2-TE

f 2 f

(Section 3), the com-

munication protocol between the robots is face-to-

face (non-wireless)—abbreviated F2F (or f2f), where

information can be exchanged only if the robots meet

at the same point anywhere. We give two algorithms:

in the former case we prove a 1 + π − α + 4sin (α/2)

and in the latter case a 1+π−α/2+3 sin(α/2) upper

bound, resp., on the treasure evacuation time, where α

is the arc distance between treasure and exit. Finally

in Section 4 we provide a lower bound for treasure-

evacuation with 2 robots in the F2F model.

Any omitted proofs, due to space limitations, can

be found in the full version of the paper (Georgiou

et al., 2016a).

2 WIRELESS MODEL

As a warm-up we present in this section an upper

bound for the wireless model, which will also serve

as a reference for the more challenging face-to-face

model. The algorithmic solution we propose is sim-

ple and it is meant to help the reader familiarize

with basic evacuation trajectories that will be used in

our main contribution pertaining to the face-to-face

model.

Theorem 2.1. For every α ∈ [0, π], problem 2-TE

can be solved in time 1 + π − α+4sin (α/2).

To prove Theorem 2.1, we propose Algorithm 1

that achieves the promised bound. Intuitively, our al-

gorithm follows a greedy like approach, adapting its

strategy as a function of the distance α of the interest-

ing points. If α is small enough, then the two robots

move together to an arbitrary point on the disk and

start exploring in opposing directions. Otherwise the

two robots move to two antipodal points and start ex-

ploring in the same direction. Exploration continues

till an interesting point is found. When that happens,

the robot that can pick up the treasure and fetch it to

the exit in the fastest time (if all locations have been

revealed) does so, otherwise remaining locations are

tried exhaustively. Detailed descriptions of the evac-

uation protocol can be seen in Algorithm 1, comple-

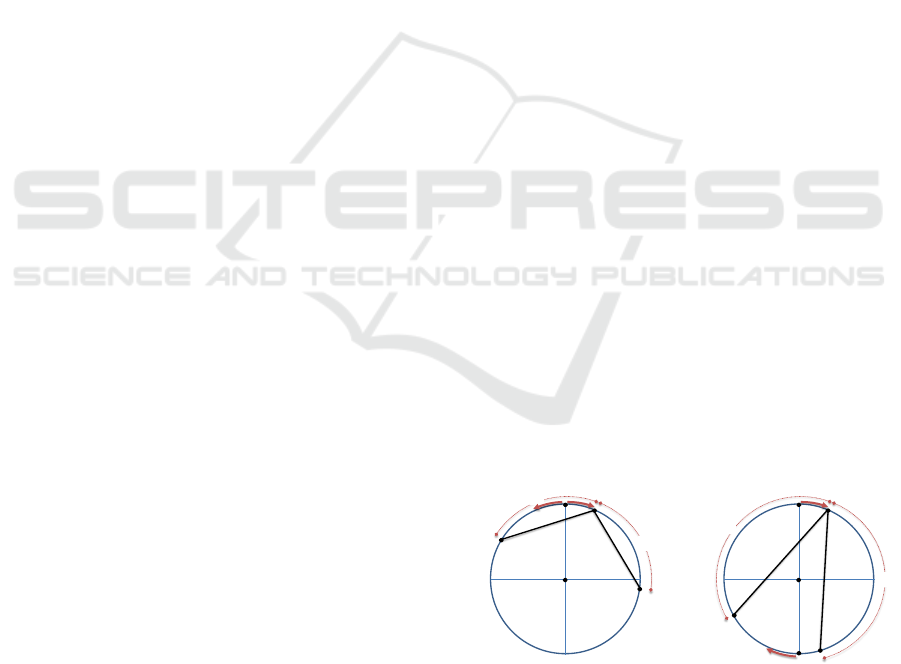
mented by Figure 1.

Noticeably, the performance analysis we give is

tight, meaning that for every α ≥ 0, there are con-

ﬁgurations (placements of the interesting points) for

which the performance of the algorithm is exactly

1 + π − α+4sin (α/2). Most importantly, the perfor-

mance analysis makes explicit that naive algorithms

that do not adapt strategies together with α are bound

to perform strictly worse than our upper bound. Also,

the achieved upper bound should be contrasted to

the upper bound for the face-to-face model (which is

achieved by a much more involved algorithm), which

at the same time is only α/2 − sin (α/2) more costly

than the bound we show in the wireless model.

Algorithm 1 takes advantage of the fact that robots

can communicate to each other wirelessly. This also

implies that lack of message transmission is effec-

tively another method of information exchange. In

what follows point A will always be the starting point

of R

, and A

denotes its antipodal point. For the sake

of the analysis and w.l.o.g. we will assume that R

the one that ﬁrst ﬁnds an interesting point I = {E,T },

say at time x := AI

. We call B,C the points that are at

clockwise and counter-clockwise arc-distance α from

I respectively. Figure 1 depicts the interesting points

encountered.





























′

 ≤ 2/3

 > 2/3

Figure 1: The points of interest for our Algorithm 1.

The description of Algorithm 1 is from the per-

spective of the robot that ﬁnds ﬁrst an interesting

point, that we always assume is R

. Next we assume

that the ﬁnding of any interesting point is instanta-

Search-and-Fetch with 2 Robots on a Disk - Wireless and Face-to-Face Communication Models

neously transmitted and received by the two robots.

Also, if at any moment, the positions of the interesting

points are learned by the two robots, then the robots

attempt a “conﬁdent evacuation” using the shortest

possible trajectory. This means for example that if the

treasure is not picked up by any robot, then the two

robots will compete in order to pick it up and return it

to the exit, moving in the interior of the disk.

Algorithm 1: Wireless Algorithm.

Step 1. If α ≤ 2π/3, then the two robots move to-

gether to an arbitrary point on the ring and start

moving in opposing directions, else they move to

arbitrary antipodal points A,A

on the cycle and

start moving in the same direction.

Step 2. Let I be the ﬁrst interesting point discov-

ered by R

, at time x := AI

. Let B,C be the points

that are at clockwise and counter-clockwise arc-

distance α from I respectively.

Step 3. If x ≥ α/2 then robots learn that the other

interesting point is in B, else R

moves to B, R

moves to C.

Step 4. Evacuate

Correctness of Algorithm 1 is straightforward,

since the two robots follow a “greedy-like evacuation

protocol” (still, they use different starting points de-

pending on the value of α). Also, the performance

analysis of the algorithm, effectively proving Theo-

rem 2.1, is a matter of a straightforward case-analysis.

We note that our worst-case analysis is tight, in that

for every α ≥ 0 there exist conﬁgurations in which the

performance is exactly as promised by Theorem 2.1.

Moreover, we may assume that α > 0 as otherwise the

problem is solved when one interesting point is found.

Note that our algorithm performs differently when

α ≤ 2π/3 and when α > 2π/3. Let x := AI

be the

time that R

ﬁrst discovers interesting point I. Then

it must be that x ≤ α/2 and x ≤ π − α for the cases

α ≤ 2π/3 and α > 2π/3 respectively (see also Fig-

ure 1). This will be used explicitly in the proof of

the next two lemmata. We also assume that R

al-

ways moves clockwise starting from point A. R

either moves counter-clockwise starting from A, if

α ≤ 2π/3, or it moves clockwise starting from the an-

tipodal point A

of A, if α > 2π/3. In every case, the

two robots move along the perimeter of the disk till

time x when R

transmits the message that it found an

interesting point.

The performance of Algorithm 1 is described in

the next two lemmata which admit proofs by case

analyses. Each of them examines the relative posi-

tion of the starting point of robot R

(which ﬁnds an

interesting point ﬁrst) and the two interesting points.

Lemma 2.2. Let A be the starting point of R

which

is the ﬁrst to discover an interesting point I. Let also

the other interesting point be at C, where CI

= α. If A

lies in the arc CI

, then the performance of Algorithm

1 is 1 + π − α+4sin (α/2), for all α ∈ [0,π].

Lemma 2.3. Let A be the starting point of R

which is

the ﬁrst to discover an interesting point I. Let also the

other interesting point be at B, where IB

= α. If A lies

outside the arc IB

, then the performance of Algorithm

1 is 1 + π − α+4sin (α/2), for all α ∈ [0,π].

It is clear now that Lemmata 2.2, 2.3 imply that for

all α ∈ [0, π], the overall performance of Algorithm 1

is no more than 1 + π − α + 4 sin(α/2) concluding

Theorem 2.1.

3 F2F MODEL

The main contribution of our work pertains to the

face-to-face model and is summarized in the follow-

ing theorem.

Theorem 3.1. For every α ∈ [0,π], problem 2-TE

f 2 f

can be solved in time 1 + π − α/2 +3sin (α/2).

Next we give the high-level intuition of the pro-

posed evacuation-protocol, i.e. Algorithm 2, that

proves the above theorem (more low level intuition,

along with the formal description of the protocol ap-

pears in Section 3.1).

Denote by β the upper bound promised by the

theorem above. It should be intuitive that when the

distance of the interesting points α tends to 0, there

is no signiﬁcant disadvantage due to lack of com-

munication. And although the wireless evacuation-

time might not be achievable, a protocol similar to

the wireless case should be able to give efﬁcient so-

lutions. Indeed, our face-to-face protocol is a greedy

algorithm when α is not too big, i.e. the two robots try

independently to explore, locate the interesting points

and fetch the treasure to the exit without coordination

(which is hindered anyways due to lack of communi-

cation). Following a worst case analysis, it is easy to

see that as long as α does not exceed a special thresh-

old, call it α

, the evacuation time is β, and the analy-

sis is tight.

When α exceeds the special threshold α

, the lack

of communication has a more signiﬁcant impact on

the evacuation time. To work around it, robots need

to exchange information which is possible only if they

meet. For this reason (and under some technical con-

ditions), robots agree in advance to meet back in the

center of the disk to exchange information about their

ﬁndings, and then proceed with fetching the treasure

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

to the exit. Practically, if the rendezvous is never re-

alized, e.g. only one robot reaches the center up to

some time threshold, that should deduce that interest-

ing points are not located in certain parts of the disk,

potentially revealing their actual location. In fact, this

recipe works well, and achieves evacuation time β, as

long as α does not exceed a second threshold, which

happens to be 2π/3.

The hardest case is when the two interesting points

are further than 2π/3 apart. Intuitively, in such a case

there is always uncertainty as to where the interesting

points are located, even when one of them is discov-

ered. At the same time, the interesting points, hence

the robots, might be already far apart when some or

both interesting points are discovered. As such, meet-

ing at the center of the disk to exchange informa-

tion would be time consuming and induces evacuation

time exceeding β. Our technical contribution pertains

exactly to this case. Under some technical conditions,

the treasure-ﬁnder might need to decide which of the

two possible exit-locations to consider next. In this

case, the treasure-holder follows a trajectory not to-

wards one of the possible locations of the exit, rather

a trajectory closer to that of its peer robot aiming for

a rendezvous. The two trajectories are designed care-

fully so that the location of the exit is revealed no mat-

ter whether the rendezvous is realized or not.

3.1 Algorithm & Correctness

In our main Algorithm 2, robots R

that start from

the centre of the circle, move together to an arbi-

trary point A on the circle (which takes time 1). Then

they start moving in opposing directions, say, counter-

clockwise and clockwise respectively till the locate

some interesting point.

In what follows we describe only the trajectory

of R

which is meant to be moving clock-wise (R

performs the completely symmetric trajectory, and

will start moving counter clock-wise). In particular

all point references in the description of our algo-

rithm, and its analysis, will be from the perspective

of R

’s trajectory which is assumed to be the robot

that ﬁrst visits either the exit or the treasure at posi-

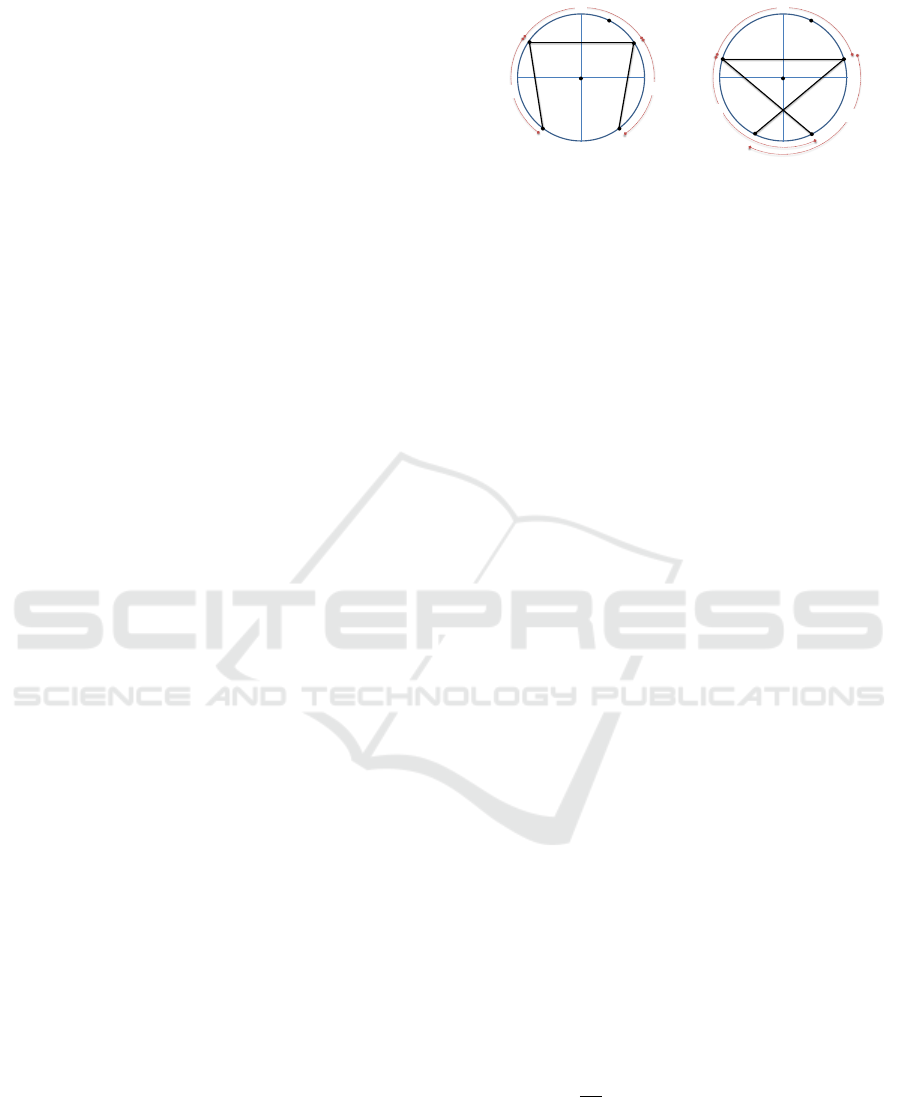
tion I. By B,C, D we denote the points on the circle

with DC

= CI

= IB

= α (see Figure 2). As before, and

in what follows, I ∈ {E,T } represents the position on

the circle that is ﬁrst discovered in the time horizon

by any robot (in particular by R

), and that holds ei-

ther the treasure or the exit. Finally, O represents the

centre of the circle, which is also the starting point of

the robots.

According to our algorithm, R

starts moving

from point A till it reaches an interesting point I at



Figure 2: The points of interest from the perspective of R

when α ≤ 2π/3 on the left, and when α ≥ 2π/3 on the right.

time x := AI

. At this moment, our algorithm will de-

cide to run one of the following subroutines with input

x. These subroutines describe evacuation protocols,

in which the treasure must be brought to the exit. Oc-

casionally, the subroutines claim that robots evacuate

(with the treasure) from points that is not clear that

hold an exit. As we will prove correctness later, we

comment on these cases by writing that “correctness

is pending”.

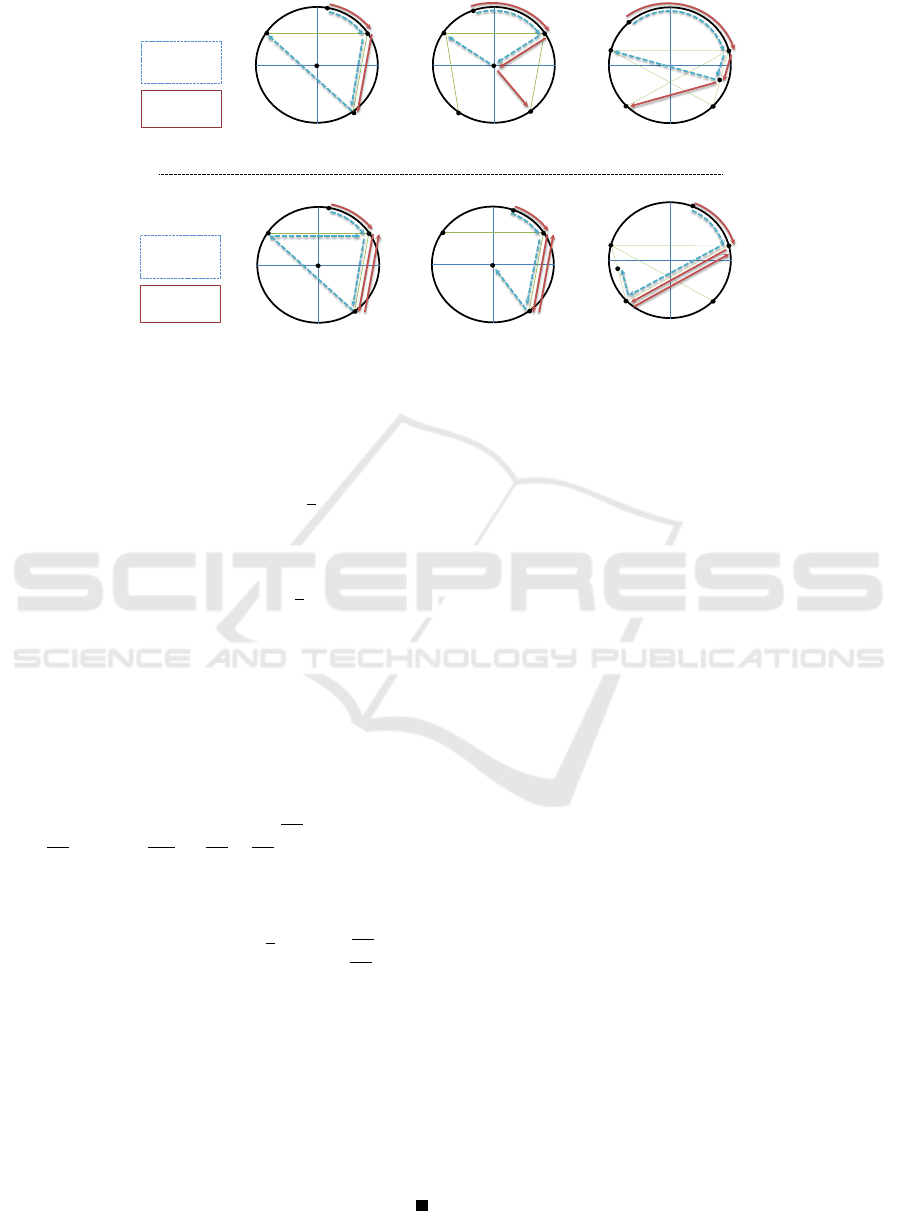
(x) (Figure 3 i): If I = T , pick up the treasure and

move to B along the chord IB. If B = E evacuate,

else go to C along the chord BC and evacuate.

(Figure 3 ii): If I = E move to B along the chord

IB. If B = T , pick up the treasure, and return to

I along the chord BI and evacuate. If B = null,

then go to C along the chord BC. If the treasure

is found at C, pick it up, and move to I along the

chord CI and evacuate (else abandon the process).

(x) (Figure 3 iii): At the moment robots leave

point A, set the timer to 0.

If I = T , pick up the treasure and go to the cen-

tre O of the circle. Wait there till the time t

max{x,α − x + 2sin (α/2)} +1. If R

arrives at O

by time t

, then go to C and evacuate (correctness

is pending). Else (if R

does not arrive at O by

time t

) go to B and evacuate (correctness is pend-

ing).

(Figure 3 iv): If I = E, move to B along the chord

IB. If B = T , pick up the treasure, and return to I

along the chord BI and evacuate. If B = null, then

go to the centre O and halt.

(x) (Figure 3 v): If I = T pick up the treasure.

If R

is already at point I go to C and evacu-

ate (correctness pending). If R

is not at point

I, then move along chord ID for additional time

y := α/2 − x + sin(α/2) + sin (α), and let K be

such that IK = y. If R

is at point K, then go to B

and evacuate (correctness is pending), else (if R

is not at point K) go to C and evacuate (correct-

ness pending).

(Figure 3 vi): If I = E, move to B along the chord

IB. If B = T , pick up the treasure, and return to I

along the chord BI and evacuate. If B = null, then

Search-and-Fetch with 2 Robots on a Disk - Wireless and Face-to-Face Communication Models

move along chord BC until you hit C (or you meet

the other robot- whatever happens ﬁrst) and halt

at the current point, call it K.

It is worthwhile discussing the intuition behind the

subroutines above. First note that if a robot ever ﬁnds

a treasure, it picks it up. The second important prop-

erty is that each robot simulates A

either till it ﬁnds

the treasure or till it fails to ﬁnd the treasure after ﬁnd-

ing the exit. At a high level, A

greedily tries to evac-

uate the treasure. This means that if the treasure is

found ﬁrst, then the robot tries successively the pos-

sible locations of the exit (using the shortest possible

paths) and evacuates. If instead the exit is found, then

it successively tries the (at most) two possibilities of

the treasure location, and if the treasure is found, it

returns it to the exit.

and A

constitute our main technical contribu-

tion. Both algorithms are designed so that in some

special cases, in which the exact locations of the in-

teresting points are not known, the two robots sched-

ule some meeting points so that if the meeting (ren-

dezvous) is realized or even if it is not, the treasure-

holder can deduce the actual location of the exit. In

other words, we make possible for the two robots to

exchange information without meeting. Indeed after

ﬁnding the treasure, in A

, R

goes to the centre of

the ring and waits some ﬁnite time till it makes some

decision of where to move the treasure, while in A

moves along a carefully chosen (and non-intuitive)

chord, and again for some ﬁnite time, till it makes a

decision to move to a point on the ring. If instead the

exit is found early, then the trajectories in A

, A

are

designed to support the other robot which might have

found the treasure in case the latter does not follow

The next non-trivial and technical step would be

to decide when to trigger the subroutines above. Of

course, once this is determined, i.e. once the trajecto-

ries are ﬁxed, correctness and performance analysis is

a matter of exhaustive analysis.

We are ready to deﬁne our main non-wireless al-

gorithm. We remind the reader that the description is

for R

that starts moving clockwise. R

performs the

symmetric trajectory by moving counter-clockwise.

Our main algorithm uses parameter

x(α) := 3α/2 − π − sin (α/2) + 2sin(α) , which

we abbreviate by x whenever α is clear from the

context. By Lemma Aa, α

≈ 1.22353 is the unique

root of x(α) = 0, while x is positive for all α ∈ (α

,π)

and negative for all α ∈ [0,α

Lemma 3.2. For every α ∈ [0,π], Algorithm 2 is cor-

rect, i.e. a robot brings the treasure to the exit.

Algorithm 2: Non-Wireless Algorithm.

Step 1. Starting from A, move clockwise until an

interesting point I is found at time x := AI

Step 2. Proceed according to the following cases:

• If α > 2π/3 and I = T and α > x ≥ α − x, then

run A

(x).

• If α > 2π/3 and I = E and x ≤ x, then run

(x).

• If α

≤ α ≤ 2π/3 and I = T and α > x ≥ α −x,

then run A

(x).

• If α

≤ α ≤ 2π/3 and I = E and x ≤ x, then run

(x).

• In all other cases, run A

(x).

Proof. First, it is easy to see that the treasure is al-

ways picked up. Indeed, if the ﬁrst interesting point I

that is discovered (by any robot) is the treasure, then

the claim is trivially true. If the ﬁrst interesting point

I found, say, by R

is an exit, then R

(in all subrou-

tines) ﬁrst tries the possible location B for the trea-

sure, and if it fails it tries location C (in other words

it always simulates A

till it fails to ﬁnd the treasure

after ﬁnding the exit). Meanwhile R

moves counter-

clockwise on the ring, and sooner or later will reach

C or B. So at least one of the robots will reach the

treasure ﬁrst. In what follows, let R

be the one who

found ﬁrst the treasure (and picks it up). We examine

three cases.

If R

is following subroutine A

, then the treasure

is brought to the exit. Indeed, in that case R

expects

no interaction from R

and greedily tries to evacuate

(see subcases i,ii in Figure 3).

If R

is following subroutine A

, then it must be

that α

≤ α ≤ 2π/3, that α − x ≤ x < α, and that

it has not found any other interesting point before

(by Lemma Aa we have α − x < α and x > 0 for all

α > α

). Figure 3 subcase iii depicts exactly this sce-

nario, where I = T . Note that from R

’s perspective,

the exit can be either in B or in C, and R

chooses to

go to the center. This takes total time x+ 1. If the exit

was at point C, then R

would have found it in time

α −x ≤ x and that would make it to follow A

. So, R

would ﬁrst check point D (where the treasure is not

present), and that would make it to go to the centre

arriving at time α−x + 2sin (α/2)+1 (an illustration

of this trajectory is shown in Figure 3 subcase iv, if

was moving clockwise). R

is guaranteed to wait

at the center till time t

(which is the maximum re-

quired time that takes each robot to reach the centre).

In that case, R

meets R

at the center (because R

did

ﬁnd the exit in C), and R

correctly chooses C as the

evacuation point. Finally, if instead the exit was not in

C, then R

would not make it to the centre by time t

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

























 = 

B =



 = 



 = 

 = 





 = 

B =



 = 

 = 

 = 





































(Subfigure )

(Subfigure )

(Subfigure )

(Subfigure )

(Subfigure )

(Subfigure )



Figure 3: The non-wireless algorithm for two robots with performance π − α/2 +3 sin(α/2).

That can happen only if the exit is at point B, and once

again R

makes the right decision to evacuate from B.

In the last case, R

is following subroutine A

, and

so it must be that α > 2π/3, that α − x ≤ x < α, and

that it has not found any other interesting point before.

Figure 3 subcase v depicts this scenario. Note that the

exit could be either in C or in D.

If the exit is in C, then α − x ≤ x, and R

would

follow A

too. This means, R

would go to point D

(where there is no treasure), and that would make it

travel along the chord DI (an illustration of this tra-

jectory is shown in Figure 3 subcase vi, if R

was

moving clockwise). If R

reaches I, it waits there,

and when R

arrives in I, R

makes the right deci-

sion to evacuate from C. Otherwise R

does not reach

I, and it moves up to a certain point in the chord ID

similarly to R

. Note that the meeting condition on

a point K on the chord, with y = IK, would be that

+ IK = CA

+ CD + (DI − IK), which translates

into y = x + sin(α/2) + sin(α) − α/2, i.e. the ex-

act segment of ID that R

traverses before it changes

trajectory. The longest R

could have traveled on the

chord ID would be when x = α−x, but then IK would

be equal to α − π + 3sin (α) ≤ 2 sin(α) = ID for all

α > 2π/3. Therefore, the two robots meet indeed in

somewhere in the chord ID. Note also that in this

case, R

makes the right decision and goes to point C

in order to evacuate.

If instead the exit is in B, then again R

travels

till point K (which is in the interior of the chord ID).

But in this case, R

will not meet R

in point K as it

will not follow A

. Once again, R

makes the right

decision, and after arriving at K it moves to point B

and evacuates.

3.2 Algorithm Analysis

In this section we prove that for all α ∈ [0,π], the evac-

uation time of Algorithm 2 is no more than 1 + π −

α/2 + 3sin (α/2), concluding Theorem 3.1. In the

analysis below we provide, whenever possible, sup-

porting illustrations, which for convenience may de-

pict special conﬁgurations. In the mathematical anal-

ysis we are careful not to make any assumptions for

the conﬁgurations we are to analyze.

It is immediate that when a robot ﬁnds the ﬁrst

interesting point at time x ≥ α after moving on the

perimeter of the disk, then that robot can also deduce

where the other interesting point is located. In that

sense, it is not surprising that, in this case, the trajec-

tory of the robots and the associated cost analysis are

simpler.

Lemma 3.3. Let x be the time some robot is the ﬁrst to

reach an interesting point I ∈ {E,T } from the moment

robots start moving in opposing directions. If x ≥ α,

then the performance of the algorithm is at most 1 +

π − α/2 + 3sin (α/2). Also, x ≥ α is impossible, if

α > 2π/3.

Proof. Note that 1 is the time it takes both robots

to reach a point, say A, on the ring. So we will

tailor our analysis to the evacuation time from the

moment robots start moving (in opposing directions)

from point A.

Let x be the time after which R

(without loss

of generality) is the ﬁrst to ﬁnd an interesting point

I ∈ {E,T }. Let also B be the other interesting point

{E, T } \ I. For R

to reach ﬁrst I, it must be the case

that R

does not have enough time to reach B, and

Search-and-Fetch with 2 Robots on a Disk - Wireless and Face-to-Face Communication Models

hence x ≤ 2π − α −x, that is x ≤ π − α/2. Since also

x ≥ α, we conclude that α ≤ 2π/3.

Next we examine the following cases. For our

analysis, the reader can use Figure 2 as reference (al-

though A is depicted in the interior of the arc CI, we

will not use that AI

≤ α).

Case 1 (I = T ): R

picks up the treasure

and moves along the chord IB = 2 sin (α/2).

The worst case treasure-evacuation time then

is max

α≤x≤π−α/2

{

x + 2 sin(α/2)

}

= π − α/2 +

2sin (α/2).

Case 2 (I = E): According to the algorithm, R

moves towards the treasure point B along the

chord IB, and reaches it in time x + 2 sin (α/2).

moves counter-clock wise and will reach the

position of the treasure in time 2π − α − x. Who-

ever ﬁnds the treasure ﬁrst will evacuate from the

exit, paying additional time 2 sin(α/2). Hence,

the total cost can never exceed

min

{

x + 2 sin(α/2) ,2π − α−x

}

+ 2 sin(α/2)

≤π − α/2 + 3sin(α/2) (by Lemma Ab)

It is easy to see that in both cases, the cost of the al-

gorithm is as promised.

By Lemma 3.3 we can focus on the (much more

interesting) case that R

, which is the ﬁrst robot that

ﬁnds an interesting point, arrives at I at time x :=

< α. A reference for the analysis below is Fig-

ure 3 which is accurately depicting point A at most

α arc-distance away from I. For the sake of better

exposition, we examine next the cases α ≤ 2π/3 and

α ≥ 2π/3 separately. Note that in the former case

robots may run subroutines A

or A

, while in the lat-

ter case robots may run subroutines A

or A

. For

both lemmata below, the reader may consult Figures 2

and 3.

Lemma 3.4. Let x be the time some robot is the ﬁrst to

reach an interesting point I ∈ {E,T } from the moment

robots start moving in opposing directions. If x < α,

then the performance of the algorithm is at most 1 +

π − α/2 + 3sin(α/2), for all α ∈ [0,π].

Proof. As before, we omit in the analysis below the

time cost 1, i.e. the time robots need to reach the pe-

riphery of the disk. We examine the following cases

for R

, which is the robot that ﬁnds I.

(I = T, B = E,C = null): If R

runs A

, then it must

be that x ≤ α − x, so the cost is x + 2 sin(α/2) ≤

α − x + 2sin (α/2) ≤ π − α/2 + 3 sin(α/2) (see

Figure 3 i).

If R

runs A

, then it must be that α − x ≤ x < α

and α ≤ 2π/3, and the robot goes to the cen-

tre in order to learn where the exit is (see Fig-

ure 3 iii). Independently of where the exit is,

and by Lemma 3.2, R

makes the right deci-

sion and evacuates in time 1+max

α−x≤x<α

{x,α−

x+2sin (α/2)}+1 ≤ max{α,x +2 sin(α/2)}+ 2

which, by Lemma Ac, is at most π − α/2 +

3sin (α/2) for all α ≤ 2π/3. Note that the analy-

sis of this case is valid, even if I = T is not the ﬁrst

interesting point that is discovered, and it is from

the perspective of the robot that ﬁnds the treasure.

If R

runs A

, then it must be that α − x ≤ x < α

and α > 2π/3. Then the trajectory of R

is as in

Figure 3 v, and the exit is found correctly due to

Lemma 3.2. For the sake of the exposition, we

will do the worst case analysis for both cases B =

E and C = E now (i.e. we only insist in that I = T

and that R

runs A

The total time for the combined cases is AI

IK +

max{

KB,KC}, where IK = y (see deﬁnition of

). Since as we have proved, K lies always in

chord ID, and since DB

= 3α − 2π we have that

BK ≤ max{BI,BD}

≤max{2 sin(α/2) ,2 sin(3α/2 − π)}

≤2sin (α/2)

We also have that KC ≤ CI = 2 sin (α/2). So the

cost becomes no more than

x + y + 2sin(α/2) = α/2 + 3sin (α/2) +sin(α)

≤π − α/2 + 3sin(α/2) (by Lemma Ad)

for all α ∈ [0,π].

(I = T, B = null,C = E): Since I is found ﬁrst, we

must have x ≤ α/2, hence both robots run A

, see

Figure 3 i. Robot R

that ﬁnds the treasure will

evacuate in time no more than x + 2 sin(α/2) +

2sin (α) ≤ α/2 + 2sin (α/2) + 2 sin(α) < π −

α/2 + 3 sin(α/2) for all α ∈ [0,π].

(I = E,B = T,C = null): If R

is the ﬁrst to ﬁnd the

treasure, then this case is depicted in Figure 3

i. This happens exactly when x + 2sin (α/2) ≤

2π − x − α, so that the total evacuation time is

x +4sin (α/2) ≤ π− α/2 +3sin (α/2) for all α ∈

[0,π].

Otherwise x > π − α/2 − sin(α/2), and R

is the

robot that reaches the treasure ﬁrst. If R

de-

cides to run A

, then the cost would be 2π −

x − α +2sin (α/2) < π − α/2 + 3sin (α/2) for all

α ∈ [0,π]. Finally, if R

decides to run A

or A

then we have already made the analysis in case

I = T, B = E,C = null above.

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems

(I = E,B = null,C = T ): Note that in all cases, both

robots will run the same subroutine. In particular,

if robots run either A

or A

, then we have already

done the analysis in case I = T,B = E,C = null

above.

Finally, if both robots run A

, it must be either

because α ≤ α

, or because x ≥ x, while the cost

is always α−x+2sin (α/2)+2 sin(α) (the case is

depicted in Figure 3 ii, with reverse direction). If

α ≤ α

, then the evacuation cost would be at most

α +2sin (α/2)+ 2 sin(α) which by Lemma Ah is

at most π − α/2 + 3 sin(α/2), for all α ∈ [0,α

If x ≥ x, then the cost would be at most α − x +

2sin (α/2) + 2 sin(α) = π − α/2 + 3sin (α/2).

Note that Lemmata 3.3, 3.4 imply that the perfor-

mance of Algorithm 2 is, in the worst case, no more

than 1 + π − α/2 + 3sin (α/2), concluding also The-

orem 3.1.

3.3 Extension to n Robots

We can easily extend our 2-robot algorithms to the

n-robot case (when n is even, otherwise we ignore

one robot) by splitting the robots into pairs, deﬁning

points in intervals of length 4π/n on the cycle, assign-

ing each pair of robots to each such point, and letting

them run the corresponding 2-robot algorithm.

4 LOWER BOUNDS

We conclude the study of treasure evacuation with 2

robots by providing the following lower bound per-

taining to distributed systems under the face-to-face

communication model.

Theorem 4.1. For problem 2-TE

f 2 f

, any algorithm

needs at least time 1 + π/3 + 4 sin(α/2) if 0 ≤ α ≤

2π/3, or 1 + π/3 + 2sin (α) + 2sin (α/2) if 2π/3 ≤

α ≤ π.

For the proof, we invoke an adversary (not neces-

sarily the most potent one), who waits for as long as

there are three points A, B,C with AB = BC = α on the

periphery such that at most one of them has been vis-

ited by a robot. Then depending on the moves of the

robots decides where to place the interesting points.

5 CONCLUSION

In this paper we introduced a new problem on search-

ing and fetching which we called treasure-evacuation

from a unit disk. We studied two online variants of

treasure-evacuation with two robots, based on differ-

ent communication models. The main point of our ap-

proach was to propose distributed algorithms by a col-

laborative team of robots. Our main results demon-

strate how robot communication capabilities affect

the treasure evacuation time by contrasting face-to-

face (information can be shared only if robots meet)

and wireless (information is shared at any time) com-

munication.

There are several open problems in addition to

sharpening our bounds. These include problems on

1) the number of robots, 2) other geometric domains

(discrete or continuous), 3) differing robot starting

positions, 4) multiple treasures and exits, 5) limited

range wireless communication, 6) robots with dif-

ferent speeds, 6) different a priori knowledge of the

topology or partial information about the targets, etc.

In particular, we anticipate that nearly optimal algo-

rithms for small number of robots, e.g. for n = 3, 4,

or any other variation of problem we consider will re-

quire new and signiﬁcantly different algorithmic ideas

than those we propose here, still in the same spirit.

REFERENCES

Ahlswede, R. and Wegener, I. (1987). Search problems.

Wiley-Interscience.

Albers, S. and Henzinger, M. R. (2000). Exploring un-

known environments. SIAM Journal on Computing,

29(4):1164–1188.

Albers, S., Kursawe, K., and Schuierer, S. (2002). Explor-

ing unknown environments with obstacles. Algorith-

mica, 32(1):123–143.

Alpern, S. (2011). Find-and-fetch search on a tree. Opera-

tions Research, 59(5):1258–1268.

Alpern, S. and Gal, S. (2003). The theory of search games

and rendezvous. Springer.

Baeza Yates, R., Culberson, J., and Rawlins, G. (1993).

Searching in the plane. Information and Computation,

106(2):234–252.

Baeza-Yates, R. and Schott, R. (1995). Parallel searching in

the plane. Computational Geometry, 5(3):143–154.

Beck, A. (1964). On the linear search problem. Israel Jour-

nal of Mathematics, 2(4):221–228.

Bellman, R. (1963). An optimal search. SIAM Review,

5(3):274–274.

Berman, P. (1998). On-line searching and navigation. In

Fiat, A. and Woeginger, G. J., editors, Online Algo-

rithms: The State of the Art, pages 232–241. Springer.

Bonato, A. and Nowakowski, R. (2011). The game of cops

and robbers on graphs. AMS.

Burgard, W., Moors, M., Stachniss, C., and Schneider,

F. E. (2005). Coordinated multi-robot exploration.

Robotics, IEEE Transactions on, 21(3):376–386.

Search-and-Fetch with 2 Robots on a Disk - Wireless and Face-to-Face Communication Models

Chrobak, M., Gasieniec, L., T., G., and Martin, R. (2015).

Group search on the line. In SOFSEM 2015. Springer.

Chung, T. H., Hollinger, G. A., and Isler, V. (2011). Search

and pursuit-evasion in mobile robotics. Autonomous

robots, 31(4):299–316.

Czyzowicz, J., Gasieniec, L., Gorry, T., Kranakis, E., Mar-

tin, R., and Pajak, D. (2014). Evacuating robots from

an unknown exit located on the perimeter of a disc. In

DISC 2014, pages 122–136. Springer, Austin, Texas.

Czyzowicz, J., Georgiou, K., Dobrev, S., Kranakis, E., and

MacQuarrie, F. (2016). Evacuating two robots from

multiple unknown exits in a circle. In ICDCN 2016.

Czyzowicz, J., Georgiou, K., Kranakis, E., Narayanan, L.,

Opatrny, J., and Vogtenhuber, B. (2015a). Evacuat-

ing robots from a disc using face to face communica-

tion. In CIAC 2015, pages 140–152. Springer, Paris,

France.

Czyzowicz, J., Kranakis, E., Krizanc, D., Narayanan, L.,

Opatrny, J., and Shende, S. (2015b). Wireless au-

tonomous robot evacuation from equilateral triangles

and squares. In ADHOC-NOW 2015, Athens, Greece,

June 29 - July 1, 2015, Proceedings, pages 181–194.

Demaine, E. D., Fekete, S. P., and Gal, S. (2006). Online

searching with turn cost. Theoretical Computer Sci-

ence, 361(2):342–355.

Deng, X., Kameda, T., and Papadimitriou, C. (1991). How

to learn an unknown environment. In FOCS, pages

298–303. IEEE.

Fekete, S., Gray, C., and Kr

oller, A. (2010). Evacuation of

rectilinear polygons. In Combinatorial Optimization

and Applications, pages 21–30. Springer.

Georgiou, K., Karakostas, G., and Kranakis, E. (2016a).

Search-and-fetch with 2 robots on a disk: Wire-

less and face-to-face communication models. CoRR,

abs/1611.10208.

Georgiou, K., Karakostas, G., and Kranakis, E. (2016b).

Search-and-fetch with one robot on a disk. In 12th

International Symposium on Algorithms and Experi-

ments for Wireless Sensor Networks.

Gluss, B. (1961). An alternative solution to the lost at

sea problem. Naval Research Logistics Quarterly,

8(1):117–122.

Hipke, C., Icking, C., Klein, R., and Langetepe, E. (1999).

How to ﬁnd a point on a line within a ﬁxed distance.

Discrete Appl. Math., 93(1):67–73.

Hoffmann, F., Icking, C., Klein, R., and Kriegel, K. (2001).

The polygon exploration problem. SIAM Journal on

Computing, 31(2):577–600.

Isbell, J. R. (1967). Pursuit around a hole. Naval Research

Logistics Quarterly, 14(4):569–571.

Jennings, J. S., Whelan, G., and Evans, W. F. (1997). Coop-

erative search and rescue with a team of mobile robots.

In ICAR, pages 193–200. IEEE.

Kao, M.-Y., Ma, Y., Sipser, M., and Yin, Y. (1998). Opti-

mal constructions of hybrid algorithms. J. Algorithms,

29(1):142–164.

Kao, M.-Y., Reif, J. H., and Tate, S. R. (1996). Searching

in an unknown environment: An optimal randomized

algorithm for the cow-path problem. Information and

Computation, 131(1):63–79.

Kleinberg, J. (1994). On-line search in a simple polygon.

In SODA, page 8. SIAM.

Koutsoupias, E., Papadimitriou, C., and Yannakakis, M.

(1996). Searching a ﬁxed graph. In ICALP 96, pages

280–289. Springer.

Nahin, P. (2012). Chases and Escapes: The Mathematics of

Pursuit and Evasion. Princeton University Press.

Papadimitriou, C. H. and Yannakakis, M. (1989). Short-

est paths without a map. In ICALP, pages 610–620.

Springer.

Stone, L. (1975). Theory of optimal search. Academic Press

New York.

Thrun, S. (2001). A probabilistic on-line mapping algo-

rithm for teams of mobile robots. The International

Journal of Robotics Research, 20(5):335–363.

Yamauchi, B. (1998). Frontier-based exploration using mul-

tiple robots. In Proceedings of the second interna-

tional conference on Autonomous agents, pages 47–

53. ACM.

APPENDIX

Lemma A. a) There exists some α

∈ (0,π) such

that 3α/2−π−sin (α/2)+2sin (α) is positive for

all α ∈ (α

,π) and negative for all α ∈ [0,α

). In

particular, α

≈ 1.22353.

b) min

{

x + 2 sin(α/2) ,2π − α−x

}

+ 2 sin(α/2) ≤

π − α/2 + 3sin(α/2) , ∀α ∈ [0,π].

c) max{α, x + 2 sin (α/2)} + 2 ≤ π − α/2 +

3sin (α/2) for all α ∈ [0, 2π/3].

d) α +sin(α) ≤ π for all α ∈ [0, π].

e) α −sin(α/2) + 2 sin(α) ≤ π for all α ∈ [0,π].

f) α/2 + 2 sin(α) ≤ π − α + 2 sin (α/2) , ∀α ∈

[0,2π/3]. .

g) max

0≤x≤π−α

{sin(π/2 −α/2 − x)} ≤

sin(α/2) , ∀α ∈ [2π/3,π]

h) max

0≤x≤α/2

{x +2 sin(α/2 − x)}+2sin (α) ≤ π −

α + 4 sin(α/2), ∀α ∈ [0,2π/3].

i) max

0≤x≤π−α

{x+2 sin (π/2 − α/2 − x)} ≤ π−α+

2sin (α/2), ∀α ∈ [2π/3,π]

j) sin (α) ≤ sin(α/2), ∀α ∈ [0,2π/3], and

sin(α) ≥ sin (α/2), ∀α ∈ [2π/3, π].

ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems