Bragg Grating Solitons in Semilinear Dual-core System with
Cubic-Quintic Nonlinearity
Jahirul Islam and Javid Atai
School of Electrical and Information Engineering, The University of Sydney, NSW 2006, Sydney, Australia
Keywords:
Bragg Grating Soliton, Fiber Bragg Grating, Cubic-Quintic Nonlinearity.
Abstract:
The existence and stability of Bragg grating solitons in a coupler, where one core is equipped with a Bragg
grating (BG) and has cubic-quintic nonlinearity and the other is linear, are studied. When the group velocity
term in the linear core is zero (i.e. c = 0), the system’s linear spectrum contains two separate bandgaps. It
is found that soliton solutions exist throughout both bandgaps. On the other hand, when the group velocity
term in the linear core is nonzero (c 6= 0), the spectrum consists of three gaps: a genuine central gap and
upper and lower gaps that overlap with one branch of continuous spectrum. In this case, soliton solutions exist
throughout the upper and lower gaps but not in the central gap. The system supports two disjoint families of
solitons (referred to as Type 1 and Type 2) that are separated by a boundary. Stability of solitons is investigated
by means of systematic numerical stability analysis. It is found that Type 2 solitons are always unstable. On
the other hand, there exist vast regions in the upper and lower bandgaps where stable Type 1 solitons exist.
1 INTRODUCTION
Fiber Bragg gratings (FBGs) are periodic optical
structures that havebeen the focus of much theoretical
and experimental research in the last few decades due
to their applications in optical communications, fil-
tering, sensing, signal processing, high speed switch-
ing and pulse compression in the nonlinear regime
(Sankey et al., 1992; Radic et al., 1995; Loh et al.,
1996; Kashyap, 1999).
One of the main characteristics of the FBGs is
their strong dispersion due to the cross coupling be-
tween the forward- and backward- propagating waves
(Desterke and Sipe, 1994). At sufficiently high in-
tensities, the FBG-induced strong dispersion may be
counterbalanced by the nonlinearity giving rise to
Bragg grating (BG) solitons. BG solitons have been
studied extensively in Kerr media, both theoretically
(Christadoulides and Joseph, 1989; Aceves and Wab-
nitz, 1989; Desterke and Sipe, 1994; Mak et al.,
2003; Neill and Atai, 2006; Neill et al., 2007) and
experimentally (Eggleton et al., 1997; Taverner et al.,
1998; Mok et al., 2006). The existence and stability
of BG solitons have also been investigated in differ-
ent nonlinear media such as quadratic (Conti et al.,
1997) and cubic-quintic nonlinearities (Atai and Mal-
omed, 2001; Atai, 2004; Dasanayaka and Atai, 2010;
Dasanayaka and Atai, 2013a; Dasanayaka and Atai,
2013b) as well as dual core fibers, where the Bragg
grating is written in one or both cores (Mak et al.,
1998; Atai and Malomed, 2000).
In the case of a semilinear dual-core fiber, where
one core has Kerr nonlinearity and is equipped with
a Bragg grating and the other is linear, it has been
shown that stability of BG solitons is dependent on
the relative group velocity in the linear core (Atai and
Malomed, 2000). In this paper, we analyze the ex-
istence and stability of BG solitons in a generalized
model of semilinear dual core system, where one core
has BG with cubic-quintic nonlinearity and the other
core is linear.
2 THE MODEL
Starting with the model outlined in (Atai and Mal-
omed, 2000) and following the procedures described
in (Atai and Malomed, 2001), we can derive the fol-
lowing normalized model for two linearly coupled
cores, assuming BG is present only in the nonlinear
core:
iu
t
+ iu
x
+

|v|
2
+
1
2
|u|
2

u−
q

1
4
|u|
4
+
3
2
|u|
2
|v|
2
+
3
4
|v|
4

u+ v+ κφ = 0
55
Islam J. and Atai J..
Bragg Grating Solitons in Semilinear Dual-core System with Cubic-Quintic Nonlinearity.
DOI: 10.5220/0005257800550059
In Proceedings of the 3rd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2015), pages 55-59
ISBN: 978-989-758-093-2
Copyright
c
 2015 SCITEPRESS (Science and Technology Publications, Lda.)

iv
t
− iv
x
+

|u|
2
+
1
2
|v|
2

v−
q

1
4
|v|
4
+
3
2
|v|
2
|u|
2
+
3
4
|u|
4

v+ u+ κψ = 0
iφ
t
+ icφ
x
+ κu = 0
iψ
t
−icψ
x
+ κv = 0
(1)
where u and v are the forward- and backward-
propagating waves in the nonlinear core and φ(x, t)
and ψ(x, t) are their counterparts in the linear core,
respectively. q > 0 is a parameter that controls the
strength of the quintic nonlinearity, and κ is the coef-
ficient of linear coupling between the cores. It should
be noted that cubic-quniticnonlinearity has been mea-
sured in chalcogenideglass (Boudebs et al., 2003) and
some transparent organic materials (Lawrence et al.,
1994; Zhan et al., 2002). Using the values of nonlin-
ear coefficients from these references and assuming a
typical value of ∆n = 5 × 10
−4
, q is found to be in
the range 0.05 < q < 0.6. Therefore, in the following
analysis, without loss of generality, we are going to
assume that q varies in the range 0 ≤ q ≤ 1. c rep-
resents the relative group velocity in the linear core
(group velocity in the nonlinear core has been set to
1). In the nonlinear core, the normalized coefficient
of the self-phase and cross-phase modulation parts in
front of the cubic terms assumed to be the usual 1 : 2
for Kerr nonlinearity (Agrawal, 1995) and 1: 6: 3
for the quintic nonlinearity as derived in (Maimistov
et al., 1999).
To analyze the system, it is necessary to first de-
termine the system’s linear spectrum within which
the solitons may exist. Substituting (u, v, φ, ψ) ∼
exp(ikx−iωt) into the system of Eqs. (1) and lineariz-
ing, the following dispersion relation can be derived
(Atai and Malomed, 2000):
ω
4
−

1+ 2κ
2
+ (1+ c
2
)k
2

ω
2
+ κ
4
+
(c
2
−2cκ
2
)k
2
+ c
2
k
4
= 0
(2)
For c = 0, the spectrum contains two disjoint
bandgaps; one in the upper half and the other in the
lower half of the spectrum and are respectively given
by



−
1
2
+
q
1
4
+ κ
2
≤ ω ≤
1
2
+
q
1
4
+ κ
2
ω > 0
−
1
2
−
q
1
4
+ κ
2
≤ ω ≤
1
2
−
q
1
4
+ κ
2
ω < 0
(3)
Note that, the width of the gaps remain constant
irrespective of the values of the coupling coefficient
κ. The upper and lower gaps merge into a single gap
when κ → 0. When c 6= 0, the shapes of the branches
of the dispersion diagram change, and as a result a
central gap (which is a genuine gap) is formed. In
this case, the lower and upper gaps overlap with one
branch of continuous spectrum and therefore they are
not genuine bandgaps. Examples of typical dispersion
diagrams are shown in Figure 1 for different values of
c and κ .
0 3
6
9
k
-8
-4
0
4
8
ω
(a)
0 3
6
9
k
-15
-10
-5
0
5
10
15
ω
(b)
Figure 1: Examples of the dispersion diagrams for (a) κ =
0.5 and (b) κ = 5.0. Solid and dashed curves correspond to
c = 2.0 andc = 0, respectively.
3 STABILITY ANALYSIS
Exact analytical solutions for Eqs. (1) can
only be found for c = 0. In the general
case c 6= 0, no analytical solution is available
and the soliton solutions must be determined nu-
merically. We sought for stationary solutions
of Eqs. (1) as {u(x, t), v(x,t),φ(x,t), ψ(x,t)} =
{U(x),V(x), Φ(x), Ψ(x)} exp(−iωt). Substitution of
these expressions into Eqs. (1) results in a set of or-
dinary differential equations that can be solved using
the relaxation algorithm. A key finding is that, sim-
ilar to the model of single core Bragg grating with
cubic-quintic nonlinearity (Atai and Malomed, 2001),
the model admits two disjoint families of BG solitons
that are separated by a border, at which solitons do
not exist. The soliton families differ in their shape,
phase structure and parities of the real and imaginary
PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology
56

1.6
2
2.4
0 0.2 0.4
0.6
0.8 1
-2.4
-2
-1.6
(a)
q
ω
Unstable (Type 2)
Unstable (Type 1)
No Solution
Stable (Type 1)
Unstable (Type 2)
Stable (Type 1)
0
0.4
0.8
1.2
0 0.2 0.4
0.6
0.8 1
-1.2
-0.8
-0.4
0 ω
(b)
q
Stable (Type 1)
Unstable (Type 1)
No Solution
Unstable (Type 2)
Unstable (Type 2)
Figure 2: Stability diagrams for (a) κ = 2.0, c = 0.0 and (b)
κ = 0.5, c = 0.2.
parts. One family (Type 1) can be regarded as the gen-
eralization of the BG solitons in the semilinear model
with cubic nonlinearity (i.e. the model of (Atai and
Malomed, 2000)) and in the other family (Type 2), the
quintic nonlinearity is dominant. In the case of c = 0,
soliton solutions exist throughout the upper and lower
gaps. On the other hand, when c 6= 0, no solutions
exist in the genuine central gap. However, Type 1 and
Type 2 solitons are found within the upper and lower
gaps (as was mentioned above, these are not genuine
gaps because they overlap with one branch of the con-
tinuous spectrum). To investigate the stability of the
BG solitons, we have performed a systematic stability
analysis by numerically solving Eqs. (1). Through the
stability analysis we have been able to identify non-
trivial stability borders in the (q, ω) plane.
The outcomes of stability analysis for two sets of
parameters are summarized in Figure 2. An important
-40 -20 0 20 40
2000
t
0
x
(a)
-40 -20 0 20 40
2000
t
0
x
(b)
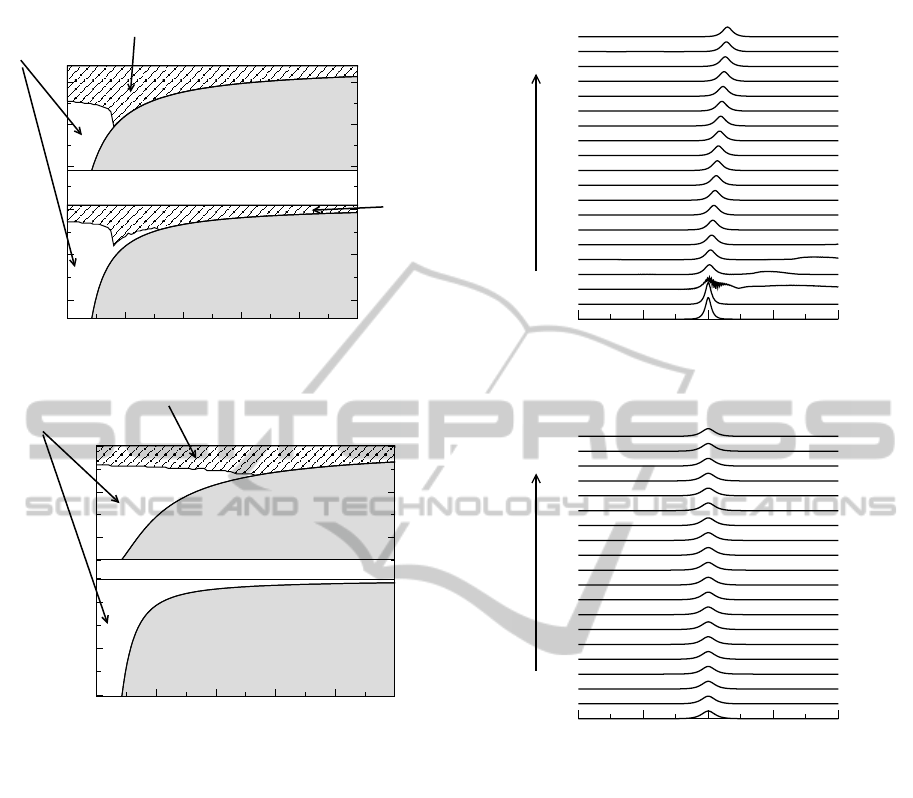
Figure 3: Examples of Type 1 soliton evolution. (a) Evolu-
tion of an unstable soliton corresponding to c= 0.0, κ= 5.0,
q = 0.10, ω = 4.90 resulting in the formation of a mov-
ing Type 1 soliton; (b) stable soliton with c = 0.2, κ = 0.5,
q = 0.20, ω = 1.05.
finding is that, unlike the case of a single core Bragg
grating with cubic-quintic nonlinearity, the Type 2
solitons are always unstable. On the other hand, vast
regions of Type 1 stable solitons have been found for
different values of κ and c in both upper and lower
gaps. An interesting feature shown in Figure 2 is that
the stable regions in both the upper and lower gaps en-
large as the strength of quintic nonlinearity increases.
Also, the stable region in the upper gap is generally
larger than that in the lower gap.
Examples of the propagation of Type 1 and Type
2 solitons are displayed in Figures 3 and 4, respec-
tively, for different values of κ, c, q and ω. Figure
3(a) shows that Type 1 solitons belonging to the the
BraggGratingSolitonsinSemilinearDual-coreSystemwithCubic-QuinticNonlinearity
57

-40 -20 0 20 40
100
t
0
x
(a)
-40 -20 0 20 40
200
t
0
x
(b)
Figure 4: Examples of Type 2 unstable soliton evolution. (a)
c = 0.2, κ = 0.5, q = 0.50, ω = 0.80, (b) c = 0.0, κ = 2.0,
q = 0.85, ω = −2.35.
unstable region initially shed some energy and conse-
quently evolve into moving solitons belonging to the
same family. Solitons in the stable region are highly
robust as shown in Figure 3(b). However, the Type
2 solitons are highly unstable and upon propagation
they radiate significant amount of energy and subse-
quently are destroyed (see Figure 4).
4 CONCLUSIONS
In this paper, we have put forward a model of semi-
linear dual core system, where one core has a cubic-
quintic nonlinearity and is equipped with a Bragg
grating and the other is linear. We have investigated
the existence and stability of quiescent Bragg grating
solitons in this model. We have derived exact analyt-
ical soliton solutions for the limiting case of c = 0.
In the case of c 6= 0, soliton solutions have been de-
termined numerically. Similar to the case of a single
core Bragg grating in cubic-quintic nonlinearity, the
model supports two disjoint families of BG solitons.
We have conducted a systematic numerical stability
analysis for various values of c and κ and identified
nontrival stability borders in the (q, ω) plane. The
analysis reveals that, for the both c = 0 and c 6= 0,
there exist vast regions within the (q, ω) plane where
Type 1 solitons are stable. On the other hand, Type 2
solitons are always unstable.
REFERENCES
Aceves, A. B. and Wabnitz, S. (1989). Self induced trans-
parency solitons in nonlinear refractive periodic me-
dia. Phys. Lett. A, 141:37–42.
Agrawal, G. P. (1995). Nonlinear Fiber Optics. Academic
Press, San Diego, 2nd edition.
Atai, J. (2004). Interaction of bragg grating solitons in a
cubic-quintic medium. J. Opt. B Quantum Semiclass.,
6:S177–S181.
Atai, J. and Malomed, B. A. (2000). Bragg-grating soli-
tons in a semilinear dual-core system. Phys. Rev. E,
62:8713–8718.
Atai, J. and Malomed, B. A. (2001). Families of bragg-
grating solitons in a cubic-quintic medium. Phys. Lett.
A, 284:247–252.
Boudebs, G., Cherukulappurath, S., Leblond, H., Troles, J.,
Smerktala, F., and Sanchez, F. (2003). Experimental
and theoretical study of higher-order nonlinearities in
chalcogenide glasses. Opt. Commun., 219:427–433.
Christadoulides, D. N. and Joseph, R. I. (1989). Slow bragg
solitons in nonlinear periodic structures. Phys. Rev.
Lett., 62:1746–1749.
Conti, C., Trillo, S., and Assanto, G. (1997). Doubly reso-
nant bragg simultons via second-harmonic generation.
Phys. Rev. Lett., 78:2341–2344.
Dasanayaka, S. and Atai, J. (2010). Stability of bragg grat-
ing solitons in a cubic-quintic nonlinear medium with
dispersive reflectivity. Phys. Lett. A, 375:225–229.
Dasanayaka, S. and Atai, J. (2013a). Moving bragg grat-
ing solitons in a cubic-quintic nonlinear medium with
dispersive reflectivity. Phys. Rev. E, 88:022921.
Dasanayaka, S. and Atai, J. (2013b). Stability and collisions
of moving bragg grating solitons in a cubic-quintic
nonlinear medium. J. Opt. Soc. Am. B, 30:396–404.
Desterke, C. M. and Sipe, J. E. (1994). Gap solitons.
Progress in Optics, 33:203–260.
Eggleton, B. J., Desterke, C. M., and Slusher, R. E. (1997).
Nonlinear pulse propagation in bragg gratings. J. Opt.
Soc. Am. B, 14:2980–2993.
PHOTOPTICS2015-InternationalConferenceonPhotonics,OpticsandLaserTechnology
58

Kashyap, R. (1999). Fiber Bragg Gratings. Academic
Press, San Diego.
Lawrence, B. L., Cha, M., Torruellas, W. E., Stegeman,
G. I., Etemad, S., Baker, G., and Kajzar, F. (1994).
Measurement of the complex nonlinear refractive-
index of single-crystal p-toluene sulfonate at 1064-
nm. Appl. Phys. Lett., 64:2773–2775.
Loh, W., Laming, R., Robinson, N., Cavaciuti, A., C. Va-
ninetti, J. A., Zervis, M., and Cole, M. (1996). Dis-
persion compensation over distances in excess of 500
km for 10 gb/s systems using chirped fiber gratings.
IEEE Photon. Technol. Lett., 8:944–946.
Maimistov, A. I., Malomed, B. A., and Desyanitkov, A.
(1999). A potential of incoherent attraction between
multidimensional solitons. Phys. Lett. A, 254:179–
184.
Mak, W. C. K., Malomed, B. A., and Chu, P. L. (1998).
Solitary waves in coupled nonlinear waveguides with
bragg gratings. J. Opt. Soc. Am. B, 15:1685–1692.
Mak, W. C. K., Malomed, B. A., and Chu, P. L. (2003).
Formation of a standing-light pulse through collision
of gap solitons. Phys. Rev. E, 68:02669.
Mok, J. T., Desterke, C. M., Litler, I. C. M., and Eggleton,
B. J. (2006). Dispersionless slow light using gap soli-
tons. Nat. Phys., 2:775–780.
Neill, D. R. and Atai, J. (2006). Collision dynamics of gap
solitons in kerr media. Phys. Lett. A, 353:416–421.
Neill, D. R., Atai, J., and Malomed, B. A. (2007). Gap soli-
tons in a hollow optical fiber in the normal dispersion
regime. Phys. Lett. A, 367:73–82.
Radic, S., George, N., and Agrawal, G. P. (1995). The-
ory of low-threshold optical switching in nonlinear
phase-shifted periodic structures. J. Opt. Soc. Am. B,
12:671–680.
Sankey, N. D., Prelewitz, D. F., and Brown, T. G.
(1992). All-optical switching in a nonlinear periodic-
waveguide structure. Appl. Phys. Lett., 60:1427–1429.
Taverner, D., Broderick, N. G. R., Richardson, D. J., Lam-
ing, R. I., and Ibsen, M. (1998). Nonlinear self-
switching and multiple gap-soliton formation in a
fiber bragg grating. Opt. Lett., 23:328–330.
Zhan, C., Zhang, D., Zhu, D., Wang, D., Li, Y., Li, D., Lu,
Z., Zhao, L., and Nie, Y. (2002). Third- and fifth-order
optical nonlinearities in a new stilbazolium derivative.
J. Opt. Soc. Am. B, 19:369–375.
BraggGratingSolitonsinSemilinearDual-coreSystemwithCubic-QuinticNonlinearity
59