
Statistical Shape Model for Simulation of Realistic Endometrial Tissue
Sebastian Kurtek
1
, Chafik Samir
2
and Lemlih Ouchchane
2,3
1
Department of Statistics, The Ohio State University, Columbus, OH, U.S.A.
2
Image Science for Interventional Techniques, UMR CNRS UdA 6284, Auvergne University, Clermont-Ferrand, France
3
Department of Biostatistics, Medical Informatics and Communication Technologies, Clermont University Hospital,
Clermont-Ferrand, France
Keywords:
Realistic Simulation, Statistical Modeling, Geodesics, Elastic Deformation, Generalized Cylinders, Re-
parametrization, Shape Analysis, Endometriosis, Karcher Mean.
Abstract:
We propose a new framework for developing statistical shape models of endometrial tissues from real clinical
data. Endometrial tissues naturally form cylindrical surfaces, and thus, we adopt, with modification, a recent
Riemannian framework for statistical shape analysis of parameterized surfaces. This methodology is based
on a representation of surfaces termed square-root normal fields (SRNFs), which enables invariance to all
shape preserving transformations including translation, scale, rotation, and re-parameterization. We extend
this framework by computing parametrization-invariant statistical summaries of endometrial tissue shapes,
and random sampling from learned generative models. Such models are very useful for medical practitioners
during different tasks such as diagnosing or monitoring endometriosis. Furthermore, real data in medical
applications in general (and in particular in this application) is often scarce, and thus the generated random
samples are a key step for evaluating segmentation and registration approaches. Moreover, this study allows us
to efficiently construct a large set of realistic samples that can open new avenues for diagnosing and monitoring
complex diseases when using automatic techniques from computer vision, machine learning, etc.
1 INTRODUCTION
Shape is an important feature of an anatomical ob-
ject. Thus, statistical shape models play a very im-
portant role in characterizing and monitoring anatom-
ical structures. Most anatomical objects are three-
dimensional and thus their boundaries form surfaces.
In this paper, we are focused on shape models of
endometrial tissue, which can be represented us-
ing cylindrical surfaces. For this purpose we uti-
lize a comprehensive Riemannian framework based
on square-root normal fields that allows registration,
comparison, deformation, averaging, and modeling of
observed shapes. Furthermore, the developed statis-
tical models are useful in subsequent tasks such as
simulation of realistic endometrial tissue shapes for
registration approaches (Yavariabdi et al., 2013).
Endometriosis is a complex gynecological disease
in which endometrial cells (glands and stroma) ap-
pear outside their usual locations in the uterine cav-
ity (Brosens et al., 2004). The main symptoms of
endometriosis may depend on the site of active en-
dometriosis and are influenced by hormonal changes.
This disease affects approximately 10% of women in
the reproductive age group and may cause chronic
pelvic pain, severe dysmenorrhea, and several diges-
tive problems including diarrhea, occasional consti-
pation, rectal bleeding and infertility. Endometrio-
sis can be found in the pelvic cavity region, specifi-
cally in the pelvic peritoneum and pelvic organs. Cur-
rently there is no ethiologic cure for endometriosis,
but it can be treated in a variety of ways, including
using pain medication, hormonal treatments, and la-
paroscopic surgery in severe cases. An accurate diag-
nosis must be made in order to obtain important med-
ical information. A key step in the diagnostic pro-
cess is to develop a statistical model of the shape of
the endometrial tissue coming from various imaging
modalities in order to evaluate segmentation and reg-
istration methods. In this paper, we consider endome-
trial tissues imaged using magnetic resonance imag-
ing (MRI). Such models provide information about
the observed variability in disease groups. Further-
more, due to data scarcity, these models can be used
for extensive simulation studies, where valid realiza-
tions of diseased endometrial tissues are randomly
generated.
While in this paper we only consider modeling
421
Kurtek S., Samir C. and Ouchchane L..
Statistical Shape Model for Simulation of Realistic Endometrial Tissue.
DOI: 10.5220/0004821904210428
In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 421-428
ISBN: 978-989-758-018-5
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

endometrial tissue surfaces, the general method de-
scribed here has many other applications. In medi-
cal imaging, researchers are often interested in mod-
eling various anatomies, including subcortical struc-
tures in the brain. Studying shapes of 3D structures
in the brain is of particular interest because many
diseases can potentially be linked to altering these
shapes, in conjunction with other physiologicalsymp-
toms. Thus, shape analysis based on imaging data
offers objective and quantitative means to aid in clas-
sification and monitoring of different disease types.
Other possible applications of shape analysis of 3D
objects include facial recognition, body shape analy-
sis, graphics, and many more.
1.1 Related Methods
Researchers have proposed numerous representations
of surfaces for the purpose of shape modeling. Sev-
eral groups have proposed to study shapes of sur-
faces by embedding them in volumes and deform-
ing the volumes (Grenander and Miller, 1998; Joshi
et al., 1997). Such methods are typically compu-
tationally expensive because of the high dimension-
ality of the resulting objects that are analyzed. An
alternative approach is based on manually-generated
landmarks also termed Kendall’s shape analysis (Dry-
den and Mardia, 1998). While this is a very popu-
lar approach in many applications, it requires a set of
registered landmarks to represent the surface, which
are difficult to obtain in practice. Others have stud-
ied 3D shape variabilities using level sets (Malladi
et al., 1996), curvature flows (Gu et al., 2007), medial
axes (Bouix et al., 2001; Gorczowski et al., 2010), or
point clouds via the iterative closest point algorithm
(Almhdie et al., 2007).
However, the most natural representation for
studying shapes of 3D anatomical objects seems to
be using their boundaries, which form parameterized
surfaces. Such a representation poses an additional
issue of handling the parameterization variability.
Some methods (Brechb¨uhler et al., 1995; Styner et al.,
2006) tackle this problem by choosing a fixed param-
eterization, similar to arc-length in the case of param-
eterized curves. A large set of papers in the litera-
ture treat the re-parameterization (or registration) and
analysis steps as separate (Cates et al., 2006; Davies
et al., 2010). Because in these approaches the two
steps are unrelated, the computed registrations tend to
be suboptimal and defining proper parameterization-
invariant geodesic distances (and statistics) between
surfaces is not possible. In a series of papers, Kurtek
et al. (Kurtek et al., 2010; Kurtek et al., 2011b; Kurtek
et al., 2012; Kurtek et al., 2011a) presented a com-
prehensive framework for parameterization-invariant
shape modeling of surfaces based on the q-map rep-
resentation. A major drawback of this method is in
the definition of the Riemannian metric, which does
not have a clear interpretation in terms of the amount
of stretching and bending needed to deform one sur-
face into another. This issue was addressed by Jermyn
et al. (Jermyn et al., 2012) using a novel representa-
tion of surfaces termed square-root normal fields. We
adopt their representation in this paper and use it to
develop statistical shape models of endometrial tis-
sue surfaces. Our main contribution is in using this
methodology to define and compute statistics such as
the mean and covariance of endometrial tissues. We
utilize these statistics in specifying generative models
of endometrial tissue shape and provide a recipe for
random sampling from these models.
1.2 Data Description
The data analyzed in this paper are ten endometrial
tissue surfaces coming from MRI images. These sur-
faces are naturally cylindrical, which motivates our
statistical model of surfaces with a cylinder parame-
terization. Figure 1 displays all surfaces in our data
set. Note that there is a lot of variation in this data,
and thus, parsimonious shape models are very impor-
tant in this application. We are able to achieve a natu-
ral shape model through elastic shape analysis of sur-
faces. This methodology uses a special Riemannian
metric to perform surface registration by achieving in-
variance to re-parameterizations of surfaces.
2 MATHEMATICAL
FRAMEWORK
Let F be the space of all smooth embeddings of a
cylinder in R
3
and let Γ be the set of all boundary-
preserving diffeomorphisms from S
1
×[0,1] to itself.
For a cylindrical surface representing endometrial tis-
sue f ∈ F , f ◦γ represents a re-parameterization of
this surface. Since F is a vector space, the tangent
space at f ∈ F , T
f
(F ) is F itself. Using two tangent
vectors v
1
,v
2
∈T
f
(F ) one can define the standard in-
ner product on F and measure distances between sur-
faces using the L
2
norm. While intuitive, this frame-
work is inappropriate for statistical shape analysis of
parameterized surfaces (Jermyn et al., 2012; Kurtek
et al., 2010; Kurtek et al., 2011b; Kurtek et al., 2012).
Thus, in this work, we will utilize the square-root nor-
mal field representation of cylindrical surfaces to per-
form the statistical analysis. This representation of
surfaces (along with the corresponding Riemannian
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
422
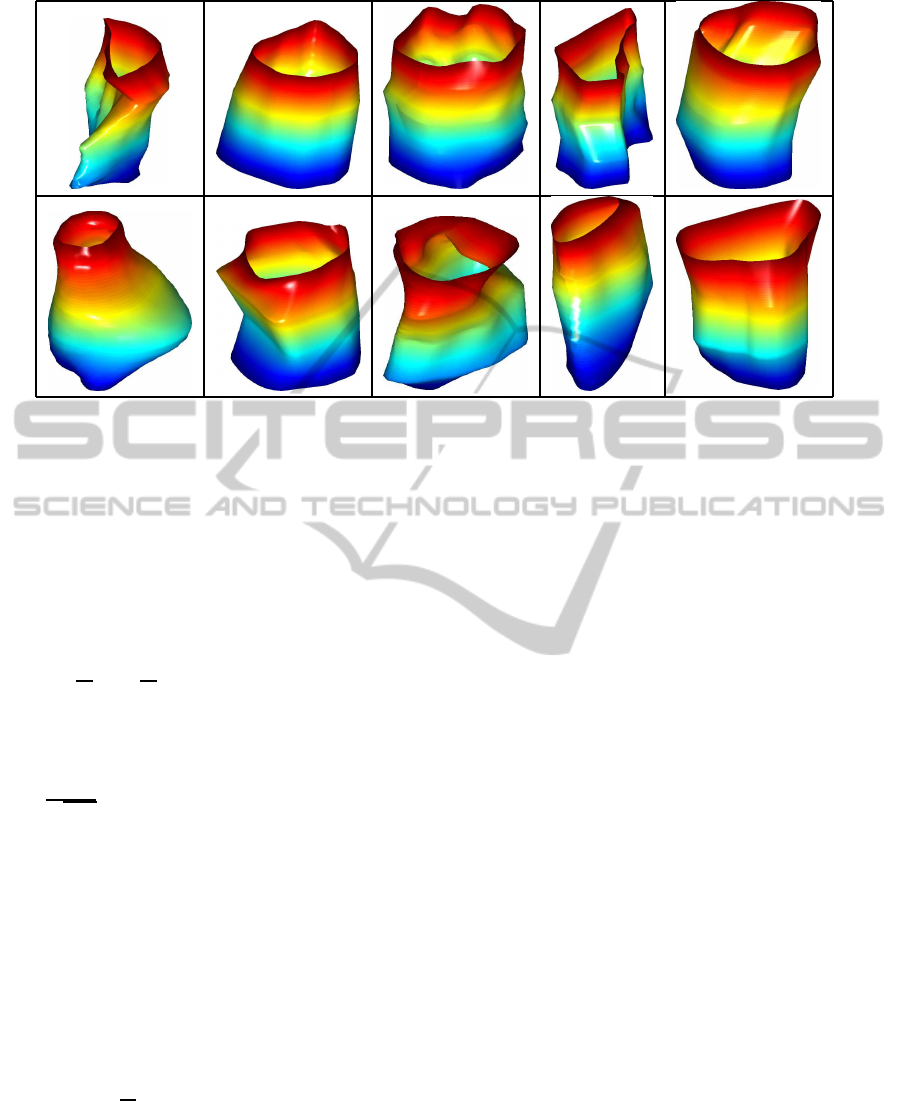
Figure 1: Data set of ten endometrial tissue surfaces coming from MRIs.
metric) were proposed by Jermyn et al. (Jermyn et al.,
2012). In the next sections, we provide some math-
ematical details as well as an algorithm to compute
geodesic paths and distances between endometrial tis-
sue surfaces.
2.1 Representation and Registration of
Endometrial Tissue Surfaces
Let n(s) =
∂f
∂u
(s)×
∂f
∂v
(s) ∈R
3
denote the normal vec-
tor to the endometrial tissue surface at the point s =
(u,v) ∈ S
1
×[0,1]. Using n(s), Jermyn et al. (Jermyn
et al., 2012) defined a mathematical representation of
surfaces termed square-root normal fields (SRNFs) as
q(s) =
n(s)
√
|n(s)|
, where |·| denotes the Euclidean norm
in R
3
. The space of all SRNFs is a subset of L
2
(S
1
×
[0,1],R
3
) hereinafter referred to as L
2
. We are in-
terested in statistical models of shapes of endome-
trial tissue surfaces. Thus, we must ensure invari-
ance to shape preserving transformations including
translation, scale, rotation and re-parameterization.
First, note that the SRNF representation is automat-
ically translation invariant. We can achieve scale in-
variance by re-scaling all surfaces to have unit area.
Furthermore, for O ∈ SO(3) and f ∈ F , the SRNF
of a rotated surface Of is Oq. Also, for γ ∈ Γ and
f ∈F , the SRNF of a re-parameterized surface f ◦γ is
(q,γ) = (q◦γ)
p
J
γ
, where J
γ
is the determinant of the
Jacobian of γ. An important property of SRNFs is that
if we rotate and re-parametrize any two surfaces in
the same way, the L
2
-norm between their SRNFs re-
mains unchanged: kq
1
−q
2
k= k(Oq
1
,γ)−(Oq
2
,γ)k.
This property is necessary to define a shape distance
between surfaces, which we later use for subsequent
statistical analysis.
In order to register endometrial tissue surfaces
with respect to rotation and parameterization, we first
define an equivalence class of an SRNF as [q] =
{(Oq,γ)|O ∈ SO(3), γ ∈ Γ}. Note that each equiva-
lence class represents a shape of an endometrial tissue
surface uniquely. Then, the registration problem can
be stated as follows:
(O
∗
,γ
∗
) = arginf
(O,γ)∈SO(3)×Γ
kq
1
−(Oq
2
,γ)k
2
. (1)
This optimization problem is solved iteratively. First,
one fixes γ and searches for an optimal rota-
tion over SO(3) using Procrustes analysis. Then,
given this rotation, one searches for an optimal re-
parameterization over Γ using a gradient descent al-
gorithm presented in (Jermyn et al., 2012) and par-
ticularized for use with cylindrical surfaces. In the
following sections, we will let f
∗
2
= O
∗
( f
2
◦γ
∗
).
2.2 Geodesics between Endometrial
Tissue Surfaces
After optimally registering the endometrial tissue
surfaces, we are interested in comparing them us-
ing geodesic paths and distances. For this pur-
pose, we utilize a numerical technique termed path-
straightening directly on F . This technique was
used for computing geodesics between spherical sur-
faces under a different representation in (Kurtek et al.,
2012). It was also specified for the SRNF representa-
tion and used in a similar fashion in the application
to analysis of cylindrical surfaces. Mainly, we use the
geodesics in the definition of the mean and covariance
StatisticalShapeModelforSimulationofRealisticEndometrialTissue
423

L(F
∗
) = 0.5334
L(F
∗
) = 0.6534
L(F
∗
) = 0.6725
Figure 2: Three examples of geodesic paths between endometrial tissue surfaces and the corresponding geodesic distances.
of endometrial tissue surfaces. Thus, we present a few
details next.
We define a Riemannian metric on F for w
1
,w
2
∈
T
f
(F ) as follows:
hhw
1
,w
2
ii
f
=
Z
S
1
×[0,1]
(n
w
1
(s) ·n
w
2
(s))
|n(s)|
ds
−
3
4
Z
S
1
×[0,1]
(n(s) ·n
w
1
(s))(n(s) ·n
w
2
(s))
|n(s)|
3
ds,
where n
w
(s) =
∂f
∂u
(s) ×
∂w
∂v
(s) +
∂w
∂u
(s) ×
∂f
∂v
(s). This
metric is the pullback metric of the L
2
metric from the
space of SRNFs. In order to compute a geodesic path
between two optimally registered endometrial tissue
surfaces f
1
, f
∗
2
∈ F , we begin by defining the length
of a path given by F : [0,1] → F , F(0) = f
1
, F(1) =
f
∗
2
using the defined metric (all arguments have been
suppressed for brevity):
L(F) =
Z
1
0
q
hhF
t
,F
t
ii
F
dt
=
Z
1
0
s
Z
[0,1]×S
1
−3(N ·N
t
)
2
4|N|
3
+
|N
t
|
2
|N|
dsdt.
In the above expression, we use N(t) to represent
∂F(t)
∂u
(s) ×
∂F(t)
∂v
(s) and we denote partial derivatives
along the t dimension using subscripts. It is a well
known result that a critical point of this path length
energy provides a geodesic between f
1
and f
∗
2
in F .
Thus, a geodesic path between two surfaces f
1
and f
∗
2
is the solution to the following minimization problem:
F
∗
= argmin
F:[0,1]→F , F(0)= f
1
, F(1)= f
∗
2
L(F). (2)
The solution to this problem is computed using a gra-
dient descent approach by approximating ∇L with di-
rectional derivatives.
In Figure 2, we present three examples of geodesic
paths between registered endometrial tissue surfaces.
In addition, we provide the resulting geodesic dis-
tance, which is useful in quantifying their shape dif-
ferences. We note that due to good registration of
features, the resulting geodesic paths represent nat-
ural deformations between endometrial tissue shapes.
This property will also lead to natural summary statis-
tics and shape models, which we consider in the next
section.
3 SHAPE STATISTICS OF
ENDOMETRIAL TISSUE
SURFACES
In this section we present tools and results for com-
puting two fundamental shape statistics, the Karcher
mean and the covariance, for a set of cylindrical sur-
faces. We then utilize these quantities to estimate a
generative Gaussian model and draw random sam-
ples.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
424
3.1 Estimation of the Karcher Mean
We begin by defining an intrinsic mean shape under
the proposed metric, called the Karcher mean. Let
{f
1
, f
2
,.. . , f
n
} ∈ F denote a sample of endometrial
tissue surfaces. Also, let F
∗
i
denote a geodesic path
between a surface f and a surface f
∗
i
that was opti-
mally registered to f. Then, the sample Karcher mean
is given by
¯
f = argmin
f∈ F
∑
n
i=1
L(F
∗
i
)
2
. A gradient-
based approach for finding the Karcher mean is given
in (Dryden and Mardia, 1998) and is repeated here for
convenience. Note that the resulting Karcher mean is
a particular element of an equivalence class of sur-
faces, because our distance (length of the geodesic) is
invariant to rotation and re-parameterization.
Algorithm 1: (Karcher Mean). Let
¯
f
0
be an initial
estimate of the Karcher mean. Set j = 0 and ε
1
, ε
2
to
be small positive values.
(1) For each i = 1,.. . , n, register f
i
to
¯
f
j
using Equa-
tion 1 to obtain f
∗
i
.
(2) For each i = 1,... ,n, compute the geodesic path
between f
∗
i
and
¯
f
j
using Equation 2.2 to obtain
F
∗
i
, F
∗
i
(0) =
¯
f
j
, F
∗
i
(1) = f
∗
i
.
(3) For each i = 1,... ,n, compute the shooting vector
v
i
=
∂
∂t
F
∗
i
|
t=0
.
(3) Compute the average direction ¯v = (1/n)
∑
n
i=1
v
i
.
(3) If k¯vk < ε
1
, stop. Else, update using
¯
f
j+1
=
¯
f
j
+ ε
2
¯v.
(4) Set j = j+ 1 and return to Step 1.
5 10 15 20
0
0.01
0.02
0.03
0.04
0.05
0.06
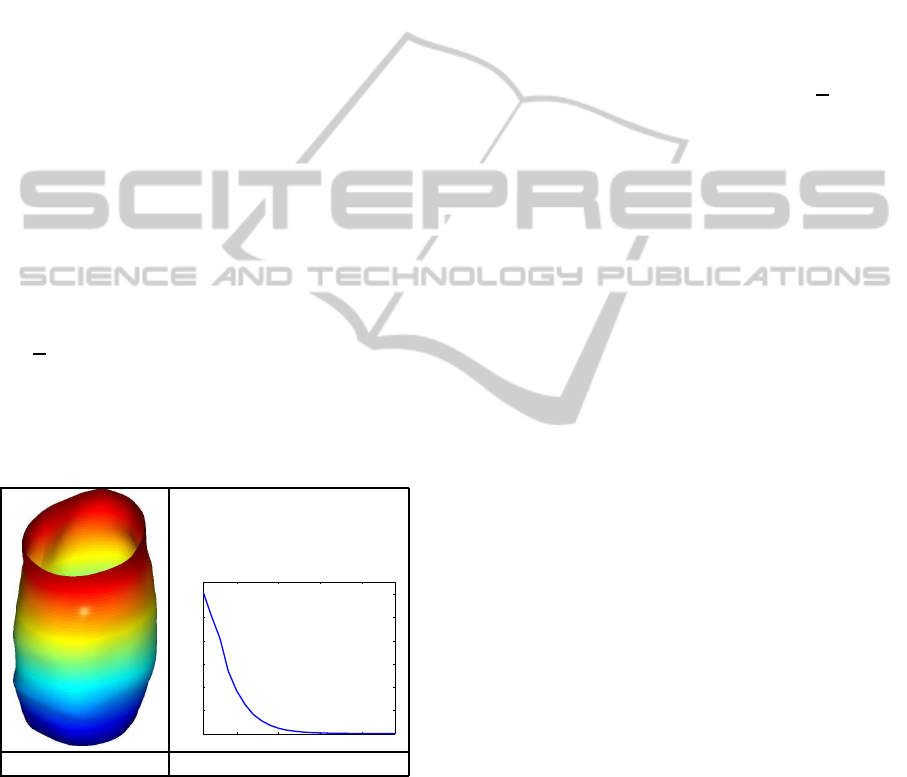
(a) (b)
Figure 3: (a) Karcher mean of the given endometrial tissue
surfaces. (b) Evolution of the energy gradient with itera-
tions on the x-axis and gradient on the y-axis.
In Figure 3 we present the result of applying Al-
gorithm 1 on our data set. In panel (a) we display the
Karcher mean and in panel (b) we show the evolution
of the gradient k¯vk. The algorithm converged in ap-
proximately 25 iterations. Also, the computed mean
is a nice representative of our data. The observed en-
dometrial tissue surfaces are all cylindrical with local
convex and concave structures. The Karcher mean is
of similar structure.
3.2 Estimation of the Karcher
Covariance
Once the sample Karcher mean has been computed,
the evaluation of the Karcher covariance is performed
as follows. The Karcher covariance captures the ob-
served variability around the Karcher mean. First,
we optimally register all surfaces in the sample to
the Karcher mean
¯
f, resulting in {f
∗
1
,.. . , f
∗
n
}. Next,
we find the shooting vectors from the mean
¯
f to each
of the registered surfaces. That is, let ν
i
=
∂
∂t
F
∗
i
|
t=0
,
where F
∗
i
(0) =
¯
f and F
∗
i
(1) = f
∗
i
, i = 1,2,.. .,n. We
then perform principal component analysis by ap-
plying the Gram-Schmidt procedure (under the cho-
sen metric hh·,·ii), to generate an orthonormal basis
{B
j
|j = 1,.. . , k}, k ≤ n, of the observed {ν
i
} in the
vector space T
¯
f
(F ). We project each of the vectors
ν
i
onto this orthonormal basis using ν
i
≈
∑
k
j=1
c
i, j
B
j
,
where c
i, j
= hhν
i
,B
j
ii
¯
f
. Now, each original surface
can simply be represented using the coefficient vec-
tor c
i
= {c
i, j
}. Then, the covariance matrix can be
computed in the coefficient space using K = (1/(n−
1))
∑
n
i=1
c
i
c
T
i
∈ R
k×k
. We can use the SVD of K to
determine the principal directions of variation in the
given data. For example, if u ∈ R
k
corresponds to a
principal singular vector of K, then the corresponding
tangent vector in T
¯
f
(F ) is given by
∑
k
j=1
u
j
B
j
. One
can then map this vector to a surface f using the ex-
ponential map. We note that the exponential map is
difficult to compute under the non-standard metric in-
troduced earlier. Thus, we use a linear approximation.
This approximation is reasonable in a neighborhood
of the Karcher mean.
In Figure 4 we display the path traced by follow-
ing the three main directions of variation from −1
standard deviation (blue) to +1 standard deviation
(red) around the Karcher mean (green). These paths
provide a natural set of representative deformations
present in our data. Furthermore, they provide an ef-
ficient summary of the observed variability. Figure 5
provides a different visualization of the principal di-
rections of variation. The first row provides the defor-
mation vector field on the mean surface correspond-
ing to each positive principal direction. The second
row is a visualization of the point-wise magnitude of
this vector field. This allows for easy identification of
areas undergoing highest amounts of deformation.
StatisticalShapeModelforSimulationofRealisticEndometrialTissue
425
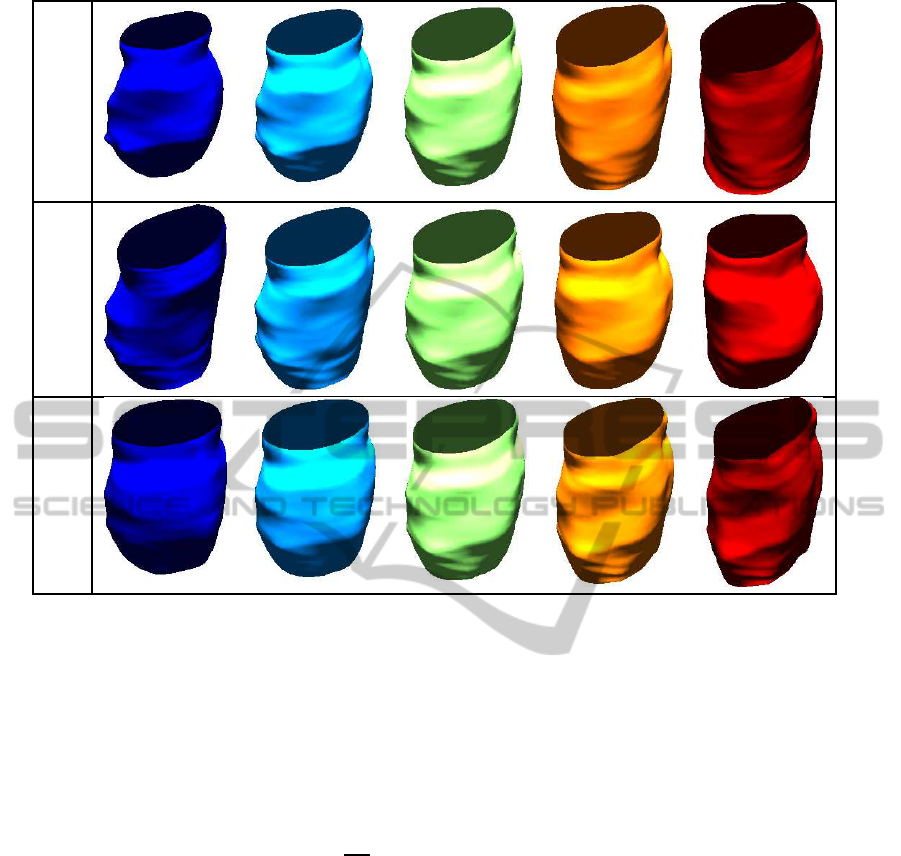
PD1
PD2
PD3
Figure 4: Three main directions of variation in the given data displayed as a path from −1 standard deviation (blue) to +1
standard deviation (red) around the Karcher mean (green).
3.3 Approximate Random Samples
from Gaussian Model
Next, we validate our model using random sampling.
For this purpose, we will utilize the Gaussian distri-
bution defined in the tangent space at the mean en-
dometrial tissue surface. A random tangent vector v ∈
T
¯
f
(F ) can be generated using v =
∑
k
j=1
z
j
p
S
j j
u
j
B
j
,
where z
j
iid
∼ N(0,1), S
j j
is the variance of the jth prin-
cipal component, u
j
is the corresponding principal
singular vector and B
j
is a basis element. One can
then obtain an approximate sample from the Gaussian
distribution using a linear mapping f =
¯
f + v.
In Figure 6, we show four randomly generated
endometrial tissue surfaces using our approximate
Gaussian model. A major motivation for random
sampling in this application is that there are only few
real data observations available. Thus, any analysis
that requires many data observations will have to uti-
lize simulation, which in turn requires a technique for
random sampling. Note that, visually, all of the ran-
dom samples generated using the described method-
ology are faithful representations of the given data,
and thus, would be useful instances in any simulation
study.
3.4 Summary
Statistical analysis of shapes of anatomical structures
plays a key role for the validation of medical imag-
ing techniques when monitoring and diagnosing com-
plex diseases. We have presented a comprehensive
framework for computing shape models of endome-
trial tissue surfaces. This framework, based on the
square root normal field representation of cylindrical
surfaces, enables one to register, compare, average
and model endometrial tissue shapes. It also allows
one to generate unobserved, random instances, which
are useful for realistic simulations, especially when
there is not enough real data for the validation pro-
cess or it is biased. The resulting statistical models
represent natural variability in observed data, and can
be used by medical practitioners to characterize the
variability in anatomical structure of the endometrial
tissues.
A future direction of research is to validate the
proposed statistical models of endometrial tissues by
relating the generated random samples to a score pro-
vided by a medical expert. Our current claim is that
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
426
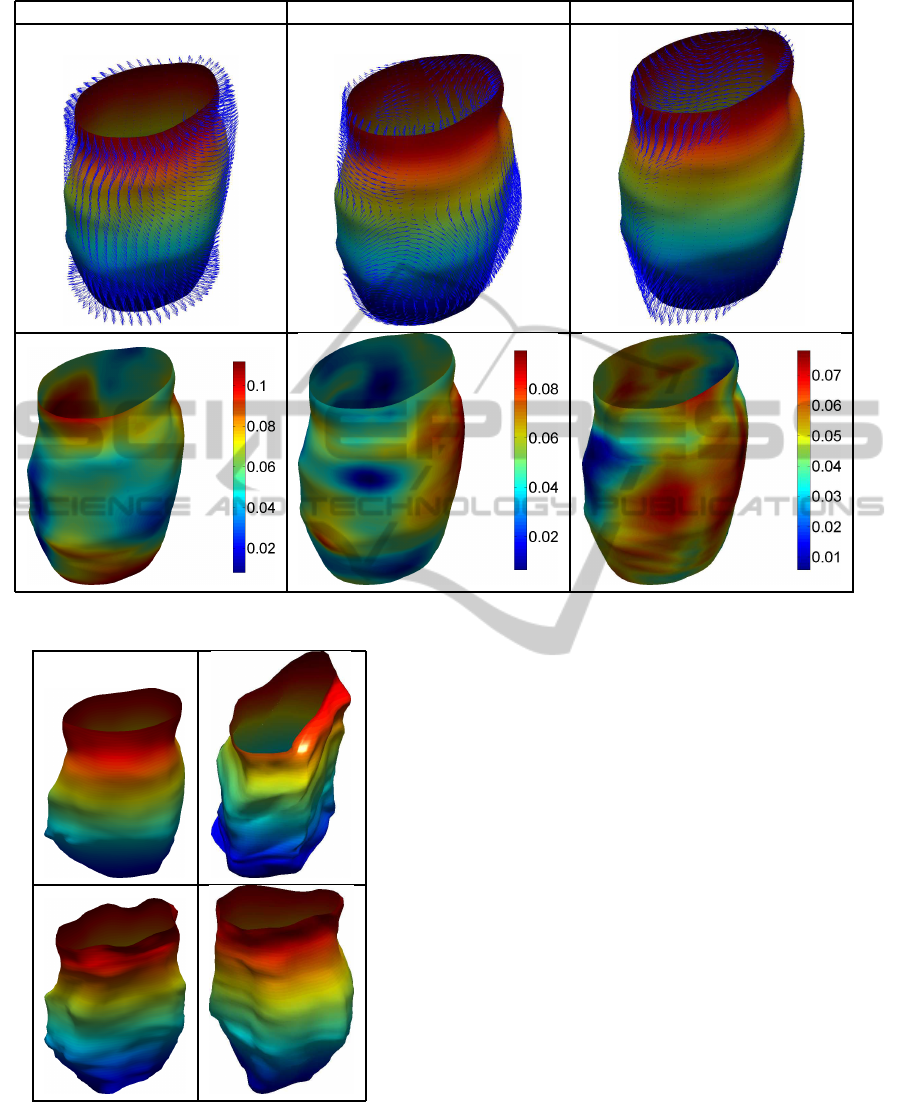
PD1 PD2 PD3
Figure 5: Principal direction deformation vector fields (top row) and their corresponding point-wise magnitudes (bottom row).
Figure 6: Four random endometrial tissue surfaces drawn
from an approximate Gaussian model.
the generated samples visually resemble natural en-
dometrial tissue surfaces. Adding a qualitative as-
sessment from a medical expert would further support
these claims. Another direction of future work can be
the evaluation of registration and classification meth-
ods using the generated random samples.
REFERENCES
Almhdie, A., L´eger, C., Deriche, M., and L´ed´ee, R. (2007).
3D registration using a new implementation of the ICP
algorithm based on a comprehensive lookup matrix:
Application to medical imaging. Pattern Recognition
Letters, 28(12):1523–1533.
Bouix, S., Pruessner, J. C., Collins, D. L., and Siddiqi, K.
(2001). Hippocampal shape analysis using medial sur-
faces. NEUROIMAGE, 25:1077–1089.
Brechb¨uhler, C., Gerig, G., and K¨ubler, O. (1995). Pa-
rameterization of closed surfaces for 3D shape de-
scription. Computer Vision and Image Understanding,
61(2):154–170.
Brosens, I., Puttemans, P., Campo, R., Gordts, S., and
Kinkel, K. (2004). Diagnosis of endometriosis: pelvic
endoscopy and imaging techniques. Best Practice
and Research Clinical Obstetrics and Gynaecology,
18:285–303.
Cates, J., Meyer, M., Fletcher, P., and Whitaker, R. (2006).
Entropy-based particle systems for shape correspon-
dence. In Proc. MICCAI Mathematical Foundations
of Computational Anatomy, pages 90–99.
StatisticalShapeModelforSimulationofRealisticEndometrialTissue
427

Davies, R., Twining, C., Cootes, T., and Taylor, C. (2010).
Building 3-d statistical shape models by direct opti-
mization. IEEE Trans. Medical Imaging, 29(4):961–
981.
Dryden, I. L. and Mardia, K.(1998). Statistical Shape Anal-
ysis. John Wiley & Son.
Gorczowski, K., Styner, M., Jeong, J., Marron, J., Piven,
J., Hazlett, H., Pizer, S., and Gerig, G. (2010). Multi-
object analysis of volume, pose, and shape using sta-
tistical discrimination. IEEE Trans. Pattern Analysis
and Machine Intelligence, 32(4):652–666.
Grenander, U. and Miller, M. I. (1998). Computational
anatomy: An emerging discipline. Quarterly of Ap-
plied Mathematics, LVI(4):617–694.
Gu, X., Wang, S., Kim, J., Zeng, Y., Wang, Y., Qin, H., and
Samaras, D. (2007). Ricci flow for 3D shape analysis.
In Proc. IEEE International Conference on Computer
Vision.
Jermyn, I., Kurtek, S., Klassen, E., and Srivastava, A.
(2012). Elastic shape matching of parameterized sur-
faces using square root normal fields. In European
Conference on Computer Vision, pages 804–817.
Joshi, S., Miller, M., and Grenander, U. (1997). On the
geometry and shape of brain sub-manifolds. Pat-
tern Recognition and Artificial Intelligence, 11:1317–
1343.
Kurtek, S., Klassen, E., Ding, Z., Avison, M., and Sri-
vastava, A. (2011a). Parameterization-invariant shape
statistics and probabilistic classification of anatomical
surfaces. In Proc. Information Processing in Medical
Imaging.
Kurtek, S., Klassen, E., Ding, Z., Jacobson, S.,
Jacobson, J., Avison, M., and Srivastava, A.
(2011b). Parameterization-invariant shape compar-
isons of anatomical surfaces. IEEE Trans. Medical
Imaging, 30(3):849–858.
Kurtek, S., Klassen, E., Ding, Z., and Srivastava, A. (2010).
A novel Riemannian framework for shape analysis of
3D objects. In Proc. IEEE Computer Vision and Pat-
tern Recognition, pages 1625–1632.
Kurtek, S., Klassen, E., Gore, J., Ding, Z., and Srivastava,
A. (2012). Elastic geodesic paths in shape space of
parametrized surfaces. IEEE Trans. Pattern Analysis
and Machine Intelligence, 34(9):1717–1730.
Malladi, R., Sethian, J., and Vemuri, B. (1996). A fast level
set based algorithm for topology-independent shape
modeling. Journal of Mathematical Imaging and Vi-
sion, 6:269–290.
Styner, M., Oguz, I., Xu, S., Brechbuhler, C., Pantazis, D.,
Levitt, J., Shenton, M., and Gerig, G. (2006). Frame-
work for the statistical shape analysis of brain struc-
tures using SPHARM-PDM. In Proc. MICCAI Open
Science Workshop.
Yavariabdi, A., Samir, C., Bartoli, A., Ines, D., and Bour-
del, N. (2013). Contour-based TVUS-MR image reg-
istration for mapping small endometrial implants. In
Abdominal Imaging. Computation and Clinical Appli-
cations, volume 8198 of Lecture Notes in Computer
Science, pages 145–154.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
428
