
A Split based Approach for the Vehicle Routing Problem
with Route Balancing
Philippe Lacomme
1
, Caroline Prodhon
2
, Christian Prins
2
,
Xavier Gandibleux
3
, Boris Beillevaire
3
and Libo Ren
1
1
Université Blaise Pascal (LIMOS UMR 6158),Campus des Cézeaux, 63177 Clermont-Ferrand, France
2
ICD-LOSI (UMR-STMR CNRS 6279), Université de Technologie de Troyes,
12 rue Marie Curie, CS 42060, 10004 Troyes Cedex, France
3
Université de Nantes (LINA UMR 6241), UFR Science et Techniques,
2 rue de la Houssinières, BP 92208, 44322 Nantes Cedex 3, France
Keywords: Vehicle Routing, Multi-objective Optimization, Split Algorithm, Meta-heuristic.
Abstract: The vehicle routing problem with route balancing is a bi-objective routing problem, in which the total route
length and the balance of routes (i.e. the difference between the maximal and minimal route length) have to
be minimized. In this paper, we propose an approach based on two solution representations: a giant tour
representing a sequence of customers (indirect representation) and a complete solution with a decomposition
of the giant tour, combined with a split algorithm to alternate between them. This approach offers a mainly
efficient way to explore the solution space. Our motivation is based on the possibility to generate efficiently
several solutions a time using an indirect representation which has been already proved to be efficient in
numerous routing problems resolution. The originality here is to tune the split algorithm considering two
objectives. An evolutionary path relinking algorithm is embedded to improve the obtained solutions. The
proposed approach is evaluated on classical vehicle routing problem instances and the results push us into
accepting that the method is competitive with the best published mono-objective methods (on criteria one :
the total route length). On a bi-objective point of view, our method is competitive with the lexicographic
solutions reported in the literature in the sense that it provides similar or better results in comparable
computational time.
1 INTRODUCTION
This paper addresses the vehicle routing problem
with route balancing (VRPRB), which is a variant of
the bi-objective vehicle routing problem (bi-
objective VRP). The VRP is a class of routing
problems that consist in visiting a set of customers
using a homogeneous fleet of capacitated vehicles
with the objective of minimizing the total route
length. The bi-objective versions of VRP consist, for
the second objective, in maximization of a profit or
equity between routes by minimizing the route
balancing. The VRPRB holds on the second.
1.1 Vehicle Routing Problems
The basic version of the VRP is the capacited
vehicle routing problem (CVRP). It can be defined
on a complete and undirected graph ,,
where 0,…, is the set of nodes and
, |∀, ∈ , is the set of edges. The depot
is represented by node 0, where an unlimited fleet of
identical vehicles with a capacity is available to
serve the demand
of each customer
corresponding to nodes from 1 to . Each edge ,
is the shortest path from node to node and
associated with a non-negative cost
. The
objective is to find the set of routes of minimal cost
to serve all customers with the following constraints:
demands cannot be split (each customer must be
served by a single visit);
each route starts and ends at the depot;
the total demand of the customers served by one
vehicle must fit its capacity.
159
Lacomme P., Prodhon C., Prins C., Gandibleux X., Beillevaire B. and Ren L..
A Split based Approach for the Vehicle Routing Problem with Route Balancing.
DOI: 10.5220/0004764801590166
In Proceedings of the 3rd International Conference on Operations Research and Enterprise Systems (ICORES-2014), pages 159-166
ISBN: 978-989-758-017-8
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

In several publications, the number of vehicles is
limited and/or a time limit is given to perform a trip.
In the latter case, a service time is added to each
customer. The CVRP is NP-hard since the mono-
vehicle case, corresponding to the traveling
salesman problem (TSP) is known to be NP-hard.
When multiple objectives are identified, they are
frequently in conflict. For this reason, adopting a
multi-objective point of view can be interesting.
1.2 VRP with Route Balancing
In the VRPRB is an extension of the CVRP in which
two objectives have to be optimized:
Minimization of the distance traveled by the
vehicles.
Minimization of the difference between the
longest and the shortest route length.
Even if very efficient methods exist to solve the
CVRP, they manage only the first objective.
Lacomme et al. (Lacomme et al., 2006) concerns the
resolution of an arc routing problem using an
NSGA-II approach. To the best of our knowledge,
the last publication on VRPRB is the one proposed
by Jozefowiez et al. (Jozefowiez et al., 2009).
Among the proposed approaches in the literature for
multi-objective (MO) problems, NSGAII (Deb,
2001) is intensively used. However, to provide
quality results on the CVRP, its general structure
requires efficient specific developments. More
generally, taking advantages of ranking schemes
seems to be a good approach in routing problem as
stressed by Coello Coello (2000) in a survey. For a
complete introduction on MO optimization, it is
possible to refer to the annotated bibliography from
Ehrgott and Gandibleux (2002) which provides a
suitable entry point for general definitions and
pertinent references.
In this paper, a new approach is proposed to
obtain a set of efficient solutions through a
technique that is based on an indirect representation
of solutions for routing problems: the mapping
function denoted split in the majority of publications
(Prins, 2004). The original version is here adapted to
tackle the multi-objective feature of the problem and
a Path Relinking (PR) algorithm is embedded to
explore the solution space.
The remainder of this paper is organized as
follows: section 2 presents the proposed approach;
computational results are introduced on Section 3
and the paper concludes with section 4.
2 PROPOSED APPROACH
The proposed algorithm is based on a Split
algorithm, a procedure that has proven its efficiency
on routing problems and that is here adapted to
handle multi-objective functions.
2.1 Split based Approaches for Routing
Problems
The split algorithm was proposed by Beasley as the
second phase in a “route-first, cluster-second”
heuristic for the CVRP (Beasley, 1983). The first
phase consists in creating a giant tour by relaxing
both vehicle capacity and maximum tour length, and
the second phase constructs a cost network and then
applies a shortest path algorithm to find least cost
feasible trips. However, the real rise of the approach
appears in 2001 when it has been implemented
within more general frameworks for routing
problems providing methods competitive with the
best published ones from 2001 to 2008 on the
Capacitated Arc Routing Problem - CARP
(Lacomme et al., 2001) (Lacomme et al., 2004) and
the VRP (Prins, 2004). In this context, the number of
split applications in routing increases strongly as
pointed by Duhamel et al. (2011) and covers now
CARP, VRP, Location routing and numerous
extensions which represent a set of more than 40
publications. Moreover, Duhamel et al. (2011) gives
a fully generic description of split functions and
proves that some ones require shortest path with
resource constraints and several labels on nodes.
The split algorithm is a function which ensures a
mapping from one indirect representation of solution
(denoted QDRS in the Figure 1) and a solution of
Figure 1: Efficient routing framework outlines according
to (Duhamel et al., 2011).
Determine a
QDRS
A quasi-direct
representation of
solution (QDRS)
A solution S.
Improved solution S’
f
A quasi-direct
representation of
solution (QDRS)
Heuristics
dedicated to the
problem
A solution S.
f
A quasi-direct
representation of
solution (QDRS)
Initial set of
QDRS
Initialization of the framework
Diversification
Process
Local Search
(LS)
f
Improvement of solution
Framework
iterations
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
160
the problem. The oscillation between the set of
QDRS (giant tours in routing problem) and the set of
solutions (solutions of the VRP for example) has
been proved to be a strongly efficient way for space
exploration.
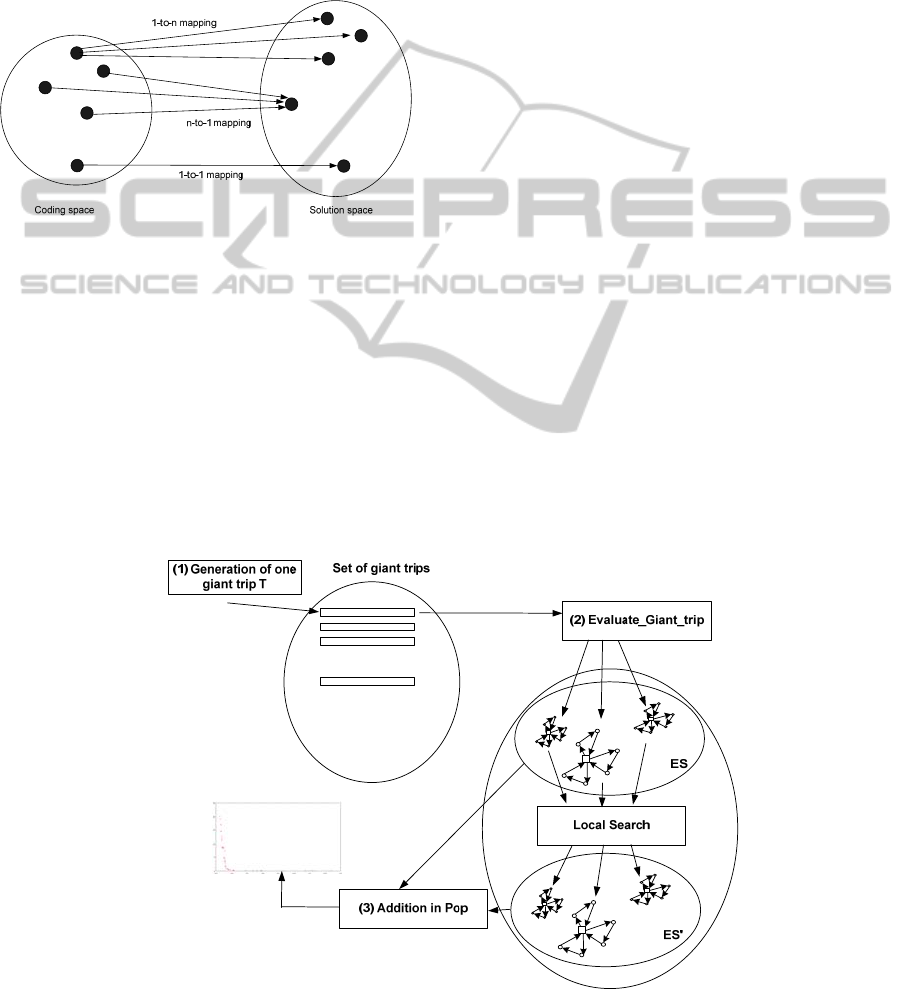
The mapping function between one QDRS and a
solution could be classified into several categories
(Figure 2) as stressed for years by Cheng et al.
(1996).
Figure 2: The mapping from coding
to solution (Cheng et al., 1996).
2.2 Search Space Exploration Strategy:
SPR
The search strategy is made by a path relinking
approach enforced by a multi-start scheme to bring
some diversity, and by an alternation between
solution spaces thanks to a new adaptation of the
classical split procedure for VRP. The resulting
method is called SPR (Split based Path Relinking
approach) and provides an approximation of the
Pareto front – referred to as GPOP - updated all
along the search process, by keeping non-dominated
solutions. Three main components characterize the
method (Figure 3):
Generation of giant tours, either heuristically
(through a randomized nearest neighbor
algorithm or a random sequencing) at the
beginning of each restart, or with PR between
existing giant tours;
Evaluation of the giant tours by transformation
into potentially non-dominated solutions through
the proposed split procedure followed by local
searches;
Inclusion of the obtained non-dominated
solutions within the current population POP, and
GPOP which model the Pareto front. The
insertion may result in some solution deletions in
the populations due to dominance rules.
The originality of the proposed approach remains
on the alternation between two search spaces taking
advantages of the split procedure. Several non-
dominated solutions can be derived from a single
giant tour. Using such an approach, a strongly
limited number of giant tours permits to obtain a
larger population with a time efficient split
algorithm. However, the population is limited to
solutions sorted by increasing solution cost.
Thus, the generation of the initial giant tours at
the beginning of each global iteration or restart (line
12 in procedure 1) aims at creating
giant tours
either with a randomized nearest neighbor algorithm
or a random sequencing. A set of solutions is
Figure 3: SPR strategy principle.
ASplitbasedApproachfortheVehicleRoutingProblemwithRouteBalancing
161

Procedure 1: Multi_Start_Split_based_Path_Relinking_Approach
1 global parameters
2 iter_max: maximal number of iterations
3. Nr : number of replications
4. input/output parameters
5. GPOP : population
6. local variables
7. POP: a population of solutions
8. begin
9. GPOP :=
10. for j:=1 to iter_max do
11. POP =
12. call Generate_new_sol_in_Population (POP)
13. call Path_relinking (iter_max ,POP,POP.n)
14 GPOP := GPOP + POP
15 end for
16. call Post-optimization(iter_max ,GPOP,GPOP.n)
17. return GPOP
obtained from the evaluation of each giant tour by
the proposed split procedure. Then, these solutions
are improved using local search procedures, and
inserted into both populations POP (the current
population made of non-dominated solutions
encounter since the beginning of the related global
iteration) and GPOP (the global population, made of
the pool of non-dominated solutions encounter since
the beginning of the whole algorithm). Once
inserted, some solution deletions in the populations
may result of the dominance rules.
The second part of the algorithm (line 13)
explores the solution space around solutions in POP
through a path relinking between them. Two inner
loops are successively called. The first one performs
a path relinking between the best solution of POP
according to the cost criteria and
randomly
selected other solutions of the population. The
second loop does the same process but with the best
solution according to the balance criteria. The
encountered solutions on the paths are tested to enter
in both POP and .
The third part (line 16) is a post optimization
that also performs a path relinking, but this time, it is
made between the subset of solutions of the
approximate efficient front contained in GPOP.
More precisely, a loop with from 1 to /2 create a
path between solutions et .
2.3 An Adaptation of Split Procedure
for Multi-objective VRP
The split procedure allows to obtain the lowest cost
feasible trips from a given giant tour . To do so, an
auxiliary acyclic graph based on a sequence of
tasks (giant tour of customers) is first constructed.
The graph contains 1 nodes numbered from 0
to , 0 being an artificial initial node. An arc ,
corresponds to a subsequence of consecutive
customer from position 1 to in tour and
visited in a single trip starting and ending at the
depot. Splitting corresponds to the computation of
a min-cost path from node 0 to node in . On
VRP, using Bellman algorithm for acyclic graph, the
splitting of the giant tour is optimal. On more
complex VRP versions, it might be useful to
compute a resource-constrained shortest path
(Desrochers, 1988) that is typically done by a label-
correcting algorithm, involving to manage several
labels per node.
In VRPRB, there exist also several labels per
node since a label can be defined as a structure
with its cost . and its balance. . This definition
does not allow for a simple comparison to claim that
one dominates or is at least equal to another, as this
is the case when only a cost is used to compare
labels. Unfortunately, the second criteria, the
balance of the routes, is not regular and the only
dominance rule which could guarantee the split
optimality is weak and does not permit to prune
enough labels to obtain strongly time efficient split
algorithm.
Thus, we introduce approximate dominance rules
which cannot guarantee the split optimality but
which are consistent with objectives and should
offer a compromise between split quality and
computation time related to the number of labels
kept on nodes.
Label
approximately dominates label
if
and only if
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
162

.
. and
.
.
or
.
. and
.
.
The dominance rule reduces the number of labels
stored at each node to a small subset. However, a
large number of labels could still be generated.
Thence, other time-saving approaches can be
proposed, such as limiting the number of labels per
node or the total number of lables generated during
the split process. Here, the number is limited only on
each label to n
. This principle, added into the
approximate dominance rules, results in some labels
pruning whereas they should not. Such restrictions
may allow to strongly reducing the CPU time, but
they are also raisons explaining why the proposed
algorithm does not guarantee to generate optimal
splitting.
For a detailed presentation of a shortest path
algorithm with resource constraints including a
specific algorithm for label comparison, it’s possible
to refer to (Duhamel et al., 2011) where a generic
algorithm dedicated to split with resource
constrained is introduced. We introduced hereafter,
basic split example decomposition from one giant
tour into a set of non dominated solutions.
2.4 Local Searches
The local search procedures implemented in the
framework rely on the first improvement selection
strategy. The local search is composed of 3 parts.
• Improvement of each trip by using classical VRP
neighborhoods such as 2-OPT and insertion
technique. It is limited to
iterations per call. It
focuses only on cost reduction.
• Closure of the shortest trip with the objective to
minimize the solution trips balance (second criterion
to minimize).
• Reduction of the longest trip by using a careful
nodes transfer technique in existing trips. During
this part of the algorithm, worsening of the criterion
1 (the cost) is acceptable in the limit of 1.1 time the
initial cost. The objective is to avoid excessive waste
of time in exploring non-promising solutions for the
criterion 1.
2.5 Path Relinking
Numerous distance measures could be investigated
as stressed in the overview of (Sörensen and
Schittekat, 2013). In this paper, the one proposed by
(Zhang 2005) is used. They design an efficient
algorithm to compute the distance relates to the
minimum numbers of permutations required to
transform a sequence into a sequence. The size
of the two sequences has to be the same and that is
totally compliant with the giant tour definition. The
proposed path relinking relies on giant tour and also
introduces progressively attributes from a guiding
solution into an initial solution to reduce the distance
defined by (Zhang 2005). Let us note as a solution
and the corresponding giant tour obtained by split
-
1
(the inverse function of the split algorithm, consiste
of concatenating the trips of a solution into a geant
tour). Given that a small change on may produce
very distant solutions from , the path relinking
works only on promising solutions (and not
necessarily distant as preconized in most of the
papers). Thus, two solutions, selected in a given
population (POP or GPOP), are transformed into
tours and then linked through a path in this reduced
solution space. Each giant tour on the path, with a
given probability
undergoes an evaluation
by split (producing potentially several solutions) and
local searches (also generating potentially several
non-dominated solutions). This strategy offers a
strong exploration.
3 NUMERICAL EXPERIMENTS
Numerical experiments were achieved on 14
classical problems first introduced by (Christofides
and Eilon, 1969) and (Christofides and al.,1979).
They are made of two groups, problems 1-5 and 11-
12 having a maximum vehicle range (travel time)
and problems 6-10 and 13-14 having not. In these
instances, the number of customers varies from 50 to
199.
3.1 Parameters
Results presented in this section have been achieved
by setting the parameters of the method (called SPR
in the sequel) as follow. Parameters were defining
using a short time tuning empirical process.
n
/5
n
25
n
100
n
5
n
/2
n
2∗
prob
3.2 Comparative Study
To provide a fair comparative study, the computational
ASplitbasedApproachfortheVehicleRoutingProblemwithRouteBalancing
163

time of each method has been scaled by the
performance factor presented in Table 2. This
coefficient takes into account the MIPS performance
of each processor. A special attention must be
directed on the RISC 6000 computer which used 8
processors and author take advantages of the 8
processors. Since the 1.1 Ghz proc. is ranked about
125 MFlops, the whole computer provides a global
performances about 1Gflops (Table 1).
Table 1: Relative performances of computers.
(Jozefowiezet
al.,2009)
Ourproposal
(SPR)
Approachof
resolution
bi‐objective bi‐objective
Computer
RISC 6000
1.1Ghs
8processors
IntelXeon
2.40Ghz
OS Unix
Language C C
MFlops 1000Mflops 4850MFlops
Speedfactor 0.2 1
3.3 Analysis of Solutions
The numerical experiments encompasses the 14
well-known instances but the comparative study
with (Jozefowiez et al., 2009) is limited to instance
1-5 and 11-12 since their method (MOEA) is only
dedicated to this subset of instances, without vehicle
range.
3.3.1 Best Solution Cost
Table 2 exposes the results on the cost criteria.
Column indicates the number of customers in the
related instance. BKS provides the best-known
solution cost.
Columns 3 (9) and 4 (10) indicate the best solution
cost obtained during the 5 runs of MOEA (SPR) and
the corresponding gap to BKS. Column 5 (11) gives
the balance associated to the solution cost.
is the
CPU time reported in (Jozefowiez et al., 2009) in
seconds.
Norm is the scaled time in seconds
according to Table 2. These times are the average
ones over the 5 replications and are representative of
the time efficiency of the method. Boldface
solutions represent dominance over the other
method.
For the first set of instances (1-5 and 11-12),
MOEA provides a gap of less than 1% for an
average computational time of 500 seconds and SPR
provides a gap of 2.24% with a computation time
350 seconds. It is possible to state that SPR
competes with the MOEA in terms of computational
time but provides a deviation greater than 2%.
However, this result is mainly due to instance 11 for
which SPR achieves very poor solution cost with a
gap around 10% from BKS. A comparison removing
this instance would lead to gaps equal to 1.12 and
0.96 for MOEA and SPR respectively, giving the
advantage to SPR. In fact, MOEA seems more stable
but it does not tackle instances with limitation on the
service provided by vehicles (problems 6-10 and 13-
14). SPR does and provides a good global
performance with a gap of 1.92% to BKS and by
retrieving 7 best known solutions. To conclude for
the solution cost, it is possible to state that SPR as a
range of application greater than MOEA. Although a
fair comparative study is difficult to manage, one
can note SPR and MOEA have similar computation
time and MOEA is quite better for a subset of
Table 2: Results for the extreme solutions on the cost criteria.
MOEA (Jozefowiez et al. 2009) SPR(ourproposal)
Instance n BKS
Cost Gap(cost) Balance
Norm
Cost Gap(cost) Balance
Norm
1 50 524.61 524.6 0.00 20.07 613.20 122.64 524.6 0.00 20.07 30.40
2 75 835.26
835.3 0.01 78.1 1522.80 304.56
843.7 1.01 93.08 142.40
3 100 826.14 827.4 0.15 67.55 2113.20 422.64 827.4 0.15 67.55 219.20
4 150 1028.14
1047.35 1.84 74.78 3936.00 787.20
1038.8 1.01 94.92 496.80
5 199 1291.45 1352.46 4.72 76.6 4968.00 993.60 1337.6 3.57 90.04 902.80
6 50 555.43 - - - - - 555.4 0.00 116.78 62.60
7 75 909.68 - - - - - 909.7 0.00 32.75 152.20
8 100 865.94 - - - - - 865.9 0.00 48.57 245.60
9 150 1162.55 - - - - - 1175.4 1.11 29.02 565.40
10 199 1395.85 - - - - - 1434.7 2.78 36.45 1363.40
11 120 1042.11 1042.11 0.00 146.67 2418.00 483.60 1145.7 9.94 135.89 419.00
12 100 819.56 819.6 0.00 93.43 2125.80 425.16 819.6 0.00 93.43 235.80
13 120 1541.14 - - - - - 1655.0 7.39 49.18 629.80
14 100 866.37 - - - - - 866.4 0.00 532.56 353.00
Avg. scale time (s) (instance
1-5 + 11-12)
505.63
349.49
Gap %
(instance 1-5 + 11-12)
0.96 2.24
Avg. scale time (s) (instance
1-14)
342.69
Gap %
(instance 1-14)
1.92
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
164

instances. A second part of the analysis can focus on
the best solutions in terms of balance.
3.3.2 Best Solution Balance
In this section, the other extreme of the Pareto front
is analyzed, i.e. the best solutions according to the
balance criteria. In Table 3, the two first columns are
related to the instance. Cost and Balance represents
respectively the cost and the balance of the best
solution on the balance criteria found over the five
replications for both MOAE and SPR. Cost' and
Balance' are respectively the cost and the balance of
the solution found by SPR over the five replications
that have the closest (but smaller) balance to the
solution reported with MOEA. Boldface solutions
represent dominance over the other method.
Firstly, let us note that on a great majority of
instances, the right end solution of the front has a
lower balance with SPR than with MOEA. For
example, with the instance 1, the right hand solution
has a balance of 0.03 with SPR and 0.24 with
MOEA. This remark holds for all the instances. This
remark pushes us into accepting than the Pareto
front is well spread in the balance with SPR.
Table 3: Results for the right hand solutions on the balance
criteria.
MOEA SPR
n Cost Balance Cost Balance Cost' Balance'
1 50 618.22 0.24 783.39 0.03
611.50 0.20
2 75 1203.98 0.59 2153.38 0.31
1194.34 0.57
3 100 1871.06 0.29
1296.07 0.11 994.85 0.28
4 150 1484.48 0.80 1704.33 0.18
1338.50 0.71
5 199 1902.64 1.38 2571.97 0.30
1767.56 1.25
6 50 690.89 1.40
7 75 1141.87 3.58
8 100 1052.83 1.71
9 150 1662.29 4.13
1
199
1943.96 5.32
1
120 2388.30 0.10
1920.21 0.03 1485.09 0.10
1
100 1429.90 1.15
1272.55 0.10 1203.57 0.85
1
120
2502.85 0.64
1
100
1383.91 0.17
Avg. 1556.94 0.65 1671.70 0.15 1233.51 0.57
Secondly, when scanning the front obtained by SPR
to identify the closest solution balance to the best
solution balance found with MOEA, it appears that
the MOEA solution is always dominated. For
example, the right hand solution for instance 1 with
MOEA is (618.22; 0.24). The closest solution in the
SPR front (with respect to the balance criteria) is the
solution (615.58; 0.22) which has a lower cost. This
analysis suggests that the Pareto front with SPR
could compete with the MOEA front.
3.3.3 Front Analysis
Our research has been directed first on the cost
minimization and on the balance but not especially
on the quality of the front. This quality varies from
replications but on a wide majority of instances and
replications, the solutions minimizing the balance
are better that solutions reported by (Jozefowiez et
al., 2009). This comment must be moderated since
(Jozefowiez et al., 2009) does not provide any
evaluation of the obtained fronts and only solutions
for instances 1-5 and 9-10 are graphically presented.
The solution (524.61;20.06) at the left is the best
known solution of the problem considering the cost
criteria, and it is retrieved by both methods. The
solution (618.22; 0.24) is the best solution found by
MOEA on the balance criteria. Table 4 gives the
details of the right part of the front with solutions
closed to the MOEA solution. On this particular run,
the best balance achieved by SPR is related to the
solution (1239.62;0.05) and the closest but better
balance that MOEA brings is the solution
(615.58;0.22) which dominates the MOEA solution
(618.22;0.24).
Table 4: Details of the front.
Cost Balance
1 524.611 20.06
2 531.643 17.09
… … …
20 610.04 0.32
21 615.58 0.22
22 666.20 0.20
23 690.79 0.17
24 785.00 0.16
25 791.00 0.15
26 935.97 0.09
27 1239.62 0.05
4 CONCLUDING REMARKS
In this paper we have proposed a split based
algorithm for a bi-objective VRP, i.e. VRP with
route balancing in which both the total length and
the balance of the routes have to be minimized
(VRPRB). The proposition encompasses all the
well-known bi-objective VRP instances including
instances with range vehicle constraints, which have
not been addressed by previous papers. Preliminary
experiments show that the proposition permits to
obtain high quality solutions for the set of 14
instances and competes for the subset of 7 instances
with previous published works. Our research is now
directed to the Pareto front and to definition of an
ASplitbasedApproachfortheVehicleRoutingProblemwithRouteBalancing
165

approach which could be validated on several bi-
objective routing problems.
REFERENCES
Beasley JE, 1983. Route-first cluster-second methods for
vehicle routing. Omega, vol. 11. pp. 403–408.
Cheng R., Gen M. and Tsujimura, Y., 1996. A tutorial
survey of job-shop scheduling problems using genetic
algorithms, Computers and industrial engineering,
vol. 30, pp. 983-997.
Christofides N., Eilon S., 1969. An algorithm for the
vehicle dispatching problem, Operational Research
Quarterly, vol. 20. pp. 309–318.
Christofides N., Mingozzi A., Toth P., Sandi C. (Eds.),
1979. Combinatorial Optimization, John Wiley,
Chichester, (Chapter 11).
Coello Coello CA., 2000. An updated survey of GA-based
multiobjective optimization techniques. ACM
Computing Surveys, vol. 32(2). pp. 109–43.
Deb, K., 2001. Multi-objective optimization. Multi-
objective optimization using evolutionary algorithms,
pp. 13-46.
Desrochers, M., 1988. An algorithm for the shortest path
problem with resource constraints. Research report G-
88-27, GERAD, Montreal, Canada.
Duhamel C, Lacomme P. and Prodhon C., 2011. Efficient
frameworks for greedy split and new depth first search
split procedures for routing problems, Computers &
Operations Research, vol. 38(4), pp. 723-739.
Ehrgott M, Gandibleux X., 2002. Multiobjective
combinatorial optimization. In: Ehrgott M.,
Gandibleux X, editors. International series in
operations research and management science, vol. 52.
Dordrecht: Kluwer; pp. 369–444.
Jozefowiez N., Semet F. and Talbi E.G., 2009. En
evolutionary algorithm for the vehicle routing problem
with route balancing. European Journal of
Operational Research, vol. 195. pp. 761-769.
Lacomme P., Prins C. and Sevaux M., 2006. A genetic
algorithm for a bi-objective capacitated arc routing
problem. Computers & Operations Research, vol. 33.
pp. 3473-3493.
Prins C., 2004. A simple and effective evolutionary
algorithm for the Vehicle Routing Problem.
Computers & Operations Research, vol. 31(12). pp.
1985-2002.
Sörensen K., Schittekat P., In Press (2013). Statistical
analysis of distance-based path relinking for the
capacitated vehicle routing problem Original
Research, Computers & Operations Research.
Zhang C, Lin Z, Zhang Q. and Lin Z., 2005. Permutation
Distance: Properties and Algorithms. MIC2005, The
6th Metaheuristics International Conference. Vienna,
Austria, August 22-26, pp. 211:216.
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
166
