DESIGNING PERSIAN FLORAL PATTERNS

USING CIRCLE PACKING

Nader Hamekasi and Faramarz Samavati

Department of Computer Science, University of Calgary, Calgary, Canada

Keywords:

Floral Patterns, Texture Generation, Circle Packing, Conformal Mapping.

Abstract:

In this paper, we present a novel approach toward generating ﬂoral patterns. We extract the essence of a

pattern aside from its appearance and geometry into combinatorial elements. As a result, existing patterns can

be reshaped while preserving their essence. Furthermore, we can create new patterns that adhere to high level

concepts such as imperfect symmetry and visual balance. By decomposing ﬂoral patterns into a conﬁguration

of circles and angles, we can reconstruct this patterns on different surfaces given a conformal mapping.

1 INTRODUCTION

Persian ﬂoral patterns have been used to decorate

books, carpets and buildings for many centuries. Ex-

amples of these patterns are illustrated in ﬁg.1. These

patterns were not only used on the plane but also on

spherical geometry to decorate domes. Like other in-

stances of Islamic art, these patterns were designed by

skilled mathematicians, and they exhibit fascinating

geometric and mathematical properties. This art was

taught by traditional practitioners through apprentice-

ship. Therefore, few resources are remained about the

design process of these patterns.

Figure 1: Example of Persian ﬂoral patterns (Takestani,

2002).

Designing ﬂoral patterns can be divided into two

aspects. First, stems are used to compose and struc-

ture the space. Second, ﬂowers and other ornamen-

tal elements are added to locations speciﬁed by the

stem structure. Although a pattern is never complete

without the second step, it is the ﬁrst step that carries

most of the beauty of the design. The composition

should comply with aesthetic concepts such as bal-

ance and repetition. With an aesthetic composition in

hand, one can use pre-designed sets of ﬂowers to dec-

orate a pattern. The main challenge of designing ﬂoral

patterns lies in ﬁnding the underlying composition or

the structure of the stems.

By analyzing existing ﬂoral patterns and study-

ing traditional literature, we realized that the under-

lying structure and design of these patterns are based

on circles. Spiral forms, ﬂowers and even the shape

of the leaves can be expressed using circle arcs. As

we explain in section 3, we can capture the essence

of a pattern into a conﬁguration of circles. There-

fore, The properties and appearance of a design can

be controlled by changing its underlying circular con-

ﬁguration. This led us to relate our problem to a

well-established ﬁeld of mathematics known as circle

packing.

Circle packing is a relatively recent ﬁeld in math-

ematics that studies the conﬁguration of circles show-

ing speciﬁed patterns of tangencies. Circle packing

is based on rich mathematical foundations such as

conformal structures and discrete analytic functions.

Capturing the essence of a ﬂoral pattern in a packing

of circles provides a powerful framework to generate

and manipulate these beautiful patterns.

By taking advantage of circle packing concepts

and tools, we can analyse, generate and edit ﬂoral pat-

terns and also formulate speciﬁc properties in their

structure. Furthermore, we can construct patterns

on non-Euclidean geometries and project designs on

135

Hamekasi N. and Samavati F..

DESIGNING PERSIAN FLORAL PATTERNS USING CIRCLE PACKING.

DOI: 10.5220/0003850101350142

In Proceedings of the International Conference on Computer Graphics Theory and Applications (GRAPP-2012), pages 135-142

ISBN: 978-989-8565-02-0

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

different surfaces without distortion using conformal

mappings.

In what follows, we ﬁrst discuss related work.

Next, in section 3 we analyze ﬂoral patterns and their

circular structure. In section 4 we present concepts

and deﬁnitions from circle packing and explain how

we apply them to control the properties of ﬂoral pat-

terns. In section 5 we provide a method for designing

a Persian ﬂoral pattern algorithmically. And ﬁnally,

section 6 concludes our discussion.

2 RELATED WORK

Ornamental design has been investigated in the con-

text of computer graphics for many years. One of the

earliest works in this area is an algorithmic approach

to generate 17 symmetry groups on the open plane

(Alexander, 1975). Later, Frieze patterns from group

theory were used to generate ornaments in bounded

areas (Glassner, 1996).

Separation of composition and ornaments was ﬁrst

applied in (Smith, 1984). In this work the branch-

ing structures of plants are generated using parallel

rewriting grammars called graphtals; then, in a post-

processing step the result is visually enhanced by

adding leaves and ﬂowers.

Although L-systems (Prusinkiewicz and Linden-

mayer, 1996) is widely used to generate plants, it is

not a suitable approach toward generating ﬂoral orna-

ments (Wong et al., 1998).

Generating spiral curves is investigated in (Xu and

Mould, 2009). These curves are generated based on

the trajectory of charged particles in a magnetic ﬁeld

and are called magnetic curves.

Islamic and Persian patterns are studied in many

works in computer graphics, because of their geo-

metric and mathematical nature. Star patterns along

with a number of algorithms to generate them are

investigated in (Kaplan and Salesin, 2004; Kaplan,

2008). Animation of Persian ﬂoral patterns is studied

in (Etemad et al., 2008). In (Djibril and Thami, 2008),

classifying symmetric patterns in decorative Islamic

art is discussed. A discussion on computer aided art

can be found in (Geng and Geng, 2010).

Our work is closely related to the computer gener-

ated ﬂoral patterns of (Wong et al., 1998). This work

presents a grammar based approach to generate ﬂoral

patterns by deﬁning a set of elements and their growth

rules. Starting with user-speciﬁed seed points, the

main role of the system is to decide which elements to

grow. In order to make this decision, the system ﬁnds

the largest empty circle inside the boundary and then

invokes the elements near that circle.

There are a number of draw backs to this method:

although aesthetic principles like visual balance are

discussed in this work, the presented algorithm does

not provide a mechanism to support these principles.

To address this issue, an interactive approach is pre-

sented, which still relies on artistic input for an aes-

thetic partitioning (Obispo and Anderson, 2007; An-

derson and Wood, 2008). Moreover, the provided al-

gorithm is costly because ﬁnding the largest circle in

every iteration is computationally expensive.

The approach we present here is not grammar

based and is able to generate patterns not only on the

plane but also on non euclidean geometries. More-

over, we are able to control high level properties of

the result such as visual balance and partial symme-

try.

3 ANALYSIS OF PERSIAN

FLORAL PATTERNS

As discussed in section 1, ornaments have two dif-

ferent aspects: composition and appearance. The

Composition involves partitioning the space inside

the boundaries of a design in a visually appealing way.

There are a number of guide lines to compose an aes-

thetic design (Wong et al., 1998):

Repetition, either in the form of simple transla-

tion or complex symmetries, implies a presence of or-

der and design in the pattern. Repetition appears in

Persian ﬂoral patterns in the form of bilateral sym-

metry and also imperfect congruency created by the

spirals.

Balance is another rule of aesthetic design, which

is related to visual weight of the components of the

design. In the case of ﬂoral patterns, visual weight

is mostly inﬂuenced by the size, number of turns and

density of elements of the spirals.

Adhering to the Boundary is another important

rule in ornament design. A pattern that exhibits this

property evokes a sense of intelligence in the design

elements, which form according to their boundary.

Conventionalization and Growth are also two

common property of ornaments (Wong et al., 1998).

Conventionalization involves representing abstract

forms of nature in the ornament. Floral patterns are

an abstraction of vines, climbing and winding to form

the composition of the design. Growth is the means of

connecting different parts of the design. In ﬂoral pat-

terns, growth is evident in spiral forms that represent

the stems. In ﬂoral patterns, and more speciﬁcally

Persian ﬂoral patterns, spirals are the main element of

composition (Etemad et al., 2008).

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications

136

Besides the composition, appearance is another

aspect of ﬂoral patterns. Ornamental elements such

as ﬂowers and leaves are added to the pattern based

on the structure to decorate the result. These ele-

ments can be reused in different designs. Hundreds of

these elements are available in several books, includ-

ing: (Jones, 1987; Aghamiri, 2004; Takestani, 2002;

Behzad, 1998; Honarvar, 2005).

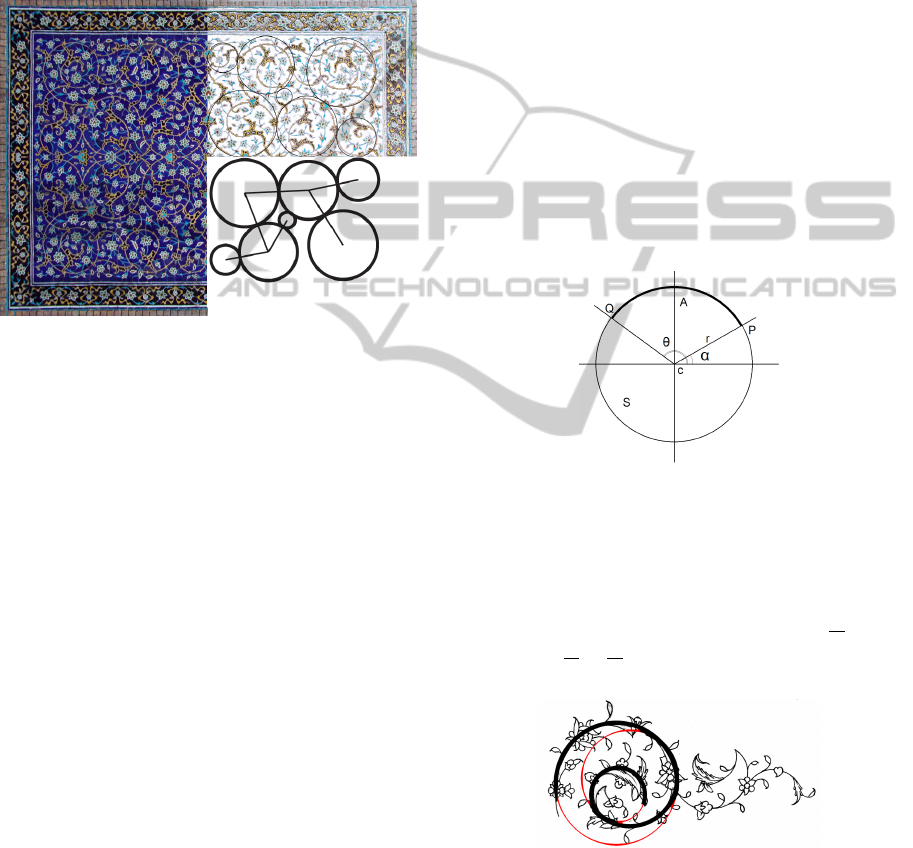
Figure 2: An example of Persian ﬂoral pattern decomposed

into underlying conﬁguration of circles.

Fig.2 shows a Persian ﬂoral pattern from Jame

mosque in Isfahan, Iran. This pattern consists of four

repeated parts using bilateral symmetry. To simplify

this pattern, we have removed the leaves and changed

the background in (ﬁg.2:top, right). This pattern con-

sists of seven spirals. Representing the spirals with a

circle, the pattern is simpliﬁed to a conﬁguration of

circles (ﬁg.2:bottom, right).

These circles and their tangencies form a graph

in which every node is a center of a circle, and ev-

ery edge represents either tangency or overlap of two

circles. We call this graph the combinatorics of the

design. The stem represents a tree (an abstraction of

a plant in nature). Likewise, it represents a tree in the

combinatorics graph. The edges of this tree represent

transitions of the stem from one circle to another.

We have simpliﬁed the design given in ﬁg.2 into

a circle packing. This enables us to not only distin-

guish between the appearance and the geometry but

also between the geometry and the combinatorics of

the pattern. In other words, such a decomposition en-

ables us to capture the essence of a design separate

from the geometry and shape, which is the most im-

portant contribution in this paper.

An important mathematical tool to manipulate

circles is the conformal transformation. This type

of transformation preserves the angle between lines.

Therefore, they map circles into circles. By captur-

ing a design in a conﬁguration of circles, we can use

conformal mapping to transfer a design to another ge-

ometries or manifold without distortion.

In order to produce a design, we need informa-

tion about spirals, their connections and also leaves

and ﬂowers. However, we should keep in mind that

we can only use circles and angles because these are

the only things that stay unchanged through confor-

mal mappings.

For the sake of simplicity throughout this paper,

we denote circle S centered at c and of radius r with

S(c,r). Since we are interested in deﬁne our orna-

ments only based on circles and angles, we deﬁne

point P on the circle S(c,r) with P(S,α) where α

is the angle of the arc between P and the x-axis, as

shown in ﬁg. 3. Therefore, an arc on the circle be-

tween two points can be expressed by its starting an-

gle and the incremental angle to the end point. For

example, the arc A on circle S starting from P(S, α) to

Q(S,θ) is denoted by A(c, r,α,θ − α).

Figure 3: Circle S centered at c and radius r is denoted by

S(c,r). Arc A from P to Q is denoted by A(c,r, α,θ − α).

Spirals consist of circular arcs with different radii

and centers. Fig.4 shows a spiral and the circle

arcs that form it. This spiral consists of three cir-

cle arcs: A

,π,−π) , A

,0,−

2π

) and

,−

2π

,−

5π

) , r

> r

Figure 4: Spirals are constructed based on circles.

There are different forms of spirals depending on

the arc angles of each arc. It is common in Persian ﬂo-

ral patterns to reduce the radius of the inner circle by

a constant value (i.e r

= r

+c = r

+2c) (Takestani,

2002).

DESIGNING PERSIAN FLORAL PATTERNS USING CIRCLE PACKING

137

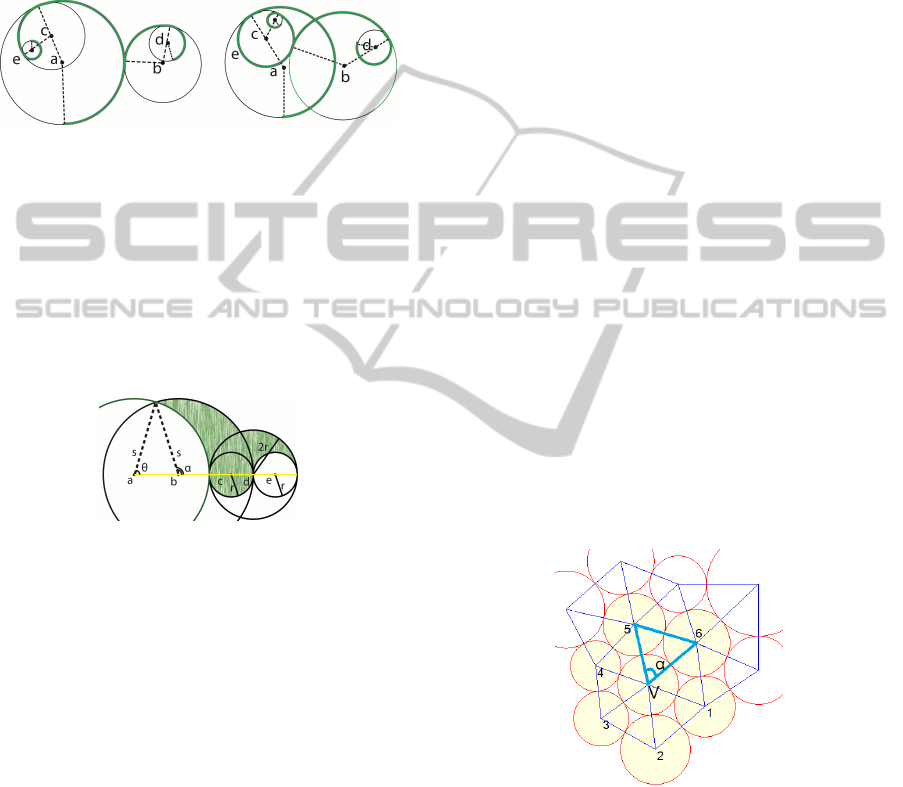
The center c

of the circle S

) which is inner

tangent to circle S

) at the point p(S

,θ) can be

found using following equations:

= c

+ (r

− r

)cos(θ)

= c

+ (r

− r

)sin(θ) (1)

Figure 5: Connections between spirals. right: Spirals are

tangent. left: Spirals overlap.

The connection between two spirals depends on

their outer circles. The outer circles of the two spi-

rals should be either tangent or overlapped in order

to make a connection. Two types of connection are

shown in ﬁg. 5. An important rule in ﬂoral pattern

design is that two connected spirals should have dif-

ferent rotation directions (Honarvar, 2005).

Figure 6: Design of a leaf based on circle arcs.

Although our main task here is to express the

structure of the ornament using circles and angles, we

realized that even the leaves and ﬂowers in Persian

ﬂoral pattern may be expressed in such terms. Fig.

6 shows how a traditional-style leaf is designed with

ﬁve circles arcs. Of course, not all the possible or-

namental elements can be expressed efﬁciently using

only arcs.

4 CIRCLE PACKING

So far, we described how we represent a ﬂoral pattern

with circle arcs and their tangencies. We can use this

analysis to generate these types of patterns automati-

cally. In order to create a new design, the underlying

conﬁguration of circles must ﬁrst be designed. There-

fore, we need a method to ﬁll a bounded area with cir-

cles of different size. Moreover, we want to be able to

control high level properties of the resulting circles.

There are different versions of the circle packing

problem depending on their constraints. For exam-

ple, some methods work with uniform circles only; or

some methods ﬁnd the maximum radii for a number

of circles inside a bounded area. A collection of some

of these different circle packing problems can be

found in (Castillo et al., 2008). Among these works,

the circle packing problem introduced by (Thurston,

1985) is the best match for our problem. This ap-

proach studies the conﬁguration of circles that exhibit

a speciﬁc pattern of tangency. Here, we present a brief

introduction to terminology and methods of this type

of circle packing. A thorough discussion on this circle

packing (which we simply call it circle packing from

this point) can be found in (Stephenson, 2005).

A packing of circles has two aspects: combina-

torics and geometry. The geometry of a packing is

deﬁned by the location of the circles and their radii,

whereas the combinatorics are deﬁned by the tan-

gency relations among circles. The tangencies studied

here are external; meaning that tangent circles have

disjoint interiors. Moreover, we limit our discussion

to tangencies among triples of circles; the tangency

relations between an n-tuble of circles can be con-

verted into triples by adding extra circles (Stephen-

son, 2005).

Combinatorics are encoded in abstract simplicial

2-complexes K which triangulate oriented topologi-

cal surfaces. Geometric realization of K is referred to

as the carrier of the packing which comes from con-

necting the center of the circles with geodesics.

Figure 7: A circle packing and its carrier.

Vertices of K can be interior or boundary. A ver-

tex V along with its neighbors U

,..,U

in K is

called a ﬂower and neighbours U

,..,U

are called

petals. We use lower case letters to refer to the radius

of a circle (e.g. v is the radius of circle represented

by vertex V ). There is a face (2-complex) associated

with each tangent triple on K and there is an angle

α associated with vertex V in each face that contains

V (see ﬁg.7). Angle α(v; u

) in face < V,U

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications

138

can be computed using law of cosines (Collins and

Stephenson, 2003):

α(v;u

) = 2 arcsin



+ v



. (2)

The summation θ(v) =

∑

α(v;u

) for all faces

adjacent to V is called the angle sum of V. To have a

non-overlapping circle packing on the plane, the an-

gle sum of every interior vertex must be 2π. This is

can be seen clearly by looking at the carrier as a geo-

metric realization of the combinatorics. Similarly, the

geometric interpretation of a vertex having angle sum

higher than 2π on the plane is an overlapped ﬂower.

Moreover, If the angle sum is less than 2π the ﬂower

can form on the sphere, and if it is greater than 2π the

ﬂower can form on the Poincare disc (Dubejko and

Stephenson, 1995).

An abstract simplicial 2-complex K can have a

feasible geometric circle packing if and only if it rep-

resents a triangulation of a space. If K has this neces-

sary and sufﬁcient condition, then it can result in dif-

ferent geometric conﬁgurations of circles. Therefore,

we can impose more restrictions to obtain a unique

packing. These restrictions can be on the size or the

angle sum of the boundary circles. We use these re-

strictions to control the boundary shape of our ﬂoral

patterns. Finding a packing that satisﬁes given bound-

ary conditions is called the boundary value problem

(the Dirichlet problem) and there exists a unique (up

to automorphism) solution for this problem (Collins

and Stephenson, 2003).

The algorithm to ﬁnd this packing is based on the

angle sums. This algorithm has two steps. The ﬁrst

step is to ﬁnd the correct radii for all the circles, and

the second step is to lay out the circles. This algorithm

is efﬁcient and guaranteed to converge to the desired

packing (Collins and Stephenson, 2003).

As stated earlier, to form a non-univalent plan-

ner packing (i.e. a packing on the plane which does

not overlap), the angle sum of every inner circle must

be 2π. Starting from an arbitrary value for the radii,

ﬁrst we initialize boundary radii with deﬁned values.

Then, we iteratively reﬁne the radius of every circle

without a radius restriction to a new value until the

angle sum condition is met (by a threshold). Assume

vertex V has k neighbors and its current angle sum is

θ. There is a radius r

so that if all the neighbors of V

had this radius, the angle sum would still be θ. Then,

there is a radius r

new

so that if V has r

new

as its radius

and all the neighbors are of radius r

the angle sum

would be A

. Replacing radii of circles with r

new

it-

eratively will adjust the angle sum of the vertices and

eventually result in a set of radii so that the circles

with that radii can ﬁt beside each other. The process

above is summarized in this equation:

new

1 − sin(

)

sin(

)

sin(

)

1 − sin(

)

(3)

In this formula k is the degree of vertex V and A

is the target angle sum for this vertex, which is 2π

for inner vertices in the case of planer packings. This

algorithm carries the angle sum from circles with a

higher angle sum to circles with a lower angle sum

until the error is less than a threshold.

The next step is to lay out the circles. Having

the combinatorics K and the radii computed above,

we traverse the combinatorics and place the circles,

which will now ﬁt together to form the packing. Start-

ing from an edge of a face on K, two circles associated

with that edge are located arbitrarily and the third cir-

cle of that face is placed based on the position of the

ﬁrst two. We then lay out faces that have a common

edge with this face, and similarly, we can place all

the circles based on the previous circles. The choice

of the ﬁrst edge and the order of traversing the faces

does not change the ﬁnal packing (Stephenson, 2005).

As explained in the previous section, the underly-

ing circles of a ﬂoral pattern can overlap. We can cre-

ate overlapped packings by adding constant values to

circles’ radii after the packing or to u

and u

in equa-

tion 2 while calculating the radii. Overlapped pack-

ings can be converted to ﬂoral patterns as depicted in

ﬁg. 5.

We use the algorithm and concepts explained

above to create new designs with speciﬁed high level

properties such as imperfect symmetry and visual bal-

ance. Repetition and symmetry can be formulated in

the combinatorics of a pattern. Symmetric combina-

torics result in a partial or perfect symmetric ﬂoral

pattern.

Visual balance of the design is a factor of the size

of the spirals and the number of turns they make.

There is a relation between the size of a circle (rel-

ative to its petals) and the degree of its corresponding

vertex in the combinatorics. This fact is supported

by the Ring Lemma (Rodin and Sullivan, 1987) :

Let S(r

) be an interior circle in a packing, and

) for i = 1..k (k ≥ 3) be its k petals. Then,

≤ a(k) in which, a(k) is a increasing function

of k. This implies that by increasing the degree of a

vertex, we can increase the radius of its correspond-

ing circle in comparison to its neighbors. Therefore, a

visually balanced result can be achieved using a bal-

anced combinatorics in which degrees of the vertices

do not deviate much. As an exaggerated example, if

all the vertices are of degree 6 (with no boundary con-

dition) then all of the resulting circles have the same

DESIGNING PERSIAN FLORAL PATTERNS USING CIRCLE PACKING

139

size.

Figure 8: Relation between the degree of a vertex and the

size of its corresponding circle compared to the petals.

5 GENERATING FLORAL

PATTERNS

With the analysis presented in section 3 and the con-

cepts provided in section 4, we propose a method to

generate ﬂoral patterns automatically.

Given boundary B, the problem is to generate a

ﬂoral pattern that ﬁlls this boundary and adheres to

high level properties such as balance and symmetry.

First, we ﬁnd M, the basic motif of B. Then, we de-

ﬁne the combinatorics K and set boundary conditions.

Next, we generate the circle packing. Having the cir-

cle packing we ﬁnd the desired tree T in K. Then

we traverse T and set the spiral types for each circle.

Finally, we apply the symmetry and repetition rules

deﬁned in ﬁrst step to ﬁll B. We will describe each

step in more details.

Symmetry is an important characteristic of the ﬂo-

ral ornaments. As the ﬁrst step, we should decide

what type of symmetry should be used for the given

boundary. There are a number of methods to detect

the symmetry in a shape automatically (Masuda et al.,

1993; Lee et al., 2008). Using these techniques, we

can detect the symmetry and specify the main mo-

tif in the boundary. We can focus only on the motif

and then repeat the generated pattern. Alternatively,

we can formulate the symmetry in the combinatorics

of the underlying circle packing and the tree. This

method results in an imperfect symmetry.

The combinatorics can come from an existing pat-

tern, or it can be deﬁned so that it exhibits some spe-

ciﬁc properties, described in section 4. The same

combinatorics can result in different ﬂoral patterns

depending on the boundary.

After specifying the combinatorics, we solve the

boundary value problem. To specify the boundary

values, we need a correspondence between the points

on the given boundary (B) and the boundary of K.

Therefore, B is converted into a polygon having an

equal number of vertices to the boundary vertices of

K. For every boundary circle, we can either ﬁx the ra-

dius or the angle sum. As shown in ﬁg.9 right, the de-

cision is based on the importance of the polygon’s an-

gle at that vertex. If the center of the circle is collinear

with its neighbors by a threshold, we ﬁx the radius.

Otherwise, we ﬁx the angle sum of that circle.

Using the algorithm discussed in section 4 we gen-

erate the circle packing. At this point, some circles

may exceed the boundary. To solve this issue, we pro-

pose three approaches. First, we can push the circles

to ﬁt within the boundary, which will result in a non-

univalent packing (i.e. overlapping circles). The sec-

ond approach is to scale the packing to ﬁt the bound-

aries which will result in empty spaces left in some

areas of the pattern (usually corners). The third ap-

proach is to “cookie cut” the packing, by which we

mean removing the circles which fall outside of the

boundary. This approaches can be used in combina-

tion with each other.

The next step, is to specify a tree inside the com-

binatorics’ graph. This tree plays an important role

in the ﬁnal appearance of the ﬂoral pattern, and of

course, the choice is not unique. Based on our ex-

periments, we present guidelines that can be used to

create more appealing results. Having the boundary

spirals as the leaves is more desired since it complies

more with conventionalization. Furthermore, it helps

to create a balanced composition by decreasing the

visual weight on the boundaries. Setting boundary

spirals as parts of the stem may result in larger arcs

with higher numbers of turns. Moreover, a combina-

torial symmetric tree results in a symmetric or imper-

fect symmetric design depending on the size of the

circles.

Similar to the discussion in section 4, the vertices

of the tree should have a balanced degree distribution

to achieve a visually balanced result. Similar to the

combinatorics, the tree can be extracted from an exist-

ing pattern designed by an artist. Many ﬂoral patterns

can be generated from a single combinatorics and a

single tree.

Figure 9: Right: Arranging boundary circles. Left: Parti-

tioning inner section of a spiral using circle packing.

After deﬁning the tree, we traverse it and specify

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications

140

the properties of the spirals (i.e. type, thickness and

number of turns). Stem’s thickness is usually uniform

in Persian ﬂoral patterns. It can also be deﬁned based

on the depth of the corresponding vertex in the com-

binatorial tree. To achieve a balanced composition,

number of the turns of a spiral should be proportional

to the size of its outer circle.

Placement of ornaments is also done in this step.

We use circle packing within the circle (Wang et al.,

2002) to partition the space inside a spiral in order to

allocate space for the ornaments. As an example, ﬁg.

9 shows a spiral partitioned based on the circles inside

its bounding circle. Circles 1, 2, 3 and 5 are available

to place an ornament, but circle 4 and 0 are occupied

by the stem and circle 6 is not attached to the stem.

Figure 10: An example on a pattern constructed on sphere.

We can construct these patterns in different ge-

ometries. As an example, in ﬁg.10, We have created

a pattern on a sphere. For patterns on the sphere,

the combinatorics should be spherical; meaning that

there should be no boundary vertices. To create spher-

ical patterns, we remove one of the vertices from the

combinatorics graph and use its petals as the combi-

natorics’ boundary. Next, we create a planar packing

on the unit disc using the combinatorics and Poincare

disc metrics. Then we use stereographic projection

to map patterns on the unit disc to one of the hemi-

spheres.

In order to map a unit disc on the hemisphere, we

use a modiﬁed version of stereographic projection.

We place the center of the stereographic sphere on

the (0,0,0) instead of (0, 0, 1). Assuming P(u, v) is

a point on the plane the projected point Q(x, y,z) on

the sphere is given by following equations:

z =

1 − (u

+ v

)

1 + (u

+ v

)

, x = u(1 + z), y = v(1 +z) (4)

Then the equator is considered as the circle removed

from the combinatorics since it is tangent to all the

boundary circles. The circle represented by equator is

larger than other circles. We can use a Mobius trans-

formation (automorphisms on sphere) to normalize

the size of the results. This method provides seam-

less packing on the sphere (Stephenson, 2005). Since

we only map the arcs and this projection is conformal,

there is no distortion in the ﬁnal results (i.e. circles re-

main circles).

We can cover arbitrary surfaces with ﬂoral pat-

terns given a conformal parametrization. Methods

such as (Bobenko et al., 2003) provide us with a circle

packings covering more general surfaces. We can use

these packing to construct ﬂoral patterns that cover an

object.

Figure 11: Final results by placing ornaments on the struc-

ture.

6 CONCLUSIONS

In this work, we presented an analysis of Persian

ﬂoral patterns based on circle packing. This ap-

proach helps us to separate the semantics and com-

binatorics of the design from its geometry and cap-

ture the essence of a design independent of its appear-

ance (i.e. the detailed ornamentation and the render-

ing style). Furthermore, the elegant mathematics sup-

porting this method enables us to generate new de-

signs that exhibit high level characteristics such as vi-

sual balance and imperfect symmetry. The presented

methodology may be applicable to other styles of ﬂo-

ral patterns.

We have implemented the proposed method to

generate Persian ﬂoral patterns. Most of the pictures

in this paper are generated using this implementation.

It is important to notice that the domain and possi-

bilities of the presented approach extend beyond this

implementation. Fig.11 shows an example of the ﬁnal

results with added ornament elements.

As future work, we would like to explore the pos-

sibility of interactive and sketch-based pattern design,

DESIGNING PERSIAN FLORAL PATTERNS USING CIRCLE PACKING

141

allowing the creation of patterns that adhere to struc-

tures provided by the user. Furthermore, animating

the generated patterns procedurally is another possi-

ble direction for future works.

ACKNOWLEDGEMENTS

The authors would like to thank Troy Alderson and

Ali Mahdavi Amiri for their detailed comments and

lively discussions during the course of this research.

This work was funded by GRAND NCE.

REFERENCES

Aghamiri, A. H. (2004). Khataei and decorative designs.

Yasavoli publications., Tehran.

Alexander, H. (1975). The computer/plotter and the 17

ornamental design types. In Proceedings of the 2nd

annual conference on Computer graphics and inter-

active techniques, SIGGRAPH ’75, pages 160–167,

New York, NY, USA. ACM.

Anderson, D. and Wood, Z. (2008). User driven two-

dimensional computer-generated ornamentation. In

Proceedings of the 4th International Symposium on

Advances in Visual Computing, ISVC ’08, pages 604–

613, Berlin, Heidelberg. Springer-Verlag.

Behzad, H. T. (1998). Design of carpets and decorations.

Yasavoli publications., Tehran.

Bobenko, A. I., Hoffmann, T., and Springborn, B. A.

(2003). Minimal surfaces from circle patterns: Ge-

ometry from combinatorics. Annals of Mathematics,

164:231–264.

Castillo, I., Kampas, F. J., and Pintr, J. D. (2008). Solving

circle packing problems by global optimization: Nu-

merical results and industrial applications. European

Journal of Operational Research, 191(3):786 – 802.

Collins, C. R. and Stephenson, K. (2003). A circle packing

algorithm. Comput. Geom. Theory Appl., 25:233–256.

Djibril, M. O. and Thami, R. O. H. (2008). Islamic ge-

ometrical patterns indexing and classiﬁcation using

discrete symmetry groups. J. Comput. Cult. Herit.,

1:10:1–10:14.

Dubejko, T. and Stephenson, K. (1995). Circle packing:

Experiments in discrete analytic function theory. MR

97f:52027, 4:307–348.

Etemad, K., Samavati, F. F., and Prusinkiewicz, P. (2008).

Animating persian ﬂoral patterns. In Eurographics

Symposium on Computational Aesthetics in Graphics,

Visualization and Imaging, pages 25–32.

Geng, W. and Geng, W. (2010). Computer-aided design of

art patterns. In The Algorithms and Principles of Non-

photorealistic Graphics, Advanced Topics in Science

and Technology in China, pages 91–112. Springer

Berlin Heidelberg.

Glassner, A. (1996). Frieze groups. Computer Graphics

and Applications, IEEE, 16(3):78 –83.

Honarvar, M. R. (2005). Golden Twist. Yasavoli publica-

tions., Tehran.

Jones, O. (1987). The grammar of ornament. Courier Dover

Publications., New York.

Kaplan, C. S. (2008). Islamic patterns. In ACM SIGGRAPH

2008 art gallery, SIGGRAPH ’08, pages 45–45, New

York, NY, USA. ACM.

Kaplan, C. S. and Salesin, D. H. (2004). Islamic star

patterns in absolute geometry. ACM Trans. Graph.,

23:97–119.

Lee, S., Collins, R. T., and Liu, Y. (2008). Rotation symme-

try group detection via frequency analysis of frieze-

expansions. Computer Vision and Pattern Recogni-

tion, IEEE Computer Society Conference on, 0:1–8.

Masuda, T., Yamamoto, K., and Yamada, H. (1993).

Detection of partial symmetry using correlation

with rotated-reﬂected images. Pattern Recognition,

26(8):1245 – 1253.

Obispo, S. L. and Anderson, R. (2007). Title: Two-

dimensional computer-generated ornamentation using

a user-driven global planning strategy. Master’s thesis,

California Polytechnic State University.

Prusinkiewicz, P. and Lindenmayer, A. (1996). The algo-

rithmic beauty of plants. Springer-Verlag New York,

Inc., New York, NY, USA.

Rodin, B. and Sullivan, D. (1987). The convergence of cir-

cle packing to the riemann mapping. Differential Ge-

ometry, pages 349–360.

Smith, A. R. (1984). Plants, fractals, and formal lan-

guages. In Proceedings of the 11th annual con-

ference on Computer graphics and interactive tech-

niques, SIGGRAPH ’84, pages 1–10. ACM.

Stephenson, K. (2005). Introduction to circle packing: the

theory of discrete analytic functions. Cambridge Uni-

versity Press., New York.

Takestani, A. M. (2002). Khataei and decorative designs.

Soroush Press., Tehran.

Thurston, W. (1985). The ﬁnite riemann mapping theorem,

invited talk at the international symposium at purdue

university on the occasion of the proof of the bieber-

bach conjecture.

Wang, H., Huang, W., Zhang, Q., and Xu, D. (2002). An

improved algorithm for the packing of unequal circles

within a larger containing circle. European Journal of

Operational Research, 141(2):440 – 453.

Wong, M. T., Zongker, D. E., and Salesin, D. (1998).

Computer-generated ﬂoral ornament. In SIG-

GRAPH’98, pages 423–434.

Xu, L. and Mould, D. (2009). Magnetic curves: Curvature-

controlled aesthetic curves using magnetic ﬁelds. In

Computational Aesthetics’09, pages 1–8.

GRAPP 2012 - International Conference on Computer Graphics Theory and Applications

142