
TWO-LEVEL METHOD FOR 3D NON-RIGID REGISTRATION
With an Application to Statistical Atlases Construction
C. Wu*, P. E. Murtha**, A. B. Mor** and B. Jaramaz* **
* Carnegie Mellon University, School of Computer Science
Robotics Institute, Pittsburgh, PA, 15213
** Institute for Computer Assisted Orthopaedic Surgery, The Western Pennsylvania Hospital Mellon Pavilion
Suite 242, 4815 Liberty Avenue, Pittsburgh, PA 15224
Keywords:
3D deformable registration, Two-level method, Statistical atlas.
Abstract:
We propose a two-level method for 3D non-rigid registration and apply the method to the problem of building
statistical atlases of 3D anatomical structures. 3D registration is an important problem in computer vision and
a challenge topic in medical image field due to the geometrical complexity of anatomical shapes and size of
medical image data. In this work we adopt a two-level strategy to deal with these problems. Compared with
a general multi-resolution framework, we use an interpolation to propagate the matching instead of repeating
registration scheme in each resolution. Our algorithm is divided into two main parts: a low-resolution solution
to the correspondences and mapping of surface models using Chui and Rangarajan’s robust point matching
algorithm, followed by an interpolation to achieve high-resolution correspondences. Experimental results
demonstrate our approach for solving the non-rigid registration and correspondences within complicated 3D
data sets. In this paper we present an example of this method in the construction of a statistical atlas of the
femur.
1 INTRODUCTION
Registration has been studied for years in computer
vision, which is still a critical problem in medi-
cal image field due to the geometrical complexity
of anatomical shapes, and computational complexity
caused by the enormous size of volume data. It has
numerous clinical applications such as statistical atlas
construction for group study and statistical parame-
ters analysis (Hill et al., 2001), mapping anatomical
atlases to individual patient images for disease anal-
ysis (Fleute et al., 2002) and segmentation (Rohlfing
et al., 2004).
According to the type of the transformation be-
ing applied, registration can be rigid or non-rigid.
In other words, as long as the shape has no change
between two images, the registration should be
rigid, such as the intra-subject(same patient)-inter-
modality(different imaging system) registration by
capturing images at the same time. However, when
we take into account the time, i.e., when two im-
ages are captured at different time, most of intra-
subject registration will be non-rigid due to the
shape variance of the anatomical structures for ex-
ample swelling, prostate poking, bone fractures, tu-
mor growth changes, intestinal movements etc. Be-
sides, inter-subject(different patient) registrations are
usually non-rigid because of the local anatomical dif-
ferences between patients. Therefore, non-rigid (also
known as deformable) registration has been an active
topic in recent years. In general, a non-rigid transfor-
mation is represented by a global rigid or affine trans-
formation plus a local non-linear deformation, which
can be described by radial basis functions (RBF) (Yu,
2005), octree-spline (Szeliski and Lavallee, 1996),
thin-plate spline (TPS) (Chui and Rangarajan, 2003),
geometric splines (Farin, 1993), finite elements (Park
et al., 1996), or free form B-spline (Rueckert et al.,
2003) etc. In order to evaluate the registration, dif-
ferent similarity measurements have been utilized ac-
cording to different features and imaging modalities.
For example, sum of squared distances (SSD) is used
for geometric features (Besl and McKay, 1992). For
the intensity features, correlation coefficients (CC)
(Kim and Fessler, 2004), Ratio Image Uniformity
(RIU) (Woods et al., 1994), or mutual information
356
Wu C., E. Murtha P., B. Mor A. and Jaramaz B. (2007).
TWO-LEVEL METHOD FOR 3D NON-RIGID REGISTRATION - With an Application to Statistical Atlases Construction.
In Proceedings of the Second International Conference on Computer Vision Theory and Applications - IFP/IA, pages 356-362
Copyright
c
SciTePress

(MI) (Wells et al., 1996) are usually considered. Reg-
istration problem can be simplified given some known
correspondences, for example using markers (Maurer
et al., 1997). Nevertheless, markers are not allowed
to use or available in many scenarios. Alternate es-
timation of correspondences and transformations are
therefore widely used for both rigid case (Besl and
McKay, 1992) and non-rigid case (Chui and Rangara-
jan, 2003; Chui et al., 2004; Glaunes et al., 2004).
Moreover, with the increase of data size and geomet-
rical complexity, multi-resolution strategy has been
adopted into the registration framework (Ellingsen
and Prince, 2006; Jaume et al., 2002; Shen, 2002).
Sparse matrices are also used to handle the computa-
tional complexity (Papademetris et al., 2003).
In this paper we propose a two-level non-rigid
registration approach for 3D surface mesh to deal
with the computational and geometrical complexity,
inspired by Chui and Rangarajan’s non-rigid regis-
tration algorithm and the previous multi-resolution
works. Since Chui and Rangarajan’s algorithm is
not able to handle more than 2000 3D points (Pa-
pademetris et al., 2003), in order to deal with more
points, we break down the registration into a two-
level process. We first apply their algorithm to the
simplified low-resolution meshes (We use Garland’s
mesh simplification technique (Garland and Heck-
bert, 1997) to compute low-resolution meshes). And
then, instead of successively matching in each reso-
lution from coarse to fine, we directly propagate the
correspondences from low resolution to the high res-
olution by an interpolation.
2 TWO-LEVEL REGISTRATION
2.1 Mesh Simplification
We use Garland’s quadric error metrics (QEM) based
mesh simplification (Garland and Heckbert, 1997)
technique to obtain low-resolution meshes. QEM is
based on the iterative contraction of vertex pairs. The
cost of contraction is noted by a quadric error and the
whole process is an iteratively minimizing the quadric
error.
A critical parameter in the simplification is the
number of vertices in the low-resolution meshes. The
less vertices, the faster low-resolution registration but
less accurate the high-resolution registration. We
make a trade off between accuracy and speed by do-
ing a series of experiments (See Sec. 4).
2.2 Low-Res Non-Rigid Registration
Point-to-Point Registration: We apply Chui and
Rangarajan’s non-rigid registration method on simpli-
fied meshes. Fuzzy correspondences and a determin-
istic annealing technique are adopted for a smoother
optimization process and efficiency. A dual update
strategy is utilized to estimate the correspondences
and transformation iteratively. The non-rigid transfor-
mation is parameterized using thin-plate splines for a
smooth spatial mapping.
Initial Alignment: Before applying Chui and Ran-
garajan’s method, we need an extra alignment due to
the particularity of our data. Our data comes from
CT scanned surfaces of human femur. Since we are
more interested in condyles, As Fig. 1 shows, only
distal femur is scanned to build meshes. According
to different patients, some meshes include more fe-
mur shaft such as mesh Y, others include less shaft
for example mesh X. Experiments shows that the reg-
istration might be very slow and may not converge
for some cases, if we only move mesh X to the center
of mesh Y at the very beginning. The reason is that
some part of mesh Y (as showed in a blue rectangle)
has no counterpart in mesh X, and we should not take
into account this part in the registration. To tackle
this problem, we estimate the pseudo center of mesh
Y and a rigid transformation between two meshes.
As Fig. 1 illustrates, we use the height of mesh
X to estimate the pseudo center of mesh Y. Assume
axis z is the scan direction from the knee to hip, we
estimate the pseudo center c
Y
′
as:
c
Y
′
=
1
N
Y
′
∑
(z
Y
−minz
Y
)<(maxz
X
−minz
X
)
p
Y
(1)
where N
Y
′
covers points p
Y
′
in mesh Y that satisfy
(z
Y
− minz
Y
) < (maxz
X
− minz
X
) (black points in 1.
We apply principal component analysis (PCA) to es-
timate the pose of each mesh. Assume
c
X
=
1
N
X
∑
p
X
(2)
is the center of mesh X. Then we can compute the
covariance matrix for {p
X
} and {p
Y
′
}:
Ψ
X
=
1
N
X
−1
[p
1
X
−c
X
,·· · ,p
N
X
X
−c
X
] · [p
1
X
−c
X
,·· · ,p
N
X
X
−c
X
]
′
Ψ
Y
′
=
1
N
X
−1
[p
1
Y
′
−c
Y
′
,·· · ,p
N
Y
′
Y
′
−c
Y
′
] · [p
1
Y
′
−c
Y
′
,·· · ,p
N
Y
′
Y
′
−c
Y
′
]
′
(3)
We compute the principle axes by decomposing the
covariance matrix using moment analysis:
Ψ
X
= U
X
Λ
X
U
X
′
, Ψ
Y
′
= U
Y
′
Λ
Y
′
U
Y
′
′
(4)
Each column of U
X
represents an principle axis of
points set {p
X
}, and U
Y
′
for {p
Y
′
}. We use three
axes to describe the pose of points set (Fig. 1): red

Mesh X Mesh Y
Move Mesh X to the pseudo center of Mesh Y
Rotate Mesh X to be the same pose as Mesh Y
Mesh X & Y
h
z
Figure 1: Illustration of the rigid transformation from mesh
X to mesh Y. The first row compares the translated mesh
X with Y. Black points in mesh Y are used to compute the
pseudo center. The second compare the translated and ro-
tated mesh X with Y. Red axes represent the principle com-
ponents of point set in mesh X, blue axes for Y.
for {p
X
} and green for {p
Y
′
}. We can estimate a
rotation from axes of X to Y
′
, which is given by
U
Y
′
·U
X
′
. Therefore, we can apply a rigid transfor-
mation [U
Y
′
·U
X
′
|(c
Y
′
−c
X
)] to points set {p
X
}. Fig.
1 shows the transformed mesh X. Experiment shows
the rate of convergence has been improved from 78%
to 95.2%.
2.3 Local Non-Rigid Registration
Point-to-Surface Registration: In the previous sec-
tion the non-rigid registration is applied to deform
only points and SSD is used as a criteria. Here we
will step further to minimize the SSD by using some
points on the surface instead of original vertices. This
idea is straightforward. As Fig. 2 shows, x
i
is a point
in the deformed mesh X, whose correspondence in
mesh Y is y
i
. SSD (
∑
|x
i
− y
i
|
2
) has been minimized
in the previous section. However, it is possible to de-
crease SSD more if we use some points on the surface
instead of y
i
. Let’s check the neighboring triangles of
y
i
, which are triangles sharing the same vertex y
i
, for
example S
1
,S
2
and S
3
in Fig. 2. We examine the dis-
tance from x
i
to each neighboring triangle, such as
d
1
, d
2
and d
3
in Fig. 2. If any of them is smaller than
d
0
= |x
i
−y
i
|, we can use the corresponding projected
point to replace y
i
such that we can have achieve a
smaller SSD.
Since the point-surface registration is a local pro-
cess, we have to take into account the case that differ-
ent points in mesh X which come up with the same
corresponding surface point in mesh Y. We use a sim-
ple rule to handle such interference: the point in mesh
X with smaller SSD will be updated with the surface
point in mesh Y.
Deformed Mesh X
Mesh Y
Figure 2: Illustration of local non-rigid registration between
point and surface. x
i
is a point in the deformed mesh X,
whose correspondence in mesh Y is y
i
. The projection of
x
i
to each triangle S
t
sharing y
i
is denoted by y
i
t
. d
t
is the
distance between x
i
and y
i
t
. (t = 1, 2,3, ·· ·).
2.4 Low-Resolution to High-Resolution
Interpolation
After the registration in low-resolution meshes, we
directly apply a surface interpolation to those coarse
meshes, in order to migrate the registration to high-
resolution meshes. The problem is to build the cor-
respondences between mesh X and Y, given corre-
spondence between a subset of X and a subset of
Y. Radial basis functions(RBF), finite element, mul-
tivariate spline such as thin-plate spline(2D bivariate
spline) and triharmonic thin-plate spline, are popular
techniques used in surface interpolation. Carr et al
(Carr et al., 1997) include multivariate splines method
into radial basis functions by using splines as kernel
functions. In this work we use Gaussian kernel based
RBF as an illustration due to it’s simple mathematical
representation and less restrictions on nodes. Specif-
ically, we use a linear affine function plus a series of
radial basis functions (RBFs) to construct the interpo-
lation function:
y
L
i
=c
1
·[ϕ(kx
L
i
,x
L
1
k),· ·· ,ϕ(kx
L
i
,x
L
N
k)]
′
+c
2
+c
3
·x
L
i
|
{z }
g(x
L
i
)
(5)
where x
L
i
is a vertex in the low-resolution mesh X
L
,
whose correspondence in the low-resolution mesh Y
L
is y
L
i
, i = 1, 2,··· , N (N is the number of vertices in
mesh X
L
). x
L
i
and y
L
i
are both 3×1 vectors with three
coordinates. c
1
is a 3×N coefficient matrix of ra-
dial basis functions. ϕ(kx
L
i
,x
L
j
k) are radially sym-
metric basis functions. We have chosen a Gaussian
kernel ϕ(u
i
,u
j
) = exp(−ku
i
− u
j
k/0.5), as suggested
by (Pighin et al., 1998). c
2
and c
3
are coefficients for
the affine component. c
2
is a 3×1 vector and c
3
is a
3×3 matrix. Given N correspondences, we have N
equations for each axis (
X , Y and Z ):

ϕ(x
L
1
,x
L
1
) ··· ϕ(x
L
1
,x
L
N
) 1 x
L
1
T
.
.
.
ϕ(x
L
N
,x
L
1
) · · · ϕ(x
L
N
,x
L
N
) 1 x
L
N
T
|
{z }
P
k
·
c
k
1
T
c
k
2
T
c
k
3
T
|
{z }
c
k
=
y
L
1
k
.
.
.
y
L
N
k
|
{z }
y
L
k
(6)
where c
1
k
, c
2
k
and c
3
k
denote the k
th
row of c
1
, c
2
and c
3
, respectively. y
L
i
k
denotes the k
th
row of y
L
i
,
k can be 1,2 or 3, corresponding to the
X , Y , and Z
axes. Therefore we have 3N equations in all:
P=[P
1
,P
2
,P
3
]
′
,c=[c
1
,c
2
,c
3
]
′
,y=[y
1
,y
2
,y
3
]
′
(7)
P is a 3N×(N+4) matrix. In order to ensure a smooth
interpolation function, we add the additional orthogo-
nality constraints
∑
i
x
L
i
T
c
1,i
= 0 (Carr et al., 2001) to
Eq. 6, where c
1,i
denotes the i
th
column of c
1
:
P
x
L
1
x
L
2
··· x
L
N
0
4×4
|
{z }
Q
· c =
y
0
4×1
|
{z }
w
(8)
The least-squares solution for this linear system,
Qc = w, is given by c = (Q
T
Q)
−1
Q
T
w.
Finally, the correspondence of a vertex x
H
j
in the
high-resolution mesh X
H
can be computed by using
Eq. 5: y
H
j
= g(x
H
j
), for j = 1, · ·· , M (M is the number
of vertices in mesh X
H
). We also apply the local non-
rigid registration for y
H
j
as described in Sec. 2.3.
3 APPLICATION: FEMUR ATLAS
CONSTRUCTION
Statistical anatomical atlases are one of powerful
analysis tool for 2D and 3D medical images (Cootes
et al., 1995; Cootes and Taylor, 2001). Due to the
anatomical variance between subjects, construction
of statistical anatomical atlases usually requires non-
rigid registrations between individual models. As an
application, we apply our registration results to build
a statistical atlas for an anatomical structure. A rigid
pose alignment has been applied to eliminate the ef-
fect of imaging pose (Goryn and Hein, 1995) before
atlas construction.
Suppose we have K aligned meshes and each
mesh can be represented by a 3M×1 vector v
i
(i =
1,·· · ,K), where M is the number of points in each
mesh and 3 denotes three coordinates
X , Y , and Z .
We compute the mean vector c =
1
K
∑
v and covari-
ance matrix Ψ=
1
M−1
[v
1
−c,· ··,v
K
−c]·[v
1
−c,· ··,v
K
−c]
′
and then apply PCA: Ψ = UΛU
′
.
Therefore, any mesh vector in the data set can be
represented by a mean vector plus a linear combina-
tion of each principal components (each column of
U):
v
i
= c+ Uη
i
(9)
where η
i
is a K×1 coefficient vector obtained by
project v
i
onto each principal axis. New models, not
included in the data set, can be generated by manipu-
lating the elements of η
i
.
4 EXPERIMENTAL RESULTS
87 CT-scanned 87 patients with healthy femur: 53
males and 34 females; 43 left femurs and 44 right.
The patients age from 39 to 78 and their femur height
ranges from 400mm to 540mm. The CT volumes are
segmented to provide triangulated surface models us-
ing Marching Cube algorithm. All surface models are
smoothed by the method in (Desbrun et al., 1999).
Each femur data includes two mesh surfaces: femoral
head and distal femur.
Fig. 3 shows two high-resolution mesh X
H
(21130
vertices, 42256 triangles, 65.84mm in z-axis) and Y
H
(26652 vertices, 53300 triangles, 105.89mm in z-axis)
for distal femur (Patient X is a 79 years old female,
with 472.55mm height femur; Patient Y is a 53 years
old female, with 477.59mm height femur). We com-
pute point-to-surface distance from X
H
to Y
H
(Aspert
et al., 2002):
d(p,Y
H
) = min
p
′
∈Y
H
kp− p
′
k
2
, p ∈ X
H
(10)
where k · k
2
is Euclidean norm. The HSV
color of each vertex in mesh X
H
denotes the
distance d(p,Y
H
). We also compute the mean
error d
m
(X
H
,Y
H
) and root mean square error
d
RMS
(X
H
,Y
H
) between mesh X
H
and Y
H
.
d
m
(X
H
,Y
H
) =
1
|X
H
|
p∈X
H
d(p,Y
H
)dX
H
d
RMS
(X
H
,Y
H
) =
q
1
|X
H
|
p∈X
H
d(p,Y
H
)
2
dX
H
(11)
With respect to the bounding box diagonal of mesh
Y
H
(158.48mm), the mean error is 6.49% and root
mean square error is 7.70%. Fig. 4 shows the low-
resolution mesh X
L
(169 vertices, 334 triangles) and
Y
L
(213 vertices, 422 triangles) after simplification.
With respect to the bounding box diagonal of mesh
Y
L
(158.28mm), the mean error is 6.53% and root
mean square error is 7.74%. Fig. 5 shows the de-
formed low-resolution mesh X
L(1)
and Y
L
after ap-
plying Chui and Rangarajan’s non-rigid registration.
With respect to the bounding box diagonal of mesh
Y
L
(158.28mm), the mean error is 1.68% and root
mean square error is 2.13%. Surface distance has
been significantly decreased after Chui and Rangara-
jan’s non-rigid registration. Fig. 6 shows the de-
formed low-resolution mesh X
L(2)
and Y
L
after ap-
plying a local deformation discussed in Sec. 2.3.

Mesh X
H
Mesh Y
H
High-Resolution
Surface Distance from X
H
to Y
H
Figure 3: Input high-resolution meshes.
Low-Resolution
Mesh X
L
Mesh Y
L
Surface Distance from X
L
to Y
L
Figure 4: After simplification.
Low-Resolution
Deformed Mesh X
L(1)
Mesh Y
L
Surface Distance from X
L(1)
to Y
L
Figure 5: After low-resolution registra-
tion.
Low-Resolution
Deformed Mesh X
L(2)
Mesh Y
L
Surface Distance from X
L(2)
to Y
L
Figure 6: After local deformation.
Mesh Y
H
High-Resolution
Deformed Mesh X
H(1)
Surface Distance from X
H(1)
to Y
H
Figure 7: After interpolation.
Mesh Y
H
High-Resolution
Deformed Mesh X
H(2)
Surface Distance from X
H(2)
to Y
H
Figure 8: After local deformation.
With respect to the bounding box diagonal of mesh
Y
L
(158.28mm), the mean error is 0.68% and root
mean square error is 1.42%, which shows local point-
to-surface registration can decrease the surface dis-
tance further. Fig. 7 shows the interpolated high-
resolution mesh X
H(1)
and Y
H
after applying an inter-
polation. With respect to the bounding box diagonal
of meshY
H
(158.48mm), the mean error is 1.65% and
root mean square error is 2.10%. The reason why the
surface distance slightly increases after interpolation
is: only 0.80% of vertices in mesh X
H(1)
have cor-
respondences obtained by non-rigid registration, oth-
ers obtain correspondences by interpolation. Fig. 8
shows the deformed high-resolution mesh X
H(2)
and
Y
H
after applying a local deformation discussed in
Sec. 2.3. With respect to the bounding box diagonal
of meshY
H
(158.48mm), the mean error is 0.28% and
root mean square error is 1.26%, which once again
demonstrates that local point-to-surface registration is
helpful for decreasing the surface distance.
The critical parameter in our algorithm is the num-
ber of vertices N used in the low-resolution meshes,
which affects the computational complexity and ac-
curacy. Due to the different length of femur shaft
within different meshes, we choose a mesh as a ref-
erence such that we could compare any other mesh
with this reference, following the procedure showed
in Fig. 3-8. By tuning the number N
ref
, we can
make a trade off between accuracy and efficiency
(in order to maintain the same points density, we set
N
other
= N
ref
×height
other
/height
ref
).
Moreover, in the application of atlas construction,
we can choose N
ref
by comparing the reconstructed
mesh from atlas with the original mesh, such that we
can also ensure the generality and accuracy of the
atlas. We conduct a series of leave-one-out experi-
ments. We first select a reference mesh(which has
all correspondences in any other meshes in the data
set) and then change N
ref
. For each N
t
ref
, we com-
pute N
t
other
(other = 1,··· , K, other 6= ref) for other
meshes and apply the two-level non-rigid registration.
After that, with K aligned meshes we apply K leave-
one-out experiments: for any v
i
(i = 1,·· · ,K), we use
other K − 1 to construct an atlas using PCA (Sec. 3).
Let U
S
i
denote the first S columns of the principal
component matrix U
i
, which consists of 95% energy.
Then v
i
(i = 1, · ·· , K) can be reconstructed by this at-
las:
e
v
i
= c+ U
S
i
U
S
i
T
(v
i
− c) (12)
We compare the surface distance between each pair of
mesh V
i
and
e
V
i
and obtain the average mean error and
(mm)
Figure 9: Reconstruction error d
m
and
d
RMS
in terms of N
ref
.
(minutes)
Figure 10: Registration processing time
T in terms of N
ref
.
Number of Principal Components
0.00%
10.00%
20.00%
30.00%
40.00%
50.00%
60.00%
70.00%
80.00%
90.00%
100.00%
1 4 7 10 13 16 19 22 25 28 31 34 37 40 43 46 49 52 55 58 61 64 67 70 73 76 79 82 85
Femoral head atlas Distal femur atlas Combined femur atlas
Energy
Figure 11: Atlases of distal femur(pink),
femoral head(blue) and entire fe-
mur(green).
root mean square error for each N
t
ref
:
d
t
m
=
1
K
d
m
(V
i
,
e
V
i
),
d
t
RMS
=
1
K
d
RMS
(V
i
,
e
V
i
) (13)
By changing N
t
ref
we can compute different
d
t
m
and
d
t
m
, also processing time T
t
of two-level registration.
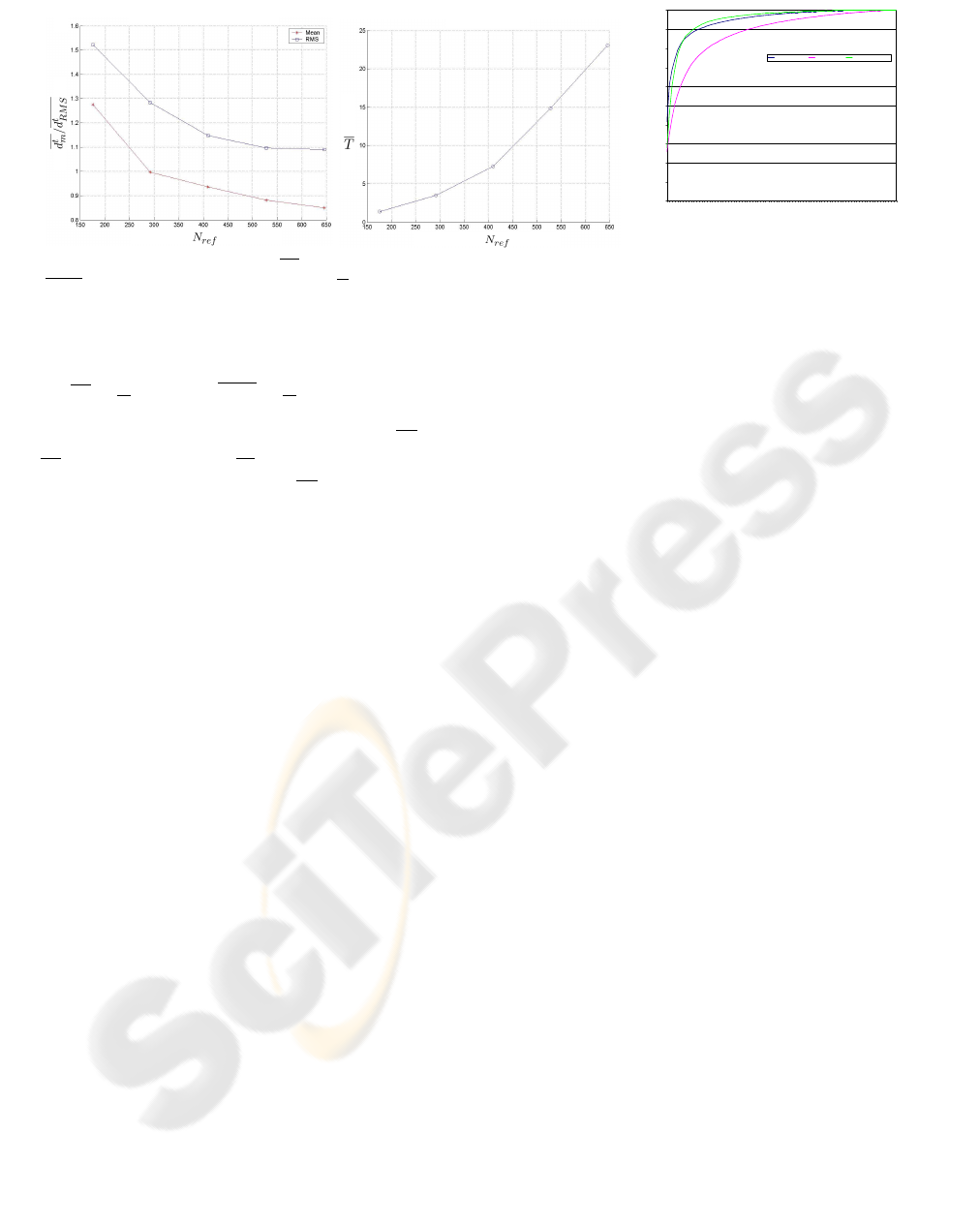
Fig. 9 shows when N
t
ref
≥ 290,
d
t
m
will be less than
1mm, which is a practical number in clinical applica-
tion. Fig. 10 shows when N
t
ref
≥ 330, average pro-
cessing time of registration of two meshes will ex-
ceed 5 mins (2.4GHz Pentium PC with 1G RAM).
Compared with original Chui and Rangranjan’s algo-
rithm, ours only need 5 mins for registering any size
of meshes (interpolation costs less than 1sec when the
number of vertices is less than 200,000), however,
their method costs 5 mins for 350 vertices, 10 mins
for 460 vertices, 20 mins for 610 vertices, etc. Our al-
gorithm significantly improve the efficiency without
losing accuracy.
Finally we select N
t
ref
= 290 and construct atlases
for distal femur, femoral head, and entire femur, re-
spectively. Fig. 11 shows the energy in terms of prin-
cipal components in each atlas.
5 CONCLUSION
In this paper we have developed a two-level algorithm
to tackle the registration problem due to the geo-
metrical and computational complexity. Experiments
demonstrate our algorithm significantly improve the
efficiency without decreasing accuracy, by comparing
with the original Chui and Rangranjan’s algorithm.
Some interesting issues such as gender effect for the
atlases, interpolation with other kernel functions, etc
will be addressed in the future work.
REFERENCES
Aspert, N., Santa-Cruz, D., and Ebrahimi, T. (2002). Mesh:
measuring errors between surfaces using the hausdorff
distance. In Proc. ICME’02, volume 1, pages 705–
708.
Besl, P. and McKay, N. (1992). A method for registration of
3-d shapes. In IEEE Trans. on PAMI’92, volume 14,
pages 239–256.
Carr, J. C., Beatson, R. K., Cherrie, J. B., Mitchell, T. J.,
Fright, W. R., Mccallum, B. C., and Evans, T. R.
(2001). Reconstruction and representation of 3d
objects with radial basis functions. In Proc. SIG-
GRAPH’01, pages 67–76.
Carr, J. C., Fright, W. R., and Beatson, R. K. (1997). Sur-
face interpolation with radial basis functions for med-
ical imaging. In IEEE Trans. on Medical Imaging,
volume 16, pages 96–107.
Chui, H. and Rangarajan, A. (2003). A new point match-
ing algorithm for non-rigid registration. In Computer
Vision and Image Understanding, volume 89, pages
114–141.
Chui, H., Rangarajan, A., Zhang, J., and Leonard, C. M.
(2004). Unsupervised learning of an atlas from un-
labeled point-sets. In IEEE Trans. on PAMI’04, vol-
ume 2, pages 160–172.
Cootes, T. and Taylor, C. (2001). Statistical models of ap-
pearance for medical image analysis and computer vi-
sion. In Proc. SPIE Image Processing, volume 4322,
pages 238–248.
Cootes, T., Taylor, C., Cooper, D., and Graham, J. (1995).
Active shape models: their training and application.
In Computer Vision and Image Understanding, vol-
ume 61, pages 38–59.
Desbrun, M., Meyer, M., Schroder, P., and Barr, A. (1999).
Implicit fairing of irregular meshes using diffusion
and curvature flow. In Proc. SIGGRAPH’99, pages
317–324.
Ellingsen, L. M. and Prince, J. L. (2006). Deformable regis-
tration of ct pelvis images using mjolnir. InProc. SPIE
Medical Imaging Conference, volume 6144, pages
329–337.

Farin, G. (1993). Curves and surfaces for cagd. In Academic
Press. New York.
Fleute, M., Lavall
´
ee, S., and Desbat, L. (2002). Integrated
approach for matching statistical shape models with
intra-operative 2d and 3d data. In Proc. MICCAI’02,
volume 2, pages 364–372.
Garland, M. and Heckbert, P. (1997). Surface simplification
using quadric error metrics. In Proc. SIGGRAPH’97,
pages 209–216.
Glaunes, J., Trouv
´
e, A., and Younes, L. (2004). Diffeo-
morphic matching of distributions: a new approach
for unlabelled point-sets and sub-manifolds matching.
In Proc. CVPR’04, volume 2, pages 712–718.
Goryn, D. and Hein, S. (1995). On the estimation of rigid
body rotation from noisy data. In IEEE Trans. on
PAMI’95, volume 17, pages 1219–1220.
Hill, D., Batchelor, P., Holden, M., and Hawkes, D. (2001).
Medical image registration. In Physics in Medicine
and Biology, volume 46, pages 1–45.
Jaume, S., Macq, B., and Warfield, S. K. (2002). Labeling
the brain surface using a deformable multiresolution
mesh. In Proc. MICCAI’02, pages 451–458.
Kim, J. and Fessler, J. A. (2004). Intensity-based image reg-
istration using robust correlation coefficients. In IEEE
Trans. on PAMI’04, volume 23, pages 1430–1444.
Maurer, C. R., Fitzpatrick, J. M., Wang, M. Y., Galloway,
R. L., Maciunas, R. J., and Allen, G. G. (1997). Regis-
tration of head volume images using implatable fidu-
cial markers. In IEEE Trans. on PAMI’97, volume 16,
pages 447–462.
Papademetris, X., Jackowski, A., Schultz, R., Staib, L., and
Duncan, J. (2003). Non-rigid brain registration using
extended robust point matching for composite multi-
subject fmri analysis. In Proc. MICCAI’03, volume
2879, pages 788–795.
Park, J., Mataxas, D., Young, A., and Axel, L. (1996). De-
formable models with parameter functions for cardiac
motion analysis from tagged mri data. In IEEE Trans.
on Medical Imaging, volume 15, pages 278–289.
Pighin, F., Hecker, J., Lischnski, D., Szeliski, R., and
Salesin, D. (1998). Synthesizing realistic facial ex-
pressions from photographs. In Proc. SIGGRAPH’98,
pages 75–84.
Rohlfing, T., Russakoff, D., and Maurer, C. (2004).
Performance-based classifier combination in atlas-
based image segmentation using expectation-
maximization parameter estimation. In IEEE Trans.
on Medical Imaging, volume 23, pages 983–994.
Rueckert, D., Frangi, A., and Schnabel, J. (2003). Auto-
matic construction of 3-d statistical deformation mod-
els of the brain using nonrigid registration. In IEEE
Trans. on Medical Imaging, volume 22, pages 1014–
1025.
Shen, D. Davatzikos, C. (2002). Hammer: hierarchical at-
tribute matching mechanism for elastic registration. In
IEEE Trans. on Medical Imaging, volume 21, pages
1421–1439.
Szeliski, R. and Lavallee, S. (1996). Matching 3-d anatomi-
cal surfaces with non-rigid deformations using octree-
splines. In IJCV’96, volume 18, pages 171–186.
Wells, W. M., Viola, P., Atsumi, H., Nakajima, S., and Kiki-
nis, R. (1996). Multi-modal volume registration by
maximization of mutual information. In Medical Im-
age Analysis, volume 1, pages 35–51.
Woods, R. P., Mazziotta, J. C., and Cherry, S. R.
(1994). Mri-pet registration with automated algo-
rithm. In Journal of Computer Assisted Tomography,
volume 17, pages 536–546.
Yu, H. (2005). Automatic rigid and deformable medical
image registration. In Ph.D. Dissertation, Mechan-
ical Engineering Department, Worcester Polytechnic
Institute, Worcester, MA.
