ACTIVE ACOUSTIC NOISE CONTROL IN DUCTS

Filipe Morais and J. M. Sá da Costa

Instituto Superior Técnico, Technical University of Lisbon,

Dept. of Mechanical Engineering / GCAR - IDMEC

Av. Rovisco Pais, 1049-001Lisboa, Portugal

Keywords: Active noise control, feedforward control, filtered-reference LMS, modified filtered-reference

LMS, filtered-u, frequency domain filtered-reference LMS.

Abstract: In this paper existing classical and advanced techniques of active acoustic noise cancellation (ANC) in ducts

are collected and compared. The laboratory plant used in experience showed a linear behaviour and so the

advanced techniques were not used. Due to delay on the plant, the feedback classical techniques could not

be applied. The best results were obtained with the modified filtered-reference LMS (MFX-LMS) and

filtered-u techniques. A very important conclusion is that the quadratic normalisation is needed to maintain

the algorithms always stable. In this paper 18dB of attenuation of white noise and 35 dB of attenuation of

tonal noise were achieved. Thus, ANC can be applied in a real situation resulting in important noise

attenuations.

1 INTRODUCTION

Acoustic noise is since a long time considered as

pollution due to the diverse problems that it causes in

the human being, both physical, as for instance

deafness, and psychological. As a consequence,

competent authorities tend to enforce restrictive laws

on the allowed sound levels, and it is thus necessary

to look for solutions leading to its fulfilment. On the

other hand, acoustic noise is a cause of lack of

productivity. By these reasons, there is a pressing

need to solve the problem of acoustic noise.

In practice passive solutions for the cancellation

of acoustic noise can be found by simple use of

absorption and reflection phenomena. However, they

are of little use for frequencies below 1000Hz. In

these other cases acoustic noise cancellation (ANC)

based on the principle of interference, should be

used.

The idea of the ANC is 70 years old. One of the

first references remounts to 1934 when P. Lueg

patented some ideas on the subject (Elliot, 2001 and

Tokhi et al., 1992). Lueg addressed ANC in ducts

and in the three-dimensional space. For ducts, Lueg

considered a microphone that captured the acoustic

noise. The signal from the microphone would pass

through the controller and feed the loudspeaker as

shown in fig. 1. The controller would result in

acoustic waves emitted by the loudspeaker with the

same amplitude of the acoustic noise but in phase

opposition, so that the two waves would cancel each

other (interference principle). This configuration is

nowadays the most used in ANC applications in

ducts.

Controller

Loudspeaker

Figure 1: Single-channel feedforward control in a duct.

The purpose of using ANC in ducts is to cancel

the plane waves that are propagated in the duct due to

fans, like in an air conditioner installation. The ANC

mostly used techniques were developed to control

stochastic disturbances, because acoustic noise can

be considered as a disturbance with significant

spectral richness. Furthermore, techniques for

stochastic disturbances can be applied in

deterministic disturbances but the inverse is not

feasible. ANC techniques for stochastic disturbances

can be divided into two main groups: classical or

advanced. Those of the first group are based on plant

linearity, and consequent validity of the superposition

principle (Ogata, 1997).

Linear techniques can also be applied to

nonlinear systems, but they usually have bad

performance. Advanced techniques were developed

214

Morais F. and Sá da Costa J. (2004).

ACTIVE ACOUSTIC NOISE CONTROL IN DUCTS.

In Proceedings of the First International Conference on Informatics in Control, Automation and Robotics, pages 214-221

DOI: 10.5220/0001141102140221

 SciTePress

to nonlinear plants, although they can be applied to

linear systems with good performance. However,

they are also more complex and demand more

computational power than the classic ones. For that

reason advanced techniques are not preferred instead

of classic ones when linear plants are concerned.

Both classic and advanced techniques can be

divided according to the type of control: feedforward

or feedback. In the feedforward control information

is collected in advance about the disturbance and so

the controller can act in anticipation; while the

feedback control has no information in advance

about the disturbance and thus the controller reacts to

the disturbance. The feedback control is useful when

the acoustic noise is created by several different

sources, or by distributed sources, or when it is not

practical or possible to get information in advance

concerning all the noise sources. However, this is not

the case of ducts because the noise source is well

defined and acoustic waves are plane and travel in a

single direction.

In this paper existing feedforward techniques for

ANC in ducts are compared to assess the

performance of these techniques in a real situation.

In ducts it is possible to have only plane acoustic

waves, rending ANC much simpler since some

acoustic effects are not to be found, as for instance

the diffraction of acoustic waves. In this work the

range of frequencies to be deal with ANC is limited

to the interval [200 Hz; 1000 Hz] since ANC is not

effective for frequencies above 1000 Hz and the

actual set-up used does not allow to go below 200

Hz.

Digital Controller

s(n)

x(n)

G (z)

W(z)

u(n)

e(n)

d(n)

f(n)

Figure 2: Block diagram of feedforward control.

2 FEEDFORWARD CONTROL

The general block diagram of the feedforward

control of acoustic plane waves in a duct is found in

fig. 2. The signal x(n) is the reference signal

measured by the reference microphone, d(n) is the

primary noise signal passed through the primary

path, e(n) is the error signal given by the error

microphone, and G

(z) is the secondary path between

the secondary source and the error sensor. It is

assumed that the controller is digitally implemented

and made up by a direct filter W(z) and a feedback

filter Ĝ

(z). The feedback filter consists of an

estimation of the natural feedback path of the system

(z), i.e., reproduces the influence of the secondary

source to the reference sensor. When Ĝ

(z) = G

(z),

the two feedback loops cancel each other and the

signal that feeds the controller is equal to x(n). In this

situation the control is purely feedforward. In the

situation in which the estimate of G

(z) is not perfect,

a residue appears from the cancellation of two loops.

If Ĝ

(z) is a good estimate of the path G

(z), the

residue has a small value and will not affect the

performance of the control. If the estimate of G

(z) is

poor, this can influence the performance of the

control, that may become unstable.

In this situation it

might be necessary to use feedback control

techniques to improve the performance or to stabilize

the control (Elliot, 2001).

Assuming that the two feedback loops cancel

each other completely and that the plants are linear

and time invariant (LTI), so that the filter W(z) and

the discrete transfer function G

(z) can be

interchanged, the error signal e(n) comes

, (1)

() () () () ()

en dn n dn n=+ =+wr r w

where w is a vector with the coefficients of the filter

and r(n) the vector with the last samples of the

iltered reference signal r(n) given by: f

, (2)

∑

−

−=

)()(

inxgnr

where the g

are the I coefficients of the discrete

transfer function G

(z), assuming that has a FIR

structure.

2.1 Filtered-reference LMS (FX-LMS)

Algorithm

This algorithm is based on the steepest descent

algorithm, which is mostly used for adapting FIR

controllers (Elliot, 2001). The expression for

adapting the coefficients of controller W(z) of fig. 2 is

iven by: g

(1) ()

∂

+= −

∂

(3)

where J is a quadratic index of performance, equal to

the error signal squared e

(n), and ∂·/∂w is the

radient: g

[

2()()

]

nen

∂

(4)

For this algorithm a simpler version than the one

given by eq. (4) is used, since the expected value of

the product is not reckoned, but only the current

alue of the gradient. Thus, v

ACTIVE ACOUSTIC NOISE CONTROL IN DUCTS

215

() ()

2() 2()()

en en

en en n

∂∂

(5)

The expression for adapting the coefficients of the

controller is given by:

(1) () ()(nnne)n

+= −wwr

(6)

where

= 2

is the convergence coefficient and

is the estimate of the filtered reference signal,

obtained with the estimate of the G

()rn

(z) model. The

algorithm is called filtered-reference LMS because

the filtered reference signal is used to adapt the

coefficients. The block diagram of the algorithm is in

iven in fig. 3. g

u(n)

xG (z)

e(n)

r(n)

G (z)

w(n)

x(n)

d(n)

Figure 3: Block diagram for FX-LMS algorithm.

If the reference signal x(n) were used instead of the

filtered reference r(n) to adapt the coefficients, the

adaptation would be wrong because there is a time

shift between the signal x(n) and the error signal

e(n). This is a consequence of the existence of a time

delay in G

(z). This algorithm is rather simple to

implement and is numerically stable, being therefore

frequently used (Elliot, 2001).

2.2 Normalized filtered-reference LMS

algorithm (NFX-LMS)

In the previous approach the adaptation of the

coefficients of the controller W(z) is directly

proportional to the coefficient of convergence

and

the vector r(n). Sometimes, when r(n) has large

values, the FX-LMS algorithm has a problem of

amplification of the gradient noise (Haykin, 2002).

The coefficients of the vector r(n) are normalized in

order to solve this problem. Haykin (2002) suggests

dividing the coefficients by the Euclidean norm of

vector r(n). The expression for adapting the

coefficients becomes:

(1) () ()()

()

nn ne

+= −

ww r

(7)

where

it is a very small and positive number. This

term allows preventing numerical difficulties when

r(n) is small because the Euclidean norm takes small

values. Elliot (2001) suggests another solution where

the coefficients of vector r(n) are divided by the

inner product of vector r(n), r

r. Whatever the

option is, algorithm NFX-LMS presents the

following advantages over algorithm FX-LMS: faster

convergence rate and sometimes better performance

of the obtained controller; the algorithm is more

stable when there is a change of the spectral richness

of the reference signal x(n). This normalization of the

filtered reference signal can be applied to other

algorithms.

2.3 Leaky LMS algorithm

For this algorithm another index of quadratic

performance is used:

(8)

()JEen

⎡⎤

⎣⎦

nen

where

is a positive constant. This performance

index weighs both the average of the error signal e(n)

squared as well as the sum of the squares of the

coefficients of the controller. This performance index

prevents the coefficients of the controller from taking

large values that can render the algorithm unstable

when both the amplitude of the reference signal, x(n),

and its spectral components undergo variations

Elliot, 2001). The adaptation becomes: (

( 1) (1 ) () ()()nn

βα

=− −wwr

. (9)

Eq. (9) is different for the FX-LMS algorithm

because of term (1-

αβ

), which is called leakage

factor. This term must take values between 0 and 1

and is normally 1. When it takes another value the

error signal e(n) is not zero and the value of

coefficients decreases with each iteration. Adding the

term (1-

αβ

) to the coefficients adapting equation

allows the increasing of the robustness of the

algorithm. On the other hand the term (1-

αβ

)

reduces the noise attenuation that can be reached.

Thus, the choice of the value for beta must take into

account the robustness of the algorithm and the

reduction of the attenuation. In most applications, the

use of a small value of beta allows a sufficient

increase of robustness and the attenuation of the

acoustic noise suffers little (Elliot, 2001). The

modification introduced in the FX-LMS algorithm

can also be implemented in the other algorithms.

2.4 Modified filtered-reference LMS

algorithm (MFX-LMS)

The FX-LMS algorithm requires a rather slow

adaptation compared with the plant dynamics so that

the error may be given by eq. (1). This is because

adapting the coefficients is somehow a nonlinearity

which influence depends on the speed of adaptation

(Elliot, 2001). Thus, to make this influence negligible

the adaptation of the coefficients must be very slow

when compared with the dynamics of the plant. This

ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

216

should be regarded as a disadvantage. The

arrangement shown in fig. 4 allows overcoming this

limitation. In this scheme, the estimated filtered

reference signal,

, in the adaptation path of the

controller is common to the adaptive filter and to the

adaptation, and has no time shift in relation to the

modified error, e’

()rn

(n).

w(n)

r(n)

G (z)

u(n)

G (z)

G (z)w(n)

e(n)

x(n)

Controller

Adaptive

filter

e' (n)

d(n)

Figure 4: Block diagram for MFX-LMS algorithm.

or this algorithm the adaptation is given by:

(1) () ()(

nnne

)

+= −wwr

(10)

here e

(n) is the modified error, given by:

. (11)

() () () ( )

mij

en dn wngxni j

−−

=+ −−

∑∑

The modified error can be seen as a prediction of the

error for the case where the coefficients of the

controller do not change at each instant. The MFX-

LMS algorithm usually presents convergence rates

larger than those of the FX-LMS algorithm (Elliot,

2001). This is because the adaptive filter and the

plant estimate were interchanged and thus the delay

between the exit of the controller and the error signal

was eliminated. For this reason it is no longer

necessary to consider the delay in the restriction of

the convergence coefficient, and larger steps may be

used with the MFX-LMS algorithm. However the

MFX-LMS algorithm has the disadvantage of

requiring more computational means.

2.5 Frequency domain filtered-reference

LMS algorithm (FX-LMS Freq)

For the FX-LMS algorithm the estimate of the

gradient of eq. (5) was used to adapt the coefficients

of the controller. The estimate of the gradient will be

assumed to be given by the average of the product

r(n)e(n) during N instants. Thus, the adaptation is

given by:

( ) ( ) () ()

nN n lel

+−

+= +

∑

ww r

(12)

In this case, the adaptation is carried only after N

time samples. The use of the average of the product

r(n)e(n) during N instants can be considered as a

more precise estimate of the gradient than the use of

the product r(n)e(n) for each time sample. In practice

adaptation with eq. (12) has a convergence rate very

similar to the FX-LMS algorithm, since though the

adaptation for eq. (12) has a lower frequency, the

value of the update of the coefficients is larger

(Elliot, 2001). The summation in eq. (12) can be

thought of as an estimate of the crossed correlation

between the filtered reference r(n) and the error

signal e(n). The estimate must be reckoned from i =

0 up to I-1, where I is the number of coefficients of

the adaptive filter. For long filters the reckoning of

the estimate can be inefficient in the time domain,

requiring a large computational effort. For large

values of I it is more efficient to calculate the cross

correlation in the frequency domain. If discrete

Fourier transform (DFT) with 2N points for the

signals e(n) and r(n) are considered, an estimate of

the cross spectral density can be calculated through:

(13)

() () ()

Sk RkEk=

where k is the index of discrete frequency and *

means the complex conjugate. Some care must be

taken to prevent the effect of circular convolution.

Thus, before reckoning the DFT of the error signal,

e(n), with 2N points, in the block with 2N points of

the error signal the first N points must be zero. This

will eliminate the non-causal part of the cross

correlation (Elliot, 2001). The expression that gives

he adaptation of the coefficients is: t

{

}

(1) () ()()

m m IFFT R k E k

+= −ww

(14)

where { }

means the causal part of the cross

correlation, IFFT is the inverse fast Fourier transform

and

is the convergence coefficient. R

(k) is directly

obtained multiplying the DFT of the reference signal

X(k) by the frequency response estimate of the

system. This algorithm is called fast LMS. Fig. 5

shows the block diagram of this algorithm.

The advantage of the fast LMS algorithm over

the FX-LMS is that it requires few computations.

Assuming that the implementation of the DFT

requires

2log2

multiplications, the FX-LMS

algorithm requires 2N

calculations per iteration

hile fast LMS needsw

(16 6 log 2 )

ACTIVE ACOUSTIC NOISE CONTROL IN DUCTS

217

W(z) G (z)

e(n)

d(n)

E(k)

R (k)

R(k)

X(k)

x(n)

G(k)

Conjugate

Get

first N

points

IFFT

FFT

Insert Zero

Block

FFT

Concatenate

two blocs

Figure 5: Block diagram for FX-LMS Freq algorithm.

2.6 Filtered-u Algorithm

Up to now Finite Impulse Response (FIR) filters

have been considered to build the controllers.

However, Infinite Impulse Response (IIR) filters can

be used as well. In this case, the equivalent to fig.2

for IIR controllers is shown in fig. 6.

t(n)

H(z)

1-A(z)

B(z)

u(n)

G (z)

e(n)

d(n)

s(n)

x(n)

Figure 6: Block diagram for IIR controller.

Compared with the block diagram of fig. 2 for the

FIR controllers, we can notice that this does not

possess a specific feedback to cancel the natural

feedback path of the system. In this case the

recursive characteristic of IIR controllers is assumed

to deal with the feedback path problem. However,

practice shows that if this estimation is included

numerical stability is guaranteed and the

performance is improved.

The filtered-u algorithm uses IIR filter as

controller. It is based on the recursive LMS (RLMS)

algorithm (see Elliot (2001) or Haykin (2002)). Fig.

7 shows the block diagram of the filtered-u

algorithm. The adaptation of the coefficients a

and b

is given by:

(1) () ()(nnen)n

+= −aa t

(15)

(1) () ()(nnen

+= −bb r

(16)

where

are the convergence coefficients, t(n)

and r(n) are respectively the filtered output and the

filtered reference, and

and

are the forgetting

factors.

H(z)

u(n)

G (z)

a (n)

b (n)

G'(z)

e(n)

d(n)

t(n)

r(n)

s(n)

x(n)

Figure 7: Block diagram for filtered-u algorithm.

The use of different convergence coefficients may be

shown in practice to allow for higher convergence

rates and the use of leakage factors slightly under 1

allows for a greater robustness of the algorithm

(Elliot, 2001). The plants modified response, G'(z), is

equal to G

(z). For that purpose, the coefficients of

the controller H(z) are assumed to be very slowly

adapted in comparison to the dynamics of the system

of the system G

(z). The same had already been

assumed for the adaptation of the FIR controller, but

for the adaptation of the IIR controller this is even

more necessary since the controller is recursive. One

of the interesting characteristics of the filtered-u

algorithm is that it presents a self-stabilising

behaviour that is also to be found in RLMS

algorithms (Elliot, 2001). During the adaptation of

the controller, if a pole leaves the unit-radius circle,

the natural evolution of filtered-u algorithm brings it

back inside. Although some researchers have

addressed this behaviour, still it was not possible to

discover the mechanism that results in this self-

stabilising property (Elliot, 2001). The self-

stabilising behaviour is found in many practical

applications, and that is why the filtered-u algorithm

is the most used in active cancellation of noise

applications (Elliot, 2001).

3 EXPERIMENTAL SET-UP

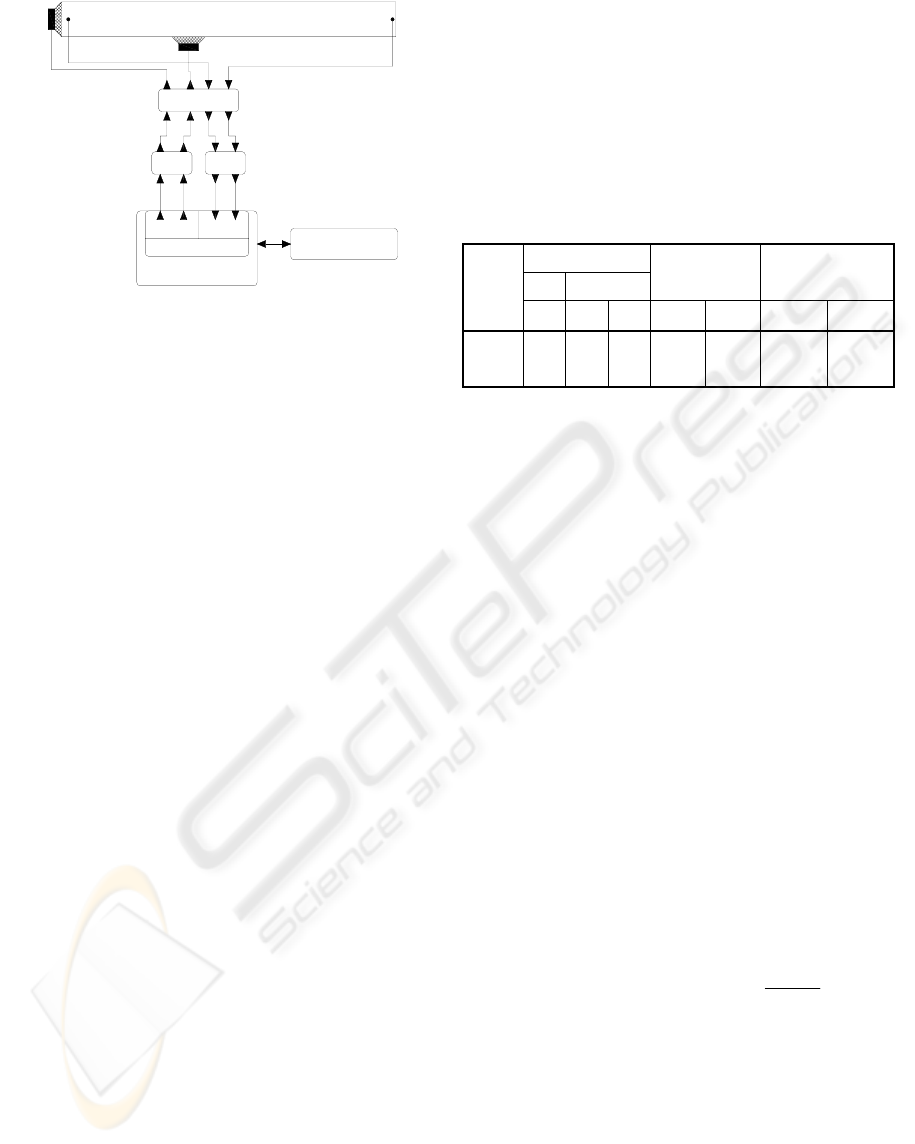
The experimental set-up used is shown in Fig. 8. A

PVC pipe with 0.125 m of diameter and 3 m of

length was used for simulating the cylindrical duct.

Given the diameter of the duct, the cut-on frequency,

which is the frequency above which waves may no

longer be considered plane, is 1360 Hz. To simulate

the acoustic noise to cancel a conventional

loudspeaker was placed in one of the ends of the

duct. At 1.25 m away from this end two loudspeakers

are placed to act as source of acoustics waves for

noise cancellation. For the detection of acoustic noise

a microphone, placed 0.08 m away from the primary

noise source, is used. The error microphone is placed

t the opposite end of the primary noise source. a

ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

218

Windows - Matlab

xPC Target

NI-DAQ 6024E

A/D

20dB0dB

Amp.

212

D/A

Fc = 1050Hz

Low-Pass Filter

Pre-Amp

Slave Computer

Master Computer

Reference

Mic.

Source

Cancellation

Error

Mic.

Noise

Source

Figure 8: Block diagram of experimental setup.

Besides the duct, loudspeakers and microphones,

the experimental set-up consists of: four low-pass

filters that allow filtering the signals to remove the

effects of aliasing and zero-order-hold; an amplifier

that allows amplifying the signals that feed the

loudspeakers; pre-amplifiers for the microphones;

and two computers, one the slave act has a digital

controller and the other the master is used for data

analysis. The slave computer is a Pentium III

733MHz with 512MB of RAM memory, running on

xPC Target, having a data acquisition board NI-DAQ

6024E. Algorithms have been implemented as S-

Functions in the Matlab/Simulink environment.

Due to hardware restrictions on the cancellation

source this set-up cannot generate relevant signals

for frequencies below 200 Hz. Therefore, the

frequency range where acoustic noise cancellation is

intended is restricted to the frequency bandwidth of

[200 Hz - 1000 Hz].

4 IDENTIFICATION

The models used are discrete in time since the

implementation of the controller is made using a

digital computer. Therefore, the simulations will be

based on discrete models. This requires the models to

include the devices associated with the discretisation

and restoration of the signals, A/D and D/A

conversions, anti-aliasing and reconstruction filters,

and the dynamic of the microphones, loudspeakers

and amplifiers associated to the experimental set-up.

Assuming that the behaviour of these devices is

linear, then each one can be represented by a discrete

ransference function. The necessary models are: t

(z) - secondary acoustic path: includes computer -

secondary source - error microphone - computer;

(z) - acoustic feedback path: includes computer-

secondary source - reference microphone-computer.

Models have been obtained for the sampling

frequency of 2500 Hz (sampling time 0.4ms) because

that allows the Nyquist frequency of 1250Hz, to be

slightly larger than the superior limit of the frequency

range to cancel, 1000 Hz. FIR and ARX models have

been obtained. Variance account for (VAF) criterion

and root mean square (RMS) have been used for

models validation. Table 1 shows the results obtained

in these identifications.

Table 1: Order, VAF and RMS of the obtained models.

Order

FIR ARX

VAF (%) RMS (V)

Model

I n

FIR ARX FIR ARX

(z) 500 150 150 99.96 99.94 0.0193 0.0195

(z) 450 150 150 99.60 99.57 0.0363 0.0373

As shown above the obtained models have

excellent performances. This shows the plant to have

a linear behaviour being unnecessary to appeal to

ANC advanced techniques.

5 EXPERIMENTAL RESULTS

The previously mentioned algorithms have been

implemented and test for different noise conditions in

the duct. However, before presenting the results it

must be point out that the use of the normalisation of

the filtered reference signal was very important.

Experiences have shown that the normalised LMS

technique has a significant influence in the behaviour

of the algorithms. In fig. 9 the evolution of the

attenuation is shown for the FX-LMS algorithm

when the variance of white noise changed, for the

following cases: the filtered reference signal was not

normalized, was normalised using the Euclidean

norm, and was normalised using quadratic

normalization. The behaviour of the other algorithms

is similar. In the figures that follow, attenuation is

iven by the expression g

() 10log

Attenuation dB

⎛

⎡⎤

⎣⎦

⎜

⎜⎟

⎡⎤

⎣⎦

⎝⎠

⎞

⎟

(18)

where e is the error signal, d the disturbance and E[ ]

is the expected value operator. In this case the

expected value is given by the average of last 50

samples.

ACTIVE ACOUSTIC NOISE CONTROL IN DUCTS

219

0 50 100 150 200

-25

-20

-15

-10

-5

Tim e (s)

Attenuation (dB)

Without normal.

Quadratic norm

Euclidean norm

Figure 9: Evolution of attenuation for the FX-LMS

algorithm.

As can be observed the normalization of the

filtered reference signal allows obtaining higher

attenuations. The quadratic norm is the only one that

ensures the stability of the algorithms when the

spectral power changes. If this were not the case

different adaptation steps would have to be used to

keep the algorithms stable.

For the comparison of the algorithms two types

of disturbances had been considered: white noise and

pure tones. The frequency range of the white noise is

[200 Hz; 1000 Hz], for the reason explained before.

Tones under 200 Hz have also not been used.

Parameters in the algorithms were chosen based

upon other experiences that had shown the influence

of parameters in algorithms performance. These

alues are: v

• FX-LMS: w = 200,

= 0.10;

• MFX-LMS: w = 400,

= 0.1;

• Filtered-u: n

= 150, n

= 100,

= 0.01,

= 0.025;

• FX-LMS Freq: w = 256,

= 0.16.

Common to all the algorithms are the leakage factor,

equal to one, and the normalization method, which

was the quadratic norm.

Results are shown in fig. 10-13 for different

types of noise to be cancelled, and Table 2 that

indicates the computational burden for the white

oise case. n

• White noise

0 50 100 150 200 250 300

-20

-18

-16

-14

-12

-10

-8

-6

-4

-2

Time (s)

Attenuation (dB)

FX-LMS

Mod FX-LMS

Filtered-U

FX-LMS Freq

Figure 10: Evolution of attenuation for white noise.

Table 2: Execution time of each iteration for the white

noise case.

Algorithm

FX-

LMS

MFX-

LMS

Filtered

-u

FX-LMS

Freq

Average time (ms) 0.044 0.067 0.081 0.027

Maximum time (ms) 0.047 0.081 0.089 0.065

• Pure tones: 320 Hz + 640 Hz + 960Hz.

All pure tones have the same spectral power. The

adaptation steps of FX-LMS and FX-LMS Freq

algorithms had to be reduced so that they would

remain stable. Steps used were

= 0,03 for the FX-

LMS and

= 0,06 for the FX-LMS Freq.

0 5 10 15 20 25 30

-40

-35

-30

-25

-20

-15

-10

-5

Time (s)

Attenuation (dB)

FX-LMS

MFX-LMS

Filtered-u

FX-LMS Freq

Figure 21: Evolution of attenuation for pure tones.

The two previous figures show that the MFX-

LMS algorithm obtains a larger attenuation sooner

but the filtered-u algorithm obtains slightly larger

attenuations. These two algorithms get the best

performances of the four. Worst of them all is the

FX-LMS Freq, even though it presents the most

reduced average time for executing each iteration.

This shows how efficient algorithms are in the

frequency domain. However, the execution time of

each iteration is not important in this case since all

times are clearly under the sampling time of 0.4ms.

ICINCO 2004 - SIGNAL PROCESSING, SYSTEMS MODELING AND CONTROL

220

This is because of the high computational power of

the slave computer.

Robustness to the variations of the model of the

eedback path f

An important question is the robustness to the

degradation of the model of the acoustic feedback

path G

(z), since when this model becomes poor the

simplification assumed on point 2.1 (that the model

cancels the feedback path exactly) is no longer

verified. If the residual of the cancellation is large,

the performance of the algorithms based on scheme

of Fig. 2 will degrade and may even be unstable.

The filtered-u algorithm can deal with the

feedback path problem. However, using the model of

Fig. 6, this algorithm has revealed to be unstable on

start. To solve this problem the adaptation steps had

to be reduced, and thus, have a slower evolution of

attenuation. Using the scheme of fig. 2 with filtered-

u algorithm has proved to be more robust and have a

faster and more regular evolution of attenuation.

That is why two experiences have been carried

out in which the performance of estimated model of

(z) was reduced. In the two following figures the

results for the MFX-LMS algorithms and filtered-u

algorithms are shown. Only those are shown because

they are the ones with better performances, as was

seen above. Parameters used in the algorithms are

those given above.

Figures 12 and 13 show that the filtered-u

algorithm is more robust to variations of the

estimated model of G

(z) model even though it leads

to more irregular evolutions. This shows that the

filtered-u algorithm is the one that should be applied

in practice since it has a performance identical to the

MFX-LMS but is more robust to modelling errors.

0 50 100 150 200 250 300

-20

-18

-16

-14

-12

-10

-8

-6

-4

-2

Time (s)

Attenuation (dB)

VAF = 99.6%

VAF = 99.0%

VAF = 95.0%

VAF = 90.0%

Figure 12: Evolution of attenuation for MFX-LMS

algorithm for different estimated models of G

(z).

0 50 100 150 200 250 300

-20

-18

-16

-14

-12

-10

-8

-6

-4

-2

Time (s)

Attenuation (dB)

VAF = 99.6%

VAF = 99.0%

VAF = 95.0%

VAF = 90.0%

Figure 13: Evolution of attenuation for filtered-u algorithm

for different estimated models of G

(z).

6 CONCLUSIONS

This paper evaluates the use of feedforward ANC to

cancel noise in ducts. The FX-LMS, NFX-LMS, Leaky

LMS, MFX-LMS, FX-LMS Freq and the Filtered-u

algorithms have been considered. The best

performance was achieved with the filtered-u

algorithm. Active cancellation of acoustic noise was

seen to be possible in practice since attenuations

obtained were about 18 dB for white noise and 35 dB

for pure tones. Moreover, algorithms were seen to be

robust when models degrade.

In what concerns the algorithms it was shown

that the normalization of the filtered reference signal

is of extreme importance allowing to ensure the

stability of the algorithms as well as better

attenuations. However this happens only for the

quadratic norm.

REFERENCES

Elliot, S. J., 2001. Signal Processing for Active

Control. Academic Press, London.

Haykin, Simon, 2002. Adaptive Filter Theory.

Prentice Hall, New Jersey, 4

edition.

Ogata, Katsuhiko, 1997. Modern Control

Engineering. Prentice Hall, New Jersey, 3

edition.

Oppenheim, Alan V., Schafer, Ronald W. and Buck,

John R., 1999. Discrete-time Signal Processing.

Prentice Hall, New Jersey, 2

edition.

Tokhi, M. and Leitch, R. R., 1992. Active Noise

Control. Oxford University Press, New York.

ACTIVE ACOUSTIC NOISE CONTROL IN DUCTS

221