Approximate Algorithms for Double Combinatorial Auctions for

Resource Allocation in Clouds: An Empirical Comparison

Diana Gudu

, Gabriel Zachmann

1,2

, Marcus Hardt

and Achim Streit

Karlsruhe Institute of Technology, Karlsruhe, Germany

Baden-Wuerttemberg Cooperative State University, Karlsruhe, Germany

Keywords:

Combinatorial Auction, Resource Allocation, Cloud Computing, Approximate Algorithm.

Abstract:

There is an increasing trend towards market-driven resource allocation in cloud computing, which can address

customer requirements for ﬂexibility, ﬁne-grained allocation, as well as improve provider revenues. We for-

mulate the cloud resource allocation as a double combinatorial auction. However, combinatorial auctions are

NP-hard problems. Determining the allocation optimally is thus intractable in most cases. Various heuristics

have been proposed, but their performance and quality of the obtained solutions are highly dependent on the

input. In this paper, we perform an extensive empirical comparison of several approximate allocation algo-

rithms for double combinatorial auctions. We discuss their performance, economic efﬁciency, and the reasons

behind the observed variations in approximation quality. Finally, we show that there is no clear winner: no

algorithm outperforms the others in all test scenarios. Furthermore, we introduce a novel artiﬁcial input gen-

erator for combinatorial auctions which uses parameterized random distributions for bundle sizes, resource

type selection inside a bundle, and the bid values and reserve prices. We showcase its ﬂexibility, required for

thorough benchmark design, through a wide range of test cases.

1 INTRODUCTION

The pay-per-use, on-demand models promoted by

cloud computing (Rappa, 2004) have enabled its ubiq-

uity in today’s technological landscape. From large

businesses moving their services to the cloud, to de-

velopers running small tests for their applications, the

requirements are becoming increasingly diverse. This

diversity is challenging for both cloud providers seek-

ing to improve their proﬁts, as well as customers try-

ing to ﬁnd a cost-effective option that aligns with their

requirements. The advent of open-source cloud tech-

nologies (CloudStack, 2017; Openstack, 2017), cou-

pled with a wide availability of low-cost server hard-

ware, has also led to an increase in cloud providers

entering the market to meet the ever-growing user de-

mands. This increases the burden on customers to

make an informed decision when choosing and com-

bining cloud resources from multiple providers.

Current trends (Buyya et al., 2008) point towards

market-driven resource allocation and pricing for a

ﬁne-grained, customizable experience for cloud cus-

tomers. Some commercial cloud providers have al-

ready adopted the concept of dynamic pricing in or-

der to maximize their resource utilization and increase

their revenue: Amazon is selling unused resources

on the so-called spot market (Amazon, 2017), where

price is regulated by the ﬂuctuating demand and sup-

ply. There is still, however, more research required

to move from existing market mechanisms which are

fast, simple, but inﬂexible (such as single-good, one-

sided auctions), towards more complex, but ﬂexible

and economically efﬁcient mechanisms.

The use of two-sided combinatorial auctions for

cloud resource provisioning is a research topic that

has been gaining interest (Nejad et al., 2015; Samimi

et al., 2014). The combinatorial aspect ensures ﬂex-

ibility in resource provisioning—clients can request

exactly the amount of resources they need without

being limited to a few predeﬁned bundles offered by

providers, such as the Amazon EC2 virtual machine

instance types (Amazon, 2017). The two-sided aspect

brings more fairness by considering both clients and

providers when making allocation decisions, and of-

ﬂoading the decision to a central entity (the auction-

eer) instead of each cloud provider.

The main reason why combinatorial auctions are

not yet widely used in practice is their computa-

tional complexity: combinatorial auctions are N P -

hard problems (De Vries and Vohra, 2003). Finding

Gudu, D., Zachmann, G., Hardt, M. and Streit, A.

Approximate Algorithms for Double Combinatorial Auctions for Resource Allocation in Clouds: An Empirical Comparison.

DOI: 10.5220/0006593900580069

In Proceedings of the 10th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2018) - Volume 1, pages 58-69

ISBN: 978-989-758-275-2

an optimal solution is intractable for large problems.

Fast, approximate algorithms exist, but they incur a

certain loss in efﬁciency that needs to be bounded.

Due to the assumed scale of cloud allocation as pre-

sented above, fast allocation needs to be prioritized

over optimal solutions. Nevertheless, any improve-

ment in solution quality can translate into large sav-

ings for clients and increases in provider revenue.

Although there is a plethora of approximate algo-

rithms for combinatorial auctions in the literature (Fu-

jishima et al., 1999; Nejad et al., 2015; Lehmann

et al., 2002; Holte, 2001; Zurel and Nisan, 2001;

Hoos and Boutilier, 2000; Chu and Beasley, 1998;

Khuri et al., 1994), to our knowledge there is no

comprehensive comparison using a consistent prob-

lem formulation and benchmarks.

With this paper, we aim to lay the groundwork for

a uniﬁed, consistent evaluation of heuristic algorithms

for combinatorial auctions. We create a portfolio of

algorithms based on existing work or well-known op-

timization methods, but adapted and improved for our

proposed problem formulation. We then introduce a

ﬂexible tool for generating artiﬁcial datasets for com-

binatorial auctions, which can be the basis for thor-

ough benchmarking of combinatorial auctions. We

perform an extensive empirical comparison of the al-

gorithms in the portfolio and discuss the differences

in performance and approximation quality.

2 PROBLEM FORMULATION

A multi-good, multi-unit two-sided combinatorial

auction is given by (Nisan et al., 2007b; Gudu et al.,

2016): a set U of n buyers or users (U = {1,..., n}), a

set P of m sellers or providers (P = {1, ... ,m}), each

offering different quantities of resources G of l types

(G = {1, ... ,l}), and an auctioneer that receives bids

and asks, and decides upon the allocation and pricing

of resources.

Each buyer i ∈ U submits a bid for a bun-

dle of resources to the auctioneer, expressed as

(hr

,. .., r

i,b

), where b

is the value the buyer is

willing to pay for the bundle, and r

is the integer

amount of requested resources of type k. Each seller

j ∈ P submits its ask to the auctioneer, expressed

as (hs

,. .., s

i,ha

,. .., a

i). That is, for each re-

source type k ∈ G, each seller offers a certain integer

quantity s

at a reserve price a

(the minimum price

for which it is willing to sell one item of the resource).

We assume that a buyer can receive the resources in a

single bundle from multiple sellers.

For example, a seller like Amazon EC2 might pro-

vide 3 types of virtual machines (t2.small, t2.medium

and t2.large) at the current on-demand prices (Ama-

zon, 2017) for the EU (London) region: 0.026$,

0.052$ and 0.106$ (per hour). If a seller provides 100

instances of each type, then its ask will be expressed

as (h100, 100,100i,h0.026, 0.052,0.104i). We can

also use our problem formulation to model ﬁner-

grained allocation: the resources being sold are com-

puting cores, memory, storage space, etc, and the cus-

tomer can request exactly the amount of resources it

needs instead of being constrained by prepackaged

VMs. For example, a customer can request a VM with

40 cores, 64 GB of memory and 1 TB disk storage,

and is willing to pay at most 10$. Then it submits the

following bid: (h40,64, 1000i,10). In this case, how-

ever, all the resources in a customer’s bundle would

have to be allocated by the same provider.

After collecting all bids and asks, the auctioneer

must ﬁnd the optimal allocation, which is deﬁned as

the allocation that maximizes the social welfare, i.e.

the sum of all trade participants’ utilities.

A buyer i’s utility for a bundle S that it bids on is

deﬁned as: u

(S) = v

(S) − p

, if i obtains bundle S,

and 0 otherwise. p

is the price the buyer pays at the

end of the trade, and v

is the buyer’s valuation, or the

real worth estimated by the buyer for the speciﬁc bun-

dle. If the buyer is truthful, then the bid b

it submits

to the auctioneer is equal to its valuation. Seller utility

can be deﬁned in a similar way.

We assume that the buyers are single-minded:

they need all the goods in the bundle (their valuation

for any subset of the requested bundle is 0). Sellers,

on the other hand, are not single-minded: any subset

of the offered goods has a positive valuation. More-

over, the seller’s valuation function is additive, mean-

ing that the value of a bundle can be computed by

summing the values of the goods in that bundle.

Then the winner determination problem

(WDP) (Lehmann et al., 2006) can be written

as an integer program that maximizes social welfare:

max

x,w

∑

i=1

−

∑

j=1

∑

k=1

∑

i=1

i jk

(1)

subject to:

∈ {0,1},∀i ∈U (2)

∑

j=1

i jk

= r

,∀i ∈U,∀k ∈ G (3)

∑

i=1

i jk

≤ s

,∀j ∈ P,∀k ∈G (4)

where x

and w

i jk

deﬁne the ﬁnal allocation: x

in-

dicates whether bidder i receives the bundle it re-

quested, and w

i jk

indicates the total number of re-

sources of type k allocated by seller j to buyer i. Con-

Approximate Algorithms for Double Combinatorial Auctions for Resource Allocation in Clouds: An Empirical Comparison

straint (2) expresses the single-mindedness of buy-

ers. Constraint (3) ensures that the total amount of

resources of a certain type that all sellers allocate to a

certain buyer is the same as the amount of resources

of that type requested by the buyer. Finally, con-

straint (4) ensures that a seller cannot sell more than

the amount of resources it offered.

2.1 Payment Scheme

Along with the WDP, the payment scheme is an es-

sential part of mechanism design. Only through an

appropriate pricing can the desired economic prop-

erties of the allocation be ensured. The following

four properties are generally targeted, although they

cannot be simultaneously satisﬁed (Myerson and Sat-

terthwaite, 1983): incentive compatibility, individual

rationality, economic efﬁciency and budget-balance.

Vickrey-Clarke-Groves (VCG) (Nisan et al.,

2007a) is a class of mechanisms that are both truth-

ful and achieve a socially optimal solution, but are

not budget-balanced—the auctioneer has to subsidize

the trade. Moreover, VCG pricing is computationally

expensive: each winner pays its social cost, i.e. one

must solve an instance of the WDP for each trade win-

ner, to compute the social welfare for the case when

it does not participate in the auction. This is why we

did not use VCG in our work.

Instead, we relax the truthfulness constraint in fa-

vor of individual rationality and budget-balance. De-

pending on the algorithm used for WDP, economic

efﬁciency might not be achieved. However, most

heuristics are asymptotically economically efﬁcient,

guaranteeing a near-optimal solution (within a fac-

tor of

√

l for the greedy algorithm (Lehmann et al.,

2002)). The κ-pricing scheme (Schnizler et al., 2008)

meets these requirements.

The general idea behind κ-pricing is to divide the

trade surplus among the trade participants in order to

ensure budget-balance. In the multi-good multi-unit

case, for a buyer i that is allocated resources from

multiple sellers, the surplus caused by the trade is:

= b

−

∑

j=1

∑

k=1

i jk

(5)

Bidder i will thus receive a discount of a κ-th part

of this surplus, resulting in payment p

= (b

−κδ

The remaining (1 −κ)δ

is divided between all the

sellers participating in the exchange generating the

surplus, proportional to each seller’s share. A seller’s

share in the trade with bidder i can be calculated by:

i j

∑

k=1

i jk

∑

j=1

∑

k=1

i jk

(6)

Adding up the surplus from all the exchanges a

seller j is involved in, the ﬁnal payment of seller j

can be calculated by:

∑

i=1

∑

k=1

i jk

+ (1 −κ)δ

i j

(7)

We used κ = 0.5 for an equal distribution of surplus.

Although the κ-pricing scheme is not incentive

compatible, non-truthful bidding increases the risk of

no allocation (Schnizler et al., 2008). Therefore, in

most cases, the competition in the market motivates

the participants to reveal their true valuations. Thus

our mechanism is budget-balanced, individually ra-

tional, asymptotically economically efﬁcient and, in

practice, truthful.

3 ALGORITHM PORTFOLIO

In the following subsections we present different al-

gorithms to solve the WDP. They are either based

on existing work or use widely known optimization

methods, but adapted to our problem formulation.

Except for branch-and-cut, the algorithms in the

portfolio aim to approximate the optimal solution in a

reasonable time rather than ﬁnd the optimal solution.

This is done by improving the ordering of bids and

asks onto which greedy algorithms are ﬁnally applied.

3.1 Branch-and-cut

The WDP can be tackled as a mixed-integer linear

program (MILP) (Gonen and Lehmann, 2000). The

most used approach for solving MILPs is branch-and-

cut (Padberg and Rinaldi, 1991). In the worst case,

this approach has exponential complexity, but it al-

ways leads to an optimal solution.

We implemented WDP for our combinatorial auc-

tion problem using ILOG’s CPLEX (IBM, 2017) soft-

ware and named this algorithm MILP. CPLEX is the

most used and most performant software for integer

and linear programming problems. Even though it is

proprietary software, IBM offers academic licenses.

3.2 Greedy Algorithms

As the name suggests, greedy algorithms are heuris-

tics that make the locally optimal choice at every step,

aiming for a globally optimal solution (Cormen et al.,

2001). Greedy algorithms thus prioritize speed over

solution quality. There is a rich literature of greedy al-

gorithms for the WDP (Lehmann et al., 2002; Samimi

et al., 2014; Nejad et al., 2015; Pfeiffer and Rothlauf,

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

2008), and they all share a simple idea: the bids are

sorted according to a certain criterion and then bids

are greedily allocated as long as there are no conﬂicts.

In the rest of this section we present our greedy algo-

rithms, adapted to our problem formulation.

We use bid and ask densities as sorting criteria,

which are deﬁned for buyer i and seller j in Eqn. 8.

√

, d

∑

k=1

(8)

Based on (Lehmann et al., 2002) and (Nejad et al.,

2015), we redeﬁne M

and M

in Eqn. 9.

∑

k=1

, M

∑

k=1

(9)

represents the relative weight of resource type

k and it can be used to express differences in value

for the resource types. We propose using different

weights for bids and asks, f

and f

, respectively.

(Nejad et al., 2015) introduce three options for cal-

culating f

in one-sided auctions, which they name

relevance factors. The ﬁrst option is a generaliza-

tion of the one-dimensional case of (Lehmann et al.,

2002), namely uniform weights. The other options

consider the scarcity of resources, either absolute

value (the inverse of the provider’s capacity of each

resource) or relative scarcity (the difference between

demand and supply, normalized by demand). We ex-

tend these options to the two-sided case as follows

(∀k ∈G):

1. f

= f

= 1

2. f

∑

j=1

, f

∑

i=1

3. f



∑

i=1

−

∑

j=1



∑

i=1

, f



∑

i=1

−

∑

j=1



∑

j=1

Densities are used to sort bids descendingly and

asks ascendingly, giving priority to clients with higher

bids and providers offering cheaper goods. For each

bid, the greedy algorithm then iterates through the

asks and allocates resources to the client until its

request is fully satisﬁed. When moving on to the

next bid in the list, previous asks are not consid-

ered in order to preserve monotonicity (Lehmann

et al., 2002)—a necessary (but not sufﬁcient) condi-

tion for a truthful mechanism. The algorithm stops

when it reaches the end of either the bid list (all re-

quests can be satisﬁed) or the ask list (there are no

more providers that can satisfy the requests), based

on (Samimi et al., 2014). We call this algorithm

Greedy-I. The main problem of Greedy-I is that it

is not individually rational. That is, some partici-

pants might have negative utility by joining the auc-

tion, since the algorithm traverses the full lists of bids

and asks; the stopping criterion does not take into ac-

count the bid and ask values, which might result in

negative utility.

In Greedy-II, we propose stopping the algorithm

when the surplus caused by satisfying the bid cur-

rently considered (as deﬁned in Eqn. 5) becomes neg-

ative. We call this bid and the ﬁrst unallocated ask

critical. A critical value is deﬁned as the value below

which a bid would not be allocated (Lehmann et al.,

2002). Although this might result in less goods be-

ing traded, the social welfare will be higher since we

are mostly eliminating trades that will result in nega-

tive utility. We use the three options of calculating the

relevance factors and name these variations Greedy-II

fk1, Greedy-II fk2 and Greedy-II fk3.

Greedy-I performs much worse for sparse

providers (offering only a subset of the resource

types), yielding a social welfare at least two or-

ders of magnitude smaller than the dense providers

case (Gudu et al., 2016). The reason for this is that,

while trying to preserve monotonicity, the algorithm

skips providers that cannot satisfy the request of the

currently considered bidder, and a large quantity of

resources remain unallocated. In Greedy-III, we pro-

pose to ﬁx this issue by considering partially allo-

cated, previously considered (i.e. lower density) asks

for each buyer request, therefore returning to the be-

ginning of the ask list for each bid. This increases the

complexity of the algorithm and violates the mono-

tonicity property, but leads to a higher social welfare.

Another consequence is that the goods allocated to

one bidder will be less likely to come from the same

provider (or a small number). Although this resource

locality is not an explicit constraint in our problem

deﬁnition, it might be a soft constraint in some cases.

Overlooking resource locality and monotonicity

led to an improved algorithm, Greedy-IV, which still

sorts the bids by density, but keeps an index of sorted

asks for each resource type, sorting them by the ask-

ing price of the respective resource type (a total of l

lists). The bids are then greedily allocated: the bid-

der with the highest density receives the cheapest re-

sources over all providers. Greedy-IV has a higher

time and memory complexity, but can also result in

higher welfare than the other algorithms.

3.3 Relaxed Linear Program-based

Relaxing the integrality constraints of the decision

variables x

and quantities w

i jk

transforms the inte-

ger program in Eqn. 1 into a linear program that can

be solved faster (weakly polynomial time when using

interior point methods, or exponential time for sim-

plex methods (Luenberger and Ye, 2015)) and that

Approximate Algorithms for Double Combinatorial Auctions for Resource Allocation in Clouds: An Empirical Comparison

provides an upper bound for social welfare. We im-

plemented two algorithms based on the relaxed linear

problem, based on (Pfeiffer and Rothlauf, 2008).

The ﬁrst one is called Relaxed LP Solution

(RLPS) and it applies Greedy-II on a set of bids and

asks sorted descendingly by their continuous decision

variables, which in our case are x

and

∑

i=1

∑

k=1

i jk

∑

k=1

for

bids and asks, respectively. By x

and w

i jk

we denote

the solutions of the relaxed linear program.

The second algorithm, Shadow Surplus (SS), uses

the solution of the dual linear program (w

i jk

) to com-

pute shadow surpluses for bids and asks as in Eqn. 10.

Shadow surpluses are then used to sort bids de-

scendingly and asks ascendingly, and then applying

Greedy-II to compute the allocation.

∑

k=1

∑

j=1

i jk

,SS

∑

k=1

∑

k=1

∑

i=1

i jk

(10)

Both algorithms use CPLEX to compute the solu-

tion of the relaxed linear problem.

3.4 Hill Climbing

Hill climbing algorithms (Russell and Norvig, 2010;

Holte, 2001) typically perform a local search in the

solution space by starting off at a random point and

moving to a neighboring solution if the cost function

of the neighbor is higher. The algorithm stops when

it ﬁnds a (local) maximum. We deﬁne a solution in

the search space as an ordering of bids (and asks)

onto which a greedy algorithm can be applied, and

the cost of a solution as its social welfare. We gen-

erate the random initial solution using a greedy algo-

rithm. Based on (Zurel and Nisan, 2001), we came up

with several ideas for generating a neighboring solu-

tion, which resulted in four algorithms.

In Hill-I, a neighboring solution is generated by

moving an unallocated bid or ask to the beginning

of the bid/ask list as proposed by (Zurel and Nisan,

2001), starting with the critical bid/ask and then go-

ing through the sorted lists. Greedy-II is used for al-

location. In Hill-II, the unallocated bid/ask replaces

the last allocated bid/ask instead. Greedy-II is used

in this case as well. Hill-III uses Greedy-IV for allo-

cation. This means that only the ordering of bids is

part of the search space. Hill-III is similar to Hill-I by

moving the bid to the top of the bid list. Hill-IV also

uses Greedy-IV for allocation and moves the unallo-

cated bid at the end of the list of allocated bids, before

the last allocated bid.

3.5 Simulated Annealing

Simulated annealing (Kirkpatrick et al., 1983) is a

well-known optimization algorithm that accepts (with

some probability) worse solutions, in order to climb

out of local optima and reach a global optimum. The

acceptance probability depends on a temperature vari-

able which decreases over time, allowing the algo-

rithm to accept worse solutions with a higher prob-

ability in the beginning of the search, but to gradually

converge as the temperature decreases.

We propose a simulated annealing algorithm with

the following features: the initial solution is generated

using Greedy-II; generating a neighboring solution is

done by choosing a random x

, toggling it, and then

ﬁnding a feasible solution using Greedy-II-like allo-

cation; the temperature decreases with a constant rate

of α = 0.9; the acceptance probability is computed us-

ing the formula ap = e

new

−w

old

)/(T

old

)

, where w

old

and w

new

are the welfare values before and after mov-

ing to the neighboring solution. For each tempera-

ture, a constant number of iterations is executed; we

named this algorithm SA-I. We derived a second al-

gorithm SA-II by having a linear number of iterations

for each temperature, proportional to the number of

bids (n/20). Then in SA-III we use Greedy-IV for

generating the initial solutions, as well as for comput-

ing the feasible allocations at every step.

3.6 Casanova

(Hoos and Boutilier, 2000) propose a stochastic lo-

cal search algorithm named Casanova which, similar

to SA, uses randomization to escape from local op-

tima. The algorithm starts with an empty allocation

and adds bids to reach a neighbor in the search space:

with a walk probability wp, a random bid is chosen

for allocation (we use a Greedy-IV-like algorithm to

select the asks to satisfy the chosen bid); with a prob-

ability of 1−wp, a bid is selected greedily by ranking

the bids according to their score. The score is de-

ﬁned as the normalized bid price (b

∑

k=1

). From

the sorted bids, the highest-ranked one is selected if

its novelty is lower than that of the second highest

ranked bid; otherwise, we select the highest ranked

bid with a novelty probability np and the second high-

est one with a probability of 1 −np. We introduced

the novelty of bids as a counterpart of the age deﬁned

by (Hoos and Boutilier, 2000), as a measure of how

often the bid was selected instead of the number of

steps since it was last selected. The search is restarted

maxTries = 10 times and the best solution from all

runs is chosen. As (Hoos and Boutilier, 2000), we set

wp = 0.15 and np = 0.5.

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

3.7 Genetic Algorithms

The multi-unit multi-good combinatorial problem can

be reduced to the multidimensional knapsack prob-

lem (Holte, 2001), which is an N P -complete prob-

lem (Kellerer et al., 2004). There are several genetic

algorithms for solving the multidimensional knapsack

problem (Chu and Beasley, 1998; Khuri et al., 1994).

We propose a genetic algorithm where individu-

als are given by the ordering of bids and asks over

which a greedy algorithm can be applied. This is dif-

ferent from other algorithms in the literature where in-

dividuals are given by the solution vectors, since our

w representation would have increased the gene space

considerably, as well as added complexity to ensure

the feasibility of each solution. Next, we describe

our steady-state (Whitley and Starkweather, 1990) ap-

proach, where offsprings replace the least ﬁt individ-

uals. The ﬁtness function is deﬁned as the welfare of

an individual. We randomly generate an initial pop-

ulation of N = 100 individuals. Two parents are se-

lected using the tournament selection method (Gold-

berg and Deb, 1991), each from a random pool of size

T = 5. They produce a child through the crossover op-

eration: a binary random number generator chooses

which parent will give the child’s next bid. Mutation

consists of swapping two random bids and two ran-

dom asks. We ﬁx the mutation rate to M = 2. The

process of parent selection, crossover, mutation and

ﬁtness evaluation is repeated t

max

= 1000 times. The

ﬁnal solution is given by the ﬁttest individual in the

population. We implemented two versions: GA-I uses

Greedy-II for allocation, while GA-II uses Greedy-IV.

3.8 Algorithm Properties

Table 1 summarizes the properties of each algorithm

in the portfolio. The proofs for time complexities are

omitted due to lack of space. However, we note that

most of the approximate algorithms run in polynomial

time, compensating with speed for the loss of welfare

compared to the optimal exponential algorithm.

The algorithms in several classes (simulated an-

nealing, stochastic local search and genetic algo-

rithms) are stochastic: they use randomization to ex-

plore the search space, which means that they can

compute different results when ran multiple times on

the same input.

Another property included in Table 1 is resource

locality. It expresses an algorithm’s preference to

allocate resources in a bidder’s bundle on the same

cloud provider. It should be noted that this is a soft

constraint: it is enforced only when possible and it

translates into bidders receiving resources from as

few providers as possible, while preserving the mono-

tonicity property. The algorithms that have this prop-

erty use a Greedy-II-like allocation after optimizing

the ordering of bids and asks.

4 INPUT GENERATION

Finding real-world data for auctions of cloud re-

sources is a difﬁcult task, since commercial cloud

providers do not typically release user bidding infor-

mation. Existing cloud auctions for dynamic pricing

of resources, such as the Amazon spot instance mar-

ket (Amazon, 2017), are simplistic and mostly one-

sided single-good auctions. Although cloud prices are

publicly available, the amount of resources offered

and their relative scarcity are not, since providers

claim inﬁnite resources. Several cloud providers have

released workload traces to be used for cloud schedul-

ing (Wilkes, 2011; Facebook, 2012). These can pro-

vide insights into typical jobs running in the cloud,

enabling us to extract the sizes of bundles requested

by clients, as well as different resource quantities and

their dependencies. However, resource types are gen-

erally limited to CPU load, memory, storage and pos-

sibly bandwidth, making the data too simple to thor-

oughly test combinatorial auctions.

Therefore, we use artiﬁcial data in all our evalua-

tions, as most papers dealing with combinatorial auc-

tions (Leyton-Brown et al., 2000; Sandholm, 2002;

De Vries and Vohra, 2003) do. An added beneﬁt of

synthetic data generation is ﬂexibility: a larger range

of use cases can be covered, rather than having just a

few real-world, but narrow-scoped datasets.

4.1 CAGE

Although there has been some work on artiﬁcial data

generation for combinatorial auctions (Leyton-Brown

et al., 2000; Sandholm, 2002; Fujishima et al., 1999;

De Vries and Vohra, 2003), to our knowledge there

is no work that deals with multi-good and multi-unit

combinatorial auctions. The Combinatorial Auctions

Test Suite (CATS) (Leyton-Brown et al., 2000) is ac-

tually the ﬁrst work that tries to create a comprehen-

sive tool for generating artiﬁcial data for combinato-

rial auctions. It supports legacy distributions (covered

in older papers), but the authors also propose more re-

alistic distributions by modeling complementarity and

substitutability of goods using graphs. We do not deal

with dependencies between goods, but the existing

work is not sufﬁcient to generate input data for our re-

source allocation problem with multi-unit multi-good

bids. We also consider the differences between buyers

Approximate Algorithms for Double Combinatorial Auctions for Resource Allocation in Clouds: An Empirical Comparison

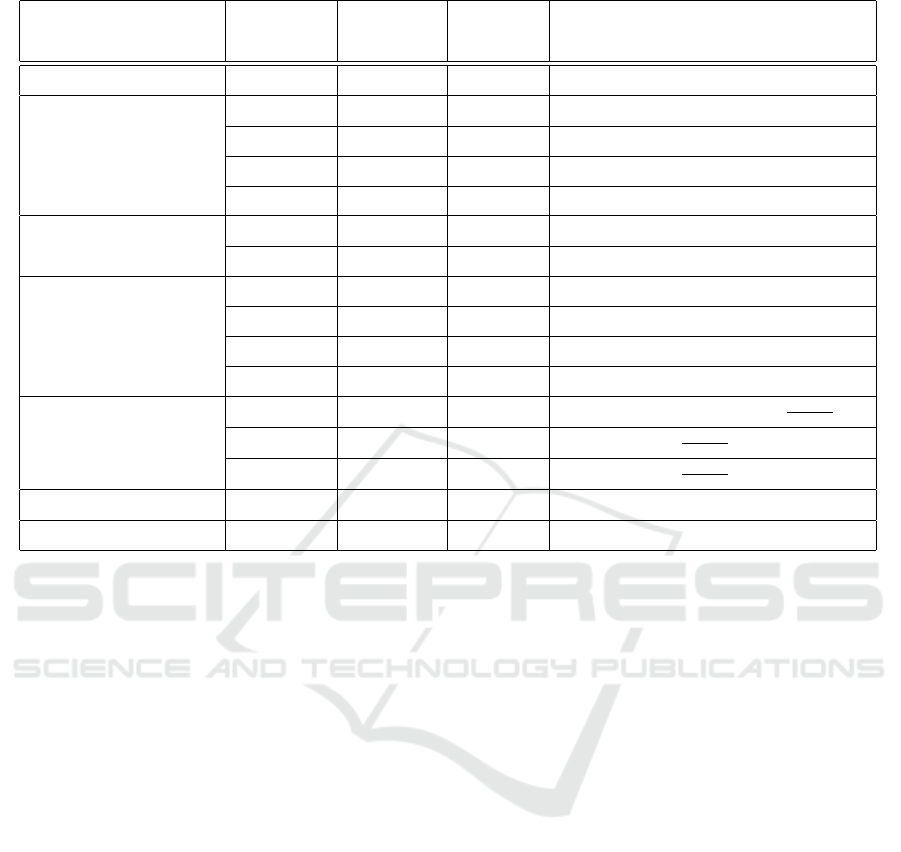
Table 1: Summary of algorithm properties.

Class Algorithm Stochastic Resource Time complexity

locality

Branch-and-cut MILP exponential

Greedy

Greedy-I X O(nlog n + m logm + l(n + m))

Greedy-II X O(nlog n + m logm + l(n + m))

Greedy-III O(nml)

Greedy-IV O(nml)

Linear relaxation

SS X exponential

RLPS X exponential

Hill climbing

Hill-I X O(nml(n + m))

Hill-II X O(nml(n + m))

Hill-III O(n

ml)

Hill-IV O(n

ml)

Simulated annealing

SA-I X X O(nlogn + m log m + nl + it

logT

min

logα

ml)

SA-II X X O(

logT

min

logα

nml)

SA-III X O(

logT

min

logα

nml)

Genetic algorithms GA-I X X O((N + l)(n + m)(N + t

max

))

Stochastic local search Casanova X O(maxTries(nml + n

))

and sellers and hence require different strategies for

generating input for each side. Thus, we propose an

improved way of generating artiﬁcial data for multi-

good multi-unit double combinatorial auctions, com-

patible with legacy distributions (Leyton-Brown et al.,

2000). Our tool CAGE (Combinatorial Auctions in-

put GEnerator) is introduced in the following.

A problem instance (deﬁned by the set of bids and

asks) can be generated using the following parame-

ters: the number of bids n, the number of asks m, the

number of resource types l and multiple random dis-

tributions with their parameters. We deﬁne the ran-

dom distributions to generate the bids as follows.

A bundle size is randomly drawn from a given

bundle size distribution, where the bundle size is the

total number of items of any type of resource.

Resource type selection: for each bundle, the re-

source type of an item is selected with a probability

given by a distribution over the number of resource

types (e.g. uniform or normal). A special case is the

sparse uniform distribution, where only a subset of

resources are requested by each bidder, with the size

of this subset given as input parameter; the resource

types in the subset can be different for each bidder.

The resource quantities of a bundle are then uniformly

distributed among the resource types in the subset.

A bid value proportional to the number of items

in each bundle is then generated; ﬁrst, the base price

distribution is used to generate a base price for each

resource type, representing the known approximate

market value of each resource type. These base prices

are the same for all trade participants. The price dis-

tribution is then used to generate an average price per

unit for each resource type, around its base price; the

total bid value is then computed by combining these

prices per unit and the number of items requested

of each resource type in one of the following ways:

1) additive: the total bid value is computed as a lin-

ear combination of the unit prices per resource type,

weighed by the number of items requested for each

type; 2) super-additive: we compute the bid value as

a quadratic function (De Vries and Vohra, 2003) pro-

portional to the bid size and parameterized with an

additivity factor (Eqn 11).

∑

k=1

∗

+ additivity

∑

k6=h

∗

(11)

In Eqn. 11, by v

∗

we denote a bidder i’s reported

(not necessarily true) valuation for one item of re-

source type k.

The same strategy is used for generating the asks,

with the difference that we generate reserve prices for

each resource type instead of a total ask value.

All the available random distributions and their

default parameters are summarized in Table 2. We

denote the base price of resource k as p

∗

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

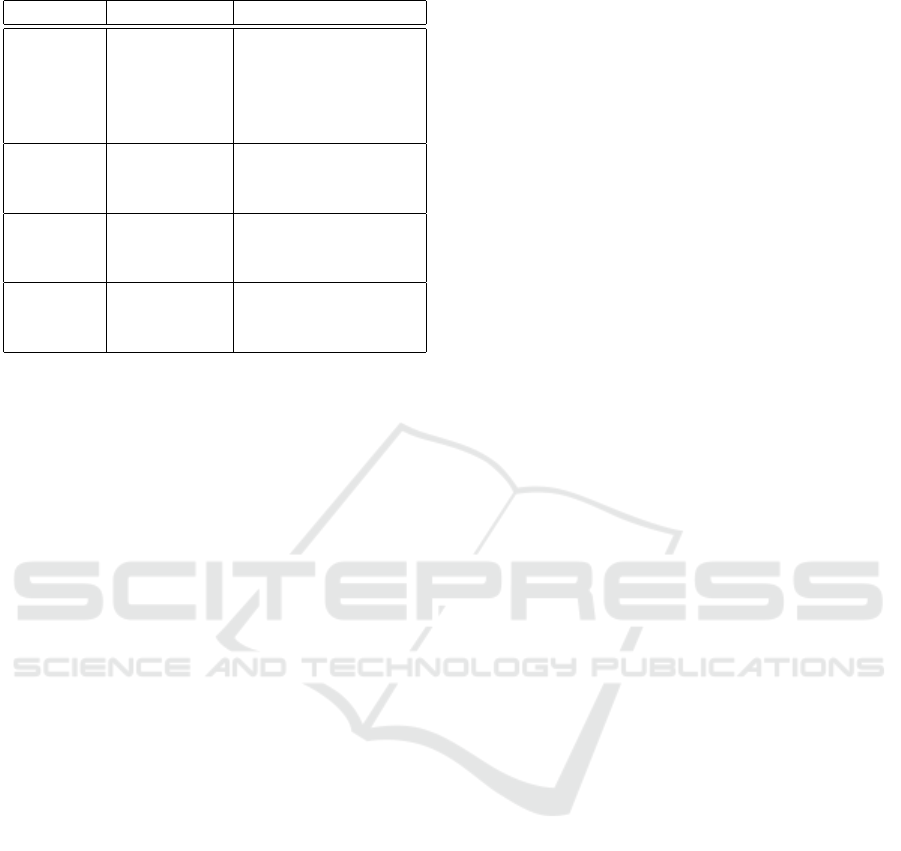
Table 2: Distributions and default parameters in CAGE.

Category Distribution Default parameters

normal µ = 1000, σ = 250

Bundle uniform min=500,max=1500

size exponential λ = 0.005, offset 20l

beta α = 5, β = 1, ×200l

constant 1000

Resource normal µ = l/2,σ = l/4

type uniform min = 0, max = l −1

sparse 2 resource types

Base uniform p

∗

: min = 0.1,

prices max = 0.9

normal p

∗

: µ = 0.5,σ = 0.2

Unit uniform v

∗

: min = p

∗

−0.1,

prices max = p

∗

+ 0.1

normal v

∗

: µ = p

∗

,σ = 0.05

5 EVALUATION

We compared all the algorithms in the portfolio un-

der various input conditions, in order to evaluate their

performance and solution quality. To that end, we se-

lected two essential metrics: execution time and so-

cial welfare. In most cases, we normalized the wel-

fare by the optimal welfare (computed with MILP).

Below we present our evaluation scenarios.

5.1 Average Case

We wish to ﬁnd the best algorithm in the average case.

Therefore, we generated 3226 problem instances us-

ing CAGE’s default parameters and different combi-

nations of the available distributions. We used both

additive bids, as well as three different positive addi-

tivity parameters. We ﬁxed the number of bids, asks

and resources as follows: n = m = 200,l = 50. We

did not increase the problem size further in order to

be able to include in our comparison the optimal al-

gorithm, which has exponential time complexity. The

results are depicted in Fig. 1.

We notice large differences in both welfare and

execution time between the algorithms in the portfo-

lio. The algorithms based on the linear relaxation of

the integer program (SS and RLPS) are the least per-

formant, since the execution time is longer than most

algorithms in the portfolio, while the social welfare is

on average less than 25% of the optimal welfare (with

high standard deviation).

The algorithms with the highest welfare are the

ones based on Greedy-IV: Hill-III, Hill-IV, SA-III and

Casanova. Although Casanova and SA-III achieve, on

average, the same or slightly lower welfare than the

hill climbing algorithms III and IV, they are 12 to 15

times faster, on average, and thus equally attractive

options. Even the Greedy-IV algorithm computes, on

average, a welfare that is almost 90% of the optimal

one, which is surprisingly high, as well as extremely

fast. We notice, however, a high standard deviation

for Greedy-IV due to the fact that ordering the bids by

density is a coarse approximation that does not work

well in all possible input scenarios. The Greedy-IV-

based algorithms achieve near-optimal welfare, which

can be explained by the fact that provider goods are

treated separately and all constraints of resource lo-

cality and bid monotonicity are relaxed. We believe

that adding such constraints to our problem formula-

tion, namely having each provider offering a bundle

to be sold to a single bidder, would make the problem

harder and most likely would make the approxima-

tions worse. This interesting hypothesis is, however,

the subject of future work, and will require adapting

all the algorithms to the new problem formulation.

The Greedy-II-based algorithms roughly enforce

the resource locality constraints, in the sense that for

each bid, they try as much as possible to allocate all

resources from the same provider. If this is a desired

feature, it must be noted that the resulting social wel-

fare is low, around 27% of the optimal welfare, for

Greedy-II (variations 1,2,3), Hill-I, Hill-II and GA-I.

The fact that the hill climbing algorithms do not sig-

niﬁcantly improve the greedy allocation suggests that

they get stuck in a local maximum close to the initial

greedy solution. This hypothesis is conﬁrmed by the

more than doubling of welfare brought on by the sim-

ulated annealing algorithms (SA-I and SA-II), which

mitigate this exact problem through randomization.

5.2 Best Algorithm

As shown in Fig. 1(a), several algorithms yield near-

optimal welfare on average. At the same time, even

the algorithms that perform poorly on average (com-

puting a welfare < 30% of the optimal one) can in a

few cases result in high welfare. These cases are de-

picted by outliers found even above the 90% line.

To obtain a clear picture of which algorithm in

the portfolio actually performs best, we analyzed the

dataset constructed for our ﬁrst test case. For each

problem instance, we compared the social welfare

computed by all the approximate algorithms and se-

lected the algorithm with the highest welfare, and,

when multiple algorithms yielded the same welfare,

the fastest algorithm. We counted the number of in-

stances for each algorithm and summarized the results

in Table 3. We notice that there is no clear winner

of the portfolio, with the results being almost equally

Approximate Algorithms for Double Combinatorial Auctions for Resource Allocation in Clouds: An Empirical Comparison

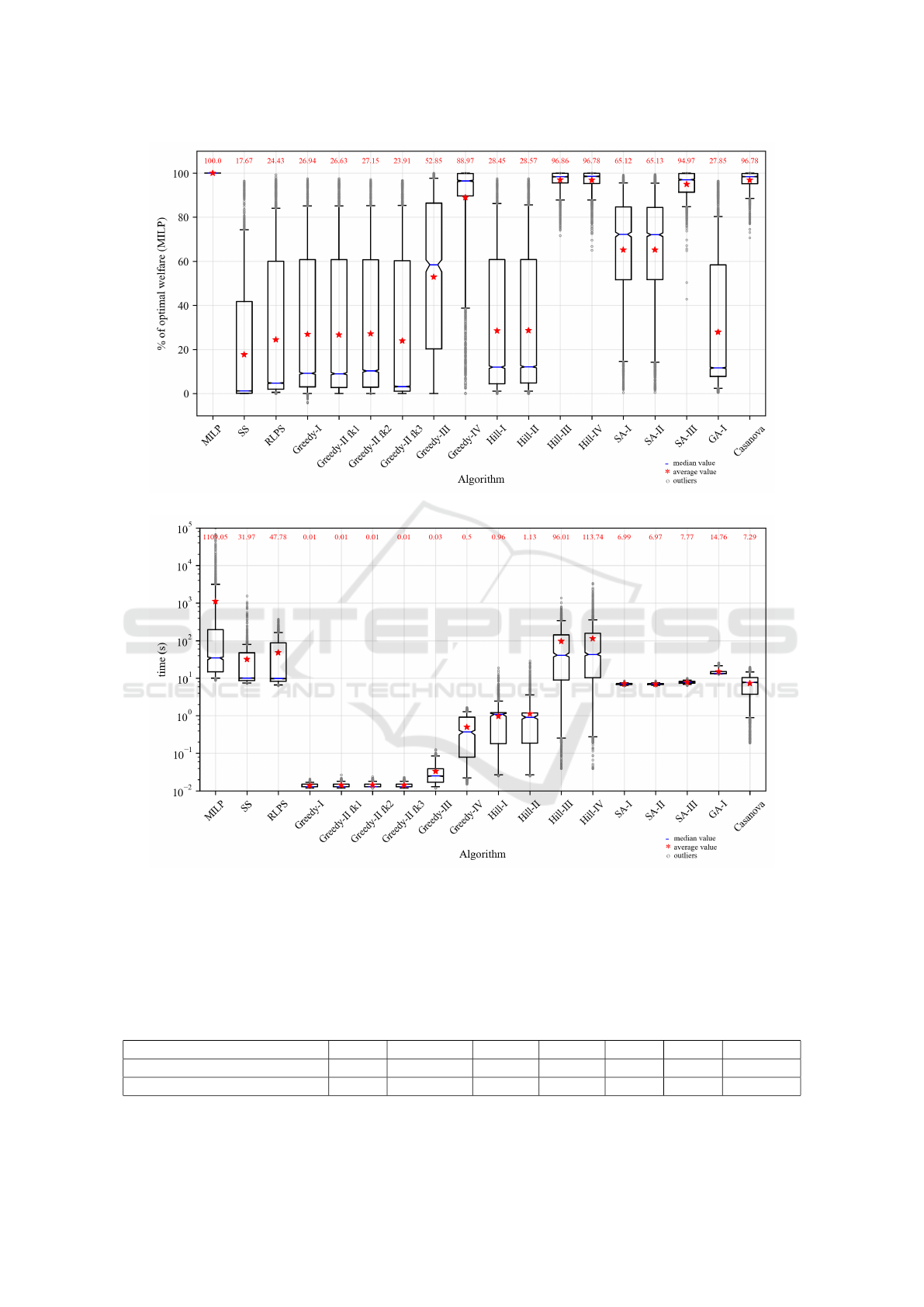
(a) Social welfare, normalized by the optimal welfare computed with MILP

(b) Execution time

Figure 1: Results from a comprehensive parameter sweep through the input space: different combinations of available dis-

tributions in CAGE with default parameters and 4 different additivity parameters. The average value for each algorithm is

represented by a red star, with the actual value attached at the top of each box. The boxes extend from the lower to the upper

quartile values of the data, with a blue line at the median. The notches around the median represent the conﬁdence interval

around the median. The whiskers reach from 5% to 95% of the data. The remaining data are represented as outliers with gray

circles. A logarithmic scale was used for the y-axis of Fig. 1(b) for better readability.

Table 3: Breakdown of results by best algorithm: number of instances where each algorithm outperforms all the other algo-

rithms in the portfolio (absolute numbers and percentage of total instances on which the portfolio was ran).

Algorithm RLPS Greedy-IV Hill-III Hill-IV SA-I SA-III Casanova

Number of instances 6 753 1021 566 2 54 824

Percentage of total instances 0.18% 23.34% 31.64% 17.54% 0.06% 1.67% 25.54%

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

distributed among a few Greedy-IV-based algorithms:

Greedy-IV, Hill-III, Hill-IV and Casanova. Further-

more, in a few cases (1.89%), other algorithms (SA-I,

SA-III, RLPS) output the highest social welfare.

This result reinforces the need for consistent

benchmarking efforts of approximate algorithms for

the WDP. A fair comparison can only be ensured

through applying the algorithm portfolio on a unique

problem formulation, coupled with a wide range of

test cases that can uncover each algorithm’s strengths.

Our work on standardizing all the existing algorithms

on the proposed problem formulation (tailored to

cloud resource allocation), as well as the novel input

generator for combinatorial auctions CAGE, aims at

tackling this issue.

5.3 Effect of Randomization

Since some algorithms in the portfolio are stochas-

tic (Casanova, genetic and simulated annealing), they

will yield different results for different runs on the

same input. It is desirable to have small variations

in welfare between runs. Thus, for each stochastic al-

gorithm we performed 100 runs on the same problem

instance, and recorded the social welfare.

Fig. 2 shows the percentual variations for each al-

gorithm with respect to the mean of the 100 runs. We

performed this normalization in order to have a com-

parative overview over all the algorithms. The plot

contains events from 100 different instances with 100

runs each. The highest variation is seen in the Greedy-

II-based algorithms, most pronounced for the GA-I

algorithm, where the lower and upper quartile values

of the data are at about −9% and +8.6% of the mean

value. This result reinforces the idea that the solution

quality of Greedy-II-based algorithms, where soft lo-

cality constraints are enforced, is highly dependent on

ordering of bids and asks, and even small changes can

lead to very different results. In order to use these al-

gorithms reliably, multiple runs are necessary, and the

best solution can be used in the end. This would, how-

ever, increase the execution time.

Fig. 3 shows the absolute welfare values from 100

runs on a single instance for Casanova and SA-III,

the algorithms based on Greedy-IV. For this particu-

lar instance, SA-III computes a higher welfare than

Casanova. Although the standard deviation is low

in both cases (0.012% and 0.36% from mean), SA-

III also produces a lower number of unique solutions,

converging to a few solutions in the search space: 9

local maxima for 100 runs. The SA-III algorithm is

more likely to converge than Casanova due to the de-

creasing temperature variable which forces a decrease

in the acceptance probability of worse solutions in the

Figure 2: Variation in social welfare for the stochastic algo-

rithms: results from 100 different input instances, with 100

runs per instance. The difference of each run to the average

value of the respective instance, normalized by that average

value, is plotted. The average value (red star) is always at 0.

The boxes extend from the lower to the upper quartile, with

a blue line at the median. The whiskers reach from 5% to

95% of the data, and the rest are outliers (gray circles).

Figure 3: Absolute welfare values computed by two algo-

rithms (SA-III and Casanova) on a single input instance,

with 100 repetitions. Average value (vertical red line), me-

dian value (vertical blue line) and ± one standard deviation

from the mean (horizontal dashed red line) are also plotted.

search space. The results in Fig. 3 conﬁrm this asser-

tion. However, there is no guarantee that SA-III will

always lead to better solutions than Casanova.

6 RELATED WORK

In the previous sections, we referred to existing work

on various approximate algorithms for solving the

WDP (Nejad et al., 2015; Lehmann et al., 2002;

Holte, 2001; Zurel and Nisan, 2001; Bertocchi et al.,

1995; Hoos and Boutilier, 2000; Chu and Beasley,

1998; Khuri et al., 1994; Fujishima et al., 1999).

While each aforementioned paper compares its newly

introduced algorithm to other algorithms in the liter-

ature, there is no attempt, to our knowledge, to ex-

perimentally compare all the existing algorithms in a

more systematic and consistent manner.

(Leyton-Brown et al., 2000) have worked in this

direction by proposing CATS, a “universal test suite”:

a wide range of economically motivated test scenar-

ios consisting of artiﬁcially generated data. However,

they focus on optimal algorithms and compare their

runtime to predict the hardness of a problem instance.

Approximate Algorithms for Double Combinatorial Auctions for Resource Allocation in Clouds: An Empirical Comparison

In contrast, we focus on approximate algorithms to

accommodate large-scale auctions and use social wel-

fare to compare them. Furthermore, our input gener-

ator can deal with multi-unit multi-good double auc-

tions, as opposed to single-unit multi-good one-sided

auctions for CATS, but we simpliﬁed our approach by

not considering dependencies between goods.

7 CONCLUSION

In this paper, we performed a systematic and com-

prehensive comparison of approximate algorithms for

winner determination in double combinatorial auc-

tions. We created an algorithm portfolio and found

that only a subset of the algorithms compute near-

optimal welfare in the average case. However, our

analysis revealed that there is no clear portfolio win-

ner, and the algorithms’ performance highly depends

on the input. In the future, we will perform a deeper

analysis to identify the input characteristics which in-

ﬂuence the solution quality and we will employ ma-

chine learning methods to predict the algorithms’ per-

formance. Moreover, we argue for the need to har-

monize benchmarking efforts and propose a ﬂexible

approach to generate artiﬁcial data. In the future, we

will integrate real cloud data in the input generator by

using up-to-date prices, as well as analyzing public

cloud workloads and extracting relevant parameters

to ﬁt them to certain random distributions.

REFERENCES

Amazon (2017). Amazon ec2 pricing. https://aws.amazon.

com/ec2/pricing. Accessed: 10. 11. 2017.

Bertocchi, M., Butti, A., Słomi

n ski, L., and Sobczyn-

ska, J. (1995). Probabilistic and deterministic lo-

cal search for solving the binary multiknapsack

problem. Optimization, 33(2):155–166. doi:

10.1080/02331939508844072.

Buyya, R., Yeo, C. S., and Venugopal, S. (2008). Market-

oriented cloud computing: Vision, hype, and reality

for delivering it services as computing utilities. In

High Performance Computing and Communications,

2008. HPCC’08. 10th IEEE International Conference

on, pages 5–13. IEEE. doi: 10.1109/HPCC.2008.172.

Chu, P. C. and Beasley, J. E. (1998). A genetic al-

gorithm for the multidimensional knapsack prob-

lem. Journal of heuristics, 4(1):63–86. doi:

10.1023/A:1009642405419.

CloudStack (2017). Apache cloudstack. https://cloudstack.

apache.org/. Accessed: 10. 11. 2017.

Cormen, T. H., Leiserson, C. E., Rivest, R. L., and Stein,

C. (2001). Greedy algorithms. Introduction to algo-

rithms, 1:329–355.

De Vries, S. and Vohra, R. V. (2003). Combinatorial auc-

tions: A survey. INFORMS Journal on computing,

15(3):284–309. doi: 10.1287/ijoc.15.3.284.16077.

Facebook (2012). Facebook workload repository.

https://github.com/SWIMProjectUCB/SWIM/wiki.

Accessed: 10. 11. 2017.

Fujishima, Y., Leyton-Brown, K., and Shoham, Y. (1999).

Taming the computational complexity of combinato-

rial auctions: Optimal and approximate approaches.

In IJCAI, volume 99, pages 548–553.

Goldberg, D. E. and Deb, K. (1991). A comparative analy-

sis of selection schemes used in genetic algorithms.

Foundations of genetic algorithms, 1:69–93. doi:

10.1016/b978-0-08-050684-5.50008-2.

Gonen, R. and Lehmann, D. (2000). Optimal solutions for

multi-unit combinatorial auctions: Branch and bound

heuristics. In Proceedings of the 2nd ACM conference

on Electronic commerce, pages 13–20. ACM. doi:

10.1145/352871.352873.

Gudu, D., Hardt, M., and Streit, A. (2016). On mas-

based, scalable resource allocation in large-scale,

dynamic environments. In Ubiquitous Intel-

ligence & Computing, Advanced and Trusted

Computing, Scalable Computing and Commu-

nications, Cloud and Big Data Computing, In-

ternet of People, and Smart World Congress

(UIC/ATC/ScalCom/CBDCom/IoP/SmartWorld),

2016 Intl IEEE Conferences, pages 567–574. IEEE.

doi: 10.1109/UIC-ATC-ScalCom-CBDCom-IoP-

SmartWorld.2016.0097.

Holte, R. C. (2001). Combinatorial auctions, knapsack

problems, and hill-climbing search. In Conference

of the Canadian Society for Computational Studies of

Intelligence, pages 57–66. Springer. doi: 10.1007/3-

540-45153-6 6.

Hoos, H. H. and Boutilier, C. (2000). Solving combinatorial

auctions using stochastic local search. In AAAI/IAAI,

pages 22–29.

IBM (2017). Ilog cplex 12.6.3. http://www-03.ibm.com/

software/products/en/ibmilogcpleoptistud. Accessed:

10. 11. 2017.

Kellerer, H., Pferschy, U., and Pisinger, D. (2004). Intro-

duction to np-completeness of knapsack problems. In

Knapsack problems, pages 483–493. Springer.

Khuri, S., B

ack, T., and Heitk

otter, J. (1994). The

zero/one multiple knapsack problem and genetic algo-

rithms. In Proceedings of the 1994 ACM symposium

on Applied computing, pages 188–193. ACM. doi:

10.1145/326619.326694.

Kirkpatrick, S., Gelatt, C. D., Vecchi, M. P., et al.

(1983). Optimization by simulated annealing.

science, 220(4598):671–680. doi: 10.1126/sci-

ence.220.4598.671.

Lehmann, D., M

uller, R., and Sandholm, T. (2006).

The winner determination problem. Combinato-

rial auctions, pages 297–318. doi: 10.7551/mit-

press/9780262033428.003.0013.

Lehmann, D., O

callaghan, L. I., and Shoham, Y. (2002).

Truth revelation in approximately efﬁcient combinato-

ICAART 2018 - 10th International Conference on Agents and Artiﬁcial Intelligence

rial auctions. Journal of the ACM (JACM), 49(5):577–

602. doi: 10.1145/585265.585266.

Leyton-Brown, K., Pearson, M., and Shoham, Y. (2000).

Towards a universal test suite for combinatorial auc-

tion algorithms. In Proceedings of the 2nd ACM con-

ference on Electronic commerce, pages 66–76. ACM.

doi: 10.1145/352871.352879.

Luenberger, D. G. and Ye, Y. (2015). Linear and non-

linear programming, volume 228. Springer. doi:

10.1007/978-3-319-18842-3.

Myerson, R. B. and Satterthwaite, M. A. (1983). Efﬁ-

cient mechanisms for bilateral trading. Journal of

economic theory, 29(2):265–281. doi: 10.1016/0022-

0531(83)90048-0.

Nejad, M. M., Mashayekhy, L., and Grosu, D. (2015).

Truthful greedy mechanisms for dynamic virtual ma-

chine provisioning and allocation in clouds. Paral-

lel and Distributed Systems, IEEE Transactions on,

26(2):594–603. doi: 10.1109/TPDS.2014.2308224.

Nisan, N. et al. (2007a). Introduction to mechanism design

(for computer scientists). Algorithmic game theory,

9:209–242.

Nisan, N., Roughgarden, T., Tardos, E., and Vazirani, V. V.

(2007b). Algorithmic game theory, volume 1. Cam-

bridge University Press Cambridge.

Openstack (2017). Openstack. https://www.openstack.org/.

Accessed: 10. 11. 2017.

Padberg, M. and Rinaldi, G. (1991). A branch-and-cut algo-

rithm for the resolution of large-scale symmetric trav-

eling salesman problems. SIAM review, 33(1):60–100.

doi: doi.org/10.1137/1033004.

Pfeiffer, J. and Rothlauf, F. (2008). Greedy heuristics

and weight-coded eas for multidimensional knapsack

problems and multi-unit combinatorial auctions. In

Operations Research Proceedings 2007, pages 153–

158. Springer. doi: 10.1007/978-3-540-77903-2 24.

Rappa, M. A. (2004). The utility business model and the

future of computing services. IBM systems journal,

43(1):32–42. doi: 10.1147/sj.431.0032.

Russell, S. and Norvig, P. (2010). Beyond classical search.

Artiﬁcial Intelligence, A Modern Approach, pages

125–128.

Samimi, P., Teimouri, Y., and Mukhtar, M. (2014). A com-

binatorial double auction resource allocation model

in cloud computing. Information Sciences. doi:

10.1016/j.ins.2014.02.008.

Sandholm, T. (2002). An algorithm for optimal win-

ner determination in combinatorial auctions. Artiﬁ-

cial intelligence, 135(1):1–54. doi: 10.1016/S0004-

3702(01)00159-X.

Schnizler, B., Neumann, D., Veit, D., and Wein-

hardt, C. (2008). Trading grid services–a multi-

attribute combinatorial approach. European Jour-

nal of Operational Research, 187(3):943–961. doi:

10.1016/j.ejor.2006.05.049.

Whitley, D. and Starkweather, T. (1990). Genitor ii: A dis-

tributed genetic algorithm. Journal of Experimental &

Theoretical Artiﬁcial Intelligence, 2(3):189–214. doi:

10.1080/09528139008953723.

Wilkes, J. (2011). More Google cluster data. Google

research blog. Posted at http://googleresearch.blog

spot.com/2011/11/more-google-cluster-data.html.

Zurel, E. and Nisan, N. (2001). An efﬁcient approx-

imate allocation algorithm for combinatorial auc-

tions. In Proceedings of the 3rd ACM conference on

Electronic Commerce, pages 125–136. ACM. doi:

10.1145/501158.501172.

Approximate Algorithms for Double Combinatorial Auctions for Resource Allocation in Clouds: An Empirical Comparison