
BM3D Image Denoising using Learning-based Adaptive Hard
Thresholding
Farhan Bashar and Mahmoud R. El-Sakka
Computer Science Department, The University of Western Ontario, London, Ontario, Canada
Keywords:
Image Denoising, Additive White Gaussian Noise, BM3D, Adaptive Threshold, Classification, Random
Forest Classifier, PSNR, SSIM.
Abstract:
Block Matching and 3D Filtering (BM3D) is considered to be the current state-of-art algorithm for additive
image denoising. But this algorithm uses a fixed hard threshold value to attenuate noise from a 3D block.
Experiment shows that this fixed hard thresholding deteriorates the performance of BM3D because it does not
consider the context of corresponding blocks. We propose a learning based adaptive hard thresholding method
to solve this problem and found excellent improvement over the original BM3D. Also, BM3D algorithm
requires as an input the value of noise level in the input image. But in real life it is not practical to pass as
an input the noise level of an image to the algorithm. We also added noise level estimation method in our
algorithm without degrading the performance. Experimental results demonstrate that our proposed algorithm
outperforms BM3D in both objective and subjective fidelity criteria.
1 INTRODUCTION
Image denoising is the process of reducing the noise
artifact from a noisy image. This domain of image
processing is very popular and old because images
are often contaminated by different types of noise due
various factors, including the quality of image sensor.
Reducing noise from these images is very important,
as noisy images in different imaging applications can
degrade the performance of that system.
Noise is a random variation of brightness or color
information in images and it can be additive or mul-
tiplicative. Additive noise is independent of image
signal and added to the image. It can be generally
modeled as:
v(x) = u(x) + η(x) (1)
where u(x) is a original signal and η(x) is the noise of
the channel. On the other hand, multiplicative noise
gets multiplied into the image signal. It can be gener-
ally modeled as:
v(x) = u(x) × η(x) (2)
Our study focused on Additive White Gaussian Noise
(AWGN). AWGN refers to the additive noise which
has constant power spectral density and follows a
Gaussian (normal) distribution.
Image denoising can be performed either in the
spatial domain or in the frequency domain. In spa-
cial domain, denoising is done by applying filter di-
rectly to the intensity values of the image. On the
other hand, in frequency domain techniques, an im-
age is transformed to the frequency domain and then
the filtering operations are performed there, and the
resulting denoised signal is transformed back into the
spatial domain.
From the early stage of image denoising, spatial
domain denoising was very popular because there is
no overhead for domain transformation and it is very
simple. Some of the basic spatial domain filters are
Mean Filter, Median Filter and Gaussian Smooth-
ing (Gonzalez and Woods, 2008). In these filtering
techniques every pixel is non-adaptively adjudicated
based on the surrounding pixels. It does not take into
account whether the pixel is from a smooth region or
an edge. So edges become blurred in these methods.
To solve this problem Perona and Malik proposed
an edge preserving image denoising technique called
Anisotropic Diffusion (Perona and Malik, 1990). The
main idea of this technique is to first identify whether
a pixel is from a smooth region or an edge and then
denoise it.
All of these spatial denoising techniques are pixel-
based denoising schemes. Non-Local Meas (NLM)
changed this idea to patch-based denoising scheme
(Buades et al., 2005). It is the most successful spa-
tial domain image denoising scheme. Instead of fil-
206
Bashar, F. and El-Sakka, M.
BM3D Image Denoising using Learning-based Adaptive Hard Thresholding.
DOI: 10.5220/0005787202040214
In Proceedings of the 11th Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2016) - Volume 3: VISAPP, pages 206-216
ISBN: 978-989-758-175-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

tering a single pixel based on its neighboring pixels,
it works with patches in a particular window. In this
algorithm, a block/patch is defined around a partic-
ular pixel, referred as the reference patch. A search
window is also defined around the pixel where sim-
ilar patches of the reference patch is searched. The
patches are given a weight based on its similarity with
the reference patch. The center pixel of the refer-
ence patch is then denoised by weighted averaging
of all the patch center pixels. A number of improve-
ments has been proposed over NLM algorithm which
have achieved a slight better accuracy over the orig-
inal NLM. Some of the algorithms are: SSIM-Based
Non Local Means (Rehman and Wang, 2011), Adap-
tive Non-Local Means (Thaipanich et al., 2010) and
Non-Local Medians (Chaudhury and Singer, 2012).
In frequency domain denoising, the basic fil-
tering technique is Low Pass Filter (Gonzalez and
Woods, 2008) which allows to pass the signal with
frequencies lower than a cutoff frequency and atten-
uates signals with frequencies higher than the cut-
off frequency. Another popular filter is Weiner Fil-
ter (Wiener, 1949). It tries to estimate the noise
from a degraded image and denoise it based on this
estimation. The current state-of-art denoising tech-
nique is Block Matching and 3D Filtering (BM3D).
Detailed description of BM3D is described in Sec-
tion 2.1. A number of improvements has been pro-
posed over the BM3D algorithm. Dabov et al. in-
troduced PCA in BM3D and proposed another algo-
rithm, BM3D-SAPCA (Dabov et al., 2009). They
have also extended BM3D for color image denois-
ing (Dabov et al., 2007b) and video denoising (Dabov
et al., 2007a). Dai et al. added adaptive distance hard
thresholding in BM3D (Dai et al., 2013) and Mittal et
al. adapted machine learning based techniques to pre-
dict the noise level parameter used in BM3D (Mittal
et al., 2012). Recently structural similarity is used in
Wiener filtering part of BM3D instead of using tradi-
tional MSE (Hasan and El-Sakka, 2015).
Although BM3D achieves excellent performance
in reducing Additive White Gaussian Noise, it posses
some limitations as well. Our main study focused
on finding these limitation and provide possible so-
lutions for them. BM3D algorithm relies on a user
provided noise level for each noisy image which is
not possible for real time systems. This noise level
is very important for estimating the denoised image.
We have incorporated a noise level estimation mech-
anism without hampering the performance in this al-
gorithm to convert this as an automated system. Also,
in BM3D a hard thresholding is used for any block of
the noisy image. We have illustrated that this thresh-
olding depends on image block’s texture and noise
level. Tuning this threshold can improve the perfor-
mance of BM3D. Thus we have proposed a learning-
based adaptive hard thresholding mechanism where
each block uses different thresholds based on their
context. From a set of training images, a classifier is
trained by providing the image block as a feature and
their best threshold as a label. From a test image, the
best threshold of its different block is predicted from
this classifier. This best threshold is used in the al-
gorithm to denoise that particular block. Experiments
show that this learning-based adaptive hard threshold-
ing improves the performance of BM3D much over
the original BM3D algorithm.
2 RELATED WORK
In recent years Block Matching and 3D Filtering
(BM3D) becomes the most popular image denoising
technique. Dabov et al. first proposed the idea in 2006
(Dabov et al., 2006) and explained it thoroughly in
2007 (Dabov et al., 2007c). BM3D achieves excel-
lent performance in reducing Additive White Gaus-
sian Noise (AWGN). It has achieved the state-of-
the-art denoising performance in terms of both peak
signal-to-noise ratio and subjective visual quality. In
our work we have tried to highlight the limitations of
this algorithm and propose modifications to improve
the performance of this method.
2.1 Block Matching and 3D Filtering
(BM3D)
BM3D follows the concept of patch-based denois-
ing mechanism where instead of denoising one single
pixel, a patch/block of pixels are denoised at a time,
a concept adapted from the Non-Local Means (NLM)
algorithm (Buades et al., 2005). It was the state-of-
the-art algorithm for image denoising before BM3D,
where a single patch is denoised by finding its similar
patches from a given window. BM3D also extended
it by denoising an image using two almost identical
steps. In the first step, a basic estimate of the noisy
image is generated. This basic estimate is then passed
to the second step to generate the final denoised im-
age. The block diagram of this algorithm is shown in
Fig. 1.
2.1.1 BM3D First Step
The first step of BM3D is known as the hard thresh-
olding step because a hard thresholding is used to
eliminate noise from the image. First, the noisy image
BM3D Image Denoising using Learning-based Adaptive Hard Thresholding
207
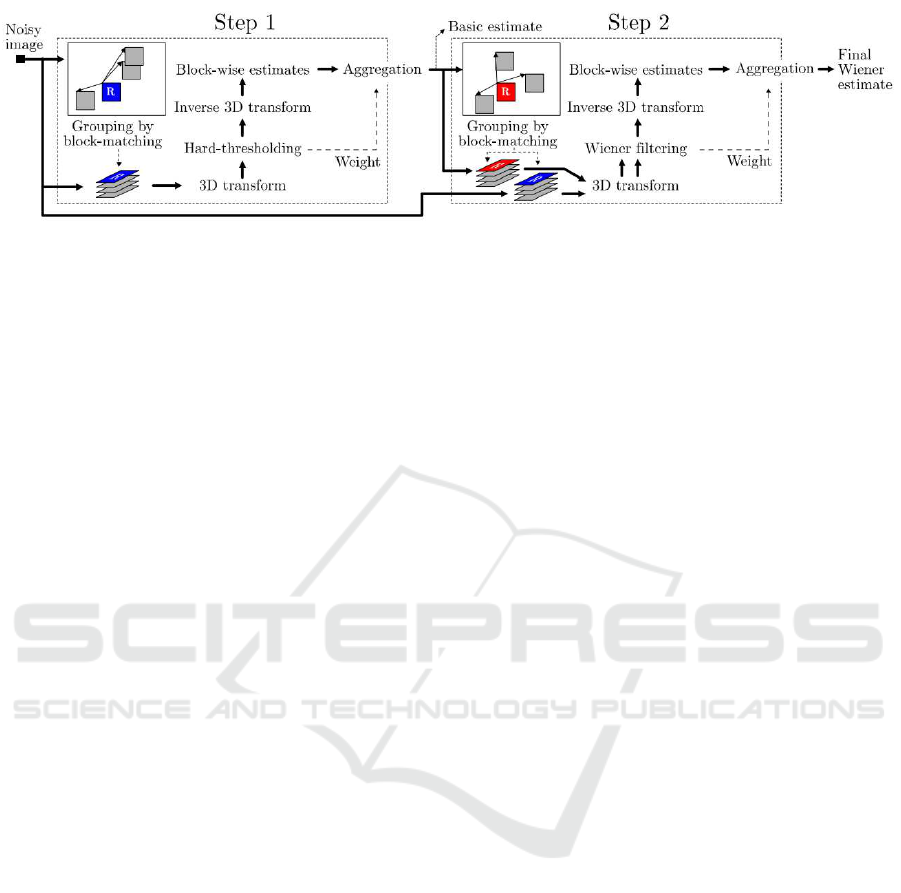
Figure 1: BM3D Block Diagram (Dabov et al., 2007c).
is divided into a number of patches or blocks. A win-
dow is defined centering each patch also referred as
the reference patch and within this window it searches
for the patches similar to the reference patch. As the
initial image is noisy, calculating similarity between
noisy blocks may degrade the performance. So, first
the blocks are filtered by using 2D transformation and
then the obtained coefficients are hard thresholded.
Next euclidean-distance between the reference block
and each of the other blocks are calculated. This
similarity measurement is called d-distance. From
this d-distance values, the similar noisy patches are
grouped together into a set, S
ht
x
R
. From this set, the
noisy blocks are grouped together in a form of 3D
array which we denote Z
S
ht
x
R
. A 3D linear transform
is applied on this 3D blocks and hard thresholding is
applied on the obtained coefficients, called collabora-
tive filtering. This thresholding attenuates the noise.
An inverse 3D transform is applied to get back to the
spatial domain. Equation (3) shows the block-wise
estimation of a 3D block.
ˆ
Y
ht
S
ht
x
R
= τ
ht
3D
−1
(ϒ(τ
ht
3D
(Z
S
ht
x
R
))) (3)
where ϒ is a hard-threshold operator and
ˆ
Y
ht
S
ht
x
R
is
stacked block-wise estimation of noisy blocks in set
S
ht
x
R
. The final operation in the first step of BM3D is
to aggregate all the estimated blocks together. Each
of the estimated sets contain a number of blocks and
these blocks contain one or more same pixel loca-
tions. That means, a single pixel can have more that
one estimation. So to get the final estimation all these
estimations are aggregated together by a weighted av-
eraging method. The basic estimate of the noisy im-
age is then passed to the second step of BM3D to gen-
erate the final estimation of the noisy image.
2.1.2 BM3D Second Step
The basic estimated image coming from the first step
has significantly attenuated noise, compared to the in-
put image. This image is used in the second step as
a reference denoised image of the input image. The
second step of BM3D is identical to the first step. At
first the similar basic estimated blocks are grouped
together for any reference block. But here, instead
of using the thresholding-based d-distance, a normal-
ized squared l
2
-distance is used to calculate the sim-
ilarity. The basic estimated blocks and noisy blocks
from input image are stacked. Wiener shrinkage co-
efficients are generated by applying a 3D transform
on the basic estimated group. The 3D transform co-
efficients of noisy blocks are multiplied, element-by-
element, with the Wiener shrinkage coefficients. This
is called Wiener collaborativefiltering. An inverse 3D
transform is applied to get the estimated pixel values.
These estimated blocks are then aggregated together
to generate the final global estimated image. Aggre-
gation is done by a weighted averaging of the esti-
mated blocks similar to first step.
3 MAIN IDEA
In our study and experiments, we tried to overcome
the limitations of BM3D. We focused on two limita-
tions of BM3D which are:
1. Noise Level: In the implementation of BM3D al-
gorithm, we have found that the actual noise vari-
ance of the image is provided to the algorithm
which is used in both first and second step. In
real time systems, the actual noise variance is not
practical to be provided as an input.
2. Fixed Hard Thresholding: In the first step of
BM3D algorithm, a hard threshold is used to at-
tenuate noise from the 3D blocks. This threshold
is fixed for all the blocks. Using fixed threshold
value deteriorates the performance of this algo-
rithm because for smooth region and textured re-
gion thresholding value should not be same.
We have done several experiments to solve these
two limitations and developed our proposed algo-
rithm. Below is a detailed description of how we
found our solution to these limitations.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
208

3.1 Automated Noise Estimation
While using the authors’ provided matlab software of
BM3D, we have found that the true noise level (stan-
dard deviation) of input noisy image is provided as in-
put. Also, we have observed that if the noise level is
changed a little, then the performanceof the algorithm
varies a lot. So, we can say that the performance of
the BM3D algorithm provided by the BM3D authors
heavily depends on the value of the input parameter.
In our proposed algorithm, we created an auto-
mated noise estimation system where the noise level
of an input image is calculated first. We found that our
noise level estimation is very close to the actual noise
level, hence eliminating such input without degrading
the performance.
For the noise level calculation, we have taken the
idea from the 2D adaptive Wiener filtering (wiener2)
algorithm (Lim, 1990). In this algorithm, image noise
level is estimated based on the local variance of the
image. The local mean and variance around each
pixel are calculated using Equation (4) and (5), re-
spectively
µ(a, b) =
1
MN
∑
x,y∈η
I(x, y) (4)
and
σ
2
(a, b) =
1
MN
∑
x,y∈η
I
2
(x, y) − µ
2
(a, b), (5)
where η is the N×M local neighborhoodof each pixel
in the image I. The noise variance is then calculated
by averaging all the local estimated variance using
Equation (6)
v
2
=
1
MN
∑
x,y∈η
σ
2
(x, y), (6)
where σ
2
(x, y) is the local estimated variance calcu-
lated from Equation (5). From this noise variance,
Equation (6), we can calculate the standard devia-
tion (sigma) of the noisy image. We have experi-
mented using various neighborhood and found that
2 × 2 neighborhood produces the closest estimation
to the actual noise level.
3.2 Context-based Hard Thresholding
In the first step of BM3D algorithm, a hard thresh-
olding is applied on the 3D noisy blocks during the
collaborative filtering. This hard thresholding atten-
uates the noise of corresponding blocks; see Section
2.1.
Note that, the hard threshold operator ϒ is fixed
for every blocks of the image.The BM3D authors
used a fixed value, ϒ = 2.7. For image having noise
level greater than 40 they have changed this value to
ϒ = 2.8. This threshold is used to attenuate the noise
of corresponding block. But using a fixed level of
threshold value is not quite a good choice, as blocks
with different properties should have different thresh-
old values.
We started our experiment to find out whether dif-
ferent blocks should use different threshold values or
not. First, we took two different images, one with
high texture and the other with smooth region and
then applied same level of noise to both of them. Next
we applied BM3D algorithm on them using various
threshold values and took the best denoised image.
We observed that different threshold values are used
to generate best denoised image in each case. The
experiment is also done using an image with various
noise levels and observed that the best threshold value
also changes with the noise level.
4 PROPOSED METHOD
Our proposed algorithm is divided into two main
parts: training and testing. Detailed description of
the algorithm is explained below.
4.1 Training
In the training phase, we developed 10 different clas-
sifier for 10 different noise levels , σ = 10, 20, 30, 40,
50, 60, 70, 80, 90 and 100. Here, image blocks are
used as feature vectors and their corresponding best
threshold value as a label of that vector. Below is a
detailed description for training a single classifier.
4.1.1 Best Threshold Calculation
From the idea of context based hard thresholding, see
Section 3.2, we know that different types of image
blocks should have different threshold values. So, we
conducted experiments on finding the best threshold
value for any reference block.
1. To build a classifier for noise level n, we have ap-
plied AWGN with σ = n to all input images from
the database.
2. The BM3D image denoising algorithm is applied
to these noisy images generated from the previ-
ous step. During collaborative filtering in the first
step, we have used various threshold values for
each block. In our experiments, we have used 22
different threshold values, ranging from 1.7 to 3.8
with step size of 0.1.
BM3D Image Denoising using Learning-based Adaptive Hard Thresholding
209

3. The 22 denoised blocks (based on applying vari-
ous threshold values) are compared with the cor-
responding block in the original true image and
the best among them is selected. The compari-
son is done based on squared euclidean distance
between these two blocks.
4. The threshold corresponding to the best denoised
block is considered to be the best threshold value
of that particular block.
5. Every block and their best threshold value is
stored in a matrix.
After taking all of the best denoised block during
collaborative filtering operation, we found the gener-
ated output to be significantly better than the output
of original BM3D algorithm in terms of PSNR and
visual quality. To asses the performance, we have
conducted this experiment and found that the PSNR
is improved by about 3 decimal (on average) when
the best threshold is used, for a given noise level.
4.1.2 Feature Generation
1. For any input image, each of the image block
is considered as a feature vector and their corre-
sponding best threshold value is considered as la-
bel of that feature.
2. Since we are considering blocks of size 7×7, thus
each feature consists of 49 noisy pixel values.
3. In an image of size M × N, a total M × N feature
vectors are generated, each of length 49 features.
4. To reduce memory and time complexities, we
have only taken 10% of the total features, by tak-
ing one feature and leaving the followingnine fea-
tures.
4.1.3 Training Features
1. The generated features and their correspondingla-
bels are used to train a classifier that will be used
in the next part of the algorithm.
In our experiment, we have used different classifica-
tion techniques namely, Naive Bayes, SVM, K Near-
est Neighborhood and Random Forest to find out the
best classifier for our algorithm. Based on their per-
formance we have decided to use Random Forest (RF)
classification algorithm. Random forests are an en-
semble learning method for classification. It is op-
erated by constructing a multitude of decision trees
(classification trees) at training time and outputting
the class that is the mode of the classes of the individ-
ual trees. To classify a new object from an input vec-
tor, put the input vector down each of the trees in the
forest. Each tree gives a classification which means
the tree votes for that class. The forest chooses the
classification having the most votes (over all the trees
in the forest) (Breiman, 2001).
4.2 Testing
In testing step, the classifier developed in the training
part is used to generate the appropriate threshold to be
used to denoise the input image. Detailed description
of the testing phase is given part by part below.
4.2.1 Noise Calculation and Classifier Selection
1. From the test image, initial noise level is calcu-
lated using the algorithm described in Section 3.1.
2. The noise is then rounded to the nearest multiple
of 10. If the value is more than 100, it is clipped
at 100.
3. From the 10 trained classifiers, we choose our
classifier based on the noise level.
4.2.2 Feature Vector Generation
1. The noisy input image is divided into several
blocks of size 7 × 7. These 49 noisy pixels are
considered the feature vector of a single block.
2. Feature vectors are generated from all of the
blocks of the noisy image.
4.2.3 Classification
1. The feature set is passed to the classifier.
2. The classifier will return the label of each feature
vector.
3. Each of the noisy blocks are then assigned their
corresponding best threshold value.
4.2.4 Output Generation
1. The noisy image is filtered using BM3D image
denoising algorithm with our predicted noise level
where in the collaborative filtering step, adaptive
thresholding is applied.
2. All other operations will remain the same as in the
original BM3D. After the second step of BM3D,
our final denoised image is generated.
5 RESULT ANALYSIS
In this section we will compare the performance of
our proposed method with the state-of-art BM3D im-
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
210

(a) Boat2 (b) Lighthouse (c) Woman (d) Sail (e) Statue (f) Model
(g) Beach (h) Bike (i) Bridge (j) Cottage
(k) Door (l) Flower (m) Raft (n) Girl
(o) Hats (p) House2 (q) Houses (r) Windows
(s) Island (t) Lake (u) Landscape (v) Lighthouse2
(w) Parrot (x) Plane
Figure 2: Training Image set (Kodak Image set).
BM3D Image Denoising using Learning-based Adaptive Hard Thresholding
211

(a) Cameraman (b) House (c) Peppers (d) Lena (e) Barbara
(f) Boat (g) Fingerprint (h) Man (i) Couple (j) Hill
Figure 3: Training Image set (Subset of BM3D Test Image set).
age denoising algorithm and the Non-Local Means
(NLM) algorithm.
5.1 Experimental Setup
The performance of our proposed algorithm is con-
ducted on two sets of images: Kodak image set and
BM3D image set. For training the classifiers, we
have used Kodak image set which contains 24 differ-
ent grayscale images. For testing, we have taken 10
grayscale images from the BM3D image set. Both of
these set have images containing textured and smooth
regions. The training and test image set is shown in
Fig. 2 and 3, respectively.
5.2 Performance Measurement Metrics
The performance of our experiments are measured us-
ing both subjective and objective fidelity criteria. Ob-
jective fidelity criteria gives us blind results which is
good for understanding the differences between the
outputs and for subjective fidelity criteria, we ob-
served how human eyes perceiving the denoising per-
formance.
For objective fidelity criteria, we have used two
standard measurement metrics. One is Peak Signal
to Noise Ratio (PSNR) which is measured by com-
paring the pixel intensities between original and es-
timated denoised image. The PSNR of an estimated
image ˆy of a true image y, is computed according to
the following standard formula:
PSNR( ˆy) = 10log
10
255
2
∑
x∈X
(y(x) − ˆy(x))
2
!
(7)
The other metric is The Structural Similarity Image
Measurement (SSIM) technique. SSIM is a measure-
ment metric measuring similarity between two im-
ages (Wang et al., 2004). SSIM is first calculated
between patches and the final score is given by av-
eraging all the patch scores. The SSIM between two
blocks is calculated using the following formula:
SSIM(x, y) =
(2µ
x
µ
y
+ c
1
)(2σ
x,y
+ c
2
)
(µ
2
x
+ µ
2
y
+ c
1
)(σ
2
x
+ σ
2
y
+ c2)
(8)
where µ and σ are mean and standard deviation of a
particular block and σ
x,y
is the co-variance between
two blocks.
5.3 Parameters Selection
In our proposed method, the parameters for best win-
dows size (for noise calculation), threshold range and
classifier selection is generated empirically by exper-
iments.
To find the best window size in automated noise
estimation step (see Section 3.1), experiment is done
on our training image set. We applied 10 different
noise levels to these images and estimated the noise
level using Equation (6). Different windows sizes are
used to find out the best window size value. It is ob-
served that for windowsize, 2×2, the estimated noise
level is almost close to the actual noise applied on
these images. Table 1 shows these results.
In our proposed method, 22 predefined threshold
values are used in the collaborative filtering step of
BM3D. From these threshold values,the best thresh-
old value is used for thresholding a particular block.
We have performed experiments based on different
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
212

Table 1: Comparing estimated noise with true noise based on different window size.
Noise Level
Window Size (η× η)
2 × 2 3× 3 5× 5 7× 7 9× 9 11× 11
10 11.21 14.19 16.79 18.89 20.68 22.25
20 20.15 22.39 24.12 25.63 26.98 28.20
30 30.58 31.64 32.88 34.01 35.04 35.99
40 40.13 41.24 42.20 43.09 43.91 44.67
50 50.24 51.00 51.77 52.50 53.17 53.81
60 60.22 60.83 61.48 62.09 62.67 63.21
70 70.19 70.71 71.27 71.80 72.30 72.77
80 80.18 80.62 81.11 81.57 82.01 82.43
90 90.15 90.55 90.98 91.39 91.79 92.16
100 100.12 100.50 100.88 101.25 101.61 101.95
Table 2: PSNR comparison for different threshold range.
Noise Level
Threshold Range (Total Number of Threshold Values)
2.7 (1) 2.3-3.1 (7) 2.1-3.4 (14) 1.9-3.6 (18) 1.7-3.8 (22) 1.5-4.0 (26)
10 34.45 35.42 35.95 36.39 36.91 36.93
20 31.21 32.27 32.82 33.32 33.95 33.98
30 29.39 30.51 31.08 31.60 32.30 32.33
40 27.95 29.43 30.05 30.58 31.28 31.31
50 27.05 28.12 28.70 29.25 29.97 30.02
60 26.25 27.33 27.91 28.47 29.20 29.25
70 25.56 26.67 27.26 27.81 28.55 28.61
80 24.97 26.10 26.69 27.25 27.99 28.05
90 24.45 25.60 26.19 26.75 27.49 27.56
100 23.98 24.47 25.75 26.30 27.05 27.12
Table 3: Performance comparison using different classifiers for testing set (Based on PSNR).
Noise Naive SVM SVM SVM K-NN (k) RF (Number of Trees)
Level Bayes (Linear) (Poly) (RBF) (1) (5) (5) (10) (15)
10 33.25 31.90 33.48 34.25 33.54 34.34 34.42 35.11 35.75
20 29.97 28.26 29.87 31.41 29.96 30.89 31.19 32.03 32.61
30 28.17 26.88 28.40 29.46 28.41 29.25 29.37 30.17 30.84
60 26.75 25.61 27.01 28.08 27.07 28.04 27.94 28.81 29.69
50 25.84 24.67 26.09 26.99 26.12 27.01 27.06 27.90 28.48
60 25.07 23.78 25.17 26.18 25.32 26.12 26.28 27.16 27.68
70 24.42 23.31 24.68 25.50 24.74 25.67 25.59 26.52 27.00
80 23.82 22.89 24.32 24.85 24.33 25.18 25.01 25.96 26.42
90 23.31 22.21 23.62 24.27 23.24 24.19 24.48 25.46 25.91
100 22.88 21.26 22.63 23.65 22.69 23.68 23.90 25.03 25.44
Average 26.35 25.08 26.53 27.46 26.54 27.44 27.52 28.41 28.98
threshold ranges to find the range which provides the
best image. Table 2 shows the result of denoised im-
age based on different threshold ranges. It can be ob-
served that if we increase the threshold range, the per-
formance increases. But using 22 and 26 threshold
values produces almost same results. However, tak-
ing 26 threshold values increases the number of class
labels. So, we have taken 22 classes to reduce the
BM3D Image Denoising using Learning-based Adaptive Hard Thresholding
213
time complexity.
Our proposed algorithm requires a classifier to
train. For finding the best classifier, we have tested
our method using various classifiers, such as Naive
Bayes, Support Vector Machine (SVM), K-Nearest
Neighbor and Random Forest. Our experiment shows
that using Random Forests provides the best accuracy
based on PSNR of the denoised image. Table 3 shows
the performance of average denoising result on our
test images.
5.4 Performance Evaluation
The performance of our proposed method is com-
pared with the original BM3D scheme. Also we have
compared with another state-of-art denoising algo-
rithm in spatial domain namely, Non-Local Means
(NLM). Table 4 and 5 shows the average PSNR and
SSIM performance for all test images. The bolded
values represent the best among all these algorithms.
From the results, we can easily observe that our pro-
posed algorithm achieved better performance in both
PSNR and SSIM metrics.
Table 4: PSNR comparison.
Noise Level NLM BM3D Proposed
10 33.10 34.45 35.75
20 29.92 31.21 32.61
30 27.79 29.39 30.84
40 26.23 27.95 29.69
50 25.01 27.05 28.48
60 24.03 26.25 27.68
70 23.21 25.57 27.00
80 22.52 24.97 26.42
90 21.90 24.45 25.91
100 21.35 23.98 25.44
Average 25.51 27.53 28.98
Table 5: SSIM comparison.
Noise Level NLM BM3D Proposed
10 0.895 0.919 0.942
20 0.812 0.865 0.903
30 0.734 0.824 0.875
40 0.660 0.786 0.854
50 0.592 0.759 0.827
60 0.531 0.733 0.807
70 0.478 0.709 0.789
80 0.431 0.687 0.773
90 0.390 0.667 0.758
100 0.355 0.647 0.744
Average 0.590 0.761 0.828
(a) (b)
(c) (d)
(e) (f)
Figure 4: Performance Comparison between BM3D and
Proposed Method (a) Original Image (b) Noisy Image
(AWGN added with σ = 100) (c) BM3D (d) Proposed
Method (e) Zoomed BM3D (f) Zoomed Proposed Method.
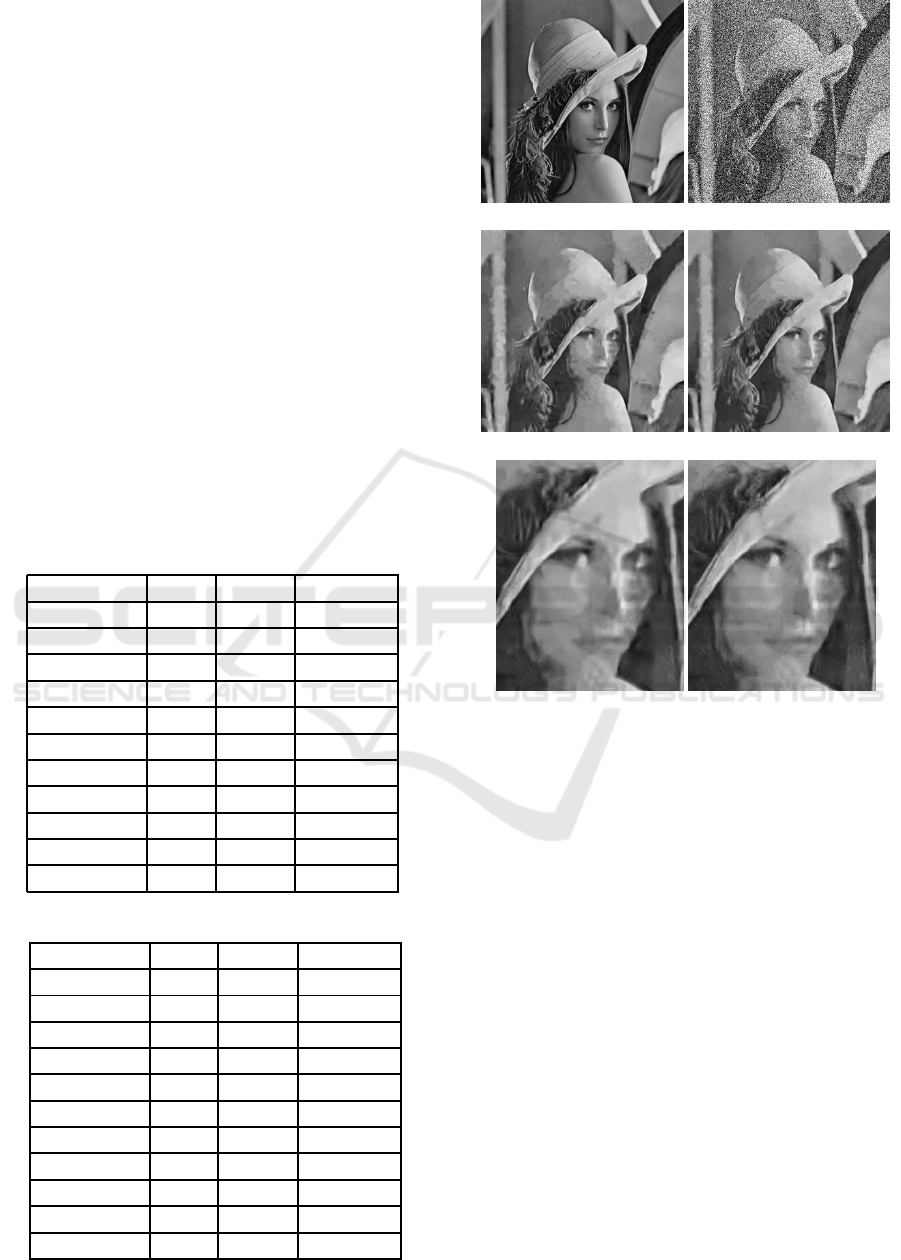
Fig. 4 shows a subjectuve comparison between
our proposed algorithm and BM3D. We have applied
AWGN noise with σ = 100 on the popular Lena im-
age and denoised it with the original BM3D and our
proposed algorithm. From the subjective viewpoint
the face of Lena is more clear in denoised image pro-
duced using our proposed method, see Fig. 3(e) and
3(f).
5.5 Intensity Profile
Intensity profile is a measure for inspecting how sharp
the edges are after denoising. In an intensity profile,
we choose one scan line on the true image, noisy im-
age and denoised image and plot them together to see
how close the denoised profile is to the original pro-
file. Also, it shows us how sharp the edges are after
achieving denoising.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
214
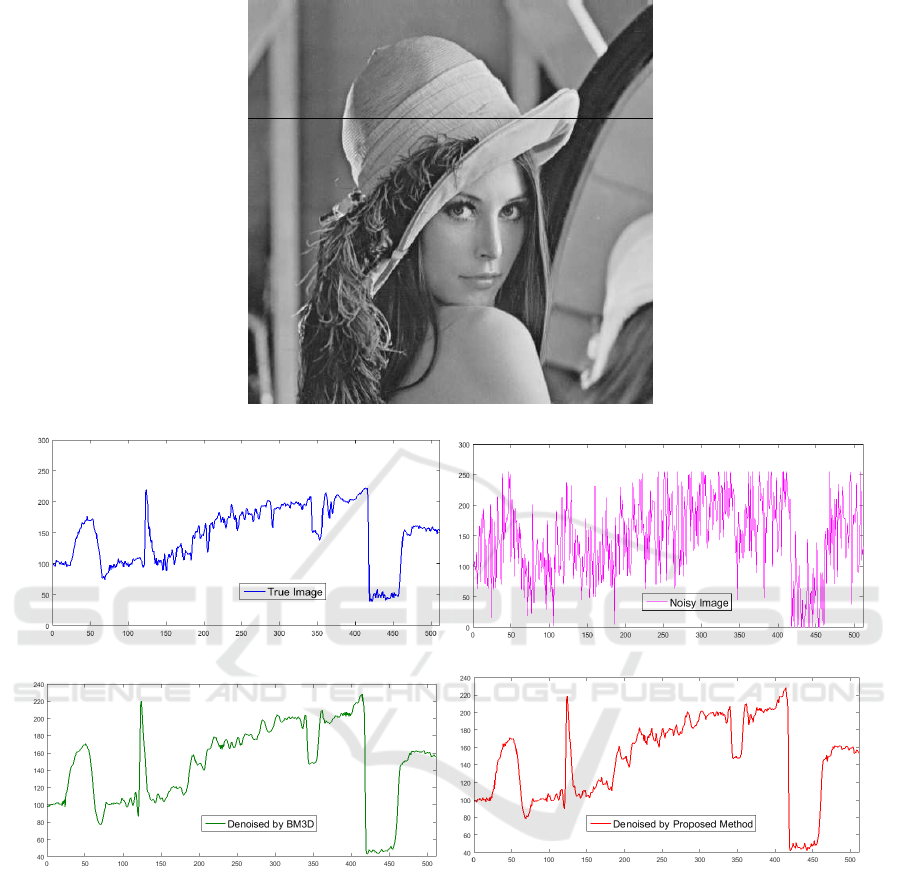
(a)
(b) (c)
(d) (e)
Figure 5: Intensity Profile for Lena Image at scan Line 100 (σ = 50) (a) Lena Image (b) Original Image (c) Noisy Image
(Pearson correlation = 0.5220) (d) Denoised by BM3D (Pearson correlation = 0.9836) (e) Denoised by Proposed Method
(Pearson correlation = 0.9934).
Let us consider the Lena image given in Figure
5(a). Here, we consider the 150
th
row (indicated by
red line) for our intensity profile calculation. A plot
of this scan line is shown in Figure 5(b). We added
AWGN with σ = 50 to the image and plot that scan
line in Figure 5(c). We can see a lot of noise added
to each of the pixel. Now, to check how close our
proposed method (as well as BM3D) is to the true
noise free image, we perform the same task. That is,
we consider the 150
th
row from our denoised image
and BM3D’s denoised image and plot them. This is
shown in Figure 5(d) and 5(e) respectively.
It is clear from these plots that our proposed meth-
ods signal is closer to the true signal versus BM3D
counterpart. Also, the Pearson correlation between
the intensity profile of the original image and the pro-
posed method is higher compared to BM3D.
6 CONCLUSION
In this paper, we have proposed a context-based adap-
BM3D Image Denoising using Learning-based Adaptive Hard Thresholding
215

tive hard thresholding to overcomethe shortcoming of
using fixed hard thresholding in BM3D. Experimen-
tal result shows that we have achieved significant im-
provement over the original algorithm. However our
algorithm requires training classifiers, hence the time
complexity is higher than the original BM3D. Once
the machines are trained, it requires little amount of
time to predict the label of each image block and
hence the time complexity is similar to BM3D. In fu-
ture, we will continue our work to adaptively adjust
other fixed parameters used in BM3D. Also, we will
extend our idea to denoise color image and video se-
quences also.
ACKNOWLEDGEMENTS
This research is partially funded by the Natural Sci-
ences and Engineering Research Council of Canada
(NSERC). This support is greatly appreciated.
REFERENCES
Breiman, L. (2001). Random forests. Machine Learning,
45(1):5–32.
Buades, A., Coll, B., and Morel, J. (2005). A non-local
algorithm for image denoising. In Proc. IEEE Inter-
national Conference on Computer Vision and Pattern
Recognition (CVPR).
Chaudhury, K. N. and Singer, A. (2012). Non-local eu-
clidean medians. IEEE Signal Processing Letters,
19(11):745–748.
Dabov, K., Foi, A., and Egiazarian, K. (2007a). Video de-
noising by sparse 3d transform-domain collaborative
filtering. In Proc. European Signal Processing Con-
ference (EUSIPCO).
Dabov, K., Foi, A., Katkovnik, V., and Egiazarian, K.
(2006). Image denoising with block-matching and 3d
filtering. In Proc. SPIE Electronic Imaging.
Dabov, K., Foi, A., Katkovnik, V., and Egiazarian, K.
(2007b). Color image denoising via sparse 3d collabo-
rative filtering with grouping constraint in luminance-
chrominance space. In Proc. IEEE International Con-
ference on Image Processing (ICIP).
Dabov, K., Foi, A., Katkovnik, V., and Egiazarian, K.
(2007c). Image denoising by sparse 3d transform-
domain collaborative filtering. IEEE Transactions on
Image Processing, 16(8):2080 – 2095.
Dabov, K., Foi, A., Katkovnik, V., and Egiazarian, K.
(2009). Bm3d image denoising with shape-adaptive
principal component analysis. In Proc. Workshop on
Signal Processing with Adaptive Sparse Structured
Representations (SPARS).
Dai, L., Zhang, Y., and Li, Y. (2013). Bm3d image denois-
ing algorithm with adaptive distance hard-threshold.
International Journal of Signal Processing, Image
Processing and Pattern Recognition, 6(6):41–50.
Gonzalez, R. C. and Woods, R. E. (2008). Digital Image
Processing. Prentice-Hall Inc.
Hasan, M. and El-Sakka, M. R. (2015). Structural similarity
optimized wiener filter: A way to fight image noise.
In Proc. International Conference on Image Analysis
and Recognition (ICIAR).
Lim, S. J. (1990). Two-Dimensional Signal and Image Pro-
cessing. Prentice Hall, New Jersey, USA.
Mittal, A., Moorthy, A. K., and Bovik, A. C. (2012). Au-
tomatic parameter prediction for image denoising al-
gorithms using perceptual quality features. In Proc.
SPIE Human Vision and Electronic Imaging.
Perona, P. and Malik, J. (1990). Scale-space and edge de-
tection using anisotropic diffusion. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
12(7):629 – 639.
Rehman, A. and Wang, Z. (2011). Ssim-based non-local
means image denoising. In Proc. IEEE International
Conference on Image Processing (ICIP).
Thaipanich, T., Oh, B. T., Wu, P., and Kuo., C. J. (2010).
Adaptive nonlocal means algorithm for image denois-
ing. In Proc. IEEE International Conference on Con-
sumer Electronics (ICCE).
Wang, Z., Bovik, A., Sheikh, H. R., and Simoncelli, E.
(2004). Image quality assessment: from error visi-
bility to structural similarity. IEEE Transactions on
Image Processing, 13(4):600–612.
Wiener, N. (1949). The Interpolation, Extrapolation and
Smoothing of Stationary Time Series. MIT press, New
York.
VISAPP 2016 - International Conference on Computer Vision Theory and Applications
216
