A Fuzzy Approach to Discriminant Analysis based on the Results of

an Iterative Fuzzy k-Means Method

Francesco Campobasso and Annarita Fanizzi

Department of Economics and Mathematics, University of Bari, Via C. Rosalba 53, 70100 Bari, Italy

Keywords: Fuzzy Discriminant Analysis, Non Linear Regression Models, Iterative Fuzzy k-Means Method,

Entrepreneurial Propensity.

Abstract: The common classification techniques are designed for a rigid (even if probabilistic) allocation of each unit

into one of several groups. Nevertheless the dissimilarity among combined units often leads to consider the

opportunity of assigning each of them to more than a single group with different degrees of membership. In

previous works we proposed a fuzzy approach to discriminant analysis, structured by linearly regressing the

degrees of membership of each unit to every groups on the same variables used in a preliminary clustering.

In this work we show that non-linear regression models can be used more profitably than linear ones. The

applicative case concerns the entrepreneurial propensity of provinces in Central and Southern Italy, even if

our methodological proposal was initially conceived to assign new customers to defined groups for

Customer Relationship Management (CRM) purposes.

1 INTRODUCTION

The statistical literature proposes two main lines of

investigation on fuzzy discriminant analysis: one is

focused on the estimation of the coefficients

associated to Fisher’s linear function by maximizing

the so called ratio of fuzzy variances (Watada et al.,

1986); the other, although particularly complex from

a computational point of view, is based on the kernel

method and captures non-linear structures of clusters

(Wu and Zhou, 2006). There have been several

successful applications and developments of such

two lines of investigation in their respective fields of

application (for example (Zhao et al., 2012); (Song

et al., 2010); (Heo and Gader 2011)).

Whatever the fuzzy clustering from which the

discriminant analysis starts, each unit of the starting

collective is in any case attributed to more than one

group with different degrees of membership ranging

in the interval [0,1]: in particular, values of the latter

closer to 1 indicate a greater similarity of such an

unit to the other elements in the group (Campobasso

et al., 2008).

We have recently used the aforesaid values in an

attempt to attribute a new observation to previously

identified fuzzy groups (Campobasso and Fanizzi,

2013). Our proposal was to linearly regress the

degrees of membership to each group on the same

variables used in a preliminary clustering operation

of the sampled units.

In this work we show that non-linear regression

models may better fit such degrees of membership.

The application case deals with economic and

demographic data extracted from the Italian Atlas of

the competitiveness of provinces and regions edited

by UnionCamere, which capture some aspects of the

entrepreneurship provincial economy in Central and

Southern Italy in 2009. In particular, after

classifying with a fuzzy approach some of the

sampled provinces in order to identify homogenous

groups for entrepreneurial propensity, the remaining

ones are assigned to such groups by means of the

estimated discriminant model. In this case the

preliminary clustering is carried out by the fuzzy k-

means method, which appears more robust than

hierarchical ones, in the sense that it is less affected

by the presence of measurement errors or other

spurious sources of variance (and, consequently,

allows us to identify more cohesive groups).

Since, however, there might be no a priori

information about the number k of groups in which

the collective ought to be allocated, it is appropriate

to implement an iterative procedure of the fuzzy k-

means method, which can suggest such a number as

a function of appropriate indices of efficiency in

grouping.

257

Campobasso F. and Fanizzi A..

A Fuzzy Approach to Discriminant Analysis based on the Results of an Iterative Fuzzy k-Means Method.

DOI: 10.5220/0004553802570264

In Proceedings of the 5th International Joint Conference on Computational Intelligence (FCTA-2013), pages 257-264

ISBN: 978-989-8565-77-8

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

The reliability of the proposed discriminant

model is verified by comparing the obtained results

with the ones of our previous suggestion (based on

linear regression models) and also of a classical

discriminant analysis.

Note that such a fuzzy algorithm was initially

designed for an automotive dealer, where new

customers had to be assigned to defined groups for a

Customer Relationship Management (CRM)

application.

2 FUZZY DISCRIMINANT

MODEL

In a recent work we proposed to evaluate, after a

preliminary fuzzy clustering, the weight that each of

the used p variables has had in determining the

degrees of membership of the sampled units to the k

identified groups. For this purpose, we estimated as

many linear regression functions as the considered

groups, thus explaining the degrees of membership

ikig2i1i

...,,...,,,



of the i.th unit to them:

.x...xx

...

,x...xx

....

,x...xx

ikipkp2i2k1i1k0kik

igipgp2i2g1i1g0gig

1iipp12i121i11101i





In so doing, we could define a discriminant model

that allows to estimate the degree of awarding of any

other not sampled unit to the previous k groups. In

other word such a model establishes a hierarchy of

assignment of a generic new observation, that can be

used as a weighting system for further analysis. It is

possible to demonstrate that, as well as the sum of

the degrees of membership to k groups of the i.th

sampled unit equals 1, also the sum of the estimated

degrees of membership of each not sampled unit

equals 1.

Some of the estimated degrees of membership of

the i.th element may be less than zero, expressing a

lack of membership to the considered group. In this

case the other degrees of the i.th unit greater than

zero can be normalized, after setting each of the

negative ones equal to zero. In particular, assuming

that



2i1i



0 in the case of four groups, it would

be sufficient to ensure





and to normalize

the remaining degrees of membership in the

following way

)

ˆˆ

(

4i3i3i





)

ˆˆ

(

4i3i4i





which leaves the total sum equal to one.

The same discriminant logic can be defined

considering non-linear regression functions,

according to which the marginal effect of a single

independent variable on the degree of membership



of the unit i.th to the g.th group is not constant.

In particular we take into account the r.th order

polynomial functions, still linear in parameters but

no longer in independent variables, which take the

following form:

....x...x...x...

...

,...x...x...x...

....

,...x...x...x...

ij)rr(pjk

ijpjkijkj0kik

ij)1r(pjg

ijpjgijjg0gig

ij)1r(pj1

ijpj1ijj1101i







Such a model better fits the degrees of membership

ikig2i1i

...,,...,,,



, which could increase as well

as decrease at rates which actually vary depending

on the values assumed by the independent variables

ikig2i1i

x...,,x...,,x,x

. In other words it may

happen that the awarding of any unit to one of the k

groups becomes more marked for certain values of

ipig2i1i

x...,,x...,,x,x

than for others.

Note that a higher order r makes the regression

function more flexible and, therefore, allows us to

express more precisely the behavior of the degrees

of membership at different levels of the independent

variables. On the other hand, a lower value of r

allows to have a more parsimonious model, which is

also easier to interpret.

In summary our proposal, framed in the context

of the relationships between clustering variables but

not focused on the fuzzy (within and between)

variances, is to express the degrees of membership

of any unit to each group as non linear functions of

the same variables used in a preliminary clustering.

Since the adjusted R

coefficient of

determination provides a measure of the residual

sum of squares of the dependent variable in relative

terms (i.e. with respect to the total deviance of such

a variable) for each regression function,

characterized by its own specification, then an index

of reliability of the discriminant model is given by

the simple average of the adjusted R

coefficients

associated to the k estimated regression functions.

Note that the simple average is allowed because the

number of the observations does not differ from one

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

258

function to another (whereas the number of

independent variables, although variable, is taken

into account by means of the adjustment of the R

coefficients of determination).

3 AN APPLICATION CASE:

THE LEVEL OF

ENTREPRENEURIAL

PROVINCIAL PROPENSITY IN

CENTRAL AND SOUTHERN

ITALY

The entrepreneurial capacity of a territory is

recognized more and more widely as an important

vehicle for economic development, or as a major

stimulus to growth in terms of productivity,

innovation and employment. In the proposed

application case we seek to analyze the provincial

level of such a capacity in Central and Southern

Italy, during the dark year 2009 of the economic

crisis (National Institute for Foreign Trade, Italy in

the International Economy - Summary Report for

2008-2009)

For this purpose, we extract specific indicators

from the Italian atlas of the competitiveness of

provinces and regions edited by UnionCamere,

which can capture some aspects of provincial

entrepreneurship for the year under review.

The business density, measured by the ratio

between the number of active companies and the

resident population (in percentage terms), and the

density of the local units, measured by the ratio

between the total number of local units and the

considered area in square kilometers (in percentage

terms), are two indicators that describe the

entrepreneurial propensity of a territory.

These indicators do not provide qualitative

information on the economy of a territory, but are

certainly useful in comparisons between

geographical areas, and between the various sectors

of an economic activity.

Another demographic indicator that can be used

in our analysis is the rate of entrepreneurial

evolution, measured by the difference between the

corresponding birth and death rates of businesses.

The first one, representative of the productive

renewal, is defined as the number of new companies

(except for farms) registered in the records kept by

the Chambers of commerce, industry, agriculture

and crafts, with respect to those existing at the

beginning of the period (in percentage terms); the

second one, instead representative of the productive

obsolescence, is defined as the number of companies

(except for farms) deleted from such records, with

respect to those existing at the beginning of the

period (in percentage terms).

The last indicator used to evaluate the territorial

dynamism is the export propensity, defined as the

ratio between the total amount of exports in one year

and the produced added value in the same time

frame (in percentage terms).

On the basis of these indicators, which are

weakly correlated with one another (Table 1), we

randomly select the 80% of the 61 provinces in

Central and Southern Italy, afterwards we identify

homogeneous groups with a fuzzy approach, and

finally we estimate the proposed discriminant model,

in order to assign the remaining 20% of the

provinces to such groups.

Table 1: Correlation coefficients between the considered

indicators.

Business

density

Density of the

local units

Rate of

evolution

Export

propensity

Business

density

- -0.15 0.19 0.03

Density of the

local units

- 0.18 0.07

Rate of

evolution

- 0.17

Export

propensity

3.1 Identification of Homogeneous

Fuzzy Groups of the Provinces

3.1.1 Fuzzy k-Means Method

In a hierarchical clustering method any improper

aggregation of units carried out in early stages of the

iterative process can undermine the aggregations in

subsequent stages (Campobasso and Fanizzi, 2013).

On the contrary, in the context of a non-hierarchical

clustering method, the allocation of every unit into

groups is modified until the classification process

does not reach convergence.

Among the non-hierarchical methods, also

defined as optimization techniques, we choose the

fuzzy k-means one (Kaufman and Rousseau, 1990),

which is a generalization of the homonymous classic

method. The corresponding iterative process

minimizes a function of the Cartesian distance

between the elements of each group, once weighted

by the degree of membership to the group itself, and

their centroid.

In particular, let



be the degree of

AFuzzyApproachtoDiscriminantAnalysisbasedontheResultsofanIterativeFuzzyk-MeansMethod

259

membership of the i-th element (i = 1, 2, …, n) to

the g-th cluster (g = 1, 2, .., k) underlying the

following two constraints: 0 ≤



≤ 1 and









Then the procedure estimates the values of



minimizing the object function







d)v,U(J



, with respect to the matrix U

of the degrees of membership



and to the

centroids vector v = (v

, v

, …, v

). The generally

used metric is the Euclidean one on standardized

variables, but it is possible to adopt other metrics

with appropriate precautions.

The main limitation of this procedure, as well as

of any non-hierarchical method, is the need to know

the number of groups in which the collective should

be shared. For this purpose we propose an iterative

process of the fuzzy k-means method for increasing

values of k.

3.1.2 An Iterative Process of the Fuzzy

k-Means Method

The iterations of the fuzzy k-means method cannot

exceed a certain limit, as it would be difficult to

analyze a number of groups too high compared to

the available observations.

Therefore, after the completion of the iterations,

it is necessary to determine such a number,

depending on the actual effectiveness of the fuzzy

clustering.

The latter is more effective when it is able to

capture the degree of fuzziness of the observed units

in belonging to different groups, without causing

difficulties in the interpretation of the final

classification.

In particular the

partition coefficient (Bezdek,

1981) of a fuzzy classification in k groups









g,i

, measures such a degree of

fuzziness and is included in [1/k,1]. A normalized

version of it, which takes values in [0,1], is

represented by

1kF



 . The higher the value of

, the more efficient the partition is.

The efficiency of a fuzzy classification in k

groups can also be expressed by the

index of entropy

(Bezdek, 1981)







g,i

g,ik

)log(



which varies from 0 up to log (k). The minimum

value is obtained in the case of hard clustering,

whereas the maximum one in the case of maximum

uncertainty (in which all the degrees of membership

equal 1/k).

A normalized version of it, which takes values in













 n/k1

)klog(

is represented by

n/k1





. The

less the value of

, the more efficient the

partition is. In correspondence of k = 2,

often

assumes a relative minimum value, to be compared

with any other.

The so far mentioned indices do not involve the

observed values, but only the membership of the

units, apart from the form taken by the obtained

clusters. Therefore they can be only used to compare

groupings obtained for different values of k through

the same clustering method.

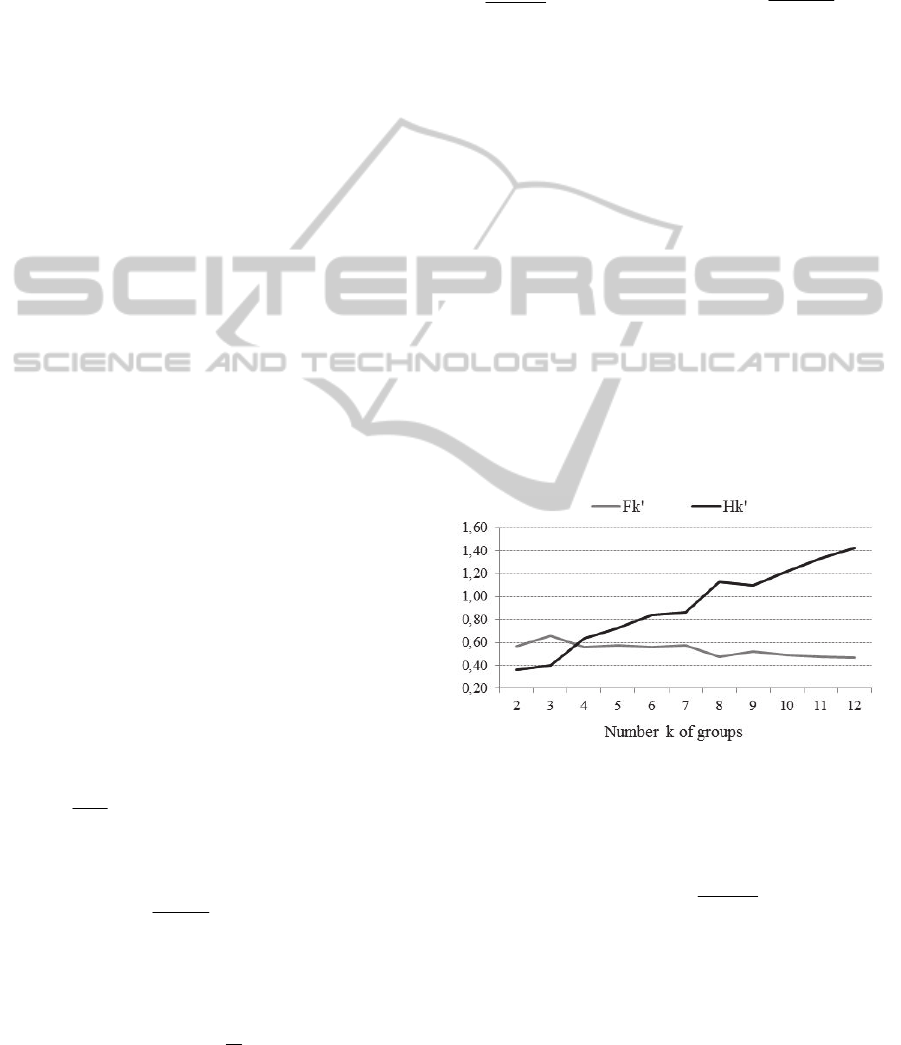
In the present case the values assumed by two

indices

and

are calculated for increasing

values of k by means of Matlab Editor. Their

graphical representation leads to divide the

provinces of Central and Southern Italy in three

groups; in correspondence of k=3, in fact,

reaches a relative maximum value and

relative minimum value.

Figure 1: Indices of efficiency in clustering for increasing

values of k.

In order to determine the "goodness" of the

clustering results, we use the so called

separation

coefficient



















gh,gk

maxg

, where

)d(maxr

k,ik,i

ni1







is the radius of the k.th group.

Such a radius is defined as the maximum distance

between its centroid and the n units of the entire

collective, weighted by the respective degrees of

membership.

The coefficient g is a functional validation index,

deliberately distinct from those used for the choice

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

260

of k, and it measures the compactness of the clusters

of a fuzzy partition, by comparing their radius with

the distance between the corresponding centroids.

Such a coefficient is obtained as the maximum ratio

of the sum of the radii of the two groups on the

distance between their centroids.

If it is less than one, then the structure of the

groupings is robust, in the sense that the minimum

distance between groups is greater than the

maximum sum of the radii. If, instead, it is equal to

one, then the clusters are tangent, i.e. the minimum

distance is equal to the maximum sum of the radii.

Finally, if it is greater than one, then the clusters

are intersecting, i.e. the minimum distance is less

than the maximum sum of the radii.

Since the separation coefficient of the identified

fuzzy partition shows a value of 0.042, then the

structure of the latter is robust and plausible.

3.2 The Identified Groups

With reference to the application case, the

preliminary analysis of the data set suggests the

subdivision of the collective into three groups.

Since the fuzzy classification generates groups to

which the elements do not belong separately, we

suggest to define the profile of each group by

calculating the weighted average of the values of the

indicators of all the sampled provinces by the

corresponding degrees of membership to all the

groups (Table 2).

Table 2: Average values of the considered indicators

weighted by the degrees of membership of each province,

by group

Business

density

Density of the

local units

Rate of

evolution

Export

propensity

Group 1 8.70 17.50 -0.41 9.94

Group 2 9.81 15.17 0.39 10.28

Group 3 9.41 21.40 0.27 21.36

The first group identifies a low level of

entrepreneurial propensity, on average characterized

by a negative

rate of evolution (equal to -0.41), but

also by a

business density and an export propensity

(respectively equal to 8.45 and 9.94) which are both

lower than the other two groups.

The second group identifies an

intermediate level

of entrepreneurial propensity

, on average

characterized by a positive

rate of evolution (equal

to 0.39), but also by a

business density and an export

propensity

(respectively equal to 9.81 and 10.28)

which are both slightly higher than the first group.

The last group identifies a

high level of

entrepreneurial propensity

, on average characterized

by an

export propensity and a density of the local

units which are both by far the highest (respectively

equal to 21.36 and 21.40).

Actually the provinces characterized by a

predominant degree of membership (greater than

0.5) to the group with a

low level of entrepreneurial

propensity are all located in the South and Islands,

while those to the group with a high level of

entrepreneurial propensity are all located in Central

Italy.

Note that a sharper clustering might be obtained

by assigning each sampled province to the group

with respect to which its degree of membership is

the highest among the three ones.

3.3 Estimation of the Fuzzy

Discriminant Model

Once the three fuzzy groups are identified, it is

possible to determine the weight of the clustering

variables in the explanation of the corresponding

degrees of membership for each sampled province.

For this purpose, as extensively discussed above, we

first estimate a linear regression model in which the

latter ones are function of the former ones (Table 3).

Table 3: Estimated coefficients of the linear regression

models, by group.

Group 1 Group 2 Group 3

Intercept 0.32*** 0.40*** 0.28***

Business density -0.14*** 0.12*** 0.02

Density of the local

units

0.00 -0.03 0.04*

Rate of evolution -0.06*** 0.06*** 0.00

Export propensity -0.05** -0.10** 0.16***

Adjusted R

0.58*** 0.52*** 0.59***

Index of reliability of the discriminant model 0.56

*** significant at 0.01 level ** significant at 0.05 level

* significant at 0.10 level

Note that the adjusted R

coefficients of

determination associated to the three linear

regressions are significant and all greater than 0.5,

so that their simple average equals 0.56. Therefore

the discriminant model reaches an acceptable level

of reliability for the collective under examination.

Now we show that the quadratic regressions are

more suitable than the linear regressions in the

estimation of the degrees of membership (Table 4).

Note that the adjusted R

coefficients of

determination associated to the three quadratic

regressions are significant and all greater than 0.6,

so that their simple average is higher (0.68) than that

obtained using linear regressions.

AFuzzyApproachtoDiscriminantAnalysisbasedontheResultsofanIterativeFuzzyk-MeansMethod

261

Table 4: Estimated coefficients of the quadratic regression

models, by group.

Group 1 Group 2 Group 3

Intercept 0.32*** 0.35*** 0.33***

Business density -0.18*** 0.18*** 0.01

Density of the local units 0.07 -0.11* 0.04*

Rate of evolution -0.11*** 0.09** 0.02

Export propensity -0.08*** -0.15*** 0.24***

Business density (^2) 0.05** -0.04* -0.01

Density of the local units

(^2)

-0.02* 0.02* -0.01

Rate of evolution (^2) -0.04*** 0.02** 0.01

Export propensity (^2) 0.01 0.03** -0.04***

Adjusted R

0.71*** 0.62*** 0.71***

Index of reliability of the discriminant model 0. 68

*** significant at 0.01 level ** significant at 0.05 level

* significant at 0.10 level

The simple average of the adjusted R

coefficients of determination still grows (0.77) in the

case of cubic regressions, because the latter ones

become even more flexible and allow a better

representation of awarding of the sampled provinces

to the three identified groups (Table 5).

Table 5: Estimated coefficients of the cubic regression

models, by group.

Group 1 Group 2 Group 3

Intercept 0,28*** 0,42*** 0,29***

Business density -0,25*** 0,27*** -0,03

Density of the local units 0,02 -0,15** 0,13**

Rate of evolution -0,13*** 0,10*** 0,03

Export propensity -0,07** -0,15*** 0,22***

Business density (^2) 0,01 0,00 -0,01

Density of the local units

(^2)

0,02 0,08* -0,09**

Rate of evolution (^2) -0,01 0,00 0,02

Export propensity (^2) 0,07* -0,12*** 0,05

Business density (^3) 0,04** -0,05*** 0,01

Density of the local units

(^3)

0,00 -0,01 0,01**

Rate of evolution (^3) 0,01 -0,01 0,00

Export propensity (^3) -0,01 0,04*** -0,02***

Adjusted R

0,76*** 0,79*** 0,77***

Index of reliability of the discriminant model 0. 77

*** significant at 0.01 level ** significant at 0.05 level

* significant at 0.10 level

Since the discriminant model defined via cubic

functions reaches a remarkable goodness of fit, we

prefer not to further increase the order of

polynomials, so as to maintain a parsimonious

number of the involved independent variables and to

allow an easier interpretability of the obtained

estimates.

The examination of the estimated regression

coefficients confirms what emerges from an

overview of the average profiles of the groups, since

the variables with a greater discriminating power in

the definition of degrees of membership seem to

correspond to those discussed above. In particular

the

business density and the rate of evolution are the

most significant variables in explaining the

assignment to the first two groups, while the

export

propensity and density of local units to the third

group (actually characterized by high average values

of the latter ones).

Note that the

business density is not significant at

all in determining the degree of membership of a

province to the third group, likely because the

corresponding average value is close to that of the

second one. Similar consideration can be done be

with reference both to the

density of the local units,

which is not significant in determining the degree of

membership to the first group, and to the

rate of

evolution

, which is not significant in determining the

degree of membership to the third group.

In general terms an independent variable,

expressed in cubic terms, helps in discriminating one

group from another when the gap between the

corresponding average values of the same

(standardized) independent variable is remarkable.

For clarity we present the average values of all

the standardized indicators for each group of

provinces in Table 6.

Table 6: Average values of the standardized indicators

weighted by the degrees of membership of each province,

by group.

Business

density

Density of

the local

units

Rate of

evolution

Export

propensity

Group 1 -0,46 0,06 -0,46 -0,20

Group 2 0,51 -0,04 0,20 -0,18

Group 3 0,20 0,23 0,10 0,68

On the basis of such an estimation procedure, it

is possible to determine the degrees of membership

to the three groups for each of the 20% of the

provinces not yet taken into account (Table 7).

Such degrees are compared with the analogue

posterior probabilities of assignment, deriving from

a classical discriminant analysis based on Bayes'

theorem, in order to evaluate their reliability. Note

that the used prior probabilities coincide with the

proportions of sampled provinces included in each

of the three groups within a classification procedure

based on the found maximum degree of

membership.

Before conducting such a classical discriminant

analysis, we have assessed – by means of the

coefficient of kurtosis defined by Mardia - the actual

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

262

multivariate normality of the indicators observed in

the three groups.

Table 7: Estimated degrees of membership to the three

identified groups, by not sampled province in Central and

Southern Italy (2009).

Sampled provinces Group 1 Group 2 Group 3

Pisa 0,22 0,32 0,47

Livorno 0,41 0,19 0,40

L'aquila 0,21 0,52 0,27

Isernia 0,31 0,46 0,24

Avellino 0,23 0,52 0,26

Brindisi 0,42 0,31 0,27

Ogliastra 0,35 0,51 0,13

Rieti 0,43 0,45 0,12

Palermo 0,50 0,41 0,09

Reggio Calabria 0,68 0,20 0,11

Enna 0,58 0,36 0,06

Medio Campidano 0,64 0,30 0,06

The achieved comparison confirms the validity

of the estimation procedure of the degrees of

membership, by means of which we assigned the

sampled provinces into homogeneous groups, since

the group with the highest degree of membership is

also the more likely one (Table 8).

Some slight discrepancies between the results of

the method proposed by us and those of the classical

discriminant analysis can happen, in the case of an

estimated not predominant membership to one of the

three groups.

See, for example, the provinces of Isernia,

Oristaglia, and Rieti, which show a degree of

membership to the first group slightly lower

(respectively equal to 0.31 0.35 and 0.43) than the

second group (respectively equal to 0.46 0.51 and

0.46), but a probability of assignment to the first

group higher than the second group. See, also, the

province of Medio Campidano, which shows a high

degree of membership to the first group (0.64), even

if the probability of assignment to the second group

is higher than the first one.

Note that the measure of probability of a

classical discriminant analysis has been used only to

assess the actual validity of the proposed model,

because such a measure represents in any case a

magnitude not directly comparable with a degree of

membership (which evokes, by definition, the

concept of a not exclusive assignment).

The latter, in particular, does not refer to the

occurrence or not of bivalent random events, but

represents the measure of a deterministic but

“vague” fact that occurs to a certain extent.

Table 8: Probability of assignment to the identified three

groups, estimated by means of a classical discriminant

analysis, by not sampled province in Central and Southern

Italy (2009).

Sampled provinces Group 1 Group 2 Group 3

Pisa 0.08 0.21 0.71

Livorno 0.51 0.16 0.33

L'Aquila 0.39 0.44 0.17

Isernia 0.68 0.30 0.02

Avellino 0,22 0.60 0.18

Brindisi 0.93 0.07 0.00

Ogliastra 0.51 0.44 0.04

Rieti 0.84 0.15 0.00

Palermo 0.69 0.22 0.10

Reggio Calabria 0.98 0.01 0.00

Enna 0.97 0,03 0.00

Medio Campidano 0.23 0.64 0.13

4 CONCLUSIONS

In this work we advance a proposal for a fuzzy

discriminant analysis, not focused on (within and

between) variances, but framed in the context of the

relationships between clustering variables.

In particular, in an attempt to regress the degrees

of membership of each unit to more groups on the

same variables used in a preliminary fuzzy

clustering, we show that polynomial functions are

more profitably than linear ones. This is because

such degrees of membership could increase as well

as decrease at rates which actually vary depending

on the values assumed by the clustering variables.

A higher order of polynomials provides more

precision in the corresponding estimates; on the

other hand, a lower value allows to have a more

parsimonious model, which is also easier to

interpret.

The reliability of our proposal is measured by the

simple average of the adjusted R

coefficients of

determination associated to the estimated regression

functions, since the number of the observations does

not differ from one function to another (whereas the

number of independent variables, although variable,

is taken into account by means of the adjustment of

the R

coefficients of determination).

As an application case we analyse the

entrepreneurial propensity in the provinces of

Central and Southern Italy on the basis of specific

indicators extracted from the Italian atlas of the

competitiveness of provinces and regions.

More specifically, we first identify a partition of

the sampled provinces in three clusters, through an

iterative procedure of the fuzzy k-means method,

AFuzzyApproachtoDiscriminantAnalysisbasedontheResultsofanIterativeFuzzyk-MeansMethod

263

which is more efficient and robust than hierarchical

methods; after we determine the degrees of awarding

of the not sampled provinces to each of the three

clusters, by means of regression cubic functions. The

latter ones show a good level of fit to the data in

addition to being sufficiently parsimonious.

The estimated degrees are compared with the

analogue posterior probabilities of assignment

deriving from a classical discriminant analysis, in

order to evaluate their reliability. Such a

discriminant analysis moves from a classification of

the sampled provinces based on their maximum

degree of membership to one of the three clusters.

The comparison confirms the validity of the

proposed procedure, since the group characterized

by the highest degree of awarding is also the more

likely one, albeit in general terms.

Note that the degrees of membership represent

measures of deterministic facts which occur to a

certain extent, while the posterior probabilities of

assignment refer to the occurrence or not of random

events; therefore the two aforesaid magnitudes are

heterogeneous, even if they are compared with each

other in order to demonstrate the actual cogency of

our proposal.

The same algorithm can be applied for a

Customer Relationship Management (CRM)

application, because of the similarity of the problem

faced to add new customers into already recognised

homogeneous groups. Actually such an algorithm

was initially conceived in the case of an Italian

automotive dealer.

ACKNOWLEDGEMENTS

The innovative contents described in this paper are

disclosed after the permission of MILLENIA S.r.l.

company, which committed to Laboratorio KAD3

S.c.a.r.l. the research project called “Data Integration

and Statistical Models per la Business Intelligence

(DISMoBI)”, co-funded by Italian Government

(Legge 12 luglio 2011, n. 106 – Credito di imposta

per le imprese che finanziano progetti di ricerca in

Università o enti pubblici di ricerca).

Although the work is the result of joint reflections by

the authors, chapters 3, 3.2, 3.3 and 4 are to be

attributed to Francesco Campobasso, and chapters

1, 2 and 3.1 to Annarita Fanizzi.

REFERENCES

Bezdek, J. C., 1981. Pattern Recognition with Fuzzy

Objective Function Algorithms. Plenum, New York.

Campobasso, F., Fanizzi, A., 2013. A Proposal for a

Discriminant Analysis Based on the Results of a

Preliminary Fuzzy Clustering. In Computational

Science and Its Applications – ICCSA 2013, LNCS,

vol. 7974, pp. 444-456. Springer, Heidelberg.

Campobasso, F., Fanizzi, A., 2013. A fuzzy approach to

Ward’s method of classification: an application case to

the Italian university system. In Statistical Methods for

spatial planning and monitoring, pp.31-46. Springer-

Verlag, Berlin Heidelberg.

Campobasso, F., Fanizzi, A., Perchinunno, P., 2008.

Homogenous urban poverty clusters within the city of

Bari. In Computational Science and its Applications -

ICCSA 2008, Part I. LNCS, vol. 5072, pp. 232-244.

Springer, Heidelberg.

Kaufman, L., Rousseau, P. J., 1990. Finding Groups in

Data - An Introduction to Cluster Analysis. John

Wiley and Sons, New York.

UnionCamera, Italain Atlas of the competitiveness of

provinces and regions, http://www.unioncamere.gov.

it/Atlante/.

Watada J., H. Tanaka, K. Asai. 1986. Fuzzy discriminant

analysis in fuzzy groups. In Fuzzy Sets and Systems,

vol. 19, pp. 261–271. Elsevier, The Netherlands.

Wu H. X., J. J. Zhou. 2006. Fuzzy discriminant analysis

with kernel methods. Pattern Recognition, vol. 39, pp.

2236-2239. Elsevier, The Netherlands.

Song X., X. Yang, J. Yang, X. Wu, Y. Zheng. 2010.

Discriminant analysis approach using fuzzy fourfold

subspaces model. In Neurocomputing, vol. 73, pp.

255–2265. Elsevier, The Netherlands.

Zhao M., T. W. S. Chow, Z. Zhang. 2012. Random walk-

based fuzzy linear discriminant analysis for

dimensionality reduction. In Soft Computing, vol. 16,

pp. 1393-1409. Springer-Verlag, Berlin, Heidelberg.

IJCCI2013-InternationalJointConferenceonComputationalIntelligence

264