DEVELOPING OF MULTISTAGE VIRTUAL SHARED MEMORY

MODEL FOR CLUSTER BASED PARALLEL SYSTEMS

Aye Aye Nwe, Khin Mar Soe, Than Nwe Aung

University of Computer Studies, Yangon, Myanmar

Thinn Thu Naing, Myint Kyi, Pyke Tin

University of Computer Studies, Yangon, Myanmar

Keywords: Multistage Virtual shared memory (MVSM), Cluster Based Parall

el System, Analytical model, Queuing

theory, Jackson queuing network.

Abstract: In this paper, we proposed a new multistage virtual shared memory model for cluster based parallel systems.

This model can be expanded in hierarchical manner and covered many of the previous clusters of parallel

system designs. Queuing theory and Jackson queuing networks are applied for constructing an analytical

model. This model gives a closed-form solution for the system performance metrics, such as processor

waiting time and system processing power. In development of this analytical model we used open queuing

network rules for analyzing a closed queuing network and calculate the input rate of each service centre as a

function of the input rate for previous service centre. The model can be used for evaluating the cluster based

parallel processing systems or optimizing its specification on design space.

1 INTRODUCTION

Cluster of workstations or symmetric

multiprocessors (SMPs) are potentially powerful

platforms for executing parallel applications (Buyya

, 1995). To simplify the programming of such

clusters, researchers have developed a number of

Virtual Shared Memory systems (VSMs) that

support a virtual shared address space across the

cluster through a layer of software (Li, 1989). The

main problem for constructing a scalable VSM

system is conflict over the common resources. The

limited service capacities of these common

resources cause an increase in the waiting time of

the processors when the number of the processor

increases. Using more powerful common resources

are the conventional method for decreasing the

waiting times, but the capacity of servicing of the

resources such as effective memory access time and

the interconnection network bandwidth is saturated

by the technology and their architectures. This

problem would be more important in parallel

processing systems that utilized a large number of

processors.

In this paper, we develop multistage VSM model

VSM) to overcome above problems. In the

propose architecture, processors are divided into the

cluster groups, and organized in several stages. The

MVSM is expandable in hierarchical manner, and is

so flexible that it covers many of the previous

clusters of parallel system designs.

In the next section, architecture of MVSM

syste

m is discussed. An analytical model is

constructed in section 3 and on base of analytical

model, the performance graphs of the system are

depicted in section 4. Conclusion is presented in the

last section.

2 MVSM CLUSTER

ARCHITECTURE

The basic MVSM system is composed of three

modules: client, provider and VSM manager. A

node that sends the user’s computation requests is

called a client. The client simply submits all requests

to a VSM manager.

263

Aye Nwe A., Mar Soe K., Nwe Aung T., Thu Naing T., Kyi M. and Tin P. (2005).

DEVELOPING OF MULTISTAGE VIRTUAL SHARED MEMORY MODEL FOR CLUSTER BASED PARALLEL SYSTEMS.

In Proceedings of the Seventh International Conference on Enterprise Information Systems, pages 263-266

DOI: 10.5220/0002554702630266

 SciTePress

The manager is responsible for handling requests

from clients and invokes computation threads on

each provider. The provider is invoked by the VSM

manager and then mutually establishes connections

with the client node.

Forward link (FL) is used to transmit remote

request from client to the manager and backward

link (BL) is used for the invocation request of the

VSM manager to the service provider.

The VSM cluster can be expanded in two ways:

increasing the number local cluster nodes (CNs) in

each stage, or using several clusters with one

additional manager that is shared by those clusters.

The unit that are located inside the basic clusters

are indicated by index 1 (M

, PC

, F

, B

) and the

units that are located outside of the cluster are

indicated by index 2 (M

, PC

, F

, B

In this system, if the number of PCs that make a

cluster will be equal for all clusters in all stage, the

system is called homogenous and if it will not be

equal at least in one stage, it will be called

heterogeneous. In next section, the homogeneous

MVSM system will be discussed and analyzed.

3 ANALYTICAL MODELING

Queuing theory and Jackson queuing network

(Cooper,1981)are applied to evaluate the

performance of the system. During job execution, it

needs to communicate with the other jobs.

Therefore, several queues would be constructed for

each service centre. We assume the following

assumptions to analyze MVSM model:

1. The no. of PCs in i

stage of system is C

and the

no. of nodes in each basic cluster is C

2. The inter job communication requests are

generated independently by processors.

3. The destination of each request will be uniformly

distributed and probability to local PCs in i

stage indicated by P

4. Both of intra-cluster and inter-cluster

communication are uniformly random.

5. Each node generates requests at rate .

6. Service rate for FL and BL are and .

7. Service rate for VSM manager and each service

provider are and .

8. Conflict over the service centre will be resolved

by queuing centre with FCFS discipline.

9. The clients must wait until they offer service as

per the above scheme; and during waiting period,

they cannot generate any other requests.

The input rate of each stage must be computed to

analyze this system. Any service centre assumed as

M/M/1 queuing centre.

We derive the input rate of each service centre as

a function of the input rate for the previous service

centre. By investigating the situation of the request

of each client, we can reach the state diagram.

....

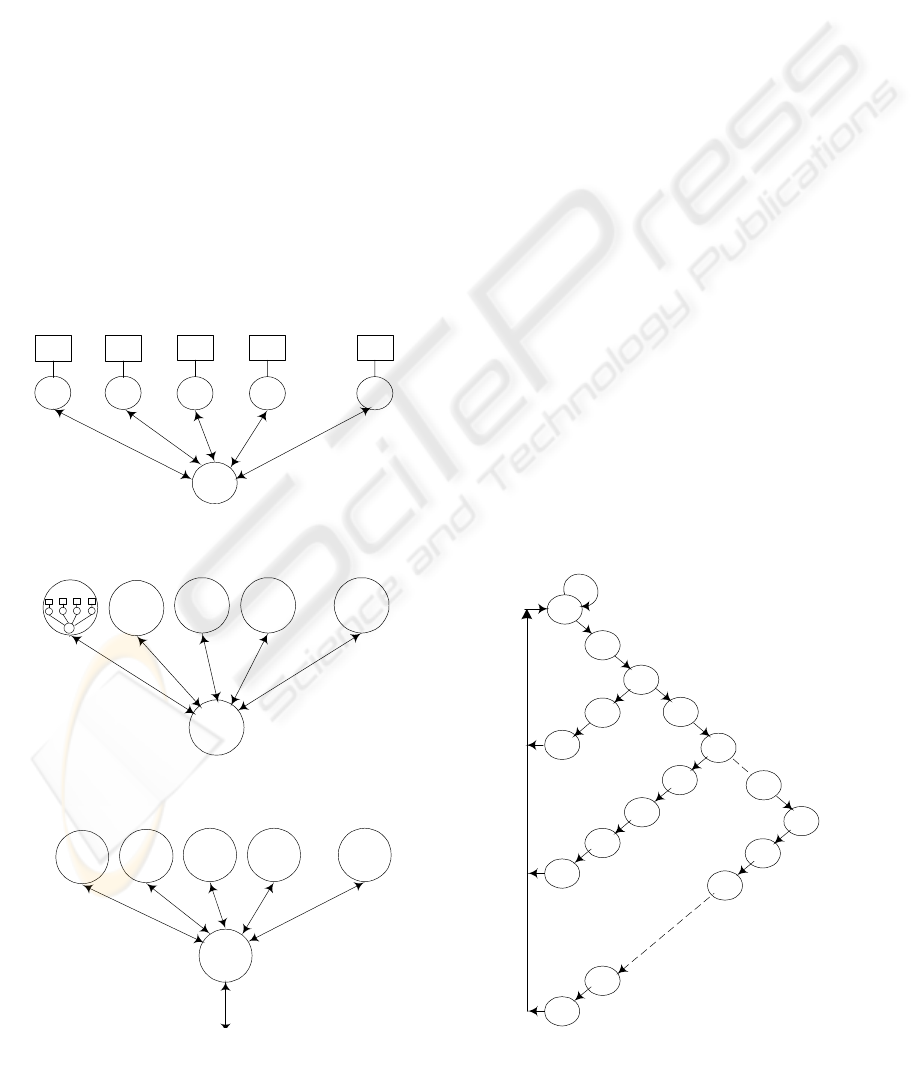
Figure 1: Basic MVSM cluster

Proc

CNs

(s-1)j

....

1C1

Figure 2: Two stage MVSM system

....

Hirerchical

Expansion

(i-1)1

(i-1)2

(i-1)3

(i-1)4

(i-1)C(i-1)

Figure 3: A cluster in i

stage of s-stages system

Figure 4: State diagram of MVSM with s-stages

ICEIS 2005 - SOFTWARE AGENTS AND INTERNET COMPUTING

264

If the probabilities of the request that directed to

itself and FL

are and r ,one can compute

the probabilities of referring a processor request to

, M

, BL

and local PCs by following equations:

(1)

(2)

is 1 for the last stage of the system.

If the request rate of a processor is , the input

rate of F

that originated from that processor will be

1 . Since there are processors in each

basic cluster, the requests that receive to F

from

other processor will be .

(14)

So the total requests of the processors that

received to service centres in 1

stage are,

(3)

(4)

In the i

stage of the system, if the input request

rate from each PC is , we can derive input rate

of each service centre by the similar method.

(5)

(6)

Based on the M/M/1 queuing equation

(Sheldon,2000), we can compute the queue lengths

of each centre for all stages. Then the average of

total waited processors can also be computed based

on the number of service centre in the system and

the number of the waited processor in each centre:

(7)

According to assumption 9, the effective

processor’s request rate would be lower than . It

will be decreased with the same ratio as the active

processors to the total processor’s number. After

determining effective request rate and waited

processor for each service centre, the waiting time

can be computed by following the equations:

(8)

(9)

(10)

(11)

(12)

Based on the average waiting time W, we can

compute the processor utilization as follows:

(13)

Finally, the most important metric for evaluating

of the system’s performance, i.e., total processing

power of the system (TPP), can be computed on the

basic of single processor power (SPP),

[]

4 PERFORMANCE METRICS

The model is useful not only to evaluate the system

performance but also to investigate the effect of

different parameters’ variation on the system

performance. The last capability of the performance

model can be used during the system design.

Table 1: System assumption

Quantity Units

Processor’s Power 400 MIPS

Total Processor 3201 Pieces

Inter Job Communication

Probability

0.25 %

Memory Reference Per

Instruction (MPI)

1.2 -

We used 3201 pieces of the 400 MIPS RISC

processors, interconnection network with 1000

Mbps and the memory access time is 20ns. It is

assume that the system is organized in a three stages

by MVSM model. To measure performance metrics,

it is based on P

and MPI.

System must give TPP of 1,280,400 MIPS for

3201 pieces of 400 MIPS. It is reachable if there is

no overhead by parallelism. To reach the maximum

PP and find the best architecture, we study the PP

corves in each stage.

Figure 6 depicted these curves when the first

stage’s cluster number (C

) varies from 1 to 100.

The curves are plotted for some values for the

second stage’s cluster number (C

) from 2 to 20.The

curves show that the maximum PP will occur on 16

clusters on the 1

and 10 clusters in 2

stages. For

this configuration the processing power will be

equal to 1,113,948 MIPS or 87% of TPP.

Figure 7 shows the variation of PU. The best

configuration will be held on 10 clusters of 16 sub-

clusters, that each sub-cluster consist 20 nodes.

∏

== )

−

fimi

)1(( −

−

∏

)1(

−

mii

bili

100011

)1(

mfm

PCPC === −

)1(( −

−−

)1)(1

)1(

101

−

mlm

λλ

)

λλλ

1(1 −− immiimi

)1( −

1−i

mili

bili

λλ

()

()()

∑

∏∏

−−

−

⎥

⎦

⎤

⎢

⎣

⎡

⎭

⎬

⎫

⎩

⎨

⎧

−++

⎭

⎬

⎫

⎩

⎨

⎧

ikkbklk

ifkmk

CCLLCLL

mkmk

λµ

−

lklk

λµ

−

fkfk

λµ

−

bkbk

λµ

−

∑

+++

bibififililimimi

WPWPWPWPW

PUlizationocessorUti

⎟

⎠

⎜ +

=××=

PUNTPP

⎞

⎜

⎝

∏

−

SPP

⎛

SPP

)1( P

−

)1( P C

−

)( P

−1

1( −i

DEVELOPING OF MULTISTAGE VIRTUAL SHARED MEMORY MODEL FOR CLUSTER BASED PARALLEL

SYSTEMS

265

2nd stage cluster no.(C2) used as plots parameter

0.2

0.4

0.6

0.8

1.2

1 3 5 7 9 1113151719

1st stage cluster no.(C1*5)

Total Processing Power (*1000000

)

MIPS

C2=2 C2=4 C2=5 C2=8

C2=10 C2=16 C2=20

2nd stage cluster no.(C2) used as plot's parameter

0.2

0.4

0.6

0.8

135791113151719

1st stage cluster no.(C1*5)

Processor Utilization

C2=2

C2=4 C2=5 C2=8

C2=10 C2=16 C2=20

Figure 7: PU vs. Cluster No. for 3-stage MVSM system

Figure 6:TPP vs. Cluster No. for 3-stage MVSMSystem

5 CONCLUSION

Mohaparta P., Das C.R., Jan 1996. Performance analysis

of finite buffered asynchronous multistage

interconnection networks, IEEE Transactions on

Parallel & Distributed Systems, pp.18-35.

We proposed a new architecture and its analytical

model for MVSM system. Analytical model was

constructed on queuing theory and the system

performance metric was expressed as mathematical

equations. The performance graphs may be used by

designer to find the optimum system configuration

for reaching to maximum performance with fixed

resources.

Mohapatra P., Das C.R. and Feng,T.Y. Jan 1994.

Performance analysis of cluster based multiprocessors,

IEEE Transaction on Computer, Vol. 43 pp. 109-114.

Nitzberg Bill and Virginia Lo, 1991. Distributed Shared

Memory: A Survey of Issues and Algorithms, IEEE

Computer, pp. 52-60.

Pinar Ali, Hendrickson Bruce., July 2004. Interprocessor

Communication with Limited Memory, IEEE

Transactions on Parallel and Distributed Systems, Vol

15, No.7

The future work focuses on improving the

analytical model for heterogeneous system to

determine the optimum point in design space. The

other subject is improving the analytical model by

applying software and scheduling features.

Shahhoseini H.S., Naderi M., Buyya R., 2000. Shared

memory multistage clustering structure: An efficient

structure for massively parallel processing systems,

The 4th International Conference on High

Performance Computing in Asia-Pacific Region (HPC

Asia 2000), Beijing, China. IEEE Computer Society

Press, USA.

REFERENCES

Buyya Rajkumar, 1995. High Performance Cluster

Computing: Architectures and Systems. vol. 1,

Prentice-Hall.

Sheldon M.Ross, 2000. Introduction to Probability Model,

Academic Press, 7

Edition.

Sohda Y., Nakada H., and Matsuoka S., 2001.

Implementation of a Portable Software DSM in Java,

Proceedings of the ACM JavaGrande/ISCOPE 2001

Conference, Stanford University, California.

Cooper Robert B., 1981. Introduction to Queuing Theory,

Elsevier North Holland. 2

Edition.

Dandamudi S.P., Eager D.L., Jun 1990. Hierarchical

interconnection networks for multiprocessor systems,

IEEE Transaction on Computer, pp. 786-797.

Stumm Michael and Zhou Songnian. 1990. Algorithms

Implementing Distributed Shared Memory, IEEE

Computer, pp.54-64.

Hayes J.P., 2002. Computer Architecture and

Organization, McGraw-Hill. 3

Edition.

Tanenbaun Andrew S., 1995. Distributed Operating

Systems,Prentice Hall, Inc.

Hennessy J. L. and Patterson D. A., 2003. Computer

Architecture: A Quantitative Approach, 3

ed: Morgan

Kaufmann Publishers Inc.

Trevisan Thobias S., Costa Vitor Santos, Whately Lauro,

Amorim Claudio L., 2002. Distributed Shared Memory

in Kernel Mode, IEEE 14

Symposium on Computer

Architecture and High Performance Computing.

Li. K., Hudak P., Nov 1989. Memory Coherence in Shared

Virtual Memory Systems, ACM Transactions on

Computer Systems, 7(4), pp 321-359.

Http://staff.um.edu.mt/simweb/mm1.htm

ICEIS 2005 - SOFTWARE AGENTS AND INTERNET COMPUTING

266