Efﬁcient Hybrid Model for Intrusion Detection Systems

Nesrine Kaaniche

, Aymen Boudguiga

and Gustavo Gonzalez-Granadillo

SAMOVAR, Telecom SudParis, Institut Polytechnique de Paris, France

Universit

e Paris-Saclay, CEA-List, Palaiseau, France

Atos Research & Innovation, Cybersecurity Laboratory, Spain

Keywords:

IDS, K-Means, Bayesian Model, Hybrid Approach, Supervised and Unsupervised Learning.

Abstract:

This paper proposes a new hybrid ML model that relies on K-Means clustering and the Variational Bayesian

Gaussian Mixture models to efﬁciently detect and classify unknown network attacks. The proposed model ﬁrst

classiﬁes the input data into various clusters using K-Means. Then, it identiﬁes anomalies in those clusters

using the Variational Bayesian Gaussian Mixture model. The model has been tested against the CICIDS 2017

dataset that contains new relevant attacks and realistic normal trafﬁc, with a reasonable size. To balance the

data, undersampling techniques were used. Furthermore, the features were reduced from 78 to 28 using feature

selection and feature extraction methods. The proposed model shows promising results when identifying

whether a data point is an attack or not with an F1 score of up to 91%.

1 INTRODUCTION

During the past decade, Machine Learning (ML) tech-

nologies have gained an expanding interest, enabling

automation, accurate predictions and classiﬁcation re-

sults from complex models, that are made possible

and more efﬁcient thanks to advanced processing re-

sources (Zhavoronkov et al., 2018). From this per-

spective, various research works started to investigate

the implementation of ML for diverse tasks such as

malware analysis, intrusion detection, log analysis,

threat classiﬁcation, etc., in order to enhance the secu-

rity by design principle in next-generation networks.

The intersection between ML and cybersecurity has

been studied for more than three decades, and both

domains are recently experiencing a blooming stage

due to the increasing deployment of next-generation

networks in the society. ML, on the one hand, of-

fers important capabilities to analyse threats and at-

tacks in various network systems, enabling compre-

hensive and in-depth defense strategies. However,

ML algorithms are raising several questions regard-

ing their effectiveness in real-world scenarios. For

instance, the lack of interpretability of many learn-

ing models makes it hard to develop defensive mech-

anisms against sophisticated attacks.

Cybersecurity, on the other hand, provides the means

to protect data from intrusions or attacks that usually

lead to high economic losses, personal information

leaks and reduced quality and productivity of organ-

isations. Intrusion Detection Systems (IDSs) are ef-

ﬁcient counter-measures for detecting inappropriate

use of host machines or networks and providing in-

formation security. IDSs monitor and analyse events

to detect any deviations from a regular behaviour.

Several machine learning methods have been im-

plemented to decrease the false positive rate of

anomaly-based IDSs, including Extreme Learning

Machine (ELM) (Singh et al., 2015) and Support Vec-

tor Machine (SVM) (Feng et al., 2014; ?; ?). How-

ever, most of these approaches only use supervised

learning algorithms that strongly rely on the accurate

labeling of the training dataset and are tested against

outdated datasets.

This paper investigates the application of ML al-

gorithms in Intrusion Detection Systems (IDSs) and

provides a detailed evaluation of existing ML meth-

ods and their applications to different network sys-

tems. It proposes a new ML-based IDS model that

relies on a hybrid approach that uses supervised and

unsupervised algorithms to efﬁciently detect complex

and sophisticated attacks (e.g., known and unknown).

The proposed model ﬁrst classiﬁes the input data

into various clusters using K-Means. Then, it iden-

tiﬁes anomalies in those clusters using the Variational

Bayesian Gaussian Mixture model. Conducted exper-

iments show promising results reaching 91% of F1-

scores in the supervised classiﬁcation and up to 86%

in the unsupervised classiﬁcation.

The remainder of this paper is as follows. Section 2

describes the proposed model and discusses the core

processing blocks. Section 3 details our methodol-

694

Kaaniche, N., Boudguiga, A. and Gonzalez-Granadillo, G.

Efﬁcient Hybrid Model for Intrusion Detection Systems.

DOI: 10.5220/0011328300003283

In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 694-700

ISBN: 978-989-758-590-6; ISSN: 2184-7711

ogy, including selected data-sets, different types of

data pre-processing and selection techniques. Sec-

tion 4 presents preliminary experimental results, be-

fore concluding in Section 5.

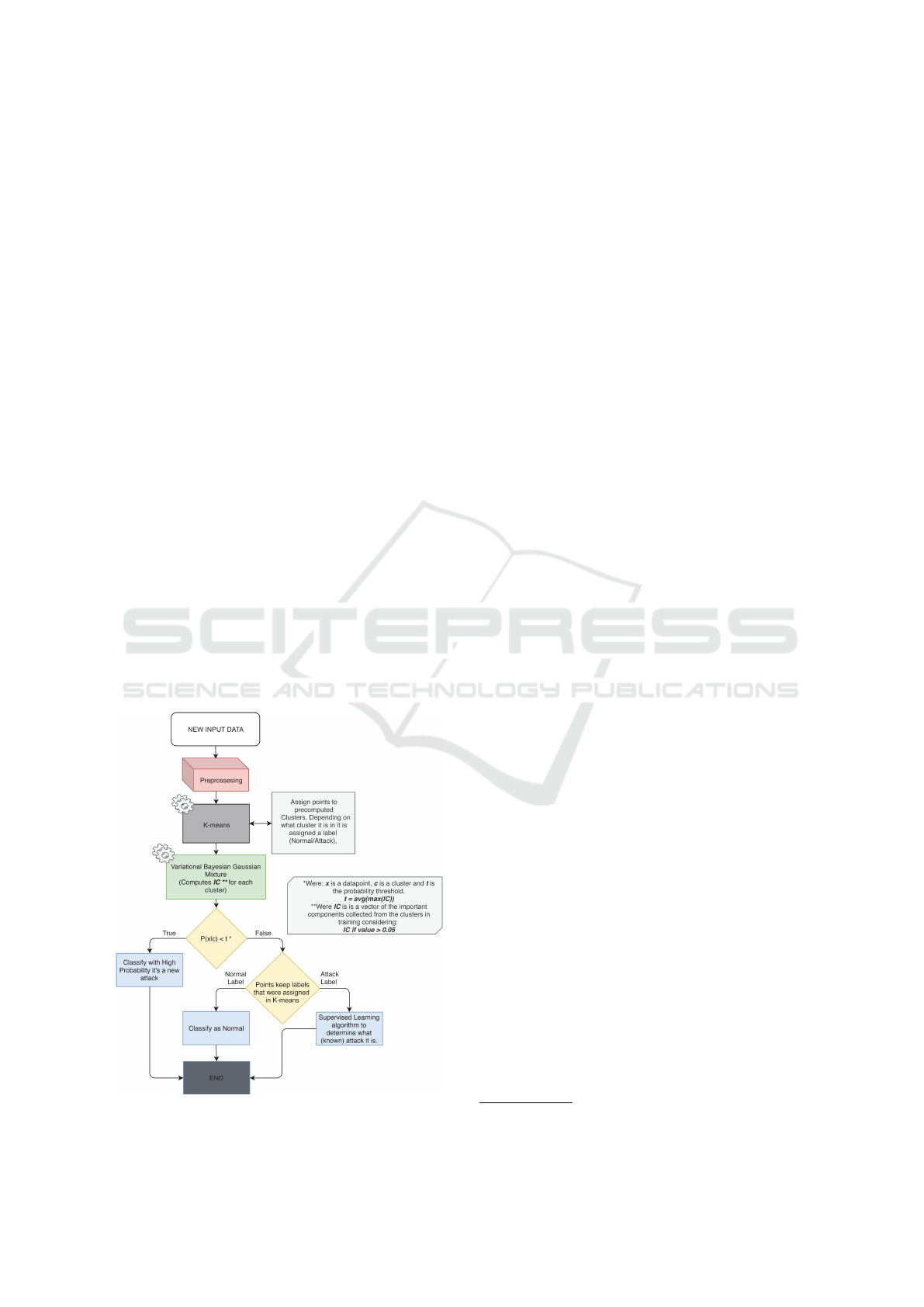
2 PROPOSED SOLUTION:

HYBRID AI-BASED MODEL

FOR IDS

The proposed solution introduces a novel ML based

IDS model that relies on a combination between su-

pervised and unsupervised learning in order to efﬁ-

ciently detect complex and sophisticated attacks, as

depicted in Figure 1. Indeed, an unsupervised clus-

tering algorithm, i.e., K-means, will ﬁrst separate

into clusters normal and abnormal behaviours. K-

means is chosen because it ensures a low computa-

tion overhead. Second, the identiﬁed clusters will

be labelled, by considering the location of the major-

ity of the points in each cluster. Then, the bound-

ary’s/thresholds for each of those datasets will be

set using the Variational Bayesian Gaussian Mixture

model. All of the points that have a probability of

belonging to a cluster smaller than the threshold will

be classiﬁed as potential new and unknown attacks.

Finally,all the points clustered as attacks by K-means

will be processed using a supervised algorithm to be

classiﬁed into different attacks. data that are classiﬁed

as normal by K-Means will keep this classiﬁcation.

Figure 1: High Level Description of Proposed Method.

2.1 Training

After the preprocessing, the data goes through the K-

Means algorithm which separates all the data points

into clusters. Then, these clusters are labelled with

respect to the majority of the classes they are com-

promised from (i.e., Normal or Attack). Next, the

Variational Bayesian Gaussian Mixture method, as

depicted in Figure 1, disregards non-important clus-

ters by giving them a weight close to zero and so not

all clusters will be considered. Note that a threshold

can be set to select only signiﬁcant clusters. Given

that the limit is set, a vector will be returned by the

model containing all the important components IC for

each point in a cluster. Lastly for each of the clusters a

threshold is computed as t = avg(max(IC), where IC

is the important components vector and the resulting t

is the probability threshold for one cluster. Once these

thresholds for all clusters are set the training phase is

over.

2.2 Prediction

After preprocessing, the prediction data are given as

inputs to the K-Means algorithm. As such, the data

points will be assigned to their respected clusters. Just

like in training, these clusters will be passed on to the

Variational Bayesian Gaussian Mixture which will re-

turn the important components of each point. Then

the max(IC) for each point of the cluster will be calcu-

lated. It corresponds to the probability that the point

belongs really to the cluster assigned by the K-Means.

This probability is formulated as P(x|c) = max(IC),

where x is a data point, c is a cluster and IC is the im-

portant components vector of that datapoint. Lastly,

once this is calculated the following expression will

be executed to see if the point belongs to the cluster,

P(x|c) < t. That is, if the probability that the point

belongs to the given cluster assigned by K-means is

lower than the threshold for that cluster which was

set in the training phase, then it will be classiﬁed as

new/unknown attack.

3 VALIDATION METHODOLOGY

3.1 Selected Datasets

Two publicly available datasets for intrusion detection

systems have been studied and compared: (i) NSL-

KDD

thanks to its large use in previous works for

https://www.unb.ca/cic/datasets/nsl.html

Efﬁcient Hybrid Model for Intrusion Detection Systems

695

fair comparison with other works; and (ii) CICIDS-

2017

one of the newest publicly available datasets.

CICIDS is more interesting than NSL-KDD as it con-

tains samples inspired from real world examples, and

it covers all criteria for building a reliable benchmark

dataset as described by Gharib et al. (Gharib et al.,

2016).

The NSL-KDD dataset is a modiﬁed version of

the KDD CUP 99 dataset. It claims to solve some

of the core problems of the of the previously widely

used KDD CUP 99 dataset by removing the redundant

records. As such, the classiﬁers will not be biased to-

wards more frequent records. Attacks in this dataset

fall into 4 distinct categories: Denial of Service At-

tack (DoS), User to Root Attack (U2R), Remote to

Local Attack (R2L), and Probing Attack (Probe).

The CICIDS-2017 consists of 14 different attacks

grouped into 9 categories: Brute Force FTP, Brute

Force SSH, DoS, Heartbleed, Web Attack, Inﬁltra-

tion, PortScan, Botnet and DDoS. All of which are

realistic and very common attacks. In addition it con-

sists of 80 features, extracted using the CICFlowMe-

ter

. Moreover, this dataset was built with the top

priority of generating realistic background trafﬁc.

This was achieved using a proposed B-Proﬁle system

(Sharafaldin et al., 2018) proﬁling human interaction

abstract behaviour and generating naturalistic, benign

background trafﬁc.

3.2 Imbalanced Datasets

The NSL-KDD dataset is class balanced with 52 per-

cent of normal labels and 48 percent of attack labels.

However, the distribution of attacks in the 4 categories

is uneven, with DoS attacks having the biggest weight

in the dataset and the U2R attack count being very

small. This can potentially bias the model. To ﬁx

this issue, it is recommended to add new attack labels

in the dataset to balance it better, since a resampling

technique would result in redundant records.

The distribution of the normal and attack labels in

the CICIDS-2017 dataset is uneven with 80 percent

of normal labels vs 20 percent of attack labels. Even

though the dataset is imbalanced, it is more realistic,

since in the real world, we do not get as many in-

stances of attacks as we get of normal network trafﬁc.

For these experiments, we used a random undersam-

pling technique to balance this large dataset.

https://www.unb.ca/cic/datasets/ids-2017.html

https://pypi.org/project/cicﬂowmeter/

3.3 Classiﬁcation Algorithms

The ﬁrst algorithm of our proposed approach deals

with unsupervised learning problem. In this case,

K-means seems to be the best ﬁt thanks to its sim-

plicity and speed at which the predictions are gener-

ated. It is crucial to have a fast prediction time when

implementing intrusion detection systems. Further-

more, algorithms like Density-Based Spatial Cluster-

ing of Applications with Noise (DBSCAN) tend to

leave outliers out of the clusters and this is not op-

timal for these kind of systems since those outliers

could be a minority of attacks. The second algorithm

of our proposed approach is used to detect anoma-

lies in clusters. The Variational Bayesian Gaussian

Mixture is the selected algorithm because there is a

smaller chance to end up in a local minimum con-

sidering that we only need to specify the maximum

number of clusters to build the model, the algorithm

will then ﬁnd the actual number of clusters and set

the weight of non-relevant clusters very close to zero

(Nasios and Bors, 2006).

3.4 Performance Metrics

This section describes our evaluation metrics:

• Accuracy: It refers to the ratio of correctly pre-

dicted observations divided by the number of all

observations, as Accuracy =

T P+T N

T P+T N+FP+FN

• Precision: It refers to the ratio of positively

predicted observations divided by the total posi-

tive observations predicted as Precision =

T P

T P+FP

High precision refers to the small false positive

rate.

• Recall: It refers to the proportion of correctly

predicted positive observations divided by all ob-

servations in a positive class, as Recall =

T P

T P+FN

• F1 Score: It refers to the weighted average of

Precision and Recall, as F1 =

2·precision·recall

precision+recall

. This

rating brings into consideration both false posi-

tives and false negatives. F1 Score is the most

suitable metric to ﬁnd an equilibrium between

Precision and Recall in a problem with irregular

distribution.

3.5 Implementation

The proposed model is implemented using Python.

The main libraries used for this model includes

pandas

, and Scikit-Learn

. As depicted in Fig-

ure 2, the initial step in the implementation process

https://pandas.pydata.org/

https://scikit-learn.org/stable/

SECRYPT 2022 - 19th International Conference on Security and Cryptography

696

is to import the data. For this implementation, we

have selected the CICIDS 2017 dataset, which has

been preprocessed, cleaned and balanced before split-

ting it in two main groups: (i) instances containing

only normal activities, and instances containing at-

tacks (e.g., Bot, Heartnleed, DoS Slowhttptest). 80%

of the dataset has been used for training and the re-

mainging 20% were used for testing. The training

dataset is further split into two subsets: (i) the train-

ing subset, containing 80% of the selected training in-

stances, (ii) the validation subset, containing 20% of

the selected training instances. The validation serves

to evaluate the model with different conﬁgurations

during pre-production.

Figure 2: Preprocessing ﬂowchart.

Once the dataset is split, all NaN values were re-

placed by the mean values of each column. Af-

ter this process, data standardisation was performed

by using the StandardScaler process from the

Scikit-Learn library. Next step is feature selec-

tion. To carry out this task, the random forest

classifier from the Scikit-Learn library was

used. It was trained with the train dataset and with

the hyperparameters of n estimators = 100 and

max depth = 2 all the others were set to default. For

the test set, only 49 out of the total of 78 features

are considered as important. Therefore, all the fea-

tures were chosen to build the models. As a fea-

ture extraction method, Principal Component Anal-

ysis (PCA) was used to ﬁt the training data to avoid

bias. The hyperparameters used were: n componets

= number of features (49 as taken from the fea-

ture selection), svd solver = ’randomized’ and

iterated power = 30. The last step in the prepross-

esing is to decide how many of PCA components are

kept by computing and plotting the PCA variances for

all clusters. Considering that after 28 features, the

variances do not change, the hyperparameters chosen

for the PCA algorithm are n components = 28, and

max iter = 200.

The implementation of our proposed model con-

siders implementing K-Means and the Variational

Bayesian Gaussian Mixture algorithms.

3.5.1 K-Means

During K-Means implementation for clustering data,

we tried two methods for ﬁxing the cluster numbers

(i) the elbow method and (ii) the cross validation with

PCA using the development dataset so that the inertia

converges. Inertia is the sum of squared distances of

samples to their closest cluster centre. Unfortunately,

when testing with the development set none of them

yielded high accuracy results. Therefore, we tested all

the accuracy’s on the training and development tests

starting with 2 clusters until reaching 50 clusters. We

then picked the number of clusters with the highest

accuracy. As shown in Figure 3, 46 clusters provide

the highest accuracy level (i.e., 91% of accuracy). All

the tests are done in 200 iterations. It is worth not-

ing that both development and train sets have almost

equal accuracy levels.

To calculate the accuracy of the model, the num-

ber of points belonging to each label (Normal or At-

tack), was measured and the cluster was assigned the

label of the class it had the majority of samples in,

since we actually had labelled data.

3.5.2 Variational Bayesian Gaussian Mixture

Bayesian Gaussian Mixture models were used to cal-

culate the probability of a point belonging to the clus-

ter. As stated in the aforementioned sections, the al-

gorithm returns the probability of a point belonging to

any of the clusters, these numbers are called compo-

nents. Since they are probabilities, their sum is one,

this means for this approach to work we must take

Efﬁcient Hybrid Model for Intrusion Detection Systems

697

Figure 3: K-Means accuracy plot.

a look at only the important components. We set a

threshold to 0.05 after testing with the train and vali-

dation sets. The algorithm takes only the components

that are equal to or bigger than the threshold for each

of the training clusters. Then, the validation set is

used to predict the probability of the points belong-

ing to each of those clusters. Once done, only the

biggest of those components is taken for each point

in the cluster and as a last step they are averaged (as

discussed in section 2.1).

4 IMPLEMENTATION RESULTS

4.1 Clusters’ Visualization

Figure 4(a) depicts the actual clusters with the real

labels of the test data that are used for evaluation pro-

poses. Let us recall that a model is considered as per-

fect if it is able to predict exact same clusters. Fig-

ure 4(b) shows the clusters that are predicted through

the different conducted experiments. We note that the

test set does not contain any new attacks. If we look

closely at Figure 4, we notice that there exist some

minor points which are wrongly classiﬁed.

In order to evaluate the classiﬁcation capabilities

of the proposed methodology, we considered a single

set composed by the concatenation of the test set and

the set of new attacks, as shown in Figure 4(c). The

resulting clusters belong to both known and unknown

attacks. We note that in Figure 4(c), there is a whole

new ”line” in purple. The data points in this line be-

long to the new attacks that were not present during

the training of the model. These are the data points

that our solution aims at detecting and classifying.

4.2 Evaluation Results

This section details the evaluation results of the pro-

posed model with different conﬁgurations and dis-

cusses the computation overheads.

(a) Real Clusters (b) Predicted Clusters

tacks

Figure 4: Real vs Predicted Clusters.

Table 1: Normal / Attack Detection with 45 and 46 Clusters

Evaluation Results.

No of Clusters 45 46

F1 score 89% 91%

Recall 94% 95%

Precision 85% 88%

Accuracy 89% 91%

4.2.1 Evaluation with 46 Clusters

The ﬁrst conﬁguration considers 46 clusters. It was

evaluated with respect to the selected metrics, as de-

tailed in section 3.4. For the K-Means algorithm, we

used the test set, to estimate the number of both at-

tacks and normal data points that are correctly pre-

dicted. The F1 score was 0.91% while the Recall

score 0.95%. Furthermore, the precision score was

0.88% and the accuracy score was 0.91% as shown in

Table 1.

To evaluate the capacity of the Variational

Bayesian Gaussian Mixture for efﬁciently detecting

new attacks, we ﬁrst implemented the prediction

pipeline with the test set. Then, we assessed the

pipeline algorithms using the attacks’ dataset. Af-

terwards, both predictions are concatenated into one

data-frame and evaluated. This concatenation permits

to identify the real labels and evaluate the results ac-

cordingly, since all of the datapoints in the unknown

attacks should be set to unknown and all the data-

points in the test set to known. The results of this

evaluation are depicted in 5(a). The results are shown

in a normalised confusion matrix in order to provide

human-centric accurate results. From Figure 5(a), we

deduce that the results of our evaluation with 46 clus-

ters are fairly good, 62% of the unknown labels are

correctly predicted.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

698

(a) Confusion matrix (46 clusters) (b) Confusion matrix (45 clusters)

Figure 5: Comparison of Confusion Matrix results obtained

for the different clusters.

4.2.2 Evaluation with 45 Clusters

As detailed in section 4.2.1, we conduct the same

evaluation pipeline while considering 45 clusters, in

order to assess their impacts on the prediction ac-

curacy. In fact, we assumed that the obtained re-

sults with 46, even though considered as good, may

be improved. For this purpose, we conduced a trial

with less clusters and evaluated the different metrics.

This second conﬁguration, i.e., 45 clusters resulted

in an improved accuracy in predicting unknown at-

tacks compared to the ﬁrst setting. However, it neg-

atively impacted the evaluation of K-Means. The F1

score dropped down to 0.89% and the Recall score

to 0.94%. Furthermore, the Precision score stepped

down to 0.85% and the total accuracy score to 0.89%.

4.3 Discussion

Figure 4(a) presents a common illustration of the real

attack and normal clusters. It is difﬁcult to distinguish

one cluster from the other one since they are merged.

This is mainly due to the close behaviour between a

normal and an attack event. In our conducted experi-

ments, two conﬁgurations are evaluated, one using 45

and another using 46 clusters. This latter showed bet-

ter results using the validation dataset, thanks to the

similar behaviour of normal and attack events. Given

that, the selected criteria to identify if a cluster is nor-

mal or malicious is the class of the majority of events,

a higher number of clusters broke down the events in

a way that could improve the classiﬁcation accuracy

of the clusters.

The number of clusters to use resolves the trade-

off between the accuracy to detect normal/attack

events and the good performance of the model to

classify known/unknown ones. Thus, based on

each setting’s requirements, i.e., to classify or detect

known/unknown attacks, our results showed that it is

more convenient to use the model with 45 clusters for

classiﬁcation and 46 clusters for detection. Moreover,

in both cases, the accuracy to classify normal/attack

events is still high (at least 89%).

The precision and recall scores for the model us-

ing 45 clusters are fairly high. The precision met-

ric indicates that 85% of the events classiﬁed by the

model as attacks, are correct, meaning that the model

has a small false positive rate. The recall metric indi-

cates that 94% of the real attacks are correctly pre-

dicted. The F1 score (or the weighted average of

precision and recall) was equal to 89%. This metric

shows that the general detection rate of the combined

models is good. The confusion matrix is helpful to

analyse the known/unknown predictions of the mod-

els. The model using 45 clusters was the best model

since only 0.1% percent of the known events were

misclassiﬁed as unknown, and only 0.14% of the un-

known events were misclassiﬁed as known.

The model using 46 clusters obtained the same re-

sults as the model using 45 clusters when predicting

the known events. This shows that the difﬁculty in the

model lies in detecting the unknown attacks. Using 46

clusters, the model misclassiﬁed 38% of the unknown

events, which are 24% more than the model using 45

clusters.

5 CONCLUSION

This paper presented a hybrid approach to tackle the

problem of implementing intrusion detection systems

using machine learning models. The CICIDS 2017

dataset has been chosen, since it contains new relevant

attacks and realistic normal trafﬁc, with a reasonable

size. The normal and attack data points were unbal-

anced, to balance the data undersampling technique

was used.

The highest performance for the K-Means clus-

tering was obtained with 46 clusters. The F1 score

was 0.91% while the Recall score 0.95% the Precision

score was 0.88% and the Accuracy score was 0.91%.

The highest performance for the Variational Bayesian

Gaussian Mixture model was obtained with 45 clus-

ters at 90% of the known attacks predicted as known

and 86% of the unknown predicted as unknown.

Future work will concentrate on evaluating other

ML models and integrating the proposed solution

into a SIEM system in a dynamic setting. This will

demonstrate the versatility of the proposed method-

ology in ever-evolving environments. In addition,

we will investigate the use of fully homomorphic

encryption as discussed by (Sgaglione et al., 2019;

Boudguiga et al., 2020) to make the intrusion detec-

tion more privacy-preserving. However, using homo-

morphic encryption will require the adaptation of the

used models and may result in a loss of accuracy.

Efﬁcient Hybrid Model for Intrusion Detection Systems

699

ACKNOWLEDGEMENTS

We acknowledge the ﬁnancial support from the Euro-

pean Commission (H2020 IMPETUS project, under

grant agreement 883286 ), and the SAMOVAR labo-

ratory of T

ecom SudParis.

REFERENCES

Boudguiga, A., Stan, O., Sedjelmaci, H., and Carpov, S.

(2020). Homomorphic encryption at work for pri-

vate analysis of security logs. In Furnell, S., Mori,

P., Weippl, E. R., and Camp, O., editors, Proceed-

ings of the 6th International Conference on Informa-

tion Systems Security and Privacy, ICISSP 2020, Val-

letta, Malta, February 25-27, 2020, pages 515–523.

SCITEPRESS.

Feng, W., Zhang, Q., Hu, G., and Huang, J. X. (2014). Min-

ing network data for intrusion detection through com-

bining svms with ant colony networks. Future Gener-

ation Computer Systems, 37:127–140.

Gharib, A., Sharafaldin, I., Lashkari, A. H., and Ghorbani,

A. A. (2016). An evaluation framework for intrusion

detection dataset. In 2016 International Conference

on Information Science and Security (ICISS), pages

1–6. IEEE.

Gonzalez-Granadillo, G., Diaz, R., Medeiros, I., Gonzalez-

Zarzosa, S., and Machnicki, D. (2019). Lads: A live

anomaly detection system based on machine learning

methods. In Conferene on Security and Cryptography.

Nasios, N. and Bors, A. G. (2006). Variational learning

for gaussian mixture models. IEEE Transactions on

Systems, Man, and Cybernetics, Part B (Cybernetics),

36(4):849–862.

Sgaglione, L., Coppolino, L., D’Antonio, S., Mazzeo, G.,

Romano, L., Cotroneo, D., and Scognamiglio, A.

(2019). Privacy preserving intrusion detection via

homomorphic encryption. In 2019 IEEE 28th Inter-

national Conference on Enabling Technologies: In-

frastructure for Collaborative Enterprises (WETICE),

pages 321–326.

Sharafaldin, I., Lashkari, A. H., and Ghorbani, A. A.

(2018). Toward generating a new intrusion detec-

tion dataset and intrusion trafﬁc characterization. In

ICISSP, pages 108–116.

Singh, R., Kumar, H., and Singla, R. (2015). An intrusion

detection system using network trafﬁc proﬁling and

online sequential extreme learning machine. Expert

Systems with Applications, 42(22):8609–8624.

Zhavoronkov, A., Mamoshina, P., Vanhaelen, Q., Scheibye-

Knudsen, M., Moskalev, A., and Aliper, A. (2018).

Artiﬁcial intelligence for aging and longevity re-

search: Recent advances and perspectives. Ageing re-

search reviews.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

700