
zkBeacon: Proven Randomness Beacon based on Zero-knowledge
Verifiable Computation
Thomas Lavaur
1,2
and J
´
er
ˆ
ome Lacan
1
1
ISAE-Supaero, Universit
´
e de Toulouse, France
2
Paul Sabatier, Universit
´
e de Toulouse, France
Keywords:
Randomness Beacon, Random Number Generation, zk-SNARK, zk-STARK, Verifiable Computation.
Abstract:
The generation of random numbers by a trusted third-party is essential to many cryptographic protocols.
Recently, the NIST proposed the standardization of randomness beacons, which are hash-based chains of
pulses. Each pulse contains a random number and is generated at regular time intervals. However, if the
owner of the beacon generator is untrusted, several attacks allow the manipulation of the provided random
numbers. In this paper, we firstly suggest protecting the first hash functions of the NIST scheme by adding
a verifiable argument of knowledge. More precisely, we propose furnishing a zk-SNARK or a zk-STARK
with the hash to make the system more transparent and resistant to randomness manipulation. Secondly, we
propose a verifiable computation-based interactive protocol to allow a client, with the help of the beacon, to
generate proven randomness. Then, we show that connecting this system to a blockchain could have several
benefits. We provide a security analysis with a model allowing a malicious beacon generator. We prove that
our first application improves the resilience of the system against randomness manipulation attacks and that
the interactive protocol rules out timing attacks for the client and ensures the non-predictability of the random
numbers. Finally, we evaluated the computation cost with zk-SNARKs.
1 INTRODUCTION
The concept of the randomness beacon was intro-
duced in (Rabin, 1983). It can be viewed as a ser-
vice that generates a new beacon at regular time in-
tervals. This beacon is called a pulse and mainly
contains a fresh random number. While Rabin used
it to build specific cryptographic applications such
as contract signing, several other applications have
been proposed such as voting protocols (Moran and
Naor, 2010) or traceable signatures (Kiayias et al.,
). In order to make compatible potential concur-
rent randomness beacons, the US National Institute
of Standards and Technology (NIST) suggests a stan-
dard draft (Kelsey et al., 2019) enabling the emis-
sion of structured random numbers starting from raw
randomness. It has also proposed its own beacon
server (Nis, 2020), as well as some projects in Chile
(UChile, 2020) and Brazil (Bra, 2020). Basically, the
main issues that must be solved by these systems are
the quality of the randomness of the outputs, their
freshness and their immutability. These issues are de-
tailed in (Kelsey et al., 2019) and some countermea-
sures are proposed. However, the system is not flaw-
less and attacks exist, especially conceivable from the
operator of the beacon.
The first objective of our paper is to make the sys-
tem more transparent and resistant to various attacks
while maintaining its interesting structure and prop-
erties i.e., a chain of pulses using external raw en-
tropy. Secondly, we propose an interactive protocol
enabling the collaboration of the randomness beacon
and another party in order to generate a new proven
random number from their raw data. Both proposals
make use of verifiable computation (VC), which al-
lows proving that a given computation has been cor-
rectly performed with public or private inputs. Used
in the context of randomness beacons, they prove that
specific steps of the system were effectively done in
the process of the generation of the given outputs.
This paper is organized as follows. The next sec-
tion presents the state of the art concerning various as-
pects related to randomness beacons. In Section 3, we
describe the NIST scheme and its weaknesses. Then,
we detail our three main propositions: the addition
of a zero-knowledge VC scheme to prove the proper
generation of the pulses, an interactive protocol to en-
sure the freshness of the generated data, and the ad-
vantages of connecting the system to a blockchain. In
the fourth section, we present a security analysis for
406
Lavaur, T. and Lacan, J.
zkBeacon: Proven Randomness Beacon based on Zero-knowledge Verifiable Computation.
DOI: 10.5220/0011327500003283
In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 406-414
ISBN: 978-989-758-590-6; ISSN: 2184-7711
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

our proposition. To this end, we analyze the poten-
tial attacks and examine how our systems respond to
them. In Section 5, we discuss the choice of certain
mechanisms (zk-SNARK or zk-STARK, hash func-
tion used, security level) and provide a performance
evaluation of an implementation of proof generation
for our systems. The last section concludes.
2 STATE OF THE ART
This section introduces the main concepts used in this
paper. First, we present the problem of reliable ran-
dom number generation and explain the principle of
the randomness beacon. The last part describes the
zero-knowledge VC schemes that will be used in this
paper to improve the trustworthiness of these random-
ness beacons.
2.1 Random Number Generation
Random numbers generated by a non-deterministic
generator are often consequently released by a trusted
third party due to the expensive equipment required.
Introduced by Micali, Rabin and Vadhan in 1999
(Micali et al., 1999), verifiable random functions
(VRF) aim to generate proven randomness. Based on
asymmetric cryptography, the inputs of this pseudo-
random function are a public value (the seed) and a
secret generation key. The output is composed of a
proof and the result. With a given public key and
the two parts of the output, anyone can verify the
proper execution of this function and thus of the ran-
dom number generation.
2.2 Public Randomness Beacons
When a system needs randomness generated by a
third-party, it is possible to use the services of a pub-
lic generator called a randomness beacon. For exam-
ple, this is the case for blockchains and some crypto-
graphic protocols. This concept of randomness bea-
cons was introduced in (Rabin, 1983) which describes
the generation of random numbers by a satellite or a
network node at regular time intervals. These regular
beacons are used to build security protocols such as
secure contract signing or confidential disclosure.
Recently, the NIST has developed a standard de-
scribing an architecture that produces a chain of ran-
dom beacons. This standard explains how to con-
vert raw data from a source of entropy into a signed
and timestamped random number with the help of
hash functions. This proposition has already been
deployed and several organizations provide random
numbers based on it, such as the NIST itself (Nis,
2020) or public organizations from Chile (UChile,
2020) or Brazil (Bra, 2020). In addition to the de-
scription of the system, (Nis, 2020) provides a se-
curity analysis by identifying potential attacks and
proposing certain countermeasures. Efficient ran-
domness beacons have been extensively studied in the
literature. For example, (Dharanikot et al., ) designed
a randomness beacon combining distributed random-
ness, by allowing users to join at any time, and cryp-
tographic delay functions.
2.3 Verifiable Computation and
Zero-knowledge Proofs
Introduced in (Goldwasser et al., 1989), a verifiable
computation is a cryptographic protocol allowing a
prover to provide a proof with the result of an NP
computation which attests to the validity of the com-
putation. Given the input, the output and the related
proof, the verifier can validate the output of a compu-
tation as being the result of a public program without
needing to run it again. This proof can be interactive
or non-interactive.
There are a multitude of verifiable computation
protocols, but three main categories have emerged
and represent the vast majority of the systems used:
Succinct Non-interactive ARgument of Knowledge
(SNARK), Scalable and Transparent ARgument of
Knowledge (STARK) and universal SNARK. We will
not go into the history of the conception of these
proofs but we will detail the functioning, the advan-
tages and the disadvantages of these two families.
With the addition of zero-knowledge, some of the
inputs can be kept secret by hiding them and the in-
termediate steps of the computation (this secret part
is call the witness). This allows the prover to justify
the result of a computation without revealing specific
inputs. If the verifier cannot retrieve the private in-
put from the output, they will not learn anything from
the proof except the result of that calculation and the
fact that the public program was computed correctly.
With this addition, the system is called zk-SNARK or
zk-STARK.
For SNARKs and STARKs the program needs to
be transformed into a polynomial representation. This
step is called arithmetization. In order to prove an
NP program, a SNARK program must be reduced to
a Rank 1 Constraint System (R1CS). A R1CS is com-
posed of polynomials extracted from multiplication
and addition gates; their number is denoted by n. For
STARKs, it must be reduces an Algebraic Intermedi-
ate Representation (AIR). An AIR is a set of polyno-
mials extracted from transition steps; their number is
zkBeacon: Proven Randomness Beacon based on Zero-knowledge Verifiable Computation
407

denoted by n. In both systems, n impacts prover com-
plexity.
SNARKs were introduced in practice in 2013
(Parno et al., 2013). The security of a zk-SNARK
protocol relies on a trusted setup. In order to limit vul-
nerabilities, we propose using the Powers of Tau cer-
emony (Bowe et al., 2017) to decentralize the trusted
setup. The Powers of Tau ceremony allows for the
decentralization of the first step of the trusted setup
which is common to all specific zk-SNARK circuits.
At the end of this protocol, the only way to compro-
mise the system and forge a fake proof is if everyone
who participated in the protocol is corrupted or mali-
cious. By attracting many diverse and reputable par-
ticipants, it becomes unrealistic that all of them would
be compromised.
The trusted setup can either be circuit specific for
SNARKs or up to a certain amount of constraints for
universal SNARKs.
The two most used SNARK systems are Groth16
(Groth, 2016) and PLONK (Gabizon et al., 2019). In
the Groth16 system, the proof size does not depend
on the program’s complexity and is shorter than 200.
That is why Groth16 is often used. PLONK is a uni-
versal SNARK protocol with great performance.
STARKs are more recent, introduced in 2018
(Ben-Sasson et al., 2018). STARKs are based on hash
functions and when a quantum collision-resistant
hash function is used, STARKs are quantum resistant.
3 A TRUSTWORTHY BEACON
3.1 NIST Randomness Beacon
The NIST generation scheme aims to furnish ran-
dom numbers at regular time intervals (Kelsey et al.,
2019). These numbers are linked through a commit-
ment scheme and form a chain. Each number is sent
along with information about it and its construction,
all of this is structured and formatted into a pulse.
The pulse contains all the information needed for the
generation of the random number. Everything is con-
structed and calculated by the beacon app. We refer
the reader to (Kelsey et al., 2019) for their system. It
can also be view through our proposition by removing
our additions describes in 3.2 and Fig. 1.
All these steps and recommendations are ex-
plained in the NIST reference (Kelsey et al., 2019).
For our proposition, we will add cryptographic tools
to this scheme to increase transparency and secure
vulnerabilities, allowing users to be more confident in
it. Indeed, this scheme is vulnerable and users should
not be convinced that what they receive is fresh and
has not been altered.
Put simply, our first idea was to apply VRFs to the
entropy seeds ρ
i,∗
. However, the verification step of
the VRF needs the inputs and thus, would force the
system to reveal the values of the seeds, which sig-
nificantly change the principle of the beacon genera-
tor. Moreover, different types of operations need to be
proved. These constraints led us to use more general
proofs, like VC arguments.
3.2 Zero-knowledge VC to Ensure the
Proper Generation of the Pulse
We propose proving the first hash functions, which
transform the raw randomness of different random
number generators into a seed used to generate the fi-
nal random number and a commitment, with the help
of VCs. In fact, the NIST model is already a bit trans-
parent in this regard but there is no guarantee about
the seed’s r
i
provenance. For a user, when they re-
ceive the pulse, they can already verify all the infor-
mation except for the r
i
value by redoing the whole
computation. However, several attacks can arise from
the user’s inability to check the origin of this value.
The hash function can be replaced in the protocol and
nobody would notice. With the addition of a VC ar-
gument, we aim to patch this vulnerability and make
the generation reliable by enabling the verification of
r
i
while keeping the inputs secret. By doing this, we
ensure that C
i
is the output of a public program: two
hash functions.
For our scheme, we propose proving the two first
hash functions: the public program is the hash func-
tions themselves. We propose furnishing the time T
i
of the pulse as a public input and ρ
i,1
, ρ
i,2
as the pri-
vate input.
Finally, we follow one of the NIST suggestions,
not present in the previous section, which consists of
adding a XOR between the output of the first hash
and the freshly-generated random number R
i
to obtain
the new randLocal value: r
i+1
= Hash(ρ
i,1
||ρ
i,2
)⊕R
i
.
All these changes are presented in the left of Fig. 1.
For the security aspect, we decided to use a deter-
ministic signature instead of an HSM due to the fact
that its security is based entirely on the trustworthi-
ness of its creator. Information inside the message M
i
changes slightly from the original proposition so as to
adapt to our scheme. We removed the external value
which is not useful in our case and added the proof of
the commitment C
i
that resulted from a VC scheme.
The verification only require redoing hash func-
tions, verifying a signature and an argument from a
VC protocol, which implies quick verification on the
user-end.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
408
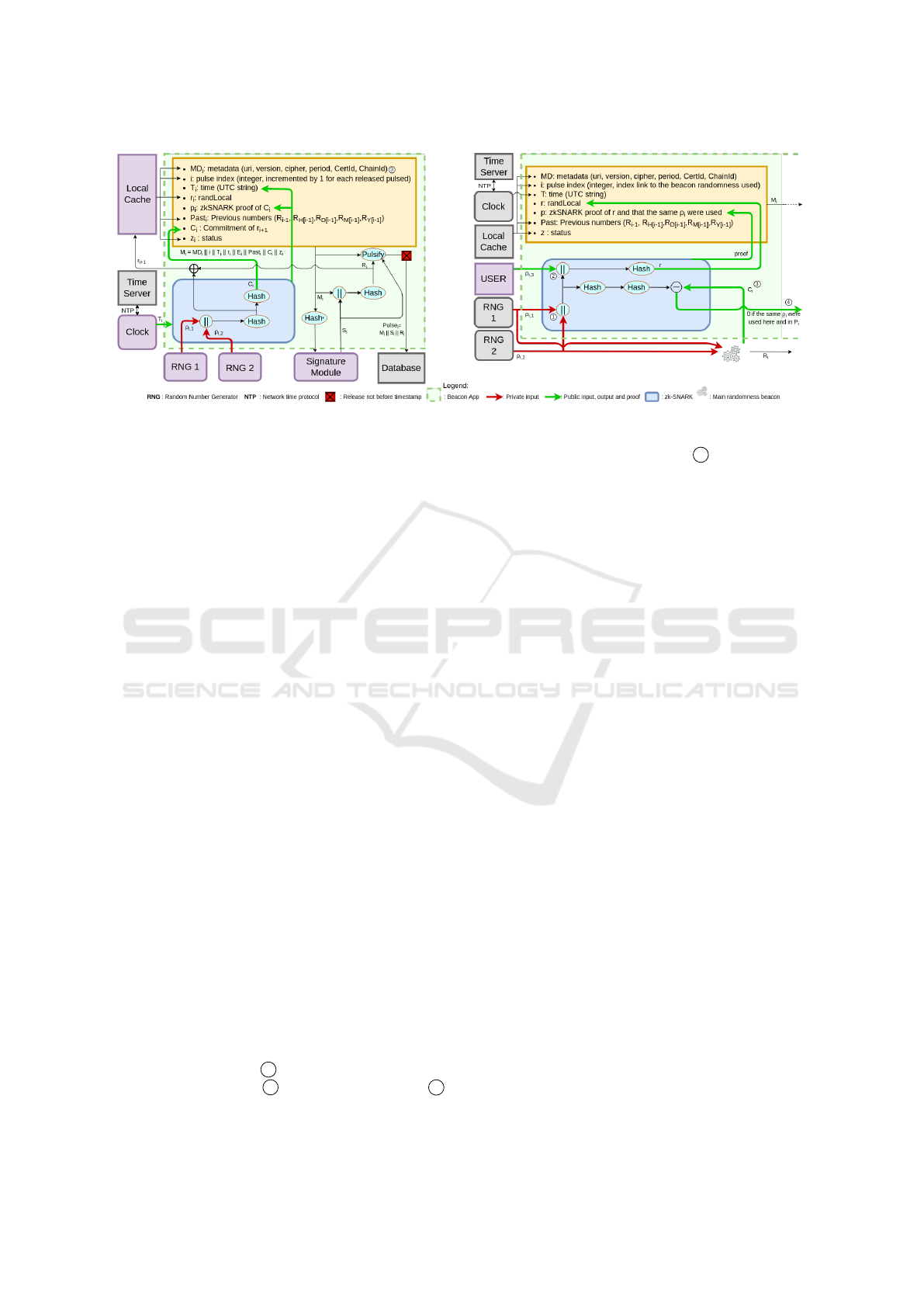
Figure 1: The zkBeacon random number generation model and the interactive protocol.
3.3 Interactive Protocol based on
Zero-knowledge VC to Ensure the
Freshness of the Pulses
Here, we exhibit our interactive protocol, allowing a
user to combine their entropy with that of the random-
ness beacon. This protocol is completely independent
of the beacon chain based on VC. Our second propo-
sition can even be applied to a classical beacon, such
as the one from the NIST.
When a client receives a new pulse from the ran-
domness beacon, even if all the computation was done
correctly, they cannot be sure that the entropy used
to generate the random number inside ρ
i,1
and ρ
i,2
is
sufficient and unmanipulated. Moreover, the pulse is
supposed to be fresh but nothing guarantees that the
pulse was not created a long time ago.
In order to counter these possibilities, we propose
an interactive protocol where a user asks the beacon
to create an orphan pulse with three inputs: the same
ρ
i,1
and ρ
i,2
used in the last pulse and a new value ρ
i,3
that they provide. This enables multiple possibilities
to counter time attacks and bias on random numbers
from a malicious owner or adversary. This will be
discussed in Section 4.
In addition to classical fields (metadata, sta-
tus, index), an orphan pulse generated by the
beacon contains the randLocal r computed as
Hash(ρ
i,1
||ρ
i,2
||ρ
i,3
) and an argument of VC which
attests to the correct computation of r and that the
same ρ
i,1
and ρ
i,2
were used in the last pulse of the
main beacon chain. Here, the VC algorithm takes
ρ
i,1
and ρ
i,2
as private inputs so as not to disclose the
(main chain) randLocal value which will be used in
the (main chain) pulse 1 , ρ
i,3
as public input to in-
clude the user’s values 2 and C
i
as public input 3
in order to certify that ρ
i,1
and ρ
i,2
correspond to the
commitment sent in the last pulse 4 . All these steps
are summarized in the right of Fig. 1. If the beacon re-
sponds quickly (an order of seconds), the user is sure
to have fresh randomness if their input is random.
Depending on the context, the user can generate a
random number as described in (Kelsey et al., 2019)
(i.e., as the hash of the message and the signature) or,
if they want to avoid any potential beacon manipula-
tion, they can use the provided randLocal value di-
rectly (as a VRF). The interactive protocol has the ad-
vantage over a VRF to provide external entropy.
In the case of a frequently consulted beacon, to
ensure smooth scaling, it is possible to include sev-
eral random seeds from different users in the same
orphan pulse. Depending on the application and the
context, the beacon must choose between one orphan
pulse per user or regrouping several users for an or-
phan pulse at a regular time interval.
3.4 Connecting the Randomness Beacon
to a Blockchain
In this Section, we show that connecting a blockchain
to our randomness beacon has several benefits for
both systems.
3.4.1 Beacon Chain Immutability
Even though the beacon chain provides a way to
link the pulse and thus, to avoid data modifications
a posteriori, we suggest decentralizing a part of the
database at the backend, storing the pulses or the ran-
dom numbers on a blockchain. This strategy should
improve the resilience of pulses against modifica-
tion and remove vulnerabilities linked to a malicious
database thanks to blockchain immutability. This part
of the proposition is independent of the protocols pro-
posed above.
zkBeacon: Proven Randomness Beacon based on Zero-knowledge Verifiable Computation
409

3.4.2 Timestamped Random Number
A user can use the interactive protocol to certify the
freshness of the randomness by submitting an entropy
input ρ
i,3
deduced from a recent block of a blockchain
to the beacon. For example, assuming Ethereum takes
approximately 14 seconds to forge a new block, if
ρ
i,3
contains the nonce of the last block mined in the
blockchain, every third party using the random num-
ber published after the protocol will be convinced that
the number was not generated before the publication
of the block on the blockchain. Indeed, if a malicious
beacon is able to know the next nonce in advance, it
can reverse a hash function, which is supposed to be
impossible. This suggestion is dependent upon the
existence of an interactive protocol or the use of a
user input. It cannot be directly applied to the offi-
cial NIST beacon, or it requires a slight modification
in order to take a user value into account.
3.4.3 Randomness for Blockchains
Blockchains often need a source of randomness for
many internal protocols. With our propositions, de-
tailed above, we can use the interactive protocol to au-
tomate the reception and use of random numbers. An
oracle can send a query to the beacon at regular time
intervals, asking it to furnish a random number with
entropy deduced using the last block as input. The
freshly generated randLocal value can be used as the
new random number inside the blockchain. Indeed,
we cannot store the whole pulse on a blockchain due
to the size of M
i
. However, we can use the randLocal
value as randomness on the blockchain by storing it
and its VC argument. By doing this, we ensure that
the randomness is not manipulated by the beacon, and
everything can be verified on the blockchain.
It should be noted that the oracle Chainlink pro-
vides a randomness service to smart contracts (Brei-
denbach et al., 2021). The principle consists of apply-
ing a Verifiable Random Function to a seed provided
by the smart contract. Like this solution, our proposal
is cryptographically verifiable, but it has the advan-
tage of using external entropy.
4 SECURITY ANALYSIS
In this section, we will follow the NIST draft (Kelsey
et al., 2019) and compare their analysis of possible at-
tacks on their system with our propositions. We will
reiterate any aspects necessary to the study of the se-
curity analysis.
4.1 Desired Properties
The main properties desired for a beacon are estab-
lished in three essential categories in (Kelsey et al.,
2019):
• relations that ensure the correct chaining process
between each pulse.
• availability of pulses with reduced human inter-
vention.
• random quality to ensure unpredictability and un-
biased, fresh randomness in each pulse; these
properties mainly come from the randLocal value.
The draft (Kelsey et al., 2019) asserts that the
properties above derive from the pulse design itself
when everything works as expected: without a breach,
with a full entropy input, with synchronous and ade-
quately fast communication and with a database that
is available and reliable.
To achieve all of these required qualities, we based
our model on cryptographic assumptions. Like in
(Kelsey et al., 2019), we will assume that the hash
functions used are one-way and collision resistant.
We will also consider that the output of the hash func-
tion used is indistinguishable from true randomness
when the input is unpredictable. Secondly, we will
assume that the signature scheme is unforgeable and
that its public key is certified correctly. For our model,
we will use a verifiable computation scheme, more
precisely, zk-SNARKs or zk-STARKs. These argu-
ments provide three additional cryptographic proper-
ties:
• completeness: if the prover (the number generator
in our case) is honest with a correct witness, they
must convince a verifier.
• knowledge soundness: an honest verifier will not
accept an invalid proof.
• zero-knowledge: the proof does not leak any in-
formation aside from the correct computation.
4.2 Adversary Model
In order to evaluate our system we need to describe
what kind of adversary can attempt an attack, what
their goal is and how they can reach it. We will con-
sider two different adversaries with different capabili-
ties. An adversary, or an attacker, can be semi-honest
or malicious. Our proposition is more general than
that of (Kelsey et al., 2019) regarding the security as-
sumptions by considering that the entire beacon can
be fully malicious and by removing the HSM which
was supposed safe.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
410

Adversaries’ goals are almost always the same but
the benefits they could reap are plentiful. Firstly,
someone may want to discover the next random num-
ber or information about the next number in advance.
For example, if someone knows the parity of the next
random number ahead of the time indicated in its
timestamp, they are twice as likely to win if the num-
ber is used in a betting game. Secondly, an attacker
may also want to directly induce a change in the be-
havior of the protocol in order to alter the next random
number and once again be able to take advantage of
it. With the same goal, an adversary can modify the
database and change pasts numbers. Finally, the last
case we studied is the ability to shut down the system,
fork a chain or anything that can block users from
accessing the random beacon for a certain period of
time.
4.3 Attacks and Countermeasures
We will now present all of the attacks evoked in
(Kelsey et al., 2019), how they can occur, which parts
of the system have to be vulnerable and what is sug-
gested in order to avoid them. For each of them, we
will study the possibility of its occurrence and we re-
fer the reader to (Kelsey et al., 2019) for more detail
of their countermeasures. For each attack, we will
specify which proposal improves the security of our
overall model. Again, each proposal is independent
and can be applied or not. We consider the complete
system all three of our proposals.
4.3.1 Bias on RNG Outputs Due to a Malicious
Beacon App
In both the NIST scheme and ours, the ρ
i
which
are outputted from the RNGs, are never revealed to
the public and an attacker could choose values to re-
place them arbitrarily. They can even directly replace
r
i
= Hash(ρ
i,1
||ρ
i,2
) due to the one-way nature of the
hash function. Adding a XOR between r
i
and R
i−1
to produce the randLocal seed has been suggested.
With this adjustment, an attacker could not com-
pletely foresee the final randLocal value which would
come from Hash(ρ
i,1
||ρ
i,2
) ⊕ R
i−1
and the commit-
ment value C
i
= Hash(Hash(ρ
i,1
||ρ
i,2
)). However, if
the adversary is able to control the beacon app for sev-
eral consecutive pulses, the fresh randomness prop-
erty is not conserved.
By adding our first proposition, this attack is not
possible. Even if the ρ
i
are not revealed, the proof
provided by the VC protocol gives the ability to ver-
ify that the proposed r
i
is the result of a concatenation
followed by a given hash function. In our case, an at-
tacker who wants to alter the randomness of a pulse
will have to anticipate all of the information within
the pulse, i.e., two consecutive hashes, and a valid
proof. The proof itself is non-deterministic by the
zero-knowledge nature of VC and it changes for each
execution due to the different random numbers used
at each step in the protocol. Moreover, our scheme
includes the modification suggested in (Kelsey et al.,
2019). This attack is completely avoided with our sys-
tem and renders the system more transparent thanks to
the guarantee of the correct r
i
computation.
4.3.2 Prediction and Exfiltration Due to a
Malicious Beacon App
As in the previous Section, a malicious adversary can
alter the r
i
or ρ
i
values. By replacing these values
with a symmetric encryption scheme that has an ap-
propriate output length and outputs indistinguishable
from random, an attacker gains the ability to commu-
nicate with someone else who shares the secret key
without anyone knowing. This communication link
can be used to exfiltrate internal information from the
beacon or from any program accessed by the attacker.
Another possible usage is the ability to completely
predict the next pulses by deterministically encrypt-
ing the index of the pulse. The draft (Kelsey et al.,
2019) does not provide any possible mitigation.
With the use of the proven beacon (first proposi-
tion), such a change is, here too, not a possibility. The
proof will not be valid if a modification has been made
on the public program and the random number will be
rejected by the users. This is a significant improve-
ment compared to the previous proposition, even if
the generation of ρ
i
can still be manipulated.
4.3.3 Bias on the Freshly-generated Random
Number Due to a Malicious Beacon App
If an adversary can make multiple requests to an hon-
est HSM, they can ask for several signatures with dif-
ferent values of r
i
until they obtain a result with a
certain property enabling them to produce a final R
i
with a desired attribute. They can also produce sev-
eral pulses in advance to give themselves more time
and be able to alter more bits of R
i
.
A mitigation proposed in (Kelsey et al., 2019) is
to use an HSM which imposes a delay between each
signature, or to partition the beacon app.
This mitigation does not solve the problem and
relies on an HSM. Moreover, the adversary may be
the operator of the system and the clients who receive
the pulses cannot verify if the system is partitioned or
not. This mitigation relies on the trustworthiness of
the owner and only avoids external attacks.
Thanks to the interactive protocol, the beacon
zkBeacon: Proven Randomness Beacon based on Zero-knowledge Verifiable Computation
411

server has a shorter time range to attempt this attack
because it cannot know the user’s input in advance.
We suggest introducing an X-second lag before the
beacon can answer, which drastically reduces the time
window for an adversary to generate multiple random
numbers.
4.3.4 Advanced Knowledge and Prediction.
It is clear that the construction of the pulse requiring
the knowledge of r
i
creates a vulnerability if the bea-
con is semi-honest. In fact, the beacon stores the rand-
Local value for the next pulse during the creation of a
new one. During this period of time, the beacon gains
the knowledge of the next randLocal, one pulse be-
fore users and thus has the information to produce R
i
.
For the same reasons, the beacon also knows R
i
before
users due to the time it needs to wait before transmit-
ting. If the beacon app is malicious, this leads to a
prediction of r
i
and R
i
. Another attack leading to ad-
vanced knowledge of R
i
relies on the internal clock. If
this clock, or time-server used by the internal clock to
synchronize itself, is malicious, it can give the beacon
app a fake time allowing for the premature creation
of a new pulse. If the beacon app remains honest, it
would release the pulse to the database. A malicious
database could then disclose the random numbers at
the right time, gaining the knowledge of every num-
ber generated in advance of other users.
The mitigations proposed by (Kelsey et al., 2019)
do not remove the above vulnerability, two of them
simply redirect trust to a timestamp service.
We followed one of the propositions and inserted
a XOR into the computation of randLocal, delaying
the knowledge of r
i+1
for the beacon. The interac-
tive protocol is not at all vulnerable to these attacks
due to the interactivity with the client. Even if the
beacon’s clock were malicious, the interactivity dras-
tically reduces the time during which the new random
number is known by the beacon, and a database is not
involved. Moreover, the client can check if the time
furnished by the beacon is in sync with their own local
clock. The beacon cannot compute the random num-
ber before it has access to the client’s input, delaying
the knowledge of the input for the beacon.
Secondly, with our third proposition, by using the
entropy from the last block of a blockchain as a part
of the public input, everyone will agree that the ran-
dom number is fresh and was not known until it was
released.
4.3.5 History Modification Due to a Malicious
Database and Signature Key Access
When an adversary has access to the database and the
signature module key stored in the HSM, they have all
the tools needed to completely alter the information
stored in the database except the commitment link be-
tween two pulses. Consequently, they can compute
their own chain of random numbers and replace the
entire chain or the end of the existing one. The NIST
draft promotes the multiplication of external reposito-
ries.
Our system highly supports the decentralization of
the database and suggests using a blockchain to store,
at least, the proofs or the random numbers, and ex-
ploiting the immutability and distributed properties of
blockchains.
5 PERFORMANCE EVALUATION
This section describes what we used to evaluate our
system. We propose using of a new generation of
tools that enable drastically reducing the memory us-
age of the prover as well as the argument generation
time. After that, we discuss the performances ob-
tained, which demonstrate that deploying our system
is realistic on a standard computer.
5.1 Hash Functions Used
Today, programs are optimized to be evaluated as
quickly as possible. This often implies the use of
operations close to the CPU and therefore Boolean
operations. However, these operations are expensive
to prove. It is therefore important to find programs
that are no longer just optimized for evaluation but
for evaluation and proving. Using arithmetic oper-
ations instead of boolean operations can increase the
evaluation time but greatly reduce the proof time, thus
improving overall complexity.
Even if VC protocols can have a succinct proof
size and verifier constant time computation, like zk-
SNARKs, the complexity of the prover is at least lin-
ear in the number of constraints. With this in mind,
classical hash functions have a lot of constraints due
to the transformation of their logic construction into
arithmetic. In section 5.2, we show that SHA256 with
a 1024-bit input has around 90, 000 constraints in the
R1CS model. It is important to note that for SNARKs,
the size of the prover key is linear in regard to the
number of constraints.
However, several propositions of an alternative
SNARK-friendly (also STARK-friendly) hash func-
SECRYPT 2022 - 19th International Conference on Security and Cryptography
412

Table 1: Evaluation of the different circuits on 100 executions.
constraints witness prover key average proving time
SHA256 (1024 bits) 89,698 2.9 MB 59.9 MB 2.710 s
Rescue (1016 bits) 1,196 38.3 KB 727 KB 382 ms
zkBeacon (Section 3.2) 1,667 53.4 KB 961.5 KB 408 ms
interactive protocol (Section 3.3) 2,390 76.6 KB 1.5 MB 447 ms
tion, which is arithmetically oriented, have appeared
in the literature over the past few years. They aim to
be more efficient regarding the number of constraints.
Following the lead of a recent survey (Ben-Sasson
et al., 2020) based on multiple security analyses, such
as (Beyne et al., 2020) and (Canteaut et al., 2020), we
will consider the usage of the Rescue hash function
(Aly et al., 2020). The Rescue function is based on
a sponge construction and can output different sizes
of data depending on the chosen parameters. In or-
der to compare the Rescue and SHA functions, we
implemented their R1CS circuits using Circom (cir,
2020) and generated their proofs and witnesses with
SnarkJS (sna, 2020). However, SnarkJS only relies on
the BN128 and BLS12 − 381 curves which are 128-bit
security curves. We decided to only evaluate 128-bit
security hash functions to remain consistent. We will
evaluate our proposition based on the SHA256 and
Rescue function. The Rescue hash function allows
faster computation and lighter memory usage. The
use of the Rescue function drastically reduces prover
and verifier key sizes for SNARKs, as well as memory
consumption.
Even though Rescue is slower to evaluate than
SHA256 which is oriented for CPU use. It is impor-
tant to differentiate the proving time and the evalu-
ation time. At our scale, with only a thousand bits
in input, the Rescue hash functions take 7 times less
time to be evaluated and proved than SHA256 with
our implementation.
5.2 Implementation and Evaluation
For our implementation, we propose the use of the
Groth16 zk-SNARK scheme (Groth, 2016) which is
very efficient in terms of communication (proof size)
and verifier computation complexity, both in O(1). In
terms of computation and memory usage, this com-
plexity is O(nlog(n)). For the trusted setup phase,
we reuse the ceremony done in 2018 on the Zcash
blockchain (zca, 2018) in order to involve many fa-
mous participants without redoing all of the organiza-
tion.
We chose the Groth16 protocol because the proof
is tiny and this is important for our global sys-
tem. Groth16 proof size is less than 200 bytes while
STARK of two Rescue with weaker parameters than
ours is around 11 KB according to the evaluation
based on winterfell (win, 2021). The blockchain’s
block size is a key parameter. Most of existing
blockchains only support a small amount of infor-
mation per transaction, or the fees paid to include
the transaction increase with size. The second is be-
cause the blockchain verification cost is feasible for
Groth16 and costly for STARKs (around 300k gas
on Ethereum for Groth16 and estimated at more than
2.5M for STARKs).
To evaluate our system, we used Circom to imple-
ment the Rescue and SHA256 circuits and evaluated
their proof generation using snarkJS. The SHA256
function has already been implemented by Circom in
the Circomlib available on github. We implemented
the Rescue function according to the Rescue-prime
specification (Szepieniec et al., 2020). We used a
32 GB RAM computer with an Intel Core i7-10850H
CPU at 2.7 GHz on a 64-bit Ubuntu 20.04.3 LTS.
We implemented Rescue using parameters related
to elliptic curve choice. Having chosen the BN128
curve, we generated all other parameters based on a
capacity of 3 elements, a state width of 4 and a secu-
rity level of 128 bits with a 40% margin. To remain
coherent with our system, we evaluated Rescue with 4
elements of F
p
as input, which is approximately 1016
bits.
We evaluated the interactive protocol with the
same hash function. As private inputs, we took the
same length of 4 elements of F
p
and for the client’s
public input, we took 2 elements of F
p
, for a total of
1524 bits. In the end, the circuit is almost entirely 3
Rescue functions: one with 6 elements of input, one
with 4 and one with 1. Our results were obtained by
averaging over 100 executions and are summarized in
Table 1.
Thanks to this evaluation, we can state that our
proposition can be easily deployed on a standard com-
puter. Indeed, according to these results evaluated
on a standard personal computer, a zk-SNARK of a
pulse and a proof for the interactive protocol can be
both generated in less than 0.5 seconds. Moreover,
SnarkJS is not optimized and most of the measured
time is dedicated to loading the verifier key and ini-
tializations.
zkBeacon: Proven Randomness Beacon based on Zero-knowledge Verifiable Computation
413

6 CONCLUSION
Our proposition aims to improve the randomness bea-
con concept standardized by the NIST.Our main ob-
jective is to keep the main interesting concepts of
randomness beacons, i.e., the use of external entropy
and the chaining of the pulses, but also to strengthen
user confidence in the outputs. For that, we proposed
the addition of a verifiable computation argument on
the first hash functions used in each pulse generation,
making our system more transparent.
The second part of our proposal is an interac-
tive protocol, limiting the possibility of timing at-
tacks and the lack of fresh randomness. We also sug-
gest connecting the database to a blockchain in order
to improve the immutability of the database, provide
timestamped random numbers and use the random-
ness beacon as a proven random number oracle for
the blockchain. We proved that our scheme supports a
security model with a malicious beacon generator. Fi-
nally, we benchmarked an implementation of our pro-
posal based on the Rescue hash function and Groth16
zk-SNARK and proved that the constraints in terms of
memory and CPU, are acceptable, even for a personal
computer.
ACKNOWLEDGEMENTS
The authors would like to thank Jonathan Detchart,
Thibault Gateau and Caroline Chanel for their help
on several aspects of this work.
REFERENCES
(2018). Zcash powers of taus ceremony attestation. Ac-
cessed: 24/03/2022.
(2020). CIRCOM: Circuit Compiler for Zero-Knowledge
Proofs. Accessed: 24/03/2022.
(2020). Inmetro Randomness Beacon. Accessed:
24/03/2022.
(2020). Nist Randomness Beacon. Accessed: 24/03/2022.
(2020). SNARKJS: JavaScript Implementation of zk-
SNARKs. Accessed: 24/03/2022.
(2021). Winterfell : A STARK prover and verifier for arbi-
trary computations. Accessed: 28/04/2022.
Aly, A., Ashur, T., Ben-Sasson, E., Dhooghe, S., and Szepi-
eniec, A. (2020). Design of symmetric-key primitives
for advanced cryptographic protocols. IACR Transac-
tions on Symmetric Cryptology, pages 1–45.
Ben-Sasson, E., Bentov, I., Horesh, Y., and Riabzev, M.
(2018). Scalable, transparent, and post-quantum
secure computational integrity. Cryptology ePrint
Archive.
Ben-Sasson, E., Goldberg, L., and Levit, D. (2020). STARK
Friendly Hash-Survey and Recommendation. IACR
Cryptol. ePrint Arch., 2020:948.
Beyne, T., Canteaut, A., Leander, G., Naya-Plasencia, M.,
Perrin, L., and Wiemer, F. (2020). On the security of
the Rescue hash function. IACR Cryptol. ePrint Arch.,
2020:820.
Bowe, S., Gabizon, A., and Miers, I. (2017). Scalable
Multi-party Computation for zk-SNARK Parameters
in the Random Beacon Model. Cryptology ePrint
Archive, Report 2017/1050. https://ia.cr/2017/1050.
Breidenbach, L., Cachin, C., Chan, B., Coventry, A., Ellis,
S., Juels, A., Koushanfar, F., Miller, A., Magauran, B.,
Moroz, D., et al. (2021). Chainlink 2.0: Next Steps in
the Evolution of Decentralized Oracle Networks.
Canteaut, A., Beyne, T., Dinur, I., Eichlseder, M., Leander,
G., Leurent, G., Plasencia, M. N., Perrin, L., Sasaki,
Y., Todo, Y., et al. (2020). Report on the Security of
STARK-friendly Hash Functions (Version 2.0).
Dharanikot, S., Jensen, M., Kristensen, S., Michno, M.,
Pignolet, Y., Hansen, R., and Schmid, S. Breeding
Unicorns: Developing Trustworthy and Scalable Ran-
domness Beacons.
Gabizon, A., Williamson, Z. J., and Ciobotaru, O. (2019).
Plonk: Permutations over lagrange-bases for oe-
cumenical noninteractive arguments of knowledge.
Cryptology ePrint Archive.
Goldwasser, S., Micali, S., and Rackoff, C. (1989). The
knowledge complexity of interactive proof systems.
SIAM Journal on computing, 18(1):186–208.
Groth, J. (2016). On the size of pairing-based non-
interactive arguments. In Annual international confer-
ence on the theory and applications of cryptographic
techniques, pages 305–326. Springer.
Kelsey, J., Brandao, L., Peralta, R., and Booth, H. (2019).
Reference for Randomness Beacons, Format and Pro-
tocol Version 2, Draft NISTIR 8213. Technical report.
Accessed: 24/03/2022.
Kiayias, A., Tsiounis, Y., and Yung, M. Traceable Sig-
natures. In Advances in Cryptology - EUROCRYPT
2004.
Micali, S., Rabin, M., and Vadhan, S. (1999). Verifiable
random functions. In 40th annual symposium on foun-
dations of computer science (cat. No. 99CB37039),
pages 120–130. IEEE.
Moran, T. and Naor, M. (2010). Split-Ballot Voting: Ev-
erlasting Privacy with Distributed Trust. ACM Trans.
Inf. Syst. Secur., 13(2).
Parno, B., Howell, J., Gentry, C., and Raykova, M. (2013).
Pinocchio: Nearly practical verifiable computation. In
2013 IEEE Symposium on Security and Privacy, pages
238–252. IEEE.
Rabin, M. O. (1983). Transaction protection by beacons.
Journal of Computer and System Sciences, 27(2):256–
267.
Szepieniec, A., Ashur, T., and Dhooghe, S. (2020). Rescue-
Prime: a standard specification (SoK). Cryptology
ePrint Archive.
UChile, R. (2020). Public, Transparent and Verifiable Ran-
domness. Accessed: 24/03/2022.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
414
