Conceptual Approach for Optimizing Air-to-Air Missile Guidance to

Enable Valid Decision-making

Philippe Ruther

, Michael Strohal

†

and Peter Stütz

‡

Institute of Flight Systems, Universität der Bundeswehr Munich, Werner-Heisenberg-Weg 39, 85577 Neubiberg, Germany

Keywords: Computer Generated Forces, Missile Guidance, Deep Reinforcement Learning, Optimal Control.

Abstract: In this paper, we briefly introduce a concept on how the workflow of a pilot in a beyond visual range mission

can be divided into different tasks in order to mimic the workflow in the behavioural control of adversary

computer generated forces in training simulations. An essential part of fighter pilots’ workflow is the decision-

making process, in which they must weigh opportunities against risks. Particularly in the weapon delivery

task, valid data are a basic prerequisite for making a confident decision when weighing one’s opportunities

against potential risks. Concerning the applicability of artificial intelligence methods, the optimization of a

missile's trajectory is used as an example to examine methods that allow an estimation of one’s chances based

on valid data to enable valid decision-making. For this purpose, we briefly introduce methods of optimal

control and in particular deep reinforcement learning. In the future, we intend to use data generated by optimal

control to validate the data provided by deep reinforcement learning methods as a basis for explainable

decision-making in training simulation and threat analysis.

1 INTRODUCTION

1.1 Overall Concept

Due to evolving technology and enhanced weapon

systems, simulating Computer-Generated Forces

(CGF) – especially the adversary side – in Beyond

Visual Range (BVR) air combat tactical scenarios is

becoming increasingly important.

A major objective in air combat training

simulators is to generate various scenarios in which

fighter pilots can apply and expand their knowledge

through new threat situations or try new tactics. In

order to achieve the main objective of any military

training centre ‘train as you fight, fight as you train’,

the artificially generated enemy forces must also be

represented in a valid manner. Therefore, two design

factors must be considered: On the one hand the

physical presence such as physical limits,

manoeuvrability, sensory systems or weapons must

be valid and on the other hand, the CGF behaviour as

described in doctrines or tactical instructions must be

appropriate and reviewable.

https://www.unibw.de/lft/personen/philippe-ruther-m-sc

†

https://www.unibw.de/lft/personen/dr-ing-akdir-michael-strohal

‡

https://www.unibw.de/lft/personen/univ-prof-dr-ing-peter-stuetz

However, generating behaviour requires expert

knowledge that is not always available. Furthermore,

once a behaviour model is implemented, its behaviour

is usually fixed and must be manually altered to

provide variations and different levels of

sophistication or challenges (Toubman et al., 2016).

There must be an ongoing process to develop new

scenarios to adapt to new threat situations using more

agile and verified opponent behaviour.

In order to represent adversary forces with higher

flexible behaviour in fighter pilots’ training

simulations, we aim to research to what extent

Artificial Intelligence (AI) methods are suitable for

this purpose. Various approaches already exist for

generating such CGF behaviour incorporating

methods of AI technology, e.g. (Xiao and Huang,

2011), (Dong et al., 2019), (Wang et al., 2021),

(Wang et al., 2020).

In general, the existing methods can be divided

into rule-based and machine learning AI methods

(Fasser, 2020).

Rule-based methods represent the behaviour of a

CGF using different predefined rules. By initiating a

304

Ruther, P., Strohal, M. and Stütz, P.

Conceptual Approach for Optimizing Air-to-Air Missile Guidance to Enable Valid Decision-making.

DOI: 10.5220/0011302800003274

In Proceedings of the 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2022), pages 304-310

ISBN: 978-989-758-578-4; ISSN: 2184-2841

predefined condition, a specific rule triggers a defined

behaviour. An example of such approaches are

behaviour trees or finite state machines (Johansson,

2018).

Machine learning AI methods like reinforcement

learning (Plaat, 2022) define a connection between a

predefined condition and a desired behaviour, thereby

establishing a suitable rule by adjusting internal

weights.

In our study, we want to investigate to what extent

machine learning approaches can be combined with

rule-based concepts to generate improved, verified

and validated behaviour models. Each of these AI

methods requires a clear definition framework. For

this reason, it is first necessary to describe the

behavioural pattern of a pilot in BVR air combat.

Therefore, the OODA loop (Observe, Orient, Decide,

Act) by Boyd (Richards, 2020) is often cited.

However, with this top-level approach, it is difficult

to describe a highly complex scenario like a BVR air

combat – a more specified and detailed concept of the

OODA loop is needed.

To tackle this, we designed a concept which

allows linking the behaviour of an enemy aircraft in

BVR air combat with potential AI methods and split

up the workflow and processes of a BVR engagement

into three main parts: attack, self-defence and decide.

Each of these has defined in- and output parameters.

This approach makes it possible to decompose the

complex application space of the OODA loop in BVR

air combat into many smaller tasks and to investigate

the suitability of various AI methods with respect to

the different tasks. A more in-depth look at the

workflow can be found in (Reinisch et al., 2022).

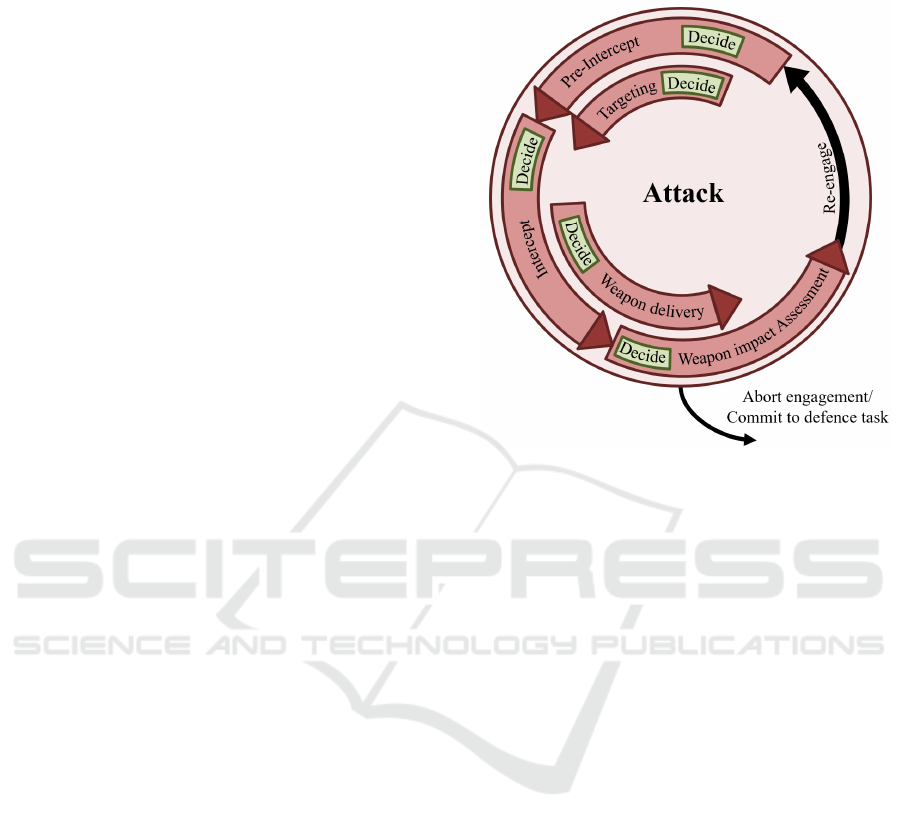
1.1.1 Attack

The main tasks of a CGF in offensive and defensive

air-to-air combat simulation are performed in the

attack loop. The tasks (see Figure 1) here are divided

into the following process tasks which will be briefly

explained here:

Pre-intercept describes the planning and

execution up to the fighting range supported by an

Airborne Warning And Control System (AWACS)

until the enemy targets are identified by the own

radar. While flying toward the enemy in the pre-

intercept phase, targeting is conducted and

coordinated by evaluating the targets. After assigning

a target, each CGF executes an intercept by flying

toward the target with the main goal of optimizing its

own aspect angle. During interception of the assigned

target, the decision whether to fire a missile or not is

made in the weapon delivery phase. The result of this

engagement is evaluated by the weapon impact

assessment.

Figure 1: Attack Loop.

1.1.2 Decide

The decide loop (see Figure 2) is executed

continuously during each task. First, scenario

information is updated. This includes static

information (e.g. predicted enemy weapon range

etc.), as well as dynamic information which, unlike

the static information, changes over the mission (e.g.

weapons status etc.). The dynamic information is

combined with the detection and identification of

enemy aircraft to form a so-called air picture. In each

cycle of the decision loop, information is first updated

to ensure the decision is made using an up-to-date air

picture.

Decisions in BVR workflow are made based on

weighing one’s own opportunity against the risk

(Stillion, 2015). Therefore, the first step is to perform

an assessment of its own situation in order to evaluate

the opportunities. The subsequent enemy assessment

allows conclusions to be made related to the current

risk. Based on this evaluation, all parameters (air

picture) that affect the execution of the specific

current task are taken into consideration.

This makes the following three decisions

possible:

 Continue/Commit to attack task

 Terminate mission

 Continue/Commit to defence task

Conceptual Approach for Optimizing Air-to-Air Missile Guidance to Enable Valid Decision-making

305

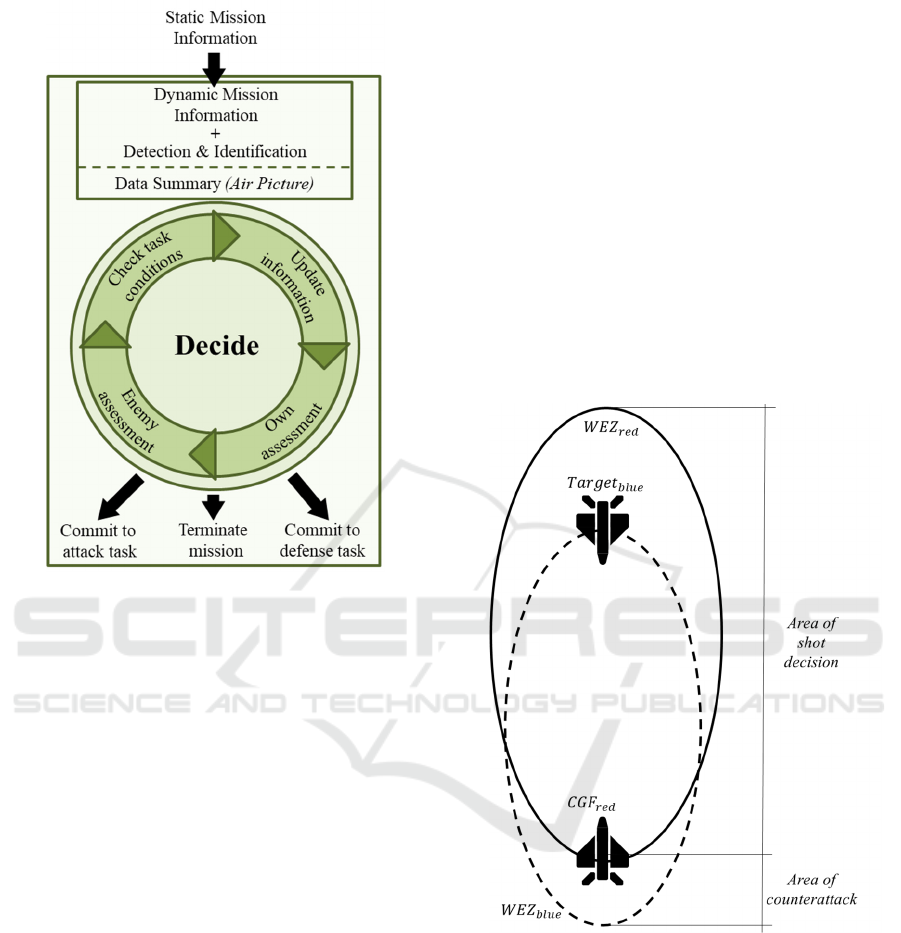
Figure 2: Decide Loop.

This continuous decision process makes it possible to

switch between the main loops attack and self-

defence at any time, as well as to abort the mission

through the self-defence loop as described in

(Reinisch et al., 2022).

1.2 Weapon Delivery Optimization

To test new tactics in a BVR air-to-air combat

simulation or to be able to evaluate a threat analysis,

the weapon range as well as an explainable time of

weapon launch have a decisive influence. Therefore,

the previously outlined weapon delivery phase

possesses a central role in defensive as well as

offensive scenarios. In this phase, after weighing up

own opportunities and risks, the decision to launch a

weapon is made.

An important parameter of this decision is the

maximum achievable range of the own Weapon

Engagement Zone (WEZ) under the condition of a

non-maneuvering target (see Figure 3). The larger the

WEZ, the sooner a potential opponent can be

engaged. Maximizing the WEZ is therefore a top

priority in BVR engagements. A large weapon range

leads to higher own security and lower own risk, as

well as more space and time to execute the own

strategy.

Another key parameter is the pilot's situational

risk level at the time of engagement. It changes

according to the air picture given in the decision loop

(Figure 2).

This risk level is especially affected by the current

threat situation (e.g. number of own aircraft, number

of enemy aircraft etc.). A low threat situation

corresponds to a pilot's low risk level. Therefore, the

pilot places a high value on flying only as deep as

necessary into the enemy WEZ, as predicted by the

static information of the decision loop. While

advancing into the enemy's WEZ increases the

probability of hitting the other aircraft, it also

negatively affects the own safety (risk of getting hit

by an incoming missile). Thus, there is a direct

correlation between risk level and the probability of

hitting the opponent as visualized in figure 3.

Figure 3: Weapon Engagement Zone of a CGF fighter

aircraft and a blue target.

In order to be able to decide on a suitable weapon

launch time within the weapon delivery phase, a valid

knowledge of the missile trajectory is an

indispensable prerequisite.

Therefore, the missile trajectory must first be

optimized using suitable methods to obtain an optimal

trajectory of the missile when given a certain risk

level which is directly related to the distance from the

target.

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

306

2 PROBLEM FORMULATION

AND OBJECTIVES

To achieve a valid decision regarding an optimal

weapon launch point, verification of the optimal

missile trajectory is of central importance. Only by

using a verified missile trajectory, it is possible to

estimate the own opportunities, which is a basic

prerequisite for the decision of launching a missile.

The underlying model determines to what extent the

weapon launch point is optimal with respect to the

own actual risk level.

Therefore, in this paper, we research a possible

implementation with respect to the optimization

procedure of the missile trajectory. The problem of

finding an optimal missile trajectory is well suitable

for studying machine learning approaches due to its

limited search space and manageable parameters

compared to learning other behavioural models

within the pre-defined BVR workflow. For this

purpose, we will use optimal control (Section 3) to

provide the verification of a machine learning

approach (Section 4). In the future, we aim to

continue investigating the most promising machine

learning approaches with respect to their applicability

to other tasks within the CGF behaviour workflow.

Because of our objective to represent valid CGFs

for a training mission, this paper employs a blue

enemy pilot and a friendly air-to-air missile, shot

from a red CGF. The blue aircraft’s position is

randomly initialized within a predefined bunch of

distances. Due to the problem formulation, a scenario

of two-dimensional planar engagement X- and Z-axis

will be discussed. The used missile model is a five

degree-of-freedom model with solid propulsion

consisting of boost and sustained thrust described in

(Zipfel and Schiehlen, 2001)

Trajectory shaping results in an advantage by

being able to fire earlier while minimizing the own

risk. The range of a missile is directly dependent on

the launch speed, the launch angle and the launch

altitude. The missile is able to achieve a higher range

through a higher climbing angle, since the drag of the

missile decreases

(

decreasing air density) with

increasing altitude (Fleeman, 2009).

To maximize the range, it’s beneficial to climb up

to an altitude with lower air density, taking advantage

of acceleration in the boost and sustain thrust phase.

Therefore, a trajectory with the maximum achievable

range R

max1

(beginning of WEZ) must first be defined.

Figure 4: Planar engagement scenario.

This trajectory can be divided into four phases

(Figure 4):

• Phase 1: In the first phase, the missile is

launched at the start of the simulation. At

initialization, the pitch angle is set to 0° in a

specified height h

and an initial speed vector

parallel to the heading of the missile. The

pitch angle is kept constant for one second to

allow a safe missile separation from the host

aircraft. Following this, an angle change is

induced by varying the acceleration a

attached perpendicular to the missile’s

velocity vector while considering the

maximum possible physical forces. The

missile propulsion system is designed to

provide a short boost phase with a subsequent

sustain phase.

• Phase 2: After the missile is burned out, a

negative acceleration is commanded

perpendicular to the speed vector in order to

control its speed despite the lack of

propulsion.

• Phase 3: The missile is in a stationary decent

within the point of containing the best lift-to-

drag ratio (L/D)

max

to reach the maximum

power-off glide range.

• Phase 4: To follow a manoeuvring target, the

missile needs excess energy. The flight path

changes to a steeper descent to speed up.

We aim to design a pitch acceleration controller,

which creates the best trajectory concerning the

current distance from the target. The climb is a

premise, to generate maximum distance. If the target

is close to the launch point, lofting may not be

necessary.

To generate an optimal trajectory with respect to

the target distance, metrics must be created that can

be used to evaluate the missile trajectory:

Conceptual Approach for Optimizing Air-to-Air Missile Guidance to Enable Valid Decision-making

307

• The time t

end

[s] between missile launch and

target contact should be minimal. A long

missile flight time reduces the distance

between the own aircraft and the target,

therefore increasing the risk of a

counterattack.

• To be able to react to a manoeuvring target, the

missile should be able to fly at least one turn

having a bigger or equal maximum turn rate

turn

[°/s] as its target. This requires a specific

range of Mach number at the target contact

point ma

end

[-]. The upper Mach limit

corresponds to the point at which the missile

can still follow the target with the same turn

rate while staying within its structural limits.

In this context, we describe a maximum speed

while considering the maximum turn rate close to the

target, a minimum flight time, as well as maximizing

the range of the missile as optimal.

3 OPTIMAL CONTROL

One approach to solving our defined problem is the

so-called optimal control theory. The objective of

optimal control is to find a control function which

transforms a system from an initial state to a final

state by optimizing pre-defined parameters,

considering the system dynamics and an arbitrary

number of specified path constraints. The time-

conditional state progression is the optimal trajectory

for the specified initial- and final state (Bryson,

Arthur E., Jr and Ho, 1975).

To describe the optimal missile trajectory and its

strong dependencies on its initial- and final state,

solutions for all states at each time step are required.

The closed-loop form of optimal control is

particularly suitable for this purpose, using a

feedback function (Figure 5), which can be used to

calculate the error in relation to the desired

parameters (which we want to be optimal). This

allows the optimization of the pitch acceleration

controller to find an optimal trajectory for any

distance to the target.

Figure 5: Feedback control loop.

The four missile trajectory phases (see section 2)

imply special constraints for the use of optimal

control theory:

• During the first phase, the system dynamics

can only be described in a nonlinear manner

since the mass of the system does change in a

non-linear way due to fuel consumption.

• The second phase represents the transition

section in which the system characteristics can

be linearized.

• At the point of best lift-to-drag ratio the

missile can be described using a linear system.

• To optimize the excess energy and turn rate

close to the target as well as taking into

account the possibility of a manoeuvring

target, the last phase can be described as

nonlinear.

Due to the described different system states,

several types of optimal control can be implemented.

Gain-scheduled model predictive control (GSMPC)

switches between a predefined set of controllers, to

control a nonlinear plant over a wide range of

operating conditions. (Wu et al., 2002) implements

the GSMPC in a missile autopilot and describes the

transformation of nonlinear missile dynamics into a

quasi-linear-parameter-varying (LPV) system and

demonstrates large performance improvements of the

controlled system.

In (Bachtiar et al., 2017) the method of nonlinear

model predictive control (MPC) is investigated. MPC

is known for its ability to handle nonlinearities and

constraints, making it suitable for high-performance

agile missiles operating near constraints for example

structural limits. However, MPC is a computationally

demanding method, therefore Bachtiar et al. present a

method to minimize the required computational

capacity.

(Sun et al., 2018) introduces the so-called

adaptive dynamic programming (ADP) method for

missile guidance. The aim here is to consider the

nonlinear behaviour of the target and therefore take

account of uncertainties.

If there are many parameter changes in initial- and

final states (e.g., varying initial altitude), optimal

control methods are very computationally intensive.

Nevertheless, in the context of verified CGF models, it

requires the possibility to test the results. (Chan and

Mitra, 2018) therefore present a Matlab tool, in which

a formal verification of an MPC could be accom-

plished. This tool provides an automated approach to

analysing MPC systems for their correctness.

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

308

4 DEEP REINFORCEMENT

LEARNING

Another method for solving the problem defined in

section 2 is deep reinforcement learning (DRL),

which is a subset of machine learning. In this method,

a computer agent based on a neural network is trained

to perform an optimal sequence of actions through

repeated trial-and-error interactions within a dynamic

environment (see Figure 6). The agent uses

observations from the environment to come up with a

series of actions to maximize the agent's cumulative

reward metric for the task. This learning takes place

without human intervention or explicit ruleset

programming. It can be used for decision problems

and as a nonlinear control application (François-

Lavet et al., 2018).

To optimize a missile trajectory, the DRL process

can be expressed using four tuples: (S, A, P, R). S

represents the state space of the air combat scenario

(e.g. position or velocity of missile and target, etc.),

A are the possible actions the agent is able to do like

in this example the commanded pitch acceleration a

described in section 2. P is representing the learned

transition probability from one state to another when

using the chosen action A, and R the reward the agent

obtains due to the status change (wrt. P) in the

environment by the selected action A.

Figure 6: DRL Concept.

The reward functions are used to teach the agent

to what extent it needs to adjust the control functions

to optimize to a maximum reward. Due to the simple

desirability of reward functions, there exist various

methods for missile guidance optimization. (Hong et

al., 2020) aims to find effective missile training

methods through reinforcement learning and

introduces its method with conditional reward

functions which are compared with the deep-

deterministic-policy-gradient (DDPG) method.

(Li et al., 2021) uses assisted deep reinforcement

learning (ARL), which predicts the acceleration of a

manoeuvring target to reduce the influence of

environmental uncertainty.

5 VERIFICATION AND

VA L I D AT I O N

Regarding the verification and validation, the

described methods need to be investigated in more

detail, since weighting in neural network layers does

not allow any conclusions to be tested. It has to be

examined to what extent the results of the DRL can

be verified and validated with the comparative

methods of optimal control.

Once the data generated by a DRL approach has

been verified and validated by optimal control, this

allows the methods to be used on additional tasks

from the attack loop described in section 1.

6 CONCLUSIONS AND

FORECAST

In this paper, we presented a concept on how to

decompose a pilots’ BVR air combat workflow to

generate the behaviour of adversary CGFs in training

simulations. Our primary goal is to investigate to

what extent machine learning approaches can be

combined with rule-based concepts to generate

verified and validated CGF behaviour models. A

major component of fighter pilots’ workflow is their

decision process, in which they have to weigh

opportunities and risks against each other. Especially

during weapon delivery, validated decisions are a

needed prerequisite to ensure success. Using the

example of missile trajectory optimization, we are

investigating methods to estimate own opportunities

based on validated data. In addition, the methods of

optimal control and in particular deep reinforcement

learning were briefly introduced.

Within the current work, we intend to use the

trajectory generated by optimal control to verify and

validate the trajectory generated by DRL methods.

The next steps of this research will focus on the

final implementation of a DRL as well as an optimal

control approach. To prove the feasibility of DRL in

our BVR air combat context, we have already set up

a sample scenario described in section 2 employing a

Deep-Q-Network (DQN). In the future, we intend to

use the trajectory generated by optimal control to

validate the trajectory generated by DRL methods to

enable valid, explainable decision-making.

Conceptual Approach for Optimizing Air-to-Air Missile Guidance to Enable Valid Decision-making

309

REFERENCES

Bachtiar, V., Manzie, C. and Kerrigan, E.C. (2017),

“Nonlinear Model-Predictive Integrated Missile

Control and Its Multiobjective Tuning”, Journal of

Guidance, Control, and Dynamics, Vol. 40 No. 11, pp.

2961–2970.

Bryson, Arthur E., Jr and Ho, Y.-C. (1975), Applied

Optimal Control, Taylor & Francis Group, New York.

Chan, N. and Mitra, S. (2018), CODEV: Automated Model

Predictive Control Design and Formal Verification

(Tool Paper).

Dong, Y., Ai, J. and Liu, J. (2019), “Guidance and control

for own aircraft in the autonomous air combat: A

historical review and future prospects”, Proceedings of

the Institution of Mechanical Engineers, Part G:

Journal of Aerospace Engineering, Vol. 233 No. 16, pp.

5943–5991.

Fasser, S. (2020), “Machine Learning vs Rules Based

Approach to Building Decisioning Software”.

Fleeman, E.L. (2009), Maximizing Missile Flight

Performance, Georgia Institute of Technology.

François-Lavet, V., Henderson, P., Islam, R., Bellemare,

M.G. and Pineau, J. (2018), “An Introduction to Deep

Reinforcement Learning”, Foundations and Trends®

in Machine Learning, Vol. 11 3-4, pp. 219–354.

Hong, D., Kim, M. and Park, S. (2020), “Study on

Reinforcement Learning-Based Missile Guidance

Law”, Applied Sciences, Vol. 10 No. 18, p. 6567.

Johansson, T. (2018), “Tactical Simulation in Air-To-Air

Combat. Evolutionary Algorithms and Behavior Tree

Framework”, Department of Computer Science,

Electrical and Space Engineering, University of

Technology, Luleå, 2018.

Li, W., Zhu, Y. and Zhao, D. (2021), “Missile guidance

with assisted deep reinforcement learning for head-on

interception of maneuvering target”, Complex &

Intelligent Systems.

Plaat, A. (2022), Deep Reinforcement Learning, a textbook.

Reinisch, F., Strohal, M. and Stütz, P. (2022), “Behaviour

Modelling of Computer-Generated-Forces in Beyond-

Visual-Range Air Combat”, Simultech2022.

Richards, C. (2020), “Boyds OODA Loop”, Necesse Vol 5,

Issue 1, pp. 142–165.

Stillion, J. (2015), Trends in Air-to-Air Combat:

Implications for Future Air Superiority, CSBA,

Washington, DC.

Sun, J., Liu, C. and Dai, J. (2018), “Robust optimal control

for missile-target guidance systems via adaptive

dynamic programming”, in 2018 Chinese Automation

Congress (CAC), Xi'an, China, 11/30/2018 - 12/2/2018,

IEEE, pp. 836–841.

Toubman, A., Roessingh, J.J., van Oijen, J., Lovlid, R.A.,

Hou, M., Meyer, C., Luotsinen, L., Rijken, R., Harris,

J. and Turcanik, M. (2016), “Modeling behavior of

Computer Generated Forces with Machine Learning

Techniques, the NATO Task Group approach”, in 2016

IEEE International Conference on Systems, Man, and

Cybernetics (SMC), Budapest, Hungary, 10/9/2016 -

10/12/2016, IEEE, pp. 1906–1911.

Wang, Z., Li, H., Wu, H. and Wu, Z. (2020), “Improving

Maneuver Strategy in Air Combat by Alternate Freeze

Games with a Deep Reinforcement Learning

Algorithm”, Hindawi.

Wang, Z., Li, H., Wu, Z. and Wu, H. (2021), “A pretrained

proximal policy optimization algorithm with reward

shaping for aircraft guidance to a moving destination in

three-dimensional continuous space”, International

Journal of Advanced Robotic Systems, Vol. 18 No. 1,

172988142198954.

Wu, F., Packard, A. and Balas, G. (2002), “Systematic

Gain-Scheduling Control Design: A Missile Autopilot

Example”, Asian Journal of Control, Vol. 4 No. 3, pp.

341–347.

Xiao, L. and Huang, J. (2011), “Maneuver Strategy in

Beyond-Visual-Range Air Combat”, IACSIT Press,

Singapore.

Zipfel, P.H. and Schiehlen, W. (2001), Modeling and

Simulation of Aerospace Vehicle Dynamics.

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

310