Threats to Adversarial Training for IDSs and Mitigation
Hassan Chaitou, Thomas Robert, Jean Leneutre and Laurent Pautet
LTCI, T
´
el
´
ecom Paris, Institut Polytechnique de Paris, Paris, France
Keywords:
Adversarial Machine Learning, GAN, Intrusion Detection System, Sensitivity Analysis.
Abstract:
Intrusion Detection Systems (IDS) are essential tools to protect network security from malicious traffic. IDS
have recently made significant advancements in their detection capabilities through deep learning algorithms
compared to conventional approaches. However, these algorithms are susceptible to new types of adversarial
evasion attacks. Deep learning-based IDS, in particular, are vulnerable to adversarial attacks based on Genera-
tive Adversarial Networks (GAN). First, this paper identifies the main threats to the robustness of IDS against
adversarial sample attacks that aim at evading IDS detection by focusing on potential weaknesses in the struc-
ture and content of the dataset rather than on its representativeness. In addition, we propose an approach to
improve the performance of adversarial training by driving it to focus on the best evasion candidates samples
in the dataset. We find that GAN adversarial attack evasion capabilities are significantly reduced when our
method is used to strengthen the IDS.
1 INTRODUCTION
Currently, networks are open to many types of at-
tacks, including denial of service (DoS), probing, and
SQL injection. Intrusion detection systems (IDSs)
are components that monitor either host machines or
network activity to detect attacks and intercept them.
Machine learning (ML)-based IDS has been identi-
fied as a solution to the common problems of expertly
configured signature-based IDS, including the large
number of rules to manage, limited detection capabil-
ities, and high maintenance costs. However, this work
concentrates on ML classifier-based IDS that use su-
pervised learning. Classifiers are parametric func-
tions with a large number of configurable parame-
ters. This is accomplished during the training process,
which optimizes their detection rates and avoids false
alarms. The classifier takes as inputs collected data
that has been divided into units describing the sys-
tem’s activity (packets, events, connections...). The
predicted class is the classifier’s output; it is either
attack or normal traffic in the simplest case. Such a
setting can be described as a two-side architecture,
with the attacker responsible for performing attacks
and attempting to evade detection and the defender
responsible for training and deploying an IDS that of-
fers the best trade-off between detection rate and false
alarms. Many works discuss the quality of datasets
that may not be sufficiently representative (Khraisat
et al., 2019). This question is also raised in more
generic works on training process quality and poten-
tial threats to classifier performances. (Gong et al.,
2019). In this paper, we study the potential weak-
nesses in the construction and content of the dataset
rather than its representativeness. To our knowledge,
the two weaknesses we focus on have received less
attention in the security domain. They impact the re-
sistance to adversarial samples attacks, a well known
approach to evade detection for IDSs based on ma-
chine learning, (Szegedy et al., 2014). Adversarial
sample attacks involve using adversarial sample gen-
eration to learn how to turn IDS-ignorant attacks into
attacks that can evade them while still having a mali-
cious impact. Such transformations are possible using
Generative Adversarial Networks (Goodfellow et al.,
2014) among other generative approaches. Nonethe-
less, evading IDS detection and ensuring the mali-
cious impact is not a trivial task as pointed out in
(Backes et al., 2016) for malware detection.
In this work, we review previous work on well-
understood models (Goodfellow et al., 2015) and
datasets. In our contributions, we identify major
threats to IDS robustness against adversarial sample
attacks designed to evade IDS detection. Next, we
propose and evaluate three approaches to mitigate
these issues.
Section 2 formalizes the main concept about IDSs
based on classifier besides identifying the known
threats that affect an IDS’s performance. Section 3
formally defines the main consequence of being able
226
Chaitou, H., Robert, T., Leneutre, J. and Pautet, L.
Threats to Adversarial Training for IDSs and Mitigation.
DOI: 10.5220/0011277600003283
In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 226-236
ISBN: 978-989-758-590-6; ISSN: 2184-7711
Copyright
c
 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: Deployed architecture of classifier based IDS.
to generate adversarial samples that remain attacks
without testing. Furthermore, it introduces the threats
this situation entails and presents mitigation strate-
gies. Sections 4 and 5 present the experimental
assessment of the risks represented by the threat
we identified and the performance of the mitigation
strategies.
2 DATASET QUALITY AND
ADVERSARIAL TRAINING
This section recalls the main concepts of adversarial
training and ML-based IDS. We study why the train-
ing set used to set up IDSs needs to be cleansed or ex-
tended to improve IDS detection capabilities and ro-
bustness. We highlight that one of the quality criteria
used to remove problematic data needs to be revisited
when creating adversarial datasets.
2.1 Classifiers with IDS
Network raw data refer to data provided by network
sensors, as depicted in Figure 1. Sensors repre-
sent observation capabilities of network activity from
routers, firewalls or host machines. This data is orga-
nized and merged into observation units correspond-
ing to an element of network activity, called a sample.
An IDS incorporating a classifier for attack detection
is fed with samples of data collected by sensors. As
depicted in figure 1, the sample goes through various
processes before being processed by a classifier that
determines for each sample whether it belongs to an
attack or not.
Definition 1 (Raw Sample). A raw sample is a tuple
of n values respectively of types T
1
, ..., T
n
. The raw
sample type T
R
is T
R
= T
1
× ... × T
n
.
The PCAP format is the type of raw sample usu-
ally used: it is sufficiently detailed that the activity
can even be replayed from the raw sample. Basically,
raw samples are expected to be detailed enough to be
able to decide whether a sample corresponds to nor-
mal activity or attack. Let L be the set of possible
labels: L = {normal, attack}.
Definition 2 (Raw Labeled Sample and Dataset). A
raw labeled sample is a couple (x, y) where x ∈ T
r
and
y ∈ L. A raw labeled dataset is a set of raw labeled
samples.
The raw sample type often relies on non-numeric
types to capture metadata about packets or applica-
tion behaviors. Therefore, the values of raw samples
can be of very diverse types (e.g., binary, categori-
cal, numeric, strings). It is extremely difficult to feed
a classifier with such data without first transforming
all these types into scalar normalized values. This
step is called pre-processing. Let call prep the func-
tion that produces IDS scalar inputs from raw samples
R. Therefore, prep function takes elements of T
R
and
produces a vector of values q in [0, 1], we now use T
P
such that T
P
= [0, 1]
q
.
Definition 3 (Preprocessed Samples and Labeled
Dataset). For any raw sample x, prep(x) is a pre-
processed sample, and for any raw labeled dataset D,
prep(D) = {{(prep(x
i
), y
i
)|(x
i
, y
i
) ∈ D}}, is the cor-
responding preprocessed labeled dataset.
To apply prep to a labeled dataset, one has to ap-
ply it to the raw sample portion of each labeled sam-
ple. In the machine learning community, a dimension
of a sample is called a feature. A labeled sample is
said to be an attack sample if its label is attack, and
a normal sample if it is normal. Each labeled dataset
can be split in two subsets respectively called normal
traffic and attack traffic.
Definition 4 (Normal and Attack Traffic of D). Given
a labeled dataset D (raw or preprocessed), the normal
traffic of D denoted N(D), and the attack traffic of D
denoted A(D) are defined as follow:
N(D) = {(x
i
, y
i
)|(x
i
, y
i
) ∈ D, y
i
= normal}
A(D) = {(x
i
, y
i
)|(x
i
, y
i
) ∈ D, y
i
= attack}
A labeled dataset is necessary when training a
classifier, or defining its parameters; such a dataset is
called a training dataset. Datasets may contain prob-
lematic samples, either due to errors in sample col-
lection or due to poor observational or pre-processing
capabilities.
Definition 5 (Contradictory Samples and Dataset).
Two labelled samples (x
1
, y
1
) and (x
2
, y
2
) are contra-
dictory samples if and only if (iff) x
1
= x
2
and y
1
6= y
2
.
A dataset D is a contradictory dataset iff it contains
contradictory samples.
Threats to Adversarial Training for IDSs and Mitigation
227

A classifier is a parametric model that must be
configured, and the training process is responsible for
determining the appropriate parameters. The training
of a deep or standard machine learning model con-
sists of feeding samples to it and tuning its parameters
to minimize a loss function (defined to penalize pre-
dicted labels from those of the training set). Hence,
a contradictory dataset impairs this process as it pre-
vents minimizing this loss function properly.
The following subsection shows how a malicious
adversarial sample can evade detection and how it can
be mitigated and improve the dataset used for train-
ing.
2.2 Adversarial Samples and Training
In (Papernot et al., 2017), the authors identify a meta-
attack procedure that can abuse the classifier’s deci-
sion by mutating a pre-processed sample. This muta-
tion aims to slightly modify the activity to change its
result while providing a different classifier label. This
type of meta-attack can be used to perform an evasion
attack: an attack to hide malicious activity.
An adversarial sample or malicious adversarial
sample (MAdv) is obtained by adding a disturbance
on each dimension (which we call a mutation) of an
existing sample so that the predicted label of the sam-
ple before and after the disturbance is added differ-
ently. In the case of evasion attacks, the attacker fo-
cuses on crafting adversarial examples for attack sam-
ples. As stated above, the purpose here is not to gen-
erate legal traffic from the attack traffic but to change
the output of the classifier and retain the malicious
impact.
Definition 6 (Adversarial sample generator). An ad-
versarial sample generator AG is a function that pro-
duces a MAdv from an input attack sample and a value
assumed to be chosen at random.
The second parameter is intended to ensure that
the attack generator is a deterministic function that
can be used to produce many different MAdv depend-
ing on the random value provided as input.
An AG is said to be correct if from an originate at-
tack sample x it only generates samples that are actu-
ally attacks (and in practice this gives the same kind of
consequences as x). The efficiency of an AG against
an IDS is measured as its likelihood of producing an
attack sample that is classified as a normal sample by
the IDS.
Note that an efficient but incorrect AG is as useless
as a correct but inefficient generator from the point of
view of the evasion attack.
Deep neural network models are known to be vul-
nerable to MAdvs (Goodfellow et al., 2015). Hope-
fully, efficient adversarial defense approaches have
been proposed to prevent these attacks (Qiu et al.,
2019). According to the literature, adversarial train-
ing or its extensions remain the most effective ap-
proaches to improve the robustness of classifiers
against MAdvs (Ren et al., 2020).
Adversarial training involves extending a training
dataset D with MAdvs before training an IDS. It re-
lies on an AG that is used by the defender to generate
MAdvs intended to evade detection of IDS trained on
D. The MAdvs generated by AG are then added to D
and the IDS is retrained on the new dataset.
The purpose of using AG is to add samples to the
training without the need to actually execute them.
Their label would be inferred. Otherwise, the cost
of significantly expanding the dataset would be pro-
hibitive.
Three aspects affect the quality of the adversar-
ial training, the number of samples added (because it
changes the distribution of D), the choice of attack
samples that are modified and the quality of the al-
teration. Surprisingly, the choice of attack generator
inputs and how adversarial training is actually imple-
mented remains poorly studied in the security com-
munity.
2.3 Problem Statement
Without dedicated guidelines, an attack generator
would alter all the features of an attack sample. A
purely random alteration of a sample may not pre-
serve the malicious impact of a sample. Yet, suppose
first that we know how to generate only MAdvs. The
problem is that, in some cases, it would be possible to
create a sample through adversarial training identical
to a sample labeled as normal in the dataset used to
train an IDS. While this is possible, although it is not
directly a contradictory data set, it still raises prob-
lems and poses threats to the approach or even to the
IDS itself.
Therefore, the issues raised by these observations
are as follows:
• Is there a concept similar to a contradictory train-
ing data set that needs to be taken into account
when applying adversarial training?
• Can the criterion used to define effective MAdvs
be exploited to boost adversarial training, either
by helping to select better MAdvs or by reducing
the cost of the approach.
In the next section, we identify the notion of the
impactful neighborhood and explain how this can be
a threat to adversarial training in the first place, but
also how understanding this concept helps to design
better sampling approaches of the MAdvs.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
228

3 THREAT TO ROBUSTNESS OF
IDS AND MITIGATION
This section presents the core concepts of our ap-
proach and contribution to better handle and under-
stands adversarial training.
3.1 Extending the Contradictory Set
Our work is motivated by the following observation:
the label of an adversarial sample is set to the label
of the sample that has been modified and can then be
added to a training dataset. Those actions are carried
out without quality checks and raise issues. Usually,
samples are obtained through observations, and thus
the label is the observed impact. Yet, in the case of
MAdvs no real activity is necessary to “obtain” a sam-
ple. From a defender, it helps to extend training sets
at almost no cost, because no real observation is nec-
essary to obtain new samples. Yet, it relies on the
assumption one can ensure an AG can only generates
attack samples. It implies that we know how to apply
perturbations in a neighborhood of each sample that
does not actually change its impact.
Definition 7 (Impactful neighborhood of an attack
sample). The impact neighborhood of an attack sam-
ple x, denoted INA(x), is the set of all possible muta-
tions applied to x that does not change its actual im-
pact.
By extension INA(A(D)) is the union of the im-
pactful neighborhood of all attack samples of D. By
definition, a correct AG only produces elements of
INA(A(D)). Because adversarial training essentially
builds training sets from subsets of D and INA(A(D))
The notion of contradictory data set should be ex-
plored for D ∪ INA(A(D)).
Definition 8 (Extended contradictory dataset). The
extended contradicting set of a dataset D, given INA
is the set of all contradictory samples contained in D∪
INA(A(D)) and is noted EC
INA
(D) (more formally
EC
INA
(D) =
S
x
{(x, normal), (x, attack)} with x such
that (x, normal) ∈ D and (x, attack) ⊆ EC
INA
(D)).
The INA index in EC
INA
will be omitted as we
only consider one version of it. EC(D) contains all
contradicting samples originally in D but also all the
contradicting samples that could be obtained through
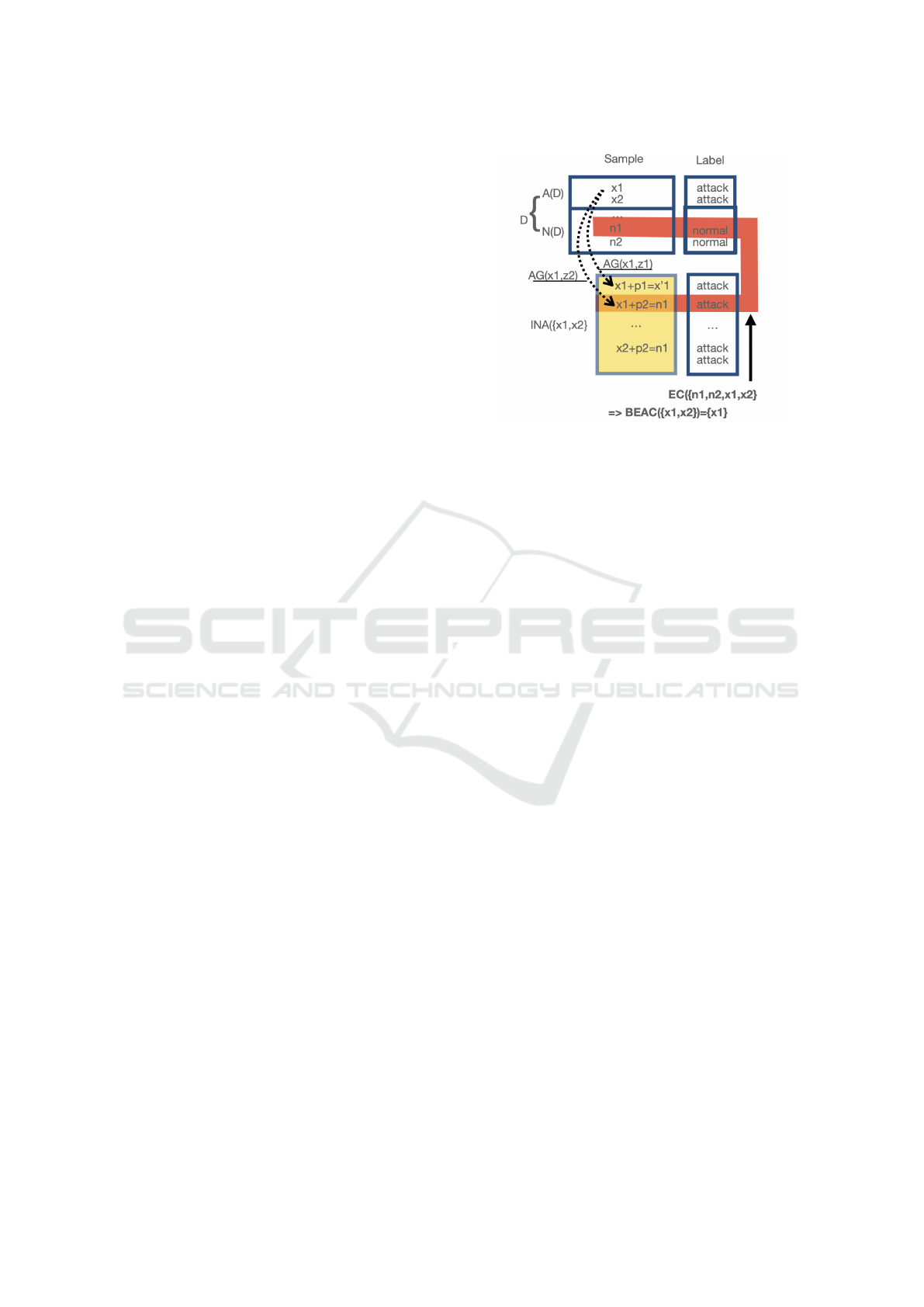
adversarial training. Figure 2 depicts a simplified
dataset D with four elements including two attacks,
x
1
and x
2
. Let assume their INA contains only four
elements : themselves plus the results of two pertur-
bations, p
1
, and p
2
. In this case, we assume x
0
1
=
x
1
+ p
1
, x
0
2
= x
2
+ p
1
, x
00
2
= x
2
+ p
2
are all samples not
Figure 2: MAdvs, BEAC and EC.
included in D, yet x
1
+ p
2
is in fact equal to n
1
. In
this context, EC(D) = {(n1, normal), (n1, attack)} as
(n
1
, attack) is an adversarial attack sample that could
be generated. Recall that a classifier trained on D, is
very likely to predict label y for sample x if (x, y) ∈ D.
Therefore, an IDS trained on a dataset containing D
has a high likelihood to predict normal as a label for
n
1
. From the attacker’s point of view, applying the
attack generator on samples that are transformed into
elements of EC(D) could represent its best chance of
success. These samples will be called Best Evasion
Attack Candidates (BEAC) and are part of D as shown
in Figure 2.
Definition 9 (Best evasion candidates of a dataset).
The set of Best Evasion Attack Candidates of a
dataset D is defined as BEAC(D) = {w | INA(w) ∩
EC(D) 6=
/
0}
Figure 2 depicts this situation in which two con-
tradicting samples can be obtained due to adversarial
training, and details the role of D, INA(D), EC(D),
and BEAC(D)
An attack generator can be created by generative
approaches (GANs, autoencoders ...). In this case, the
attack samples of EC(D) thus contain the right sam-
ples for training an attack generator to attack an IDS
trained with D as is. Thus, the knowledge of EC(D)
and BEAC(D) can be the source of various threats to
IDSs performances.
3.2 Adversarial Training Threats
The concept of the extended contradictory dataset
raises several questions on the way MAdvs for IDSs
are generated and handled.
Assume the attacker knows the INA of its attack
samples. An attack generator is either in a white box
Threats to Adversarial Training for IDSs and Mitigation
229

or black box setting. Black box assumption is consid-
ered equivalent to assuming that the attacker knows
a dataset equivalent (same distribution) to the one
used to train the IDS (before any adversarial train-
ing). Thus, both have similar EC(D). We study the
case where the attacker knows BEAC(D), but the de-
fender applies adversarial training without particular
care.
The first threats to IDS performances are due to a
defender that does not know how to explore INA(x)
of an attack sample x. This situation must be taken
into account as we have noticed that to our knowledge
only NSL-KDD explicitly provided insights to define
the notion of impactful neighborhood.
The consequence of this situation is that the at-
tack generator used by the defender does not guar-
antee that generated samples are actual attacks. We
assumed previously to use only correct attack genera-
tors for simplicity. However, in practice, this situation
is not guaranteed for the defender. Recall that adver-
sarial training extends a dataset D with samples for
which the label is set to attack without actually ob-
serving the activity. Therefore, we have two cases,
either the defender sets blindly labels to attack, or it
checks whether MAdvs are actual attacks. The for-
mer case is called the poisoning threat, and the latter
is called the testing cost threat.
Definition 10 (Poisoning Threat). If adversarial train-
ing is performed for an IDS using an AG for which
it cannot prove that AG(w, z) ∈ INA(w), then this
training procedure is said to poison the IDS training
dataset.
Indeed, there is a chance that the generated sam-
ples correspond to actual normal activities instead of
attacks. If such a normal activity is labeled as an at-
tack, then it is a dataset poisoning situation that threat-
ens the availability of normal activities.
The alternative approach is to test each adversarial
attack sample that would be added for training (sec-
ond case). The activity has to be carried out and ob-
served. This is no longer adversarial training as it
requires real observation. It is a regular dataset ex-
tension for which the defender must pay the cost of
executing each sample and observing it.
Definition 11 (Testing Cost Threat). Consider that
adversarial training is performed for an IDS using an
attack generator AG for which it cannot be proven that
∀z, AG(w, z) ∈ INA(w), and that the defender tests
the impact of each generated MAdv, then this training
procedure is said to suffer from a testing cost threat.
If someone applies this approach given the usual
size of adversarial training dataset, it can be in-
tractable or too costly. Now suppose the impactful
neighborhood of an attack sample is defined and used
by the defender to avoid previous threats. In this con-
text, if we do not remove normal samples of D that do
belong to EC(D), then we risk adding to D, through
adversarial training, attack samples that are very sim-
ilar or equal in value but with different labels. Even
if samples are not contradictory, adding samples very
similar with distinct labels might significantly disrupt
the training process (having a large gradient even with
small changes on input makes training difficult). This
increases the risk of false prediction.
Definition 12 (Confusing Normal Sample Threat). If
D
0
is a training dataset that extends D with adversarial
samples, then D
0
is said to be subject to confusing nor-
mal sample threat if it contains normal samples that
belong to EC(D).
Indeed, if a dataset with MAdv does contain con-
fusing normal samples, this can increase the likeli-
hood of evasion attack success for attack samples in
BEAC(D) (attack samples that once modified may be-
long to EC(D)). The last case is related to the sam-
pling strategy of the different attack samples. Indeed,
if a category of attack is more likely to happen, it is
relevant to acquire more samples of it to improve de-
tection capability. Conversely, if an attacker knows
that an evasion attack is more likely to succeed for an
element of BEAC(D), then it is more likely that this
attack will be carried out because of a higher evasion
rate a priori.
Definition 13 (Best Evasion Attack Threat). The best
evasion attack threat corresponds to the situation
where an attacker focuses on applying evasion attacks
only for elements of BEAC(D) for an IDS trained on
D.
This threat account for attackers that focus on ap-
plying evasion attacks only on attack samples with the
highest likelihood to evade detection. We now pro-
vide the mitigation strategies for these threats.
3.3 Mitigation Strategy
We identified four threats to an efficient usage of ad-
versarial training related to INA. Note that the first
two threats cannot be mitigated; they represent situa-
tions in which adversarial training is either too costly
or risky as it may significantly reduce the system’s
availability. In practice, even if there is no formal def-
inition of the impactful neighborhood, the concept is
implicitly defined. So now, let us consider the two
last threats: the confusing sample threat and the best
evasion attack focus threat.
Definition 14 (Sample Removal). This mitigation
strategy consists in removing normal samples from D
SECRYPT 2022 - 19th International Conference on Security and Cryptography
230

that belong to EC(D).
This approach avoids normal samples for mem-
bers of EC(D). Yet, these samples can still be ob-
tained through adversarial training. In order to reduce
the likelihood of detection miss, we can change their
label in D instead of removing them.
Definition 15 (Pessimistic Relabelling). Relabel any
normal sample from D ∩ EC(D) as attacks.
We now introduce mitigation for the last threat.
MAdv generation is based on the selection of attack
samples on which an evasion attack generator is ap-
plied. The selection of attack samples on which the
attack generator is applied is called attack sampling.
Attack sampling is almost never discussed on the at-
tack side and is assumed to be uniform. Yet, attackers
that restrict themselves to BEAC(D) elements would
be less likely to do so either because they do not
have enough samples in this area or because the at-
tack generator creates an element of EC(D). Our mit-
igation strategy would be to change the proportion of
BEAC(D) elements when sampling A(D) during ad-
versarial training.
Definition 16 (Oversampling of BEAC). This strat-
egy consists in increasing the likelihood of generating
MAdvs from elements of BEAC.
It allows training the IDS to be more efficient in
detecting them. A first expected effect is to obtain
samples in EC(D) to force predicting the attack for
this set. A second expected effect is that a good detec-
tion on BEAC(D) could be generalized to other sam-
ples. First, the impact of confusing sample and best
evasion attack focus threats need to be assessed on
IDS without mitigation. Secondly, it is also neces-
sary to check that the proposed mitigation approach
actually mitigates them. Next section details the ex-
perimentation campaign conducted to assess all these
aspects on a dataset for which the INA concept is de-
fined.
4 ASSESSMENT METHOD AND
ARCHITECTURE
This section discusses the different assessment objec-
tives and metrics used. The experimental framework
and dataset are then described.
4.1 Metrics and Objectives
First, we need to determine the performance met-
rics for evasion attacks and adversarial training. The
objective is to identify the extent to which the per-
formance of the attack generator correlates with the
content of the Extended Contradictory set and how
the proposed mitigation strategies perform to ad-
dress the identified threats. We use the usual IDSs
performance metrics derived from confusion matri-
ces (Wang, 2018). Testing an IDS requires a labeled
test dataset without evasion attack, e.g. an Original
Test Dataset OT D. To test the IDS without evasion
attack, we simply submit OT D samples to the IDS. To
test the IDS against evasion attack, an attack genera-
tor is applied to the members of OT D before submit-
ting them to the IDS. We check IDS predicted labels
for the submitted samples to compute the number of
true positives TP, false negatives FN, false positives
FP, and true negatives TN.
The Recall is one of the most used metrics to
determine if an attack would be detected. Let sup-
pose T P and FN are computed for an IDS tested with
OT D, on which F is first applied. F is either the iden-
tity function, noted id, or an attack generator. The
recall of this experiment is noted and defined as:
Recall
IDS
F
(OT D) =
T P
T P + FN
Then, Recall
IDS
id
is the recall of IDS tested without
evasion attack applied, and Recall
IDS
G
is the recall of
IDS tested against the attack generator G. We are in-
terested in the extent to which the Recall is affected
by evasion attacks and measure it through the evasion
increase rate (EIR) of a generator G defined as fol-
lows:
EIR
IDS
G
(OT D) = 1 −
Recall
IDS
G
(OT D)
Recall
IDS
id
(OT D)
The last metric used is the evasion reduction rate
(ERR) which compares EIR for the same attack gen-
erator but against different IDSs.
ERR
IDS
1
,IDS
2
G
(OT D) = 1 −
EIR
IDS
2
G
(OT D)
EIR
IDS
1
G
(OT D)
ERR compares how well IDS
2
resists to G com-
pared to IDS
1
. We use ERR only to compare an
IDS trained without adversarial training to the various
IDSs that take advantage of the mitigation strategies.
4.2 Dataset, Dataset Extension
This subsection describes the dataset and how we use
the GAN-based generator.
4.2.1 Dataset
The choice of the dataset was difficult. To our knowl-
edge, the only one to provide a clear definition of INA
Threats to Adversarial Training for IDSs and Mitigation
231

is NSL-KDD. Still, this dataset is considered outdated
as it does not cover recent attacks. However, many
papers used it and overlooked the threats we identi-
fied. Therefore, we decided to conduct the assess-
ment on NSL-KDD because it provides a clear defi-
nition of the INA, and this dataset is well understood.
This dataset categorizes attacks as Denial of Service
(DoS), User to Root (U2R), Root to Local (R2L), and
Probe. The NSL-KDD training dataset includes 41
features and class identifiers for each record. The con-
cept of INA is defined through the notion of function
features: the dimension that should not change (Lee
and Stolfo, 2000). Hence, the INA is obtained by
changing all non-function features of a sample. NSL-
KDD samples’ features are split into four groups: In-
trinsic, Time-based, Content, and Host-based. Not
surprisingly, the functional features are different for
each attack category:
• DoS attacks: Intrinsic and Time-based
• U2R attacks: Intrinsic and Content
• R2L attacks: Intrinsic and Content
• Probe attacks: Intrinsic, Time-based and Host-
based
In order to stick to our models, binary classifiers, the
dataset is split in 4 datasets, one per attack type, which
only retain the targeted attack type. We will focus
on normal, DoS, and probe samples as the others are
too few. It should be noted that after searching for
the BEAC set on the training dataset of NSL-KDD
restricted to DoS and Probe attacks, we found that
BEAC(D) contained only DoS samples that represent
3.74% of DoS samples. In this dataset, the samples
contain categorical attributes, such as protocol type
or flags. We applied the usual pre-processing ap-
proaches on these samples to obtain fully scalar at-
tributes.
4.2.2 Generative Adversarial Network (GAN)
We assume that GAN-based generators are black-box
evasion attack generators. GAN-based attacks target
pre-trained IDS models and repeatedly update the pa-
rameters of two components, the Generator and the
Discriminator. The Generator is trained to mutate the
non-functional features of the attack samples to gen-
erate MAdvs. The generator input is made of an attack
sample concatenated with a random vector (it is com-
pliant with the attack generator definition). The Gen-
erator is trained to evade discriminator detection, but
the discriminator is trained to mimic the IDS. Each
component has its own loss function: Discriminator
is penalized when a sample is classified differently by
the IDS, and the generator is penalized when generat-
ing samples that do not evade the IDS. Thus, among
the key parameters of the Generator and Discrimi-
nator, there is the number of update iterations called
epochs. We consider GAN trained here either on 100
or 1000 epochs as both are well-spread constants in
security. A Generator of type GAN−N would de-
note a Generator trained in N epochs. We also con-
sider the best Generator ever observed against the IDS
as the optimization process is not guaranteed to be
monotonous. We implement training set extension
and adversarial training as explained in algorithm 1 to
produce MAdvs using GAN−100 type of generators.
Generators are used on both sides: to extend the IDS
training set but also on the attack side to apply evasion
attacks and thus test our approaches. They all suffer
from variability issues. On the attack side, we handle
it by independently repeating the training of 50 gen-
erators to assess a generator type performance against
an IDS. On the defense side, we ensure that the train-
ing continues or is restarted as long as the generator
does obtain an EIR threshold (here 0.99 for DoS at-
tacks). This ensures that the defense, to its knowl-
edge, is using a decent generator.
Algorithm 1: Adversarial training of an IDS.
Input: OD (an original dataset), IDS (an IDS
trained on OD), S (an extension size factor), r (a
rate of sampling of BEAC(OD);
Output: Best Generator best G, re-trained IDS on
extended dataset D
ext
;
1: procedure ADV-TRAIN IDS(OD, IDS, S, r)
2: initialize Gen and Disc, initial generator and
discriminator of a GAN of type GAN−100
3: Train Gen, Disc, using Gen(OD) labeled by
IDS, store each Generator with its evasion
score.
4: Choose the best attack generator Gen, noted
best G;
5: Use best G to generate MAdvs from elements
of A(OD) to create D
ext
so that the added ele-
ments represent S times the size of OD. More-
over, the proportion of added elements created
from elements of BEAC(OD) has to be r.
6: Re-train IDS on D
ext
;
7: end procedure
5 EXPERIMENTS AND RESULTS
Our experimentation consists in testing IDS trained
on different datasets with adversarial training and/or
mitigation strategies. In order to identify those IDSs,
we follow this notation: IDS−X−sr−option where sr
and option are both optional. X represents the dataset
SECRYPT 2022 - 19th International Conference on Security and Cryptography
232

considered for training (detailed later). The parame-
ter sr denotes the sampling rate chosen for BEAC(X)
if applied (not provided if unchanged). The option
parameter indicates whether removing confusing nor-
mal sample, noted wn for without normal, or rela-
belling them as attacks, noted na for normal as attack,
have been applied.
5.1 Threat Level Without Mitigation
We need to determine whether the existence of a non-
empty BEAC set is problematic. As previously stated,
probe and DoS attacks illustrate two distinct situa-
tions. If we compute the BEAC set of NSL-KDD,
it contains no probe attack sample but DoS samples.
Let thus train two IDSs, one for Probe and on for DoS
attacks and see how they behave. We need a training
dataset to detect DoS samples, it contains normal and
DoS samples of NSL-KDD training dataset, noted
OD
DoS
. The second data set contains normal and
Probe samples of NSL-KDD training dataset, noted
OD
Pr
.
We train two batches of 50 GANs, following
the architecture of GAN−100, respectively against
IDS−OD
Pr
and IDS−OD
DoS
. We observe that eva-
sion attacks reach an average EIR of above 0.99 for
IDS−OD
DoS
and is 0 for IDS−OD
Pr
. It shows two
situations that are consistent with our claim of the
role of BEAC in evasion attack success. Note that
the IDS trained has shown usual performances, e.g.,
as in (Vinayakumar et al., 2019), of ML-based IDSs.
Hence, we have a 0.85 recall (ability to detect attacks)
for IDS−OD
dos
on non adversarial samples. The next
step is to understand how efficient is the adversarial
training for different size factor parameters. Here,
we test an adversarial training for size factors of 1,
2, 5 and 10, leading to extended datasets for AT 1,
AT 2, AT 3, and AT4. Each dataset is used to train
an IDS without any particular mitigation of identified
threats. These IDS have been tested against strong
Figure 3: The average EIR for fifty GAN−1000 Generators
vs IDS−AT
1
, IDS−AT
2
, IDS−AT
3
and IDS−AT
4
.
attack generators of type GAN−1000 to better under-
stand their performances, and results are presented in
Figure 3. We notice that the risk of the adversarial
evasion attacks drops significantly from 100% EIR
on IDS−OD to reach 9% EIR on a very costly IDS
in terms of training, which is IDS−AT
4
. Adversar-
ial training works well but at the expense of scaling
factors that are 5 or 10 times the size of the original
dataset. Training an IDS on 10 times larger datasets
has a linear effect on the training cost and may not be
accepted. Note that this adversarial training has not
impaired the performance of IDSs when no evasion
attack is applied, as shown in the first three lines in
Table 1.
In the following subsections, we perform experi-
ments to evaluate our mitigation strategies described
in 3.3.
5.2 Confusing Samples Mitigation
This subsection evaluates the impact on the perfor-
mance of both regular and robust IDS when the two
mitigation strategies, sample removal, and sample
pessimistic relabeling (section 3.3) are applied.
5.2.1 Effect on Regular IDS Performance
As pointed out, confusing samples can make it harder
for the IDS to resist attack generators. To assess
the confusing sample threat on the regular IDS re-
silience, we train two IDSs. The first one is called
(IDS−OD−wn) trained on OD without the normal
samples applying the sample removal mitigation. The
second one is IDS−OD−na trained on OD in which
we relabeled the confusing normal samples as attacks
as proposed in the sample pessimistic relabelling mit-
igation. These IDS are not designed to be resilient
Table 1: Performance metrics of various IDS models.
IDSs Precision Accuracy F1 score Recall
IDS−OD 85.8 86.4 84.4 85.1
IDS−AT
2
82.4 86.2 84.6 86.9
IDS−AT
4
88.4 87.6 85.2 82.2
IDS−OD−na 88.1 87.9 85.7 83.4
IDS−AT
2
− 25 87.6 87.3 84.9 82.5
to evasion attacks. Thus, we use only Generator of
type GAN−100 trained specifically against IDS−OD
and test them on IDS−OD−wn and IDS−OD−na.
We observe that the attacks still manage to evade
IDS−OD−wn completely.
However, the average ERR for IDS−OD−na is
0.5 in this case. Note that we use weaker generators in
this subsection compared to before. These results are
Threats to Adversarial Training for IDSs and Mitigation
233

encouraging as relabelling is a very cheap adversarial
training. Indeed, the number of confusing samples
is very limited compared to all normal samples (less
than 1%). Yet, normal samples related to EC(OD)
seem very useful for adversarial training.
Let now consider adversarial training with these
mitigation strategies.
5.2.2 Effect on Robust IDS Performance
We investigate the mitigation approaches of confus-
ing samples combined with IDS reinforced with reg-
ular adversarial training. We assess the performance
using IDS−AT
2
, IDS−AT
2
−wn e.g. with sample re-
moval mitigation and IDS−AT
2
−na using the sample
pessimistic relabeling mitigation. This time, we use
50 GAN−1000 generators against each of these IDSs.
Table 2 summarizes the results.
Table 2: ERR mean over the fifty GAN−A
1
−1000 attacks
on IDS−AT
2
, IDS−AT
2
−wn and IDS−AT
2
−na.
IDS−AT
2
IDS−AT
2
−wn IDS−AT
2
−na
ERR mean over 0.39 0.57 0.43
50 experiments
The ERR of the IDS without mitigation but with
adversarial training on AT
2
remains low at 0.39. How-
ever, the first mitigation strategy, sample removal,
performs significantly better this time. It increase the
ERR by almost 50% to 0.57. Surprisingly, the rela-
belling strategy did not perform as expected, with a
very small increase in ERR. Without mitigation, there
is a real gap on the ERR of adversarial training of scal-
ing factor 2, i.e. 0.39, and scaling factor 5, i.e. 0.83.
Hence, we observe that simply removing few normal
samples from the training data set reduces this gap by
50%. It provides a mean to reach a given ERR level
with a significantly lower scaling factor.
In the next subsections, we examine the effect of
the oversampling strategies on the BEAC set com-
pared to regular adversarial training with uniform
sampling.
5.3 Adversarial Training on BEAC Set
Here, we consider adversarial training datasets built
by controlling the sampling rate of elements from
BEAC.
This last set of experiments aims to compare
the effect of the last proposed mitigation com-
pared to the sample removal and sample relabel-
ing ones. We consider sampling rates of BEAC in
{0.10, 0.20, 0.25, 0.35, 0.50, 0.75}. We define the sr
parameter value to denote percentages. Hence, IDS−
AT
2
−25represents an adversarial training on a dataset
with a size factor of 2 and a sampling rate of 0.25.
Again, we test GAN−1000 generators against IDSs
trained with an adversarial training set of size factor
of 2, e.g., IDS−AT
2
− j family.
Figure 4: Average ERR on 50 GAN−1000 generators
against IDS−AT
2
− j for various j.
Figure 4 outlines the result of this experiment.
The results reveal that the adversarial evasion at-
tacks are significantly less effective in the majority
of these IDSs when compared to IDS−AT
2
but for
IDS−AT
2
− 75. However, this situation is expected as
a too high sampling rate prevents the IDS from cor-
rectly detecting evasion attacks applied to attacks in
A(D)−BEAC(D). A sampling rate between 20% and
50% seems to be equivalent. This mitigation yields
similar results to the sample removal approach with
an ERR close to 0.6. Moreover, it seems not too diffi-
cult to take advantage of it, as the interval of sampling
rates yielding similar ERR is large. Furthermore, us-
ing oversampling of BEAC mitigation narrows the
margin between the performance of IDS −AT
2
−25
and IDS−AT
3
as the difference in ERR is almost di-
vided by two, as one can see in Figure 4.
6 RELATED WORK
(Gong et al., 2019) provide criteria to define better
sampling strategies for datasets and the use of diversi-
fication approaches to improve the training of generic
classifiers. Yet, they do not consider the specificity
of IDS as security classifiers or even the specificity of
adversarial samples. With the recent advancements in
machine learning research, adversarial attacks piqued
the interest of researchers in a wide variety of do-
mains. As a result, network security faces critical
challenges from adversarial attacks as a sensitive and
complex field. However, a few researches focus on
the sampling strategy of MAdvs in order to establish
a fair balance between IDS training performance and
SECRYPT 2022 - 19th International Conference on Security and Cryptography
234

detection capabilities against adversarial evasion at-
tacks. In (Khamis et al., 2020), they generated MAdvs
using two methods, either by mutating all the dimen-
sions of attack samples or by mutating the 16 ob-
tained principal components using Principal Compo-
nent Analysis (PCA) as a dimensionality reduction
technique. However, in either case, the MAdv gen-
eration was obtained without taking into account the
impactful neighborhood of the attack samples. There-
fore, the preservation of attack behaviors is not as-
sured following the mutation process.
To our knowledge, all techniques that take INA
into account define attributes that split attack sam-
ples as functional or non-functional. This separa-
tion of features is typically performed manually by
a domain expert such as in NSL-KDD or through
statistical or machine learning methodologies. (Lin
et al., 2018), (Zhao et al., 2021) and (Usama et al.,
2019) proposed to craft MAdvs using GANs. Dur-
ing the mutation process, they considered the impact-
ful neighborhood of attack samples into account as
they preserved the attack behavior by keeping the
functional features of these samples unaltered, using
the same criteria described for NSL-KDD. Whereas
in (Alhajjar et al., 2021), (Chauhan and Shah Hey-
dari, 2020), and (Msika et al., 2019), each of these
works makes use of statistical tools or deep learn-
ing methods such as Shapley Additive Explanations
(SHAP) (Lundberg and Lee, 2017) to define the im-
pactful neighborhood of the attack samples. However,
those tools define the attack’s functionality solely
based on the dataset’s statistical properties, not on
the attack samples’ semantics. Although both cate-
gories perform very powerful adversarial evasion at-
tacks, one shortcoming of these works lacks an ex-
amination of the effect of the confusion samples or
BEAC set on the robustness of the IDSs when adver-
sarial training is used.
To our knowledge, no work in the literature fo-
cuses on assessing the dataset after the mutation of
MAdvs . This paper aims to examine the threats
linked to the current generation process used in ad-
versarial training. Furthermore, we propose a new
method to improve the performance of the adversarial
training for IDS by adjusting the sampling strategies
of adversarial samples to account for confused sam-
ples and the BEAC set.
7 CONCLUSIONS
This paper examined the effect of a non-empty con-
tradictory dataset on IDS robustness performance in
the presence of adversarial samples. First, we iden-
tify the main threats that could lead to extending the
contradictory set during adversarial training, includ-
ing the poisoning threat, the threat of confusing nor-
mal samples, and the threat of the best evasion attack
candidates (BEAC). In addition, we proposed three
mitigation strategies to improve the performance of
adversarial training by taking advantage of the im-
pactful neighborhood of attack samples and focusing
adversarial training on the BEAC set.
In future work, we will investigate the effect of
the overall training approach on the IDS performance
by specifying one IDS to detect regular attacks and
another one to detect adversarial evasion attacks (in
particular BEAC samples). In addition, we want to
investigate the applicability of the proposed approach
used with different sampling strategies such as those
in (Picot et al., 2021).
ACKNOWLEDGEMENTS
This research is part of the chair CyberCNI.fr with
support of the FEDER development fund of the Brit-
tany region.
REFERENCES
Alhajjar, E., Maxwell, P., and Bastian, N. (2021). Adver-
sarial machine learning in network intrusion detection
systems. Expert Syst. Appl.
Backes, M., Manoharan, P., Grosse, K., and Papernot, N.
(2016). Adversarial perturbations against deep neural
networks for malware classification. CoRR.
Chauhan, R. and Shah Heydari, S. (2020). Polymorphic
adversarial ddos attack on ids using gan. In ISNCC.
Gong, Z., Zhong, P., and Hu, W. (2019). Diversity in ma-
chine learning. IEEE Access.
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B.,
Warde-Farley, D., Ozair, S., Courville, A., and Ben-
gio, Y. (2014). Generative adversarial nets. In NIPS.
Goodfellow, I. J., Shlens, J., and Szegedy, C. (2015). Ex-
plaining and harnessing adversarial examples.
Khamis, R. A., Shafiq, M. O., and Matrawy, A. (2020).
Investigating resistance of deep learning-based ids
against adversaries using min-max optimization. In
ICC.
Khraisat, A., Gondal, I., Vamplew, P., and Kamruzzaman, J.
(2019). Survey of intrusion detection systems: tech-
niques, datasets and challenges. Cybersecur.
Lee, W. and Stolfo, S. J. (2000). A framework for con-
structing features and models for intrusion detection
systems. ACM TISSEC.
Lin, Z., Shi, Y., and Xue, Z. (2018). IDSGAN: Generative
Adversarial Networks for Attack Generation against
Intrusion Detection. arXiv e-prints.
Threats to Adversarial Training for IDSs and Mitigation
235

Lundberg, S. M. and Lee, S.-I. (2017). A unified approach
to interpreting model predictions. In NeurIPS.
Msika, S., Quintero, A., and Khomh, F. (2019). Sigma :
Strengthening ids with gan and metaheuristics attacks.
Papernot, N., Mcdaniel, P., Goodfellow, I. J., Jha, S., Ce-
lik, Z. B., and Swami, A. (2017). Practical black-box
attacks against machine learning. ACM ASIACCS.
Picot, M., Messina, F., Boudiaf, M., Labeau, F., Ayed, I. B.,
and Piantanida, P. (2021). Adversarial robustness via
fisher-rao regularization. ArXiv.
Qiu, S., Liu, Q., Zhou, S., and Wu, C. (2019). Review
of artificial intelligence adversarial attack and defense
technologies. Applied Sciences.
Ren, K., Zheng, T., Qin, Z., and Liu, X. (2020). Adversarial
Attacks and Defenses in Deep Learning. Engineering.
Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan,
D., Goodfellow, I. J., and Fergus, R. (2014). Intriguing
properties of neural networks. In ICLR.
Usama, M., Asim, M., Latif, S., Qadir, J., and Ala-Al-
Fuqaha (2019). Generative adversarial networks for
launching and thwarting adversarial attacks on net-
work intrusion detection systems. IWCMC.
Vinayakumar, R., Alazab, M., Soman, K. P., Poornachan-
dran, P., Al-Nemrat, A., and Venkatraman, S. (2019).
Deep learning approach for intelligent intrusion detec-
tion system. IEEE Access.
Wang, Z. (2018). Deep learning-based intrusion detection
with adversaries. IEEE Access.
Zhao, S., Li, J., Wang, J., Zhang, Z., Zhu, L., and Zhang, Y.
(2021). attackgan: Adversarial attack against black-
box ids using generative adversarial networks. Proce-
dia Computer Science.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
236