
Membership Inference Attacks on Aggregated Time Series with Linear
Programming
Antonin Voyez
1,3 a
, Tristan Allard
1 b
, Gildas Avoine
1,2 c
, Pierre Cauchois
3
,
Elisa Fromont
1,5,4 d
and Matthieu Simonin
4
1
Univ Rennes, CNRS, IRISA, France
2
INSA Rennes, CNRS, IRISA, France
3
ENEDIS, France
4
Inria, IRISA, France
5
IUF (Institut Universitaire de France), France
Keywords:
Privacy, Time Series, Membership Inference Attack, Subset Sum Problem, Gurobi.
Abstract:
Aggregating data is a widely used technique to protect privacy. Membership inference attacks on aggregated
data aim to infer whether a specific target belongs to a given aggregate. We propose to study how aggregated
time series data can be susceptible to simple membership inference privacy attacks in the presence of adver-
sarial background knowledge. We design a linear programming attack that strongly benefits from the number
of data points published in the series and show on multiple public datasets how vulnerable the published data
can be if the size of the aggregated data is not carefully balanced with the published time series length. We
perform an extensive experimental evaluation of the attack on multiple publicly available datasets. We show
the vulnerability of aggregates made of thousands of time series when the aggregate length is not carefully
balanced with the published length of the time series.
1 INTRODUCTION
Private organizations and public bodies worldwide
are nowadays engaged in ambitious open data pro-
grams that aim at favoring the sharing and re-use
of data (The World Wide Web Foundation, 2017).
Opening data is rooted in century-old principles
1
and,
with today’s data collection capacities, is expected to
yield important and various benefits (Deloitte, 2017;
The World Wide Web Foundation, 2017; The Euro-
pean Data Portal, 2015; OECD, 2020) (e.g., driving
public policies, strengthening citizens trust into gov-
ernments, fostering innovation, facilitating scientific
studies). Personal data are part of the open data move-
a
https://orcid.org/0000-0003-3248-1497
b
https://orcid.org/0000-0002-2777-0027
c
https://orcid.org/0000-0001-9743-1779
d
https://orcid.org/0000-0003-0133-3491
1
See, e.g., the XV
th
article of the Declaration of the
Rights of Man and of the Citizen (1789).
ment
2
and an ever-increasing quantity of information
about individiduals is made available online, often in
an aggregated form (e.g., averaged, summed up) in
order to comply with personal data protection laws
(e.g., the European GDPR
3
, the Californian CCPA
4
)
and (try to) avoid jeopardizing individual’s right to
privacy. In particular, datasets associating various
attributes, coming from the same data provider or
not, are especially valuable for understanding com-
plex correlations (e.g., gender, socio-economic data,
and mobility (Gauvin et al., 2020)).
Time series are considered as valuable data for
open data publication. They are unbounded se-
quences of measures performed over a given popula-
tion at a given sampling rate. For example, current
smart-meters enable the collection of fine-grained
2
See, e.g., the GovLab Data Collaboratives effort (https:
//datacollaboratives.org/).
3
https://eur-lex.europa.eu/legal-content/EN/TXT/
HTML/?uri=CELEX:32016R0679
4
https://leginfo.legislature.ca.gov/faces/billTextClient.
xhtml?bill id=201720180SB1121
Voyez, A., Allard, T., Avoine, G., Cauchois, P., Fromont, E. and Simonin, M.
Membership Inference Attacks on Aggregated Time Series with Linear Programming.
DOI: 10.5220/0011276100003283
In Proceedings of the 19th International Conference on Security and Cr yptography (SECRYPT 2022), pages 193-204
ISBN: 978-989-758-590-6; ISSN: 2184-7711
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
193

electrical power consumption with one measure ev-
ery 30 minutes. Electrical consumption records are
then published under a variety of aggregated time
series
5
. Today, the publication of such datasets is
often encouraged by laws such as the EU directive
2019/1024
6
imposing to the states members to set up
open data programs for various information, includ-
ing energy consumption (Directive 2019/1024 Article
66).
The main protection measure, called threshold-
based aggregation in the following, consists in guar-
anteeing that the number of individuals per aggregate
is above a given threshold. The threshold is chosen
with the goal to preserve the subtle equilibrium be-
tween individual’s privacy and data utility (B
¨
uscher
et al., 2017). Threshold-based aggregation may come
with additional protection measures (e.g., suppression
of outsiders, noise addition) but is often considered
as being sufficient in real-life, even for sensitive data
(e.g., power consumption in France
7
), provided that
the threshold is high enough.
However, and despite its wide usage in real-life,
the lack of formal privacy guarantees of threshold-
based aggregation, together with the length of the
time series allowed to be published, does not allow to
formally claim that personal data is indeed protected.
In particular, powerful attackers may exist that hold
most of the raw data (if not all) and may use them for
performing membership inference attacks.
This new threat model is relevant in real-life situ-
ations, when the raw data are illegitimately accessed
after a (partial or total) disclosure, either acciden-
tally by careless employees or following an active at-
tack. Such threats must not be overlooked today as
witnessed by the ever-increasing list of major data
breaches. For example, the Ponemon Institute re-
ported in 2020 a strong rise in the number of insider-
caused cybersecurity incidents (+47% between 2018
and 2020)
8
. As another example, the 2021 Verizon
Data Breach Investigation Report shows the large
diversity of industries concerned (from finance and
healthcare to energy or transportation) and the distri-
bution of attack patterns having led to the breaches
9
.
Membership inference attacks form an important
part of the privacy attacks. They aim to infer whether
a specific target is present or absent from a dataset
5
See, e.g., the open data portal of the French national
electrical network manager (https://data.enedis.fr).
6
https://eur-lex.europa.eu/eli/dir/2019/1024/oj
7
https://www.legifrance.gouv.fr/codes/id/
LEGISCTA000034381202/2017-04-08
8
https://www.observeit.com/cost-of-insider-threats/
9
https://www.verizon.com/business/resources/reports/
dbir/2021/data-breach-statistics-by-industry/
using various methods such as statistical tests (Dwork
et al., 2017) and machine learning (Rigaki and Garcia,
2020). The presence of a target in a published aggre-
gate is a valuable knowledge for an attacker when the
aggregate is, or can be, publicly associated to other,
possibly sensitive, attributes.
Contributions. In this paper, we introduce (Sec-
tion 2) a new threat model where the attacker has ac-
cess to the published aggregates (e.g., averages, sums)
that are, or can be, associated to additional attributes,
and to the disclosed raw times series. He/she then
aims to determine whether (the time series of) a given
target is associated to the additional attribute(s). This
can actually be framed as a membership inference at-
tack. We then show (Section 3) that this member-
ship inference attack can be reduced to the subset sum
problem, which can be solved as a constraint pro-
gramming problem when data consist of time series.
Each time point serves as a constraint to efficiently
solve a subset sum problem. Based on this approach,
we perform (Section 4) experiments on real-life data
using the Gurobi solver, and show that our mem-
bership inference attack is successful in most cases.
Our findings demonstrate that breaking privacy when
aggregate-based techniques are used to publish time
series is much easier than expected. We analyse the
limit cases to eventually help publishers enforcing in-
dividuals’ privacy.
Table 1: Notations.
Notation Description
I Set of individuals
T Set of timestamps
S Full multiset of time series
S
A
Multiset of time series participating in
the aggregates
A Vector of aggregates published
θ Time budget of the attacker
p Pool size (number of solutions asked
to the solver)
P Set of solutions found by the attacker
G Adversarial guesses
| · | Cardinality
2 PROBLEM STATEMENT
2.1 Time Series
A time series is a timestamped sequence of data.
In the following, we consider fixed-length univariate
integer-valued time series. We represent the full mul-
SECRYPT 2022 - 19th International Conference on Security and Cryptography
194

tiset of time series as a |I |∗|T | matrix S (all notations
are defined in Table 1) where the |I | rows represent
the time series of each individual and the |T | columns
represent the timestamps (i.e., a sequence of integers
from 1 to |T | for simplicity, see eq. 1). Each cell
S
i,t
∈ [d
min
, d
max
] thus represents the value of the i
th
individual at the t
th
timestamp. Without loss of gen-
erality, and unless explicitly stated, we consider in the
rest of the paper that d
min
= 0.
S =
S
1,1
··· S
1,|T |
.
.
.
.
.
.
.
.
.
S
|I |,1
··· S
|I |,|T |
(1)
2.2 The Publishing Environment
Publisher. As shown in Figure 1, the publishing en-
vironment considered consists of a publisher and an
attacker (described in Section 2.3). The publisher col-
lects from a set of individuals I a multiset of time se-
ries (where each individual produces a single fixed-
length time series) associated to, possibly personal
and/or sensitive, additional attributes contextualizing
the time series (e.g., income, house surface, socio-
demographic information, electrical appliances).
Individuals
Collect
Get access
Publisher
Attacker
Publish aggregates
+ sensitive information
Who is in ?
(infer sensitive information)
Figure 1: The SUBSUM Attack.
Published Aggregates. The publisher selects a sub-
matrix S
A
of S and computes and publishes a vector
of aggregates A over S
A
. In this paper, we focus on
aggregates that are sums (we use the two terms in-
distinctly below). Note that all sum-based aggrega-
tion methods (e.g., average) can also be tackled by
our proposed attack with minor changes in the attack
constraints. Each aggregate is computed for a specific
timestamp t by summing the values of each individ-
ual in S
A
: A
t
=
∑
∀i
S
A
i,t
. The set of individuals se-
lected in S
A
represents the ground truth. We model
the ground truth as a vector of probability telling, for
each individual of S, which one is part of S
A
. The
probabilities of the i
th
individual is set to 1 if and only
if the i
th
individual is in S
A
, and to 0 otherwise. It is
worth noting that the sequences of aggregates A usu-
ally come along with the timestamps and the number
of time series aggregated.
Published Additional Attributes. To make the pub-
lished aggregates more valuable, they are usually as-
sociated with additional information that character-
izes the subpopulation in the aggregates. Such char-
acterizing attributes can be for example the average
surface of the households in the aggregates, the av-
erage age of the individuals, the incomes, the region,
etc. To illustrate this point, a practical case is the pub-
lication of the average daily electricity consumption
(time series) per region (attribute).
2.3 Threat Model
The usual threat model obviously considers an at-
tacker who aims to retrieve from the published aggre-
gates, protected through various privacy-preserving
measures, the identity (or associated valuable infor-
mation) of the people concerned by these data (Ja-
yaraman et al., 2021) (Bauer and Bindschaedler,
2020) (Pyrgelis et al., 2018). A step further consists
in considering a threat model where the attacker has
access both to the (published) aggregated time series
and to the (leaked) raw time series (while the addi-
tional attributes remain secret and the goal of the at-
tack remains unchanged). Two points should then be
discussed: the relevance of this scenario and the at-
tacker’s motivation to perform an attack in such a sce-
nario.
Due to legal requirements and widespread security
best practices, publishers usually store direct iden-
tifiers and raw time series in separate databases
10
applying for example traditional pseudonymization
schemes. Dedicated access control policies, archival
rules, or security measures can then be applied to each
database (e.g., retention period limited to a couple of
years for fine-grained electric consumption time se-
ries). Isolating direct identifiers from time series in-
deed prevents direct re-identifications from malicious
employees or external attackers exploiting a leak
11
.
The same security principles might apply to the stor-
age of the additional, possibly sensitive, attributes.
Note that variants of the above context can be eas-
ily captured by our model. An example of a vari-
ant, common in real-life, is when the additional at-
tributes come from another data provider collaborat-
ing with the publisher for computing cross-database
10
We use the term database for simplicity without any
assumption on the underlying storage mechanisms.
11
The wealth of information contained in
pseudonymized time series still allows massive re-
identifications, but publishers seldom apply destructive
privacy-preserving schemes to the time series that they
store for preserving their utility.
Membership Inference Attacks on Aggregated Time Series with Linear Programming
195

statistics. Whatever the scenario, this results in a set
of databases, isolated one from the other, either for se-
curity reasons in order to mitigate the impacts of data
leaks, or simply because multiple data providers col-
laborate. Because data leaks are common, whether
they are due to insider attackers or to external ones,
we believe that considering that raw data may even-
tually leak is a conservative approach that deserves
to be explored. Obviously, if the identifiers, the time
series, and the additional attributes all leak together,
attacking the published aggregates is useless. How-
ever, in cases where only the raw times series leak, at-
tackers need to deploy membership inference attacks
for learning the association between a target individ-
ual (or more) and its attributes. In the following, we
consider this threat model. We show on a real-life ex-
ample that an attacker is able to efficiently retrieve the
attributes of a target using linear programming.
More formally, the adversarial background knowl-
edge consists of the full multiset of time series S.
Given his/her background knowledge S, the vector A
of timestamped aggregates, and the number of time
series aggregated, the attacker outputs a vector of
guesses G over the participation of each individual
to the vector of aggregates. The vector of guesses is
similar to the ground truth vector s.t. the i
th
value
of the vector of guesses represents the probability of
the participation of the i
th
individual to the aggregate.
The closer to the ground truth the guesses, the better
for the attacker.
3 THE SUBSUM ATTACK
The SUBSUM attack is based on solving the subset
sum problem (Kellerer et al., 2004) over the vector A
of aggregates given the set of time series S.
3.1 Constraint Programming and
Solvers
Constraint programming (CP) is a computation
paradigm that can be used to model mathematical op-
timization problems such as the subset sum problem.
The problem is modeled by a set of variables and for-
mulas, called constraints, that describe and bound the
problem, and an optimization objective. The objec-
tive can be to prove (or disprove) the feasibility of the
problem, or to find real solutions matching the con-
straints, if any. Integer Programming (IP) focuses on
problems where all the variables are integers. An in-
teger programming set of constraints for solving the
subset sum problem has the following form:
∑
i≤n
(X[i] ·V [i]) == s (2)
where s is the sum to reach, V is a vector of integer
values and X a vector of Boolean values indicating
whether to add a specific weight to the bag (i.e., set to
1) or not (i.e., set to 0).
A wide variety of solvers are able to solve such
problem (e.g., Gurobi (Gurobi Optimization, 2020),
Choco (Charles Prud’homme et al., 2016), OR-
Tools (Laurent Perron, 2019)).
3.2 Attack Formulation
The SUBSUM attack solves a well known NP-hard
problem and would be highly inefficient and not scale
in the general case. This is, in part, due to the fact that
for a given timestamp, an important set of individuals
may have similar values which may further increase
the combinatorics. By exploiting the different time
points (with different aggregate values but originating
from the same set of individuals), the solver is able
to prune the unsatisfactory solutions much faster and
converge, with enough constraints, to possibly unique
solutions if all individuals do not have identical values
as another individual in all time points.
Algorithm 1 thus combines multiple subset sum
problems, one for each aggregate (each timestamp),
into a single set of IP constraints. Let X be a vector
of |S | Boolean variables denoting the time series that
are (possibly in case of multiple solutions) part of the
aggregate. We define one constraint per aggregate in
A :
∑
i≤n
(X[i] · S
i,t
) == A
t
(3)
Once these constraints are defined, we define one
final constraint representing the attacker knowledge
of the number |S
A
| of individuals present in the ag-
gregates.
∑
i≤n
X[i] == |S
A
| (4)
Our objective is to find less than p solutions (ide-
ally p = 2) to infer meaningful information about the
aggregate members within a reasonable time (the wall
time θ). The solver runs until one of the following
conditions is satisfied: (1) all the existing solutions
are found, (2) the maximum number of solutions, p,
is reached, (3) the time budget θ is exhausted. The
solver outputs a set P of up to p candidate solutions
together with a status code. Each solution is a vector
of probability, similarly to the ground truth vector, in-
dicating the individuals from S that, when summed up
together on the right timestamp(s), solve the given set
SECRYPT 2022 - 19th International Conference on Security and Cryptography
196

Algorithm 1: SUBSUM attack.
Input: The set of time series (S), the
aggregates (A), the time budget (θ),
the number of solutions to look for (p)
Output: The solutions found (P), the guesses
(G), the status code (status)
set time limit(θ)
set pool size( p)
for i ∈ |S| do
add variable(X
i
, {0, 1})
end
for t ∈ |A| do
add constraint(
∑
∀i∈S
X
i
S
i,t
== A
t
)
end
solve()
P = get solutions()
G = to probability vector(P )
status = get status()
return P , G, status
Functions used in the algorithm :
add variable(bounds): Define an integer
variable bounded to a given set of values.
add constraint(constraint): Define a
constraint binding the model.
set pool size(p): Define an upper bound p
on the number of solutions to search for.
set time limit(θ): Set the time budget θ of
the solver.
solve(): Solves the problem.
get status(): Get the status of the solver af-
ter its termination. We assume that at least the
two following statuses are available : OPTIMAL
(i.e., either p solutions are found or less than
p solutions are found but no more solutions
exist), TIMELIMIT (i.e., the time budget θ is
over) and INFEASIBLE (i.e., the model cannot
be solved).
get solutions(): Get the solutions found
by the solver (if any).
of constraints X. Finally, the attacker computes the
frequency of each individual in the set of solutions in
order to obtain his guesses G.
4 EXPERIMENTS
We perform an extensive experimental survey of the
attack using two open datasets: the CER ISSDA
dataset (CER, 2012) and the London Households En-
Table 2: Values of the parameters used in our experiments.
Parameter Value
S {ISSDA-30m, London-30m}
|S| {1000, 2000, 3000, 4000, 4500}
|S
A
| {0%, 10%, . . . , 100%} × |S |
|A| {0%, 10%, . . . , 100%} × |S |
θ {1000, 2000, 4000, 8000, 86400}
p {2, 100}
ergy Consumption dataset. Our results show that
the SUBSUM attack is highly efficient (e.g., absolute
success) when it’s requirements are met, i.e., when
the vector of aggregates published contains a suffi-
cient number of aggregates (sufficient number of con-
straints) and when the attacker has sufficient comput-
ing power.
4.1 Settings
Experimental Environment. It consists of two soft-
ware modules
12
.
First, the driver module, written in Python, is in
charge of driving the complete set of experiments :
deploying the experiments, launching them, stopping
them, and finally fetching the experimental results.
Based on the driver, we deployed our experiments
on our own OAR2 (Linux)
13
computing cluster, allo-
cating 2 cores (2.6 GHz) and 2 GB RAM at least to
each experiment. Each experiment is a SUBSUM at-
tack fully parameterized (e.g., full set of time series,
aggregates published). We describe it below.
The second software module is the solver in
charge of performing a SUBSUM attack given a set
of parameters. We use in our experiments the Gurobi
solver (Gurobi Optimization, 2020), a well-known
and efficient IP solver, but any other solver can be
used provided that it implements an API similar to
the one used in Algorithm 1.
Datasets. We performed our experiments over the
real-life ISSDA CER public dataset (CER, 2012)
which contains power consumption time series of
6435 individuals for over 1.5 years at a 30 mins rate.
Removing the time series containing at least one miss-
ing value left us with 4622 time series. We changed
the unit from kWh to Wh obtaining thus only inte-
ger values (required by our solver). We refer to this
cleaned dataset as ISSDA-30m.
14
We replicate the experiments on the real-life Lon-
12
Available here: https://gitlab.inria.fr/avoyez1/subsum
13
https://oar.imag.fr/
14
https://www.ucd.ie/issda/data/
commissionforenergyregulationcer
Membership Inference Attacks on Aggregated Time Series with Linear Programming
197

don Households Energy Consumption dataset (UK
Power Networks, 2013) containing 5567 individuals
for over 2.5 years at a 30 mins rate. As this dataset
contains a lot of missing values (all individuals have
at least one missing value), we filled the missing
values using the consumption of the previous week.
Then, we removed the individuals that have missing
values along several weeks. This left us with 5446 in-
dividuals. We also changed the unit from kWh to Wh
in order to obtain only integer values. We refer to this
cleaned dataset as London-30m.
Experimental Protocol. We consider three main pa-
rameters impacting the SUBSUM attack: the size |S|
of the set of time series, the size |A| of the vector of
aggregates published (number of constraints), and the
number of values aggregated in each aggregate |S
A
|.
Table 2 shows the parameter values we use in our ex-
periments. For each triple of parameters, we generate
20 experiments
15
where each experiment is a SUB-
SUM attack over (1) a set of time series, (2) a vector
A of aggregates published, and (3) a time budget θ.
At each experiment, the full population S, together
with the individuals S
A
that are part of the vector of
aggregates, are randomly selected. We log for each
experiment the ground truth (i.e., the exact set of in-
dividuals in S
A
), the candidate solution(s) found by
the solver, the status of the solver, and the wall-clock
time elapsed during the attack.
Success Definition. Our experimental validation con-
siders a flexible success definition. An attack is con-
sidered to be a success if the solver finds strictly less
than p solutions in the allowed time θ
16
. Indeed, this
implies (1) that the solution is part of the pool of so-
lutions and (2) that the solver found all the solutions.
We will especially focus on a pool size equals to 2.
In this case, a success occurs when the solver outputs
a single solution: the membership inference is per-
fect. However, a pool size equals to 2 is not always
sufficient. In these cases, we increase the pool size
and analyze the solutions more deeply found by the
solver, showing the distribution of the guess vector
on the individuals that are part of the ground truth.
15
Performing 20 times the SUBSUM attack on the same
set of parameters is sufficient for obtaining a stable success
rate for the given set of parameters.
16
Note that this is a somewhat precautionary success
measurement since the attacker will draw conclusions only
when he/she is certain that all solutions have been found
by the solver. Other success metrics can be considered in
which the attacker gains information from incomplete sets
of solutions returned by the solver. However, when the
solver reaches the time budget or when the pool p is filled,
the solver fails to prove the non-existence of other solutions.
Inference on incomplete results might be refuted by new, yet
undiscovered solutions.
4.2 Experimental Results
Our experiments aim at providing clear insights on
the conditions leading to successful SUBSUM attacks.
First, we start in Section 4.2.1 by studying the SUB-
SUM success rate according to the total number of
time series in the full population (population size),
the number of time series aggregated in the published
vector of aggregates (aggregate size), and the length
of this vector (number of constraints). We set here the
time budget to a value sufficiently high for not inter-
fering with the attack. Through this study, we observe
a clear relationship between the population size and
the published vector of aggregates (size and length)
for a successful SUBSUM attack. This allows us to
express both the size of the published vector of ag-
gregates and its length relatively, as a fraction of the
population size. Then, we study in Section 4.2.2 the
impact of the time budget on the success rate, setting
the other parameters to fixed values. Finally, we study
in Section 4.2.3 the efficiency of the SUBSUM attack
on the full population available in our datasets.
4.2.1 Relationship between the Number of
Individuals and the Success
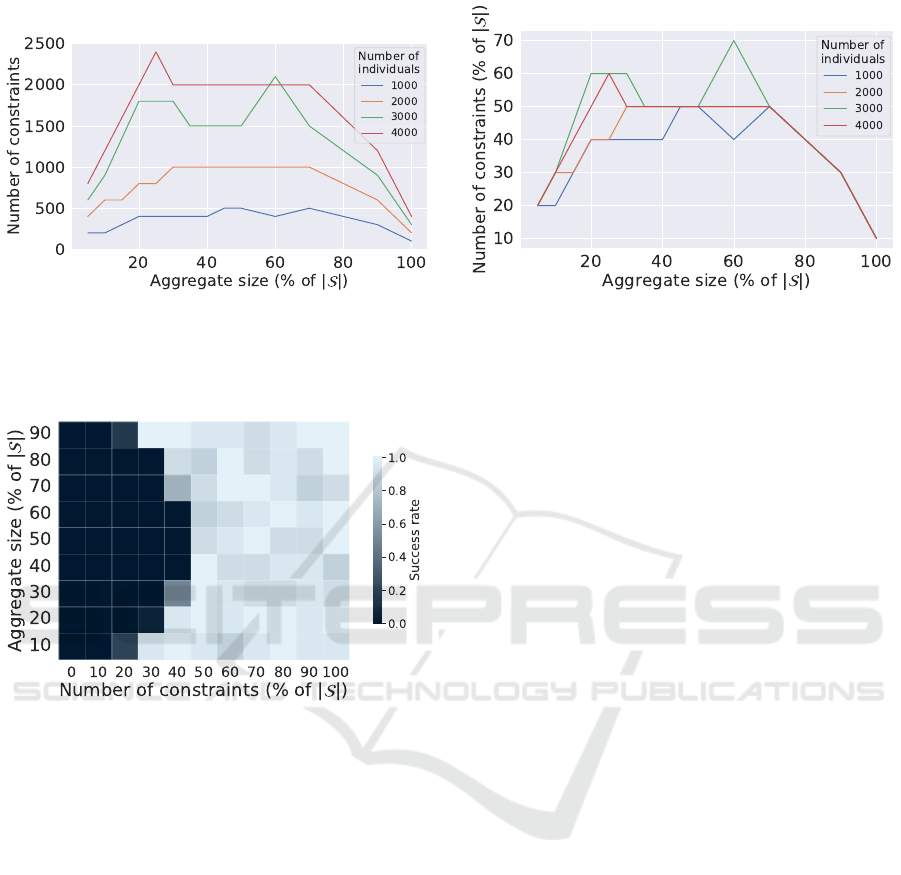
Figure 2 shows the minimal number of constraints re-
quired to have at least one success for several pop-
ulation sizes and for a time budget large enough for
not interfering (i.e., θ = 24h). We can see that, even
if the required number of constraints before getting a
success increases with the population size, it follows
a parabolic shape for all population sizes. Figure 3
shows the results of attacks with respect to the aggre-
gate size and the number of constraints for a small
dataset of 1000 individuals and a small time budget
of 1000s (approximately 15 minutes).
As already seen in Figure 2, Figure 3 shows that
the attacks fail in a parabolic area centered around ag-
gregates of half the population size. These failures
are due to the fact that the solver reaches the maxi-
mum allocated time. Outside this area of failure, the
attacks are mostly successful with the exception of a
few, randomly distributed, failed experiments which
depend on the original aggregate and population sam-
ples. In this ”light” area, the few failures are due to
the existence of several possible solutions (we provide
below in Section 4.2.3 an advanced analysis of the
cases where several solutions exist). After reaching
an aggregate size corresponding to 50% of the pop-
ulation, it is expected that the number of constraints
needed goes down again which comes from the fact
that knowing S, identifying |S
A
| individuals in S is at
least as difficult as identifying |S| − |S
A
| individuals.
With a small aggregate size (lower than 50% of the
SECRYPT 2022 - 19th International Conference on Security and Cryptography
198
(a) Y axis: absolute number of constraints. (b) Y axis: number of constraints (% of the number of indi-
viduals).
Figure 2: Minimal number of constraints before getting at least one success. Parameters : Dataset = ISSDA-30m, |S | = {1000,
2000, 3000, 4000}, θ=24h, p=2, 20 repetitions.
Figure 3: Success rate (0 : all failed, 1 : all succeed). Pa-
rameters : Dataset = ISSDA-30m, |S| = 1000, θ=1000s,
p=2, 20 repetitions.
population size) the number of constraints needed is
often twice the size of the aggregate: in general the
number of constraints needed to successfully attack a
population of size |S| should be at least in the order of
the aggregate size |S
A
|. Conversely, if the number of
constraints is much lower than the aggregate size, the
dataset is deemed safe (relatively to the time budget θ
and to the pool size p) to the SUBSUM attack. Build-
ing on this result, in the following, both the aggregate
size |S
A
| and the length |A| of the vector of aggre-
gates (number of constraints) are expressed as a frac-
tion of the population size |S |. Note that the length
of the vector of aggregates might be larger than the
population size, resulting thus in fractions larger than
100% the population size.
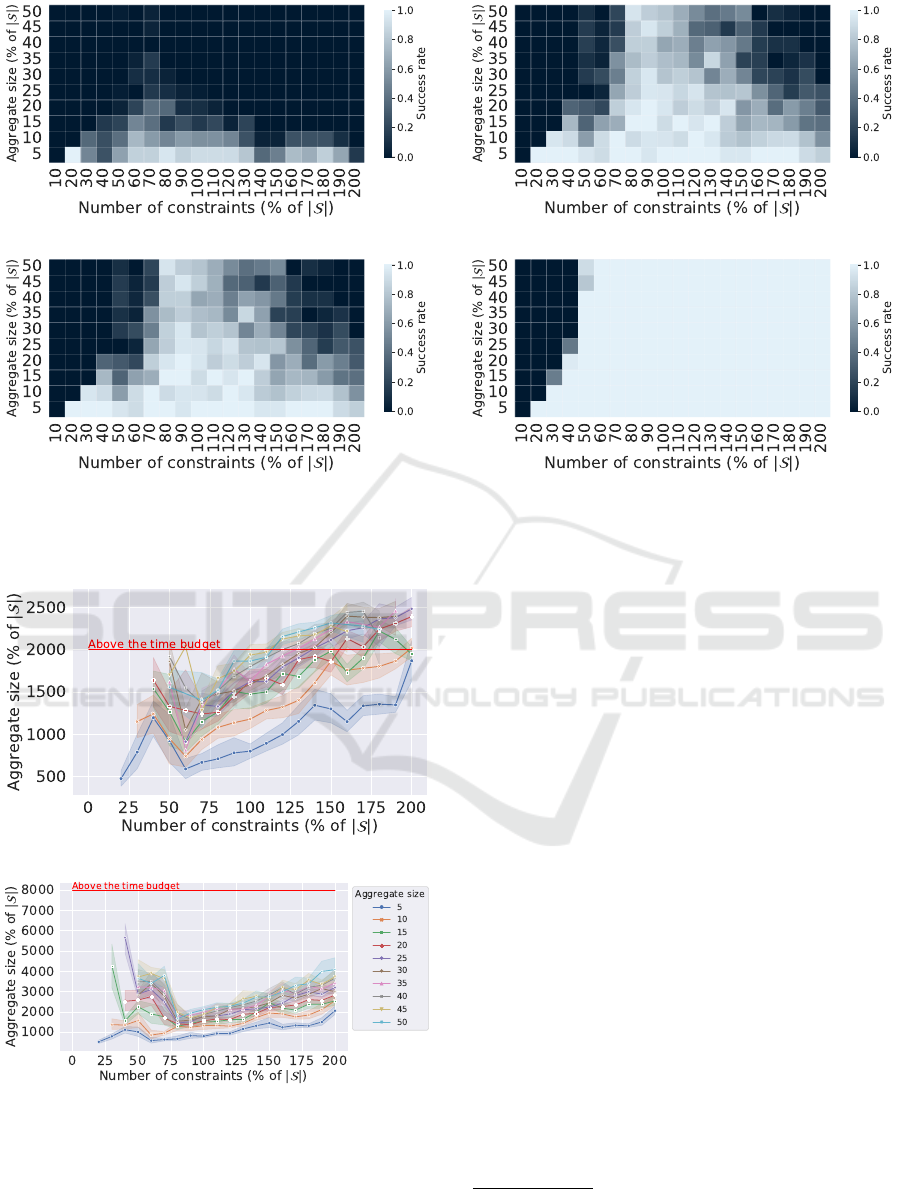
4.2.2 Impact of the Time Budget
For practical reasons, we evaluate the impact of the
time budget on a rather small dataset with |S| = 2000.
As can been seen in Figure 4, the time budget θ has an
impact on the attack success: the higher the time bud-
get, the higher the success rate. However, as shown
in Figure 4d, even with a high time budget, attacking
an aggregate with a small number of constraints (the
left dark sides of Figures 4b, 4c and 4d) will be un-
successful. Conversely, if the time budget is too low
and the number of constraints is too high (the right
black / grey area of the Figures 4a, 4b and 4c), the
solver does not have the time to solve the problem
with its given parameters. Figure 5 shows the experi-
ments time (in seconds). We note three areas of inter-
est: 1) an area with missing points (before reaching
25% of constraints) corresponding to the, previously
defined, parabolic area of failures 2) the failures due
to reaching the allowed solver time and 3) when in-
creasing the number of constraints, the sudden drop
in execution time until a point where the attack is the
fastest for all aggregate sizes. After this point, the
execution time increases again linearly with the num-
ber of constraints up to the point where the execution
time reach the allowed time again (Figure 5b). There
is thus a clear compromise to make between the num-
ber of constraints used (that needs to be in the order of
the aggregate size) and the time budget. If the attacker
has a short time budget, he/she might prefer not using
all the available constraints at his/her disposal.
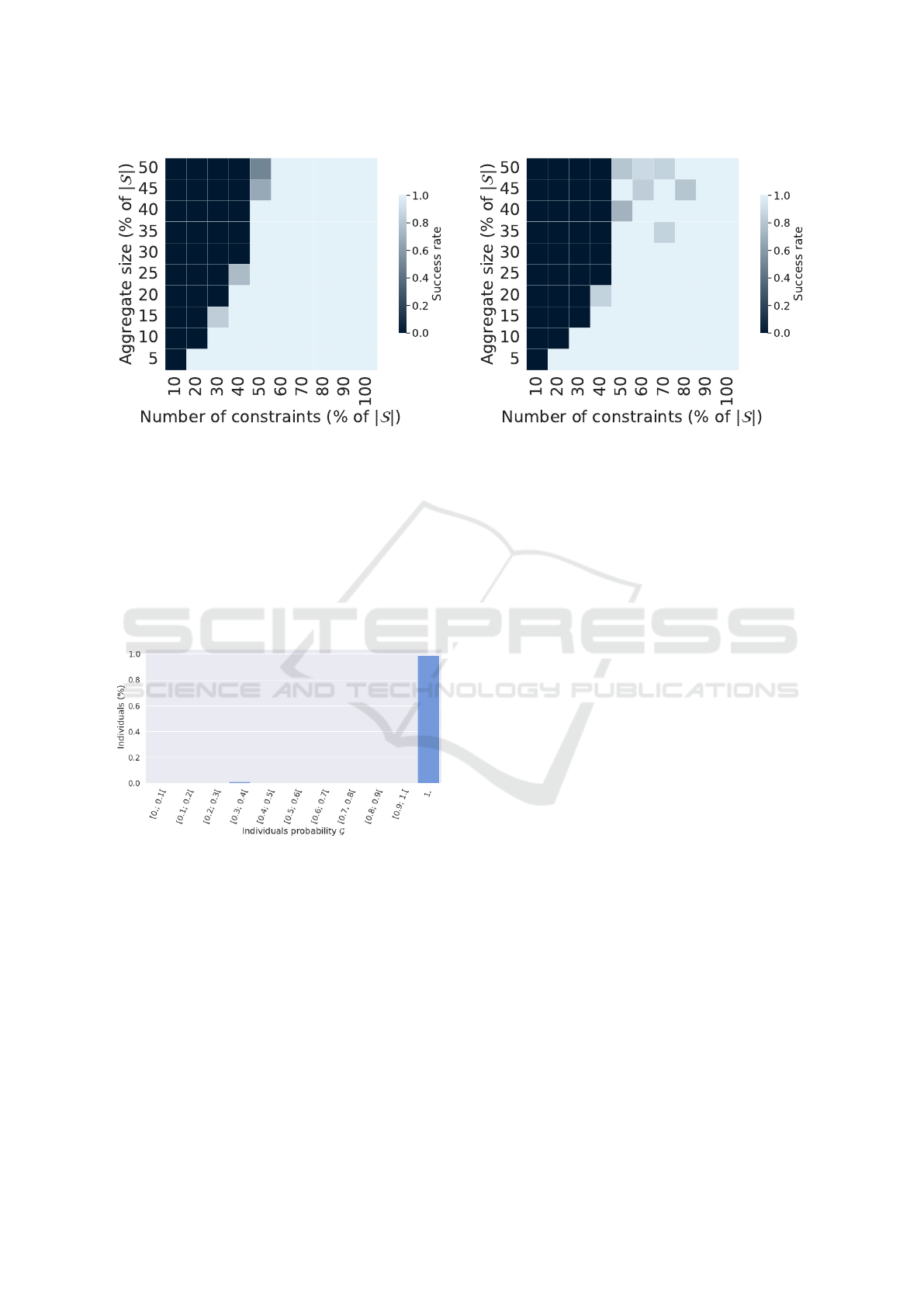
4.2.3 Attacking Large Populations
The attacks on our largest dataset provide results sim-
ilar to the ones previously described. However, since
the dataset is larger, we need to increase the time bud-
get to 24h to observe the same phenomena. As shown
in Figure 6, the relationship between the dataset size,
the aggregate size and the number of aggregates re-
Membership Inference Attacks on Aggregated Time Series with Linear Programming
199
(a) θ = 1000s. (b) θ = 2000s.
(c) θ = 4000s. (d) θ = 8000s.
Figure 4: Evolution of the success (0 : all failed, 1 : all succeed) depending on the time budget. Parameters : dataset =
ISSDA-30m, |S | = 2000, θ = {1000s, 2000s, 4000s, 8000s}, p = 2, 20 repetitions.
(a) θ = 2000s.
(b) θ = 8000s.
Figure 5: Evolution of experiments time depending on the
time budget. Parameters : dataset = ISSDA-30m, |S| =
2000, θ = {2000s, 8000s}, p = 2, 20 repetitions.
quired for the attack to succeed is similar to what
we observed in the other experiments. In particular,
in this case, we need roughly twice more constraints
than the aggregate size until we reach an aggregate
size of 25% of |S|. After that, the number of con-
straints needed to reach a success remains stable at
50% of |S|.
It is worth to note that we set the pool size to
p = 100 in these experiments, meaning that the at-
tack is considered to be successful if the number of
solutions found is between 1 and 99. This allows us
to study the cases where several solutions are found,
which make G worth analyzing. We chose the experi-
ment in which the solver returned the highest number
of solutions and where the intersection of these solu-
tions is the smallest (in other words, where the num-
ber of individuals that are part of several solutions is
the highest). This case occurred in one of the 20 repe-
titions of the attack performed with the following pa-
rameters: dataset = ISSDA-30m, |S| = 4500, θ = 24h,
p = 100, |S
A
| = 225 (5%) and |A| = 900 (20%). It
resulted in a pool containing 3 solutions. We repre-
sent in Figure 7 the part of the guess vector limited to
the individuals found in the 3 solutions. Figure 7 is a
histogram showing the fraction of individuals (Y-axis)
associated to eleven possible ranges of guess in G
17
(X-axis). The figure shows that 224 (98.7%) individ-
uals appear in all the solutions: their membership can
17
Recall that the vector of guesses G contains for each
individual the probability that the individual participates to
A.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
200
(a) Dataset = London-30m. (b) Dataset = ISSDA-30m.
Figure 6: Attack success (0 : all fail, 1 : all succeed) for datasets of 4500 individuals. Parameters : dataset = {ISSDA-30m,
London-30m}, |S| = 4500, θ = 24h, p = 100, 20 repetitions.
thus be completely inferred with certainty while only
one individual differs in all three solutions: the mem-
bership probability of the corresponding individuals
is thus equal to 1/3. This shows that the SUBSUM at-
tack manages to gain significant knowledge about the
aggregate members even when multiple solutions are
provided.
Figure 7: Focus on the experiment in which the solver re-
turned the highest number of solutions and where the inter-
section of these solutions is the smallest (3 solutions found
in this case). We show here the fraction of individuals as-
sociated to each possible adversarial guess value (organized
within eleven ranges). Parameters : dataset = ISSDA-30m,
|S| = 4500, θ = 24h, p = 100, |S
A
| = 225 (5%), |A| = 900
(20%).
5 RELATED WORKS
In the literature, attacks applicable against the
privacy-preserving publication of electrical consump-
tion data can be separated in three categories. First,
there is the Linear reconstruction attacks where the
attackers aim at finding back the original dataset from
a publication. Secondly, the Membership Inference
Attacks (MIA in short) looks if a specific individual
is part of a publication. Lastly, NonIntrusive Load
Monitoring (or NILM) tries to infers valuable infor-
mation (e.g., the devices used) from an electrical con-
sumption time series. We consider our attack as be-
ing a membership inference attack (we try to know
which individuals take part in a publication) by using
methodologies explored by the reconstruction attacks
(the usage of linear programming solvers).
5.1 Linear Reconstruction Attacks
Linear reconstruction attacks (Cohen and Nissim,
2020; Dinur and Nissim, 2003; Dwork et al., 2007;
Dwork and Yekhanin, 2008; Lacharit
´
e et al., 2018;
Quadrianto et al., 2008), illustrated by Cohen & al.
(Cohen and Nissim, 2020), are probably the closest
from our attack. In these attacks, an attacker is given
access to an interface allowing him to generate ag-
gregates from limited queries on the dataset. The at-
tacker sends a set of queries, each of them getting a
new aggregate from a randomly selected subset of the
dataset. Each query is then used to build a set of con-
straints that are then solved by a linear programming
solver. As for our attack, the goal is to extract private
information from a set of constraints. However, the
SUBSUM attack differs in several ways. First, the lin-
ear reconstruction attack aims to reconstruct a private
dataset (e.g., the values of the dataset elements) while
our attack aims to reconstruct private aggregates from
known data. The attack aims to infer the presence
or the absence of individuals in an aggregate and not
Membership Inference Attacks on Aggregated Time Series with Linear Programming
201

their values. Second, due to the different objective
of the attack, the attacker does not require the same
background knowledge. Our attack does not require
access to a query interface and can be performed on a
static set of aggregates as they are generally published
in open data programs. However, the large number of
queries required by the linear reconstruction attack is
somewhat balanced by the requirement of the individ-
uals’ values.
5.2 Membership Inference Attacks
Membership inference attacks are another family of
attacks where the attacker wishes to infer the pres-
ence or the absence of a target inside a dataset or
whether a target has played a part in the result of
a function (Dwork et al., 2017; Rigaki and Garcia,
2020). Datasets can broadly take the form of ag-
gregates (Bauer and Bindschaedler, 2020; B
¨
uscher
et al., 2017; Jayaraman et al., 2021; Pyrgelis et al.,
2020a; Pyrgelis et al., 2018; Pyrgelis et al., 2020b;
Zhang et al., 2020), data used to train machine learn-
ing model (Long et al., 2020; Melis et al., 2019;
Salem et al., 2019; Shokri et al., 2017; Truex et al.,
2019; Yeom et al., 2018), genomics database (Homer
et al., 2008; Samani et al., 2015; Sankararaman
et al., 2009) or original data used to generate synthetic
ones (Stadler et al., 2020).
5.2.1 Membership Inference Attacks on
Aggregates
When membership inference attacks are applied to
aggregates (Bauer and Bindschaedler, 2020; B
¨
uscher
et al., 2017; Jayaraman et al., 2021; Pyrgelis et al.,
2020a; Pyrgelis et al., 2018; Pyrgelis et al., 2020b;
Zhang et al., 2020), as in our approach, the aim is to
find whether an individual is part of an aggregate or a
set of aggregates. In (Pyrgelis et al., 2018), an attacker
has access to a set of aggregates representing the num-
ber of people visiting a specific geographic point at a
particular time. Similarly to time series, each geo-
graphic point generates a new record at given periods.
Prior to the attack, the attacker has access to incom-
plete background knowledge about a target (a single
person) telling where it was at a given time. The target
can be present in the set of observed points or not. The
attacker will then train a machine learning classifier
which will be able to infer whether or not the target
is present on at least one geographic point at a given
time outside his training range. Compared to our at-
tack, this attack required far less background knowl-
edge: only a few points where the target is present or
not. However its scale is limited: it is only able to
infer the presence or the absence of the target inside a
set of aggregates while our attack can reconstruct up
to every record present in the aggregate. Membership
inference can be applied to more generic data (Bauer
and Bindschaedler, 2020; Jayaraman et al., 2021). In
these cases a similar method is used: an attack model
is trained with similar data as the one attacked. This
model is then used to deduce the presence or the ab-
sence of a specific target in an aggregate.
5.2.2 Membership Inference Attack on ML
Models
These attacks (Long et al., 2020; Melis et al., 2019;
Salem et al., 2019; Shokri et al., 2017; Truex et al.,
2019; Yeom et al., 2018) aim to find whether an in-
dividual is part of the dataset used to train a ma-
chine learning model. The attacker has access to un-
limited queries to a black box model and to records
sampled from the same distribution as the original
training data. Usually (Shokri et al., 2017; Truex
et al., 2019), the attacker will train an ML-based at-
tack model against multiple shadow models which
replicate the behavior of the attacked model and are
trained with some known datasets (with and without
the target individual). The attack model will then be
applied against the real model to attack. Membership
attacks on ML models requires knowledge of distri-
bution of the attacked records and large amount of
data to train the shadow models. However, they do
not need to get access to the real data used by the at-
tacked model. These attacks are, for now, limited to
attacking machine learning models and not aggregate
data.
5.3 Non Intrusive Load Monitoring
(NILM) introduced by Hart (Hart, 1992) in 1992 is
a field of study aiming to extract information con-
tained in electric consumption time series such as the
occupancy of a household, the electric devices used
and even the TV program watched. NILM algorithms
can use a wide variety of methods to reach this goal
from finite state machines to knapsack-based algo-
rithms and machine learning classifiers. Despite not
being considered as privacy attacks, these algorithms
can be used as a tool to retrieve private information
contained in time series. To the best of our knowl-
edge, no attempt has been made to adapt NILM prin-
ciples to extract information contained in an aggrega-
tion of multiple electric load consumption time series.
NILM-based attacks may be used as a complement
of our attack either to filter a set of loads potentially
present in the aggregates or to train a NILM model
from the consumption values of the aggregates.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
202

6 CONCLUSION
Membership inference attacks aim to infer whether
a specific individual belongs to a given aggregate.
In this work, we introduced a new technique to per-
form inference attacks on (threshold-based) aggre-
gated time series. Given a publicly known dataset
of time series, and aggregated values (one value per
timestamp) calculated from a private subset of that
dataset, the adversary that we consider is able to re-
identify the individuals belonging to the private sub-
set. To do so, we modeled the membership inference
attack as a subset sum problem and we used Gurobi to
solve it. We completed experiments on two real-life
datasets containing power consumption time series,
from UK and Ireland, respectively. We showed that
if the number of available aggregated values is larger
than the aggregate size (i.e., the number of individ-
uals in the private subset), then the SUBSUM attack
is highly likely successful. Interesting future works
include relaxing the background knowledge required
by the SUBSUM attack (e.g., missing time series, ap-
proximate values) and coping with advanced privacy-
preserving approaches (e.g., differential privacy).
ACKNOWLEDGEMENTS
We would like to thank Charles Prud’homme (TASC,
IMT-Atlantique, LS2N-CNRS) for his help on the
choice of the solver. Some of the authors are sup-
ported by the TAILOR (”Foundations of Trustworthy
AI - Integrating Reasoning, Learning and Optimiza-
tion” - H2020-ICT-2018-20) project.
REFERENCES
Bauer, L. A. and Bindschaedler, V. (2020). Towards realistic
membership inferences: The case of survey data. In
ACSAC ’20: Annual Computer Security Applications
Conference, pages 116–128. ACM.
B
¨
uscher, N., Boukoros, S., Bauregger, S., and Katzen-
beisser, S. (2017). Two is not enough: Privacy as-
sessment of aggregation schemes in smart metering.
Proc. Priv. Enhancing Technol., 2017(4):198–214.
CER (2012). CER Smart Metering Project - Electricity
Customer Behaviour Trial. Irish Social Science Data
Archive. (accessed may 11 2022). https://www.ucd.
ie/issda/data/commissionforenergyregulationcer.
Charles Prud’homme, Jean-Guillaume Fages, and Xavier
Lorca (2016). Choco solver documentation. http:
//www.choco-solver.org.
Cohen, A. and Nissim, K. (2020). Linear Program Recon-
struction in Practice. J. Priv. Confidentiality, 10(1).
Deloitte (2017). Assessing the value of tfl’s open data and
digital partnerships.
Dinur, I. and Nissim, K. (2003). Revealing informa-
tion while preserving privacy. In Proceedings of
the Twenty-Second ACM SIGACT-SIGMOD-SIGART
Symposium on Principles of Database Systems, pages
202–210.
Dwork, C., McSherry, F., and Talwar, K. (2007). The price
of privacy and the limits of LP decoding. In Proceed-
ings of the 39th Annual ACM Symposium on Theory
of Computing, pages 85–94.
Dwork, C., Smith, A., Steinke, T., and Ullman, J. (2017).
Exposed! a survey of attacks on private data. Annual
Review of Statistics and Its Application, 4:61–84.
Dwork, C. and Yekhanin, S. (2008). New efficient attacks
on statistical disclosure control mechanisms. In Ad-
vances in Cryptology - CRYPTO 2008, 28th Annual
International Cryptology Conferences, volume 5157
of Lecture Notes in Computer Science, pages 469–
480.
Gauvin, L., Tizzoni, M., Piaggesi, S., Young, A., Adler,
N., Verhulst, S., Ferres, L., and Cattuto, C. (2020).
Gender gaps in urban mobility. Humanities and Social
Sciences Communications, 7(1):1–13.
Gurobi Optimization, L. (2020). Gurobi optimizer. http:
//www.gurobi.com.
Hart, G. (1992). Nonintrusive appliance load monitoring.
Proceedings of the IEEE, 80(12):1870–1891.
Homer, N., Szelinger, S., Redman, M., Duggan, D., Tembe,
W., Muehling, J., Pearson, J. V., Stephan, D. A., Nel-
son, S. F., and Craig, D. W. (2008). Resolving in-
dividuals contributing trace amounts of dna to highly
complex mixtures using high-density snp genotyping
microarrays. PLoS Genet, 4(8):e1000167.
Jayaraman, B., Wang, L., Knipmeyer, K., Gu, Q., and
Evans, D. (2021). Revisiting membership inference
under realistic assumptions. Proc. Priv. Enhancing
Technol., 2021(2):348–368.
Kellerer, H., Pferschy, U., and Pisinger, D. (2004). The
subset sum problem. In Knapsack Problems, pages
73–115. Springer.
Lacharit
´
e, M., Minaud, B., and Paterson, K. G. (2018). Im-
proved reconstruction attacks on encrypted data using
range query leakage. In IEEE Symposium on Security
and Privacy, SP, pages 297–314.
Laurent Perron, Vincent Furnon, G. (2019). Or-tools. https:
//developers.google.com/optimization/.
Long, Y., Wang, L., Bu, D., Bindschaedler, V., Wang, X.,
Tang, H., Gunter, C. A., and Chen, K. (2020). A prag-
matic approach to membership inferences on machine
learning models. In IEEE European Symposium on
Security and Privacy, EuroS&P 2020, pages 521–534.
Melis, L., Song, C., Cristofaro, E. D., and Shmatikov, V.
(2019). Exploiting unintended feature leakage in col-
laborative learning. In 2019 IEEE Symposium on Se-
curity and Privacy, SP 2019, pages 691–706.
OECD (2020). Oecd open, useful and re-usable data (our-
data) index: 2019. https://www.oecd.org/gov/digital-
government/policy-paper-ourdata-index-2019.htm.
Membership Inference Attacks on Aggregated Time Series with Linear Programming
203

Pyrgelis, A., Troncoso, C., and Cristofaro, E. D. (2018).
Knock knock, who’s there? membership inference on
aggregate location data. In 25th Annual Network and
Distributed System Security Symposium, NDSS. The
Internet Society.
Pyrgelis, A., Troncoso, C., and Cristofaro, E. D. (2020a).
Measuring membership privacy on aggregate location
time-series. Proc. ACM Meas. Anal. Comput. Syst.,
4(2):36:1–36:28.
Pyrgelis, A., Troncoso, C., and Cristofaro, E. D. (2020b).
Measuring Membership Privacy on Aggregate Loca-
tion Time-Series. Proc. ACM Meas. Anal. Comput.
Syst., 4(2):36:1–36:28.
Quadrianto, N., Smola, A. J., Caetano, T. S., and Le, Q. V.
(2008). Estimating labels from label proportions. Pro-
ceedings of the Twenty-Fifth International Conference
on Machine Learning (ICML 2008), pages 776–783.
Rigaki, M. and Garcia, S. (2020). A survey of privacy at-
tacks in machine learning. CoRR, abs/2007.07646.
Salem, A., Zhang, Y., Humbert, M., Berrang, P., Fritz, M.,
and Backes, M. (2019). Ml-leaks: Model and data in-
dependent membership inference attacks and defenses
on machine learning models. In 26th Annual Network
and Distributed System Security Symposium, NDSS
2019.
Samani, S. S., Huang, Z., Ayday, E., Elliot, M., Fellay,
J., Hubaux, J., and Kutalik, Z. (2015). Quantifying
genomic privacy via inference attack with high-order
SNV correlations. In 2015 IEEE Symposium on Secu-
rity and Privacy Workshops, SPW 2015, pages 32–40.
Sankararaman, S., Obozinski, G., Jordan, M. I., and
Halperin, E. (2009). Genomic privacy and limits
of individual detection in a pool. Nature genetics,
41(9):965–967.
Shokri, R., Stronati, M., Song, C., and Shmatikov, V.
(2017). Membership Inference Attacks Against Ma-
chine Learning Models. In 2017 IEEE Symposium on
Security and Privacy, SP 2017, pages 3–18.
Stadler, T., Oprisanu, B., and Troncoso, C. (2020).
Synthetic data - A privacy mirage. CoRR,
abs/2011.07018.
The European Data Portal (2015). Creating value through
open data : Study on the impact of re-use of public
data resources. https://op.europa.eu/en/publication-
detail/-/publication/51ec011a-e13b-11e6-ad7c-
01aa75ed71a1.
The World Wide Web Foundation (2017). Open data barom-
eter - global report (4th ed.).
Truex, S., Liu, L., Gursoy, M. E., Wei, W., and Yu, L.
(2019). Effects of differential privacy and data skew-
ness on membership inference vulnerability. In First
IEEE International Conference on Trust, Privacy and
Security in Intelligent Systems and Applications, TPS-
ISA 2019, pages 82–91.
UK Power Networks (2013). SmartMeter Energy Con-
sumption Data in London Households (Accessed
May 11 2022). https://data.london.gov.uk/dataset/
smartmeter-energy-use-data-in-london-households.
Yeom, S., Giacomelli, I., Fredrikson, M., and Jha, S. (2018).
Privacy risk in machine learning: Analyzing the con-
nection to overfitting. In 31st IEEE Computer Security
Foundations Symposium, CSF 2018, pages 268–282.
Zhang, G., Zhang, A., and Zhao, P. (2020). Locmia: Mem-
bership inference attacks against aggregated location
data. IEEE Internet Things J., 7(12):11778–11788.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
204
