Code-based Key Encapsulation Mechanism Preserving Short Ciphertext

and Secret Key

Jayashree Dey and Ratna Dutta

Department of Mathematics, Indian Institute of Technology Kharagpur, Kharagpur-721302, India

Keywords:

Public Key Encryption, Key Encapsulation Mechanism, MDS Code, Companion Matrix.

Abstract:

Post-quantum cryptography has recently drawn considerable attention from both industry and academia due

to the impending threat by quantum computers. Developing key encapsulation mechanism (KEM) that resists

attacks equipped with quantum computers has become relevant as KEM is used in practice quite heavily.

Coding theory is an attractive option to guarantee secure communication in the post-quantum world. Motivated

by the goal of improving efﬁciency, we revisit code-based KEM in this article. We present basicPKE, a public

key encryption (PKE) scheme using a parity check matrix of maximum distance separable (MDS) code. Our

construction is built on top of a companion matrix in deriving an MDS code. This signiﬁcantly reduces the

secret key size. We support the conjectured security of basicPKE by analysis and prove that the scheme

achieves security against indistinguishability under chosen plaintext attacks (IND-CPA) in the random oracle

model. Following the design framework of basicPKE, we construct fullPKE that leads to the design of fullKEM.

We have shown that fullPKE is secure against one-wayness under plaintext and validity checking attacks (OW-

PCVA) and fullKEM achieves security against indistinguishability under chosen ciphertext attacks (IND-CCA)

in the random oracle model. An appealing feature of fullKEM is that it exhibits better performance guarantee

in terms of communication bandwidth and secret key size when contrasted with existing similar approaches.

1 INTRODUCTION

With the proliferation of a wide range of Internet of

Things (IoT), IoT devices are increasingly used to

store secrets that are used to authenticate users or

enable secure payments. Many IoT devices are not

equipped with proper environments to store secret

keys and provide developers with little programma-

bility for their applications. It is therefore desirable to

leverage the fact that users own multiple devices such

as smart phone, smart watch, smart TV, etc. and en-

able multi-device cryptographic functionalities with-

out making strong assumptions about a device’s se-

curity features. Given the limited computation and

communication power of IoT devices, it is essential

to come up with cryptographic primitives that meet

short communication bandwidth as well as short se-

cret key.

Key encapsulation mechanism (KEM) is an im-

portant building block in cryptography which plays

a vital role in transmitting symmetric key information

securely utilizing asymmetric algorithms. Although

public key cryptosystems are incompetent to commu-

nicate long messages in practice, KEM is beneﬁcial

to exchange relatively short symmetric key which is

then used for encrypting a longer message. More pre-

cisely, one can encrypt a random symmetric key us-

ing the preferred public key algorithm. The receiver

recovers the symmetric key by the decryption proce-

dure of the public key algorithm.

Given the rapidly expanding set of KEM ap-

plications and public key encryption (PKE), there

is a strong interest in making PKE and KEM

post-quantum secure. Error-correcting codes play

a signiﬁcant role in designing quantum-safe alter-

natives while offering reasonable performance with

solid security guarantees as code-based cryptographic

schemes are usually very fast and can be implemented

on several platforms.

Our Contribution. Since its introduction by

McEliece (McEliece, 1978) in 1978, numerous

proposals in constructing PKEs and KEMs based on

error correcting codes have been presented yielding

various improvements in security and efﬁciency. A

line of recent work are offered to NIST call in 2016

for standardization of quantum safe cryptography

(Barreto et al., 2017), (Bardet et al., 2017), (Yamada

et al., 2017), (Bernstein et al., 2017), (Kim et al.,

374

Dey, J. and Dutta, R.

Code-based Key Encapsulation Mechanism Preserving Short Ciphertext and Secret Key.

DOI: 10.5220/0011273900003283

In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 374-381

ISBN: 978-989-758-590-6; ISSN: 2184-7711

2018), (Aguilar-Melchor et al., 2018), (Albrecht

et al., 2019), (Aragon et al., 2017a), (Banegas et al.,

2018), (Baldi et al., 2018), (Szepieniec, 2017),

(Wang, 2017), (Aragon et al., 2017b), (Melchor et al.,

2017), (Aragon et al., 2017c), (Aragon et al., 2017b),

(Melchor et al., 2017), (Aragon et al., 2017c), (Mel-

chor et al., 2019), focusing on constructing KEM

offering improvements in security and efﬁciency. The

challenge lies in the requirement of low communi-

cation bandwidth and short key size while providing

strong security guarantee. This motivates our search

for a code-based KEM featuring indistinguishability

under chosen ciphertext attacks (IND-CCA) security

under the hardness of the syndrome decoding with

relatively short ciphertext and short secret key. Using

the structure of a companion matrix, we form an

MDS code and integrate it to design basicPKE by

coupling with the Niederreiter encryption (Nojima

et al., 2008). We have shown that basicPKE achieves

indistinguishability against chosen plaintext attacks

(IND-CPA). More speciﬁcally, we use the parity

check matrix of the MDS code as the public key

matrix and keep the last row of the companion

matrix as secret key. Our approach yields signiﬁcant

reduction in the secret key size and communication

overhead, making the scheme useful in applications

with limited communication bandwidth. Moreover,

use of parity check matrix instead of generator matrix

enables faster encapsulation. MDS codes satisfy

the Singleton bound and have efﬁcient decoding

algorithm which is employed to decode ciphertext

during decryption.

We extend basicPKE to fullPKE which is proven

to be one-wayness under plaintext and validity check-

ing attacks (OW-PCVA) secure in the random oracle

model. Finally, we build indistinguishability under

chosen ciphertext attacks (IND-CCA) secure fullKEM

from fullPKE. We brieﬂy discuss our fullKEM in refer-

ence to the previous similar works.

• As exhibited in Table 1, our fullKEM offers sev-

eral strong advantages over the existing approaches

((Albrecht et al., 2019), (Aragon et al., 2019), (Bern-

stein et al., 2017), (Baldi et al., 2018), (Bardet et al.,

2017), (Banegas et al., 2018), (Dey and Dutta, 2019))

that are constructed over ﬁnite ﬁelds with character-

istic 2. The most appealing feature of our fullKEM is

that we use MDS code in our work owning the bi-

nary structure and the use of the companion matrix

helps to reduce the secret key size. A bit more pre-

cisely, the secret key size of our construction is com-

paratively shorter than the schemes ((Albrecht et al.,

2019), (Bernstein et al., 2017), (Bardet et al., 2017),

(Baldi et al., 2018),(Banegas et al., 2018), (Dey and

Dutta, 2019)) although the size of public key remains

large. The BIKE variants and LEDAkem are efﬁcient

in terms of public key sizes and achieve IND-CCA se-

curity. However, they experience a small decoding

failure rate unlike our candidate.

• More interestingly, our fullKEM supports low

communication overhead and performs better in terms

of ciphertext size over DAGS (Banegas et al., 2018)

and (Dey and Dutta, 2019). It uses parity check ma-

trix during encapsulation instead of generator matrix

which leads faster encapsulation in contrast to DAGS

and NTS-KEM. In fact, the encapsulation procedure

of fullKEM is closest to the work in (Bardet et al.,

2017).

• To prove the security of fullKEM, we follow the

generic transformations by Hofheinz et al. (Hofheinz

et al., 2017). More concretely, our basicPKE sup-

ports IND-CPA security in random oracle model un-

der the hardness of syndrome decoding problem and

the indistinguishability of the public key matrix from

a random matrix. We prove that breaking OW-PCVA

security of our fullPKE would lead to breaking the

IND-CPA security of basicPKE in the random ora-

cle model. Achieving IND-CCA security of fullKEM

seems quite tricky despite of its potential for compar-

ative simplicity. As OW-PCVA security always im-

plies one-wayness under validity attacks (OW-VA) se-

curity with zero queries to the plaintext checking ora-

cle, the OW-PCVA security and consequently the OW-

VA security of fullPKE follows from the IND-CPA se-

curity of basicPKE. We show that the OW-VA security

of fullPKE implies the IND-CCA security of fullKEM

in the random oracle model. We can further extend

our security proof in the quantum random oracle fol-

lowing the work by Hofheinz et al. (Hofheinz et al.,

2017).

2 PRELIMINARIES

In this section, we provide mathematical background

and preliminaries that are necessary to follow the dis-

cussion in the paper.

Notation. We use the notation x

←− X for choosing a

random element from a set or distribution, a ←− A for

the sampling according to some distribution A, wt(x)

to denote the weight of a vector x, (x||y) for the con-

catenation of the two vectors x and y. The matrix I

the n × n identity matrix. We let GF(q) to denote the

Galois ﬁeld of cardinality q and Z

to represent the

set {a ∈ Z|a ≥ 0} where Z is the set of integers. We

denote the transpose of a matrix A by A

and concate-

nation of two matrices A and B by [A|B]. The uniform

distribution over c × d random q-ary matrices is de-

Code-based Key Encapsulation Mechanism Preserving Short Ciphertext and Secret Key

375

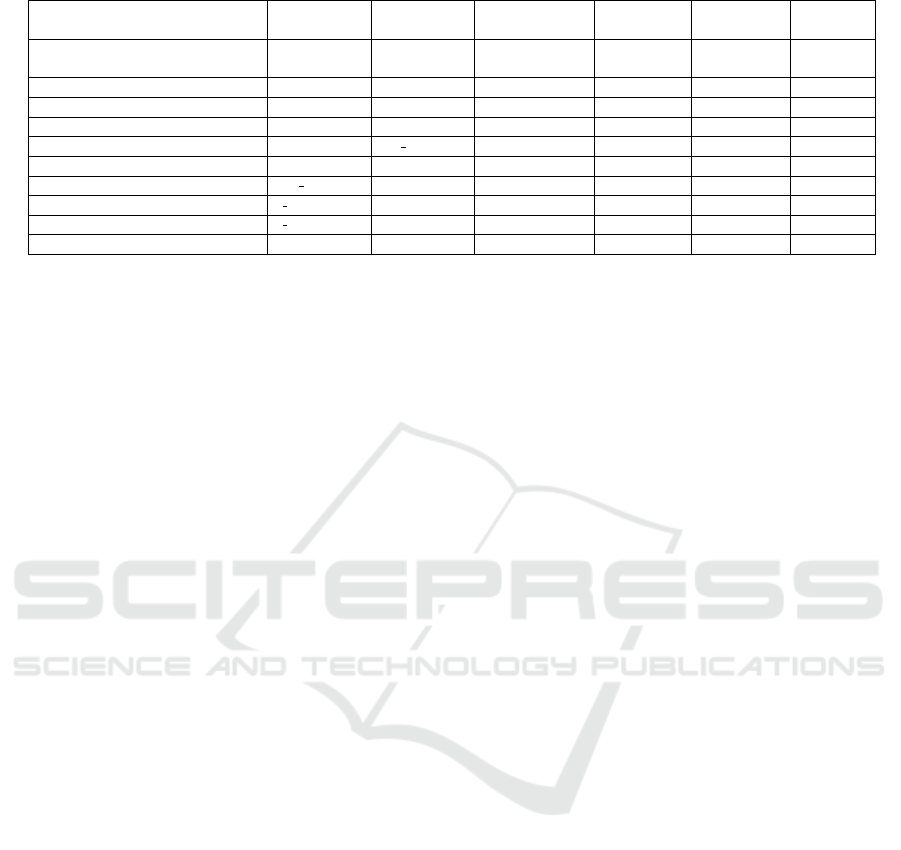
Table 1: Comparative summary of IND-CCA secure KEMs.

Scheme pk size (in bits) sk size (in bits) CT size (in bits) Code used Cyclic/Dyadic Correctness

error

NTS-KEM (Albrecht et al., 2019) (n − k)k 2(n − k + r)m (n − k + r) Binary Goppa – No

+nm + r

BIKE-1 (Aragon et al., 2019) n n + w · ⌈log

k⌉ n MDPC Quasi-cyclic Yes

BIKE-2 (Aragon et al., 2019) k n + w · ⌈log

k⌉ k MDPC Quasi-cyclic Yes

BIKE-3 (Aragon et al., 2019) n n + w · ⌈log

k⌉ n MDPC Quasi-cyclic Yes

LEDAkem (Baldi et al., 2018) n − ℓ

ℓ

wlog

ℓ ℓ LDPC Quasi-cyclic Yes

Classic McEliece (Bernstein et al., 2017) k(n − k) n + mt + mn (n − k) + r Binary Goppa – No

BIG QUAKE (Bardet et al., 2017)

ℓ

(n − k) mt + mn (n − k) + 2r Binary Goppa Quasi-cyclic No

DAGS (Banegas et al., 2018)

(n − k) log

q 2mnlog

q [n + k

′

]log

q GS Quasi-dyadic No

(Dey and Dutta, 2019)

(n − k) log

q 2mnlog

q [k

′

+ (n − k)]log

q GS Quasi-dyadic No

fullKEM k

km 2k

′

+ km MDS – No

pk=public key, sk=secret key, CT=ciphertext, k=dimension of the code, n=length of the code, ℓ=length of each blocks, t=error correcting capacity,

′

< k, s,r,w, p

, p

are positive integers (ℓ << s), s = 2

, q = 2

, λ=security parameter, m= the degree of ﬁeld extension, r=the desired key length,

GS=Generalized Srivastava, MDPC=Moderate Density Parity Check, LDPC=Low Density Parity Check

noted by U

c,d

2.1 MDS Codes

Deﬁnition 1. (MDS Code (MacWilliams and

Sloane, 1977)). An [n,k,d] linear code with length

n, dimension k and minimum distance d is said to

be a maximum distance separable (MDS) code if

k = n − d + 1.

Deﬁnition 2. (MDS Matrix (Gupta and Ray,

2013)). Let GF(q) be a ﬁnite ﬁeld and m, n be two in-

tegers. Let x → M ×x be a mapping from (GF(q))

(GF(q))

deﬁned by the n × m matrix M. We say that

M is an MDS matrix if the set of all pairs (x, M × x)

is an MDS code, i.e. a linear code of dimension m,

length m + n and minimum distance n + 1.

Theorem 1. (MacWilliams and Sloane, 1977) An

[n,k,d] linear code with generator matrix G = [I|M] ∈

(GF(q))

k×n

is MDS code if and only if every square

submatrix of M is nonsingular where M is a k × (n −

k) matrix over GF(q). We say M is an MDS matrix if

the corresponding code is MDS.

Deﬁnition 3. (Companion Matrix (Gupta et al.,

2017a)). Let g(X ) = z

+ z

X + ·· · + z

k−1

+ X

be a monic polynomial over GF(q) of degree k. The

k × k companion matrix C

associated to the polyno-

mial g is given by







0 1 ·· · 0

·· · ·· · ·· · ·· ·

0 0 ·· · 1

−z

·· · −z

k−1







Theorem 2. (Blaum and Roth, 1999) Let GF(q) be

the ﬁnite ﬁeld containing q elements with character-

istic 2, Mat(m,GF(q)) be the ring of m × m matri-

ces over GF(q) and Mat(n,m) be the set of n × n

block matrices over Mat(m,GF(2)). A matrix M ∈

Mat(n,GF(q)) is MDS if and only if every square sub-

matrix of M is nonsingular. Similarly, a block matrix

M ∈ Mat(n,m) is MDS if and only if every square

block submatrix of M is nonsingular.

The following result follows easily from the above

theorem.

Lemma 1. A block matrix M ∈ Mat(n,m) is MDS if

and only if its transpose M

is MDS.

The order of a polynomial g(X) ∈ GF(q)[X]

(g(0) ̸= 0), denoted by ord(g), is the least positive in-

teger n such that g(X) divides X

− 1. The weight of

a polynomial is the number of its coefﬁcients that are

nonzero.

Theorem 3. (Gupta et al., 2017a) Let g(X ) ∈

GF(q)[X] be a monic polynomial of degree k with

ord(g) ≥ 2k. Then the matrix M = (C

)

is MDS if

and only if the weight of any nonzero multiple of de-

gree ≤ 2k − 1 of the polynomial g(X) is greater than

Deﬁnition 4. (Permutation Equivalent Matrices

(Kesarwani et al., 2019)) Two matrices M and M

′

are said to be permutation equivalent, denoted by

M ∼

′

, if there exist two permutation matrices P,Q

such that M

′

= PMQ.

Lemma 2. (Kesarwani et al., 2019) Suppose that

two matrices M and M

′

are permutation equivalent.

Then M is MDS if and only if M

′

is MDS.

Deﬁnition 5. (Expanded Codes (Khathuria et al.,

2019)). Let n, k be positive integers with k ≤ n, q be

a prime power and m be an integer. Let C be a lin-

ear code of length n and dimension k over GF(q

The expanded code of C with respect to a primitive

element γ ∈ GF(q

) is a linear code over the base

ﬁeld GF(q) deﬁned as

C = {φ

: (GF(q

))

−→ (GF(q))

is the GF(q)-linear

isomorphism deﬁned by γ as

(α

,α

,. .. ,α

n−1

) = (φ(α

),φ(α

),. .. ,φ(α

n−1

))

SECRYPT 2022 - 19th International Conference on Security and Cryptography

376

and φ : GF(q

) −→ (GF(q))

is given by

φ(a

+ a

γ + ·· · + a

m−1

) = (a

,. .. ,a

m−1

Lemma 3. (Khathuria et al., 2019). Let C be a

linear code in (GF(q

))

, γ ∈ GF(q

) be a primi-

tive element and φ

: (GF(q

))

−→ (GF(q))

be the

GF(q)-linear isomorphism deﬁned by γ as in Deﬁni-

tion 5.

(i) If G = [g

,. .. ,g

]

is a generator matrix of

C where g

,. .. ,g

are vectors in (GF(q

))

then the expanded code

C of C over GF(q) with

respect to the primitive element γ ∈ GF(q

) has

the expanded generator matrix

G = [φ

),φ

(γg

),. .. ,φ

(γ

m−1

),φ

(γg

),. .. ,φ

(γ

m−1

),. .. ,φ

),φ

(γg

.. ., φ

(γ

m−1

)]

(ii) If H = [h

,. .. ,h

] is a parity check matrix of

C where h

,. .. ,h

are vectors in (GF(q

))

n−k

then the expanded code

C of C over GF(q) with

respect to the primitive element γ ∈ GF(q

) has

the expanded parity check matrix

H = [φ

n−k

)

,φ

n−k

(γh

)

,. .. ,φ

n−k

(γ

m−1

)

n−k

)

,φ

n−k

(γh

)

,. .. ,φ

n−k

(γ

m−1

)

.. ., φ

n−k

)

,φ

n−k

(γh

)

,. .. ,φ

n−k

(γ

m−1

)

(iii) φ

(xG) = φ

(x)

G for all x ∈ (GF(q

))

(iv) φ

n−k

(Hy

) =

H(φ

(y))

for all y ∈ (GF(q

))

2.2 Hardness Assumptions

Deﬁnition 6. ((Search) (q-ary) Syndrome Decoding

(SD) Problem (Barg, 1997)). Given a full-rank matrix

(n−k)×n

over GF(q), a vector c ∈ (GF(q))

n−k

and a

non-negative integer w, the search version of q-ary SD

problem is to ﬁnd a vector e ∈ (GF(q))

of weight w

such that the syndrome He

of e satisﬁes He

= c.

Assumption 1. The public key matrix, output by

the key generation algorithm of a code-based PKE

scheme, is computationally indistinguishable from a

uniformly chosen matrix of the same size.

3 basicPKE: AN IND-CPA SECURE

PUBLIC KEY ENCRYPTION

We now present the details of our public key encryp-

tion scheme basicPKE = (Setup, KeyGen,Enc,Dec).

• basicPKE.Setup(λ)−→ pp

basicPKE

: Taking secu-

rity parameter λ as input, a trusted authority pro-

ceeds as follows to generate the global public pa-

rameters pp

basicPKE

(i) Sample k (≥ 2),m ∈ Z

, set q = 2

. Let γ ∈

GF(q) be a primitive element of GF(q).

(ii) Set w ≤ k/2 and sample k

′

∈ Z

(iii) Choose a cryptographic hash function H

{0,1}

∗

−→ {0,1}

′

(iv) Publish the global parameters pp

basicPKE

(k, k

′

,w,q,m, γ,H

• basicPKE.KeyGen(pp

basicPKE

) −→ (pk,sk): A

user on input pp

basicPKE

, performs the following

steps to generate public key pk and secret key sk.

(i) Select z

,. .. ,z

k−1

∈ GF(q) where q = 2

. Let

g(X) ∈ GF(q)[X] be a monic polynomial of de-

gree k ≥ 2 given by g(X) = z

+ z

X + z

·· · + z

k−1

+ X

with ord(g) ≥ 2k such that

g(X) has no nonzero multiple of degree ≤ 2k − 1

with weight ≤ k. Such polynomials can be con-

structed using the approaches proposed by Gupta

et al. ((Gupta et al., 2017b), (Gupta et al., 2019)).

(ii) The companion matrix associated with the

polynomial g(X) is







0 1 0 ··· 0

0 0 1 ··· 0

·· · ·· · ·· · ·· · ···

0 0 0 ··· 1

·· · z

k−1







∈ (GF(q))

k×k

(iii) Compute

M = (C

)

which is MDS by Theo-

rem 3 as g(X ) satisﬁes the conditions stated in

this theorem. Therefore, every square submatrix

M is non-singular by Theorem 2. Hence by

Theorem 1, the matrix G = [I|

M] ∈ (GF(q))

k×n

a generator matrix of an MDS code C having code

length n = 2k, dimension k and minimum distance

k + 1. Then the parity check matrix of the code C

is H = [

n−k

] ∈ (GF(q))

(n−k)×n

(iv) Let

H be the expanded parity check matrix of the

expanded code

C of C with respect to the prim-

itive element γ of GF(q) where q = 2

and the

isomorphism φ

as in Deﬁnition 5. Here

H is an

(n−k)m×nm matrix over GF(2) by Lemma 3 (ii).

(v) Write

H ∈ (GF(2))

(n−k)m×nm

in systematic form

[

M|I

(n−k)m

] where

M is an (n − k)m × km matrix

and n − k = k.

(vi) Publish the public key pk =

M and keep the se-

cret key sk = (z

,. .. ,z

k−1

) secret to itself.

• basicPKE.Enc(pp

basicPKE

,pk, m; r) −→ c: Given

system parameters pp

basicPKE

, public key pk =

M and a message m ∈ (GF(2))

′

, an encryptor

proceeds as follows to generate a ciphertext c ∈

(GF(2))

km+k

′

Code-based Key Encapsulation Mechanism Preserving Short Ciphertext and Secret Key

377

Algorithm 1: Function G: Error vector derivation.

Input: A binary seed vector σ of any length, integers nm,t.

Output: A binary error vector e = (e

,. .. ,e

nm−1

) of length nm, weight t.

1: Set e ←− 1

||0

nm−t

; b ← σ;

2: for (i = 0 to t − 1) do

3: j ← F (b) mod (nm − i − 1); // see Remark 1

4: Swap entries e

and e

i+ j

in e; b ← Hsh(b); // Hsh is a hash function

5: end for

6: return e = (e

,. .. ,e

nm−1

)

(i) Select a random vector σ.

(ii) Run Algorithm 1 to generate a unique binary er-

ror vector e of length nm and weight w using σ as

a seed, i.e, e = G(σ). Here, r = e is the random-

ness used in the procedure.

(iii) Using the public key

M, construct the parity

check matrix

H = (

M|I

(n−k)m

) for the MDS code

where n − k = k.

(iv) Compute the syndrome c = (c

) = (m ⊕

(e),

) ∈ (GF(2))

(n−k)m+k

′

(v) Publish the ciphertext c.

• basicPKE.Dec(pp

basicPKE

,sk,c)−→ m

′

: On re-

ceiving a ciphertext c = (c

), a decryptor exe-

cutes the following steps using public parameters

basicPKE

and its secret key sk = (z

,. .. ,z

k−1

(i) First proceed as follows to decode c

and ﬁnd bi-

nary error vector e

′

of length nm and weight w :

(a) Use sk = (z

,. .. ,z

k−1

) to form k × k com-

panion matrix







0 1 0 ··· 0

0 0 1 ··· 0

·· · ·· · ·· · ·· · ···

0 0 0 ··· 1

·· · z

k−1







associated with the monic polynomial g(X) =

+ z

X + z

+ · ·· + z

k−1

+ X

∈

GF(q)[X] of degree k ≥ 2 and ord(g) ≥ 2k that

has no nonzero multiple of degree ≤ 2k − 1

with weight ≤ k. Then compute

M = (C

)

and the parity check matrix H = [

n−k

] ∈

(GF(q))

(n−k)×n

for n = 2k.

(b) Compute c

′

= φ

−1

n−k

) where c

is a col-

umn vector of length (n − k)m over GF(2), c

′

is a column vector of length (n − k) over GF(q)

and φ

n−k

is the GF(2)-linear isomorphism de-

ﬁned by γ (Deﬁnition 5). The (n − k) × n parity

check matrix H is used to decode c

by ﬁrst

computing the syndrome S = H(c

′

||0)

where

0 is a vector consisting of k zeros and then by

running the decoding algorithm for MDS codes

to ﬁnd the vector

e ∈ (GF(q))

to get e

′

= φ

(

e) ∈ (GF(2))

(ii) Compute m

′

= c

⊕ H

′

(iii) Return m

′

Remark 1. The function G in Algorithm 1 uses a

hash function Hsh in line 4 and in F in line 3. Note

that, G returns a binary vector of length nm and

weight t on input an arbitrary binary string and in-

tegers nm, t. For simplicity, we use the notation

G(σ) to denote the output of the error vector genera-

tion algorithm instead of G(σ, nm,t). The subroutine

F (b) mod (nm − i − 1) −→ j outputs an integer j on

input a binary vector b of length k as follows.

Step 1. Truncate Hsh(b) to a string of s bytes where

s is larger than the byte size of nm.

Step 2. Convert this s–bytes string to an integer A.

(a) If A > 2

− (2

mod (nm − i − 1)) then go to

Step 1.

(b) else set j = A mod (nm − i − 1).

Correctness. While decoding c

, we form an

(n − k) × n parity check matrix H over GF(q) using

the secret key sk and ﬁnd the syndrome H(c

′

||0)

to estimate the error vector e

′

∈ (GF(2))

with

wt(e

′

) = w. Note that, the ciphertext component

H(e)

is the syndrome of e where the matrix

H is a parity check matrix in the systematic form

over GF(2) which is indistinguishable from a random

matrix over GF(2). At the time of decoding c

, we

need a parity check matrix over GF(q). The matrix

a parity check matrix of MDS code in the systematic

form derived from the public key pk, does not help

to decode c

as the SD problem is hard over GF(2).

The decoding algorithm in our decryption procedure

uses the parity check matrix H derived from the

secret key sk. This procedure can correct upto k/2

errors. In our scheme, the error vector e used in the

procedure basicPKE.Enc satisﬁes wt(e) = w ≤ k/2.

Consequently, the decoding procedure will recover

the correct e by Lemma 3 (iv).

The method for achieving an indistinguishable

public key matrix by mixing secret key matrix by two

matrices is rather old and shows vulnerability to the

scheme according to Strenzke et al.(Strenzke, 2010).

The most reliable method suggested by Biswas and

Sendrier (Biswas and Sendrier, 2008) to obtain the

public key matrix is to compute the systematic form

of the secret key matrix. In our scheme, we start with

choosing z

, i = 0,1, ...,n −1 randomly to construct a

companion matrix and then proceed to obtain a parity

check matrix of an MDS code. After that, we ﬁnd the

expanded parity check matrix over base ﬁeld GF(2)

and write it in the systematic form to obtain public

key.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

378

Theorem 4. If SD problem (Deﬁnition 6 in Sub-

section 2.2) is hard and the public key ma-

trix

H (derived from the public key pk which is

generated by running basicPKE.KeyGen(pp

basicPKE

)

where pp

basicPKE

←− basicPKE.Setup(λ)) is in-

distinguishable, then the public key encryption

scheme basicPKE = (Setup,KeyGen,Enc,Dec) de-

scribed above is IND-CPA secure in the random oracle

model.

4 fullPKE: AN OW-PCVA SECURE

PUBLIC KEY ENCRYPTION

We now discuss a public key encryption fullPKE =

(Setup,KeyGen,Enc, Dec) that is constructed from

the framework of basicPKE.

• fullPKE.Setup(λ) −→ pp

fullPKE

: A trusted author-

ity runs basicPKE.Setup(λ) and sets global pa-

rameters pp

fullPKE

= (k,k

′

,w,q,m, γ,H

) taking se-

curity parameter λ as input.

• fullPKE.KeyGen(pp

fullPKE

) −→ (pk,sk) : A user

generates public-secret key pair (pk, sk) by run-

ning basicPKE.KeyGen(pp

fullPKE

) where pk =

and sk = (z

,. .. ,z

k−1

• fullPKE.Enc(pp

fullPKE

,pk, m; r) −→ CT : An en-

cryptor encrypts a message m ∈ M = (GF(2))

′

using public parameters pp

fullPKE

and its public

key pk as input and produces a ciphertext CT as

follows.

(i) Run Algorithm 1 using m as a seed to obtain an

error vector e of length nm and weight w i.e. e =

G(m). Let r = e = G(m). Compute d = H

(m) ∈

(GF(2))

′

(ii) Use the public key pk =

M to construct the matrix

H = (

M|I

(n−k)m

(iii) Compute c = (c

) = (m ⊕ H

(e),

) ∈

(GF(2))

(n−k)m+k

′

. Here, n = 2k.

(iv) Return the ciphertext CT = (c, d) ∈ C =

(GF(2))

km+2k

′

• fullPKE.Dec(pp

fullPKE

,sk, CT) −→ m

′

: On receiv-

ing the ciphertext CT, the decryptor executes the

following steps using public parameters pp

fullPKE

and its secret key sk = (z

,. .. ,z

k−1

(i) Use the secret key sk = (z

,. .. ,z

k−1

) to form

a parity check matrix H and then ﬁnd error vector

′

of weight w and length nm as in the procedure

basicPKE.Dec.

(ii) Compute m

′

= c

⊕ H

′

) ∈ (GF(2))

′

= H

′

) ∈ (GF(2))

′

and e

′′

= G(m

′

) ∈

(GF(2))

(iii) If (e

′

̸= e

′′

) ∨ (d ̸= d

′

), output ⊥ that indicates

decryption failure. Otherwise, return m

′

Correctness. The decoding algorithm in fullPKE.Dec

uses the parity check matrix H (derived from the

secret key sk) and can correct upto k/2 errors. In

our scheme, the error vector e used in the procedure

fullPKE.Enc satisﬁes wt(e) = w ≤ k/2. Consequently,

the decoding procedure will recover the correct e as

Lemma 3 (iv) holds. We regenerate e

′′

and compare it

with e

′

obtained after decoding. Since the error vector

generation algorithm G uses a deterministic function

to obtain a ﬁxed low weight error vector, e

′

= e

′′

oc-

curs.

Theorem 5. If the public key encryption scheme

basicPKE =(Setup, KeyGen, Enc, Dec) as described

in Section 3 is IND-CPA secure, then the scheme

fullPKE = (Setup,KeyGen,Enc,Dec) as described

above achieves OW-PCVA security considering the

hash function G as a random oracle.

As the OW-PCVA security for an encryption

scheme trivially implies the OW-VA security of the

scheme considering zero queries to the PCO(·,·) or-

acle, we can obtain the following corollary as an im-

mediate consequence.

Corollary 1. If the PKE scheme basicPKE =(Setup,

KeyGen, Enc, Dec) as described in Section 3

is IND-CPA secure, then the scheme fullPKE =

(Setup,KeyGen,Enc, Dec) as described in Section 4

is OW-VA secure considering the hash function G as

a random oracle.

5 fullKEM: AN IND-CCA SECURE

KEY ENCAPSULATION

MECHANISM

We now present the details of our key encapsulation

mechanism fullKEM = (Setup, KeyGen,Encaps,

Decaps).

• fullKEM.Setup(λ)−→ pp

fullKEM

: A trusted au-

thority runs fullPKE.Setup(λ), chooses another

cryptographic hash function H

: {0, 1}

∗

−→

{0,1}

and sets public parameters pp

fullKEM

(k, k

′

,w,r, q,m, γ,H

) taking security parame-

ter λ as input.

• fullKEM.KeyGen(pp

fullKEM

) −→ (pk,sk): A user

generates public-secret key pair (pk, sk) by run-

ning fullPKE.KeyGen(pp

fullKEM

) where pk =

and sk = (z

,. .. ,z

k−1

Code-based Key Encapsulation Mechanism Preserving Short Ciphertext and Secret Key

379

• fullKEM.Encaps(pp

fullKEM

,pk)−→ (CT, K): Given

system parameters pp

fullKEM

and public key pk =

M, an encapsulator proceeds as follows to gener-

ate a ciphertext header CT ∈ (GF(2))

km+2k

′

and an

encapsulation key K ∈ {0,1}

(i) Sample m

←− (GF(2))

′

(ii) Run Algorithm 1 using m as a seed to obtain

an error vector e of length nm and weight w i.e.

e = G(m). Compute d = H

(m) ∈ (GF(2))

′

(iii) Use the public key pk =

M to construct the ma-

trix

H = (

M|I

(n−k)m

(iv) Compute c = (c

) = (m ⊕ H

(e),

) ∈

(GF(2))

(n−k)m+k

′

where n = 2k.

(v) Set the ciphertext header CT = (c, d) ∈ C =

(GF(2))

km+2k

′

and the encapsulation key K =

(m) ∈ {0, 1}

(vi) Publish the ciphertext header CT = (c,d) and

keep K as secret.

• fullKEM.Decaps(pp

fullKEM

,sk,CT)−→ K: On re-

ceiving a ciphertext header CT = (c,d), a decap-

sulator executes the following steps using public

parameters pp

fullKEM

= (k, k

′

,w,r, q,m, γ,H

)

and its secret key sk = (z

,. .. ,z

k−1

(i) Using the secret key sk, form a parity check ma-

trix H and then proceed to ﬁnd error vector e

′

of weight w and length nm as in the procedure

fullPKE.Dec (i.e as in basicPKE.Dec).

(ii) Compute m

′

= c

⊕ H

′

) ∈ (GF(2))

′

= H

′

) ∈ (GF(2))

′

and e

′′

= G(m

′

) ∈

(GF(2))

(iii) If (e

′

̸= e

′′

) ∨ (d ̸= d

′

), output ⊥ indicating de-

capsulation failure. Otherwise, compute the en-

capsulation key K = H

′

Correctness. Correctness of fullKEM follows from

that of fullPKE.

Theorem 6. If the scheme fullPKE = (Setup, KeyGen,

Enc,Dec) as described in Section 4 is OW-

VA secure, then the scheme fullKEM =

(Setup,KeyGen,Encaps, Decaps) as described

above provides IND-CCA security modelling hash

function H

as a random oracle.

Theorem 7. Depending on the hardness of SD prob-

lem (Deﬁnition 6 in Subsection 2.2) and indistin-

guishability of the public key matrix

H that is derived

from the public key pk by running key generation al-

gorithm of fullKEM, the scheme fullKEM described in

Section 5 provides IND-CCA security considering G

and H

as random oracles.

Proof. This is an immediate consequence of The-

orem 4, Corollary 1 and Theorem 6. Due to limited

space, proofs of Theorem 4, Theorem 5 and Theorem

6 will appear in the full version of the paper.

Remark 2. To prove security in quantum random or-

acle model, it is necessary to show post-quantum se-

curity of a scheme where the adversary can submit

queries to the random oracle having quantum access.

In this scenario, the adversary has quantum access to

the random oracles besides having classical access to

some other oracles like plaintext checking oracles, ci-

phertext validity checking oracles, decapsulation or-

acles, etc. The scheme basicPKE provides IND-CPA

security in random oracle model as the SD problem

is hard and the public key matrix is indistinguish-

able (see Theorem 4). Note that IND-CPA security

always implies OW-CPA security. Following the work

of (Hofheinz et al., 2017), we can show that OW-CPA

security of the encryption scheme basicPKE indicates

OW-PCA security of fullPKE considering G as a quan-

tum random oracle. Then, we can prove that OW-PCA

security of fullPKE implies the IND-CCA security of

fullKEM modeling H

as quantum random oracles.

Thus we can get the following theorem.

Theorem 8. Depending on the hardness of SD prob-

lem (Deﬁnition 6 in Subsection 2.2) and indistin-

guishability of the public key matrix

H derived from

the public key pk by running key generation algorithm

of fullKEM, our scheme fullKEM described in Section

5 achieves IND-CCA security considering the hash

functions G,H

and H

as quantum random oracles.

6 CONCLUSION

In this work, we give a proposal to design a key encap-

sulation mechanism exploiting the structure of a com-

panion matrix. We have shown that our KEM proto-

col provides IND-CCA security in the random oracle

model and quantum random oracle model. However,

the issue regarding the public key size needs to be ex-

plored in near future. In terms of secret key size and

ciphertext size, our work seems promising. There-

fore, we believe that our proposal to design a KEM

will offer an attractive approach in the area of code-

based cryptography.

ACKNOWLEDGEMENTS

The authors would like to thank Dr. Ayineedi

Venkateswarlu for his valuable opinions that helped

to improve the manuscript.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

380

REFERENCES

Aguilar-Melchor, C., Blazy, O., Deneuville, J.-C., Gaborit,

P., and Z

emor, G. (2018). Efﬁcient encryption from

random quasi-cyclic codes. IEEE Transactions on In-

formation Theory, 64(5):3927–3943.

Albrecht, M., Cid, C., Paterson, K. G., Tjhai, C. J., and

Tomlinson, M. (2019). Nts-kem. NIST submissions.

Aragon, N., Barreto, P., Bettaieb, S., Bidoux, L., Blazy, O.,

Deneuville, J.-C., Gaborit, P., Gueron, S., Guneysu,

T., Melchor, C. A., et al. (2017a). Bike: Bit ﬂipping

key encapsulation. NIST submissions.

Aragon, N., Barreto, P., Bettaieb, S., Bidoux, L., Blazy, O.,

Deneuville, J.-C., Gaborit, P., Gueron, S., Guneysu,

T., Melchor, C. A., et al. (2019). Bike: Bit ﬂipping

key encapsulation. NIST submissions.

Aragon, N., Blazy, O., Deneuville, J.-C., Gaborit, P.,

Hauteville, A., Ruatta, O., Tillich, J.-P., and Z

emor,

G. (2017b). Lake-low rank parity check codes key ex-

change.

Aragon, N., Blazy, O., Deneuville, J.-C., Gaborit, P.,

Hauteville, A., Ruatta, O., Tillich, J.-P., and Z

emor,

G. (2017c). Locker-low rank parity check codes en-

cryption.

Baldi, M., Barenghi, A., Chiaraluce, F., Pelosi, G., and San-

tini, P. (2018). Ledakem: a post-quantum key encap-

sulation mechanism based on qc-ldpc codes. In Inter-

national Conference on Post-Quantum Cryptography,

pages 3–24. Springer.

Banegas, G., Barreto, P. S., Boidje, B. O., Cayrel, P.-L.,

Dione, G. N., Gaj, K., Gueye, C. T., Haeussler, R.,

Klamti, J. B., N’diaye, O., et al. (2018). Dags: Key

encapsulation using dyadic gs codes. Journal of Math-

ematical Cryptology, 12(4):221–239.

Bardet, M., Barelli, E., Blazy, O., Canto-Torres, R., Cou-

vreur, A., Gaborit, P., Otmani, A., Sendrier, N., and

Tillich, J.-P. (2017). Big quake. NIST submissions.

Barg, A. (1997). Complexity issues in coding theory.

Electronic Colloquium on Computational Complexity

(ECCC), 4(46).

Barreto, P. S., Gueron, S., G

uneysu, T., Misoczki, R., Per-

sichetti, E., Sendrier, N., and Tillich, J.-P. (2017).

Cake: Code-based algorithm for key encapsulation. In

IMA International Conference on Cryptography and

Coding, pages 207–226. Springer.

Bernstein, D. J., Chou, T., Lange, T., von Maurich, I., Mis-

oczki, R., Niederhagen, R., Persichetti, E., Peters,

C., Schwabe, P., Sendrier, N., et al. (2017). Clas-

sic mceliece: conservative code-based cryptography.

NIST submissions.

Biswas, B. and Sendrier, N. (2008). Mceliece cryptosys-

tem implementation: Theory and practice. In Inter-

national Workshop on Post-Quantum Cryptography,

pages 47–62. Springer.

Blaum, M. and Roth, R. M. (1999). On lowest density

mds codes. IEEE Transactions on Information The-

ory, 45(1):46–59.

Dey, J. and Dutta, R. (2019). Secure key encapsulation

mechanism with compact ciphertext and public key

from generalized srivastava code. In International

Conference on Information Security and Cryptology,

pages 175–193. Springer.

Gupta, K. C., Pandey, S. K., and Venkateswarlu, A. (2017a).

On the direct construction of recursive mds matrices.

Designs, Codes and Cryptography, 82(1-2):77–94.

Gupta, K. C., Pandey, S. K., and Venkateswarlu, A. (2017b).

Towards a general construction of recursive mds diffu-

sion layers. Designs, Codes and Cryptography, 82(1-

2):179–195.

Gupta, K. C., Pandey, S. K., and Venkateswarlu, A. (2019).

Almost involutory recursive mds diffusion layers. De-

signs, Codes and Cryptography, 87(2-3):609–626.

Gupta, K. C. and Ray, I. G. (2013). On construc-

tions of mds matrices from companion matrices for

lightweight cryptography. In International Confer-

ence on Availability, Reliability, and Security, pages

29–43. Springer.

Hofheinz, D., H

ovelmanns, K., and Kiltz, E. (2017). A

modular analysis of the fujisaki-okamoto transforma-

tion. In Theory of Cryptography Conference, pages

341–371. Springer.

Kesarwani, A., Sarkar, S., and Venkateswarlu, A. (2019).

Exhaustive search for various types of mds matrices.

IACR Transactions on Symmetric Cryptology, pages

231–256.

Khathuria, K., Rosenthal, J., and Weger, V. (2019). Encryp-

tion scheme based on expanded reed-solomon codes.

arXiv preprint arXiv:1906.00745.

Kim, J.-L., Kim, Y.-S., Galvez, L., Kim, M. J., and Lee, N.

(2018). Mcnie: A code-based public-key cryptosys-

tem. arXiv preprint arXiv:1812.05008.

MacWilliams, F. J. and Sloane, N. J. A. (1977). The theory

of error-correcting codes, volume 16. Elsevier.

McEliece, R. J. (1978). A public-key cryptosystem based

on algebraic coding theory. Coding Thv, 4244:114–

116.

Melchor, C. A., Aragon, N., Bardet, M., Bettaieb, S.,

Bidoux, L., Blazy, O., and Deneuville, J.-C. (2019).

Rollo-rank-ouroboros, lake & locker.

Melchor, C. A., Aragon, N., Bettaieb, S., Bidoux, L.,

Blazy, O., Deneuville, J.-C., Gaborit, P., Hauteville,

A., Z

emor, G., and Bourges, I.-C. (2017). Ouroboros-

Nojima, R., Imai, H., Kobara, K., and Morozov, K. (2008).

Semantic security for the mceliece cryptosystem with-

out random oracles. Designs, Codes and Cryptogra-

phy, 49(1-3):289–305.

Strenzke, F. (2010). A timing attack against the secret per-

mutation in the mceliece pkc. In International Work-

shop on Post-Quantum Cryptography, pages 95–107.

Springer.

Szepieniec, A. (2017). Ramstake. Technical report, Tech-

nical report, National Institute of Standards and Tech-

nology.

Wang, Y. (2017). Rlcekey encapsulation mechanism (rlce-

kem) specifcation. NIST Submission.

Yamada, A., Eaton, E., Kalach, K., Lafrance, P., and Par-

ent, A. (2017). Qc-mdpc kem: A key encapsulation

mechanism based on the qc-mdpc mceliece encryp-

tion scheme. NIST Submission.

Code-based Key Encapsulation Mechanism Preserving Short Ciphertext and Secret Key

381