Generalized Mutant Subsumption

Samia Al Blwi

, Imen Marsit

, Besma Khaireddine

, Amani Ayad

, JiMeng Loh

and Ali Mili

NJIT, Newark, NJ, U.S.A.

University of Sousse, Sousse, Tunisia

University of Tunis El Manar, Tunis, Tunisia

Kean University, Union, NJ, U.S.A.

mili@njit.edu

Keywords:

Mutation Testing, Mutant Subsumption, Differentiator Sets.

Abstract:

Mutant Subsumption is an ordering relation between the mutants of a base program, which ranks mutants

according to inclusion relationships between their differentiator sets. The differentiator set of a mutant with

respect to a base program is the set of inputs for which execution of the base program and the mutant produce

different outcomes. In this paper we propose to reﬁne the deﬁnition of mutant subsumption by pondering, in

turn: what do we consider to be the outcome of a program’s execution? under what condition do we consider

that two outcomes are comparable? and under what condition do we consider that two comparable outcomes

are identical? We ﬁnd that the way we answer these questions determines what it means to kill a mutant, how

subsumption is deﬁned, how mutants are ordered by subsumption, and what set of mutants is minimal.

1 INTRODUCTION

1.1 Program Executions and Outcomes

The mutants of a program are generated by applying

localized syntactic alterations to the source code of a

program, and are typically used to assess the quality

of test suites: a good test suite is one that yields dif-

ferent outcomes (from the base program) for all the

mutants that are not semantically equivalent to the

program. Mutation testing is a reliable way to as-

sess the effectiveness of test suites, but it is also an

expensive proposition. As a consequence, it is sen-

sible to try to reduce the size of mutant sets, without

loss of effectiveness. In (Marsit et al., 2021), Mar-

sit et al. propose an algorithm to reduce the size of a

set of mutants by partitionning the set of mutants into

equivalence classes, modulo semantic equivalence,

and retaining one mutant from each equivalence class.

While this criterion is non-controversial (two seman-

tically equivalent mutants are as good as just one), it

may be sub-optimal: In (Guimaraes et al., 2020; Par-

sai and Demeyer, 2017; Souza, 2020; Li et al., 2017;

Jia and Harman, 2008; Kurtz et al., 2014; Kurtz et al.,

2015; Tenorio et al., 2019), a more sophisticated cri-

https://orcid.org/0000-0002-6578-5510

terion is used: a partial ordering is deﬁned between

mutants of a given base program P, whereby a mutant

M is said to subsume a mutant M

′

if and only if M

produces a different outcome from P for at least one

input, and any input for which M produces a different

outcome from P, M

′

produces necessarily a different

outcome from P.

The original deﬁnition of mutant subsumption

(Kurtz et al., 2014) refers to program outcomes be-

ing identical or distinct, but does not dwell on what

exactly is the outcome of a program and when can

we consider that two program outcomes are identical.

In this paper we propose to generalize the concept of

subsumption by seeking to ponder the following ques-

tions:

• What Is the Outcome of a Program? Programs

and mutants do not always terminate normally and

produce a well-deﬁned/ agreed upon outcome.

Programs may fail to terminate (if they enter an

inﬁnite loop, and eventually time out), or they

may encounter an exceptional condition, such as

an array reference out of bounds, a reference to

a nil pointer, a division by zero, an undeﬁned ex-

pression (e.g. the logarithm of a negative num-

ber), an overﬂow, an underﬂow, etc. In fact many

mutation operators are prone to create the condi-

tions of divergence even when the original pro-

Al Blwi, S., Marsit, I., Khaireddine, B., Ayad, A., Loh, J. and Mili, A.

Generalized Mutant Subsumption.

DOI: 10.5220/0011166700003266

In Proceedings of the 17th International Conference on Software Technologies (ICSOFT 2022), pages 46-56

ISBN: 978-989-758-588-3; ISSN: 2184-2833

gram terminates normally. The question that we

must ponder is: when a program fails to converge,

do we consider that it has no outcome, or that fail-

ure to converge is itself an outcome.

Also, even when a program does terminate nor-

mally, it is not always clear what we consider to

be its outcome: is it its ﬁnal state or the output

that the program delivers as a projection of the

ﬁnal state? For example, if a program permutes

two variables x and y using an auxiliary variable

z, what is the outcome of the program? is it the

ﬁnal values of x, y and z, or just the ﬁnal values of

x and y? This can get more complicated/ ambigu-

ous when we consider global variables, parame-

ter passing, communication channels, operations

with side effects, etc.

• Under what condition do we consider that the

Outcomes of Two Programs Are Comparable?

When the execution of a program on some input

terminates after a ﬁnite number of steps without

causing any exception, such as an array reference

out of bounds, a reference to a nil pointer, a run-

time stack overﬂow, or an illegal operation (such

as a square root of a negative number, the log of

zero or a negative number, a division by zero, an

arithmetic overﬂow, etc) we say that the execu-

tion converges (or: terminates normally); else we

say that the execution diverges. When two pro-

grams converge, comparing their outcomes poses

no problem; but we must decide whether their out-

comes are comparbale when one of them or both

of them diverge.

• When Do We Consider That Two Program Out-

comes Are Identical or Distinct? If we consider

that the outcome of a program that converges and

the outcome of a program that diverges are com-

parable, then it is sensible to consider that their

outcomes are distinct. But if two programs di-

verge for a given input, do we consider that their

outcomes are incomparable, or that they are com-

parable and identical? What if the divergence is of

the same type (e.g. both fail to terminate, or both

attempt a division by zero, etc)? What if both fails

at the same statement of the source code?

In this paper we argue that the deﬁnition of subsump-

tion depends critically on how we answer these three

questions. Speciﬁcally, we present three possible def-

initions of subsumption, which correspond to differ-

ent interpretations of program outcomes and how to

compare them. Then we show on a concrete exam-

ple how these yield different ordering relations on the

mutants of a base program, and different minimal mu-

tant sets. It appears that the original deﬁnition of mu-

tant subsumption (Kurtz et al., 2014) makes no provi-

sion for the possibility of divergence, hence assumes

implicitly that programs and mutants converge for all

inputs; it also seems to assume that the outcome of

a program that converges is well-understood, hence

requires no careful consideration.

1.2 Motivation

While the discussion of what is a program outcome

and when two program outcomes are considered iden-

tical may sound like an academic exercise in hair-

splitting, we argue that it is fact an important con-

sideration in mutation testing, because many muta-

tion operators are prone to cause programs to diverge,

even when the base program converges:

• if we consider a loop that addresses an array at

indices 0 through N − 1

while (i<N)

{

a[i]=..;...;i++;

}

and the logical operator

is changed to

then

the resulting mutant will diverge due to an array

index out of bound.

• If we consider a guarded assignment statement

such as:

if ((x!=0) && (x!=1))

{

y=1/x(x-1);

}

and the

is replaced by a logical OR

, then

the resulting mutant will diverge for x = 0 and for

x = 1, due to a division by zero.

• If we consider a loop that decrements an integer

variable by 2 at each iteration while the variable

is positive,

x=5; while (x>0)

{

x=x-2;..;

}

and we change the comparison operator

then (if the initial value is odd) the resulting mu-

tant will diverge due to an inﬁnite loop.

In theory, we should also consider cases where the

base program itself may fail to converge for some test

data; of course one may wonder why we would test

a program outside its domain, but it is the domain of

the speciﬁcation, not the domain of the program, that

determines what test data to run.

1.3 Agenda

To discuss these questions, we need to introduce a

framework for deﬁning and analyzing program func-

tions; this is the subject of section 2. In section 3

we introduce the concept of differentiator set, which

serves as a basis for redeﬁning subsumption, and in

section 4 we present three distinct deﬁnitions of sub-

sumption. In section 5 we consider a benchmark pro-

gram, generate its mutants, then we analyze subsump-

tion relationships between these mutants, using the

Generalized Mutant Subsumption

three deﬁnitions introduced in section 4; we show that

(not surprisingly) these three deﬁnitions give three

distinct subsumption graphs, and three distinct min-

imal mutant sets. In section 6 we summarize our ﬁnd-

ings and suggest venues for further investigation.

2 MATHEMATICS FOR

PROGRAM ANALYSIS

2.1 Sets and Relations

In this paper, we use relations and functions (Brink

et al., 1997; Schmidt, 2010) to capture program spec-

iﬁcations and program semantics. For the sake of sim-

plicity, and without loss of generality, we consider ho-

mogeneous relations on sets represented by program-

like declarations. Modeling the program behavior by

homogeneous relations encompasses the case where

we want to model it by a relation from inputs to out-

puts: it sufﬁces to add an input stream and an output

stream as state variables. We generally denote sets

(referred to as spaces) by S, elements of S (referred to

as states) by lower case s, speciﬁcations (binary rela-

tions on S) by R and programs (functions on S) by P,

Q. We denote the domain of a relation R (or a func-

tion P) by dom(R) (dom(P)). Because we model pro-

grams and speciﬁcations by homogeneous relations /

functions, we usually talk about initial states and ﬁnal

states; we may talk about inputs to refer to the initial

value of the input stream and outputs to refer to the

ﬁnal value of the output stream.

2.2 Programs and Speciﬁcations

A speciﬁcation R includes all the initial state / ﬁnal

state pairs that the speciﬁer considers correct; hence

the domain of a speciﬁcation R (dom(R)) includes all

the initial states for which candidate programs must

make provisions. A program P includes all the ini-

tial state/ ﬁnal state pairs (s, s

′

) such that if P starts

execution in initial state s it terminates normally (i.e.

after a ﬁnite number of steps, without raising an ex-

ception) in state s

′

. From this deﬁnition, it stems that

the domain of program P (dom(P)) is the set of initial

states s such that execution of P on s terminates after

a ﬁnite number of steps, and does not raise an excep-

tion (such as an overﬂow, underﬂow, division by zero,

array reference out of bounds, etc).

For the sake of simplicity, we restrict our study

to deterministic programs, i.e. programs which map

each initial state to at most one ﬁnal state. It would be

interesting to include non-deterministic programs (in-

cluding concurrent programs), but this would compli-

cate our model, and introduce other mutation-speciﬁc

difﬁculties (Vercammen et al., 2021).

2.3 Absolute Correctness

We consider a program P on space S and a speciﬁca-

tion R on S; without loss of generality, we model the

semantics of a program by the (homogeneous) rela-

tion that the program deﬁnes from its initial states to

its ﬁnal states.

Deﬁnition 1. We say that a program P on space S is

correct with respect to speciﬁcation R on S if and only

if:

dom(R) = dom(R∩ P).

Intuitively, a program P is correct with respect to

a speciﬁcation R if and only if for all s in dom(R), ex-

ecution of P on s converges and produces a ﬁnal state

that satisﬁes the condition (s, P(s)) ∈ R. The domain

of the intersection of R and P represents the set of

initial states for which program P behaves as R man-

dates; it is called the competence domain of P with

respect to R. Figure 1 shows a simple example of a

(non-deterministic) speciﬁcation R and two programs

P and P

′

such that P is correct with respect to R and P

′

is not; the competence domains of P and P

′

are shown

by the ovals.

Deﬁnition 2. We say that a program P on space S is

partially correct with respect to speciﬁcation R on S if

and only if:

dom(R) ∩ dom(P) = dom(R∩ P).

Intuitively, a program P is partially correct with

respect to a speciﬁcation R if and only if for all s

in dom(R), if execution of P on s converges then

it produces a ﬁnal state that satisﬁes the condition

(s, P(s)) ∈ R. When we want to contrast correct-

ness with partial correctness, we may refer to the for-

mer as total correctness. Our deﬁnitions of total and

partial correctness are equivalent, modulo differences

of notation, to traditional deﬁnitions with respect to

pre/post speciﬁcations (Hoare, 1969; Gries, 1981; Di-

jkstra, 1976; Manna, 1974). See Figure 2: Program Q

is partially correct with respect to R because for any

initial state of dom(R) for which it terminates, pro-

gram Q delivers a ﬁnal state that satisﬁes speciﬁca-

tion R; by contrast, program Q

′

is not partially correct

with respect to R, even though it terminates normally

for all initial states in dom(R), because it does not sat-

isfy speciﬁcation R; neither Q nor Q

′

is totally correct

with respect to R. We admit without proof that if P is

totally correct with respect to R then it is necessarily

partially correct with respect to R.

ICSOFT 2022 - 17th International Conference on Software Technologies

✘

✘✿

❳

❳③

✲

✘

✘✿

❳

❳③

✲

❳

❳③

❳

❳③

❳

❳③

✲

✘

✘✿

✟

✟✯

✚

✚❃

✄

✂



✁

✄

✂



✁

P R

′

dom(R ∩ P) = {1, 2}

= dom(R) ⇒ P correct

dom(R∩ P

′

) = {1}

6= dom(R) ⇒ P

′

incorrect

Figure 1: Total Correctness.

✘

✘✿

❳

❳③

✲

✘

✘✿

❳

❳③

✲

✘

✘✿

✘

✘✿

❍

❍❥

✟

✟✯

✄

✂



✁

′

dom(R∩ Q) = {1}

= dom(R) ∩ dom(Q)

⇒ Q part. correct

dom(R∩ Q

′

) = {}

6= dom(R) ∩ dom(Q

′

)

⇒ Q

′

not part. correct

Figure 2: Partial Correctness.

2.4 Relative Correctness

Whereas total correctness and partial correctness de-

ﬁne a property between a program and a speciﬁca-

tion, relative correctness deﬁnes a property between

two programs and a speciﬁcation.

Deﬁnition 3. Given a speciﬁcation R on space S and

two programs P and P

′

on S, we say that P

′

is more-

correct than P with respect to R (denoted by: P

′

⊒

or P ⊑

′

) if and only if:

dom(R∩ P) ⊆ dom(R∩ P

′

In other words, P

′

is more-correct than P with re-

spect to R if and only if it has a larger competence

domain with respect to R. Whenever we want to con-

trast correctness (deﬁnition 1) with relative correct-

ness, we may refer to the former as absolute correct-

ness. See Figure 3; it shows two instances of relative

correctness. Q

′

is more-correct than Q by virtue of

imitating the correct behavior of Q; by contrast, P

′

more-correct than P by virtue of a differentcorrect be-

havior; because speciﬁcation R is non-deterministic,

correct behavior is not unique.

3 DIFFERENTIATOR SETS

In section 1, we had argued that while the deﬁnitions

of mutant subsumption refer to program outcomes

and to the condition under which two program out-

comes are identical, they are not perfectly clear about

what constitutes the outcome of a program, when

two program outcomes are comparable, and if they

are when can we consider them to be identical. In

this section, we address this ambiguity by introducing

several deﬁnitions of differentiator sets, which reﬂect

different interpretations to the questions above.

Given two programs, say P and Q, the differentia-

tor set of P and Q is the set of initial states for which

execution of P and Q yield different outcomes. For

the purposes of this paper, we adopt the three deﬁni-

tions of differentiator sets proposed by Mili in (Mili,

2021):

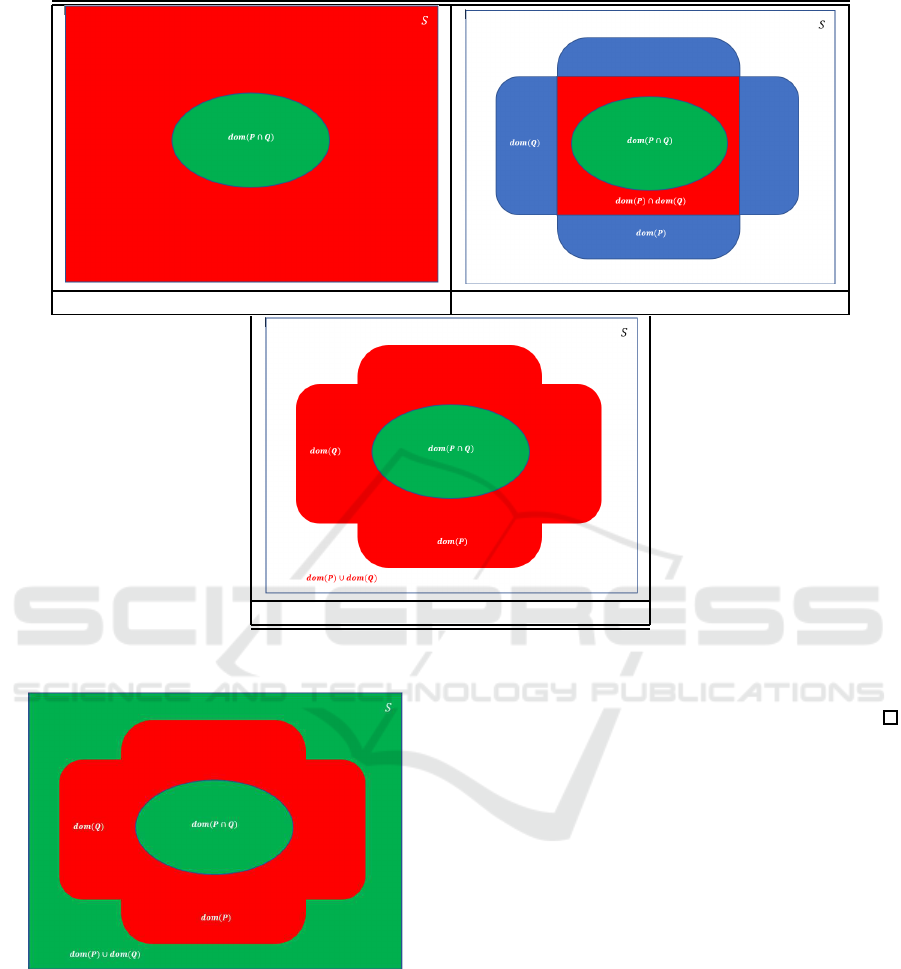
• Basic Differentiator Set. The basic differentiator

set of two programs P and Q on space S is deﬁned

only if P and Q converge for all s in S; it is the

set of states s such that P(s) 6= Q(s). This set is

denoted by δ

(P, Q) and deﬁned by:

(P, Q) =

dom(P∩ Q).

• Strict Differentiator Set. The strict differentiator

set of two programs P and Q on space S is de-

ﬁned regardless of whether P and Q converge for

all initial states. It includes all the states for which

executions of P and Q both converge and yield

distinct outcomes. This set is denoted by δ

(P, Q)

and deﬁned by:

(P, Q) = dom(P) ∩ dom(Q)∩

dom(P∩ Q).

• Loose Differentiator Set. The loose differentiator

set of two programs P and Q on space S is de-

ﬁned regardless of whether P and Q converge for

all initial states. It includes all the states for which

executions of P and Q both converge and yield

distinct outcomes, as well as the states for which

only one of the programs converges and the other

diverges. This set is denoted by δ

(P, Q) and de-

ﬁned by:

(P, Q) = (dom(P) ∪ dom(Q)) ∩

dom(P∩ Q).

Generalized Mutant Subsumption

✲

✲✘

✘

✘✿

✘

✘✿

❳

❳③✘

✘

✘✿

❳

❳③

❳

❳③

❳

❳③

❳

❳③

❳

❳③

❳

❳③

❳

❳③

✲

❳

❳③

❳

❳③

✘

✘✿

✘

✘✿

✘

✘✿

′

R P

′

✞

✝

☎

✆

✞

✝

☎

✆

✞

✝

☎

✆

✞

✝

☎

✆

Preserving Correct Behavior

((R∩ Q) ⊆ (R∩ Q

′

))

Preserving Correctness

((R∩ P)L ⊆ (R∩ P

′

)L)

Figure 3: Relative Correctness: (Q

′

⊒

Q), (P

′

⊒

P).

Figure 4 illustrates the three deﬁnitions of differentia-

tor sets (represented in red in each case). To gain an

intuitive understanding of these deﬁnitions, it sufﬁces

to note the following details:

• The domain of program P (dom(P)) is the set of

initial states on which execution of P converges

(i.e. terminates normally after a ﬁnite number of

steps without raising any exception or attempt-

ing any illegal operation). We assume that when

a program enters an inﬁnite loop, it gets timed

out by the run-time environment, so that non-

termination is an observable outcome.

• The domain of (P ∩ Q) is the set of inputs for

which programs P and Q converge and return the

same outcome.

• The complement of the domain of (P∩ Q) is the

set of inputs for which program P and Q converge

and return distinct outcomes. In other words,

dom(P∩ P) = {s : P(s) 6= Q(s)}.

A possible fourth interpretation is to consider that

when two programs diverge, they have the same out-

come; we illustrate this situation in Figure 5, to high-

light its contrast with the situations represented in

Figure 4. Notice that it has the same differentiator

set as δ

, but differs from it in the way it interprets si-

multaneous divergence: whereas δ

considers that in

the case of simultaneous divergencewe cannot decide

whether the outcomes are identical, the interpretation

of Figure 5 considers that simultaneous divergence is

a case of identical outcome. Because this interpreta-

tion is controversial (and perhaps of limited interest),

we do not consider it further in this paper.

Given that differentiator sets reﬂect the extent of

behavior differencebetween two programs, we expect

that when a differentiator set is empty, the programs

have some measure of identity/ similarity. This is dis-

cussed in the following Propositions; ﬁrst, we brieﬂy

introduce a lemma from relational algebra (Brink

et al., 1997; Schmidt, 2010).

Lemma 1. If two functions F and G satisfy the con-

ditions F ⊆ G and dom(G) ⊆ dom(F) then F = G.

Proposition 1. Given two programs P and Q on

space S such that dom(P) = S and dom(Q) = S. The

basic differentiator set of P and Q is empty if and only

if P = Q.

Proof. The proof of sufﬁciency is trivial.

Proof of necessity: If δ

(P, Q) =

0 then dom(P ∩

Q) = S. By hypothesis, dom(P) = S. By set theory,

we have (P∩ Q) ⊆ P. By the lemma above, we infer

(P ∩ Q) = P, whence by set theory we infer P ⊆ Q.

By permuting P and Q in the argument above, we ﬁnd

Q ⊆ P.

For the sake of convenience, we often equate a

program with its function; this may give rise to some

odd-sounding statements such as the claim that some

program is correct with respect to another. When we

say that program P is correct with respect to program

Q, we really mean that P, as a program written in

some programming language, is correct with respect

to the function of program Q, which we interpret as

a speciﬁcation on space S. With this qualiﬁcation in

mind, we proceed with the next propositions linking

differentiator sets with properties of correctness.

Proposition 2. Given two programs P and Q on

space S, the strict differentiator set of P and Q is

empty if and only if program P is partially correct

with respect to the function of program Q (interpreted

as a speciﬁcation).

Proof. The proof of sufﬁciency stems readily from

the deﬁnition of partial correctness (Deﬁnition 2) and

the deﬁnition of strict differentiator sets.

Proof of Necessity. From δ

(P, Q) =

0 we in-

fer dom(P) ∩ dom(Q) ⊆ dom(P ∩ Q). By set theory

(and monotonicity of the dom()) we infer dom(P ∩

Q) ⊆ dom(P) and dom(P ∩ Q) ⊆ dom(Q), whence

dom(P ∩ Q) ⊆ dom(P) ∩ dom(Q). From dom(P ∩

Q) = dom(P) ∩ dom(Q) we infer that P is partially

correct with respect to the function of Q.

Proposition 3. Given two programs P and Q on

space S, the loose differentiator set of P and Q is

empty if and only if program P is totally correct with

ICSOFT 2022 - 17th International Conference on Software Technologies

(P, Q) δ

(P, Q)

Figure 4: Three Deﬁnitions of Differentiator Sets.

Figure 5: Fourth Interpretation of Identical Outcome.

respect to the function of program Q (interpreted as a

speciﬁcation).

Proof. The proof of sufﬁciency stems readily from

the deﬁnition of total correctness (Deﬁnition 1) and

the deﬁnition of loose differentiator sets.

Proof of Necessity. From δ

(P, Q) =

0 we infer

dom(P)∪ dom(Q) ⊆ dom(P∩ Q). From which we in-

fer, a fortiori: dom(P) ⊆ dom(P ∩ Q). The reverse

incluse is a tautology. From Deﬁnition 1 we infer that

P is totally correct with respect to the function of Q.

In Propositions 2 and 3, the roles of P and Q can

be permuted: each is (partially/ totally) correct with

respect to the function of the other; in the context of

mutation testing, we use these propositions asymmet-

rically,

4 MUTANT SUBSUMPTION

In (Kurtz et al., 2014; Kurtz et al., 2015), Kurtz et al

deﬁne the concept of true subsumption as follows:

Deﬁnition 4. Given a program P on S and two mu-

tants M and M

′

, we say that M subsumes M

′

with

respect to P if and only if:

P1 There exists an initial state s for which P and M

produce different outcomes.

P2 For all s in S such that P and M produce different

outcomes, so do P and M

′

Since this deﬁnition makes no mention of P, M

or M

′

failing to converge, we assume that P, M and

Generalized Mutant Subsumption

′

are considered to converge for all initial states.

The following Proposition formulates subsumption

by means of basic differentiator sets.

Proposition 4. Given a program P on space S and

two mutants M and M

′

of P, M subsumes M

′

if and

only if:

0 ⊂ δ

(P, M) ⊆ δ

(P, M

′

Proof. We consider the ﬁrst condition

0 ⊂ δ

(P, M)

⇔ {deﬁnition of δ

(P, M)}

∃s : s ∈

dom(P∩ Q)

⇔ {interpreting the complement}

∃s : ¬(s ∈ dom(P∩ Q))

⇔ {interpreting dom(P∩ Q)}

∃s : ¬(P(s) = Q(s)))

⇔ {deﬁnition 4}

Condition P1.

As for the second conditions,

(P, M) ⊆ δ

(P, M

′

)

⇔ {deﬁnition of δ

(, )}

∀s : s ∈

dom(P∩ M) ⇒ s ∈ dom(P∩ M

′

)

⇔ {interpreting the complement}

∀s : ¬(s ∈ dom(P∩ M)) ⇒ ¬(s ∈ dom(P∩ M

′

))

⇔ {interpreting the domain}

∀s : ¬(P(s) = M(s)) ⇒ ¬(P(s) = M

′

(s))

⇔ {deﬁnition 4}

Condition P2.

The following Proposition reformulates subsump-

tion by means of relative correctness.

Proposition 5. Given a program P on space S and

two mutants M and M

′

of P, M subsumes M

′

if and

only if M is not equivalent to P and it is more-correct

than M

′

with respect to (the function of) P.

Proof. According to Proposition 1, condition P1 is

equivalent to: P and M are not equivalent.

On the other hand, we have shown above that con-

dition P2 is equivalent to:

(P, M) ⊆ δ

(P, M

′

)

⇔ {deﬁnition of δ

(, )}

∀s : s ∈

dom(P∩ M) ⇒ s ∈ dom(P∩ M

′

)

⇔ {Boolean identity}

∀s : s ∈ dom(P∩ M

′

) ⇒ s ∈ dom(P∩ M)

⇔ {set theory}

dom(P∩ M

′

) ⊆ dom(P∩ M)

⇔ {Deﬁnition 3}

M ⊒

′

Proposition 4 provides an alternative formula to

deﬁne mutant subsumption in the case where we as-

sume that all programs and mutants terminate for all

initial states. This Proposition is formulated in terms

of basic differentiator sets, which are deﬁned when

the program and its mutants are assumed to converge

for all initial states; but in section 3, we have in-

troduced two more deﬁnitions of differentiator sets,

which do not assume universal convergence of pro-

grams and mutants, and take a liberal interpretation

of program outcomes and when to consider outcomes

as identical or distinct. The following deﬁnitions gen-

eralize the concept of subsumption to the case when

programs and their mutants do not necessarily con-

verge for all initial states.

Deﬁnition 5. Strict Subsumption. Given a program

P on space S and two mutants M and M

′

of P, we say

that M strictly subsumes M

′

if and only if:

0 ⊂ δ

(P, M) ⊆ δ

(P, M

′

Deﬁnition 6. Loose Subsumption. Given a program

P on space S and two mutants M and M

′

of P, we say

that M loosely subsumes M

′

if and only if:

0 ⊂ δ

(P, M) ⊆ δ

(P, M

′

In the next section,we will see that the distinction

between the basic deﬁnition of subsumption (Deﬁni-

tion 4, (Kurtz et al., 2014; Kurtz et al., 2015)), strict

subsumption, and loose subsumption is not a mere

academic exercise. These deﬁnitions yield vastly dif-

ferent subsumption graphs.

5 ILLUSTRATION

We consider the Java benchmark pro-

gram of jTerminal (available online at

http://www.grahamedgecombe.com /projects /jtermi-

nal), an open-source software product routinely used

in mutation testing experiments (Parsai and Demeyer,

2017). We apply the mutant generation tool Lit-

tleDarwin in conjunction with a test generation and

deployment class that includes 35 test cases (Parsai

and Demeyer, 2017); we augmented the benchmark

test suite with two additional tests, intended speciﬁ-

cally to trip the base program jTerminal, by causing

to diverge. We let T designate the test augmented

test suite codiﬁed in this test class; all our analysis

of mutant equivalence, mutant redundancy, mutant

survival, etc is based on the outcomes of programs

and mutants on this test suite (and carefully selected

subsets thereof). Execution of LittleDarwin on

jTerminal yields 94 mutants, numbered m1 to m94;

the test of these mutants against the original using

the selected test suite kills 48 mutants; for the sake of

documentation, we list them below:

m1, m2, m7, m8, m9, m10, m11, m12, m13,

ICSOFT 2022 - 17th International Conference on Software Technologies

m14, m15, m16, m17, m18, m19, m21, m22,

m23, m24, m25, m26, m27, m28, m44, m45,

m46, m48, m49, m50, m51, m52, m53, m54,

m55, m56, m57, m58, m59, m60, m61, m62,

m63, m83, m88, m89, m90, m92, m93.

The remaining 46 mutants are semantically equiva-

lent to the pre-restriction of jTerminal to T. The ﬁrst

order of business is to partition these 48 mutants into

equivalence classes modulo semantic equivalence;

we ﬁnd that these 48 mutants are partitioned into 31

equivalence classes, and we select a member from

each class; we let µ be the set of selected mutants:

µ =

m1, m2, m7, m11, m13, m15, m19, m21, m22,

m23, m24, m25, m27, m28, m44, m45, m46, m48,

m49, m50, m51, m52, m53, m55, m56, m57, m60,

m63, m92, m93

We resolve to draw the subsumption graphs of

these mutants according to the three deﬁnitions:

• Basic/ True Subsumption:

0 ⊂ δ

( jTerminal, M) ⊆ δ

( jTerminal, M

′

• Strict Subsumption:

0 ⊂ δ

( jTerminal, M) ⊆ δ

( jTerminal, M

′

• Loose Subsumption:

0 ⊂ δ

( jTerminal, M) ⊆ δ

( jTerminal, M

′

To this effect, we must compute the differ-

entiator sets δ

( jTerminal, M), δ

( jTerminal, M),

( jTerminal, M) for all 31 mutants selected above,

with respect to jTerminal. For the sake of illustration,

we show in Table 1 the output ﬁle of the base program

jTerminal, as well as that of mutant M22; the number

at the start of each line identiﬁes the input. Using this

table, we can derive the differentiator set of M22 with

respect to jTerminal; this is shown in Table 2, under

all. three interpretations (basic, strict, loose) of dif-

ferentiator sets; these sets can be inferred from the

deﬁnitions, by analyzing the output ﬁles of the base

program and the mutant. The ﬁrst observation that we

can make about these output ﬁles is that divergence,

far from being an exceptional circumstance, is in fact

a very frequent occurrence; notwithstanding the two

instances of divergence that we have triggered on pur-

pose at lines 9 and 10, mutant M22 fails to converge

for several other inputs, which are part of the original

benchmark test suite.

Note that this experiment is artiﬁcial in the sense

that whereas the strict and loose deﬁnitions of differ-

entiator sets can be applied to the same combination

of program and test suite, the basic deﬁnition can only

be applied when we know, or assume, that the base

program and all the mutants converge for all the ele-

ments of the test suite. In the case of jTerminal and its

mutants, this assumption does not hold, as virtually

all of them fail to converge on at least some elements

of T. We obviate this difﬁculty by considering that

divergence is itself an execution outcome, but this is

merely a convenient assumption for the sake of the

experiment.

By computing the basic, strict and loose differen-

tiator sets of all the mutants with respect to jTermi-

nal and comparing them for inclusion, we derive the

subsumption relations between the mutants, which we

can represent by graphs; these graphs are given in, re-

spectively, Figures 6, 7 and 8. Nodes in these graphs

represent mutants and arrows represent subsumption

relations: whenever there is an arrow from mutant M

to mutant M

′

, it means that M subsumes M

′

(hence

′

can be eliminated from the mutant set without

affecting its effectiveness). When two mutants sub-

sumes each other (for example M27 and M28 in 7),

this means that though these mutants are distinct from

each other (they compute functions functions), they

have the same differentiator set with respect to jTer-

minal.

From these graphs, we derive minimal mutant sets

by selecting the maximal nodes in the subsumption

ordering. Once we have the minimal mutant sets, we

derive minimal test suites that kill all the mutants in

these sets. We verify, in each case, that the test suites

that kills all the mutants of the minimal mutant sets

actually kill all the 48 non-equivalent mutants derived

in our experiment; this comes as no surprise, since

this precisely the rationale for deleting subsumed mu-

tants.

For strict subsumption, for example, we ﬁnd the

following minimal mutant set:

m22, m23, m27, m28, m44, m45, m48, m50,

m51, m54, m56, m61, m83, m92, m93

Using this mutant set, we derive minimal test suites

that kill all these mutants; we ﬁnd 6 minimal test

suites, of size 7:

Suite 1:

{

t7,t16,t18,t20,t21,t22,t25

}

Suite 2:

{

t7,t16,t18,t20,t21,t22,t26

}

Suite 3:

{

t16,t18,t20,t21,t22,t23,t25

}

Suite 4:

{

t16,t18,t20,t21,t22,t25,t27

}

Suite 5:

{

t16,t18,t20,t21,t22,t23,t26

}

Suite 6:

{

t16,t18,t20,t21,t22,t26,t27

}

By virtue of subsumption, these test suites kill all 31

mutants selected above; by virtue of equivalence, they

necessarily kill all 48 killable mutants of jTerminal.

Using the basic interpretation of subsumption, we

ﬁnd 96 minimal test suites, all of them of size 12; for

the loose interpretation of subsumption, we ﬁnd 48

minimal test suites, all of them of size 11. Due to

Generalized Mutant Subsumption

Table 1: Outputs of jTerminal and Mutants.

t3, null

t4, c

t5, c

t6, a

t7, null

t8, B

t1, h

t23, com.grahamedgecombe.jterminal.TerminalCell@47089e5f

t24, X

t25, java.awt.Color[r=255,g=0,b=0]

t26, java.awt.Color[r=255,g=255,b=0]

t27, com.grahamedgecombe.jterminal.TerminalCell@4141d797

t28, X

t29, java.awt.Color[r=0,g=0,b=0]

t30, java.awt.Color[r=192,g=192,b=192]

t33, H

t34, i

t35, null

t36, 1

t37, 3

t2, h

t9, java.lang.IndexOutOfBoundsException

t10, java.lang.IndexOutOfBoundsException

t31, 3

t32, 17

t11, A

t12, null

t13, 5

t14, 2

t15, 7

t16, 3

t17, 0

t18, 3

t19, 0

t20, 2

t21, 3

t22, 7

t3, null

t4, java.lang.NullPointerException

t5, java.lang.NullPointerException

t6, java.lang.NullPointerException

t7, com.grahamedgecombe.jterminal.TerminalCell@5f8ed237

t8, java.lang.NullPointerException

t1, h

t23, null

t24, java.lang.NullPointerException

t25, java.lang.NullPointerException

t26, java.lang.NullPointerException

t27, null

t28, java.lang.NullPointerException

t29, java.lang.NullPointerException

t30, java.lang.NullPointerException

t33, java.lang.NullPointerException

t34, java.lang.NullPointerException

t35, java.lang.NullPointerException

t36, 1

t37, 3

t2, h

t9, java.lang.ArrayIndexOutOfBoundsException

t10, java.lang.ArrayIndexOutOfBoundsException

t31, 3

t32, 17

t11, java.lang.ArrayIndexOutOfBoundsException

t12, java.lang.ArrayIndexOutOfBoundsException

t13, 5

t14, 2

t15, 7

t16, 3

t17, 0

t18, 3

t19, 0

t20, 2

t21, 3

t22, 7

Output of Base Program, jTerminal Output File, mutant M22

Table 2: Differentiator Sets of Mutant M22.

Mutant δ

M22

{t4, t5, t6, t7, t8, t23, t24, t25, t26, t27,

t28, t29, t30, t33, t34, t35, t11, t12}

{t23, t27}

{t4, t5, t6, t7, t8, t23, t24, t25, t26, t27,

t28, t29, t30, t33, t34, t35, t11, t12}

space limitations, we do not include these test suites.

Sufﬁce it to say that their number and their size are

vastly different from those found under the strict in-

terpretation.

6 CONCLUSION

In this paper, we seek to generalize the concept of mu-

tant subsumption by analyzing what can be consid-

ered as the outcome of a program, when two program

outcomes can be compared, and under what condition

two comparable program outcomes can be considered

as identical or distinct. To this effect, we introduce

the concept of differentiator set, and ﬁnd that we can

deﬁne three versions of differentiator sets, depending

on how we answer the above-cited questions. Specif-

ically, we consider the following deﬁnitions:

• Basic Differentiator Set. The basic differentiator

set of two program P and Q (denoted by δ

(P, Q))

is deﬁned only if P and Q converge for all initial

states, and it includes all initial states for which P

and Q yield distinct ﬁnal states.

ICSOFT 2022 - 17th International Conference on Software Technologies

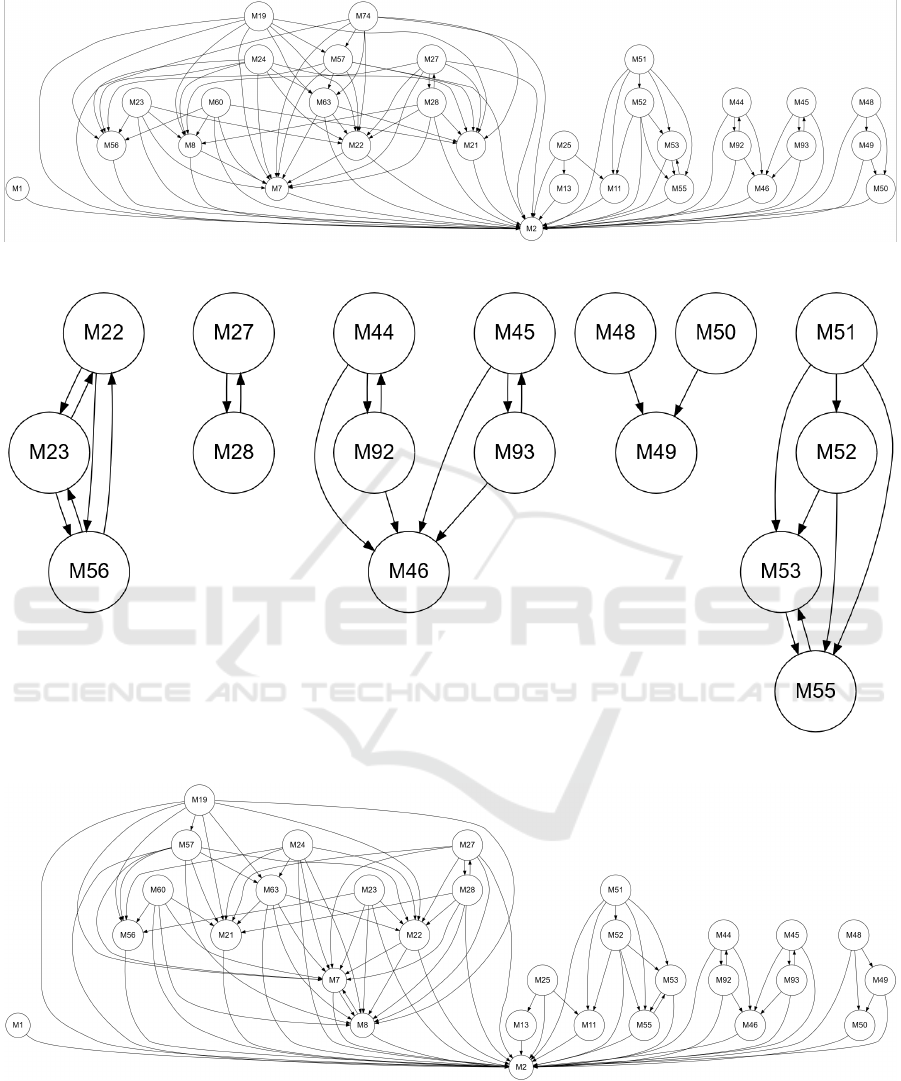
Figure 6: Basic Subsumption Graph, jTerminal Mutants.

Figure 7: Strict Subsumption Graph, jTerminal Mutants.

Figure 8: Loose Subsumption Graph, jTerminal Mutants.

• Strict Differentiator Set. The strict differentiator

set of two programs P and Q (denoted by δ

(P, Q))

can be deﬁned regardless of whether P and Q con-

verge for all initial states; it contains all initial

states for which P and Q converge and produce

distinct ﬁnal states.

• Loose Differentiator Set. The loose differentia-

tor set of two programs P and Q (denoted by

(P, Q)) can be deﬁned regardless of whether P

and Q converge for all initial states; it contains all

Generalized Mutant Subsumption

initial states for which P and Q converge and pro-

duce distinct ﬁnal states, as well as all initial states

for which one of them diverges and the other con-

verges, regardless of the ﬁnal state produced by

the program that converges.

Using these three deﬁnitions of differentiator sets, we

get three distinct versions of mutant subsumption:

Mutant M subsumes mutant M

′

with respect to base

program P if and only if:

0 ⊂ δ

(P, M) ⊆ δ

(P, M

′

)

0 ⊂ δ

(P, M) ⊆ δ

(P, M

′

)

0 ⊂ δ

(P, M) ⊆ δ

(P, M

′

)

depending on our interpretation of program outcomes,

the condition under which we consider that two out-

comes are comparable, and the condition under which

two comparable outcomes are identical.

These three deﬁnitions of differentiator sets yield

three distinct deﬁnitions of what it means for a test to

kill a mutant; they also yield three distinct subsump-

tion graphs, and three distinct minimal mutant sets.

Indeed, a test t kills a mutant M with respect to base

program P if and only if

t ∈ δ(P, M),

where δ(P, M) can be δ

(P, M), δ

(P, M),

depending on the interpretation we adopt. Also, a test

suite T kills a mutant M with respect to base program

P if and only if

T ∩ δ(P, M) 6=

where δ(P, M) can be δ

(P, M), δ

(P, M),

depending on the interpretation we adopt.

We show by means of a simple example that

different interpretations yield different subsumption

graphs. Among other things, this example highlights

the need to take into consideration the possibility of

divergence, since many of its mutants diverge for

many of the tests included in its benchmark test suite.

ACKNOWLEDGEMENT

The authors are very grateful to the anonymous re-

viewers for their valuable feedback, which has greatly

enhanced the content and presentation of the paper;

they are also genuinely impressed by the thorough-

ness, proﬁciency and precision of the reviewers’ feed-

back.

This research is partially supported by NSF grant

DGE1565478.

REFERENCES

Brink, C., Kahl, W., and Schmidt, G. (1997). Relational

Methods in Computer Science. Advances in Computer

Science. Springer Verlag, Berlin, Germany.

Dijkstra, E. (1976). A Discipline of Programming. Prentice

Hall.

Gries, D. (1981). The Science of Programming. Springer

Verlag.

Guimaraes, M. A., Fernandes, L., Riberio, M., d’Amorim,

M., and Gheyi, R. (2020). Optimizing mutation test-

ing by discovering dynamic mutant subsumption rela-

tions. In Proceedings, 13th International Conference

on Software Testing, Validation and Veriﬁcation.

Hoare, C. (1969). An axiomatic basis for computer pro-

gramming. Communications of the ACM, 12(10):576–

583.

Jia, Y. and Harman, M. (2008). Constructing subtle faults

using higher order mutation testing. In Proceed-

ings, Eighth IEEE International Working Conference

on Software Code Analysis and Manipulation, pages

249–258, Beijing, China.

Kurtz, B., Amman, P., Delamaro, M., Offutt, J., and Deng,

L. (2014). Mutant subsumption graphs. In Proceed-

ings, 7th International Conference on Software Test-

ing, Validation and Veriﬁcation Workshops.

Kurtz, B., Ammann, P., and Offutt, J. (2015). Static analy-

sis of mutant subsumption. In Proceedings, IEEE 8th

International Conference on Software Testing, Veriﬁ-

cation and Validation Workshops.

Li, X., Wang, Y., and Lin, H. (2017). Coverage based dy-

namic mutant subsumption graph. In Proceedings,

International Conference on Mathematics, Modeling

and Simulation Technologies and Applications.

Manna, Z. (1974). A Mathematical Theory of Computation.

McGraw-Hill.

Marsit, I., Ayad, A., Kim, D., Latif, M., Loh, J., Omri,

M. N., and Mili, A. (2021). The ratio of equivalent

mutants: A key to analyzing mutation equivalence.

Journal of Systems and Software.

Mili, A. (2021). Differentiators and detectors. Information

Processing Letters, 169.

Parsai, A. and Demeyer, S. (2017). Dynamic mutant sub-

sumption analysis using littledarwin. In Proceedings,

A-TEST 2017, Paderborn, Germany.

Schmidt, G. (2010). Relational Mathematics. Number 132

in Encyclopedia of Mathematics and its Applications.

Cambridge University Press.

Souza, B. (2020). Identifying mutation subsumption rela-

tions. In Proceedings, IEEE / ACM International Con-

ference on Automated Software Engineering, pages

1388–1390.

Tenorio, M. C., Lopes, R. V. V., Fechina, J., Marinho,

T., and Costa, E. (2019). Subsumption in mutation

testing: An automated model based on genetic algo-

rithm. In Proceedings, 16th International Confer-

ence on Information Technology –New Generations.

Springer Verlag.

Vercammen, S., DeMeyer, S., Borg, M., and Claessens, R.

(2021). Flaky mutants: Another concern for mutation.

In Proceedings, IEEE 2021 International Cconference

on Software Testing, Porto de Galinhas, Brazil.

ICSOFT 2022 - 17th International Conference on Software Technologies