
Towards Decentralized Parameter Servers for Secure Federated
Learning
Muhammad El-Hindi, Zheguang Zhao and Carsten Binnig
Department of Computer Science, Technical University of Darmstadt, Germany
Keywords:
Federated Learning, Privacy, Parameter Server, Decentralization, Sharding, Asynchronous Updates.
Abstract:
Federated learning aims to protect the privacy of data owners in a collaborative machine learning setup since
training data does not need to be revealed to any other participant involved in the training process. This
is achieved by only requiring participants to share locally computed model updates (i.e., gradients), instead
of the training data, with a centralized parameter server. However, recent papers have shown that privacy
attacks exist which allow this server to reconstruct the training data of individual data owners only from the
received gradients. To mitigate this attack, in this paper, we propose a new federated learning framework
that decentralizes the parameter server. As part of this contribution, we investigate the configuration space of
such a decentralized federated learning framework. Moreover, we propose three promising privacy-preserving
techniques, namely model sharding, asynchronous updates and polling intervals for stale parameters. In our
evaluation, we observe on different data sets that these techniques can effectively thwart the gradient-based
reconstruction attacks on deep learning models, both from the client side and the server side, by reducing the
attack results close to random noise.
1 INTRODUCTION
Motivation. Federated learning (FL) (McMahan
et al., 2017) enables organizations to learn predictive
models in a collaborative way. There are several rea-
sons for using federated learning. One is that each
individual organization has too little training data and
thus data of multiple organizations is needed to train
a deep model. Moreover, FL is interesting since the
training data does not leave organizational boundaries
(Kairouz et al., 2019; Li et al., 2020). This is espe-
cially helpful if the data contains private information
that needs to be protected. A prime example for FL
is healthcare. There, multiple hospitals want to learn
a model over their joint data for the classification of
a new disease, but need to keep patient data local due
to legal and privacy regulations (Brisimi et al., 2018).
The predominant architecture for federated learn-
ing today is to use a central parameter server (PS)
that collects the model updates from all participants
and aggregates them. In this setup, the data owners
participate in the training process by sending their lo-
cally computed model updates to the central server,
which combines these updates into a global model
(McMahan et al., 2017). The original assumption was
that such an approach is able to protect the privacy
of each participant’s training data, since only model
updates and not the training data itself is exchanged
with the server. Yet, recent works (Zhu et al., 2019;
Zhao et al., 2020) have shown that privacy attacks ex-
ist that allow an attacker to successfully extract in-
formation about the training data by observing the
model updates (i.e., exchanged gradients). More sur-
prisingly, these attacks showed that it is possible to
successfully reconstruct individual training examples
with high accuracy (e.g., a full picture used for train-
ing) (Zhu et al., 2019; Zhao et al., 2020). Even worse,
these attacks are also applicable for different model
architectures (Geiping et al., 2020; Wei et al., 2020).
Meanwhile existing defense strategies remain lim-
ited in preventing privacy attacks in federated learning
(Zhu et al., 2019; Geiping et al., 2020; Phong et al.,
2018; Bonawitz et al., 2017; Abadi et al., 2016). Most
strategies either significantly reduce the learning ac-
curacy (e.g., using noisy gradients can result in 30%
less accuracy (Zhu et al., 2019)) or have other limita-
tions such as assuming a trusted central PS, or being
incompatible with widely used model architectures
(e.g., secure aggregation (Bonawitz et al., 2017)).
Generic cryptographic primitives such as homomor-
phic encryption, although not affecting accuracy, typ-
ically incur significant overhead resulting in longer
training times (e.g., by 100x (Phong et al., 2018)).
Contributions. In this work we take a differ-
ent, system-driven approach by modifying the fed-
erated learning framework. We propose to ar-
El-Hindi, M., Zhao, Z. and Binnig, C.
Towards Decentralized Parameter Servers for Secure Federated Learning.
DOI: 10.5220/0011146300003269
In Proceedings of the 11th International Conference on Data Science, Technology and Applications (DATA 2022), pages 257-269
ISBN: 978-989-758-583-8; ISSN: 2184-285X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
257

chitect the training system around decentralize pa-
rameter servers. Further, we initiate the study of
the configuration space of such a decentralized FL
framework, called P2Sharding, w.r.t. its security
against client-side and server-side attacks. We pro-
pose three promising privacy-preserving techniques,
namely model sharding, asynchronous updates and
polling intervals on stale parameters. Our evalua-
tion on the CIFAR10 and MNIST datasets shows
that these configurations can effectively thwart the
gradient-based reconstruction attacks on deep learn-
ing models by reducing the attack outcome close to
random noise.
Outline. The remainder of this paper is organized
as follows. Section 2 gives an overview of federated
learning and the common basis for existing privacy
attacks. We present our privacy-preserving sharding
framework based on a decentralized parameter server
architecture in Section 3. We evaluate these config-
urations in Section 4 and conclude with related work
and a summary.
2 BACKGROUND
In the following, we briefly discuss the basics of fed-
erated learning and the typical structure of privacy at-
tacks on federated learning. Finally, we review exist-
ing defense strategies when using a central parameter
server and their limitations.
2.1 Federated Learning
Federated learning is a collaborative learning set-
ting in which multiple parties jointly train a machine
learning model. To coordinate the learning process,
federated learning typically uses a central parame-
ter server to initialize a global model, and interacts
with a set of participants (clients) to collect updates
to the model. One distinct aspect of this setting is
that participants never upload their data to the server,
and the only information the server collects is model
updates computed on privately held data (McMahan
et al., 2017; Kairouz et al., 2019; Bonawitz et al.,
2019). The de facto class of training algorithms
deployed in the federated setting for deep learning
is stochastic gradient descent (SGD). SGD updates
are gradients of model weights towards minimizing
a loss function computed on batches of the training
data (Kone
ˇ
cn
´
y et al., 2016). Training data is possibly
iterated through multiple times locally before sending
the final update to be averaged to the server (McMa-
han et al., 2017). The parameter server aggregates
…
Parameter Server (Centralized)
<latexit sha1_base64="EmxjjITA3lVgFEkDU/lAZEWSaRQ=">AAAB6HicdVDJSgNBEK2JW4xb1KOXxiB4GmY0khyDXjwmYBZIhtDTqUna9Cx09whhyBd48aCIVz/Jm39jZxFcHxQ83quiqp6fCK6047xbuZXVtfWN/GZha3tnd6+4f9BScSoZNlksYtnxqULBI2xqrgV2Eok09AW2/fHVzG/foVQ8jm70JEEvpMOIB5xRbaRGu18sOXbZqVTL5+Q3cW1njhIsUe8X33qDmKUhRpoJqlTXdRLtZVRqzgROC71UYULZmA6xa2hEQ1ReNj90Sk6MMiBBLE1FmszVrxMZDZWahL7pDKkeqZ/eTPzL66Y6qHoZj5JUY8QWi4JUEB2T2ddkwCUyLSaGUCa5uZWwEZWUaZNNwYTw+Sn5n7TObPfCdhrlUu1yGUcejuAYTsGFCtTgGurQBAYI9/AIT9at9WA9Wy+L1py1nDmEb7BePwAmbY0t</latexit>
W
Data
SGD
Participant 1
Data
SGD
Participant 2
Data
SGD
Participant N
Data
SGD
Participant 1
Data
SGD
<latexit sha1_base64="W3dqUP2gEyynIkY7A0JcNAsNjYs=">AAAB73icbVBNS8NAEJ3Ur1q/qh69LBbBU0lE0WPRi8cK9gPaUCbbTbt0s0l3N0IJ/RNePCji1b/jzX/jts1BWx8MPN6bYWZekAiujet+O4W19Y3NreJ2aWd3b/+gfHjU1HGqKGvQWMSqHaBmgkvWMNwI1k4UwygQrBWM7mZ+64kpzWP5aCYJ8yMcSB5yisZK7a7EQCBp9coVt+rOQVaJl5MK5Kj3yl/dfkzTiElDBWrd8dzE+Bkqw6lg01I31SxBOsIB61gqMWLaz+b3TsmZVfokjJUtachc/T2RYaT1JApsZ4RmqJe9mfif10lNeONnXCapYZIuFoWpICYms+dJnytGjZhYglRxeyuhQ1RIjY2oZEPwll9eJc2LqndVdR8uK7XbPI4inMApnIMH11CDe6hDAygIeIZXeHPGzovz7nwsWgtOPnMMf+B8/gCDy4+f</latexit>
rW
<latexit sha1_base64="EmxjjITA3lVgFEkDU/lAZEWSaRQ=">AAAB6HicdVDJSgNBEK2JW4xb1KOXxiB4GmY0khyDXjwmYBZIhtDTqUna9Cx09whhyBd48aCIVz/Jm39jZxFcHxQ83quiqp6fCK6047xbuZXVtfWN/GZha3tnd6+4f9BScSoZNlksYtnxqULBI2xqrgV2Eok09AW2/fHVzG/foVQ8jm70JEEvpMOIB5xRbaRGu18sOXbZqVTL5+Q3cW1njhIsUe8X33qDmKUhRpoJqlTXdRLtZVRqzgROC71UYULZmA6xa2hEQ1ReNj90Sk6MMiBBLE1FmszVrxMZDZWahL7pDKkeqZ/eTPzL66Y6qHoZj5JUY8QWi4JUEB2T2ddkwCUyLSaGUCa5uZWwEZWUaZNNwYTw+Sn5n7TObPfCdhrlUu1yGUcejuAYTsGFCtTgGurQBAYI9/AIT9at9WA9Wy+L1py1nDmEb7BePwAmbY0t</latexit>
W
1
2
3
Figure 1: Federated learning with a centralized parameter
server using stochastic gradient descent (SGD). Each par-
ticipant
1
downloads global model parameters W from the
server;
2
computes local model updates ∇W based on pri-
vately held data;
3
sends local updates to the server. The
server aggregates the local updates to global parameters.
updates from each client, and applies changes to the
model parameters either synchronously (Chen et al.,
2017) (accepting one update per client in a round) or
asynchronously (Dean et al., 2012) (allowing clients
to progress independently).
Figure 1 illustrates the basic steps. Each client k
downloads the parameters W , computes the gradient
∇
W
L(W ;x
k
,y
k
) for the loss function L on its local data
(x
k
,y
k
) (denoted as ∇W (x
k
,y
k
)) . The server collects
each gradient and aggregates it into the global model
W ← W −η
∑
K
k=1
β
k
∇W (x
k
,y
k
) with the weights β
k
and the learning rate η. The interactive process iter-
ates until convergence.
2.2 Privacy Attacks
Since its inception, federated learning has emerged
as a common paradigm to train on real-world privacy
sensitive data. It was commonly believed that the in-
formation transmitted over the network in federated
settings contains only minimal updates for improving
the model, and therefore reveals much less informa-
tion about the private training data (Kone
ˇ
cn
´
y et al.,
2016; McMahan et al., 2017). However, this con-
ceived advantage has been cast into doubt by recent
work on privacy attacks that revealed that even the
model updates contain enough information to com-
promise the data privacy (Melis et al., 2018; Zhu
et al., 2019; Geiping et al., 2020).
The authors (Melis et al., 2018) show that gradi-
ents carry valuable information that can be leveraged
by attackers to leak unintended knowledge about the
private data. The authors of (Zhu et al., 2019) were
the first to show that it is even possible to reconstruct
full images and text data with high precision from gra-
dients sent by clients and thus breach the privacy of
the learning process. This class of reconstruction at-
tacks only requires access to the exposed model up-
dates (i.e., the gradients ∇W ), plus the parameters W
and is therefore applicable to most federated settings.
The common basis for these attacks is the follow-
ing optimization problem: Find some estimated data
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
258

x
0
(e.g., an image) and its label y
0
(e.g., the classifi-
cation of the image) such that its gradient ∇
W
L(x
0
,y
0
)
is closest to the transmitted client gradient ∇W for its
private input x and label y. In other words, the dis-
tance of the two gradients with regard to a distance
function D() is minimized:
argmin
x
0
,y
0
D
∇W,∇
W
L(W, x
0
,y
0
)
(1)
The original attack (Zhu et al., 2019) used an L-
BFGS solver (Liu and Nocedal, 1989) with randomly
initialized (x
0
,y
0
) to optimize Eq. (1) based on the
euclidean distance for a training batch size of 1. The
attack accuracy was improved by (Zhao et al., 2020)
in which the private labels y are recovered analytically
from the direction of the gradients. More recently,
(Geiping et al., 2020) used cosine similarity in Eq.
(1) to yield a stronger attack for larger batch sizes.
2.3 Existing Defense Strategies
The key ingredients for the reconstruction attacks in
Eq. (1) are: (a) the access to the entire model pa-
rameters W , and (b) the view of the entire gradi-
ent ∇W . Several countermeasures based on differ-
ential privacy (Zhu et al., 2019), gradient compres-
sion (Lin et al., 2018; Zhu et al., 2019) and cryptogra-
phy (Bonawitz et al., 2017; Phong et al., 2018) were
proposed. Yet, they have several limitations:
Differential Privacy Approach. The differential
privacy-based approach in (Zhu et al., 2019) adds La-
pacian and Gaussian noise to the local model updates
before transmission, but larger noise is often neces-
sary for enough privacy protection, which tends to de-
grade the training accuracy significantly.
ML-based Approach. Gradient compression (Lin
et al., 2018) by dropping out small gradient compo-
nents has shown to be effective only when the sparsity
of the gradient exceeds 20% (Zhu et al., 2019). Yet,
this method does not prevent a corrupt server from in-
verting the gradients from observed model iterates, a
crucial step for reconstruction (cf. Sec. 3.2.2).
Cryptographic Approach. Some cryptographic proto-
cols are still ineffective against the attack in (Geip-
ing et al., 2020), e.g., secure aggregation (Bonawitz
et al., 2017) or, in the case of Homomorphic en-
cryption (Phong et al., 2018), incur prohibitive over-
head and are limited to integer fields. A multi-party
computation-based approach (Goldreich, 1998) also
has large overhead when scaling to more than two
servers or clients or is not directly applicable to the
federated setting as is the case for the approach in
(Mohassel and Zhang, 2017).
3 DECENTRALIZED SECURE FL
In the following, we present an alternative, system-
driven approach for enhancing privacy in federated
learning without the drawbacks seen in the above
mentioned approaches. We first give an overview of
our decentralized parameter server that partitions the
model into shards. We then discuss how these model
shards are created and updated on different server in-
stances in order to enhance data privacy.
3.1 Decentralized Parameter Server
Centralized parameter server presents a single point
of security vulnerability because a corrupt server
can see all updates from all clients and launch the
gradient-based reconstruction attack as is. By con-
trast, we proposed to base our defense mechanism on
decentralizing the parameter server.
Instead of congregating the model parameters on
a centralized PS, our framework, called P2Sharding,
distributes trust among several independent parameter
server instances, each hosting a fraction of the model,
called a shard. No single server instance holds the
entire model W , nor receives the entire gradient ∇W .
Thus just by design, sharding enhances data privacy
by preventing the adversary from having a consistent
view of the entire gradients and the model parameters,
both the key elements in the reconstruction attacks.
Federated Settings. We consider a set of K clients
who participate to train a model on their joint
data. The model W is partitioned into M shards
W
1
,··· ,W
M
using a configurable strategy, and each
shard W
m
is hosted on a separate parameter server in-
stance. Each server instance W
m
receives the gradient
shard ∇W
m
from each client k. Each client downloads
the full model iterates W = (W
1
,··· ,W
M
) by sending
requests (i.e., polling) to the M server instances.
Note that the amount of exchanged data between
clients and the parameter server shards is similar to
the classical central parameter server setting. In both
cases, clients need to download the full model W or
send all gradients ∇W to a remote location. The only
additional overhead introduced by our framework are
additional messages/connections since clients have to
communicate with multiple remote endpoints.
The framework can adapt to several federated set-
tings using different configurations. For example, for
enterprise clients where each has enough computa-
tion resource, each of the M server instances can be
co-located with a client. An example is shown in Fig-
ure 2. In contrast, a server-aided model can be used to
outsource the M server instances onto M independent
Towards Decentralized Parameter Servers for Secure Federated Learning
259

Parameter Server (Decentralized)
PS Instance 1 PS Instance 2 PS Instance 3
<latexit sha1_base64="x7hHGBDEz4SEbeBXJSvRqUuRzU4=">AAAB7HicdVDLSsNAFL2pr1pfVZduBovgKiR9kLorunFZwbSFNpbJdNoOnUzCzEQood/gxoUibv0gd/6N04egogcuHM65l3vvCRPOlHacDyu3tr6xuZXfLuzs7u0fFA+PWipOJaE+iXksOyFWlDNBfc00p51EUhyFnLbDydXcb99TqVgsbvU0oUGER4INGcHaSH77LqvM+sWSazsLIMf2LspuzTOk6nj1agV9WSVYodkvvvcGMUkjKjThWKmu6yQ6yLDUjHA6K/RSRRNMJnhEu4YKHFEVZItjZ+jMKAM0jKUpodFC/T6R4UipaRSazgjrsfrtzcW/vG6qh/UgYyJJNRVkuWiYcqRjNP8cDZikRPOpIZhIZm5FZIwlJtrkU/gewv+kVbbdmu3cVEuNy1UceTiBUzgHFzxowDU0wQcCDB7gCZ4tYT1aL9brsjVnrWaO4Qest0/zqo7K</latexit>
W
3
<latexit sha1_base64="np9xBWt4CtC5x8WN3I/3Me3vNu8=">AAAB7HicdVBNS8NAEJ34WetX1aOXxSJ4CklNjd6KXjxWMG2hjWWz3bZLN5uwuxFK6G/w4kERr/4gb/4btx+Cij4YeLw3w8y8KOVMacf5sJaWV1bX1gsbxc2t7Z3d0t5+QyWZJDQgCU9kK8KKciZooJnmtJVKiuOI02Y0upr6zXsqFUvErR6nNIzxQLA+I1gbKWje5ZVJt1R2bO+0WrnwkGP7/pnnu4ZU3SlDru3MUIYF6t3Se6eXkCymQhOOlWq7TqrDHEvNCKeTYidTNMVkhAe0bajAMVVhPjt2go6N0kP9RJoSGs3U7xM5jpUax5HpjLEeqt/eVPzLa2e6fx7mTKSZpoLMF/UzjnSCpp+jHpOUaD42BBPJzK2IDLHERJt8iiaEr0/R/6RRsd2q7dx45drlIo4CHMIRnIALPtTgGuoQAAEGD/AEz5awHq0X63XeumQtZg7gB6y3Tx/Qjug=</latexit>
W
2
<latexit sha1_base64="se9iSvRH+DMnR0T44fUBk5Whf7o=">AAAB7HicdVDLSsNAFJ3UV62vqks3g0VwFTIlbequ6MZlBdMW2lgm00k7dDIJMxOhhH6DGxeKuPWD3Pk3Th+Cih64cDjnXu69J0w5U9pxPqzC2vrG5lZxu7Szu7d/UD48aqskk4T6JOGJ7IZYUc4E9TXTnHZTSXEcctoJJ1dzv3NPpWKJuNXTlAYxHgkWMYK1kfzOXY5mg3LFsd2q59YQdOw6Ql69ZshF3fEaLkS2s0AFrNAalN/7w4RkMRWacKxUDzmpDnIsNSOczkr9TNEUkwke0Z6hAsdUBfni2Bk8M8oQRok0JTRcqN8nchwrNY1D0xljPVa/vbn4l9fLdNQIcibSTFNBlouijEOdwPnncMgkJZpPDcFEMnMrJGMsMdEmn5IJ4etT+D9pV21Us50bt9K8XMVRBCfgFJwDBDzQBNegBXxAAAMP4Ak8W8J6tF6s12VrwVrNHIMfsN4+ARVXjuE=</latexit>
W
1
<latexit sha1_base64="EmxjjITA3lVgFEkDU/lAZEWSaRQ=">AAAB6HicdVDJSgNBEK2JW4xb1KOXxiB4GmY0khyDXjwmYBZIhtDTqUna9Cx09whhyBd48aCIVz/Jm39jZxFcHxQ83quiqp6fCK6047xbuZXVtfWN/GZha3tnd6+4f9BScSoZNlksYtnxqULBI2xqrgV2Eok09AW2/fHVzG/foVQ8jm70JEEvpMOIB5xRbaRGu18sOXbZqVTL5+Q3cW1njhIsUe8X33qDmKUhRpoJqlTXdRLtZVRqzgROC71UYULZmA6xa2hEQ1ReNj90Sk6MMiBBLE1FmszVrxMZDZWahL7pDKkeqZ/eTPzL66Y6qHoZj5JUY8QWi4JUEB2T2ddkwCUyLSaGUCa5uZWwEZWUaZNNwYTw+Sn5n7TObPfCdhrlUu1yGUcejuAYTsGFCtTgGurQBAYI9/AIT9at9WA9Wy+L1py1nDmEb7BePwAmbY0t</latexit>
W
Participant 3
Data
Participant 2
Data
Participant 1
Data
Figure 2: Decentralized Parameter Server Architecture for
an example with 3 shards (W
1
,W
2
,W
3
). The parameter
space W is partitioned across several independent PS in-
stances managed by different participants. In the example,
the PS instances are co-located with each participant, but
they can also be hosted by independent physical servers.
physical servers, which is more suitable for resource-
constrained clients running on edge devices such as
mobile phones.
Security Model. The P2Sharding framework as-
sumes all parties to be semi-honest, that is each client
and server follow their prescribed protocol and only
attempts to extract more information from the other
client’s data
1
. Moreover, at least one client and
one shard are assumed to be non-colluding with the
other parties (i.e., we have at least two non-colluding
shards). Otherwise, the security reduces to that of a
centralized server.
We also consider cases where (1) a subset of PS
instances or (2) client and server instances collude
(e.g., due to being co-located as shown in Figure 2).
In the first case, the goal of the colluding PSs is to ex-
tend their knowledge about exchanged gradients. In
the second case, the attacker only wants to get access
to the full model iterates W
1
,··· ,W
M
since the client
regularly receives the latest global model. This pro-
vides crucial information for reconstruction because
the attacker can estimate the full gradients from the
history of the received model iterates.
In P2Sharding, we provide several configurations
to help reduce the risk of both PS-side and client-side
attacks as explained next.
3.2 Privacy-preserving Configurations
We turn to investigate several configurations within
the P2Sharding framework that can enhance privacy.
These configurations are rooted in system designs,
and therefore present a different tool for protecting
private training data than differential privacy or end-
to-end cryptographic approaches.
1
Protocols that assume a semi-honest setup prevent in-
advertent leakage of information between parties, and are
thus useful if this is the concern. In addition, protocols in
the semi-honest model are quite efficient, and are often an
important first step for achieving higher levels of security.
3.2.1 Model Sharding
Since a shard contains only a partition of the model,
the information leakage to a corrupt server is lim-
ited to its hosted shard. Which data can be recon-
structed from a shard depends on how the model pa-
rameters are distributed. For example, if the penulti-
mate layer in a feed-forward, softmax-output neural
network were allocated to the same shard, its corrupt
server may learn the training label (Zhao et al., 2020).
In the following, we describe three sharding strategies
that provide strong privacy in our evaluation, and we
show how to vary the shard size to increase resilience
against collusion of multiple shards.
Uniform Sharding. The idea of the Uniform-
strategy is to create S similar-sized shards that store
the same fraction of parameters from each layer, as
depicted in Figure 3. As shown in the figure, all three
shards have the same size and equally span all layers.
In order to achieve this partitioning, the strategy
uniformly assigns the parameters p
i
to the shards W
j
.
This can be expressed by selecting a shard for a pa-
rameter at index i using a shared hash function P :
S (i) =
P (i) mod S
+ 1 (2)
Uniform sharding creates equally-sized partitions.
However, it is completely oblivious of the different
layers and hence a participant might possess parame-
ters from all layers.
Slicing Sharding. Another model-oblivious tech-
nique is the Slicing-strategy. In this strategy, the pa-
rameter space is contiguously divided into S equally-
sized partitions, as depicted in Figure 3. More for-
mally, this strategy can be described by the following
function:
S (i) =
&
i
|W |
S
'
(3)
Intuitively, we can linearly iterate over all parameters
in W and assign the first
1
S
parameters to the first shard
(blue) and the second
1
S
to the second (green) shard
and so on.
In terms of shard size, this strategy creates equally
sized shards as shown in Figure 3.Moreover, shards
span only a few layers of a NN as depicted in the ex-
ample. There, the blue and yellow shard span mul-
tiple layers but the green shard is limited to a single
parameter-layer. Hence, this strategy differs from the
Uniform-strategy since it reduces the number of lay-
ers from which a participant holds parameters.
Boundary-aware Sharding. In contrast to the pre-
vious strategies, this strategy guarantees that a par-
tition does not hold any parameters of adjacent
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
260
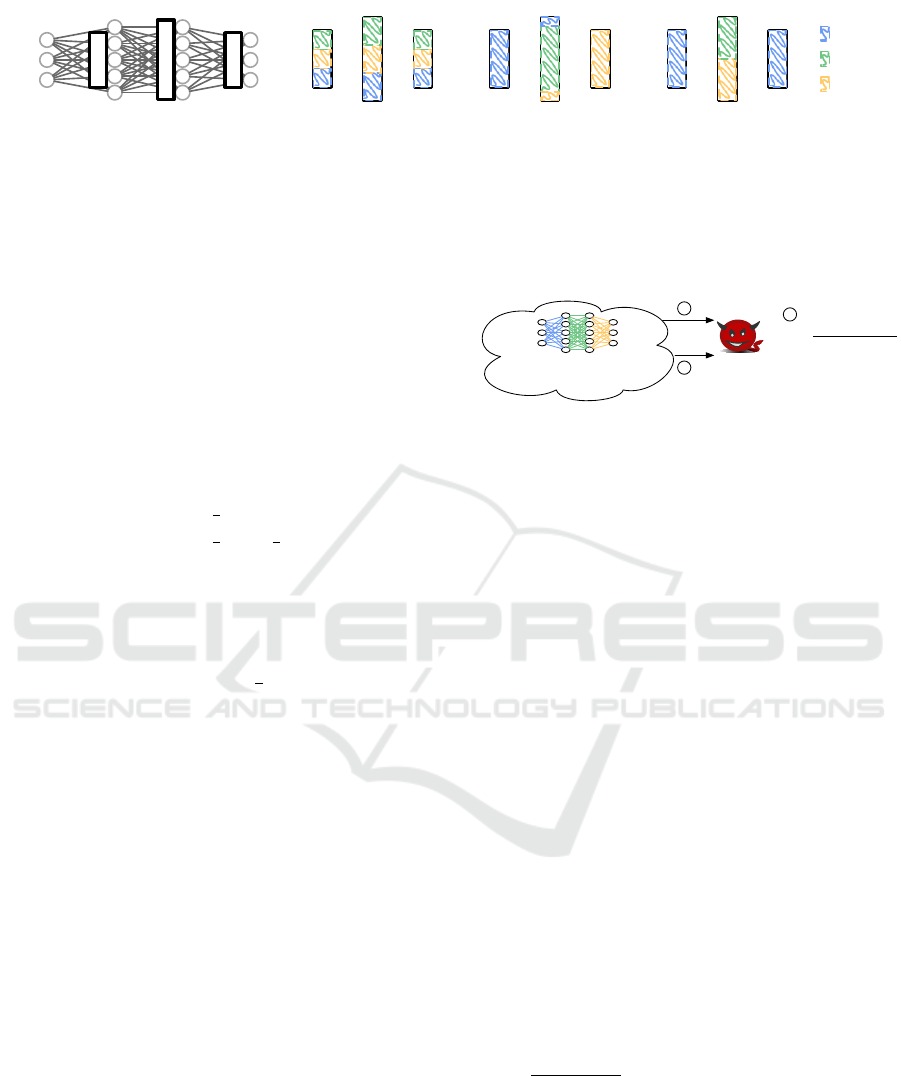
l
1
l
2
l
3
(a) Layers of model parameters.
l
1
l
2
l
3
(b) Uniform.
l
1
l
2
l
3
(c) Slicing.
l
1
l
2
l
3
Shards
<latexit sha1_base64="x7hHGBDEz4SEbeBXJSvRqUuRzU4=">AAAB7HicdVDLSsNAFL2pr1pfVZduBovgKiR9kLorunFZwbSFNpbJdNoOnUzCzEQood/gxoUibv0gd/6N04egogcuHM65l3vvCRPOlHacDyu3tr6xuZXfLuzs7u0fFA+PWipOJaE+iXksOyFWlDNBfc00p51EUhyFnLbDydXcb99TqVgsbvU0oUGER4INGcHaSH77LqvM+sWSazsLIMf2LspuzTOk6nj1agV9WSVYodkvvvcGMUkjKjThWKmu6yQ6yLDUjHA6K/RSRRNMJnhEu4YKHFEVZItjZ+jMKAM0jKUpodFC/T6R4UipaRSazgjrsfrtzcW/vG6qh/UgYyJJNRVkuWiYcqRjNP8cDZikRPOpIZhIZm5FZIwlJtrkU/gewv+kVbbdmu3cVEuNy1UceTiBUzgHFzxowDU0wQcCDB7gCZ4tYT1aL9brsjVnrWaO4Qest0/zqo7K</latexit>
W
3
<latexit sha1_base64="np9xBWt4CtC5x8WN3I/3Me3vNu8=">AAAB7HicdVBNS8NAEJ34WetX1aOXxSJ4CklNjd6KXjxWMG2hjWWz3bZLN5uwuxFK6G/w4kERr/4gb/4btx+Cij4YeLw3w8y8KOVMacf5sJaWV1bX1gsbxc2t7Z3d0t5+QyWZJDQgCU9kK8KKciZooJnmtJVKiuOI02Y0upr6zXsqFUvErR6nNIzxQLA+I1gbKWje5ZVJt1R2bO+0WrnwkGP7/pnnu4ZU3SlDru3MUIYF6t3Se6eXkCymQhOOlWq7TqrDHEvNCKeTYidTNMVkhAe0bajAMVVhPjt2go6N0kP9RJoSGs3U7xM5jpUax5HpjLEeqt/eVPzLa2e6fx7mTKSZpoLMF/UzjnSCpp+jHpOUaD42BBPJzK2IDLHERJt8iiaEr0/R/6RRsd2q7dx45drlIo4CHMIRnIALPtTgGuoQAAEGD/AEz5awHq0X63XeumQtZg7gB6y3Tx/Qjug=</latexit>
W
2
<latexit sha1_base64="se9iSvRH+DMnR0T44fUBk5Whf7o=">AAAB7HicdVDLSsNAFJ3UV62vqks3g0VwFTIlbequ6MZlBdMW2lgm00k7dDIJMxOhhH6DGxeKuPWD3Pk3Th+Cih64cDjnXu69J0w5U9pxPqzC2vrG5lZxu7Szu7d/UD48aqskk4T6JOGJ7IZYUc4E9TXTnHZTSXEcctoJJ1dzv3NPpWKJuNXTlAYxHgkWMYK1kfzOXY5mg3LFsd2q59YQdOw6Ql69ZshF3fEaLkS2s0AFrNAalN/7w4RkMRWacKxUDzmpDnIsNSOczkr9TNEUkwke0Z6hAsdUBfni2Bk8M8oQRok0JTRcqN8nchwrNY1D0xljPVa/vbn4l9fLdNQIcibSTFNBlouijEOdwPnncMgkJZpPDcFEMnMrJGMsMdEmn5IJ4etT+D9pV21Us50bt9K8XMVRBCfgFJwDBDzQBNegBXxAAAMP4Ak8W8J6tF6s12VrwVrNHIMfsN4+ARVXjuE=</latexit>
W
1
(d) Boundary-aware.
Figure 3: Partitioning Strategies for a neural network (NN) model architecture with four layers (a); i.e., three layers of
parameters since the input layer has no parameters. (b) The Uniform strategy creates equally sized partitions that span
across all layers. (c) The Slicing strategy divides the parameters into equally sized consecutive slices (only some of which
span layers). (d) The Boundary-aware strategy guarantees that while a shard may posses parameters from multiple layers,
these layers are not adjacent. This strategy might create shards of different sizes.
parameter-layers, e.g., the blue shard in Figure 3 does
not hold any parameters from layer l
2
. Further, this
strategy might create partitions with a different num-
ber of parameters in order to prevent a shard from
storing parameters from adjacent layers. This situa-
tion can be seen in Figure 3 since the blue shard is
bigger than the remaining two shards.
Such a mapping can be expressed as follows:
S (i,l) =
(
P (i) mod b
S
2
c
+ 1, l mod 2 = 1
P (i) mod d
S
2
e
+ d
S
2
e, l mod 2 = 0
(4)
That is, we distinguish two sets of shards, one
is responsible for odd layers (l mod 2 == 1) while
the other stores the parameters of the even layers
(l mod 2 == 0). We create these two sets by split-
ting the shards in two halves (b
S
2
c). For example, we
can observe in Figure 3 that shard W
1
is responsible
for the odd layers, while shard W
2
and W
3
are re-
sponsible for the even layer. Moreover, within every
set of shards, the parameters are uniformly distributed
with the help of a uniform shared hash function P (i).
Note that, we have decided to assign more shards to
the even layers (i.e., using bc as first bound), since
even layers tend to contain more parameters (cf. Fig-
ure 3) than, e.g., the odd in-/output layers. While
the Boundary-aware-strategy does not create equally-
sized partitions, it takes the layer boundaries of the
model architecture into account and avoids that shards
receive gradients of two adjacent layers.
Shard Sizes. The P2Sharding framework provides
the shard size configuration parameter for adjusting
the privacy of sharding in light of collusion attacks.
The effect of a collusion attack is the same as if sev-
eral shards were combined to form a larger subset of
the model. Hence, the shard size is privacy-sensitive
in that it can be used to control for the expected num-
ber of collusions. Intuitively, if C server instances
collude, their knowledge is the union of their shards.
If the number of colluding shards becomes large
enough the reconstruction attack becomes easier. So
Parameter Server
(Decentralized)
1
2
<latexit sha1_base64="Gjbm7FvdLuUkiAonNkN/Mk+hxKI=">AAAB63icbVBNS8NAEJ3Ur1q/qh69LBahXkoiih6LXjxWsB/QhrLZbtqlu0nYnQil9C948aCIV/+QN/+NmzYHbX0w8Hhvhpl5QSKFQdf9dgpr6xubW8Xt0s7u3v5B+fCoZeJUM95ksYx1J6CGSxHxJgqUvJNoTlUgeTsY32V++4lrI+LoEScJ9xUdRiIUjGImtat43i9X3Jo7B1klXk4qkKPRL3/1BjFLFY+QSWpM13MT9KdUo2CSz0q91PCEsjEd8q6lEVXc+NP5rTNyZpUBCWNtK0IyV39PTKkyZqIC26kojsyyl4n/ed0Uwxt/KqIkRR6xxaIwlQRjkj1OBkJzhnJiCWVa2FsJG1FNGdp4SjYEb/nlVdK6qHlXNffhslK/zeMowgmcQhU8uIY63EMDmsBgBM/wCm+Ocl6cd+dj0Vpw8plj+APn8wdQtI3C</latexit>
W (t)
<latexit sha1_base64="hjDN3s8Y18nsH+9SgSoEz6hbjIQ=">AAAB7XicbVDLSgNBEOyNrxhfUY9eBoMQEcKuKHoMevEYwTwgCWF2MpuMmZ1dZnqFsOQfvHhQxKv/482/cZLsQRMLGoqqbrq7/FgKg6777eRWVtfWN/Kbha3tnd294v5Bw0SJZrzOIhnplk8Nl0LxOgqUvBVrTkNf8qY/up36zSeujYjUA45j3g3pQIlAMIpWajTLeOad9oolt+LOQJaJl5ESZKj1il+dfsSSkCtkkhrT9twYuynVKJjkk0InMTymbEQHvG2poiE33XR27YScWKVPgkjbUkhm6u+JlIbGjEPfdoYUh2bRm4r/ee0Eg+tuKlScIFdsvihIJMGITF8nfaE5Qzm2hDIt7K2EDammDG1ABRuCt/jyMmmcV7zLint/UareZHHk4QiOoQweXEEV7qAGdWDwCM/wCm9O5Lw4787HvDXnZDOH8AfO5w8odo4y</latexit>
W (t + 1)
…
<latexit sha1_base64="Il3JBfzwGkuIgwGXkaGM4hqwVLQ=">AAACDHicbVDLSgMxFM3UV62vqks3wSIoYpkRRTeC6Malgu0InUHupJk2NJMZkjtCGfoBbvwVNy4UcesHuPNvTB8LXwcSDuecS3JPlElh0HU/ndLU9MzsXHm+srC4tLxSXV1rmjTXjDdYKlN9E4HhUijeQIGS32SaQxJJ7ke986Hv33FtRKqusZ/xMIGOErFggFa6rdYCBZEE6tMTGsQaWOFv486evXa9nUERcISBTbl1dwT6l3gTUiMTXN5WP4J2yvKEK2QSjGl5boZhARoFk3xQCXLDM2A96PCWpQoSbsJitMyAblmlTeNU26OQjtTvEwUkxvSTyCYTwK757Q3F/7xWjvFxWAiV5cgVGz8U55JiSofN0LbQnKHsWwJMC/tXyrpgK0HbX8WW4P1e+S9p7te9w7p7dVA7PZvUUSYbZJNsE48ckVNyQS5JgzByTx7JM3lxHpwn59V5G0dLzmRmnfyA8/4F2biZmg==</latexit>
rW =
W (t) W (t + 1)
⌘
3
Figure 4: Attackers recovering full gradients from model
iterates. The estimation takes three steps: Downloading
all parameters from all shards repeatedly (
1
and
2
) and
assembling the global model at t and t + 1. Finally, both
models are used to recompute the gradients that were used
to update W
t
to W
t+1
3
. For the Stochastic Gradient De-
scent (SGD) algorithm, the gradients can be recomputed
with the shown formula.
by reducing the maximum shard size S, P2Sharding
can control the amount of leakage during C shard-
collusion to be ≤C ·S gradient components.
3.2.2 Asynchronous Updates
This configuration aims to reduce the risk of mali-
cious client and server collusion.
Leakage from Synchronous Updates. Under syn-
chronous training, with the help of a colluding server,
a malicious client can retrieve model snapshots of dif-
ferent iterations for a targeted victim, then uncover the
full gradient to launch the gradient-based attack. As
depicted in Figure 4 an attacker could continuously
retrieve (i.e., poll) the latest model from all param-
eter servers to determine W (t)
1
and W (t + 1)
2
and re-compute the gradients ∇W based on the re-
trieved models
3
. This observation especially holds
true for standard SGD which uses the update rule
W (t + 1) = W (t) −η ∗∇W with learning rate η (i.e.
∇W =
W (t)−W (t+1)
η
) for computing the new model pa-
rameters. In other SGD variants, gradients may only
be estimated from the full history of model iterates
{W (t)}
t
.
Perturbation by Asynchronous Updates. Our ap-
proach to mitigate the aforementioned gradient recov-
ery is to use asynchronous federated updates. In this
setting, concurrent client updates to the same model
Towards Decentralized Parameter Servers for Secure Federated Learning
261

shard are applied without a global order, which may
lead to the effect of different clients overwriting each
other’s model updates, or some clients update some
shards more often than others. As a result, data recon-
struction becomes harder as shown in our evaluation.
Intuitively, if multiple updates to each shard are
incorporated asynchronously in parallel, then the full
model iterates may contain out-of-sync values. This
leads to non-uniform directional perturbation in the
estimated full gradients. Following the model iterate
analysis for asynchronous SGD (Mania et al., 2017),
such perturbation can be modeled as essentially in-
jecting random noises E (t) on the model iterates to
the adversary’s view g:
∇
b
W = g
W (t) + E (t)
t
(5)
where E (t) is a vector that describes perturbation per
shard j at time t. Thus the attacker only sees a gra-
dient with noisy rotation and stretch. Since it is the
angle of the gradient that contains most information
about the data (Geiping et al., 2020), our evaluation
shows that perturbed gradients indeed make data re-
construction harder while maintaining model accu-
racy high.
3.2.3 Polling Intervals
Asynchronous updates can lead to degraded model
quality for some models and datasets (Mania et al.,
2017). For these cases where asynchronous updates
are not applicable, we introduce polling intervals as
another means to perturb model iterates for privacy.
The idea is to create stale parameters, while still al-
lowing for synchronous updates to the entire model
for more stable training.
More specifically, each server instance j can in-
dependently implement a manual random delay τ
j
,
called the polling interval, for each connecting client.
For each request, the server instance checks the
client’s identity, and answers with an outdated model
shard W
j
(t − τ
j
). All such artificially out-of-sync
model shards form a client’s view on the entire model,
which crucially still contains inconsistent values at all
time. As such this setting can also resist the recon-
struction attack. Specifically, the difference between
the latest but hidden model shard W
j
(t) and the polled
model shard W
j
(t −τ
j
) can be viewed as the source
for the perturbation E (t) in Eq. (5) at a particular time
t. As such, polling intervals provide a deterministic
way for inducing perturbation through staleness.
An important point to note here is that each pa-
rameter server instance is assigned to a separate trust
domain with its internal states hidden from the envi-
ronment, that is, it only exposes its interface to the
other parties. Hence, each PS instance can actually
implement different strategies of which data can be
read from the local shard. That way, each server in-
stance in P2Sharding can control parameter stale-
ness local to its shard by keeping track of the updated
model versions (i.e., one version per iteration) and re-
turn a model with a definable staleness to the client.
Finally, another interesting observation is that
model iterates with the same increasing polling inter-
val actually also produce a similar effect of increasing
the batch size, since it results in accumulated updates
across multiple training examples. As shown in (Zhu
et al., 2019) and in (Geiping et al., 2020) an increased
batch size makes privacy attacks harder. We validated
the effectiveness of polling interval in Section 4 for
both privacy and performance.
4 EXPERIMENTS
Overall the goal of the evaluation is to analyze the ef-
fects of the different configurations of P2Sharding
on privacy protection. We first demonstrate that
the privacy of the training data can be significantly
strengthened with the help of P2Sharding’s decen-
tralized setting when compared to a centralized pa-
rameter server. We then decompose P2Sharding into
each of its configurations. We show that for varying
data and model complexities P2Sharding is able to
provide configurations under which the attack results
remained unrecognizable, i.e., close to random noise.
4.1 Setup and Metrics
In our evaluation we used a similar setup as the orig-
inal reconstruction attack (Zhu et al., 2019; Geiping
et al., 2020), because our goal is to show that the
range of configurations in P2Sharding can mitigate
such attacks successfully. More details on the setup
are provided below:
Dataset Complexities. We used the MNIST (LeCun,
1998) and CIFAR10 (Krizhevsky, 2009) datasets as
representatives for less and more complex datasets.
MNIST is considered less complex than CIFAR10 for
it contains only black-and-white images of handwrit-
ten digits, whereas CIFAR10 contains colored images
of more complex objects.
Model Complexities. As models, we used
LeNetZhu as in (Zhu et al., 2019) and ConvNet
as in (Geiping et al., 2020) to represent lower and
higher model complexities. Both models are widely-
used convolutional neural networks. However, one
noticeable difference is their depth, or number of
layers, since ConvNet is deeper than LeNetZhu.
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
262

Another important difference from a reconstruction
attack perspective is the used activation function.
LeNetZhu uses a Sigmoid function which makes the
network inherently twice-differentiable, resulting in a
smoother optimization problem in attack formulation
(Eq. 1). ConvNet by contrast uses ReLU which is
non-smooth and non-differentiable at 0.
Attack Implementation. For the attacks, we used
the code in (Geiping et al., 2020) (cosine similarity
based reconstruction attack) and adapted their hyper-
parameters for the actual learning process (i.e., SGD
with learning rate η = 0.1). We integrated our parti-
tioning strategies by implementing a separate module
that limits the gradients that are accessible to the at-
tacker (i.e., a PS instance).
In the following, we always execute 5 attacks on
randomly selected training batches. Thereby, we set
the batch size to 1, as done in (Zhu et al., 2019), since
this represents the worst-case that P2Sharding has to
defend against — as mentioned in (Zhu et al., 2019),
a bigger batch size makes the attack harder. Further,
we executed each experiment three times.
Privacy Metrics. In order to evaluate the privacy
against reconstruction attacks, we measured the struc-
tural dissimilarity (DSSIM) of a reconstructed image
from its targeted private image. The DSSIM is derived
from the structural similarity (SSIM) (Wang et al.,
2004) as DS SIM(x, y) =
1−SSIM(x ,y)
2
. We used this
measure instead of the mean squared error (MSE) as
in (Zhu et al., 2019) or the MSE-based peak noise-
to-signal ratio as in (Geiping et al., 2020), because
DSSIM not only captures pixel-local deviation but
more importantly the structural differences. Hence, it
has been shown to be a superior measure for signal fi-
delity such as perceptual distortion or recognizability
(Brunet et al., 2012). For example, a color-inverted
MNIST image (a black-and-white digit) will have ex-
tremely high MSE, but it does not correlate with the
privacy of the image as the structure of the digit re-
mains obviously the same. In contrast, the DSSIM
value for the same image will be kept low to reflect the
structural similarity. In general, a higher DSSIM sug-
gests the reconstructed image deviates more from the
private image and may even be unrecognizable. We
show a sample of images from MNIST and CIFAR10
with varying DSSIM in Figure 5. Three reconstructed
images were randomly selected to represent differ-
ent DSSIM intervals. It can be observed that when
the DSSIM reaches a value > 0.45 the reconstruc-
tion become unrecognizable, which coincides with
the DSSIM of random noise.
In our evaluation, we recorded the empirical dis-
tribution of DSSIM over MNIST and CIFAR10 under
DSSIM in
(0.0, 0.4)
DSSIM in
(0.4, 0.45)
DSSIM in
(0.45, 0.5)
DSSIM in
(0.5, 0.55)
DSSIM in
(0.0, 0.4)
DSSIM in
(0.4, 0.45)
DSSIM in
(0.45, 0.5)
DSSIM in
(0.5, 0.55)
Figure 5: Visualization of different DSSIM ranges for at-
tacks on the MNIST (left) and CIFAR10 (right) dataset. A
higher DSSIM value means that an attack was unsuccessful
and privacy is protected. For MNIST and CIFAR10 privacy
is protected beginning with a DSSIM > 0.45.
repeated attacks, and reported the average and mini-
mum DSSIM as average and worst-case performance.
Baselines. In the following we compared
P2Sharding to two baselines. As the first base-
line, we compared against a centralized parameter
server with no sharding. This setting represents
an insecure setup and we show that P2Sharding
configurations achieve much stronger privacy. This
baseline will be shown as red dashed line in the
experiment plots. On the other hand, the best privacy
against reconstruction is to have attack results close
to random noise. Hence, we also compared against
a randomly generated picture in which each pixel
is sampled i.i.d. from a uniform range (shown as a
green dotted line in the following figures).
4.2 Decentralized vs. Centralized PS
In the first experiment we evaluate the privacy gain
from sharding the model parameters in the decentral-
ized parameter server setting, as compared to the cen-
tralized parameter server without sharding.
To that end, we used P2Sharding to partition
the parameter space using the three proposed shard-
ing techniques. Additionally, we varied the num-
ber of shards used to partition the model parameters
in order to capture the effect of varying shard sizes
(size =
1
#shards
). For instance, a shard size of 0.5 refers
to the fact that the model was split into 2 partitions.
We then randomly selected a resulting partition and
measured the DSSIM when executing reconstruction
attacks across all datasets and model architectures.
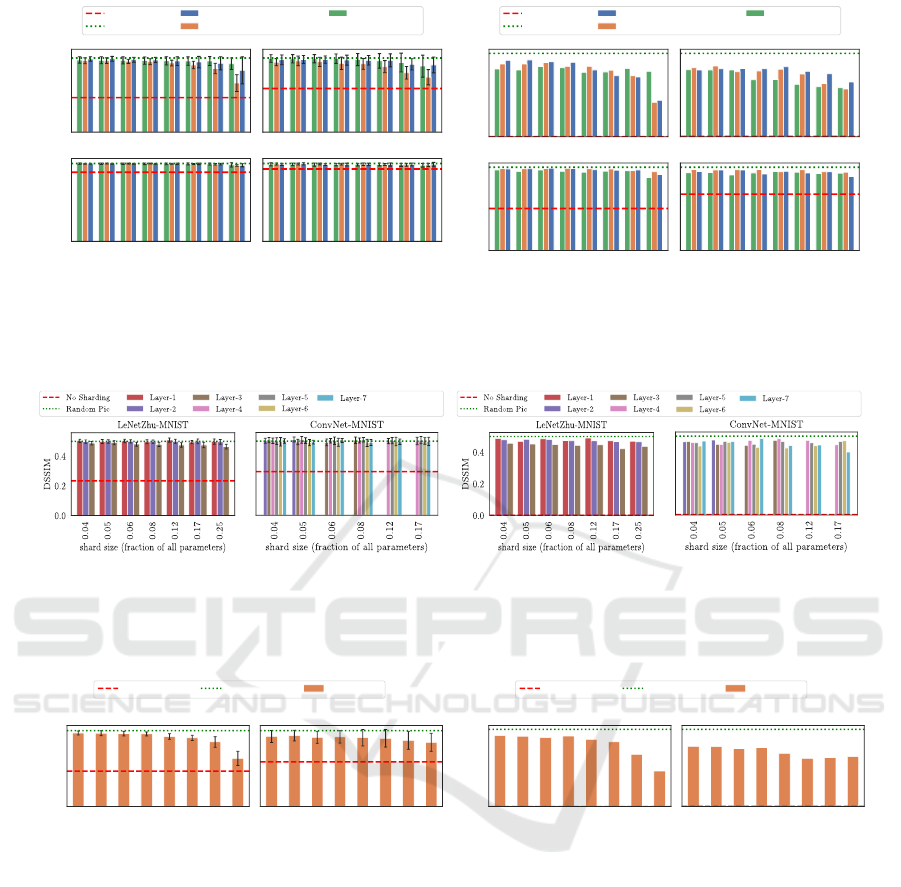
The results of this experiment can be seen in Fig-
ure 6. All sharding techniques show a clear improve-
ment over the centralized parameter server baseline
(dashed red line). In particular, the benefit of shard-
ing is most visible when looking at the success of
the best attack (called worst-case scenario) in Fig-
ure 6. Without sharding the centralized setting is con-
sistently able to recover some private image. How-
ever, with P2Sharding we were able to find config-
Towards Decentralized Parameter Servers for Secure Federated Learning
263

urations (e.g., shard size = 0.12) that result in DSSIM
values close to random noise even in the worst-case.
While Figure 6 illustrates that all partitioning
strategies improve privacy clearly when compared to
the baseline without sharding, it also reveals subtle
differences among the different strategies, i.e., not all
strategies get close to the upper bound of a random
picture (green dotted line) for all settings. In the fol-
lowing, we analyze these difference in more detail.
4.3 Effects of Model Sharding
P2Sharding provides configurations for different
sharding strategies. Each sharding strategy deter-
mines which parameters are stored in the same shard.
Since an attacker sees at least one shard of gradients,
it is important to understand the privacy impact of dif-
ferent ways of sharding. In the following, we shed
more light on when to use which sharding strategy.
In Figure 6, we compared the three proposed
sharding strategies across data and model character-
istics. The first important observation is that the at-
tack becomes consistently harder on more complex
datasets (i.e., CIFAR10 bottom row). This observa-
tion is in line with what was reported in previous work
(Zhao et al., 2020; Geiping et al., 2020). Therefore,
we mainly used the simpler MNIST dataset to differ-
entiate the privacy impact of the sharding strategies.
In the case of the MNIST data (upper row) we
make the following observations. For the sim-
ple LeNetZhu model, both the uniform and the
boundary-aware strategy result in lower DSSIM val-
ues than the slicing sharding technique. This can
be observed in terms of both the average (Figure 6)
and the worst-case performance (Figure 6). With de-
creasing shard size (ie., higher number of shards) both
strategies improve and eventually achieve similar or
slightly better (in terms of the worst-case) privacy
protection than the slicing strategy.
For the more complex ConvNet model, the op-
posite effect is noticeable: Initially the uniform and
the boundary-aware strategy show a better (worst-
case) performance than the slicing strategy (see
Figure 7). Yet, with decreasing shard size again all
strategies provide comparable performance.
We found that this effect can be explained by the
boundary-awareness of the different strategies, as will
be outlined next.
Figure 7 reveals two key observations: First, limit-
ing the gradients of a shard to only one layer yields (as
in the slicing strategy) a relatively consistent perfor-
mance across different shard sizes. Secondly, in the
case of the MNIST dataset the last layer (Layer-3) en-
ables more successful attacks (lower DSSIM) even for
smaller shard sizes (e.g., 0.06). This is the case for
both average as well as the worst-case performance
shown in Figure 7. For the ConvNet model, however,
this effect is not as significant and is only partially
observable in the worst-case performance.
This experiment highlights that different layers of
a deep learning model can carry more information
than others. Further, and even more importantly, lim-
iting the information of a shard to one layer provides
a more robust privacy protection compared to the
uniform and boundary-aware strategy (Figure 6).
Yet, as shown next, the ability of P2Sharding to
control the shard size helps to improve the privacy
protection of sharding strategies.
4.3.1 Reducing Shard Sizes
The main idea of the P2Sharding framework is to
partition the global model into several shards hosted
on independent parameter server instances. Intu-
itively, with smaller shard sizes a corrupted parame-
ter server learns less about the gradients of the model,
which increases the resistance to data reconstruction.
To evaluate this concept, we used the uniform
strategy to create shards of different sizes and mea-
sure the success of reconstruction attacks for different
model complexities on the MNIST dataset. We used
the uniform strategy, since out of the three proposed
strategies it had the most sensitivity to changing shard
sizes. Hence, using this setup we show that reducing
the shard size is another effective measure to make the
privacy for sharding more robust.
Figure 8 shows the result of this experiment for
various shard sizes on the x-axis. We can see, that
by reducing the shard size the privacy protection is
improved significantly. Starting from a shard size
below 0.12, P2Sharding is able to achieve a pri-
vacy protection that was otherwise only reached by
boundary-aware sharding.
4.4 Effects of Asynchronous Updates
If P2Sharding is used for asynchronous updates the
different parameter shards can be updated at differ-
ent points in time. In general, with more clients con-
currently training and updating the model shards, the
more staleness on average one can observe, and the
larger such variance across shards becomes (Mania
et al., 2017).
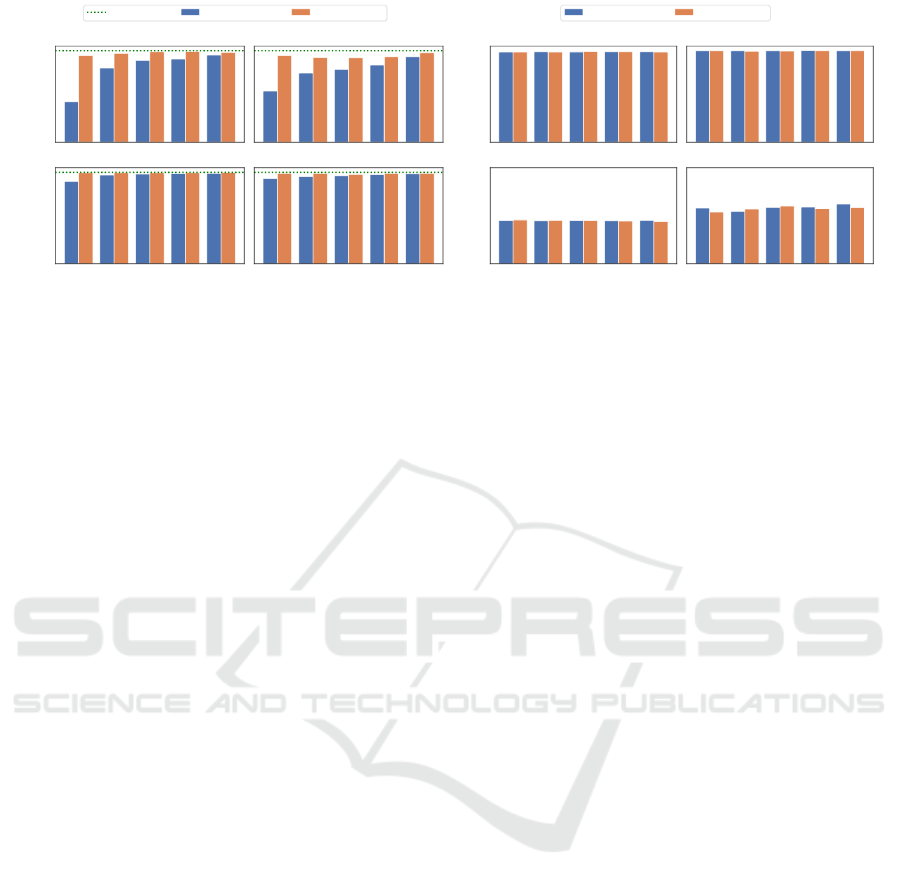
In the experiment shown in Figure 9, we simulated
the effect of concurrent activities and stale shards (i.e.,
delayed parameter updates) by randomly delaying the
incorporation of an update in a shard. We studied
the effects of staleness with no additional polling (i.e.,
polling interval = 1) and with a high polling interval.
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
264
0.0
0.2
0.4
DSSIM
LeNetZhu-MNIST ConvNet-MNIST
0.5
0.25
0.17
0.12
0.08
0.06
0.05
0.04
shard size (fraction of all parameters)
0.0
0.2
0.4
DSSIM
LeNetZhu-CIFAR10
0.5
0.25
0.17
0.12
0.08
0.06
0.05
0.04
shard size (fraction of all parameters)
ConvNet-CIFAR10
No Sharding
Random Pic
Boundary-aware Sharding
Uniform Sharding
Slicing Sharding
(a) Average Performance
0.0
0.2
0.4
DSSIM
LeNetZhu-MNIST ConvNet-MNIST
0.50.250.170.120.080.060.050.04
shard size (fraction of all parameters)
0.0
0.2
0.4
DSSIM
LeNetZhu-CIFAR10
0.50.250.170.120.080.060.050.04
shard size (fraction of all parameters)
ConvNet-CIFAR10
No Sharding
Random Pic
Boundary-aware Sharding
Uniform Sharding
Slicing Sharding
(b) Worst-case Performance
Figure 6: Evaluation of the proposed sharding techniques in terms of (a) the average success and (b) the success of the best
attack (called worst-case scenario). All sharding techniques show a clear improvement over the baseline (dashed red line).
(a) Average Performance (b) Worst-case Performance
Figure 7: Relative Importance of Layers. An attack based on the later layers of a model seem to have a higher chance for a
successful attack (lower DSSIM value). This effect is most noticeable for simple data as well as models and when looking at
the worst-case performance (Figure 7).
0.04
0.05
0.06
0.08
0.12
0.17
0.25
0.5
shard size (fraction of all parameters)
0.0
0.2
0.4
DSSIM
LeNetZhu-MNIST
0.04
0.05
0.06
0.08
0.12
0.17
0.25
0.5
shard size (fraction of all parameters)
ConvNet-MNIST
No Sharding Random Pic p2Sharding
(a) Average Performance
0.04
0.05
0.06
0.08
0.12
0.17
0.25
0.5
shard size (fraction of all parameters)
0.0
0.2
0.4
DSSIM
LeNetZhu-MNIST
0.04
0.05
0.06
0.08
0.12
0.17
0.25
0.5
shard size (fraction of all parameters)
ConvNet-MNIST
No Sharding Random Pic p2Sharding
(b) Worst case Performance
Figure 8: Influence of the shard size on privacy attacks (zoom-in into Figure 6). Decreasing the shard size is an effective
measure to prevent attacks. This is shown by the increasing DSSIM (less successful attack) for small shard sizes (e.g., 0.12).
In our setup, already with an average staleness
per shard increased to 2, we observed that all data
and models started to have increased resistance to re-
construction. That is, the average DSSIM (Figure 9)
increases. With more concurrency, such as when
the average staleness reached 8, the privacy becomes
close to the ideal privacy of random noise, even for
a simple model and dataset. This effect was even
stronger when a polling interval of 8 was used in addi-
tion, which suggests that polling intervals contribute
significantly towards an increased privacy protection.
Hence, we will study the effect of polling intervals in
more detail in the next section.
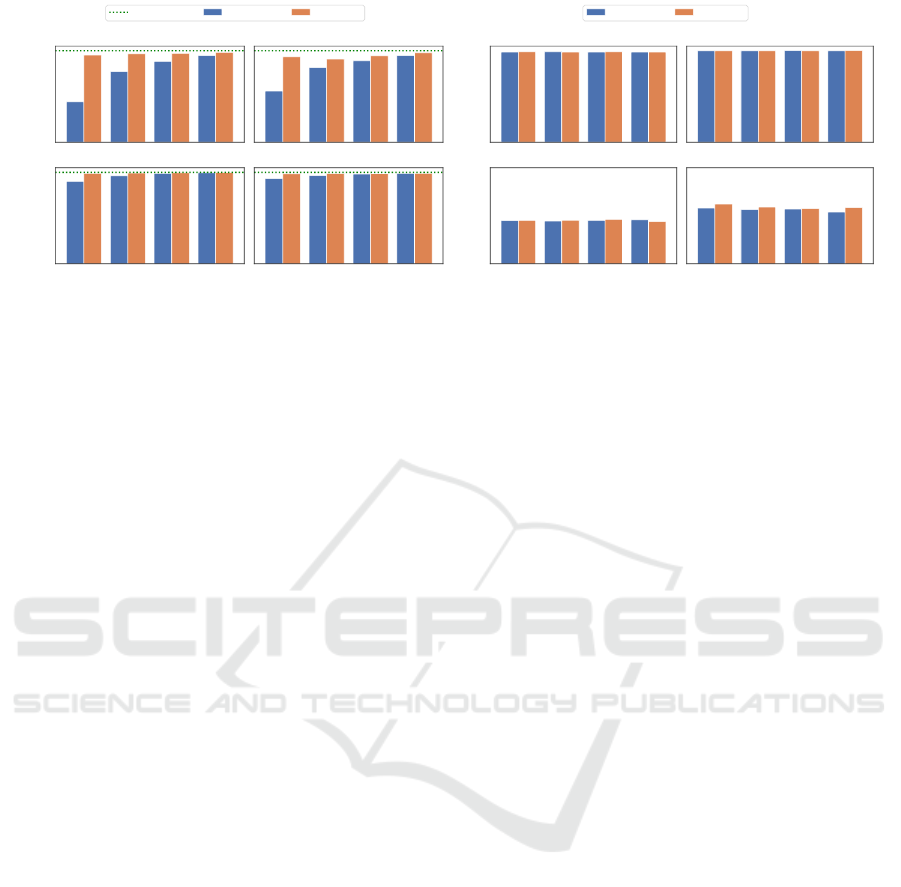
4.5 Effects of Polling Intervals
Similar to asynchronous updates, polling intervals
aim at preventing client-side attacker from uncover-
ing the full gradient, a crucial step in reconstruction.
However, polling intervals rely on serving parameters
with randomly varying staleness to perturbe the at-
tacker’s view on the entire model. The added benefit
is that polling intervals can work with synchronous
updates to all the model shards such that the training
becomes more stable.
In the experiment of Figure 10, we observed that
with increasing polling intervals, the resistance to
Towards Decentralized Parameter Servers for Secure Federated Learning
265
0.0
0.2
0.4
DSSIM
LeNetZhu-MNIST ConvNet-MNIST
0
1
2
4
8
staleness
0.0
0.2
0.4
DSSIM
LeNetZhu-CIFAR10
0
1
2
4
8
staleness
ConvNet-CIFAR10
Random Pic PollingInterval-1 PollingInterval-8
(a) Average Performance
0.00
0.25
0.50
0.75
1.00
ACC
LeNetZhu-MNIST ConvNet-MNIST
0
1
2
4
8
staleness
0.00
0.25
0.50
0.75
1.00
ACC
LeNetZhu-CIFAR10
0
1
2
4
8
staleness
ConvNet-CIFAR10
PollingInterval-1 PollingInterval-8
(b) Accuracy
Figure 9: Influence of staleness on privacy attacks. Staleness makes the model iterates inconsistent across all shards as in a
typical asynchronous learning setup since the shards incorporate client updates with a delay. An increased staleness helps to
improve the privacy protection, i.e., increase the DSSIM (9) while not affecting the resulting model accuracy (9).
construction also became stronger. This effect was
most obvious when the staleness due to asynchronous
updates was controlled for and set to 0 (i.e., no stale-
ness created by asynchronous updates, blue bar). We
note that this setting is essentially polling interval
combined with synchronous updates. With the only
effect left due to polling intervals, we observed that
a higher average interval at 8 consistently achieved
higher resistance to attacks than without the polling
interval (i.e., 1) across all data and model complexi-
ties (cf. Figure 10).
On a final note, in both experiments of the asyn-
chronous training and polling intervals we observed
consistently high test accuracy as reported in Figure 9
and Figure 10. This finding is consistent with previ-
ous work on asynchronous learning that showed that
asynchronous updates achieve robust training qual-
ity (Dean et al., 2012; Mania et al., 2017).
5 RELATED WORK
Privacy Preserving Machine Learning. While
Federated Machine Learning represents a recent tech-
nique to protect the privacy of training data, preserv-
ing the privacy in machine learning is a much broader
area of research (Shokri and Shmatikov, 2015; Abadi
et al., 2016; Mohassel and Zhang, 2017; Bonawitz
et al., 2017; Phong et al., 2017; Phong et al., 2018).
In particular, (Mohassel and Zhang, 2017) consid-
ers a non-federated setting where users upload se-
cret shares of their data on two non-colluding servers.
(Shokri and Shmatikov, 2015) uses a central param-
eter server to host the up-to-date model. It allows
clients to train on the latest model while only send-
ing selective gradients. However, it cannot prevent
gradient-based attacks from colluding clients or a cor-
rupt server.
Privacy in Federated Machine Learning (ML).
There have already been several existing approaches
for enhancing privacy in Federated ML. In fact,
cryptographic techniques such as differential privacy
(McMahan et al., 2018), homomorphic encryption
(Liu et al., 2020) or secure multi-party computation
(Bonawitz et al., 2017) have also been proposed to im-
prove the privacy in the context of federated learning.
However, as mentioned previously these techniques
show several limitations such as limited compatibil-
ity with different model architectures or an increased
learning overhead.
Recently, papers also explored non-cryptographic
techniques to protect privacy in Federated ML, such
as gradient compression (Lin et al., 2018; Zhu et al.,
2019). In this technique, gradients with small values
are pruned to zero such that the number of useful gra-
dients that are sent to the server are limited. While
this technique also limits the amount of information
available to an attacker, it depends heavily on whether
gradients can be pruned or not and can influence the
training process negatively.
Decentralized Architectures and Sharding.
Moreover, there has been a lot of work in the context
of decentralized machine learning (Lian et al., 2017;
Orm
´
andi et al., 2013). This works mainly focus on
how to enable ML without using any central (parame-
ter) server component. In contrast, our approach does
not eliminate the parameter server, but decentralizes
this component itself. The most similar approach
with this regard is the work in (El-Mhamdi et al.,
2020). However, compared to their architecture,
which assumes a full replication of parameters across
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
266
0.0
0.2
0.4
DSSIM
LeNetZhu-MNIST ConvNet-MNIST
1
2
4
8
pollingInterval
0.0
0.2
0.4
DSSIM
LeNetZhu-CIFAR10
1
2
4
8
pollingInterval
ConvNet-CIFAR10
Random Pic Staleness-0 Staleness-8
(a) Average Performance
0.00
0.25
0.50
0.75
1.00
ACC
LeNetZhu-MNIST ConvNet-MNIST
1
2
4
8
pollingInterval
0.00
0.25
0.50
0.75
1.00
ACC
LeNetZhu-CIFAR10
1
2
4
8
pollingInterval
ConvNet-CIFAR10
Staleness-0 Staleness-8
(b) Accuracy
Figure 10: Influence of polling intervals on privacy attacks. Polling intervals enable P2Sharding to introduce asynchronous
effects even to synchronous training. As for staleness, an increased polling interval improves the privacy protection, i.e.,
increases the DSSIM (10) while not affecting the resulting model accuracy (10).
all server instances to make the overall training
robust against potentially misbehaving parameter
servers and thus to tolerate Byzantine failures, our
approach utilizes sharding to distribute parameters
across server instances to achieve privacy.
Lastly, sharding or partitioning in general has
widely been used in both database systems (DeWitt
and Gray, 1992) and ML systems (Dean et al., 2012;
Chilimbi et al., 2014; Li et al., 2014; Xing et al.,
2015) to improve scalability and performance or re-
duce communication costs (Zhang et al., 2020). How-
ever, to the best of our knowledge, looking at sharding
from a privacy perspective is a new proposal.
6 CONCLUSION AND FUTURE
WORK
The security of federated learning was recently called
into question by works on gradient-based attacks to
reconstruct private trainnig data. In this work, we
initiated the study of secure FL based on a differ-
ent, decentralized parameter server architecture called
P2Sharding. We proposed three configurations on
how to partition, serve and update the model param-
eters for better privacy. Empirical evidence on CI-
FAR10 and MNIST showed noticeably stronger re-
silience against gradient-based data reconstruction at-
tacks by limiting the attack outcome close to random
noise. In future work, we aim to further establish the
formal security analysis of our FL framework.
Several areas for other future work exist. Our
framework can be extended with differential privacy
or cryptographic tools to further strengthen the se-
curity such as against malicious adversaries or sup-
port secure synchronous non-stochastic optimization.
Another work is to develop an automatic mechanism
to optimally configure our framework given a wider
range of models and datasets. Lastly our framework
may also be extended for other security concerns in
federated learning such as data and model poisoning.
ACKNOWLEDGEMENTS
This work was partially funded by the National Re-
search Center ATHENE, the BMWK project SafeF-
BDC (01MK21002K), and the BMBF project Trust-
DBle (16KIS1267). We also thank hessian.AI for the
support.
REFERENCES
Abadi, M., Chu, A., Goodfellow, I. J., McMahan, H. B.,
Mironov, I., Talwar, K., and Zhang, L. (2016). Deep
learning with differential privacy. In Weippl, E. R.,
Katzenbeisser, S., Kruegel, C., Myers, A. C., and
Halevi, S., editors, ACM SIGSAC, CCS 2016, pages
308–318, Vienna, Austria. ACM.
Bonawitz, K., Eichner, H., Grieskamp, W., Huba, D., Inger-
man, A., Ivanov, V., Kiddon, C., Konecn
´
y, J., Maz-
zocchi, S., McMahan, B., Overveldt, T. V., Petrou, D.,
Ramage, D., and Roselander, J. (2019). Towards fed-
erated learning at scale: System design. In Talwalkar,
A., Smith, V., and Zaharia, M., editors, MLSys 2019,
pages 374–388, Stanford, CA, USA. mlsys.org.
Bonawitz, K. A., Ivanov, V., Kreuter, B., Marcedone, A.,
McMahan, H. B., Patel, S., Ramage, D., Segal, A.,
and Seth, K. (2017). Practical secure aggregation for
privacy-preserving machine learning. In Thuraising-
ham, B. M., Evans, D., Malkin, T., and Xu, D., editors,
ACM SIGSAC, CCS 2017, pages 1175–1191, Dallas,
TX, USA. ACM.
Towards Decentralized Parameter Servers for Secure Federated Learning
267

Brisimi, T. S., Chen, R., Mela, T., Olshevsky, A., Pascha-
lidis, I. C., and Shi, W. (2018). Federated learning
of predictive models from federated electronic health
records. Int. J. Medical Informatics, 112:59–67.
Brunet, D., Vrscay, E. R., and Wang, Z. (2012). On
the Mathematical Properties of the Structural Similar-
ity Index. IEEE Transactions on Image Processing,
21(4):1488–1499.
Chen, J., Pan, X., Monga, R., Bengio, S., and Jozefowicz,
R. (2017). Revisiting distributed synchronous sgd.
arXiv, pages 1–10.
Chilimbi, T. M., Suzue, Y., Apacible, J., and Kalyanara-
man, K. (2014). Project adam: Building an efficient
and scalable deep learning training system. In Flinn,
J. and Levy, H., editors, OSDI 2014, pages 571–582,
Broomfield, CO, USA. USENIX Association.
Dean, J., Corrado, G., Monga, R., Chen, K., Devin, M., Le,
Q. V., Mao, M. Z., Ranzato, M., Senior, A. W., Tucker,
P. A., Yang, K., and Ng, A. Y. (2012). Large scale
distributed deep networks. In Bartlett, P. L., Pereira,
F. C. N., Burges, C. J. C., Bottou, L., and Weinberger,
K. Q., editors, NIPS 2012, pages 1232–1240, Lake
Tahoe, NV, USA. Curran Associates, Inc.
DeWitt, D. J. and Gray, J. (1992). Parallel database sys-
tems: The future of high performance database sys-
tems. Commun. ACM, 35(6):85–98.
El-Mhamdi, E., Guerraoui, R., Guirguis, A., Hoang, L. N.,
and Rouault, S. (2020). Genuinely distributed byzan-
tine machine learning. In Emek, Y. and Cachin, C.,
editors, ACM PODC 2020, Virtual Event, pages 355–
364, Italy. ACM.
Geiping, J., Bauermeister, H., Dr
¨
oge, H., and Moeller, M.
(2020). Inverting gradients - how easy is it to break
privacy in federated learning? In Larochelle, H., Ran-
zato, M., Hadsell, R., Balcan, M., and Lin, H., editors,
NeurIPS 2020, 2020, virtual.
Goldreich, O. (1998). Secure multi-party computation.
Manuscript. Preliminary version, 78.
Kairouz, P., McMahan, H. B., Avent, B., Bellet, A., Ben-
nis, M., Bhagoji, A. N., Bonawitz, K. A., Charles, Z.,
Cormode, G., Cummings, R., D’Oliveira, R. G. L.,
Rouayheb, S. E., Evans, D., Gardner, J., Garrett, Z.,
Gasc
´
on, A., Ghazi, B., Gibbons, P. B., Gruteser, M.,
Harchaoui, Z., He, C., He, L., Huo, Z., Hutchinson,
B., Hsu, J., Jaggi, M., Javidi, T., Joshi, G., Kho-
dak, M., Kone
ˇ
cn
´
y, J., Korolova, A., Koushanfar, F.,
Koyejo, S., Lepoint, T., Liu, Y., Mittal, P., Mohri, M.,
Nock, R.,
¨
Ozg
¨
ur, A., Pagh, R., Raykova, M., Qi, H.,
Ramage, D., Raskar, R., Song, D., Song, W., Stich,
S. U., Sun, Z., Suresh, A. T., Tram
`
er, F., Vepakomma,
P., Wang, J., Xiong, L., Xu, Z., Yang, Q., Yu, F. X., Yu,
H., and Zhao, S. (2019). Advances and open problems
in federated learning.
Kone
ˇ
cn
´
y, J., McMahan, H. B., Yu, F. X., Richt
´
arik, P.,
Suresh, A. T., and Bacon, D. (2016). Federated Learn-
ing: Strategies for Improving Communication Effi-
ciency. pages 1–10.
Krizhevsky, A. (2009). Learning multiple layers of fea-
tures from tiny images. Technical report, University
of Toronto.
LeCun, Y. (1998). The mnist database of handwritten digits.
Li, M., Andersen, D. G., Park, J. W., Smola, A. J., Ahmed,
A., Josifovski, V., Long, J., Shekita, E. J., and Su, B.
(2014). Scaling distributed machine learning with the
parameter server. In Flinn, J. and Levy, H., editors,
OSDI 2014, pages 583–598, Broomfield, CO, USA.
USENIX Association.
Li, T., Sahu, A. K., Talwalkar, A., and Smith, V. (2020).
Federated learning: Challenges, methods, and future
directions. IEEE Signal Process. Mag., 37(3):50–60.
Lian, X., Zhang, C., Zhang, H., Hsieh, C., Zhang, W., and
Liu, J. (2017). Can decentralized algorithms outper-
form centralized algorithms? A case study for decen-
tralized parallel stochastic gradient descent. In Guyon,
I., von Luxburg, U., Bengio, S., Wallach, H. M., Fer-
gus, R., Vishwanathan, S. V. N., and Garnett, R., edi-
tors, NIPS 2017, pages 5330–5340, Long Beach, CA,
USA.
Lin, Y., Han, S., Mao, H., Wang, Y., and Dally, B. (2018).
Deep gradient compression: Reducing the commu-
nication bandwidth for distributed training. In ICLR
2018, Vancouver, BC, Canada. OpenReview.net.
Liu, D. C. and Nocedal, J. (1989). On the limited mem-
ory BFGS method for large scale optimization. Math.
Program., 45(1-3):503–528.
Liu, Y., Kang, Y., Xing, C., Chen, T., and Yang, Q. (2020).
A secure federated transfer learning framework. IEEE
Intelligent Systems, 35(4):70–82.
Mania, H., Pan, X., Papailiopoulos, D., Recht, B., Ram-
chandran, K., and Jordan, M. I. (2017). Perturbed iter-
ate analysis for asynchronous stochastic optimization.
SIAM Journal on Optimization, 27(4):2202–2229.
McMahan, B., Moore, E., Ramage, D., Hampson, S., and
y Arcas, B. A. (2017). Communication-efficient learn-
ing of deep networks from decentralized data. In
Singh, A. and Zhu, X. J., editors, AISTATS 2017 ,
pages 1273–1282, Fort Lauderdale, FL, USA. PMLR.
McMahan, H. B., Ramage, D., Talwar, K., and Zhang, L.
(2018). Learning differentially private recurrent lan-
guage models. In ICLR 2018, Vancouver, BC, Canada.
OpenReview.net.
Melis, L., Song, C., Cristofaro, E. D., and Shmatikov, V.
(2018). Inference attacks against collaborative learn-
ing. CoRR, abs/1805.04049:1–16.
Mohassel, P. and Zhang, Y. (2017). SecureML: A Sys-
tem for Scalable Privacy-Preserving Machine Learn-
ing. In IEEE SP 2017, pages 19–38, San Francisco,
CA, USA. ISSN: 2375-1207.
Orm
´
andi, R., Heged
¨
us, I., and Jelasity, M. (2013). Gossip
learning with linear models on fully distributed data.
Concurr. Comput. Pract. Exp., 25(4):556–571.
Phong, L. T., Aono, Y., Hayashi, T., Wang, L., and Moriai,
S. (2017). Privacy-Preserving Deep Learning: Revis-
ited and Enhanced. In Batten, L., Kim, D. S., Zhang,
X., and Li, G., editors, Applications and Techniques in
Information Security, Communications in Computer
and Information Science, pages 100–110, Singapore.
Springer.
Phong, L. T., Aono, Y., Hayashi, T., Wang, L., and
Moriai, S. (2018). Privacy-Preserving Deep Learn-
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
268

ing via Additively Homomorphic Encryption. IEEE
Transactions on Information Forensics and Security,
13(5):1333–1345.
Shokri, R. and Shmatikov, V. (2015). Privacy-Preserving
Deep Learning. In ACM SIGSAC,CCS 2015, pages
1310–1321, Denver, Colorado, USA. ACM Press.
Wang, Z., Bovik, A. C., Sheikh, H. R., and Simoncelli, E. P.
(2004). Image quality assessment: from error visibil-
ity to structural similarity. IEEE Trans. Image Pro-
cess., 13(4):600–612.
Wei, W., Liu, L., Loper, M., Chow, K. H., Gursoy, M. E.,
Truex, S., and Wu, Y. (2020). A framework for eval-
uating gradient leakage attacks in federated learning.
CoRR, abs/2004.10397:1–25.
Xing, E. P., Ho, Q., Dai, W., Kim, J. K., Wei, J., Lee, S.,
Zheng, X., Xie, P., Kumar, A., and Yu, Y. (2015).
Petuum: A new platform for distributed machine
learning on big data. In Cao, L., Zhang, C., Joachims,
T., Webb, G. I., Margineantu, D. D., and Williams, G.,
editors, ACM SIGKDD 2015, pages 1335–1344, Syd-
ney, NSW, Australia. ACM.
Zhang, Z., Wu, W., Jiang, J., Yu, L., Cui, B., and Zhang, C.
(2020). Columnsgd: A column-oriented framework
for distributed stochastic gradient descent. In IEEE
ICDE 2020, pages 1513–1524. IEEE.
Zhao, B., Mopuri, K. R., and Bilen, H. (2020). idlg:
Improved deep leakage from gradients. CoRR,
abs/2001.02610:1–5.
Zhu, L., Liu, Z., and Han, S. (2019). Deep leakage from
gradients. In Wallach, H. M., Larochelle, H., Beygelz-
imer, A., d’Alch
´
e-Buc, F., Fox, E. B., and Garnett, R.,
editors, NeurIPS 2019, pages 14747–14756, Vancou-
ver, BC, Canada. Curran Associates, Inc.
Towards Decentralized Parameter Servers for Secure Federated Learning
269
