CRGC: A Practical Framework for Constructing Reusable Garbled

Circuits

Christopher Harth-Kitzerow

, Georg Carle

, Fan Fei

, Andre Luckow

and Johannes Klepsch

Department of Informatics, Technical University of Munich, Garching, Germany

Faculty of Electrical Engineering and Computer Science, Leibniz University Hannover, Hannover, Germany

Group IT, The BMW Group, Munich, Germany

Keywords:

Secure Multiparty Computation, Garbled Circuits, Privacy Enhancing Technologies.

Abstract:

In this work, we introduce two schemes to construct reusable garbled circuits (RGCs) in the semi-honest

setting. Our completely reusable garbled circuit (CRGC) scheme allows the generator (party A) to construct

and send an obfuscated boolean circuit along with an encoded input to the evaluator (party B). In contrast to

Yao’s Garbled Circuit protocol, B can securely evaluate the same CRGC with an arbitrary number of inputs.

As a tradeoff, CRGCs predictably leak some input bits of A to B. We also propose a partially reusable garbled

circuit (PRGC) scheme that divides a circuit into reusable and non-reusable sections. PRGCs do not leak

input bits of A. We benchmark our CRGC implementation against the state-of-the-art garbled circuit libraries

EMP SH2PC and TinyGarble2. Using our framework, evaluating a CRGC is up to twenty times faster, albeit

with weaker privacy guarantees, than evaluating an equivalent garbled circuit constructed by the two existing

libraries. Our open-source library can convert any C++ function to a CRGC at approx. 80 million gates per

second and repeatedly evaluate a CRGC at approx. 350 million gates per second. Additionally, a compressed

CRGC is approx. 75% smaller in ﬁle size than the unobfuscated boolean circuit.

1 INTRODUCTION

Secure Multiparty Computation enables parties to ex-

ecute functions on obliviously shared inputs without

revealing them (Lindell, 2020). Yao’s Garbled Cir-

cuits protocol (Yao, 1982; Yao, 1986) is a popular

Secure Multiparty Computation protocol for realiz-

ing semi-honest two-party computation. Following

the protocol, a circuit generator A sends its encoded

inputs and the encrypted and permuted gate output ta-

bles of a boolean circuit to a circuit evaluator B. B

can obtain only one encoded input per circuit through

Oblivious Transfer. Thus, each time B wants to obtain

an output from a different input, it needs to request an-

other garbled circuit. Garbled circuits get large in ﬁle

size. Our Reusable Garbled Circuit (RGC) schemes

allow B to re-use a garbled circuit for multiple eval-

uations with different evaluator inputs. They signiﬁ-

cantly reduce communication overhead compared to

sending a new garbled circuit for each evaluation.

RGCs enable party A to send obfuscated data to an un-

trusted party B while ensuring that sent data remains

secret and can only be used for its intended purpose

implemented by the circuit. B can evaluate an RGC

with an arbitrary number of inputs without revealing

A’s input.

Existing RGC schemes usually rely on crypto-

graphic primitives that are too complex for real-

world use cases. Our key idea instead is to uti-

lize information-theoretic techniques to obfuscate the

wire labels that A sends to B in a way that hinders B

from learning A’s secret inputs. With this approach,

B can repeatedly evaluate the same obfuscated circuit

with arbitrary inputs. Only when A

′

s input changes

it needs to construct a new RGC. While constructing

an RGC can take longer than constructing a garbled

circuit, it pays off over time due to faster evaluation

speed. Not all gates in a circuit can be obfuscated

without leaking input bits. Thus, A has two options:

1. It obfuscates only those gates with our techniques

that do not leak information. It then groups the

remaining unobfuscated gates into n non-reusable

sub-circuits and prepares n Yao’s Garbled Circuit

protocols. With this approach, we obtain reusable

and non-reusable sections in a circuit. We call the

resulting circuit a partially reusable garbled cir-

cuit (PRGC).

2. It obfuscates all gates with our techniques and

tolerates a certain number of leaked input bits.

We call the resulting circuit a completely reusable

garbled circuit (CRGC).

Harth-Kitzerow, C., Carle, G., Fei, F., Luckow, A. and Klepsch, J.

CRGC: A Practical Framework for Constructing Reusable Garbled Circuits.

DOI: 10.5220/0011145300003283

In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 83-95

ISBN: 978-989-758-590-6; ISSN: 2184-7711

Our CRGC scheme essentially transforms a

boolean circuit C that computes a functionality f (a,b)

into a boolean circuit C

′

and obfuscated input a

′

such

that C

′

,b) = C(a,b) for a speciﬁc input a and any

arbitrary input b. Evaluating C

′

is as efﬁcient as evalu-

ating C. Given C

′

, C, and a

′

it is difﬁcult to infer input

bits of a even with repeated evaluations. Our PRGC

scheme divides a CRGC C

′

into reusable sub-circuits

(sections) and non-reusable sections. Reusable sec-

tions do not leak inputs of a. Non-reusable sections

contain gates that may leak input bits of a. Thus,

A and B engage in a Yao’s Garbled Circuit protocol

for each non-reusable section in C

′

for each repeated

evaluation. As a result, our PRGC scheme guaran-

tees the same level of input privacy as Yao’s Garbled

Circuit protocol.

Our framework compiles any user-deﬁned C++

program and a set of inputs into a CRGC and a set of

encoded inputs. A can send these compressed over the

network to B. B can use our implementation to eval-

uate the CRGC with an arbitrary number of inputs.

We tested several programs such as linear search, set

intersection, and data analysis but also elementary

operations such as addition and multiplication. Our

benchmarks show that an Amazon M5ZN instance

can construct CRGCs at approx. 80 million gates per

second and evaluate them at approx. 350 million gates

per second. The construction is only necessary once

per input of party A. EMP SH2PC (Wang et al., 2016)

and TinyGarble2 (Hussain et al., 2020) can evaluate

the same programs at up to 55 million gates per sec-

ond but without leaking any input bits to B.

2 OUR APPROACH

In this section, we show how A can construct a CRGC

and a PRGC. Any boolean circuit C and generator in-

put a can be converted into an RGC C

′

and an obfus-

cated input a

′

using three different kinds of obfusca-

tion techniques: Bit Flipping, obfuscating ﬁxed gates,

and obfuscating intermediary gates. After applying

our obfuscation techniques, C

′

is tied to a single a

′

meaning that ∃a∀b : C

′

,b) = C(a, b) but for inputs

not equal to a

′

the output equality of C and C

′

is not

ensured.

We call XNOR and XOR gates balanced gates,

and all other gates imbalanced gates. We refer to a

gate as a passive gate if modifying its truth table does

not alter the circuit’s output. A gate provides indis-

tinguishability obfuscation if B has an advantage of

0 to distinguish between a gate’s truth table entry re-

sulting from a generator’s input of 0 and 1. In our

PRGC protocol, only truth tables of gates that provide

indistinguishability obfuscation and ﬁnal output gates

are contained in the reusable section. A uses Yao’s

Garbled Circuit protocol to ensure that the remain-

ing gates also do not leak any input bits of a. In our

CRGC protocol, A instead also sends these remaining

gates to B without additional obfuscation, thus toler-

ating a predictable number of leaked input bits.

2.1 Bit Flipping

Bit Flipping refers to applying a one-time pad r over

the input bits of a and all wires in the circuit C to

obtain C

′

and a

′

. Only inputs from B and ﬁnal output

wires do not get ﬂipped. Whenever, a wire w is ﬂipped

by r, A needs to modify the truth table of w’s child

gates to recover the integrity of C

′

. For instance, if the

left input wire of a gate g with functionality f (u,v) is

ﬂipped, A can modify g

′

s truth table to f (¬u,v) to

ensure that C

′

,b) = C(a, b).

Since an RGC should be dependent on one ﬁxed a

with a bitlength l, truth table entries that contain ¬a

(i < l) can be modiﬁed arbitrarily while maintaining

the integrity of C

′

. Algorithm 1 realizes Bit Flipping.

Since a one-time pad is only secure for a single input,

A has to construct a new RGC if a changes. However,

B can use C

′

and a

′

for multiple of its own inputs b.

With Bit Flipping, all balanced gates (XOR, XNOR)

in C

′

achieve indistinguishability obfuscation.

Algorithm 1: Bit Flipping.

1: for each generator input a[i] do

2: a

′

[i] ← generateRandomBit()

3: f lipped[i] ← a

′

[i] == a[i]

4: for each gate g do

5: recoverIntegrity(g)

6: f lipped[g] ← generateRandomBit()

7: if f lipped[g] == true & g ̸∈ Output then

8: f lipTruthTable(g)

2.1.1 Examples

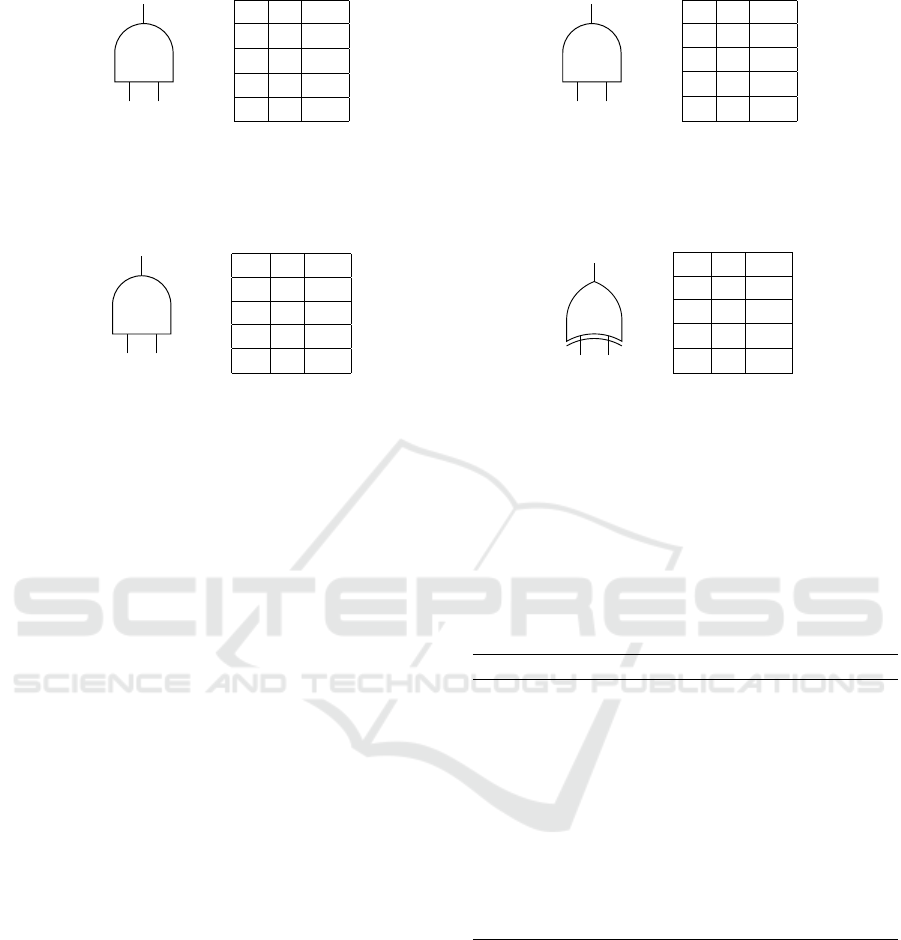
Figure 1 illustrates the achieved indistinguishability

of randomly ﬂipping balanced gates. Note that truth

tables shown in Figure 1a and 1b are identical, even

though their generator inputs u differ. Figure 1c, 1d

show the other two identical truth tables constructed

from different inputs and ﬂips. Since B can obtain two

identical truth tables from a generator’s value of 0 and

1, it cannot infer u from inspecting the truth table of a

potentially ﬂipped balanced gate.

Bit Flipping does not lead to an indistinguishabil-

ity obfuscation for imbalanced gates. All four com-

binations of randomly ﬂipping the generator’s input

u and the output wire w yield distinct truth tables.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

u v

XOR

u v w

0 0 1

0 1 0

1 0 0

1 1 1

(a) XOR gate, left parent ﬂipped.

u v

XOR

u v w

0 0 1

0 1 0

1 0 0

1 1 1

(b) XOR gate, output ﬂipped.

u v

XOR

u v w

0 0 0

0 1 1

1 0 1

1 1 0

u v

XOR

u v w

0 0 0

0 1 1

1 0 1

1 1 0

(d) XOR gate, left parent & output ﬂipped.

Figure 1: Flipping balanced gates yields indistinguishable truth tables.

Thus, even though a

′

is obfuscated by r

, B can in-

fer a

by inspecting any imbalanced gate with func-

tionality f (a

′

). Our following two techniques also

obfuscate imbalanced gates.

2.2 Obfuscating Fixed Gates

We deﬁne ﬁxed gates as gates that always return the

same value given the generator input a. For instance,

an AND gate that takes a generator input of 0 is a ﬁxed

gate. The problem with an imbalanced gate on level 1

is that B can immediately infer A

′

s input by observing

if its output changes when changing B

′

s input bit. A

can effectively obfuscate those gates by ﬂipping one

of the output values in the truth table and adjusting

child gates accordingly. This way, a ﬁxed imbalanced

gate at level 1 is indistinguishable from an unﬁxed

one. When obfuscating a ﬁxed gate, we break the

gate’s integrity, i.e., we might return a value of 1 even

though its correct value is 0. The integrity of C

′

has

to be recovered to yield the correct output. Algorithm

2 identiﬁes all ﬁxed gates and ensures that modifying

ﬁxed gates maintains the correctness of C

′

2.2.1 Examples: Obfuscating Fixed Gates

Figure 2 illustrates the following examples. Consider

an AND gate g at level 1 in C that depends on one

input u of A and one input v of B. Suppose A’s input is

1 (Figure 2a). In this case, the relevant output entries

for g are 1|0|0 and 1|1|1 (left input|right input|output).

A can modify the other two entries arbitrarily as they

depend on a different generator input. Thus, A can

obfuscate g to an XNOR gate by assigning the unused

truth table entries to 0|0|1 and 0|1|0.

Suppose A’s input is 0 (Figure 2b). In this case,

g is a ﬁxed gate since the two relevant entries in its

Algorithm 2: Identify ﬁxed gates.

1: for each generator input a[i] do

2: f ixedValue[i] ← a[i]

3: isFixed[i] ← true

4: for each gate g do

5: l ← g.le f tParent

6: r ← g.rightParent

7: T ← g.truthTable

8: v

← f ixedValue[l]

9: v

← f ixedValue[r]

10: if isFixed[l] & isFixed[r] then

11: f ixedValue[g] ← T [v

][v

]

12: isFixed[g] ← true

13: else

14: if isFixed[l] & T [v

][0] == T [v

][1] then

15: f ixedValue[g] ← T [v

][0]

16: isFixed[g] ← true

17: if isFixed[r] & T [0][v

] == T [1][v

] then

18: f ixedValue[g] ← T [0][v

]

19: isFixed[g] ← true

20: if !isFixed[g] then

21: recoverIntegrity(g)

truth table 0|0|0 and 0|1|0 both return a 0 independent

of B’s input. The ﬁxed output immediately reveals u

to B if it knows the gate type. A obfuscates a ﬁxed

gate by choosing one of these entries at random and

ﬂipping its output wire. For instance, A can change

the entry 0|0|0 to 0|0|1. This way, we again created a

truth table indistinguishable from XNOR. We showed

before that A can apply Bit Flipping to a balanced

gate like X NOR to achieve indistinguishability obfus-

cation. Again, truth tables shown in Figure 2a and

2b are identical, even though their generator inputs u

differ.

CRGC: A Practical Framework for Constructing Reusable Garbled Circuits

u = 1 v

AND

u v w

0 0 1

†

0 1 0

†

1 0 0

1 1 1

(a) Unﬁxed AND gate, obfuscated.

u = 0 v

AND

u v w

0 0 1

⋆

0 1 0

1 0 0

†

1 1 1

†

(b) Fixed AND gate, obfuscated.

†

These entries do not depend on the generator’s input and can be re-assigned arbitrarily.

⋆

One relevant entry in a ﬁxed gate gets ﬂipped.

Figure 2: Obfuscated imbalanced gates on level 1.

w (0) x

AND

w x y

0 0 0

0 1 0

1 0 0

1 1 0

†

(a) Child AND gate.

⋆

w (0) x

XOR

w x y

0 0 0

0 1 1

1 0 0

†

1 1 1

†

(b) Child XOR gate.

†

Left parent’s true value is 0. Truth table gets recovered accordingly.

⋆

Adjusting the truth table transformed the child gate into a ﬁxed gate. This gate gets obfuscated in the next iteration of algorithm 2.

Figure 3: Gates with a ﬁxed left parent.

2.2.2 Examples: Modifying Child Gates

Figure 3a shows an AND gate g with a ﬁxed obfus-

cated AND gate as its left parent. A can recover g’s

integrity by changing the entry 1|1|1 to 1|1|0. A just

transformed g into a ﬁxed gate that always returns 0.

Thus, A can apply our obfuscation technique to this

gate as well. Figure 3b shows an XOR gate with a

ﬁxed obfuscated AND gate as its left parent. A can

recover its integrity by changing the entries 1|0|1 and

1|1|0 to 1|0|0 and 1|1|1. Notice that the resulting truth

table is not a balanced gate. Thus, it does not provide

indistinguishability obfuscation.

2.3 Obfuscating Intermediary Gates

Some gates g

do not affect the circuit’s output as all

paths from g

to a ﬁnal output gate g

include at least

one ﬁxed gate g

. We call these gates between the

ﬁrst level of the circuit and the dependant ﬁxed gates

intermediary gates.

If A modiﬁes an intermediary gate g

, each ﬁxed

gate’s output wire may change its value due to chang-

ing the truth table of a gate it depends on. However,

we know that changing an obfuscated ﬁxed gate’s

value does not change the ﬁnal output of C

′

. By def-

inition we also know that no ﬁnal output gate g

di-

rectly depends on g

without a ﬁxed gate g

between

and g

. Thus, arbitrary modiﬁcations of interme-

diary gates do not break the integrity of C

′

. Due to

this property, ﬁxed and intermediary gates are passive

gates. A can modify each passive gate’s truth table

to be indistinguishable from its active version. At the

end of Algorithm 3, all gates where ob f uscatable[g]

has not been set to f alse are passive gates. Our proto-

col re-generates each gate on level 1 to a random bal-

anced gate and all other passive and balanced gates to

provide indistinguishability obfuscation.

Algorithm 3: Identify passive gates.

1: for each ﬁnal output gate g

2: queue.push(g

) ▷ output gates are

non-intermediary

3: while ! queue.empty() do

4: g ← queue.pop()

5: ob f uscatable[g] ← f alse

6: for each parent p of g do

7: if !isFixed[p] & !pushed[p] then

8: pushed[p] ← true

9: queue.push(p)

▷ non-intermediary gates get pushed

2.3.1 Example

Figure 4 illustrates a section of a circuit with two ﬁxed

gates. Note that all paths from the unﬁxed gates in the

section end up as an input wire of a ﬁxed gate. Thus,

all four unﬁxed gates in this section are intermediary

gates. Modifying their truth tables may change the

output of one of the ﬁxed gates. However, this modi-

ﬁcation will not affect the output of the circuit.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

fixed

⋆

Properties hold for every gate type.

Figure 4: Section of a circuit containing four intermediary

gates

⋆

2.4 Constructing a CRGC

The whole process of constructing a CRGC can be

summarized as follows:

1. Obtain C

′

and a

′

by applying Bit Flipping to a and

all gates in C using algorithm 1.

2. Identify all ﬁxed gates and modify all children of

ﬁxed gates in C

′

using algorithm 2.

3. Identify all intermediary gates in C

′

using algo-

rithm 3.

4. Obfuscate all imbalanced, ﬁxed, and intermediary

gates on level 1 randomly to XOR/XNOR. Ob-

fuscate all passive gates in C

′

beyond level 1 to

achieve indistinguishability obfuscation.

After these steps, an evaluator that receives C

′

and

′

can evaluate C

′

any number of times with varying

inputs b. For all gates g

that do not provide indistin-

guishability obfuscation, B has an advantage > 0 to

infer the true wire labels of g

’s parents. Thus, some

of these gates may leak input bits of A. A can predict

the leakage of a CRGC before constructing it and de-

cide whether to send the CRGC that leaks some input

bits or to construct a PRGC instead. PRGCs do not

leak generator inputs. In the appendix, we show how

A can predict input leakage of a constructed CRGC

and achieve n-party computations from our CRGC

scheme. We also give a step-by-step example of ap-

plying our obfuscation techniques to a circuit.

2.5 Constructing a PRGC

After applying the three described obfuscation tech-

niques, there is a subset of gates left in C

′

that do

not provide indistinguishability obfuscation, i.e. B

might be able to infer input bits of a when inspect-

ing those gates. Our PRGC scheme prevents B from

inferring inputs when inspecting these gates by intro-

ducing non-reusable sections.

2.5.1 Non-reusable Sections

Each gate that does not provide indistinguishability

obfuscation has to be contained in a non-reusable sec-

tion. At the start of a non-reusable section s of C

′

, A

and B engage in Oblivious Transfer (OT) for each in-

put wire on the ﬁrst level of s to let B obtain keys to

be used in a Yao’s Garbled Circuit protocol. A non-

reusable section ends if each ﬁnal output gate of the

non-reusable section provides indistinguishability ob-

fuscation. A needs to apply a new Bit Flipping to each

of these output gates to hinder B from inferring inputs

by evaluating the circuit multiple times. With this ap-

proach, A and B have to engage in a Yao’s Garbled

Circuit protocol for each non-reusable section. With

the output bits obtained from Yao’s Garbled Circuit

protocol, B continues evaluating the circuit.

By ”refreshing” Bit Flipping at the end of a non-

reusable section, all balanced gates again provide in-

distinguishability obfuscation. To ensure correctness,

both parties need to engage in OT for each ﬁnal out-

put gate of C

′

to let A reverse Bit Flipping applied

in the non-reusable sections. Note that a simpler

protocol could consist of evaluating each gate that

does not provide indistinguishability obfuscation by

an OT with a bit ﬂipped result. However, if a non-

reusable section spans multiple levels in the circuit,

using Yao’s Garbled Circuit protocol is more efﬁcient.

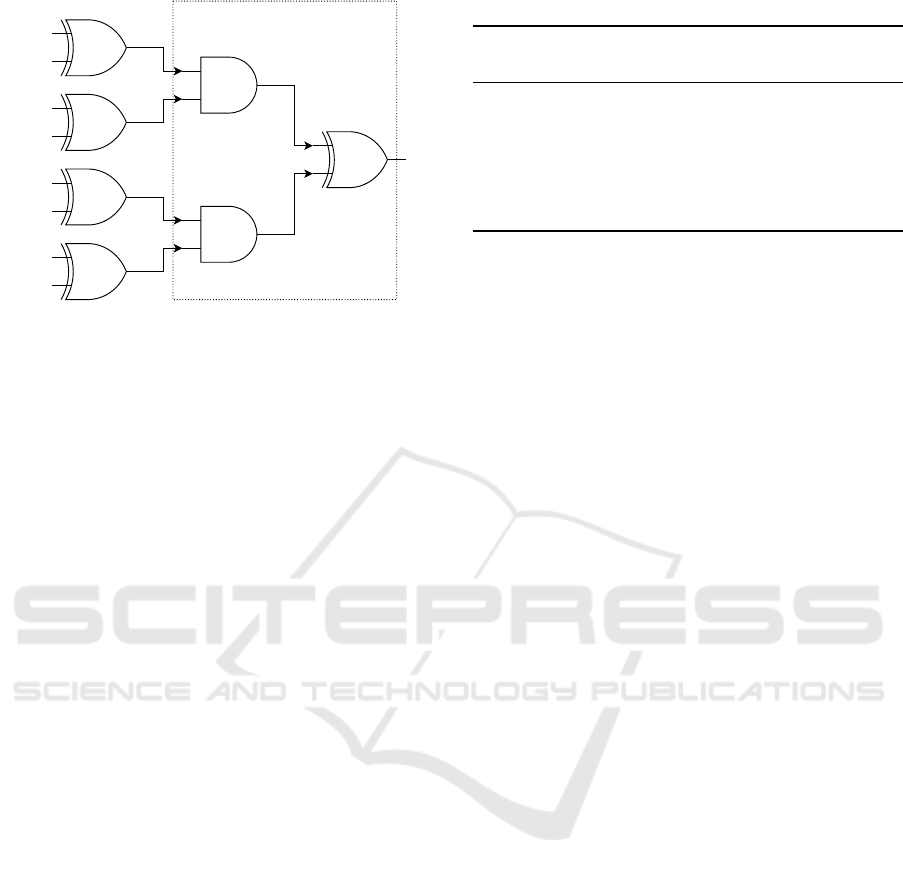
Figure 5 illustrates a circuit with a non-reusable

section. Inputs a

mark A’s inputs, inputs b

mark B’s

inputs. Observe that both AND gates cannot be ﬁxed

gates and reveal A’s input even if obfuscated by our

techniques. The ﬁnal XOR gate marks the end of the

non-reusable section by providing indistinguishabil-

ity obfuscation. A only sends the gates in the reusable

section (ﬁrst level) to B. By assigning the two AND

gates and the ﬁnal XOR gate to a non-reusable sec-

tion, B has to stop evaluating the PRGC after the ﬁrst

level. For each input wire of each AND gate, it has to

receive an input key via OT and obtain a Yao’s Gar-

bled Circuit from A containing the remaining three

gates. For each repeated evaluation of the circuit with

different inputs b, it can reuse the gates on the ﬁrst

level of the circuit.

PRGCs provide input privacy without leakage. A

security proof of PRGCs can be found in the ap-

pendix. There, we also cover how to achieve indis-

tinguishability obfuscation for passive gates in the

reusable section. In high latency environments, it

might be favorable to split C

′

into only one reusable

and one non-reusable section. This way, a PRGC

can be evaluated in constant communication rounds

where one batch of OTs is processed in parallel.

CRGC: A Practical Framework for Constructing Reusable Garbled Circuits

AND

XOR

AND

XOR

Non-reusable Section

Figure 5: A circuit containing a non-reusable section.

3 BENCHMARKS

Our open-source library is available on GitHub. With

our library, A can construct a CRGC from any user-

deﬁned C++ function, compress it, predict leaked in-

put bits, and send it over the network to B. B can

evaluate the CRGC and store it on its hard drive for

future use. For compiling a C++ function to a boolean

circuit, we mainly rely on modules provided by EMP.

We tested our implementation on two AWS

M5ZN metal instances with 24 cores, 48 threads, and

192GB of RAM connected via 100 Gbit/s network

connections to the internet in a WAN setting. A can

construct a CRGC at a speed of up to 85 million gates

per second, perform leakage prediction with up to

115 million gates per second and evaluate a circuit

with up to 395 million gates per second. For com-

parison, we also implemented our test programs with

EMP SH2PC and TinyGarble2. Since EMP SH2PC

and TinyGarble2 implement a regular garbled circuit

protocol, an evaluation must always be performed to-

gether with circuit construction. In all tests, EMP per-

forms better than TinyGarble2 and achieves a speed of

up to 55 million gates per second. Thus, after only a

few evaluations, our CRGC library outperforms both

libraries. All CRGCs we constructed leak at most two

input bits to B. We use the Turbo Pfor integer com-

pression algorithm (Lemire et al., 2014) before send-

ing a CRGC over a network or storing it locally. As

a result, a CRGC is approx. 75% smaller in ﬁle size

than the original uncompressed boolean circuit.

3.1 Basic Circuits

Table 1 shows the results of applying our protocol to

elementary circuits. |C| shows the number of gates in

a circuit. Inputs leaked refers to the number of gen-

Table 1: Evaluation time for basic circuits.

Circuit |C| Inputs Evaluation

leaked time (µs)

64-bit Adder 376 1/64 2

64-bit Subtract 439 1/64 2

64-bit Multiplier 13675 2/64 36

AES-256(k,m) 50666 0/256 94

SHA256 135073 0/512 205

SHA512 349617 0/1024 551

erator inputs a CRGC leaks. All tested basic circuits

can be evaluated in under 1ms by our library.

3.2 Large Circuits

We also tested more complex circuits that implement

three real-world use cases: Finding an element in an

unsorted list (query), identifying the maximum ele-

ment in a speciﬁc coordinate range of a 2D array, and

ﬁnding the intersect of two datasets. The resulting cir-

cuits have up to 1.9 billion gates and leak at most one

input bit to B. These larger circuits demonstrate that

our library is practical for real problems.

Our programs may serve as references for other

functionalities. Table 2 shows that our library can

process a dataset containing millions of entries in just

a few seconds for simple functionalities. For com-

plex functions such as the demonstrated set intersec-

tion, it can process a few thousand elements per sec-

ond. These results may serve as a rough estimation

of whether CRGCs can cope with a certain problem

size.

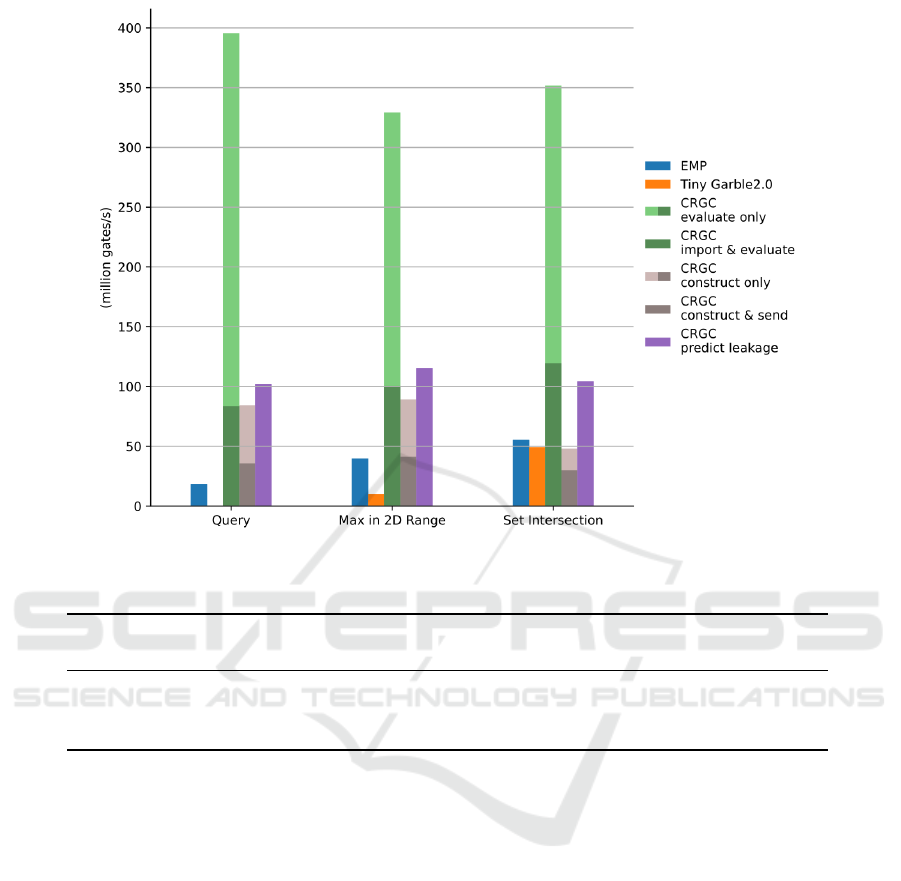
Figure 6 shows the results of benchmarking our

framework against EMP SH2PC and TinyGarble2.

Recall that A has to perform leakage prediction only

once per circuit, independent of its inputs. It has to

generate a CRGC once per unique generator input a.

B has to evaluate a CRGC once per changing evalu-

ator input b. Thus, we measured all three tasks inde-

pendently.

The bars with different shades of colors show ad-

ditional costs that might occur along with a CRGC

component: After A constructs a CRGC, it needs

to send it to B over the network (brown bar). If B

does not store the circuit in memory after evaluat-

ing it, it needs to import the circuit from the hard

drive again before performing an additional evalua-

tion (green bar).

Our benchmark shows that our library can con-

sistently evaluate different circuits at approx. 350

million gates per second. Constructing a CRGC and

sending it to B is sometimes slower than perform-

ing a regular garbled circuit protocol with EMP once.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

400

350

300

Mmm

=EMP

Tiny

Garble2.0

—~

250

CRGC

evaluate

only

CRGC

import

evaluate

200

CRGC

construct

only

CRGC

construct

send

150

wes

CRGC

predict

leakage

100

Query

Max

Range

Set

Intersection

Figure 6: Performance Comparison of EMP SH2PC, TinyGarble2, and CRGC Components.

Table 2: Evaluation time for large circuits.

Functionality |C| Elements

Evaluation time (Elements/s)

CRGC EMP SH2PC TinyGarble2

Query 9,100,000 140,000 6,086,956 281,690 1,924

Max in 2D Range 123,815,518 148,996 396,265 48,094 11,860

Set Intersection 1,910,780,159 40,000 7,362 1,163 1,027

However, evaluating a CRGC is 5-20 times faster than

performing a garbled circuit protocol using EMP. In

all tests, using our library compared to EMP and Tiny-

Garble2 pays off after less than three evaluations.

Note that beyond our implementation, a generator

can always construct a PRGC with only one reusable

and non-reusable section. Since evaluating a CRGC

is faster than evaluating a regular garbled circuit, it

follows that for most circuits C, we can construct a

PRGC that can be evaluated faster than performing

Yao’s Garbled Circuit protocol with C.

4 RELATED WORK

Reusable garbled circuits have been gaining popular-

ity in the Secure Multiparty Computation community

during the last decade. (Saleem et al., 2018) sum-

marizes and discusses recent advancements in gar-

bled circuits. The authors state that one important

future step is constructing a reusable garbled circuit

scheme with low computational complexity. In con-

trast to our approach, existing proposals tried to build

CRGCs without leakage that do not scale well. To

achieve practicability, we propose a trade-off between

the extent of reusability and performance (PRGC), or

between security and performance (CRGC).

(Goldwasser et al., 2013) proposed the ﬁrst

reusable garbled circuit scheme that is based on func-

tional encryption. Functional encryption allows a user

to generate secret keys that enable a key holder to

learn a speciﬁc function output of encrypted data but

learn nothing about the data (Boneh et al., 2011).

However, their scheme relies on fully homomorphic

encryption and other computationally expensive tech-

niques to achieve functional encryption. Since then,

there have been optimizations to the computational

complexity of reusable garbled circuits that also rely

on fully homomorphic- or attribute-based encryption

(Boneh et al., 2014).

As both prior mentioned schemes for reusable

garbled circuits combine multiple complex crypto-

CRGC: A Practical Framework for Constructing Reusable Garbled Circuits

graphic primitives, it is difﬁcult to assess their efﬁ-

ciency. According to (Wang et al., 2017) both so-

lutions are not practical. Thus, (Wang et al., 2017)

constructed a reusable garbled circuit scheme with a

trade-off between security and privacy. Their solu-

tion does not contain any benchmarks or implementa-

tions. (Gorbunov et al., 2015) proposed a step towards

reusable garbled circuits by encrypting each garbled

value with a seed. For each wire and each gate, a dif-

ferent encryption key is used. The evaluator obtains

an encoded seed in the beginning to evaluate the cir-

cuit. However, their scheme does not achieve input

privacy.

Due to the lack of an existing reusable garbled cir-

cuit implementation, we compare our library with the

alternative of constructing a new Yao’s Garbled Cir-

cuit for each evaluation with a state-of-the-art frame-

work. Multiple libraries have been proposed that

implement Yao’s Garbled Circuit protocol with var-

ious optimizations such as Free XOR (Kolesnikov

and Schneider, 2008). Libraries that offer state-of-

the-art performance and rich functionalities are Tiny-

Garble2 (Hussain et al., 2020), Obliv-C (Zahur and

Evans, 2015), ABY (Demmler et al., 2015), and

EMP SH2PC (Wang et al., 2016). Since (Hussain

et al., 2020) demonstrated that TinyGarble2 outper-

forms Obliv-C and ABY, we chose EMP and Tiny-

Garble2 as our benchmark.

5 CONCLUSION

In this work, we proposed obfuscation-based tech-

niques for constructing completely reusable garbled

circuits (CRGCs) and partially reusable garbled cir-

cuits (PRGCs). We showed that our CRGC library

can evaluate constructed circuits up to 20 times faster

than current state-of-the-art garbled circuit libraries.

CRGCs come with predictable input leakage.

While we were not able to not infer multiple input

bits from our test circuits, certain functionalities or

more sophisticated analyses may do so. In this case,

the generator and evaluator can engage in our hybrid

PRGC protocol to only use a CRGC for evaluating the

sections of the underlying circuit that do not pose in-

put leakage. The remaining sub-circuits can be evalu-

ated by Yao’s Garbled Circuit protocol. Future work

may introduce techniques to increase the number of

gates in the reusable section or ﬁnd more efﬁcient

ways to construct RGCs for n-party computation.

REFERENCES

Boneh, D., Gentry, C., Gorbunov, S., Halevi, S., Niko-

laenko, V., Segev, G., Vaikuntanathan, V., and

Vinayagamurthy, D. (2014). Fully key-homomorphic

encryption, arithmetic circuit abe and compact gar-

bled circuits. In Annual International Conference on

the Theory and Applications of Cryptographic Tech-

niques, pages 533–556. Springer.

Boneh, D., Sahai, A., and Waters, B. (2011). Functional

encryption: Deﬁnitions and challenges. In Theory of

Cryptography Conference, pages 253–273. Springer.

Demmler, D., Schneider, T., and Zohner, M. (2015). Aby-

a framework for efﬁcient mixed-protocol secure two-

party computation. In NDSS.

Goldwasser, S., Kalai, Y., Popa, R. A., Vaikuntanathan, V.,

and Zeldovich, N. (2013). Reusable garbled circuits

and succinct functional encryption. In Proceedings of

the forty-ﬁfth annual ACM symposium on Theory of

computing, pages 555–564.

Gorbunov, S., Vaikuntanathan, V., and Wee, H. (2015).

Attribute-based encryption for circuits. Journal of the

ACM (JACM), 62(6):1–33.

Hussain, S., Li, B., Koushanfar, F., and Cammarota, R.

(2020). Tinygarble2: Smart, efﬁcient, and scalable

yao’s garble circuit. In Proceedings of the 2020

Workshop on Privacy-Preserving Machine Learning

in Practice, pages 65–67.

Kolesnikov, V. and Schneider, T. (2008). Improved garbled

circuit: Free xor gates and applications. In Interna-

tional Colloquium on Automata, Languages, and Pro-

gramming, pages 486–498. Springer.

Lemire, D., Boytsov, L., and Kurz, N. (2014). Simd com-

pression and the intersection of sorted integers. Soft-

ware: Practice and Experience, 46.

Lindell, Y. (2017). How to simulate it–a tutorial on the sim-

ulation proof technique. Tutorials on the Foundations

of Cryptography, pages 277–346.

Lindell, Y. (2020). Secure multiparty computation (mpc).

IACR Cryptol. ePrint Arch., 2020:300.

Lindell, Y. and Pinkas, B. (2009). A proof of security of

yao’s protocol for two-party computation. Journal of

cryptology, 22(2):161–188.

Saleem, A., Khan, A., Shahid, F., Alam, M. M., and Khan,

M. K. (2018). Recent advancements in garbled com-

puting: how far have we come towards achieving se-

cure, efﬁcient and reusable garbled circuits. Journal

of Network and Computer Applications, 108:1–19.

Wang, X., Malozemoff, A. J., and Katz, J. (2016). Emp-

toolkit: Efﬁcient multiparty computation toolkit.

Wang, X. A., Xhafa, F., Ma, J., Cao, Y., and Tang, D.

(2017). Reusable garbled gates for new fully homo-

morphic encryption service. International journal of

web and grid services, 13(1):25–48.

Yao, A. C. (1982). Protocols for secure computations. In

23rd annual symposium on foundations of computer

science (sfcs 1982), pages 160–164. IEEE.

Yao, A. C. (1986). How to generate and exchange secrets. In

27th Annual Symposium on Foundations of Computer

Science (sfcs 1986), pages 162–167.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

Zahur, S. and Evans, D. (2015). Obliv-c: A language for

extensible data-oblivious computation. IACR Cryptol.

ePrint Arch., 2015:1153.

APPENDIX

Security Proof of PRGCs

To prove input privacy of a one-time protocol π

against semi-honest adversaries one can use the fol-

lowing two simulation proofs (Lindell, 2017):

,x, f

(x,y))}

x,y∈{0,1}

∗

;n∈N

≡ {view

(x,y,n)}

x,y∈{0,1}

∗

;n∈N

(1)

,y, f

(x,y))}

x,y∈{0,1}

∗

;n∈N

≡ {view

(x,y,n)}

x,y∈{0,1}

∗

;n∈N

(2)

Simulating A’s view is trivial as it does not interact

with B when constructing reusable sections. Simu-

lating B’s view is possible by constructing a PRGC

with a random generator input. Using the knowledge

of f

(x,y), the simulator can modify the Oblivious

Transfers required to obtain the ﬁnal output bits by

always returning the correct output, independent of

′

s choice bit. Thus, we only need to show if, in B’s

view, a PRGC based on a random generator input is

indistinguishable from a PRGC based on the actual

generator input.

Claim. A PRGC computing an arbitrary functionality

f (a,b) expressed by a circuit C for a ﬁxed input a and

an unﬁxed input b provides input privacy.

Without loss of generality, assume C only consists of

balanced gates (XOR, XNOR) and the following im-

balanced gates: AND, NAND, OR, NOR. Assume G

is a PRG that can sample a uniformly random b from

U = {0, 1}. Assume that B knows every gate g in C.

For each value v

at wire w in C, A samples a b

from U and sets v

′

= v

⊕ b

. Each wire label v

′

is now obfuscated by a one time pad. B receives b

only for its own input bit wires. Let g be a gate in

C with functionality f (v

) = v

,i, j, k < |w|. Let B

receive only the last column of the truth table T

from

A that contains all four combinations for f (v

′

) =

′

. Table 3 shows a truth table after Bit Flipping. p

refers to the position in the of the last column’s entry

in the truth table. B knows up to one input wire v

(c ∈ {i, j}) of g in advance (let c = j).

If all wires satisfy the following equation, then any

two PRGCs based on different generator inputs fol-

low the same distribution of wire labels and are thus

indistinguishable from B’s perspective.

PR[v

= 0]

= PR[v

= 1]

. (3)

Thus, we reduce the proof that a PRGC provides input

privacy against a semi-honest evaluator to equation 3

holding for all wires under said conditions. We split

up the proof into four Lemmas. Prooﬁng Lemma 1-3

shows that the reusable sections of a PRGC provide

input privacy. Prooﬁng Lemma 4 shows that non-

reusable sections of a PRGC provide input privacy.

In combination, we prove that PRGCs provide input

privacy for any circuit C.

Lemma 1. The position p of an entry v

in the truth

table T

does not leak v

under the security assump-

tions of G.

Proof: In the unmodiﬁed truth table of g, B can infer

the following from p:

p ∈ {0,1} =⇒ v

= 0 (4)

p ∈ {2,3} =⇒ v

= 1 (5)

After Bit Flipping B can infer the following from p:

p ∈ {0,1} =⇒ v

⊕ b

= 0 (6)

p ∈ {2,3} =⇒ v

⊕ b

= 1 (7)

Since B does not hold b

, it cannot infer v

from its

position p in the truth table without breaking the se-

curity assumptions of G.

Lemma 2. A balanced gate g in the reusable section

does not leak v

under the security assumptions of G.

Proof: The following equation holds if g is an X OR

gate:

′

= v

′

⊕ v

′

= v

⊕ b

= v

⊕ b

⊕ v

⊕ b

(8)

The following equation holds if g is an XNOR gate:

⊕ b

= ¬(v

⊕ b

⊕ v

⊕ b

) (9)

Since B does not hold any values of {v

⊕ b

B cannot distinguish between the entries in T

where

= 1, v

= 0, v

= 1. Thus, B cannot infer v

and v

when inspecting the truth table T

of balanced

gate g without breaking the security assumption of G.

Lemma 3. An imbalanced gates g in the reusable sec-

tion does not leak v

under the security assumptions of

Proof: The following equation holds if g is an AND

gate:

⊕ b

= v

⊕ b

∧ v

⊕ b

(10)

With a certain probability q, A replaces g by a NOR

gate:

⊕ b

= ¬(v

⊕ b

∨ v

⊕ b

) (11)

CRGC: A Practical Framework for Constructing Reusable Garbled Circuits

Table 3: Flipped gate with arbitrary functionality, denoted by ⋆.

p v

′

+ b

0 ⊕ b

[(0 ⊕ b

) ⋆ (0 ⊕ b

)] ⊕ b

+ 1 − b

0 ⊕ b

1 ⊕ b

[(0 ⊕ b

) ⋆ (1 ⊕ b

)] ⊕ b

2 − 2b

+ b

1 ⊕ b

0 ⊕ b

[(1 ⊕ b

) ⋆ (0 ⊕ b

)] ⊕ b

2 − 2b

+ 1 − b

1 ⊕ b

[(1 ⊕ b

) ⋆ (1 ⊕ b

)] ⊕ b

Only v

= 1 can lead to the unique output of an AND

gate (v

= 1). Only v

= 0 can lead to the unique out-

put of a NOR gate (v

= 1). By inspecting the truth

table of this term B ﬁnds identical values of v

′

for

three cases. In the other case it can infer that v

pro-

duces the unique output of g. However, if it cannot

distinguish if A replaced g before Bit Flipping it can-

not infer the value of v

. Thus A

′

s goal is to replace

g with a probability q such that from B

′

s perspective

Pr[g ∈ NOR] = Pr[g ∈ AND].

Replacing g does not maintain the integrity of C

′

Thus, A can only replace g if it is a passive gate.

Let s be the set of possible input combinations for

a where g is a passive gate. A and B can calculate

p = Pr[g ∈ {passive gates}] =

|s|

|a|

. A sets the proba-

bility to replace g to:

pq = (1 − p) + (1 − q)p

⇔ 2q =

1 − p

+ 1

⇔ q =

(12)

If q ≤ 1, A replaces g with probability q to achieve:

Pr[g ∈ NOR]

= Pr[g ∈ AND]

. (13)

If q > 1, A must not add g to the reusable section of C

′

With the same procedure, A can securely obfuscate

NOR gates (AND gates as replacement), NAND gates

(OR gates as replacement), and OR gates (NAND

gates as replacement). After replacing (or not replac-

ing) g, A applies Bit Flipping to g.

By prooﬁng Lemma 1-3, we showed that a

reusable section containing only the balanced gates

of C and imbalanced gates that meet the conditions

above satisﬁes equation 3. All other gates of C

′

are

contained in a non-reusable section.

Lemma 4. A gate g in the non-reusable section does

not leak v

under the security assumptions of Yao’s

Garbled Circuit protocol.

Proof: For each gate g in the ﬁrst level of a non-

reusable section s, B holds both input wires v

′

, v

′

By engaging in two Oblivious Transfers per gate with

A, B obtains two input keys per gate. A garbles the

circuit s according to Yao’s Garbled Circuit protocol.

Yao’s Garbled Circuit protocol was proven to be se-

cure before (Lindell and Pinkas, 2009). Each ﬁnal

output gate of s is either also a ﬁnal output gate of

C or meets the conditions of a gate contained in the

reusable section. In the former case, there is no dif-

ference to Yao’s Garbled Circuit protocol. In the latter

case, equation 3 holds as proven in lemma 1-3 .

If A does not need to learn the output of the com-

putation, a PRGC is secure against a malicious B

when utilizing a compatible OT protocol.

Enabling n-Party Computation with

CRGCs

Our CRGC protocol can be easily extended to enable

n-party computation. The following steps are necces-

sary for 3-PC:

1. A sends C

′

and a

′

to party B.

2. Party B further obfuscates C

′

and its inputs b and

sends C

′′

, a

′

, and b

′

to party C.

3. Party C can evaluate C

′′

with a

′

, b

′

, and arbitrary

inputs c.

If party C wants to evaluate C

′′

with different in-

puts of B, the parties have to repeat steps 2-3. For dif-

ferent inputs of party A, they have to repeat all steps.

Thus, the order of parties receiving and further obfus-

cating a CRGC is relevant. We can generalize this ob-

servation for n-party computation. If any party wants

to evaluate the circuit with a different input of a party

at position i in the receiving order, all parties at posi-

tion p with i ≤ p ≤ n − 1 need to repeat obfuscation.

Predicting Leakage of a CRGC

To predict leaked input bits of a CRGC, we have to

take the evaluator’s perspective when it receives C

′

and a

′

from A. By default, B does not know whether

a gate in C

′

is obfuscated or ﬂipped except for a ﬁ-

nal output gate (that is never obfuscated nor ﬂipped).

However, if it knows C’s exact construction, it can

identify gates that are not passive or balanced with

certainty. These gates do not provide indistinguisha-

bility obfuscation and may reveal input bits of A.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

Potentially Fixed Gates

First, we introduce the concept of potentially ﬁxed

gates. From B’s perspective, any imbalanced gate on

level 1 is a potentially ﬁxed gate. As we showed be-

fore, we achieved indistinguishability obfuscation for

all gates on level 1. However, in deeper levels of C, B

may identify gates that A could not have obfuscated.

To identify potentially ﬁxed gates, B can use the

following ruleset. It can consider all generator inputs

as potentially ﬁxed and all evaluator inputs as not po-

tentially ﬁxed. A balanced gate that has at least one

not potentially ﬁxed parent is not potentially ﬁxed it-

self. This property holds because evaluating a bal-

anced gate such as XOR with one ﬁxed and one un-

ﬁxed bit always returns two different output bits. An

imbalanced gate instead is only not potentially ﬁxed

if both parents are not potentially ﬁxed. This property

holds because evaluating an imbalanced gate such as

AND with at least one ﬁxed bit may always return

the same output bit. B can iterate through the whole

circuit with this ruleset to identify all not potentially

ﬁxed gates. Algorithm 4 applies this ruleset to a

CRGC.

Algorithm 4: Identify potentially ﬁxed gates.

1: for each generator input a

′

2: p f [a

′

] ← true ▷ p f b= potentially ﬁxed

3: for each evaluator input b

4: p f [b

] ← f alse

5: for each gate g do

6: switch type(g) do

7: case type(g) ∈ imbalancedGates

8: p f [g] = p f [l] ∨ p f [r]

9: case type(g) ∈ {XOR,XNOR}

10: p f [g] = p f [l] ∧ p f [r]

11: case type(g) ∈ {{0,0,1,1},{1,1,0,0}}

12: p f [g] = p f [l]

13: case type(g) ∈ {{0,1,0,1},{1,0,1,0}}

14: p f [g] = p f [r]

15: case De f ault ▷ {0,0,0,0} or {1,1, 1, 1}

16: p f [g] = true

Potentially Intermediary Gates

Recall that intermediary gates and ﬁxed gates provide

indistinguishability obfuscation. Thus, B also needs

to identify all potentially intermediary gates. If it as-

sumes all potentially ﬁxed gates to be ﬁxed gates, it

can identify intermediary gates by algorithm 3. As

the set of ﬁxed gates is a subset of all potentially ﬁxed

gates, B can identify all potentially intermediary gates

this way.

Potentially Revealing Gates

Recall that Bit Flipping provides indistinguishability

obfuscation only for balanced gates. Thus, B can

identify the true values of both parents of a gate with

certainty if the gate is not balanced and not poten-

tially passive. However, identifying such a gate does

not yield input leakage yet. Thus, we call those gates

potentially revealing gates.

Suppose there is a potentially revealing gate on

level 1. Since a potentially revealing gate, g

always

reveals the true value of its parents to B (if it knows

C), a potentially revealing gate on level 1 would leak

its input bits. However, each revealing gate is located

at a deeper level of C

′

. Therefore, its leakage does not

always reveal an input bit of A.

Consider a potentially revealing gate g

. B can

only infer a generator input bit a

′

if there is at most

one balanced gate on the path of g

to a

′

since it does

not know whether a balanced gate’s input wires are

ﬂipped. This approach is utilized by our library to

predict the number of inputs leaked in a CRGC.

However, B could combine the knowledge of mul-

tiple potentially revealing gates by setting up a system

of boolean equations from each input bit to each re-

vealed value. Calculating solutions to this system of

equations may require an exhaustive search and is in-

feasible for large circuits. Thus, we do not provide an

implementation for this approach. This means, how-

ever, that our implemented leakage prediction only

serves as a lower bound. We also do not exclude

the possibility that there are more ways to infer input

bits from potentially revealing gates. In case a CRGC

leaks multiple input bits, A can construct a PRGC in-

stead.

Alternative threat models than discussed here may

assume that B does not know C’s construction. In this

case, passive gates can be re-generated completely at

random instead of providing indistinguishably obfus-

cation. This is the default setting of our library.

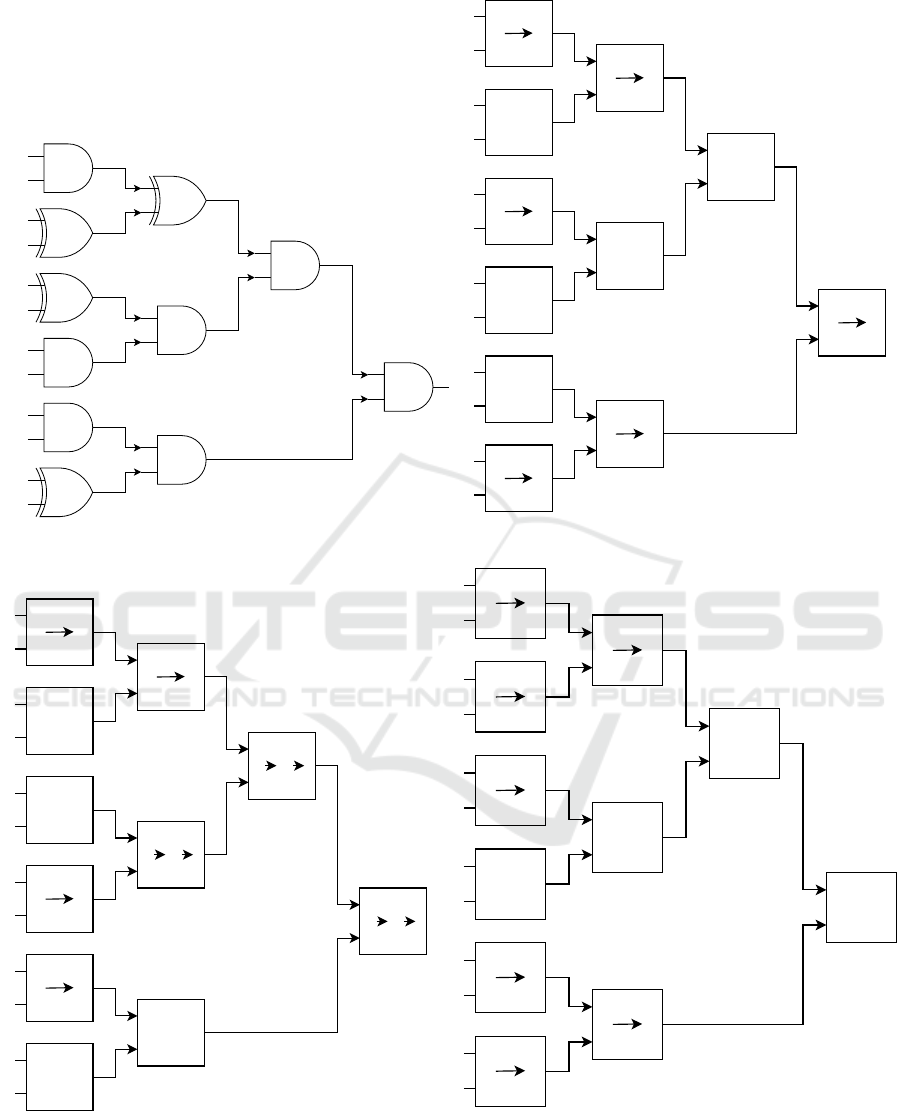
Example - Constructing a CRGC

Figure 7 illustrates an exemplary section s of a circuit

and shows the key modiﬁcations when using our three

obfuscation techniques. Figure 7a shows the plain cir-

cuit and its inputs. For simplicity, we use only AND

and XOR gates to cover one type of balanced and one

type of imbalanced gates. In the example, the left par-

ent of each gate on level 1 is always A’s input, and

the right parent is always B’s input. Since useful real-

world circuits are too large to illustrate in an example,

we assume that the shown sequence of gates is only a

section of a bigger circuit.

CRGC: A Practical Framework for Constructing Reusable Garbled Circuits

Bit Flipping

Figure 7b illustrates how each gate and input bit is

modiﬁed when Bit Flipping is applied. At ﬁrst, A gen-

erates obfuscated inputs. The sufﬁx (!) next to a wire

value indicates that the obfuscated input is the ﬂipped

version of the original input. Bit Flipping ﬁrst recov-

ers the integrity of each gate if one of its parents got

ﬂipped. Afterward, with a probability of

, the output

wire of each gate gets ﬂipped as well. In the ﬁgure,

the four values inside each gate show the output en-

tries of the sorted truth table after the recovery step.

Two columns inside a gate indicate that the gate also

got ﬂipped afterward. In this case, the values on the

left show the truth table after recovering the gate’s in-

tegrity, while the values on the right show the truth

table after the output wire got ﬂipped. Notice that the

XOR gate with evaluator input bit b (X OR

) provides

indistinguishability obfuscation since B cannot distin-

guish XOR

’s truth table from the one where A

′

s input

is 0 and XOR

is ﬂipped.

Obfuscating Fixed Gates

Figure 7c illustrates how ﬁxed gates and their parents

get modiﬁed after Bit Flipping is applied. The four

most left values inside each gate show the truth ta-

ble of each gate after Bit Flipping. obf/o indicates

that a gate is ﬁxed and shows the truth table after ob-

fuscating it. Recall that all gates on level 1 of the

circuit get obfuscated to a gate indistinguishable from

XOR/XNOR. L1 indicates that an unﬁxed imbalanced

gate gets obfuscated into a balanced gate. rec/r indi-

cates that the child g

of a ﬁxed gate gets modiﬁed

to recover the circuit’s integrity. If this modiﬁcation

leads to g

being ﬁxed, it gets obfuscated afterward

(indicated by o).

Notice that after applying this obfuscation tech-

nique to all gates on level 1, each gate’s truth table

is indistinguishable from either XOR or X NOR. Ob-

serve that after recovering a gate’s integrity, each truth

table gets modiﬁed to be independent of its obfus-

cated parent. After recovery, any modiﬁcation to the

obfuscated gate does not change the output of its chil-

dren. All ﬁxed gates get modiﬁed to provide indistin-

guishability obfuscation.

Obfuscating Intermediary Gates

Figure 7d illustrates how intermediary gates get mod-

iﬁed after obfuscating ﬁxed gates. Recall that each

gate g where each path from g to a ﬁnal output gate

contains a ﬁxed gate g

is an intermediary gate.

A can modify these gates to achieve indistinguisha-

bility obfuscation without breaking the circuit’s in-

tegrity. The four most left values inside each gate

show the truth table of each gate after obfuscating

ﬁxed gates.obf indicates that this intermediary gate

gets obfuscated. Since the ﬁnal gate of s in this ex-

ample is an obfuscated ﬁxed gate, all other gates are

intermediary gates. Thus, A can obfuscate all gates to

provide indistinguishability obfuscation. After apply-

ing our obfuscation techniques to the whole circuit, A

can send C

′

and a

′

to B.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

AND

XOR

(a) Section of a circuit.

1(!)

(b) Bit Flipping.

rec

obf

r o

obf

(d) Obfuscating intermediary gates.

Figure 7: Constructing a CRGC.

Codebase: https://github.com/chart21/CRGC

CRGC: A Practical Framework for Constructing Reusable Garbled Circuits