Comparison-based MPC in Star Topology

Gowri R. Chandran

, Carmit Hazay

, Robin Hundt

and Thomas Schneider

TU Darmstadt, Germany

Bar-Ilan University, Israel

Keywords:

Secure Multi-party Computation, k

Ranked Element, Scheduling Problems, Optimisation Problems.

Abstract:

With the large amount of data generated nowadays, analysis of this data has become eminent. Since a vast

amount of this data is private, it is also important that the analysis is done in a secure manner. Comparison-based

functions are commonly used in data analysis. These functions use the comparison operation as the basis.

Secure computation of such functions have been discussed for median by Aggarwal et al. (EUROCRYPT’04)

and for convex hull by Shelat and Venkitasubramaniam (ASIACRYPT’15).

In this paper, we present a generic protocol for the secure computation of comparison-based functions. In order

to scale to a large number of participants, we propose this protocol in a star topology with an aim to reduce the

communication complexity. We also present a protocol for one speciﬁc comparison-based function, the

ranked element. The construction of one of our protocols leaks some intermediate values but does not reveal

information about an individual party’s inputs. We demonstrate that our protocol offers better performance than

the protocol for k

ranked element by Tueno et. al. (FC’20) by providing an implementation.

1 INTRODUCTION

Data is being constantly generated by organisations as

well as individuals. To leverage this massive volume

of unstructured data, organisations seek to use data

analysis techniques. Data analysis can beneﬁt organi-

sations in various ways. For example, businesses can

learn more about their target group by running analy-

sis on the consumers trends, multiple companies can

run analysis on their combined data to compare vari-

ous data points such as salaries of employees, the key

performance indicator, etc., hospitals and healthcare

companies analyse their data using artiﬁcial intelli-

gence and machine learning to obtain faster and more

accurate diagnosis. In addition to using the data for

analytics, these organisations, at times, wish to keep

the data private as it contains sensitive information. In

all the above mentioned examples the data being anal-

ysed is sensitive. In cases such as that of healthcare

companies, the sharing of patient’s data is forbidden by

law. The analysis therefore has to be done in a manner

which does not reveal the inputs. This is where secure

Multiparty Computation (MPC) comes into play.

For the past couple of decades, MPC has been a

prominent ﬁeld of research. Starting with the seminal

works of (Yao, 1982; Goldreich et al., 1987; Beaver

et al., 1990) it is still a widely researched topic with re-

cent works like (Lindell et al., 2015; Wang et al., 2017;

Choudhuri et al., 2020). The problem of secure MPC

focuses on a group of parties that do not trust each

other, but still wish to compute a function

of their

inputs while keeping their inputs private. Namely, it

allows a set of mutually distrusting parties to securely

compute a function on their joint inputs without re-

vealing anything about their inputs except what can

be inferred by the output. In the real world, there are

adversaries present that may act maliciously to gain

more information than they are supposed to. Semi-

honest adversaries follow the protocol as it is but try

to learn more information from the messages. In cases

where companies or organisations run the protocol,

semi-honest security is a realistic assumption, as the

organisations would not deviate from the protocol for

their reputation’s sake. Another factor that is consid-

ered for the construction of an MPC protocol is the

number of parties that are corrupted by the adversary.

In our work, we consider semi-honest adversaries and

a dishonest majority, i.e.,

n−1

parties can be corrupted

by the adversary.

One of the standard approaches to implement con-

stant round MPC used in (Beaver et al., 1990; Ben-

David et al., 2008; Kolesnikov et al., 2009; Lindell

et al., 2015; Lindell et al., 2016) is by using Garbled

Circuits proposed by Yao (Yao, 1982), by converting

the function to be computed to a boolean circuit and

privately evaluating the gates. Alternatively, the MPC

protocol by Goldreich, Micali and Wigderson (Gol-

dreich et al., 1987), which also uses a boolean rep-

Chandran, G., Hazay, C., Hundt, R. and Schneider, T.

Comparison-based MPC in Star Topology.

DOI: 10.5220/0011144100003283

In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 69-82

ISBN: 978-989-758-590-6; ISSN: 2184-7711

resentation, works by secret sharing the wire values

amongst the parties. This protocol has been improved

and implemented in (Choi et al., 2012; Boyle et al.,

2021). All the aforementioned protocols are generic

MPC protocols which can be used to implement any

function f by converting it to a boolean circuit.

Another line of works considers the development

of protocols for speciﬁc functions to achieve im-

proved efﬁciency by exploiting the properties of the

underlying function and optimising the concrete pro-

tocols accordingly. Several works have proposed

protocols for speciﬁc functions such as private set-

intersection (Hazay and Venkitasubramaniam, 2017;

Inbar et al., 2018; Pinkas et al., 2018; Rosulek and

Trieu, 2021) for ﬁnding the intersection of multiple

sets, secure pattern matching (Hazay and Lindell,

2008; Hazay and Toft, 2010; Yasuda et al., 2013; Faust

et al., 2013) for ﬁnding matching patterns in texts and

RSA key generation (Frederiksen et al., 2018; Hazay

et al., 2019; Chen et al., 2021) for generation of the

RSA modulus. Relevant to our work, in (Garay et al.,

2007; Damg

ard et al., 2007; Damg

ard et al., 2008;

Kolesnikov et al., 2009; Couteau, 2016), protocols for

the secure comparison of integers have been proposed

using various techniques.

The computation of these speciﬁc functions can be

optimised by reducing the function

to the compu-

tation of smaller/easier computable primitives. One

method is to reduce the secure computation of

into

the secure evaluation of a boolean circuit. Another

technique is to reduce the function

to multiple in-

stances of a smaller function and perform a secure

computation of this primitive. The latter reduction

technique is used in (Shelat and Venkitasubramaniam,

2015) to reduce

to the comparison function, which

takes two integer inputs and returns

if the ﬁrst input

is smaller than the second and

otherwise. Here the

authors present a two-party protocol for the compu-

tation of a class of functions, where the parties only

interact for implementing the comparison function.

This reduction results in a much more efﬁcient proto-

col, as the parties only communicate to evaluate the

comparison function.

The comparison-based functions considered

in (Shelat and Venkitasubramaniam, 2015) are widely

used for various data analytic purposes. They include

functions such as ﬁnding the convex hull, ﬁnding the

median, job scheduling problems, matroid optimisa-

tions and many more optimisation problems. One of

the functions that we discuss in detail in our work is

the convex hull. The convex hull of a set of points is

the smallest convex set which contains all the points

in that set. We also discuss job scheduling, which is

an optimisation algorithm where multiple parties have

jobs that require the use of a common resource and the

jobs are assigned to the resource at a speciﬁc time.

These functions have important real world appli-

cations. For instance, the secure computation of the

convex hull of a set is useful in tracking a disease epi-

demic, where the extent of the spread of a disease can

be monitored without revealing all the locations of the

infected patients. A two-party variant of this problem

is discussed in (Shelat and Venkitasubramaniam, 2015)

where the authors use the Gift Wrapping Algorithm

for computing the convex hull. Scheduling problems,

such as job scheduling, have many applications in set-

tings where the resources are limited and more than

one user wishes to use them. Secure job scheduling

can be used in applications where the details of the job

(e.g. duration, amount of resource used etc.) are to be

kept private, for instance in booking appointments at a

doctor’s, where the time taken is kept private.

Another functionality that we consider is ﬁnding

the

ranked element of the union of multiple sorted

sets. This function has applications in ﬁnancial and

medical analysis. (Aggarwal et al., 2004) present a

secure protocol for the computation of the

ranked

element, where the

ranked element is computed

using the binary search algorithm. Following that, a

constant round protocol for this function is presented

in (Tueno et al., 2020), where the protocol is presented

in a star topology with all the parties communicating

only with a dedicated server.

In instances where multiple organisations wish to

jointly analyse their data, often the communication

occurs via WAN connections, making communication

the bottleneck for running the protocol, as most organ-

isations have high computational power. Therefore,

protocols with low communication complexity are cru-

cial. One method to achieve this is by constructing

the protocols in a star network topology. The parties

would then only need to communicate to one central

party. The central party has its own input for the com-

putation and also interacts with all the other parties in

a series of secure two-party computations. This elimi-

nates the need for broadcast channels, thus reducing

the communication complexity.

1.1 Our Contribution and Outline

In this paper, we explore the concrete efﬁciency of

comparison-based functions, i.e. a class of functions

that can be reduced to a secure computation of compar-

ison of integers. We present two different protocols for

this class of functions. The ﬁrst is a generic protocol

(see §3) for secure computation of a class of functions

called the Greedy Compatible functions (see §2.1)

where we extend the two-party protocol from (She-

SECRYPT 2022 - 19th International Conference on Security and Cryptography

lat and Venkitasubramaniam, 2015). We implement a

reduction technique to reduce the computation of the

function to a multi-party computation of the minimum

integers and propose an efﬁcient new method

for computing the minimum. Next, we give concrete

instantiations (see §3.2) of a few functions demonstrat-

ing the practical applications of our protocol. To the

best of our knowledge, there have not been any pre-

vious works on speciﬁc multi-party protocols for the

other two problems, i.e. convex hull and job schedul-

ing. We show that our multi-party protocol can be used

for the computation of these functions and that it has

better performance compared to speciﬁc approaches

and to generic MPC protocols that can be used for any

of these functions.

Lastly, we present an alternative way of comput-

ing the

ranked element (see §4) by using reduction

techniques similar to the generic protocol. Our proto-

col is the ﬁrst that uses these reduction techniques to

compute this function in a star topology. If the proto-

col is instantiated in a star topology, the computation

of this function can be reduced to a secure computation

of a summation function. Then communication only

occurs during the computation of the summations, and

the remaining computations are done locally by the

parties and the comparisons are done locally by the

central party. In particular, we reduce the computation

of the

ranked element to a computation of secure

summation which is instantiated using a threshold ho-

momorphic encryption scheme and is implemented in

a star topology where one of the participating parties

plays the central party which interacts with the rest of

the parties.

We note that our protocol for the

ranked ele-

ment leaks the intermediate result of the summations

to the central party. This leakage can reveal the dis-

tribution of the data in the union of sets. For some

applications, revealing the distribution of data is a

tolerable leakage. A potential approach for protect-

ing this leakage can be by using differential privacy

by revealing only the differentially private leakage.

Combining MPC with differentially private tools has

been used previously in (Groce et al., 2019) to achieve

cheaper private set intersection by allowing differen-

tially private leakage. In (He et al., 2017) the problem

of private record linkage with differentially private

leakage is studied. Sometimes, allowing some leakage

can result in a more efﬁcient protocol. There have

been many works that discuss this trade-off on privacy

for better performance. In (Cash et al., 2013; Pappas

et al., 2014) some information related to the search

queries is leaked in order to achieve more efﬁcient

database search functionalities. We leave the idea of

using differentially private leakage for future work.

1.2 Related Work

Here, we mention several closely related works.

The development of general-purpose MPC started

with (Goldreich et al., 1987) and is still a major area of

research with seminal works like (Franklin and Haber,

1996; Cramer et al., 2001; Ben-Efraim et al., 2016; Lin-

dell et al., 2016; Ananth et al., 2019). These protocols

can be used to instantiate the function for ﬁnding the

minimum integer, which is one of the major underly-

ing computations of our generic protocol. If we use the

multi-party protocol in (Ananth et al., 2019) to instan-

tiate the computation of minimum function, the result-

ing communication complexity is

O(κnd log nlogd)

with

rounds, where

is the security parameter,

the number of parties, and

is the input size. This pro-

tocol uses functional encryption combiners to achieve

a constant round multi-party computation protocol,

and although introducing good asymptotic results, it is

not practical enough for an implementation.

Often speciﬁc purpose protocols are developed to

replace the use of generic MPC and improve the per-

formance. There has been abundant work done to de-

velop protocols speciﬁcally for the secure comparison

of two integers. In (Damg

ard et al., 2007; Damg

ard

et al., 2008), homomorphic encryption is used to build

a protocol for the two-party comparison of integers.

Using either of these protocols for computing the mini-

mum, a communication complexity of

O(nd(d +κ))

achieved with

O(logn)

rounds. In (Garay et al., 2007),

a two-party protocol for the comparison of integers

is presented using the encryption scheme of (Cramer

et al., 2001). Using this protocol to implement the min-

imum function the online communication complexity

O(nd)

with a round complexity of

O(logn logd)

In (Couteau, 2016), the authors use a block decompo-

sition technique to compare the blocks of the integer

and execute the comparison with Oblivious Transfer

as a building block. By implementing the minimum

function using (Couteau, 2016), an online communi-

cation complexity of

O(nd)

is achieved with a round

complexity of

O(logn loglogd)

. We compare the efﬁ-

ciency of our implementation of the minimum function

with that of instantiating it with any of the above pro-

tocols in Tab. 1.

In (Tueno et al., 2020), a constant round protocol

for the computation of the

ranked element is pre-

sented. The protocol is presented in a star network

topology where the clients interact with a server. Un-

like this setup, the central party in our protocol is one

of the parties participating in the protocol and also

provides input. Tueno et al. present several protocols

in (Tueno et al., 2020), using different building blocks.

The protocol using the garbled circuit approach has a

Comparison-based MPC in Star Topology

Table 1: Comparison of complexities for the computation of minimum function for

parties, using generic multi-party protocols

((Franklin and Haber, 1996; Ananth et al., 2019)) or two-party comparison protocols ((Garay et al., 2007; Damg

ard et al., 2007;

Damg

ard et al., 2008; Couteau, 2016)) with our garbled circuit-based approach. Here,

is the security parameter,

is the

length of the input and n is the number of parties.

(Franklin and Haber, 1996) (Garay et al., 2007) (Damg

ard et al., 2007; Damg

ard et al., 2008) (Couteau, 2016) (Ananth et al., 2019) This work

Ofﬂine comm. — O(κnd/logκ) — O(κd/logκ) — O(κd)

Online comm. O(n

) O(nd) O(nd(d + κ)) O(nd) O(κnd logn logd) O(κnd)

Rounds O(logn) O(log nlog d) O(logn) O(logn loglog d) 2 O(logn)

Assumption DDH OT DGK OT LWE OT

Table 2: Comparison of protocols for secure computation

of the

ranked element. We compare our protocol with

the one in (Aggarwal et al., 2004) and the three protocols

presented in (Tueno et al., 2020) that are based on Yao’s

garbled circuit (YGC) and additively homomorphic encryp-

tion(AHE).

is the number of parties,

is the security pa-

rameter,

is the bit-length of the input,

is the threshold

of the additive homomorphic scheme, and

is the range of

elements in the database.

(Aggarwal et al., 2004) (Tueno et al., 2020) This work

YGC AHE1 AHE2

Comm. O(n

logS) O(κn

) O(κn

dt) O(κn

dt) O(nlog S)

Rounds logS 4 4 4 logS

total communication complexity of

O(κn

)

, while the

protocol using an additively homomorphic encryption

scheme has a communication complexity of

O(κn

dt)

where

is the threshold of the homomorphic encryp-

tion scheme. Our work achieves a communication

complexity of

O(κnlog S)

, where

is the range of el-

ements in the database, and a round complexity of

O(logS)

rounds. We provide a comparison of our

work and the previous works on the

ranked ele-

ment in Tab. 2.

2 PRELIMINARIES

In this section we deﬁne some basic cryptographic

primitives that are used in our protocols.

2.1 Greedy Compatible Functions

A function

is said to be Greedy Compatible (Shelat

and Venkitasubramaniam, 2015), if

on the union of

given sets can be deﬁned using two functions

MIN

and

UPT

, such that these functions have a few speciﬁc

properties as speciﬁed in deﬁnition 1.

Deﬁnition 1 (Greedy Compatible Functions). The nec-

essary and sufﬁcient conditions for a function

to be

Greedy Compatible are:

Unique solution: Given inputs

i = [1,n]

there

is a unique solution.

Unique order: The output

,...c

)

is released in

a unique order, i.e.,

f (X

,...,X

) = (c

,...c

)

where

= F

UPT

(⊥,

)

and

i+1

UPT

((c

,...,c

) for i = [1,l − 1].

Local updatability: The function

UPT

on the union

of all sets can be computed by computing the func-

tion

UPT

on each set individually and then com-

puting F

MIN

on its result. Namely,

UPT

((c

,...,c

[

) =

MIN

UPT

((c

,...,c

),X

),...,F

UPT

((c

,...,c

),X

)).

2.2 Oblivious Transfer

1-out-of-2 Oblivious Transfer (OT) is a two-party pro-

tocol run between a sender

and a receiver

. The

sender

inputs a pair of

-bit strings

∈ {0,1}

and

inputs a choice bit

b ∈ {0, 1}

. At the end of

the protocol,

learns the chosen string

, but noth-

ing about the unchosen string

1−b

, whereas

learns

nothing about the choice bit b.

Oblivious Transfer Extension. OT protocols require

costly public-key cryptography, but their performance

can be improved using OT extension (Ishai et al., 2003;

Asharov et al., 2013). OT extension allows extending a

few public key-based base OTs using only symmetric

cryptography and a constant number of rounds.

2.3 Garbled Circuits

An efﬁcient way to evaluate a boolean circuit

a constant number of rounds is Yao’s garbled cir-

cuit (Yao, 1986; Lindell and Pinkas, 2004). In this

approach, the circuit constructor

creates a garbled

circuit

as follows: for each wire

of the circuit,

randomly chooses two garbled values

, where

represents the value

. Further, for each gate

creates a garbled table

with the following prop-

erty: given a set of garbled values of

’s inputs,

allows to recover the garbled value of the correspond-

ing

’s output, but nothing else.

sends these garbled

tables, called garbled circuit

to the evaluator

. Ad-

ditionally,

obliviously (via OT) obtains the garbled

inputs

corresponding to the inputs of both parties.

Now

can evaluate the garbled circuit by evaluating

gate by gate, using the garbled tables

. Finally,

SECRYPT 2022 - 19th International Conference on Security and Cryptography

translates the garbled output into the output values

given for the respective parties.

2.4 Gift-Wrapping Algorithm

The Gift Wrapping algorithm (Jarvis, 1973) for ﬁnding

the convex hull of a set works as follows: the ﬁrst point

in the convex hull is the leftmost point of the set. From

this point a vertical line is considered. Then this line is

rotated in a clockwise direction until it touches another

point in the set. The ﬁrst point that touches this line

is the second point of the convex hull. Then a vertical

line is considered from this point and again rotated in

a clockwise direction. This process continues till the

last point that falls on the rotation line is the ﬁrst point

of the convex hull.

3 COMPARISON-BASED

FUNCTIONS

Here we propose an extension to the two-party proto-

col in (Shelat and Venkitasubramaniam, 2015), where

a secure protocol to compute a class of functions called

Greedy Compatible functions(cf. §2.1) is discussed.

We extend their protocol to the multi-party setting and

propose optimisations for the multi-party computation

of the minimum function.

The Greedy Compatible functions can be deﬁned in

an iterative manner with all the computations done lo-

cally by each party except for computing the minimum.

After each iteration, the output is slowly released so

that the ﬁnal output of the computation is the tuple of

outputs from each iteration. Furthermore, the output

of each iteration is given as the input for the next it-

eration. The only step where the parties interact with

each other is for computing the minimum. We propose

to reduce the communication between the parties by

constructing the protocol in a star topology. Thus the

parties only communicate with one central party which

eliminates the need for broadcast channels.

As discussed above, the parties ﬁrst compute a

part of the function locally and then the minimum

together. Consequently, the protocol

(Fig. 3)

for computing the function

involves instantiating

two sub-functionalities: ﬁrst, the local update func-

tion

UPT

(Fig. 1) and second, the minimum function

MIN

(Fig. 2). The functionality

UPT

updates the in-

put of each party for the computation of the minimum

functionality. The output of

UPT

is the input of

MIN

for the next iteration of the protocol.

UPT

is computed

locally by each party, where its inputs are the party

’s

set of elements

and the output of

MIN

. The output

UPT

is the pair

,δ

)

MIN

takes

,δ

)

as input

and computes the minimum of all values

and then

returns the x

corresponding to the smallest δ

Now, combining these two functionalities we de-

scribe the protocol

for securely computing

. In

the initialisation step, the parties locally compute their

ﬁrst input pair by calling the functionality

UPT

on the

set

. Then the iteration begins; for the ﬁrst iteration,

the parties send their input pair

,δ

)

to the func-

tionality

MIN

, which computes

min{δ

,δ

,...,δ

}

and

returns some

= x

corresponding to the smallest

. Then the parties update their inputs for the next

iteration by calling

UPT

and

. The protocol

runs for

j = 1,...,l

iterations, with

depending on the

computed function. As mentioned earlier, the protocol

releases the output slowly, i.e., after each iteration, the

parties receive

, which is a part of the ﬁnal output

,...,c

Functionality F

UPT

This functionality is computed locally by each party P

Input: The set of elements

and the outputs

,...,c

)

obtained by the previous iterations.

•

In the initial step, given input

(⊥,X

)

UPT

computes

party

’s input for

MIN

for the ﬁrst iteration denoted

by (x

,δ

•

In the

iteration, given input

((c

,...,c

),X

)

UPT

computes party

’s input for

MIN

for the

( j + 1)

iteration denoted by (x

j+1

,δ

j+1

Output:

j+1

,δ

j+1

)

where

j+1

∈ X

and

j+1

is the

associated index.

Figure 1: Local update function.

Functionality F

MIN

Parties P

,..., P

participate in this computation.

Input: Each party

sends the pair

,δ

)

, where

an integer.

• Compute δ

= min{δ

,...,δ

•

Sets

c = x

, where

has the corresponding index

Output: c.

Figure 2: Minimum function.

Security. We state and prove the security of this proto-

col next.

Theorem 1. The class of Greedy Compatible func-

tions (cf. deﬁnition 1) is securely computed by protocol

(Fig. 3) in the presence of semi-honest adversaries

for n ≥ 2 in the F

MIN

-hybrid.

Proof.

We prove the security of the protocol in a hy-

brid model, where the function

MIN

is computed by

Comparison-based MPC in Star Topology

Protocol π

Input: Each party P

has a set of distinct elements X

The Protocol:

Each party

locally computes

,δ

) ←

UPT

(⊥,X

2. For j = [1,l] :

(a)

The parties call functionality

MIN

for inputs

,δ

) to obtain output c

(b)

Each party

locally applies functionality

UPT

on its input

((c

,...,c

),X

)

, computing the output

j+1

,δ

j+1

)

, which will serve as its input in the

next iteration.

Output: c

,...,c

Figure 3: Semi-honest protocol for a greedy compatible

function f .

a trusted third party. Consider

to be an adversary

that corrupts a subset

of the parties. Let

,...c

)

be the ﬁnal output of the computation. We construct

a simulator

that generates the view of

i ∈ I

given

’s input

and the output

,...,c

)

, then

works as follows:

Given

i ∈ I

and

,...,c

)

, the simulator

in-

vokes the corrupted parties on their corresponding

inputs.

2. S

plays the honest parties’ role against the cor-

rupted parties on arbitrary sets of inputs.

In the

iteration, given the inputs

{(x

,δ

)}

i∈I

to F

MIN

, S simulates c

as the output of F

MIN

In this case, the view of the corrupted party in the

simulation is identical to that in the real execution of

the protocol. From the unique ordering property of

the solution, the two views are identical. Hence, the

protocol

securely computes any function

in the

presence of semi-honest adversaries.

Complexity. In protocol

, communication occurs

only during the execution of

MIN

. Let

O(C)

be the

communication complexity of

MIN

and

be the num-

ber of rounds of the protocol. Since the parties execute

MIN

once per round, the total communication com-

plexity is

O(lC)

. We discuss the total complexity of

the protocol in §3.1.

3.1 Realising F

MIN

Recall that during the execution of

, communica-

tion between the parties only occurs during the in-

stantiation of

MIN

. To reduce this communication,

we propose an efﬁcient way of computing the mini-

mum function by splitting the multi-party computation

MIN

into a series of two-party computations. We

achieve this by performing the comparisons pairwise.

Thus, we implement

MIN

in a star network topology

where all the parties interact with one central party

(say

) and not with any other party. This implies that

the protocol

can be implemented in a star topology

as well. We deﬁne the pairwise computation of

MIN

in Fig. 4.

Protocol F

MIN

Parties P

,..., P

participate in this computation.

Input: Each party

sends the pair

,δ

)

, where

an integer.

Let a and b be variables.

• (a,b) = (x

,δ

• For i = [2, n],

(a,b) = (x

,δ

), i f δ

< b

• c = a

Output: Each party receives

c = x

such that

min{δ

,...,δ

} for t ∈ [1,n].

Figure 4: Protocol for minimum function using pairwise

comparisons.

Correctness. The correctness follows directly from a

linear search algorithm.

Instantiation. We instantiate the pairwise compar-

isons using garbled circuits and construct the protocol

in a star topology. Therefore, all communications be-

tween the parties happen via party P

Our protocol is based on the idea of mobile

agents (Cachin et al., 2000) that chains together mul-

tiple garbled circuit computations. We consider party

to be the originator of the mobile agents protocol.

Then the remaining parties are the hosts. The proto-

col works as follows:

generates the message for

n − 1

parallel OTs. The next party, i.e.,

constructs

a circuit using the output of

and sends it to

via

then generates a circuit using

’s output and

sends it to

via

. The parties continue similarly

till the last party

sends the circuit to

and

eval-

uates the ﬁnal circuit to obtain the ﬁnal output. This

construction can be modiﬁed to a binary tree based

structure, where parties

, for

i = 1,...,⌊n/2⌋

can par-

allely run the second step and send the circuits to

2i+1

for

i = 1, ...,⌊(n−1)/2⌋

. In the third step, parties

2i+1

construct their circuits based on the received circuits

and send it to party

4i+1

, for

i = 1,..., ⌊n/4⌋

. We can

also view this communication pattern as an evaluation

of a hypercube, as presented in (Inbar et al., 2018),

where each party represents a vertex of the cube.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

Complexity. We ﬁrst discuss the complexity for com-

puting F

MIN

and then compute the total complexity of

the protocol π

The number of rounds required for the computation

of the minimum is

O(logn)

. To increase the computa-

tion efﬁciency, we use OT extensions instead of plain

OTs. As the precomputation for the OT extensions can

be done in parallel, the communication complexity of

the precomputation is

O(κd)

, where

is the size of

the input. The total number of comparisons performed

for each minimum function is

n − 1

, hence the total

communication complexity is O(κnd).

We can instantiate the minimum functionality us-

ing either speciﬁc two-party protocols, or speciﬁc

multi-party protocol or even using generic multi-party

protocols. We now compare our results with those

of using existing protocols. If we instantiate the pair-

wise comparisons using a two-party protocol for in-

teger comparison (Couteau, 2016), it would require

O(logn loglogd)

rounds and would have a communi-

cation complexity of

O(nd)

. Using a generic MPC pro-

tocol (Ananth et al., 2019), we can compute the mini-

mum value in a constant number of rounds, with a com-

munication complexity of

O(κnd log nlogd)

. In Tab. 1,

we give a detailed comparison of the protocols.

Thus, we see that our garbled circuit-based ap-

proach gives the most efﬁcient instantiation of

MIN

terms of communication complexity.

3.2 Concrete Instantiations of f

As discussed in §3, the protocol

computes a class

of functions

. The main challenge in implementing

is to deﬁne the functionalities

UPT

and

MIN

, such

that correctness still holds. For each

, the deﬁnition

of these functionalities changes according to

. Now

we discuss some examples of

in detail and show

how we can deﬁne

UPT

and

MIN

to realise the func-

tions. Speciﬁcally, we consider the following func-

tions: convex hull of a set and job scheduling. Two-

party protocol for computation of convex hull have

been given in (Shelat and Venkitasubramaniam, 2015).

We give the multi-party protocol for this function and

also present a new protocol for secure job schedul-

ing. We also discuss the computation of median of the

union of n sets in the full version of our paper.

3.2.1 Convex Hull

The convex hull of a set of points is the smallest convex

set, which contains all the points in that set. Suppose

there are

parties, each having a set of points. Then

the convex hull of the union of these sets is the small-

est convex set that contains all the points of all the

sets. There are various algorithms that are used to ﬁnd

the convex hull of a set. Here we consider the Gift

Wrapping algorithm (Jarvis, 1973) (see §2.4) which is

the most efﬁcient algorithm for this function.

Now, consider

parties and suppose each party

has a set

, then our objective is to compute the convex

hull of the union of these sets. Each element in

a point on a plane which is represented as

= (x

)

where

and

are the

and

coordinate of the

point, respectively. Now we apply the Gift Wrapping

Algorithm and deﬁne the functionality F

UPT

•

For

j = 1

UPT

(⊥,X

) = (p

,δ

)

, where

is the

leftmost point in the set

(i.e., the point with the

smallest

-coordinate) and

is the

-coordinate

of p

•

For

j > 1

, if

∈ {c

,...,c

j−1

}

, then

sends

terminate

MIN

. Else,

UPT

((c

,..,c

j−1

),X

) =

,δ

)

, where

is the point that makes the small-

est clockwise angle (larger than zero) with the ver-

tical dropped from

j−1

and

is the magnitude

of the angle between the line joining

j−1

and

and the vertical from

j−1

. (The next point in the

convex hull is the point that makes the least clock-

wise angle with the point

j−1

. Hence, each party

sets its input for the next iteration by comparing

the angles.)

The functionality

MIN

is deﬁned exactly as in Fig. 2.

Thus, the ﬁnal output is

,...,c

)

, where each

a point of the convex hull. The number of iterations

of the protocol is equal to the number of points on

the convex hull.

If there are three collinear points in

, the ro-

tation line will touch two points at the same time,

which will give the same angle

for two points

which does not satisfy the properties of

in deﬁni-

tion 1. Hence, we assume that no three points in the

set are collinear.

3.2.2 Job Scheduling

Job scheduling is an optimisation algorithm where

multiple parties have jobs that require the use of a

common resource and these jobs are assigned to the

resource at a particular time. Secure job scheduling

can be used in applications where the details of the job

(e.g., duration, amount of resource used, etc.) are to

be kept private, for example in a car-sharing service

where the clients would like to protect the information

about the usage of the car.

Here we consider a job scheduling problem with

one shared resource and multiple jobs. Consider

par-

ties, each party

having a set of jobs

= {b

,...,b

}

The goal is to ﬁnd the order in which to assign these

jobs to a common resource

. We consider the Short-

est Job First (SJF) algorithm for the scheduling as this

Comparison-based MPC in Star Topology

algorithm gives the best average waiting time for the

parties. We instantiate the generic protocol in Fig. 3

to realise the function. The functionality

MIN

runs

exactly like in Fig. 2 and we deﬁne the functionality

UPT

as follows:

•

For

j = 1

UPT

(⊥,X

) = (b

,δ

)

, where

is the

shortest job in

and

is the completion time

for b

•

For

j > 1

, if

⊆ {c

,...c

j−1

}

, then

UPT

((c

,...c

j−1

),J

) = (⊥,δ

)

where

= ∞

∈ {c

,...c

j−1

}

, then

UPT

((c

,...c

j−1

),J

) =

,δ

)

where

∈ J

\ {b

}

is the smallest job with

completion time

. Else if

∈ {c

,...c

j−1

}

then

UPT

((c

,...c

j−1

),J

) = (b

,δ

)

where

∈ J

is the shortest job and its completion time is δ

The ﬁnal output is

,...,c

)

, which gives the or-

der in which to assign the jobs to the resource

. The

protocol runs for N =

∑

| iterations.

4 LEAKY k

RANKED ELEMENT

Now we focus on one speciﬁc comparison-based func-

tion, namely ﬁnding the k

ranked element of a set.

Recalling that protocol

(in §3) computes

comparison-based functions that possess the proper-

ties speciﬁed in deﬁnition 1, it can therefore be im-

plemented for computing the

ranked element of a

union of sets. In this section, we construct a special

protocol for the computation of the

ranked element.

The protocol discussed here has a smaller communica-

tion complexity than a generic protocol computing this

function, as well as previous protocols for the com-

putation of this function. We also see that using this

speciﬁc protocol is more efﬁcient than

(from §3)

for computing the k

ranked element.

The functionality for ﬁnding the

ranked element

for

parties is deﬁned by

,...D

) 7→ (x

,...,x

)

where

is the

element of the union over all input

sets

. We present a Leaky

Ranked Element pro-

tocol

Leaky

(Fig. 7) that securely realises functionality

Leaky

(Fig. 6). We use the binary search algorithm for

ﬁnding the

element. This protocol works iteratively

and requires two summations and two comparisons per

iteration. We construct the protocol in a star network

topology, hence splitting the computations into a series

of secure two-party computations. By doing this, we

reduce the communication complexity, but leak the

result of the summations to the parties. This leakage

is discussed in detail in §4.1.

Now we present the Leaky protocol in detail. The

functionality

Leaky

(Fig. 6) computes the

ranked

Functionality F

Functionality

communicates with all parties

,...,P

and an adversary Sim.

•

Upon receiving

from each party, compute

where

is the

ranked element in

i=1

. Send

to the adversary

Sim

. If

Sim

responds OK, transmit

to all parties.

Figure 5: Functionality for computing the

ranked element

of a union of n sets.

Functionality F

Leaky

Functionality

Leaky

communicates with all parties

,...,P

and an adversary Sim.

• Receives (x

) from each party.

•

Upon receiving

from party

, if

m = x

, where

is the

ranked element, the functionality sends

to all parties. If

m > x

, then

Leaky

sends

to all the

parties. Else, if m < x

, F

Leaky

sends 0 to all parties.

Figure 6: Leaky functionality for computing the

ranked

element of a union of n sets.

element of the union of

sets. It takes inputs from

the parties for computing the sum. The result of this

addition is then returned to all the parties. Next, the

functionality receives an input from party

. If this

input is equal to the

ranked element, then

Leaky

sends

(the

ranked element) to all the parties.

Otherwise, if the input is smaller than

Leaky

sends

to all the parties and if the input is greater, it sends

The functionality is called

leaky

as it reveals the inter-

mediate sum in each iteration to all the parties. This

provides additional information to the parties which

otherwise an adversary could not compute from the

output alone.

The protocol

Leaky

, which realises functionality

Leaky

, works in iterations and as follows: in the pre-

computation phase, each party computes

m = [a+b/2]

and counts the number of elements in its database that

are smaller than

(and larger than

). The parties

encrypt inputs using a threshold homomorphic encryp-

tion scheme and send them to

. Party

computes

the sum of these encrypted inputs and all the parties

jointly decrypt the result and obtain the plaintext. Next,

compares the result of the sum to conclude whether

the

ranked element is smaller than

(or larger than

). Based on the result of the comparison, the value

is updated for the next iteration. Note that each

party only communicates with party

throughout the

execution. This reduces the communication cost as

compared to the multi-party protocol given in (Aggar-

SECRYPT 2022 - 19th International Conference on Security and Cryptography

wal et al., 2004) that computes the same functionality.

Leaky k

Ranked Element (π

Leaky

)

Input: Each party

has a database

. The rank

, the

range of elements in the union of databases (

[a,b]

) and

the size of each database (|D

|) are public.

Primitives: A homomorphic encryption scheme

(Gen,Enc,Dec) having a key generation protocol π

Gen

Initial Phase: Each party

ranks its elements in ascend-

ing order.

N = Σ

is the total number of elements in

Key Generation Phase: The parties engage in a semi-

honestly secure protocol

Gen

to generate a public key

and their respective shares of secret key sk

of sk.

Local Computation Phase: Each party

does the fol-

lowing:

1. Computes m = ⌊(a + b)/2⌋.

Computes the number of elements

)

less than

and the number of elements (g

) greater than m.

Multi-party Phase:

Each party

encrypts its masked inputs,

Enc

)

and

′

= Enc

)

, and sends the cipher-

texts to P

5. P

computes [L] =

∑

i=1

and [G] =

∑

i=1

′

The parties jointly decrypt

[L]

and

[G]

to obtain the

sums

and

, respectively. Party

receives the

decrypted values L and G.

7. P

does the following comparisons

(a)

L < k

and

G ≤ N − k

, then

is the

ranked

element and P

sends Foundk to all the parties.

(b)

L ≥ k

, then

sends

to all parties. Then each

party sets

b = m − 1

and repeats the protocol from

the local computation phase.

(c)

G > N − k

, then

sends

to all parties and

each party sets

a = m +1

and repeats the protocol

from the local computation phase.

Output: x

(the k

element of

Figure 7: Leaky protocol for passively secure computation

of the k

ranked element.

Correctness. We prove the correctness of the protocol

in the following argument. Let

[a,b]

be the range

of elements in the union of all the sets and

be the

number of elements in the union. Let

be the element

at the

position in the union of the sets where the

elements are arranged in ascending order. Let

the value of

in the

iteration. In the

iteration,

each party counts the number of elements smaller than

and the number of elements greater than

and the

sum of these values from all the parties is computed

respectively. Let

and

be the total number of

elements smaller than and larger than

respectively,

in the i

iteration. Then three cases arise.

•

< m

, then

∈ [a,m

− 1]

. Then the number

of elements smaller than

is greater than the

number of elements smaller than

, i.e.,

> k −1

Thus,

i+1

will be computed as



a + m

− 1



and

the procedure is repeated.

•

> m

, then

∈ [m

+ 1,b]

. Then, the number

of elements larger than

will be greater than the

number of elements larger than

, i.e.,

> N − k

Thus,

i+1

is computed as



+ 1 + b



and the

procedure is repeated with m

i+1

•

Now if

< k

and

≤ N −k

, then

̸∈ [a, m

−1]

and x

̸∈ [m

+ 1,b], which implies x

= m

Hence, the protocol correctly computes the

ele-

ment.

Security. The protocol

Leaky

securely realises

Leaky

in the presence of semi-honest adversaries for

n ≥ 2

We discuss the proof of security in detail in §B.

Instantiations of the threshold PKE. The thresh-

old homomorphic encryption in protocol

Leaky

can

be instantiated using any homomorphic encryption

schemes (see §A). In the implementation of our pro-

tocol, described in §4.3, we use the threshold Paillier

PKE (Paillier, 1999). The threshold Paillier can be im-

plemented with distributed RSA modulus generation,

as discussed in (Hazay et al., 2019).

4.1 Leakage

Now we discuss the leakage mentioned above in pro-

tocol

Leaky

. In each iteration of

Leaky

, the sum of the

number of elements smaller than

(

) and the sum of

the number of elements greater than

(

) is leaked to

party

. Therefore for each

, the number of elements

greater or smaller than

in the union of all databases,

i.e.,

, is revealed. Using this leakage from each

iteration, an adversary can calculate the number of

elements that lie between two values of

. This shows

the distribution of the elements in

and

, for

j = [2,n]

. However, this leak only reveals a collec-

tive information about the union of the databases, and

the distribution of elements in each individual set

cannot be computed from this leakage.

In some applications certain leakage may be tol-

erable as a tradeoff between privacy and efﬁciency.

This can be demonstrated by several works like (Cash

et al., 2013; Pappas et al., 2014; Kolesnikov et al.,

2015; Schoppmann et al., 2018) that leak some infor-

mation in order to obtain more efﬁcient protocols. For

instance, in (Cash et al., 2013; Pappas et al., 2014;

Schoppmann et al., 2018) DBMS search protocols

Comparison-based MPC in Star Topology

are presented that allow leakage of some information

to improve the efﬁciency of the search. (Kolesnikov

et al., 2015) studies the dual-execution paradigm (Mo-

hassel and Franklin, 2006) where the efﬁciency of

two-party computation is improved by revealing a sin-

gle bit of the honest party’s input to the adversary.

These works demonstrate tradeoffs between privacy

and efﬁciency, where some leakage may be accepted

in order to achieve higher efﬁciency. Moreover, if the

leakage is to be reduced, a potential solution may be

to use differential privacy. Then the leakage in the

protocols would be the differentially private leakage

as demonstrated in (Groce et al., 2019).

4.2 Complexity

Let

S = b − a+ 1

, where

[a,b]

is the range of elements

. Then, the maximum number of rounds is

logS

. The communication occurs at the setup phase for

generating correlated randomness and the multi-party

phase for ﬁnding the

element. The communication

complexity of the key generation phase is

O(κ · n

)

where

is the number of parties participating. In the

multi-party phase, in each round, the communication

occurs for:

encryptions,

decryption and

broadcast

. Hence, the communication complexity of the

online phase protocol is

O(κnd log S)

, where

is the

length of the inputs.

The protocol in (Aggarwal et al., 2004) also

uses the binary search algorithm and requires

logS

rounds. The circuit consists of two summations and

two integer comparisons, therefore the circuit size

O(nlog S)

. Hence, using an efﬁcient MPC proto-

col (Ananth et al., 2019) for the computation of the

circuit, the total complexity for the protocol becomes

O(κnd log nlogd logS).

The protocol in (Tueno et al., 2020) uses a star

topology to achieve a constant round protocol. Using

the additively homomorphic encryption as the basis,

they obtain a

round protocol. They compute the

rank of the element by comparing each element with

every other element. The communication complexity

of their protocol is therefore quadratic in the number

of participating parties, i.e.,

O(κn

. We give the

comparison of the complexities of the above protocols

with our work in Tab. 2.

4.3 Implementation

We implemented the protocol

Leaky

in the Rust pro-

gramming language and instantiated the threshold ho-

momorphic encryption with the threshold Paillier PKE

using a 3072 bit modulus

. The implementation

of the threshold encryption is based on the C library

libhcs (Tiehuis, 2018) and the Java library Paillier

Threshold Encryption Toolbox (UTD Data and Privacy

Lab, 2010).

4.4 Benchmarks

Benchmark Environment: We ran our benchmarks

on a server with 2

Intel Xeon Gold 6144

3.5 GHz

(8 physical cores) and

16 × 32 = 512

GB DDR4 RAM.

We created 20 containers, each with 32 GB RAM and

one core. The containers, running Arch Linux, were

connected via a simulated WAN with a bandwidth of

100 Mbits and latency of 100 ms.

For our benchmarks, we consider the worst-case

scenario for our protocol, i.e., when

k = 1

. We assume

that each party holds a set of elements and the range of

the elements in the union of these sets is S. Therefore,

the protocol runs for

logS

rounds. We benchmark

values of S from 10

to 10

. We benchmark the total

communication of the protocol execution for 3 to 19

parties, where each party’s database has a size of 1 GB

(Fig. 8b). To emulate the setting of (Tueno et al., 2020),

we also evaluate the runtime for 20 to 200 parties

with a single element each (Fig. 8a). The results are

averaged over 10 runs for each conﬁguration.

4.4.1 Results

Our experimental results match with the expected

asymptotic complexities. We see that the total com-

munication scales linearly with the number of par-

ties, and increasing the number of parties does not

affect the individual communication. Moreover, the

communication increases logarithmically with the

range of the database.

The outliers in Fig. 8a are due to thread scheduling

issues on the container executing party P

Table 3: Performance comparison of our protocol

Leaky

(Fig. 7) for computing the

ranked element among

100 parties connected via WAN with the numbers reported

in (Tueno et al., 2020) based on Yao’s garbled circuit (YGC)

and additively homomorphic encryption (AHE). Comm. is

the communication from the client to the server in MB.

the range of elements in the database.

(Tueno et al., 2020) (no leakage) This work (leaky)

YGC AHE1 AHE2 S = 10

S = 10

Time (s) 197 1749 441 112.6 222.2

Comm. (MB) 0.31 1.11 0.32 0.040 0.143

Comparison: We compare our results with the exper-

imental results of the previous work in (Tueno et al.,

2020). The comparison of results for 100 parties with

a database range of either

is given in Tab. 3.

In the case of

S = 10

, our protocol reduces the client

communication by more than a factor of two compared

SECRYPT 2022 - 19th International Conference on Security and Cryptography

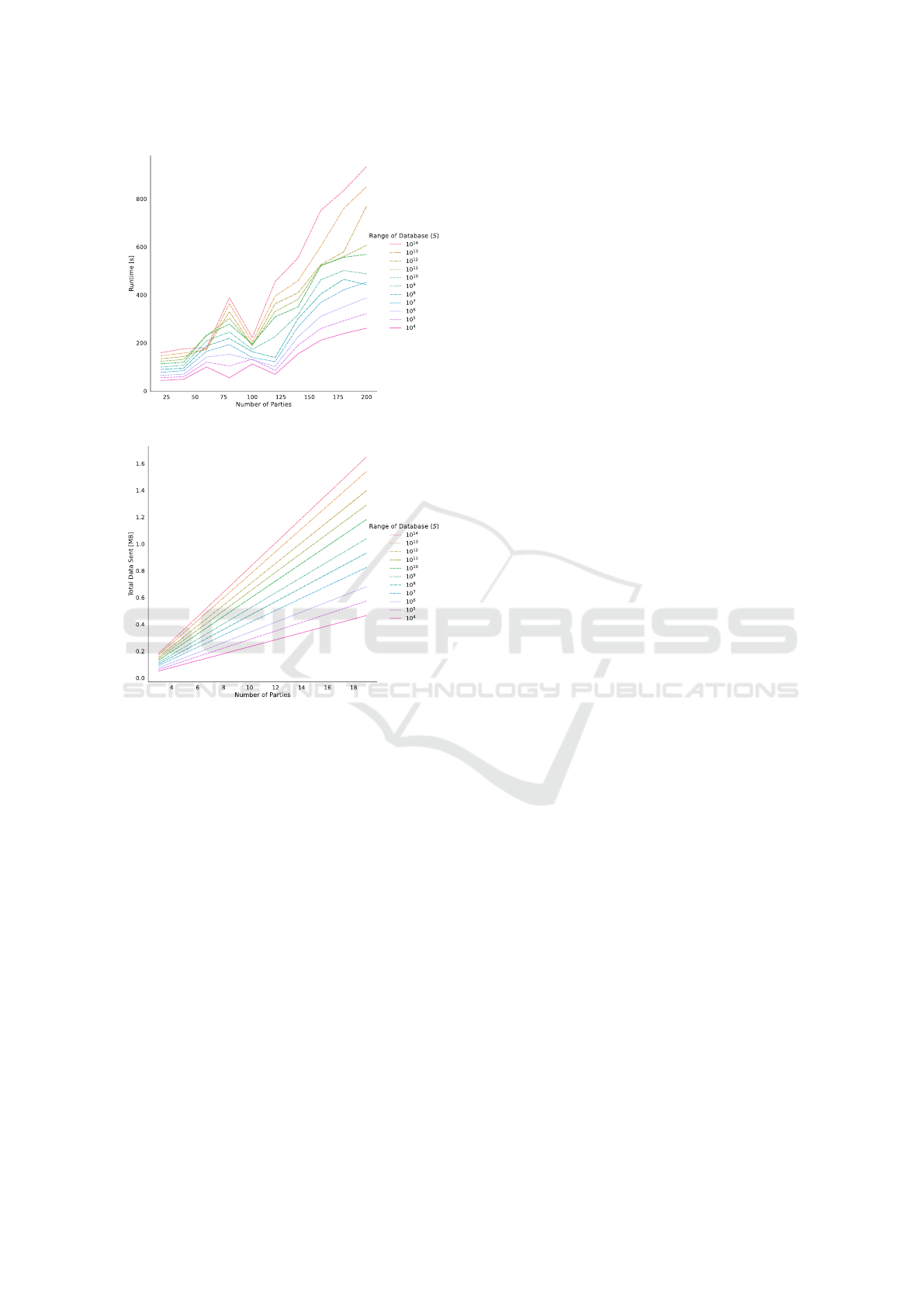
(a) Runtime

(b) Communication

Figure 8: Experimental analysis of protocol

Leaky

(Fig. 7),

which computes the

ranked element of the union of

sets, for varying number of parties

. The plots show the

results for different ranges of values in the database.

to the best protocol of (Tueno et al., 2020).

5 CONCLUSION

In this paper, we have presented two multi-party pro-

tocols, one for computing a class of comparison-based

functions and the second for computing the

ranked

element. The protocols that we constructed have better

communication complexities as compared to the previ-

ous works on these speciﬁc functions, and to generic

multi-party protocols that can be used for these func-

tions. We reduce the functions to a computation of

some high-level primitives and perform the compu-

tations in a star network topology, where one party

communicates with every other party to execute a se-

ries of two-party computations. We show that such

a design improves the efﬁciency of the protocols as

the communication between parties during the execu-

tion are reduced to a minimum. Our protocols have

communication complexities linear in the number of

parties, which makes it easily scalable.

ACKNOWLEDGEMENTS

This project received funding from the European Re-

search Council (ERC) under the European Union’s

Horizon 2020 research and innovation program (grant

agreement No. 850990 PSOTI). It was co-funded by

the Deutsche Forschungsgemeinschaft (DFG) within

SFB 1119 CROSSING/236615297 and GRK 2050 Pri-

vacy & Trust/251805230, and by the German Federal

Ministry of Education and Research and the Hessen

State Ministry for Higher Education, Research and the

Arts within ATHENE.

This project was also supported by the BIU Cen-

ter for Research in Applied Cryptography and Cyber

Security in conjunction with the Israel National Cy-

ber Bureau in the Prime Minister’s Ofﬁce, and by ISF

grant No. 1316/18.

REFERENCES

Aggarwal, G., Mishra, N., and Pinkas, B. (2004). Secure

computation of the k th-ranked element. In EURO-

CRYPT.

Ananth, P., Badrinarayanan, S., Jain, A., Manohar, N., and

Sahai, A. (2019). From FE combiners to secure MPC

and back. In TCC (1).

Asharov, G., Lindell, Y., Schneider, T., and Zohner, M.

(2013). More efﬁcient oblivious transfer and exten-

sions for faster secure computation. In CCS.

Beaver, D., Micali, S., and Rogaway, P. (1990). The round

complexity of secure protocols (extended abstract). In

STOC.

Ben-David, A., Nisan, N., and Pinkas, B. (2008). Fair-

playMP: a system for secure multi-party computation.

In CCS.

Ben-Efraim, A., Lindell, Y., and Omri, E. (2016). Optimiz-

ing semi-honest secure multiparty computation for the

internet. In CCS.

Boyle, E., Gilboa, N., Ishai, Y., and Nof, A. (2021). Sublin-

ear GMW-style compiler for MPC with preprocessing.

In CRYPTO (2).

Cachin, C., Camenisch, J., Kilian, J., and M

uller, J. (2000).

One-round secure computation and secure autonomous

mobile agents. In ICALP.

Cash, D., Jarecki, S., Jutla, C. S., Krawczyk, H., Rosu, M.,

and Steiner, M. (2013). Highly-scalable searchable

Comparison-based MPC in Star Topology

symmetric encryption with support for boolean queries.

In CRYPTO (1).

Chen, M., Hazay, C., Ishai, Y., Kashnikov, Y., Micciancio,

D., Riviere, T., Shelat, A., Venkitasubramaniam, M.,

and Wang, R. (2021). Diogenes: Lightweight scalable

RSA modulus generation with a dishonest majority. In

S&P.

Choi, S. G., Hwang, K., Katz, J., Malkin, T., and Ruben-

stein, D. (2012). Secure multi-party computation of

boolean circuits with applications to privacy in on-line

marketplaces. In CT-RSA.

Choudhuri, A. R., Ciampi, M., Goyal, V., Jain, A., and

Ostrovsky, R. (2020). Round optimal secure multiparty

computation from minimal assumptions. In TCC (2).

Couteau, G. (2016). Efﬁcient secure comparison protocols.

IACR Cryptol. ePrint Arch., page 544.

Cramer, R., Damg

ard, I., and Nielsen, J. B. (2001). Mul-

tiparty computation from threshold homomorphic en-

cryption. In EUROCRYPT.

Damg

ard, I., Geisler, M., and Krøigaard, M. (2007). Efﬁcient

and secure comparison for on-line auctions. In ACISP.

Damg

ard, I., Geisler, M., and Krøigaard, M. (2008). Ho-

momorphic encryption and secure comparison. Int. J.

Appl. Cryptogr.

Damg

ard, I., Jurik, M., and Nielsen, J. B. (2010). A general-

ization of Paillier’s public-key system with applications

to electronic voting. Int. J. Inf. Sec.

Faust, S., Hazay, C., and Venturi, D. (2013). Outsourced

pattern matching. In ICALP (2).

Franklin, M. K. and Haber, S. (1996). Joint encryption and

message-efﬁcient secure computation. J. Cryptol.

Frederiksen, T. K., Lindell, Y., Osheter, V., and Pinkas, B.

(2018). Fast distributed RSA key generation for semi-

honest and malicious adversaries. In CRYPTO (2).

Gamal, T. E. (1985). A public key cryptosystem and a

signature scheme based on discrete logarithms. IEEE

Trans. Inf. Theory.

Garay, J. A., Schoenmakers, B., and Villegas, J. (2007).

Practical and secure solutions for integer comparison.

In PKC.

Gilboa, N. (1999). Two party RSA key generation. In

CRYPTO.

Goldreich, O., Micali, S., and Wigderson, A. (1987). How

to play any mental game or A completeness theorem

for protocols with honest majority. In STOC.

Groce, A., Rindal, P., and Rosulek, M. (2019). Cheaper pri-

vate set intersection via differentially private leakage.

PoPETs.

Hazay, C. and Lindell, Y. (2008). Efﬁcient protocols for set

intersection and pattern matching with security against

malicious and covert adversaries. In TCC.

Hazay, C., Mikkelsen, G. L., Rabin, T., Toft, T., and Ni-

colosi, A. A. (2019). Efﬁcient RSA key generation and

threshold Paillier in the two-party setting. J. Cryptol.

Hazay, C. and Toft, T. (2010). Computationally secure pat-

tern matching in the presence of malicious adversaries.

In ASIACRYPT.

Hazay, C. and Venkitasubramaniam, M. (2017). Scalable

multi-party private set-intersection. In PKC (1).

He, X., Machanavajjhala, A., Flynn, C. J., and Srivastava,

D. (2017). Composing differential privacy and secure

computation: A case study on scaling private record

linkage. In CCS.

Inbar, R., Omri, E., and Pinkas, B. (2018). Efﬁcient scalable

multiparty private set-intersection via garbled Bloom

ﬁlters. In SCN.

Ishai, Y., Kilian, J., Nissim, K., and Petrank, E. (2003).

Extending oblivious transfers efﬁciently. In CRYPTO.

Jarvis, R. A. (1973). On the identiﬁcation of the convex hull

of a ﬁnite set of points in the plane. Inf. Process. Lett.

Kolesnikov, V., Mohassel, P., Riva, B., and Rosulek, M.

(2015). Richer efﬁciency/security trade-offs in 2PC. In

TCC (1).

Kolesnikov, V., Sadeghi, A., and Schneider, T. (2009). Im-

proved garbled circuit building blocks and applications

to auctions and computing minima. In CANS.

Lindell, Y. and Pinkas, B. (2004). A proof of Yao’s protocol

for secure two-party computation. Electron. Collo-

quium Comput. Complex.

Lindell, Y., Pinkas, B., Smart, N. P., and Yanai, A. (2015).

Efﬁcient constant round multi-party computation com-

bining BMR and SPDZ. In CRYPTO (2).

Lindell, Y., Smart, N. P., and Soria-Vazquez, E. (2016). More

efﬁcient constant-round multi-party computation from

BMR and SHE. In TCC (B1).

Mohassel, P. and Franklin, M. K. (2006). Efﬁciency tradeoffs

for malicious two-party computation. In PKC.

Paillier, P. (1999). Public-key cryptosystems based on com-

posite degree residuosity classes. In EUROCRYPT.

Pappas, V., Krell, F., Vo, B., Kolesnikov, V., Malkin, T., Choi,

S. G., George, W., Keromytis, A. D., and Bellovin,

S. M. (2014). Blind Seer: A scalable private DBMS.

In S&P.

Pinkas, B., Schneider, T., and Zohner, M. (2018). Scalable

private set intersection based on OT extension. ACM

Trans. Priv. Secur.

Rosulek, M. and Trieu, N. (2021). Compact and malicious

private set intersection for small sets. In CCS.

Schoppmann, P., Gasc

on, A., and Balle, B. (2018). Private

nearest neighbors classiﬁcation in federated databases.

IACR Cryptol. ePrint Arch.

Shelat, A. and Venkitasubramaniam, M. (2015). Secure

computation from millionaire. In ASIACRYPT (1).

Tiehuis, M. (2018). libhcs. https://github.com/tiehuis/libhcs.

Accessed: 29.11.2021.

Tueno, A., Kerschbaum, F., Katzenbeisser, S., Boev, Y., and

Qureshi, M. (2020). Secure computation of the k

ranked element in a star network. In FC.

UTD Data and Privacy Lab (2010). Paillier threshold en-

cryption toolbox. http://cs.utdallas.edu/dspl/cgi-bin/

pailliertoolbox/index.php. Accessed: 29.11.2021.

Wang, X., Ranellucci, S., and Katz, J. (2017). Global-scale

secure multiparty computation. In CCS.

Yao, A. C. (1982). Protocols for secure computations (ex-

tended abstract). In FOCS.

Yao, A. C. (1986). How to generate and exchange secrets

(extended abstract). In FOCS.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

Yasuda, M., Shimoyama, T., Kogure, J., Yokoyama, K., and

Koshiba, T. (2013). Secure pattern matching using

somewhat homomorphic encryption. In CCSW.

A Additively Homomorphic

Encryption

A public key encryption (PKE) scheme is said to

be additively homomorphic if for two ciphertexts

= Enc

)

and

= Enc

)

, we can

efﬁciently compute

Enc

+ m

;r)

with an inde-

pendent

and without the knowledge of the secret

key sk.

Threshold PKE. In a distributed scheme, shares of the

secret key are held by the parties so that the combined

key remains secret. In order to decrypt, the parties use

their shares to compute intermediate values, which are

combined eventually to form the decrypted plaintext.

Threshold encryption scheme thus comprises of two

functionalities: a generate functionality to generate

the shares of the secret key and share among the par-

ties, and a decryption functionality where the parties

perform the decryption together.

Homomorphic Encryption Schemes. A popular in-

stantiation of the homomorphic encryption is the Pail-

lier encryption scheme (Paillier, 1999), which is based

on the Decisional Composite Residuosity (DCR) hard-

ness assumption for its security. In (Gilboa, 1999;

Damg

ard et al., 2010) threshold variant of the Paillier

scheme is presented. Another instantiation of homo-

morphic encryption is the El Gamal scheme (Gamal,

1985). Its security is implied by the Decisional Difﬁe-

Hellman hardness assumption.

B Security of π

Leaky

Theorem 2. (Security of

Leaky

). Assume that

(Gen,Enc,Dec)

is an IND-CPA secure threshold ho-

momorphic encryption scheme. Then the proto-

col (Fig. 7) securely realises

Leaky

in the presence

of semi-honest adversaries for n ≥ 2.

Proof.

We construct a simulator

, where

is provided

with the inputs of the corrupted parties and the output

of the computation. Let

be an adversary corrupting

a subset of the parties, then two cases arise:

Case 1:

corrupts a strict subset

of the parties

excluding

. Let

be the

ranked element in the

union of all the sets. The simulator

has input

i ∈ I and x

, and is deﬁned as follows:

Given

, i ∈ I

and

, the corrupted parties are

invoked by S on their corresponding inputs.

2. S

generates

(pk,sk) ← Gen(1

)

and invokes

Gen

for the key generation phase.

3. S

plays the role of

on an arbitrary set of inputs,

against the corrupted parties.

For each iteration

, let

= [a + b/2]

be the me-

dian of the range as computed by each party. If

< m

, then

returns

to all parties. If

> m

S returns 0 to the parties.

In this case, the view generated by the simulator is

identical to the view of the honest parties in the real

protocol. In the case when

< m

, it implies that

(number of elements less than

m) ≥ k

, then in the

real execution as well as in the simulation,

b = m −

. When

> m

, it implies that

(the number of

elements greater than

m) ≥ N − k + 1

, then in the real

execution and in the simulation,

a = m + 1

. When

= m

(number of elements less than

m) ≤ k − 1

and

(number of elements greater than

m) ≤ N −k

then in both executions

is the

element. Hence,

the view of the honest parties in both executions are

identical.

Case 2:

corrupts a strict subset

of parties including

. Let

be the

ranked element of the union of all

databases

. Here the simulator

has input sets

i ∈ I and x

, and is deﬁned as follows:

Given

, i ∈ I

and

, the corrupted parties are

invoked by the simulator on their corresponding

inputs.

2. S

generates

(pk,sk) ← Gen(1

)

and invokes the

simulator

Gen

(pk)

for

Gen

in the key generation

phase.

3. S

plays the honest parties’ role against

in the

protocol. For the

iteration, let

= [a+b/2]

computed by

. The simulator sends encryptions

of two arbitrary inputs to

and

computes two

sets of sums

(a)

< x

, the simulator invokes

Dec

)

for

the decryption of

and

Dec

(N − k +r

)

for the

decryption of

′

, where

∈ Z

. Then

returns 0 and the simulator sets a = m

+ 1.

(b)

> x

, the simulator invokes

Dec

(k + r

)

for the decryption of

and

Dec

)

for the de-

cryption of

′

, where

∈ Z

. Then

re-

turns 1 and the simulator sets b = m

− 1

= x

, then m

is the k

element.

In this case the difference lies in the encryptions sent to

. In the real execution, the parties send encryptions

Comparison-based MPC in Star Topology

of their input to

whereas the simulator sends en-

cryptions of arbitrary inputs to

. Hence, the indistin-

guishability of the two views follows from the privacy

of the threshold homomorphic encryption scheme.

Thus, the above protocol securely computes the

ranked element of the union of n sets.

SECRYPT 2022 - 19th International Conference on Security and Cryptography