
Interval-based Robot Localization with Uncertainty Evaluation
Yuehan Jiang, Aaronkumar Ehambram and Bernardo Wagner
a
Real Time Systems Group (RTS), Institute for Systems Engineering, Leibniz Universit
¨
at Hannover,
D-30167 Hannover, Germany
Keywords:
Landmark-based Localization, Uncertainty Estimation, Interval Analysis, Factor Graph, Probabilistic
Uncertainty.
Abstract:
Being able to provide trustworthy localization for a robot in a map is essential for various tasks with safety-
related requirements. In contrast to classical probabilistic approaches that represent the uncertainty as a Gaus-
sian distribution, we use interval error bounds for the uncertainty estimation of a localization problem. To
tackle and identify the limitations of probabilistic localization uncertainty estimation, we carry out compari-
son experiments between an interval-based method and a factor graph-based probabilistic method. Different
measurement error models are propagated by the two methods to derive the robot pose uncertainty estimates.
Results show that the probabilistic approach can provide very good pose uncertainty when there is no non-
Gaussian systematic sensor error. However, if the measurements have unmodeled systematic errors, the in-
terval approach is able to robustly contain the true poses whereas the probabilistic approach gives completely
wrong results.
1 INTRODUCTION
For safe navigation and operation, a mobile robot not
only has to accurately determine its localization in
the environment but also needs to provide trustwor-
thy results. In indoor environments where no Global
Positioning System (GPS) is available, the robot usu-
ally localizes itself by using sensory information (e.g.
wheel odometry, 3D point cloud, or camera images)
and updates its belief of position with respect to a
given map. A variety of probabilistic techniques have
been proposed to reach the localization goal on a prior
map (Gutmann et al., 1998) (Wilbers et al., 2019).
Nevertheless, most approaches focus on providing ac-
curate point-wise solutions, while the quality of the
uncertainty estimation of environmental perception
and localization results are not thoroughly investi-
gated.
In probabilistic localization, the Kalman filter
and graph-based optimization approaches provide ex-
plicit estimates of robot poses efficiently, with the as-
sumption that the measurement and pose uncertainty
have zero-mean Gaussian distributions (Chen, 2012)
(Kummerle et al., 2011). The Gaussian uncertainty
assumption, however, could be inaccurate and unreli-
able due to the following reasons.
a
https://orcid.org/0000-0001-5900-0935
On one hand, there exist non-Gaussian sensor
errors which are hard to be identified. For exam-
ple, light detection and ranging (LiDAR) sensors are
widely used for robot localization applications. It
has been pointed out by (Voges, 2020) that stochas-
tic distributions can not always truly represent the er-
ror model of LiDARs due to the presence of unmod-
eled systematic errors. Moreover, analysis in (Mal-
let et al., 2008) shows that the LiDAR measurement
model is subject to mixed effects of geometric (e.g.
the incidence angle between the laser beam and the
surface) and radiometric object properties (e.g. dif-
ferent materials of the surface). These problems in-
duce non-Gaussian measurement uncertainty, which
can not be represented by the mean and variance. On
the other hand, due to the nonlinearity of the system, a
linearization process is required which can only give
an approximation of the uncertainty estimate. Due to
these limitations of probabilistic approaches, the re-
sulting pose estimation and its uncertainty might be
erroneous and may significantly differ from the true
result.
In this paper, we aim to tackle and identify the lim-
itations of probabilistic localization uncertainty when
the Gaussian assumption is violated. First, we provide
a solution to a 2D landmark-based localization prob-
lem using interval analysis (Jaulin et al., 2001). In
296
Jiang, Y., Ehambram, A. and Wagner, B.
Interval-based Robot Localization with Uncertainty Evaluation.
DOI: 10.5220/0011143700003271
In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 296-303
ISBN: 978-989-758-585-2; ISSN: 2184-2809
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

comparison to probabilistic methods that use Gaus-
sian distributions for the measurement model (i.e.
range and bearing) as well as the robot pose (position
and heading), the interval method models them with
interval boxes with lower and upper bounds, where
no probability distribution is assumed. The interval-
based solution can provide guaranteed uncertainty es-
timation for the robot poses that enclose the true val-
ues. We focus on the uncertainty estimation of the lo-
calization problem and compare the results from the
interval-based method and a factor graph-based prob-
abilistic method, to find advantages and limitations
of both. In particular, we investigate the uncertainty
propagation from the measurement model to the re-
sulting robot pose.
The contributions of the paper are:
• We evaluate the uncertainty estimation of an
interval-based solution and a factor graph-based
probabilistic solution for a localization problem
by designing four simulated experiments.
• We find failure cases where the probabilistic ap-
proach leads to incorrect uncertainty estimation
with the presence of non-Gaussian measurement
error, whereas the results of the interval-based
method still hold true.
In the remainder of this paper, we first introduce
the related work in Section 2. In Section 3 we in-
troduce the basics of interval analysis. Subsequently,
we formulate our localization problem and establish
our interval-based localization solution, as well as the
state-of-the-art probabilistic solution in Section 4. In
Section 5, we evaluate the uncertainty estimation of
the two solutions by four small simulated experiments
and analyze the results.
2 RELATED WORK
In the existing map-based localization literature,
landmark-based methods are widely used by differ-
ent sensor modalities benefiting from the identifiable
landmarks in the environments like poles (Brenner,
2010) (Schaefer et al., 2019), visual features (Wilbers
et al., 2019) and natural landmarks (Rohou et al.,
2020). In this work, we also use a set of landmarks
as the prior map. Typically, the landmarks observed
by the sensor are associated with the map to track the
robot in the map. The data association problem is
challenging and false associations introduce outliers
that need to be dealt with. Since data association is
not the focus of this paper, we assume that the asso-
ciation between locally-observed landmarks and the
map landmarks is known.
In recent years, interval methods have shown their
potential in robot localization and simultaneous local-
ization and mapping problems. The work in (Rohou
et al., 2020) solves the localization problem for an un-
derwater vehicle in a known map but with unreliable
data association. By formulating a constraint network
with a constellation contractor, the data association
and state estimation problems are solved together. In
an unmanned aerial vehicle (UAV) localization appli-
cation (Kenmogne et al., 2017) interval has been used
to compute the 6 DOF pose of the UAV by tracking
known image features with bounded-error. The work
in (Voges and Wagner, 2021) firstly proposes a guar-
anteed visual-LiDAR odometry for autonomous ve-
hicles that uses LiDAR and a monocular camera to
compute the 6 DOF pose estimate with bounded un-
certainty. Evaluation of real data from large-scale ex-
periments shows that the vehicle’s real poses are en-
closed in a guaranteed way. Authors in (Ehambram
et al., 2021) extend this work (Voges and Wagner,
2021) by fusing information from LiDAR and stereo
cameras to solve the dead-reckoning of a vehicle and
use the interval contraction method for consecutive
robot pose estimation. The above methods show that
interval analysis can provide robust uncertainty es-
timates of the robot pose which always enclose the
ground truth data. However, few investigations have
been done to compare the interval results with those
of the probabilistic methods. Interval analysis has
the benefit of providing a guaranteed estimation of
the robot pose, however, it can also suffer from pes-
simism due to large initial intervals, wrapping effect,
and dependencies of parameters (Jaulin et al., 2001).
Thus, we think it is important to validate the use of in-
terval analysis by showing under what cases interval
has advantages over probability approaches and also
disadvantages in terms of uncertainty estimation.
Recently, graph-based optimization has become
the standard solution for SLAM and widely applied
for localization applications (Kummerle et al., 2011)
(Kaess et al., 2011) (Wu et al., 2017) (Wilbers et al.,
2019). The graph representation allows adding robot
poses and landmark positions as nodes in the graph,
while the constraints between the nodes are added as
edges (or factors). A non-linear least-squares prob-
lem is formulated and the error function is minimized
in a bundle-adjustment manner to determine the opti-
mal robot pose and landmark positions. In this paper,
we use the factor graph (Kaess et al., 2011) to formu-
late a 2D localization problem. We establish a factor
graph-based localization solution as the state-of-the-
art probabilistic approach. The uncertainty estimation
of this method will be compared with the interval-
based uncertainty and evaluated.
Interval-based Robot Localization with Uncertainty Evaluation
297
3 INTERVAL ANALYSIS
Interval analysis is a numerical tool based on the idea
of enclosing real numbers in intervals (Jaulin et al.,
2001). Instead of an exact value, variables are de-
fined by an interval that is a subset of R , denoted
by [x] = [x, x]. The variable is bounded by a lower
bound x and an upper bound x , without any assump-
tions about its probability distribution. By using the
simple error bounds, interval provides a guaranteed
way to represent the uncertainty of a variable. For
example, if we know that the accuracy of a distance
measurement is ± 0.3 m, then the true value x
∗
is en-
closed by an interval x
∗
∈ [x] , with an uncertainty of
the radius r([x]) = (x−x)/2 = 0.3 m. An interval box
[x] is define as a vector of intervals.
Interval computation enables classical real arith-
metic operations, +,−,×, and ÷, as well as elemen-
tary functions like sin,cos, exp ... on intervals based
on set theory. Here is an example of addition opera-
tion on intervals:
[−2, 4] + [5, 6] = [−2 + 5, 4 + 6] = [3, 10] (1)
For a 2D robot localization problem, where we
consider the set of possible robot poses described in
the interval domain X , the problem can be character-
ized as:
X = {x ∈ R
3
| f (x) ∈ Y} = f
−1
(Y), (2)
where f : R
3
→ R
2
is a non-linear function, which
can be the measurement constraint, and Y the land-
mark positions. The robot pose X can be obtained
by using Set Inverter Via Interval Analysis (SIVIA)
(Jaulin et al., 2001) to calculate a subpaving solution
set from an initial search domain.
Alternatively, this can also be solved by formulat-
ing a Constraint Satisfaction Problem (CSP) as a set
of constraints and variables. We give an exemplary
CSP:
H :
Variable : x
n
Constraint : g(x
n
) = 0
Domain : [x
n
]
, (3)
where x
n
∈ [x
n
] is the unknown variable vector, and
g(x
n
) is the constraints to fulfill in the CSP H .
Contractors (Jaulin et al., 2001) can be built to
contract the variable’s initial domain, to get a result-
ing interval box that satisfies all the constraints. Here
the contraction means that the initial interval domain
is reduced by removing all values that do not sat-
isfy the constraints. The forward-backward contrac-
tor is the most convenient contractor to contract the
domain of CSP H where all constraints are decom-
posed into primitive constraints (i.e. a sequence of
functions containing only a single operator) and each
of the primitive constraints is contracted until the in-
terval boxes converge towards the smallest possible
sizes. The benefit of contraction is that all possible
solutions are guaranteed to be contained in the con-
tracted domain.
In this work, interval analysis is used for solving a
2D robot localization problem. A CSP is formulated
to compute the uncertainty of the robot pose. Contrac-
tors are built to propagate the uncertainty of the map
landmarks and measurement constraints, resulting in
a guaranteed robot pose uncertainty that satisfies the
constraints in CSP H .
4 PROBLEM FORMULATION
The goal is to track a moving robot in a known map
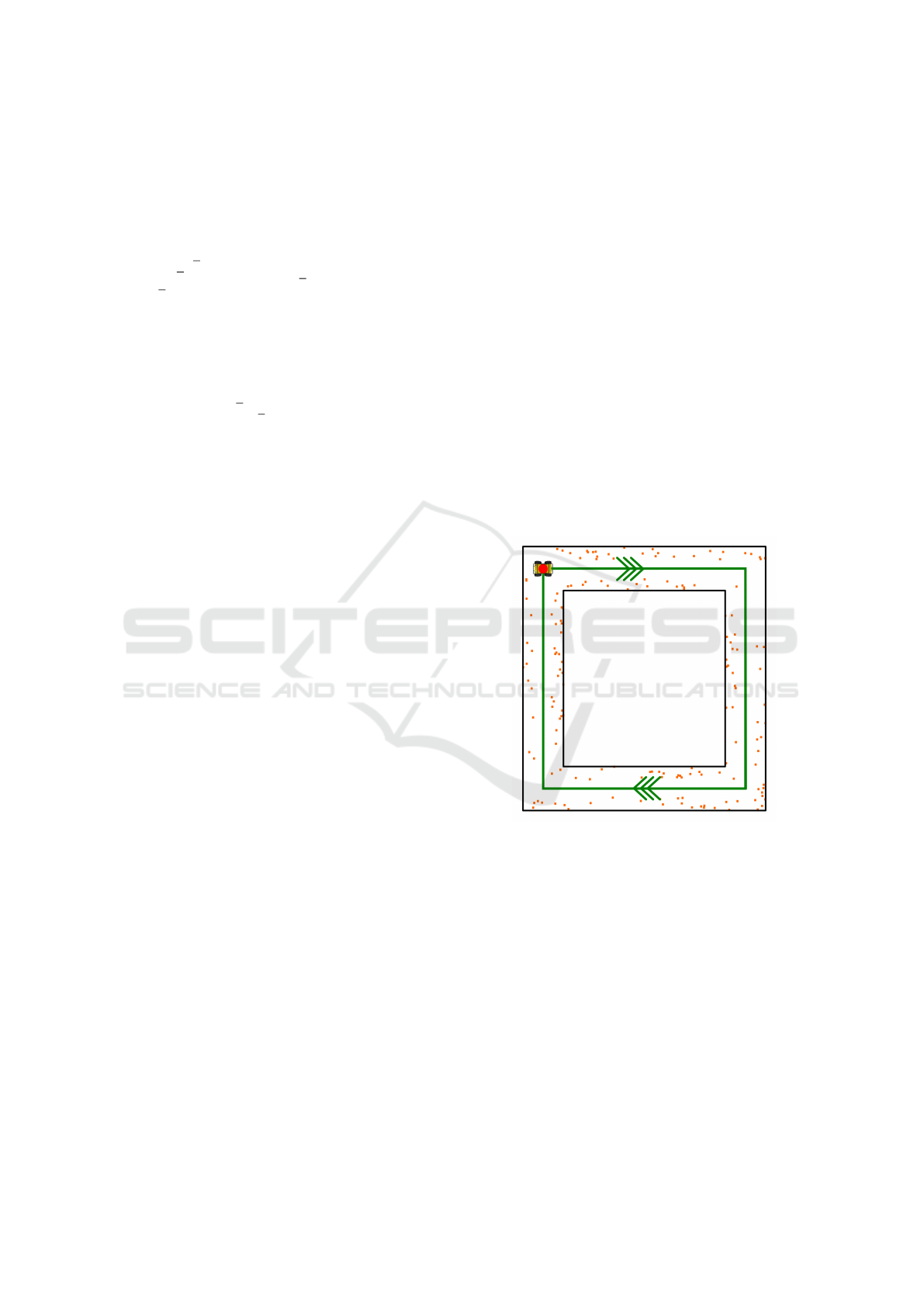
of landmarks M . As shown in Figure 1 the robot
moves in a square-shaped indoor corridor from a start-
ing point.
Figure 1: The 2D view of a robot moving in a 10m × 10 m
square-shape corridor (bounded by two black boxes). The
robot starts from the red point (0, 0) and follows the clock-
wise green trajectory (ground truth). Orange dots are land-
marks to be measured.
The robot carries a LiDAR sensor and measures
the radial distance r and horizontal angle θ of its
surrounding landmarks to the robot itself. For each
LiDAR scan a subset of the map landmarks m
l
can
be measured, where l ∈ {1,..., L} . L is the num-
ber of landmarks the robot observes from its current
scan. Note that this scenario is built in simulation,
with the positions of map landmarks M known. The
landmarks are assumed to be randomly distributed in
the environment and can be perceived by the LiDAR
accurately. Furthermore, the locally observed land-
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
298
marks m
l
are acquired according to the robot mo-
tion model and the geometry of the corridor which
we establish by simulation. We assume that a feature
extraction algorithm provides measurements of land-
marks in the current scan and association between the
locally observed landmarks m
l
and the map M is al-
ready solved.
This localization problem can be formulated by
the state estimation equations:
(
Measurement : G(x, z , m
l
) = 0
Association : m
l
∈ M
, (4)
where we denote x = (x y ψ)
T
as the unknown robot
pose, z = (r θ)
T
as the measurement for each m
l
in current scan, and m
l
= (m
l
x
m
l
y
)
T
the position
of the landmark. More specifically, the measurement
constraint in Equation 4 can be broken down as fol-
lows:
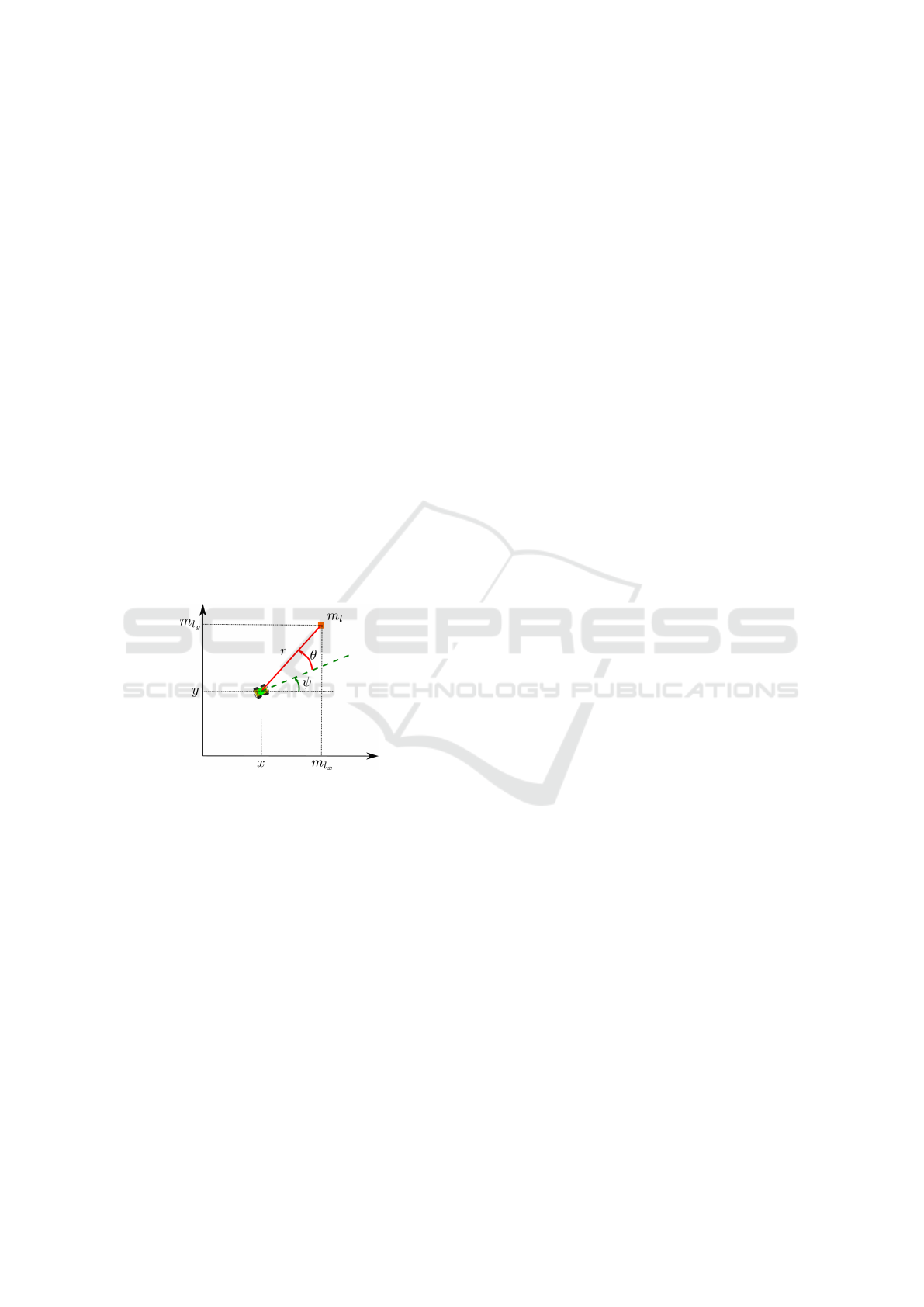
G(x, z ) =
x + r · cos(ψ + θ) − m
l
x
y + r · sin(ψ + θ) − m
l
y
. (5)
We illustrate the above measurement model in Figure
2 where the robot measures its distance and azimuthal
angle with respect to a landmark.
Figure 2: The robot measurement model.
Next, we will introduce our interval-based so-
lution and factor graph-based probabilistic solution
for the aforementioned localization problem, respec-
tively.
4.1 Interval-based Localization
All variables in Equation 4 are described in the inter-
val domain. This allows us to formulate a CSP L:
L :
Variable : x, z, m
l
, M
Constraint :
G(x, z , m
l
) = 0
m
l
∈ M
Domain : [x], [z], [m
l
], [M]
, (6)
where [x] is the set of feasible robot poses that we
want to determine and [z] = ([r] [θ])
T
is our land-
mark measurement. Interval boxes are suitable to
represent the uncertainty of LiDAR measurements
because we usually only know the accuracy of the
distance and beam divergence (Voges, 2020). Be-
sides the measurement uncertainty, the uncertainty of
known map landmarks M is also specified. The un-
certainty of map landmarks can be provided by the
accuracy of the given map or feature extraction algo-
rithm. In this CSP we assume no information about
the prior robot position, thus its initial domain is set
to [x] = ([−∞, ∞] [−∞, ∞] [−π, π])
T
.
Then, we build forward-backward contractors for
solving each constraint in CSP L and get the inter-
section to contract the interval pose. Before using the
contractors, we first break down our constraints into
simple equations according to Equation 5 and 6 (Ro-
hou et al., 2020):
a = ψ + θ
d
x
= r · cos (a)
d
y
= r · sin (a)
m
l
x
= x + d
x
m
l
y
= y + d
y
m
l
∈ M
, (7)
where a and d = (d
x
d
y
)
T
are intermediate variables
for decomposing complex constraints into elementary
equations. Subsequently, we apply addition contrac-
tor C
+
(e.g. C
+
([a], [ψ], [θ]) ) for addition equations
and polar contractor C
polar
([d
x
], [d
y
], [r], [a]) for the
polar equations in Equation 7 (Desrochers and Jaulin,
2016). As a result, related interval domains are re-
duced until smallest interval boxes are reached.
In our localization problem, the CSP L will be
solved for each robot pose, which means that when-
ever the robot measures landmarks from one LiDAR
scan, the contractors will be applied to contract the
initial box [x] for the contracted robot pose. The re-
sulted interval box represents the uncertainty of the
robot pose.
4.2 Factor Graph-based Localization
A factor graph includes variables and factors which
represent constraints between variables in a graph and
solve a maximum a posteriori (MAP) estimate prob-
lem (Kaess et al., 2011). Here we illustrate the factor
graph of our localization problem in Figure 3.
As a probabilistic approach, all quantities and fac-
tors involved are labeled with a probability distribu-
tion. Given that all measurements are affected by
Gaussian noise, the goal of our localization problem
is to estimate a Gaussian approximation of the poste-
rior of the robot poses. In the following, we formulate
our localization problem as an optimization problem
Interval-based Robot Localization with Uncertainty Evaluation
299

Figure 3: Factor graph representation of the localization
problem. We have robot poses x (grey circles), observed
landmarks m
l
(orange circles) as variables. Blue boxes are
the measurement factors between poses and observed land-
marks m
l
. Green boxes represent the map factors between
the observed landmarks and map M .
that determines the robot poses and landmark posi-
tions based on a set of measurements.
Let v = (x m
l
)
T
be the state vector that consists
of robot poses x = (x
1
... x
T
) and landmarks m
l
=
(m
l
1
... m
l
K
) where T, K are the numbers of all poses
and landmarks, respectively. Here we define the robot
poses as x
t
∈ SE(2) and landmarks as m
l
k
∈ R
2
. The
optimization problem can be represented as a MAP
estimate according to Bayes’ law:
v
∗
= argmax
v
p(v|z) = argmax
v
p(z|v) p(v) (8)
where z is the measurements gathered by the robot.
The term p(v) is the prior over all states which re-
quire to be given. With the assumption of indepen-
dent Gaussian noise on the measurements, Equation
8 can be written as:
v
∗
= argmin
v
∑
i
e
i
(v, z
i
)
T
Ω
i
e
i
(v, z
i
) + F
map
(m
l
)
(9)
where e
i
(v, z
i
) is the error function that measures
how well the state vector v satisfy the constraint z
i
,
Ω
i
is the information matrix of measurement z
i
and
F
map
is the prior knowledge of the map landmarks.
In our localization problem, apart from defining mea-
surement factors which can be described by the left
part on the right side of Equation 9, we also de-
fine the map factors, which is a Gaussian prior about
the landmark positions in the known map (similarly,
in the interval approach we define the prior of map
landmarks as interval boxes). To solve Equation 9
and compute the Gaussian approximation of the robot
poses as well as landmark positions, we use the stan-
dard least-squares optimization method Levenberg-
Marquardt using the GTSAM solver for factor graphs
(Dellaert, 2012).
5 EXPERIMENTAL EVALUATION
Our simulated experiments are designed to 1) support
the claim that the interval-based localization method
can ensure a guaranteed uncertainty estimation with-
out assuming any probability distribution over the
measurement; 2) compare the uncertainty estimation
of the interval-based method and the factor graph-
based probabilistic method; 3) to find out the advan-
tages and disadvantages of using interval method and
probabilistic method when there are unidentified non-
Gaussian measurement errors.
We use simulated data (as explained in Section 4)
for our experiments to leave out the influence of in-
accurate data association and outliers so that we can
investigate how the measurement model and uncer-
tainty propagation strategy can affect the final uncer-
tainty estimation. Firstly, we introduce important pa-
rameters that we use for the experiments.
We assume the robot moving in a 10 m × 10 m
square-shaped indoor corridor with an initial position
at (0, 0) as illustrated in Figure 1. To calculate com-
parable uncertainty estimations for the interval-based
and factor graph-based methods, we carefully choose
the uncertainty of map landmarks and measurements.
For the factor graph based method, we define the
standard deviations for the prior map landmarks as
σ
M
x
= σ
M
y
= 0.01 m , and for the angle and dis-
tance measurements as σ
θ
= 0.01° , σ
r
= 0.1 m . For
the interval-based method, we intend to define the in-
terval box region of the map and measurements as
such, that it will always include the 99% confidence
region of Gaussian error ellipse. According to the χ
2
distribution, we choose 3 σ as the radius of the in-
tervals. Specifically, for the map landmarks the un-
certainty is [∆
M
x
] = [∆
M
y
] = [−0.03, 0.03]m , and
for the measurements the uncertainties are [∆
θ
] =
[−0.03, 0.03]°, [∆
r
] = [−0.3, 0.3]m.
In the following sections, we design four small ex-
periments to compare the uncertainty estimation re-
sults of the two methods. We assign non-Gaussian
measurement noises in the measurement model to find
out how the two methods handle it. For the interval
method, the measurement model always follows the
interval uncertainty. For the probabilistic methods, no
matter there is or not non-Gaussian noise in the mea-
surements, it always assume it to be Gaussian. First,
we compare the interval uncertainty with the proba-
bilistic uncertainty when the measurements of given
map landmarks follow Gaussian distributions. The
non-zero Gaussian measurement is just a perfect as-
sumption, while in real cases, the LiDAR measure-
ments could contain systematic errors that are hard to
identify. Thus in the second and third experiment, we
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
300
simulate systematic errors for both methods and show
how the two approaches handle the uncertainty prop-
agation. In the last experiment, we suppose that the
actually measured map landmarks are uniformly dis-
tributed in the interval uncertainty box of map land-
marks, then apply the two methods with interval and
probabilistic measurement models as in the first ex-
periment.
5.1 Comparison of the Uncertainty
Estimation
Our first experiment is designed to show the compari-
son of the robot pose uncertainty estimation using the
interval-based localization algorithm and the factor
graph-based optimization algorithm. Here the mea-
surements are acquired according to the given map
landmark positions. The measurements in the factor
graph are inserted using Gaussian distribution while
the measurements in the interval method follow inter-
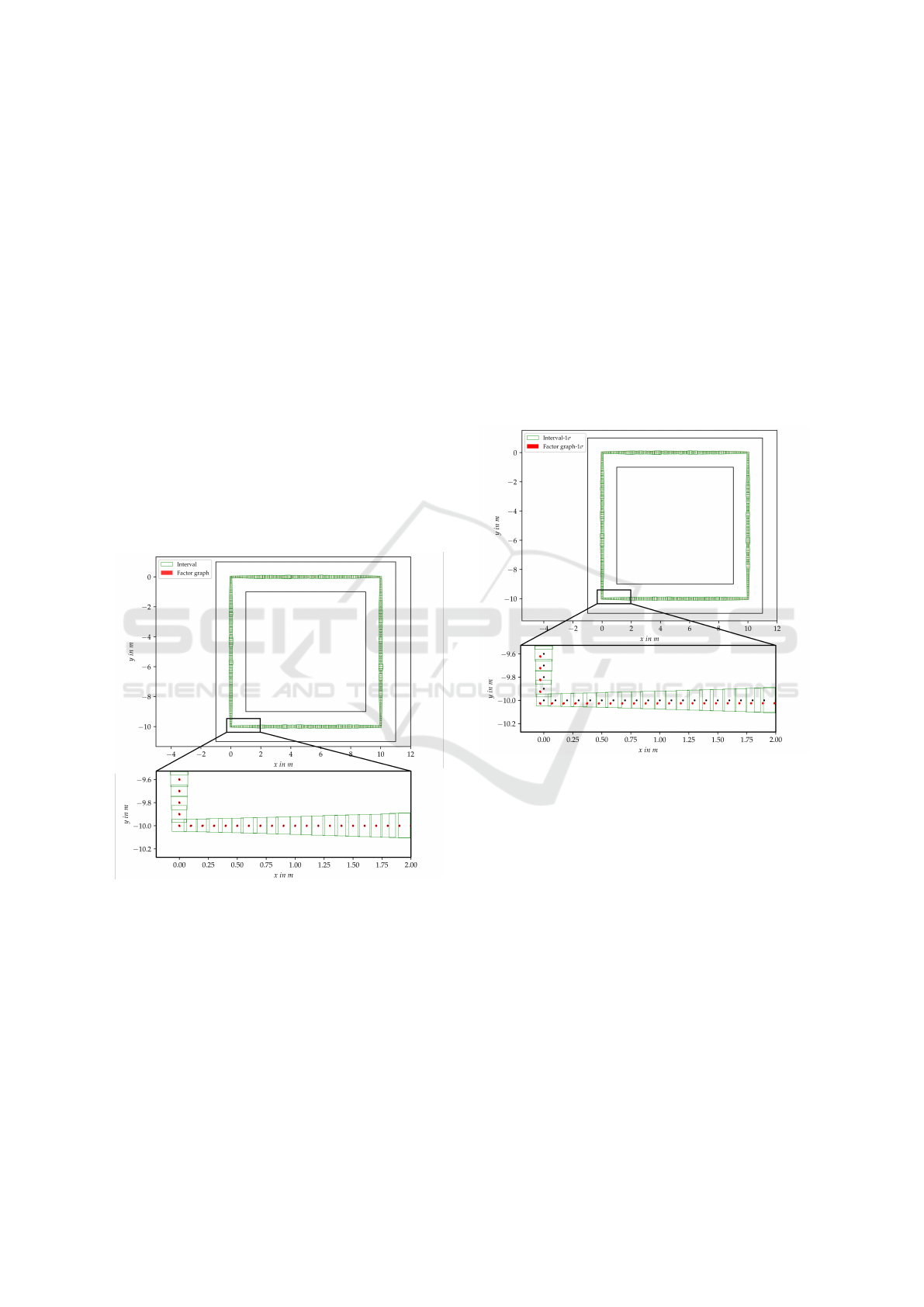
val uncertainty. We show in Figure 4 the result of both
methods.
Figure 4: Uncertainty of robot poses given by interval
method and factor graph method. The green boxes repre-
sent the interval pose uncertainty. Red ellipses represent the
probabilistic pose uncertainty which is the 99% confidence
region. The black dots inside the red ellipses are the ground
truth value.
As can be seen, the green boxes represent the
interval pose uncertainty and the red error ellipses
which are the 99% confidence region represent the
probabilistic uncertainty. It is clear that throughout
the trajectory the probabilistic uncertainty is much
smaller than the interval uncertainty. Moreover, 100%
ground-truth poses are enclosed by both the interval
and probabilistic pose uncertainties. The results show
that both methods can give guaranteed results while
the probabilistic method can provide more accurate
pose estimation (i.e. the mean value) than the interval
method, as the interval results can only give a region
of all possible robot positions, but not explicit poses
like the probabilistic method do.
5.2 Impact of 1-σ Systematic Error
In the second experiment, we add a positive 1-σ
r
sys-
tematic error to the distance measurements of both
methods. This is to resemble unidentified systematic
errors in the range measurements from a LiDAR. The
results are shown in Figure 5.
Figure 5: Green boxes represent the interval pose uncer-
tainty. Red ellipses represent the 99% confident region of
probabilistic uncertainty. Black dots are the ground truth
value.
Note that interval uncertainty boxes still enclose
the ground truth. Also, the interval boxes shrink
slightly because solutions that are not consistent with
the new measurement constraints are removed. The
probabilistic uncertainty (red ellipse) shows an ob-
vious shift to the outer bound of the interval box,
and no longer includes the ground-truth value. The
results imply that the probabilistic method underes-
timates the uncertainty and gives wrong estimates,
while the interval method is still able to enclose the
ground truth.
5.3 Impact of 2-σ Systematic Error
In the third experiment, we decide to further investi-
gate the influence of systematic errors of the measure-
Interval-based Robot Localization with Uncertainty Evaluation
301
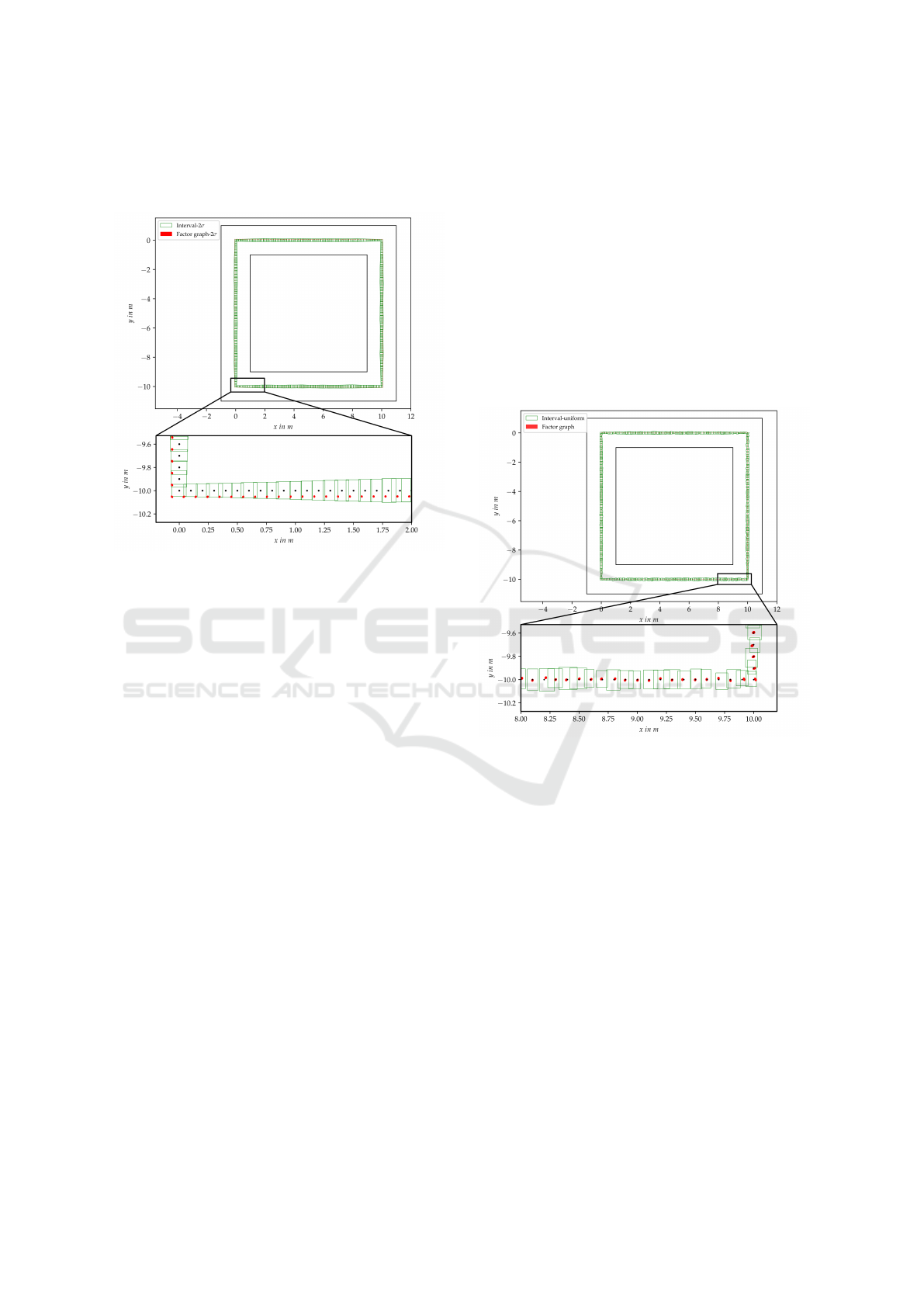
ments. We add a positive 2-σ
r
systematic error to the
distance measurements of both methods. The results
are shown in Figure 6.
Figure 6: Green boxes represent the interval pose uncer-
tainty. Red ellipses represent the 99% confident region of
probabilistic uncertainty. Black dots are the ground truth
value.
We can clearly see that interval boxes are still en-
closing the ground truth, however, most of the prob-
abilistic error ellipses go even further away from the
true value. We believe that in this case, the probabilis-
tic method gives very wrong uncertainty estimation
that some of the error ellipses are even partly outside
of the guaranteed interval uncertainty.
To conclude, we find that the interval method is
robust to systematic errors of measurements, while
the probabilistic method becomes significantly unre-
liable. The results of the second and third experiment
show that the probabilistic method tends to underesti-
mate the uncertainty of pose estimation and can even
give totally wrong uncertainty estimation in the pres-
ence of large systematic errors. The interval method,
on the contrary, can guarantee to provide trustworthy
uncertainty estimates and not underestimate the pose
uncertainty.
5.4 Impact of a Uniformly Distributed
Measurement
In this part, we assume our measured map landmarks
are no longer on the given positions, but uniformly
distributed in the interval uncertainty box we defined
for the map landmarks. This is a more realistic as-
sumption since the actually measured landmarks by
a LiDAR sensor could reside in the close vicinity of
the real landmark positions. In other words, we cre-
ate our map landmark positions that follow a uni-
form distribution inside the interval region [M
i
] =
M
i
+ [−0.03, 0.03] m × [−0.03, 0.03]m and create
the measurements which follow interval uncertainty
and Gaussian uncertainty according to this new map.
In this experiment, the non-Gaussian measurement
error comes from the uncertainty of measured map
landmarks, but not the uncertainty in the measure-
ment models, as in the previous two experiments. The
purpose of this design is to see how the probabilistic
method copes with a known map with interval uncer-
tainty. Results are displayed in Figure 7.
Figure 7: Green boxes represent the interval pose uncer-
tainty. Red ellipses represent the 99% confident region of
probabilistic uncertainty. Black dots are the ground truth
value.
As seen from the result, the interval uncertainty
boxes encloses the ground truth poses throughout the
whole trajectory. However, the probabilistic error el-
lipses are not always able to include the ground truth
poses with some black dots completely outside the red
ellipse region, which shows that the probabilistic un-
certainty is overconfident. This experiment implies
that, when the uncertainty of map landmarks is an in-
terval, then modeling the measurements as Gaussian
can lead to underestimated pose uncertainty. Unlike
the interval-based method that gives a worst-case un-
certainty but ensures the inclusion of real result, the
probabilistic method tends to underestimate the un-
certainty.
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
302

6 CONCLUSIONS
We compare an interval-based solution and a factor
graph-based probabilistic solution for a 2D localiza-
tion problem for robot pose uncertainty estimation.
For this purpose, we design four comparison exper-
iments with different measurement models. From the
results, we find out that the probabilistic method can
provide more accurate pose estimation and smaller
uncertainty estimation than the interval method given
Gaussian measurement noise. However, the uniden-
tified non-Gaussian errors in measurements can sig-
nificantly impede the performance of the probabilis-
tic approach, causing wrong pose estimates and un-
derestimated uncertainty. In comparison, the inter-
val method is not sensitive to systematic measure-
ment errors or uncertainty of measured map positions,
which is able to robustly provide guaranteed pose un-
certainty estimation. It also shows that the interval
method usually gives pose estimation with larger un-
certainty compared to the probabilistic method. How-
ever, the benefits of using intervals for solving robot
localization problems is that no prior information of
the robot pose is required, and the ability to provide
all possible solutions with guarantee.
In the further work, we aim to apply the interval-
based method to real data. We plan to tackle the land-
mark extraction and association problem which can
introduce more sources of error that will influence
the uncertainty estimation. Besides, we would like
to investigate again the uncertainty estimation perfor-
mance of interval methods and probabilistic methods
with noisy real measurement data for which the real
distribution is unknown.
ACKNOWLEDGEMENTS
This work was supported by the German Academic
Exchange Service (DAAD) as part of the Research
Training Group i.c.sens [RTG 2159].
REFERENCES
Brenner, C. (2010). Vehicle localization using landmarks
obtained by a lidar mobile mapping system.
Chen, S. Y. (2012). Kalman filter for robot vision: A
survey. IEEE Transactions on Industrial Electronics,
59(11):4409–4420.
Dellaert, F. (2012). Factor graphs and gtsam: A hands-on
introduction. Technical Report GT-RIM-CP&R-2012-
002, GT RIM.
Desrochers, B. and Jaulin, L. (2016). A minimal contrac-
tor for the polar equation: Application to robot local-
ization. Engineering Applications of Artificial Intelli-
gence, 55:83–92.
Ehambram, A., Voges, R., and Wagner, B. (2021). Stereo-
visual-LiDAR sensor fusion using set-membership
methods. In 2021 IEEE 17th International Confer-
ence on Automation Science and Engineering (CASE).
IEEE.
Gutmann, J.-S., Burgard, W., Fox, D., and Konolige, K.
(1998). An experimental comparison of localiza-
tion methods. In Proceedings. 1998 IEEE/RSJ Inter-
national Conference on Intelligent Robots and Sys-
tems. Innovations in Theory, Practice and Applica-
tions (Cat. No.98CH36190). IEEE.
Jaulin, L., Kieffer, M., Didrit, O., and Walter,
´
E. (2001).
Interval analysis. In Applied Interval Analysis, pages
11–43. Springer London.
Kaess, M., Johannsson, H., Roberts, R., Ila, V., Leonard, J.,
and Dellaert, F. (2011). iSAM2: Incremental smooth-
ing and mapping with fluid relinearization and incre-
mental variable reordering. In 2011 IEEE Interna-
tional Conference on Robotics and Automation. IEEE.
Kenmogne, I.-F., Drevelle, V., and Marchand, E. (2017).
Image-based UAV localization using interval meth-
ods. In 2017 IEEE/RSJ International Conference on
Intelligent Robots and Systems (IROS). IEEE.
Kummerle, R., Grisetti, G., Strasdat, H., Konolige, K., and
Burgard, W. (2011). g2o: A general framework for
graph optimization. In 2011 IEEE International Con-
ference on Robotics and Automation. IEEE.
Mallet, C., Soergel, U., and Bretar, F. (2008). Analysis of
full-waveform lidar data for classification of urban ar-
eas. In ISPRS Congress 2008.
Rohou, S., Desrochers, B., and Jaulin, L. (2020). Set-
membership state estimation by solving data associ-
ation. In 2020 IEEE International Conference on
Robotics and Automation (ICRA). IEEE.
Schaefer, A., Buscher, D., Vertens, J., Luft, L., and Bur-
gard, W. (2019). Long-term urban vehicle local-
ization using pole landmarks extracted from 3-d li-
dar scans. In 2019 European Conference on Mobile
Robots (ECMR). IEEE.
Voges, R. (2020). Bounded-error visual-lidar odometry on
mobile robots under consideration of spatiotemporal
uncertainties.
Voges, R. and Wagner, B. (2021). Interval-based visual-
LiDAR sensor fusion. IEEE Robotics and Automation
Letters, 6(2):1304–1311.
Wilbers, D., Merfels, C., and Stachniss, C. (2019). Local-
ization with sliding window factor graphs on third-
party maps for automated driving. In 2019 In-
ternational Conference on Robotics and Automation
(ICRA). IEEE.
Wu, C., Huang, T. A., Muffert, M., Schwarz, T., and Grater,
J. (2017). Precise pose graph localization with sparse
point and lane features. In 2017 IEEE/RSJ Interna-
tional Conference on Intelligent Robots and Systems
(IROS). IEEE.
Interval-based Robot Localization with Uncertainty Evaluation
303
