Structural Extensions of Basis Pursuit:

Guarantees on Adversarial Robustness

avid Szeghy

2,3 a

, Mahmoud Aslan

1 b

Aron F

othi

1 c

, Bal

azs M

esz

aros

1 d

Zolt

am Milacski

4 e

and Andr

as L

orincz

1 f

Department of Artiﬁcial Intelligence, Faculty of Informatics, ELTE E

otv

os Lor

and University,

1/A. P

azm

any P

eter s

any, Budapest, 1117, Hungary

Department of Geometry, Faculty of Natural Sciences, ELTE E

otv

os Lor

and University,

1/C. P

azm

any P

eter s

any, Budapest, 1117, Hungary

AImotive Inc., 18-22 Sz

epv

olgyi

ut, Budapest, 1025, Hungary

Former Member of Department of Artiﬁcial Intelligence, Faculty of Informatics, ELTE E

otv

os Lor

and University,

1/A. P

azm

any P

eter s

any, Budapest, 1117, Hungary

Keywords:

Sparse Coding, Group Sparse Coding, Stability Theory, Adversarial Attack.

Abstract:

While deep neural networks are sensitive to adversarial noise, sparse coding using the Basis Pursuit (BP)

method is robust against such attacks, including its multi-layer extensions. We prove that the stability theorem

of BP holds upon the following generalizations: (i) the regularization procedure can be separated into disjoint

groups with different weights, (ii) neurons or full layers may form groups, and (iii) the regularizer takes

various generalized forms of the

norm. This result provides the proof for the architectural generalizations

of (Cazenavette et al., 2021) including (iv) an approximation of the complete architecture as a shallow sparse

coding network. Due to this approximation, we settled to experimenting with shallow networks and studied their

robustness against the Iterative Fast Gradient Sign Method on a synthetic dataset and MNIST. We introduce

classiﬁcation based on the

norms of the groups and show numerically that it can be accurate and offers

considerable speedups. In this family, linear transformer shows the best performance. Based on the theoretical

results and the numerical simulations, we highlight numerical matters that may improve performance further.

The proofs of our theorems can be found in the supplementary material

∗

1 INTRODUCTION

Considerable effort has been devoted to overcom-

ing the vulnerability of deep neural networks against

‘white box’ adversarial attacks. These attacks have

access to the network structure and the loss function.

They work by modifying the input towards the sign

of the gradient of the loss function (Goodfellow et al.,

2014) that can spoil classiﬁcation at very low levels

of perturbations. Furthermore, this white box attack

gives rise to successful transferable attacking samples

to other networks of similar kinds (Liu et al., 2016),

https://orcid.org/0000-0002-2934-7732

https://orcid.org/0000-0003-4844-1860

https://orcid.org/0000-0002-1662-7583

https://orcid.org/0000-0002-1261-4523

https://orcid.org/0000-0002-3135-2936

https://orcid.org/0000-0002-1280-3447

∗

https://arxiv.org/pdf/2205.08955.pdf

called ‘black box attack’. This underlines the need for

network structures exhibiting robustness against white

box adversarial attacks.

Sparse methods exploiting

norm regularization

and the Basis Pursuit (BP) algorithm (Figs. 1(a) and

1(c)) exhibit robustness against such attacks, including

their multilayer Layered Basis Pursuit (LBP) exten-

sions (Romano et al., 2020) (Fig. 1(d)). (Cazenavette

et al., 2021) (Cazenavette et al., 2021) found a solu-

tion to the LBP’s drawback that layered basis pursuit

accumulates errors: they put forth an architectural gen-

eralization of LBP to modify the cascade of layered

basis pursuit steps of the deep neural network in such a

way that the entire network becomes an approximation

to a single structured sparse coding problem that they

call deep pursuit (Figs. 1(e) and 1(e

∗

)). Note that their

generalization goes beyond the structure depicted in

Fig. 1(e). This architectural generalization points to

the relevance of a single sparse layer BP that we study

Szeghy, D., Aslan, M., Fóthi, Á., Mészáros, B., Milacski, Z. and L

orincz, A.

Structural Extensions of Basis Pursuit: Guarantees on Adversarial Robustness.

DOI: 10.5220/0011138900003277

In Proceedings of the 3rd International Conference on Deep Learning Theory and Applications (DeLTA 2022), pages 77-85

ISBN: 978-989-758-584-5; ISSN: 2184-9277

Figure 1: Steps of Basis Pursuit (BP) generalizations. Equa-

tions with argmin: the minimization tasks.

(a):

Recurrent

BP with sparse representation. Blue (light green) rectangle:

representation (input) layer. Blue (dashed light green) ar-

rows: channels that deliver quantities in the actual (in the

previous) time step. Red (light yellow) circles: active (non-

active) units of the sparse representation.

: input.

and

: representation and error at the

iteration.

j,t

: same at

the

layer of the deep unrolled network. Matrices

dictionaries,

: identity matrix,

softmax with

bias.

(b):

group sparse case:

norm is replaced with the

1,2

norm.

(c): Unrolled

feedforward network with ﬁnite number of

iterations.

(d):

Cascaded unrolled deep network.

(e):

Non-

cascaded modiﬁcation of the unrolled deep sparse cascade.

∗

The minimization task of

(e)

(f):

The general case still

having warranties against adversarial attacks. Within layer

groups are not shown. More details: text and supplementary

material.

here.

A long-standing problem is that sparse coding is

slow. An early effort utilized an associative correlation

matrix (Gregor and LeCun, 2010). Recent efforts, put

forth the ﬁrst approximation of BP combined with

speciﬁc loss terms during training (see (Murdock and

Lucey, 2021) and the references therein). Although the

approach is attractive, theoretical stability warranties

are missing.

We propose group sparse coding as an additional

means for the resolution. Sparse coding that exploits

norm regularization to optimize the hidden represen-

tation can be generalized to group sparse coding that

uses the `

1,2

norm or the elastic `

β,1,2

norm instead.

We present theoretical results on the stability of a

family of group sparse coding that alike to its sparse

variant can robustly recover the underlying represen-

tations under adversarial attacks. Yet, group sparse

coding offers fast and efﬁcient feedforward estima-

tions of the groups either by traditional networks or

by transformers that the classiﬁcation step can follow.

Previous work (L

orincz et al., 2016) suggested the

feedforward estimation of the groups to be followed

by the pseudoinverse estimation of the group activi-

ties for learning and ﬁnding a group sparse code but

without targeting classiﬁcation or adversarial consider-

ations.

Our feedforward method estimates the

norms of

the active groups followed by the classiﬁcation step,

achieving further computational gains by eliminating

the pseudoinverse computations. We consider how to

combine the fast estimation with the robust BP compu-

tations based on our theoretical and numerical results.

However, the speed considerations and test will be

presented in a separate paper, now will focus on the

robustness results.

Our contributions are as follows:

•

we extend the theory of adversarial robustness of

Basis Pursuit to a family of networks, including

groups, layers, and skip connections between the

layers both to deeper and to more superﬁcial layers,

•

we introduce group norm based classiﬁcation and

its group pooled variant,

• suggest and study gap regularization,

•

execute numerical computations and test feedfor-

ward shallow, deep, transformer networks trained

on sparse and group sparse layers with a synthetic

and the MNIST dataset,study the performance of

these fast algorithms, and

•

we point to bottlenecks in the training procedures.

We present our theoretical results in Sect. 2. It is

followed by the experimental studies (Sect. 3). We

examine the properties of the group sparse structures

outside of the scope of the theory to foster further

works. Section 4 contains the discussions of our re-

sults. We conclude in Section 5. Details of the theoret-

ical derivations are in the supplementary material of

Footnote

∗

2 THEORY

We start with the background of the theory including

the notations. It is followed by our theoretical results.

2.1 Background and Notation

We denote the Sparse Coding (SC) problem by

X =

DΓ

, where given the signal

X ∈ R

and the unit-

normed dictionary

D ∈ R

N×M

, the task is to recover

the sparse vector representation Γ

Γ ∈ R

min

subject to X

X = D

DΓ

Γ,

, (P

)

where

denotes the

norm. For an excellent

book on the topic, see (Elad, 2010) and the references

therein.

DeLTA 2022 - 3rd International Conference on Deep Learning Theory and Applications

One may try to approximate the solution of Eq.

)

via the unconstrained version of the Basis Pursuit (BP,

or LASSO) method (Tibshirani, 1996; Chen et al.,

2001; Donoho and Elad, 2003):

argmin





de f

= argmin



X −D



+ γ ·



(BP)

where γ > 0.

Given

X = D

DΓ

, we may assume that

can be

further decomposed in a way similar to X

X = D

, (1)

= D

K−1

= D

The layered problem then tries to recover Γ

,. . . , Γ

Deﬁnition 1.

The Layered Basis Pursuit (LBP) (Pa-

pyan et al., 2017a) ﬁrst solves the Sparse Coding prob-

lem

X = D

via Eq.

(BP)

with parameter

, obtain-

ing

. Next, it solves another Sparse Coding problem

= D

again by Eq.

(BP)

with parameter

, de-

noting the result by

, and so on. The ﬁnal vector

is the solution of LBP. The vector

LBP

contains the

weights γ

in Eq. (BP) for each layer i.

It was shown in (Papyan et al., 2016) and (Papyan

et al., 2017b) that there is strong relationship between

the LBP and the CNN, showing that the forward pass

of the CNN is in fact identical to a layered pursuit

thresholding algorithm, moreover the layered version

can improve the system. There was also shown that

LBP suffers from error accumulation. To alleviate this

obstacle, (Cazenavette et al., 2021) rewrote LBP into

a single joint Eq.

(BP)

-like minimization scheme (i.e.,

all layers are processed simultaneously) that can be

equipped with skip connections. However, the solu-

tions of the two programs differ, and the stability has

not been proven for the latter that we do in the sup-

plementary material of Footnote

∗

, see Figs. 1(e*), and

(f).

We want to extend these methods to allow different

norms on different parts of

with different

weights

(as in the layered case) and prove a stability result for

this more general case. This will also allow to relieve

the condition on the dictionary

that its columns have

unit length in the `

norm.

Let us introduce a slightly modiﬁed version of the

notation used by (Papyan et al., 2016) and (Papyan

et al., 2017b). Let

be a subset of

{

1,. . . , M

}

which

is called a subdomain, and the components, or atoms

corresponding to

form the subdictionary

. Let

ω ∈

{

1,. . . , M

}

denote the atom corresponding to

the index ω.

de f

{

ω |

6= 0

}

and

is its

cardinality, then the restriction

∈ R

Γ ∈ R

to the indices in Λ

D) is given by,





de f







, if θ ∈ Λ

D),

0, otherwise.

(2)

Now let

0,st,D

de f

= max



(3)

be the stripe norm with respect to

, a generalization

of the deﬁnition in (Papyan et al., 2017b).

is ﬁxed, then we will use the shorter

form

0,st

0,st,D

. Further, let

µ(D

D) =

max

i6= j





be the mutual coherence of the dic-

tionary (since

is unit-normed the division by



is dropped).

We want to use 4 different norms the

, `

and the

elastic

β,1,2

norm deﬁned as

β,1,2

de f

= β ·

(1 − β)

, i.e., it is the convex combination of the

and

norms, and ﬁnally, the

1,2

group-norm, some-

times referred to as the Group LASSO (Yuan and Lin,

2006; Bach et al., 2011). To deﬁne this we need a

group partition of the index set.

If the index set

{

1,. . . , M

}

is partitioned into

groups

, i ∈

{

1,. . . , k

}

(i.e.,

i=1

{

1,. . . , M

}

and

∩ G

for

i 6= j

), then the

1,2

norm ( see,

e.g., (Bach et al., 2011) and the references therein) is

1,2

de f

∑

i=1



, (4)

where

∑

j∈G

· e

with the standard basis vec-

tors e

∈ R

, i.e. z

-s are the coordinates of Z

To extend the regularizer of Eq.

(BP)

, if

, i ∈

{

1,. . . , k

}

is a partition of the index set

{

1,. . . , M

}

then let

l : R

→ R

, l

l (Γ

Γ)

de f





,. . . , l





(5)

where

is one of the

, `

β,1,2

norm. For different

groups the parameter

can be different as well. So

this is a vector which elements are norms evaluated

on different parts of

corresponding to the different

groups and for each group, we can individually decide

which norm to use. Let

de f

= (γ

,. . . , γ

)

be a weight

vector for the different groups (more precisely for the

norms of the different groups), where

> 0, ∀i

. We

want use the regulariser

γ,l

l (Γ

Γ)

∑

i=1





. (6)

Structural Extensions of Basis Pursuit: Guarantees on Adversarial Robustness

Note that if for some groups we use the

norm

with the same weight

, then we think of this as using

the

1,2

group norm for this group of groups with the

weight γ being a special case.

Now if we ﬁx a partition

and a regularizer

(i.e. norms for the groups), then let

Γ,G

∈ R

be the

2-norm group characteristic vector of Γ

Γ, i.e.,



Γ,G



de f











1, if j ∈ supp Γ

Γ, or

j ∈ G

∩ supp Γ

Γ 6=

0 and l

= `

0, otherwise,

(7)

where supp Γ

de f

{

ω | Γ

6= 0

}

is the support of Γ

Γ.

For Z

Z ∈ R

, we deﬁne



supp d



de f







, if θ ∈ supp d

0, otherwise.

(8)

We call

L,D

de f

= max



supp d



(9)

the local amplitude of

with respect to the dictionary

For a ﬁxed

, we use the shorthand

L,D

Both the stripe norm deﬁned previously, and the

local amplitude seem difﬁcult to calculate. However,

as in (Papyan et al., 2017b) if

corresponds to a

CNN architecture, then both become quite natural and

the calculation is easy. Moreover, it is easier to keep

mutual coherence of the dictionary low.

2.2 Theoretical Results

The proofs of the results can be found in the supple-

mentary material of Footnote

∗

Here, we will investigate the stability of Eq.

(BP)

and two closely related algorithms. To unify the sev-

eral different cases, we introduce the following deﬁni-

tion.

Deﬁnition 2.

First, ﬁx a partition

, i ∈

{

1,. . . , k

}

norms for this partition

l (Γ

Γ)

and the weights

for the

norms. The unconstrained Group Basis Pursuit (GBP)

is the solution of the problem:

argmin





de f

= argmin



X −D





γ,l





(GBP)

Theorem 3.

Let

X = D

DΓ

be a clean signal and

Y = X

X + E

be its perturbed variant. Let

GBP

the minimizer of Eq. GBP where

is the weight vec-

tor. If among the norms of

we used the elastic

norm, let

{

,. . . , β

}

be the set of the parameters

used in the elastic norms and

de f

= min

{

1,β

,. . . , β

}

Moreover, let

max

de f

= max

{

,. . . , γ

}

and

min

de f

min

{

,. . . , γ

}

for the weight vector

and

de f

λγ

min

max

Assume that



Γ,G



0,st

≤ c

1+θ



1 +

µ(D



λ(1−c)

≤ γ

min

where

0 < c < 1

. If

supp χ

Γ,G

has full column rank,

then

1) supp Γ

GBP

⊆ supp χ

Γ,G

2) the minimizer of Eq. GBP is unique.

If we set γ

min

λ(1−c)

, then

GBP

− Γ

∞

1+θ

(1+µ(D

D))θ(1−c)



1+θ

(1+µ(D

D))θ(1−c)

⊆ supp Γ

GBP

where

1+θ

(1+µ(D

D))θ(1−c)

≤

1+θ

θ(1−c)

yields a

weaker bound in 3) and 4) without the mutual co-

herence.

Roughly speaking, if the perturbation is not too

large, the support of the noisy representation stays

within its clean equivalent, and the indices that are

above the threshold level in 4) are recovered. More-

over, we can compare our result to the original Eq. BP,

Theorem 6 in (Papyan et al., 2016), as in the pure

norm case

λ = 1

and if we set

c =

, we get the same

bound

0,st



1 +

µ(D



, but we have

≤ γ

instead of the original

in b). Similarly, our

weaker bound in 3) and 4) is

instead of their

7.5

Interestingly, this single sparse layer theorem for

Eq. GBP extends to multiple layers, where on each

layer we can add group partitioning, can choose norms

and weights. The precise convergence theorem can

be found in the supplementary material of Footnote

∗

It is a generalized version of Theorem 12 in (Papyan

et al., 2017a), but that suffers from error accumulation

(Romano et al., 2020).

As mentioned earlier, we can rewrite a layered

GBP into a single sparse layer GBP. The solution will

differ a bit, but the error accumulation is not present,

see the supplementary material of Footnote

∗

for the

details. However, the new dictionary describing all the

layers won’t have unit normalization being a problem

in the ‘classical’ case but not in ours. This is because

if the dictionary

is not unit-normed, but the columns

belonging to a group

(where we choose the

the

β,1,2

norm) have the same

norm, then we can

push the ”normalization weights” of the columns of

to the weight

through the solutions of the

DeLTA 2022 - 3rd International Conference on Deep Learning Theory and Applications

(GBP)

. The problem and the solution change, but the

solution will be equivalent to the original problem, see

the supplementary material of Footnote

∗

for further

details. This allows us to extend our result for more

general sparse coding problems, see Fig. 1f and the

supplementary material of Footnote

∗

Now, if we stack a linear classiﬁer onto the top

of GBP (or onto a layered GBP) as it was done in

(Romano et al., 2020), we have several classiﬁcation

stability results, see in the supplementary material of

Footnote

∗

Also if we solve Eq.

(GBP)

with positive coding,

i.e. restrict the problem to non-negative

vectors, and

the solution

+GBP

is group-full (i.e.

supp Γ

+GBP

supp χ

+GBP

) then a weak stability theorem holds

for

+GBP

, more in the supplementary material of

Footnote

∗

3 EXPERIMENTAL STUDIES

We turn to the description of our numerical studies. We

want to explore the limitations of Group Basis Pursuit

(GBP) methods and our experiments are outside of the

scope of the present theory. We ﬁrst review the meth-

ods. It is followed by the description of the datasets

and the experimental results. Throughout these stud-

ies we used fully connected (dense) networks imple-

mented in PyTorch (Paszke et al., 2019).

3.1 Methods

3.1.1 Architectures

To evaluate the empirical robustness of our GBP with

norm regularization, we compared two variants of it

with Basis Pursuit (BP) and 3 Feedforward networks.

For our BP experiments, we used a single BP

layer to compute the hidden representation

, then

stacked a classiﬁer w

w on top.

Next, for GBP, we considered two scenarios. First,

we applied GBP on its own to compute a full

GBP

code. Second, we introduced Pooled GBP (PGBP):

after computing

GBP

with GBP, we compressed it

with a per group

norm calculation into

PGBP

, and

used this smaller code as input to a smaller classiﬁer

PGBP

Finally, we employed

feedforward neural net-

works trained for approximating

PGBP

: a Linear

Transformer (Katharopoulos et al., 2020), a single

dense layer, and a dense deep network having parame-

ter count similar to the Transformer. Network structure

details can be found in the supplementary material of

Footnote

∗

. For the nonnegative norm values, we used

Rectiﬁed Linear Unit (ReLU) activation at the top of

these networks. To migitate vanishing gradients, we

also added a batch normalization layer in some cases.

After obtaining the approximate pooled

PGBP

, we

applied the smaller w

PGBP

as the classiﬁer.

3.1.2 Loss Functions

Whenever training was necessary for classiﬁcation (see

Sect. 3.2.2), we pretrained our methods to minimize

the unsupervised reconstruction loss

X −D

DΓ

(G)BP

During classiﬁcation and attack phase, we used a

total loss function

J (D

D,w

w,b

b,X

X,class (X

X))

consisting

of a common classiﬁcation loss term with an optional

regularization term.

For the classiﬁcation loss, we made our choice de-

pending on the number of classes. For the

class (bi-

nary classiﬁcation) case we used hinge loss, whereas

for the multiclass case we applied the categorical cross-

entropy loss.

The regularization loss was speciﬁcally employed

to test whether it can further improve the adversarial

robustness. For this, we introduced a gap regulariza-

tion term to encourage a better separation between

active and inactive groups. We intended to increase

the smallest difference of preactivations between the

smallest active and the largest inactive group norm

within a mini-batch of Γ

(G)BP

samples:

gap

= − min

i=1,...,N



min

j : φ



||Γ

(i)

(G)BP,G



6=0

||Γ

(i)

(G)BP,G

− max

j : φ



||Γ

(i)

(G)BP,G



||Γ

(i)

(G)BP,G



(10)

where

is the sample index,

||Γ

(i)

(G)BP,G

is the

norm of group

within

(i)

(G)BP

(i.e., an element of

(i)

PGBP

) and

is an appropriate proximal operator.

For the BP case we applied group size 1.

For the training of the feedfoward networks, we

applied mean squared error against Γ

PGBP

3.1.3 Adversarial Attacks

To generate the perturbed input

Y = X

X + E

, we used

the Iterative Fast Gradient Sign Method (IFGSM) (Ku-

rakin et al., 2016). Speciﬁcally, this starts from

and

takes

bounded steps wrt.

∞

and

norms according

to the sign of gradient of the total loss

to get

Y = Y

= X

t−1

= ∇

t−1

J (D

D,w

w,b

b,Y

t−1

,class (X

X))

= clamp (Y

t−1

+ a · sgn (G

t−1

)).

(11)

Structural Extensions of Basis Pursuit: Guarantees on Adversarial Robustness

where for the learning rate we set

a =

and

clamp

a clipping function. Throughout our experiments, we

used

T = 20

; for our values of

, see Sect. 3.3. For

most cases, the attack was white box and if applicable,

the total loss

included the optional gap regulariza-

tion term. However, for the

Feedforward networks

we computed

using PGBP, resulting in a black box

attack.

3.2 Datasets

We used three datasets; two synthetic ones and MNIST.

3.2.1 Synthetic Data

We generated two synthetic datasets, one without

and another with group pooling, according to the

following procedure. First, we built a dictionary

D ∈ R

100×300

using normalized Grassmannian pack-

ing with

groups of size

(Dhillon et al., 2008). We

generated two normalized random classiﬁers

w ∈ R

300

and

PGBP

∈ R

with components drawn from the

normal distribution

N (0, 1)

and set the bias term to

zero (

b = 0

). Next, we created the respective input

sets. We kept randomly generating

Γ ∈ R

300

vectors

having

nonzero groups of size

with activations

drawn uniformly from

[1,2]

and computed

X = D

DΓ

We collected two sets of

10,000 X

vectors that satis-

ﬁed classiﬁcation margin

O(X

X) ≥ η ∈ {0.03,0.1, 0.3}

in terms of the classiﬁers

and

PGBP

acting on top

(no pooling) and the

norms of the groups of

(pooled), respectively. While running our methods, we

used a single dense layer and a linear classiﬁer layer

with the true parameters (D

D, w

(PGBP)

3.2.2 MNIST Data

We employed image classiﬁcation on the real MNIST

dataset. The images were vectorized and we prepro-

cessed to zero mean and unit variance. We used a

fully connected (dense) dictionary

D ∈ R

784×256

, hid-

den representation

(G)BP

∈ R

256

with optionally

groups of size

for our grouped methods, and a fully

connected softmax classiﬁer

mapping to the

class

probabilities acting either on top of the full

(G)BP

(i.e.,

∈ R

256

i = 1,. . . ,10

) or the compressed

PGBP

(i.e.,

PGBP,i

∈ R

i = 1,. . . , 10

). Since in this case

the true parameters (

) were not available for

our single layer methods, we tried to learn these via

backpropagation over the training set. For this, we

applied Stochastic Gradient Descent (SGD) (Bottou

et al., 2018) over

500

epochs with early stopping pa-

tience

. To prevent dead units in

, we increased

linearly between

and its ﬁnal value over the initial

epochs.

In agreement with the sparse case (Sulam et al.,

2020), we found that pretraining the dictionary using

reconstruction loss (see Sect. 3.1.2) is beneﬁcial in the

group case, too.

3.3 Experimental Results

We note that our numerical studies are outside of the

scope of the theory as shown in the supplementary

material of Footnote

∗

since (i) only about 50% of the

perfect group combinations could be found in the syn-

thetic case and (ii) the group assumption is not war-

ranted for the MNIST dataset.

3.3.1 Synthetic Experiments

We used three margins,

0.03

0.1

, and

0.3

on the syn-

thetic data. Results for margin

0.1

of the no group

pooling and group pooled synthetic experiments are

shown in Fig. 2 a) and b), respectively. See the supple-

mentary material of Footnote

∗

for the rest.

For the no group pooling experiment, we found that

BP achieves low accuracy even without attacks, and

it breaks down rapidly for increasing

. In contrast,

our GBP achieves perfect scores for low

, since it

has access to the ground truth group structure of the

data, and it is able to leverage it. For large

values, it

still breaks down and is slower than BP in the studies

domain. Note, however, that the search space is much

larger for BP than for GBP.

For the group pooled experiment, the dense, deep

dense and transformer networks were trained to ap-

proximate PGBP instead of the ground truth, hence

they score worse for zero attack. Up to

ε ≈ 0.14

val-

ues, PGBP reaches perfect accuracy. Beyond that and

due to the different nature of the attack (white box for

PGBP and black box for the others), the breakdown

is faster for PGBP than for the other methods. The

effect is more pronounced for smaller margins (see the

supplementary material of Footnote

∗

). Out of the three

feedforward estimations, the transformer performed

the best.

3.3.2 MNIST Experiment

On MNIST, we compared BP, GBP, PGBP, their re-

spective gap regularized variants and the 3 feedfoward

networks. Our results are depicted in Fig. 2 c).

Among the white box attacked pursuit methods,

PGBP gave the best results for both the non-attacked

and for the attacked case, indicating the beneﬁts of

the pooled representation, i.e., it is more difﬁcult to

attack group norms than the elements within groups.

We think that this result deserves further investigation.

DeLTA 2022 - 3rd International Conference on Deep Learning Theory and Applications

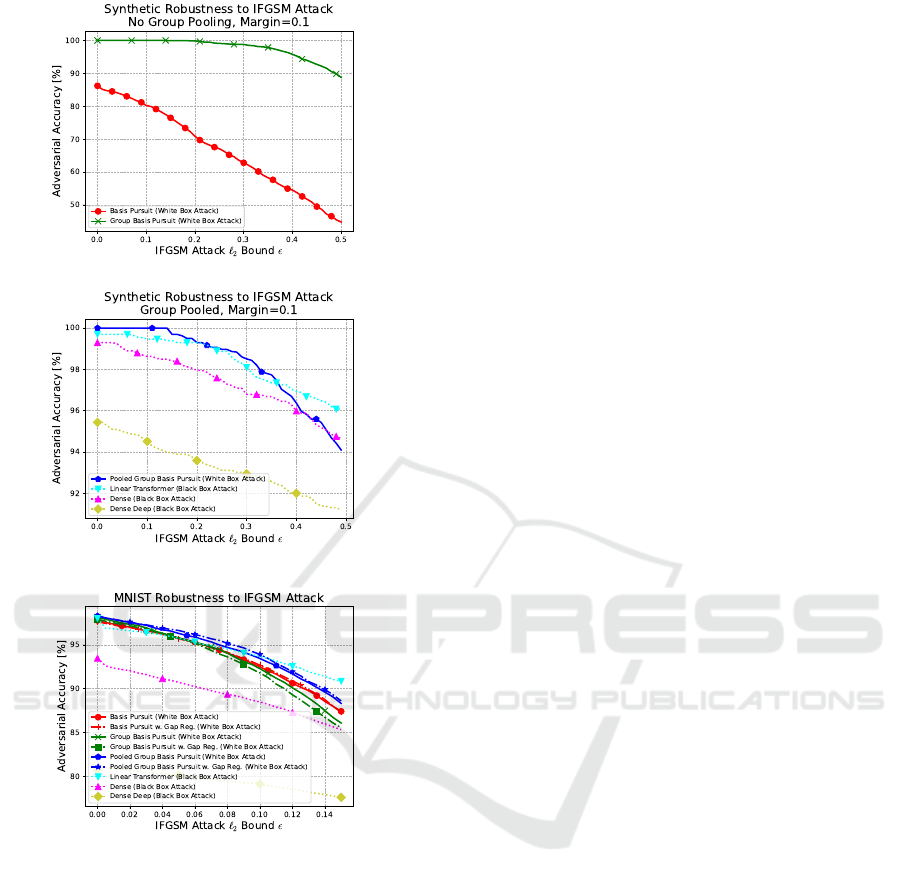
(a)

(b)

(c)

Figure 2: Results for adversarial robustness against Itera-

tive Fast Gradient Sign Method (IFGSM) attack. Datasets

differ for all subﬁgures. Best viewed zoomed in.

(a):

Syn-

thetic dataset, no group pooling: our Group Basis Pursuit

(GBP, green) obtains

100%

accuracy for small

and consid-

erably outperforms Basis Pursuit (BP, red) as it can exploit

the given group structure.

(b):

Synthetic dataset, group

pooling: Pooled Group Basis Pursuit (PGBP, blue) achieves

perfect scores for small

. Break down is faster than for

the Linear Transformer (LT, cyan) and the Dense (magenta)

networks due to the difference between white box and black

box attacks. Deep network (yellow) having parameter count

similar to LT is overﬁtting.

(c)

: MNIST dataset: PGBP is

the best for small

, and it also consistently outperforms all

BP and GBP variants for large

. For some methods, gap reg-

ularization (dash-dotted) increases performance. For large

, black box attacked LT scores the highest. Deep network

overﬁts.

BP and GBP were worse and their curves crossed each

other.

Gap regularization (Eq. (3.1.2)) slightly increased

performance for BP and PGBP, but it impairs GBP.

We believe that this technique may be improved by

making it less restrictive, similarly to the modiﬁcations

for mutual coherence in (Murdock and Lucey, 2020),

e.g., by averaging the terms.

Feedforward nets were attacked by the black box

method. The Linear Transformer obtained the best

results. Deep Network was difﬁcult to teach; it was

overﬁtting.

4 DISCUSSION

We have dealt with the structural extensions of basis

pursuit methods. We have extended the stability the-

ory of sparse networks and their cascaded versions as

follows:

The non-cascaded extension (Cazenavette et al.,

2021) that includes skip connections beyond the

off-diagonal identity blocks of the matrix depicted

in Fig. 2 that is the lower triangular part of the

matrix can be ﬁlled by general blocks has stability

proof.

Stability proof holds if non-zero general block ma-

trices occur in the upper triangular matrix repre-

senting unrolled feedback connections.

Stability proof holds if representation elements

within any layers are grouped.

Different layers and groups can have different bi-

ases, diverse norms, such as

1,2

, and the elastic

norm.

The theorem is valid for Convolutional Neural Net-

works.

Proofs are valid for positive coding for the sparse

case and under certain conditions, for the group

case, too.

Feedforward estimations are fast and our experiments

indicate that they are relatively accurate especially for

the Linear Transformer for the group structures when

there is no attack. In case of attacks, the transformer

shows reasonable robustness against black box attacks.

However, it seems that transformers are also fragile

for white box attacks (Bai et al., 2021). Attacks can be

detected as shown by the vast literature on this subject.

For recent reviews, see (Akhtar et al., 2021; Salehi

et al., 2021) and the references therein. Detection of

the attacks can optimize the speed if all (P)GBP and

feedforward estimating networks are run in parallel

and the detection is fast so it can make the choice in

time.

Structural Extensions of Basis Pursuit: Guarantees on Adversarial Robustness

Performances could be improved by introducing

additional regularization loss terms (Murdock and

Lucey, 2021). We could improve our results by adding

a loss term aiming to increase the gap between the

groups that will become active and the groups that

will be inactive after soft thresholding. Our results are

promising and the present loss term (Eq.

(3.1.2)

) may

be too strict. Another interesting loss term could be the

minimization of the mutual coherence of

(Murdock

and Lucey, 2020) and we leave this examination for

future works.

Our experimental studies can be generalized in sev-

eral ways. Firstly, a single layer can not be perfect for

all problems. The hierarchy of layers is most promis-

ing for searching for groups of different sizes. As an

example, edge detectors can be built hierarchically

using CNNs, see, e.g., (Poma et al., 2020).

Further, we restricted the investigations to groups

of the same size and the same bias, even though that

inputs may be best ﬁt by groups of different sizes, or

even by including a subset of single elements, and the

bias may also differ. This is an architecture optimiza-

tion problem, where the solution is unknown. Learn-

ing of the sparse representation is however, promising

since under rather strict conditions, high-quality sparse

dictionaries can be found (Arora et al., 2015). The

step to search for groups is still desired since (a) the

search space may become smaller by the groups and

(b) the presence of the active groups may be estimated

quickly and accurately using feedforward methods, es-

pecially transformers (in the absence of attacks). In

turn, feedforward estimation of the groups followed

by (P)GBP with different group sizes including single

atoms seems worth studying.

5 CONCLUSIONS

We studied the adversarial robustness of sparse coding.

We proved theorems for a large variety of structural

generalizations, including: groups within layers, di-

verse connectivities between the layers and versions

of optimization costs related to the

norm. We also

studied group sparse networks experimentally. We

demonstrated that our GBP can outperform BP, and

that our PGBP works better than both using 8 times

smaller representation. We found that PGBP offers

fast feedforward estimations and the transformer ver-

sion shows considerable robustness for the datasets we

studied. Finally, we showed that gap regularization

can improve robustness even further, as suggested by

condition 4) of Theorem 3.

Yet, the scope of our studies are limited from mul-

tiple perspectives. First, the suprisingly great perfor-

mance of our PGBP despite its small representation

calls for further investigations using more complex

datasets and attacks, as MNIST and IFGSM are too

simple and specialized compared to real world sce-

narios. Second, we believe that theoretical extensions

to PGBP are possible, and that varying group sizes

and other loss functions may provide performance im-

provements.

Defenses against noise, novelties, anomalies and,

in particular, against adversarial attacks may be solved

by combining our robust, structured sparse networks

with out-of-distribution detection methods.

ACKNOWLEDGEMENTS

The research was supported by (a) the Ministry of Inno-

vation and Technology NRDI Ofﬁce within the frame-

work of the Artiﬁcial Intelligence National Laboratory

Program, (b) Application Domain Speciﬁc Highly Re-

liable IT Solutions project of the National Research,

Development and Innovation Fund of Hungary, ﬁ-

nanced under the Thematic Excellence Programme

no. 2020-4.1.1.-TKP2020 (National Challenges Sub-

programme) funding scheme and (c) D. Szeghy was

partially supported by the NKFIH Grant K128862.

REFERENCES

Akhtar, N., Mian, A., Kardan, N., and Shah, M. (2021). Ad-

vances in adversarial attacks and defenses in computer

vision: A survey. IEEE Access, 9:155161–155196.

Arora, S., Ge, R., Ma, T., and Moitra, A. (2015). Simple,

efﬁcient, and neural algorithms for sparse coding. In

Conf. on Learn. Theo., pages 113–149. PMLR.

Bach, F., Jenatton, R., Mairal, J., and Obozinski, G.

(2011). Optimization with sparsity-inducing penalties.

arXiv:1108.0775.

Bai, Y., Mei, J., Yuille, A. L., and Xie, C. (2021). Are

transformers more robust than cnns? Adv. in Neural

Inf. Proc. Syst., 34.

Bottou, L., Curtis, F. E., and Nocedal, J. (2018). Optimiza-

tion methods for large-scale machine learning. Siam

Review, 60(2):223–311.

Cazenavette, G., Murdock, C., and Lucey, S. (2021). Ar-

chitectural adversarial robustness: The case for deep

pursuit. In IEEE/CVF Conf. on Comp. Vis. and Patt.

Recogn., pages 7150–7158.

Chen, S. S., Donoho, D. L., and Saunders, M. A. (2001).

Atomic decomposition by basis pursuit. SIAM Review,

43(1):129–159.

Dhillon, I. S., Heath, J. R., Strohmer, T., and Tropp, J. A.

(2008). Constructing packings in Grassmannian mani-

folds via alternating projection. Exp. Math., 17(1):9–

35.

DeLTA 2022 - 3rd International Conference on Deep Learning Theory and Applications

Donoho, D. L. and Elad, M. (2003). Optimally sparse repre-

sentation in general (nonorthogonal) dictionaries via

minimization. Proc. Natl. Acad. Sci., 100(5):2197–

2202.

Elad, M. (2010). Sparse & Redundant Representations and

Their Applications in Signal and Image Processing.

Springer Science & Business Media.

Goodfellow, I. J., Shlens, J., and Szegedy, C. (2014).

Explaining and harnessing adversarial examples.

arXiv:1412.6572.

Gregor, K. and LeCun, Y. (2010). Learning fast approxi-

mations of sparse coding. In 27th Int. Conf. on Mach.

Learn., pages 399–406.

Katharopoulos, A., Vyas, A., Pappas, N., and Fleuret, F.

(2020). Transformers are rnns: Fast autoregressive

transformers with linear attention. In Int. Conf. on

Mach. Learn., pages 5156–5165. PMLR.

Kurakin, A., Goodfellow, I. J., and Bengio, S.

(2016). Adversarial examples in the physical world.

arXiv:1607.02533.

Liu, Y., Chen, X., Liu, C., and Song, D. (2016). Delving

into transferable adversarial examples and black-box

attacks. arXiv:1611.02770.

orincz, A., Milacski, Z. A., Pint

er, B., and Ver

o, A. L.

(2016). Columnar machine:

ast estimation of struc-

tured sparse codes. Biol. Insp. Cogn. Arch., 15:19–33.

Murdock, C. and Lucey, S. (2020). Dataless model selection

with the deep frame potential. In IEEE/CVF Conf. on

Comp. Vis. and Patt. Recogn., pages 11257–11265.

Murdock, C. and Lucey, S. (2021). Reframing neural net-

works: Deep structure in overcomplete representations.

arXiv:2103.05804.

Papyan, V., Romano, Y., and Elad, M. (2017a). Convo-

lutional neural networks analyzed via convolutional

sparse coding. J. Mach. Learn. Res., 18(1):2887–2938.

Papyan, V., Sulam, J., and Elad, M. (2016). Working locally

thinking globally-Part II: Stability and algorithms for

convolutional sparse coding. arXiv:1607.02009.

Papyan, V., Sulam, J., and Elad, M. (2017b). Working locally

thinking globally: Theoretical guarantees for convo-

lutional sparse coding. IEEE Trans. Signal Process.,

65(21):5687–5701.

Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,

Chanan, G., Killeen, T., Lin, Z., et al. (2019). PyTorch:

An imperative style, high-performance deep learning

library. arXiv:1912.01703.

Poma, X. S., Riba, E., and Sappa, A. (2020). Dense extreme

inception network: Towards a robust CNN model for

edge detection. In IEEE/CVF Winter Conf. on Apps. of

Comp. Vis., pages 1923–1932.

Romano, Y., Aberdam, A., Sulam, J., and Elad, M. (2020).

Adversarial noise attacks of deep learning architectures:

Stability analysis via sparse-modeled signals. J Math.

Imag. and Vis., 62(3):313–327.

Salehi, M., Mirzaei, H., Hendrycks, D., Li, Y., Ro-

hban, M. H., and Sabokrou, M. (2021). A uniﬁed

survey on anomaly, novelty, open-set, and out-of-

distribution detection: Solutions and future challenges.

arXiv:2110.14051.

Sulam, J., Muthukumar, R., and Arora, R. (2020). Adversar-

ial robustness of supervised sparse coding. In Adv. in

Neural Inf. Proc. Syst., volume 33, pages 2110–2121.

Tibshirani, R. (1996). Regression Shrinkage and Selection

via the LASSO. J. R. Stat. Soc. Series B (Methodol.),

58(1):267–288.

Yuan, M. and Lin, Y. (2006). Model selection and estimation

in regression with grouped variables. J. R. Stat. Soc.

Series B (Methodol.), 68(1):49–67.

APPENDIX

Due to space constraints, we were only able to state

our main result of Theorem 3 here. The rest of our

theorems and all proofs can be found in the supple-

mentary material of Footnote

∗

, the url is located right

below the abstract.

Structural Extensions of Basis Pursuit: Guarantees on Adversarial Robustness