Online Non-metric Facility Location with Service-Quality Costs

Christine Markarian

Department of Engineering and Information Technology,

University of Dubai, Dubai, U.A.E.

Keywords:

Online Non-metric Facility Location, Service-quality Costs, Optimization, Online Algorithms, Competitive

Analysis, Randomized Algorithms, Rounding.

Abstract:

In this paper, we study the Online Non-metric Facility Location with Service-Quality Costs problem (Non-

metric OFL-SQC), a generalization of the well-known Online Non-metric Facility Location problem (Non-

metric OFL), in which facilities have, in addition to opening costs, service-quality costs. Service-quality costs

are determined by the quality of the service provided by each facility so as the higher the quality, the lower

the service-quality cost. These are motivated by companies wishing to incorporate the quality of third-party

services into their optimization decisions. Clients are scattered around facilities and arrive in groups over

time. Each arriving group is composed of a number of clients at different locations. Non-metric OFL-SQC

asks to serve each client in the group by connecting it to an open facility. Opening a facility incurs an opening

cost and connecting a client to a facility incurs a connecting cost, which is the distance between the client

and the facility. Moreover, for each group, the algorithm needs to pay the sum of the service-quality costs

associated with the facilities serving the clients of the group. The aim is to serve each arriving group while

minimizing the total facility opening costs, connecting costs, and service-quality costs. We develop the ﬁrst

online algorithm for non-metric OFL-SQC and analyze it using the standard notion of competitive analysis, in

which the online algorithm’s worst-case performance is measured against the optimal ofﬂine solution that can

be constructed optimally given all the input sequence in advance.

1 INTRODUCTION

Facility Location problems, that aim to place one

or more facilities in a way that meets a given opti-

mization objective, are one of the most well-studied

combinatorial optimization problems, with a wide

range of applications in operations research, urban

planning, management science, economics, market-

ing, computer science, and many others (Drezner and

Hamacher, 2004).

Facility Location problems have an online nature,

in which the input sequence is revealed in portions

over time, and the so-called online algorithm reacts to

each portion by targeting the given optimization goal.

In its most general form, each such sequence is com-

posed of a single client that needs to be connected to

an open facility. The online algorithm needs to de-

cide at which locations to open facilities, while mini-

mizing the total facility opening costs and connecting

costs or distances between clients and facilities.

Facility Location problems are known as metric

and non-metric variants. In the former case, clients

and facilities are assumed to reside in the metric

space and the distances respect the triangle inequal-

ity. The metric properties are normally used in the

analysis of the online algorithms for the metric vari-

ants. Both metric (Meyerson, 2001; Fotakis, 2008;

Anagnostopoulos et al., 2004) and non-metric (Alon

et al., 2006; Markarian, 2021; Markarian et al., 2021;

Markarian and auf der Heide, 2019; Markarian and

Khallouf, 2021; Markarian and El-Kassar, 2021) vari-

ants have been well investigated, in many settings and

as many variations.

In this paper, we study an online non-metric vari-

ant of Facility Location, known as the Online Non-

metric Facility Location With Service-Quality Costs

problem (Non-metric OFL-SQC).

1.1 Online Non-metric Facility Location

with Service-Quality Costs

(Non-metric OFL-SQC)

Given a collection of potential facility locations. Each

facility location has an opening cost and a service-

quality cost. Service-quality costs are determined by

the quality of the service provided by each facility

so as the higher the quality, the lower the service-

quality cost. These are motivated by companies wish-

ing to incorporate the quality of third-party services

616

Markarian, C.

Online Non-metric Facility Location with Service-Quality Costs.

DOI: 10.5220/0011101900003179

In Proceedings of the 24th International Conference on Enterprise Information Systems (ICEIS 2022) - Volume 1, pages 616-622

ISBN: 978-989-758-569-2; ISSN: 2184-4992

into their optimization decisions. Clients are scattered

around facilities and arrive in groups over time. Each

arriving group is composed of a number of clients

at different locations. Non-metric OFL-SQC asks to

serve each client in the group by connecting it to an

open facility. Opening a facility incurs the associ-

ated facility opening cost and connecting a client to

a facility incurs a connecting cost, which is the dis-

tance between the client and the facility. Moreover,

for each group, the algorithm needs to pay the sum

of the service-quality costs associated with the facil-

ities serving the clients of the group. The aim is to

serve each arriving group while minimizing the total

facility opening costs, connecting costs, and service-

quality costs.

2 OUR CONTRIBUTION

We design the ﬁrst online algorithm for non-metric

OFL-SQC and measure its performance using com-

petitive analysis, a notion commonly used in the anal-

ysis of online algorithms (Sleator and Tarjan, 1985;

Borodin and El-Yaniv, 2005). An online algorithm is

said to be c-competitive or has competitive ratio c if

its cost is at most c times that of an optimal solution

constructed ofﬂine given, in advance, all the knowl-

edge about the input sequence, over all possible in-

stances of the problem. The input sequence is given

by an adversary that is trying to trick the algorithm so

that its competitive ratio is maximized. The algorithm

is given each portion of the input and needs to react

to it with its eyes closed to the future portions. Hence

the only information the algorithm has at any point in

time, is the present and the past. Competitive anal-

ysis is a worst-case analysis, that can reveal how the

algorithm performs against its worst input sequence.

Hence, by proving the competitive ratio of the algo-

rithm, one is able to give a provable guarantee about

the solution being constructed, in comparison to an

optimal solution that could only be constructed given

all the input sequence in advance. In our analysis, we

assume an oblivious adversary, which does not know

the random choices made by the algorithm.

2.1 Competitive Ratio

We prove that our randomized algorithm for non-

metric OFL-SQC has an O(logm logn) competitive

ratio, where:

– m is the number of potential facility locations

– n is the total number of clients

2.2 Algorithmic Techniques

Our online algorithm for non-metric OFL-SQC draws

on ideas from the online algorithms for the Online

Non-metric Facility Location problem (Alon et al.,

2006) and its variant (Markarian, 2021). We ﬁrst for-

mulate the problem as a directed connectivity graph

problem and then run a randomized algorithm based

on randomized rounding, a technique widely used in

the design and analysis of online algorithms.

3 OBSERVATIONS ABOUT THE

MODEL

It is worth noting that if each arriving portion is com-

posed of a single client, rather than a group of clients,

then the problem can be solved as follows. Each

client’s connecting cost to a facility will be incre-

mented by adding to it the corresponding service-

quality cost of the facility. We can then run any on-

line algorithm for the special case of non-metric OFL-

SQC, the Online Non-metric Facility Location prob-

lem (Non-metric OFL) (Alon et al., 2006) to solve this

variant.

One might also wonder whether it helps to break

down the given portion containing a group of clients

into single clients, each arriving as a distinct portion

and then adding the service-quality costs as above.

However, this is not possible, since, we would then

have to pay the service-quality cost of a facility mul-

tiple times for the same group of clients and in our

model, we assume clients arrive as groups. The

groups of clients are motivated by scenarios in which

portions represent companies, and each of the clients

are the employees of the company. The goal would

be to serve each company with the minimum possible

service-quality costs of the joint facilities serving the

company.

As mentioned earlier, the service-quality costs are

motivated by scenarios of companies wishing to take

into consideration the quality of the services they are

offering through third-party companies when mak-

ing their decisions. In the classical Facility Location

models, the goal is to minimize the total facility open-

ing costs and the distances between the clients and

the facilities. Clients are indeed happy when they are

served by a nearby facility, but if the service is not

up to standard, then this would affect the image of

the company. So, the service quality also matters as

much as the distance. In many cases, the clients need

to be compensated to make up for the poor service.

Hence, the company would accompany each facility

with a service-quality cost to represent the compensa-

Online Non-metric Facility Location with Service-Quality Costs

617

tion costs.

Therefore, the Online Non-metric Facility Loca-

tion with Service-Quality Costs problem (Non-metric

OFL-SQC) is motivated by intrinsic client-serving

scenarios, in which companies with employees are

represented as groups of clients. Each client or em-

ployee needs to be connected to an open facility. Fa-

cilities are third-party service providers, each associ-

ated with an opening cost and a service-quality cost

that represents the quality of the service provided by

the facility.

Furthermore, the service-quality costs of non-

metric OFL-SQC are analogous to the so-called rat-

ing costs of the Online Set Cover With Rated Sub-

sets problem (OSC-RS), which we have recently in-

troduced in (Markarian, 2022). OSC-RS generalizes

the Online Set Cover problem (Alon et al., 2009),

in which we are given a universe of elements and a

collection of subsets of the universe, each associated

with a subset cost and a rating cost. The algorithm is

given, in each step, a request that contains a subset of

the elements. To serve a request the algorithm needs

to assign it to a number of subsets purchased by the

algorithm that jointly cover the requested elements.

The algorithm pays the subset costs associated with

the subsets purchased and for each request, it pays the

sum of the rating costs associated with the subsets as-

signed to the request. The aim is to serve all requests

as soon as revealed, while minimizing the total subset

and rating costs paid.

4 LOWER BOUNDS

The Online Set Cover problem (OSC) (Alon et al.,

2009) is a special case of the Online Non-metric

Facility Location problem (Non-metric OFL) (Alon

et al., 2006), which in turn is a special case of the

Online Non-metric Facility Location with Service-

Quality Costs problem (Non-metric OFL-SQC), in

which all service-quality costs are 0.

– There is an Ω(

lognlogm

loglogn+loglogm

) lower bound on the

competitive ratio of any deterministic algorithm

for OSC, where m is the number of subsets and

n is the number of elements, due to (Alon et al.,

2009).

– There is an Ω(log nlog m) lower bound on the

competitive ratio of any randomized polynomial-

time algorithm for OSC, under the assumption

that BPP 6= NP, due to (Korman, 2005).

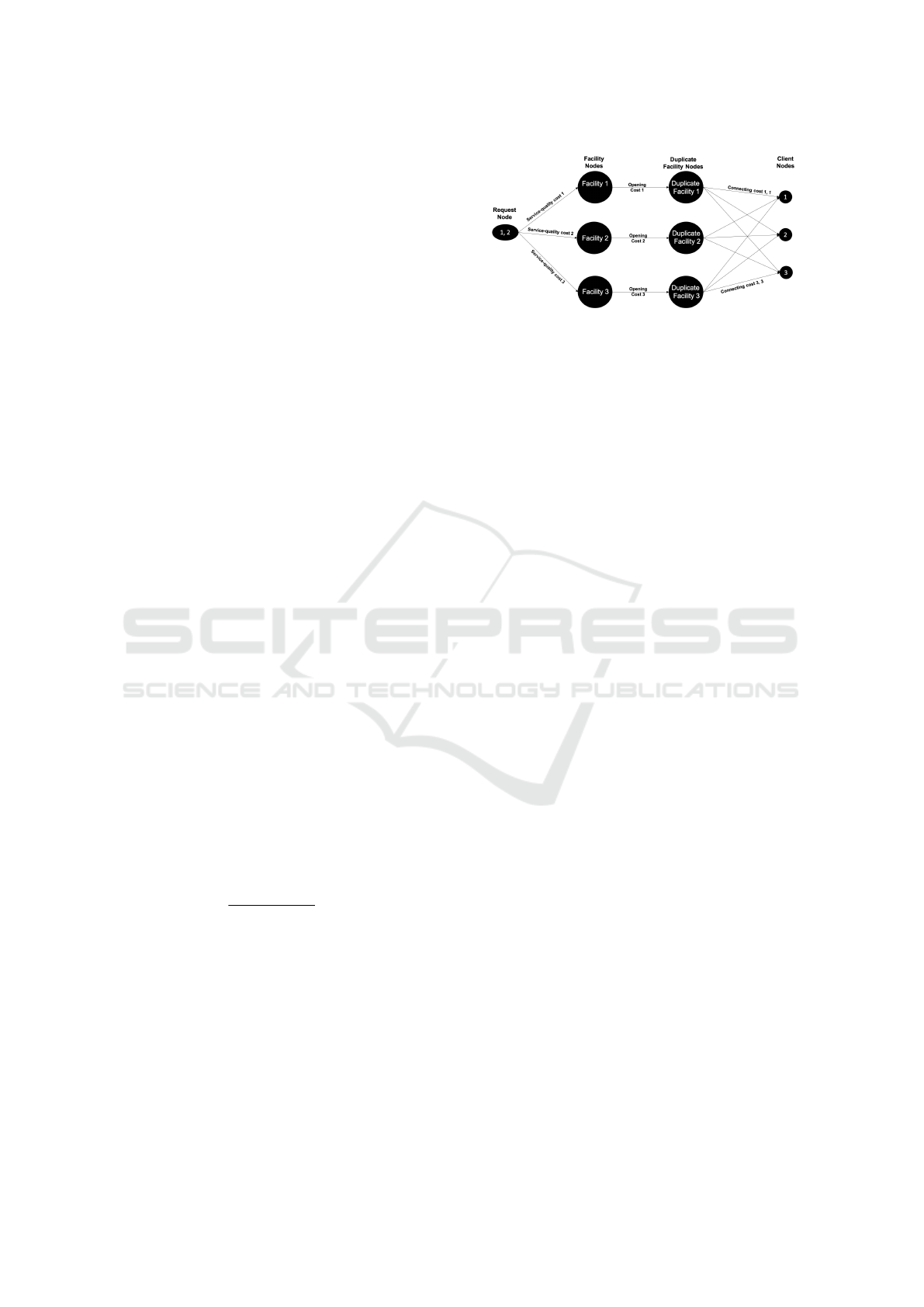
Figure 1: Non-metric OFL-SQC instance of three facilities,

three clients, and a request, formulated as a connectivity

digraph problem.

5 FORMULATION OF

NON-METRIC OFL-SQC AS A

CONNECTIVITY DIGRAPH

PROBLEM

We formulate a given instance I of non-metric OFL-

SQC as a connectivity digraph problem, as follows.

We refer to each group of arriving clients as a request.

The reader is referred to Figure 1 for an illustration.

I will be represented as a graph G = (V, E), where

V denotes the request nodes, the facility nodes, and

the client nodes, and E is a collection of weighted

directed edges connecting these nodes.

We Construct the Set V of Nodes as Follows:

– For each arriving request, we create a request

node.

– For each facility i, we create two facility nodes,

namely, facility node i and duplicate facility node

– For each client, we create a client node.

We Construct the Set E of Edges as Follows:

– From each request node, we add a directed edge to

each facility node, of weight equal to the service-

quality cost of the corresponding facility.

– From each facility node, we add a directed edge to

its duplicate facility node, of weight equal to the

opening cost of the facility.

– From each duplicate facility node, we add a di-

rected edge to each client node, of weight equal

to the connecting cost between the client and the

corresponding facility.

The facility nodes, the duplicate facility nodes,

and the client nodes along with the edges in between

are constructed before the execution of the algorithm.

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

618

Each request node and its outgoing edges are formed

as soon as a request is revealed.

Upon the Arrival of a New Request:

– A request node and its edges are added.

– The algorithm outputs, for each client in the re-

quest, a directed path from the request node to the

corresponding client node.

Solution Mapping:

– The algorithm pays each facility opening cost,

each service-quality cost, and each connecting

cost associated with the edges in the directed

paths outputted by the algorithm. The algorithm

opens each facility if its facility nodes are in the

directed paths of the outputted solution.

– For each client, the algorithm outputs a directed

path containing at least one facility node and its

duplicate. This is true since every directed path

from the request node to the client node contains

a facility node and its duplicate node. The algo-

rithm connects each client to the corresponding

facility of the directed path.

– According to this mapping, any feasible solution

for the transformed instance implies a feasible so-

lution for I, of the same cost.

6 ONLINE ALGORITHM

In this section, we present an online randomized al-

gorithm for the Online Non-metric Facility Loca-

tion with Service-Quality Costs problem (Non-metric

OFL-SQC).

The algorithm solves the connectivity digraph

problem described in the previous section. It uses

an approach similar to that used in other online prob-

lems in the literature (Hamann et al., 2018; Markar-

ian, 2021; Alon et al., 2006; Markarian et al., 2021;

Markarian, 2018).

6.1 Preliminaries

Given the input graph G = (V,E) with a positive edge-

weight function. We refer to the weight of an edge e

by w

A fraction f

is assigned to each edge e in G.

All fractions are set initially to 0 and will be non-

decreasing throughout the run of the algorithm. The

maximum ﬂow from a node u to a node v is the small-

est sum of fractions of edges which would disconnect

u from v if removed. These edges form a minimum

cut.

The algorithm generates the number q, indepen-

dently among 2

logn

random variables uniformly

distributed in the interval [0, 1], where n is the total

number of clients. q represents the randomized aspect

of the algorithm, that will determine which edges will

be purchased by the algorithm.

6.2 Execution

Given a request node r at time step t and a client node

j associated with the request. We let S

be the collec-

tion of edges of G outputted by the algorithm before

and at time step t.

At time step t:

If the edges in S

form a directed path in G from

r to j, the algorithm moves on to the next client as-

sociated with r. Else, it performs the following three

steps:

Step 1. The algorithm checks the maximum ﬂow

from r to j. While it is less than 1, the algorithm

outputs a minimum cut Q and increases the fraction

of each edge in Q , using the equation below:

← f

(1 +

) +

|Q | · w

Step 2. The algorithm adds each edge with fraction

above q (the value generated before the execution of

the algorithm) to the solution.

Step 3. The algorithm could have outputted a set of

edges that form an infeasible solution. To guarantee

feasibility, the algorithm performs the following. If S

does not contain edges that form a directed path from

r to j, the algorithm ﬁnds a shortest weighted directed

path from r to j and outputs the edges of this path to

the solution.

The three steps of the algorithm are depicted in

Algorithm 1 below.

7 COMPETITIVE ANALYSIS

In this section, we analyze the competitive ratio of the

online algorithm presented above.

Given an instance I of non-metric OFL-SQC. Ac-

cording to the solution mapping given above, any fea-

sible solution for the graph instance problem corre-

sponding to I implies a feasible solution for I, of the

same cost.

Online Non-metric Facility Location with Service-Quality Costs

619

Algorithm 1: Online Algorithm for Non-metric OFL-SQC.

Step 1. While the maximum ﬂow from r to j is less

than 1:

Construct a minimum cut Q from r to j and in-

crease the fraction f

of each edge e ∈ Q , using the

equation below:

← f

(1 +

) +

|Q | · w

Step 2. Output each edge e to the solution if its

fraction f

is above q.

Step 3. If the edges in S

do not form a directed

path from r to j, output the edges of a smallest

weighted directed path from r to j.

Thus, in order to measure the performance of the

algorithm, we analyze the total cost of edges pur-

chased by the algorithm in comparison to the cost of

the optimal ofﬂine solution.

Let Opt be the cost of an optimal ofﬂine solution.

The algorithm purchases edges in steps 2 and 3. Let

and S

be the collection of edges purchased by the

algorithm in Step 2 and Step 3, respectively. We ana-

lyze the expected cost of each step separately.

Step 2. In Step 2, the algorithm purchases each edge

whose fraction is at least q (generated before the ex-

ecution of the algorithm). We ﬁx an edge e and

i : 1 ≤ i ≤ 2

logn

. We denote by X

e,i

the indicator

variable to indicate if e has or has not been purchased

by the algorithm. We let w

and f

be the weight and

fraction of edge e, respectively. The expected cost C

of the collection S

of Step 2 can be expressed as fol-

lows:

∑

e∈S

logn

∑

i=1

· Exp [X

e,i

] (1)

= 2

logn

∑

e∈S

(2)

To compare to the edges in the optimal ofﬂine

solution, we need to understand when the algorithm

purchases. We will observe the minimum cuts con-

structed in Step 1 of the algorithm. Notice that each

minimum cut constructed must contain at least one

optimal edge. This is because each optimal solution

must also contain a directed path to the client at hand.

Let us now observe the number of times a mini-

mum cut is constructed by the algorithm. It is possi-

ble to upper bound this number by O(Opt · log |Q|),

where |Q| is the size of the largest minimum cut con-

structed. We prove this as follows.

Proof. Let us ﬁx the edges in the optimal solution.

We can prove that each optimal edge appears in a

bounded number of minimum cuts. This is true be-

cause the fractional value of each such edge eventu-

ally reaches 1. After reaching 1, it can’t appear in any

future minimum cut, as per the algorithm’s condition.

Let us observe any optimal edge and the equa-

tion of the algorithm. After O(w

log|Q|) fraction in-

creases, the value of the edge reaches at least 1. Recall

that, each minimum cut contains at least one optimal

edge. Hence, O(Opt · log |Q|) minimum cuts must be

constructed by the algorithm, where |Q| is the size of

the largest minimum cut constructed.

We now give an upper bound on |Q|. Fix a request

node and a client node. Each directed path from the

request node to the client node represents one of the

facility locations available. Therefore, |Q| is at most

m, the number of potential facility locations.

Thus, the number of minimum cuts constructed is

at most O(Opt · log m).

Next, we show that the total fractional increase ac-

companying each minimum cut is at most 2.

Lemma 1. Each minimum cut constructed is accom-

panied with a fractional increase of at most 2.

Proof. We ﬁx a minimum cut Q. The fraction of each

edge e in Q is increased by w



·w



, as per

the equation in the algorithm. Before fractions in-

crease, the maximum ﬂow was less than 1, as per the

algorithm. Thus,

∑

e∈Q

< 1. Therefore, we have

that:

∑

e∈Q



· w



< 2

Thus,

≤ O(Opt · logn · logm) (3)

Step 3. It remains to bound the expected cost C

the collection S

of edges purchased by the algorithm

in Step 3.

The ﬂow of a path is the minimum fraction among

the edge fractions of a given path. We ﬁx a client

node u and an i: 1 ≤ i ≤ 2

logn

. We measure the

probability that, for a single i, there is no directed path

purchased by the algorithm in Step 2 feasible for u. In

terms of ﬂow, this probability is the probability that q

is more than the ﬂow of each directed path to u. We let

Q be any minimum cut constructed at the end of Step

2. Before executing Step 3, we had that the sum of

ﬂow associated with all directed paths to u was at least

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

620

1 as per the algorithm. Hence, the probability that

there is no directed path purchased by the algorithm

in Step 2 feasible for u, for a single i, is:

∏

e∈Q

(1 − f

) ≤ e

−

∑

e∈Q

≤

Next, we calculate the probability for all i: 1 ≤

i ≤ 2

logn

and imply the following. The probability

that there is no directed path purchased by the algo-

rithm in Step 2 feasible for u is at most

Thus, the algorithm purchases a smallest weighted

path from the request node to u with probability at

most

. Clearly, this path is upper bounded by Opt,

since it is a smallest weighted path.

Since the total number of clients is at most n, we

have that:

≤ n ·

Opt

Hence, the theorem below follows.

Theorem 1. There is an O(log mlog n)-competitive

randomized algorithm for the Online Non-metric Fa-

cility Location with Service-Quality Costs problem

(Non-metric OFL-SQC), where m is the number of

potential facility locations, and n is the number of

clients.

8 CONCLUDING THOUGHTS

In this paper, we have initiated the service-quality

costs model by addressing the non-metric variant of

Online Facility Location. A next step would be to

investigate the metric variant in which facilities and

clients are assumed to reside in the metric space.

A next research direction is to explore other ways

to express service-quality costs. In our model, the ser-

vice quality of a facility is expressed as a ﬁxed cost,

given to the algorithm, and does not change over time.

It could be that this quality improves over time and

it would be interesting to add this dynamics into the

model and study its effect in the competitive ratio of

the algorithms.

Our adversary assumes the algorithm has no

knowledge at all about the future input portions. One

may want to investigate, for instance, other types of

adversary and probability distributions for the client

arrival.

We have assumed in our model that a client ar-

rives exactly once and this assumption is used in the

analysis of the proposed algorithm. In real-world sce-

narios, one client may appear in more than one group,

and a different approach would be needed to solve this

variant of the problem.

Finally, it is always interesting to observe how the

algorithm performs in simulated or real-world envi-

ronments. This would give us a better understanding

about the performance of the algorithm in average-

case scenarios, thus complementing our worst-case

scenario analysis.

REFERENCES

Alon, N., Awerbuch, B., Azar, Y., Buchbinder, N., and

Naor, J. (2006). A general approach to online net-

work optimization problems. ACM Transactions on

Algorithms (TALG), 2(4):640–660.

Alon, N., Awerbuch, B., Azar, Y., Buchbinder, N., and

Naor, J. (2009). The online set cover problem. SIAM

Journal on Computing, 39(2):361–370.

Anagnostopoulos, A., Bent, R., Upfal, E., and Van Henten-

ryck, P. (2004). A simple and deterministic competi-

tive algorithm for online facility location. Information

and Computation, 194(2):175–202.

Borodin, A. and El-Yaniv, R. (2005). Online computation

and competitive analysis. cambridge university press.

Drezner, Z. and Hamacher, H. W. (2004). Facility location:

applications and theory. Springer Science & Business

Media.

Fotakis, D. (2008). On the competitive ratio for online fa-

cility location. Algorithmica, 50(1):1–57.

Hamann, H., Markarian, C., auf der Heide, F. M., and

Wahby, M. (2018). Pick, pack, & survive: Charg-

ing robots in a modern warehouse based on online

connected dominating sets. In Ito, H., Leonardi,

S., Pagli, L., and Prencipe, G., editors, 9th Inter-

national Conference on Fun with Algorithms, FUN

2018, June 13-15, 2018, La Maddalena, Italy, volume

100 of LIPIcs, pages 22:1–22:13. Schloss Dagstuhl -

Leibniz-Zentrum f

ur Informatik.

Korman, S. (2005). On the use of randomization in the on-

line set cover problem. Master’s thesis, Weizmann In-

stitute of Science, Israel.

Markarian, C. (2018). An optimal algorithm for online

prize-collecting node-weighted steiner forest. In Il-

iopoulos, C. S., Leong, H. W., and Sung, W., editors,

Combinatorial Algorithms - 29th International Work-

shop, IWOCA 2018, Singapore, July 16-19, 2018, Pro-

ceedings, volume 10979 of Lecture Notes in Computer

Science, pages 214–223. Springer.

Markarian, C. (2021). Online non-metric facility location

with service installation costs. In Filipe, J., Smi-

alek, M., Brodsky, A., and Hammoudi, S., editors,

Proceedings of the 23rd International Conference on

Enterprise Information Systems, ICEIS 2021, Online

Streaming, April 26-28, 2021, Volume 1, pages 737–

743. SCITEPRESS.

Markarian, C. (2022). Online set cover with rated subsets.

In To appear in the Proceedings of the 24th Interna-

tional Conference on Enterprise Information Systems

(ICEIS), 2022, Online Streaming, April 25-27, 2022.

Online Non-metric Facility Location with Service-Quality Costs

621

Markarian, C. and auf der Heide, F. M. (2019). Online

algorithms for leasing vertex cover and leasing non-

metric facility location. In Parlier, G. H., Liberatore,

F., and Demange, M., editors, Proceedings of the 8th

International Conference on Operations Research and

Enterprise Systems, ICORES 2019, Prague, Czech

Republic, February 19-21, 2019, pages 315–321.

SciTePress.

Markarian, C. and El-Kassar, A. N. (2021). Algorith-

mic view of online prize-collecting optimization prob-

lems. In Filipe, J., Smialek, M., Brodsky, A., and

Hammoudi, S., editors, Proceedings of the 23rd Inter-

national Conference on Enterprise Information Sys-

tems, ICEIS 2021, Online Streaming, April 26-28,

2021, Volume 1, pages 744–751. SCITEPRESS.

Markarian, C., Kassar, A., and Yunis, M. M. (2021). An

algorithmic approach to online multi-facility location

problems. In Parlier, G. H., Liberatore, F., and De-

mange, M., editors, Proceedings of the 10th Interna-

tional Conference on Operations Research and En-

terprise Systems, ICORES 2021, Online Streaming,

February 4-6, 2021, pages 29–35. SCITEPRESS.

Markarian, C. and Khallouf, P. (2021). Online facility ser-

vice leasing inspired by the covid-19 pandemic. In

18th International Conference on Informatics in Con-

trol, Automation and Robotics, ICINCO 2021, pages

195–202.

Meyerson, A. (2001). Online facility location. In Proceed-

ings 42nd IEEE Symposium on Foundations of Com-

puter Science, pages 426–431. IEEE.

Sleator, D. D. and Tarjan, R. E. (1985). Amortized efﬁ-

ciency of list update and paging rules. Commun. ACM,

28(2):202–208.

ICEIS 2022 - 24th International Conference on Enterprise Information Systems

622