A Framework for Robust Remote Driving Strategy Selection

Michael Kl

oppel-Gersdorf

and Thomas Otto

Fraunhofer IVI, Fraunhofer Institute for Transportation and Infrastructure Systems, Dresden, Germany

Keywords:

Driving Strategy Selection, Yard Automation, Particle Filter, Robust Optimization, Valet Parking, V2X, IEEE

802.11p.

Abstract:

In this paper, a framework for assisting Connected Vehicle (CV) is proposed, with the goal of generating

optimal parameters for existing driving functions, e.g., parking assistant or Adaptive Cruise Control (ACC),

to allow the CV to move autonomously in restricted scenarios. Such scenarios encompass yard automation as

well as valet parking. The framework combines Model predictive control (MPC) with particle ﬁlter estimators

and robust optimization.

1 INTRODUCTION

Remote control of Connected Vehicles (CVs) is an ac-

tive topic of research, spanning questions from gen-

erating feasible movements, e.g., in yard automation

(Belov et al., 2021), to the efﬁcient transmission of the

calculated maneuvers (Tsukada et al., 2020) as well

as, of course, generating non-intersecting (in space-

time) trajectories (Scheffe et al., 2021). The goal of

this paper is to take a step back from the newest de-

velopments and to implement automatic driving capa-

bilities on an existing vehicle using existing technol-

ogy, which requires to retroﬁt the vehicle with com-

munication capabilities as well as gaining access to

driving functions. A centralized approach is used as

most vehicles will not provide the necessary compu-

tation power. Here, the goal is not to completely re-

mote control the vehicle (this might be difﬁcult due

to latency reasons and missing sensors), but rather

to generate useful set points for the local assistance

functions, called driving strategies (Manzinger et al.,

2017). Following these strategies is then left to the ve-

hicle. A robust optimization approach is used to ac-

count for the inherent uncertainties when predicting

the future movement of vehicles. The framework is

not intended to provide general automated driving ca-

pabilities, rather it is mainly concerned with restricted

areas like parking lots or yards, where the driver can

drop of the vehicle at an entry point. As such, we are

commonly dealing with uninhabited vehicles.

The paper is organized as follows: In the next sec-

tion preliminaries and requirements for employing the

https://orcid.org/0000-0001-9382-3062

presented approach are discussed, whereas the third

section introduces the framework, which is used in a

case study in Section 4. The ﬁnal section concludes

the paper.

2 PRELIMINARIES

In this section, the necessary inputs, their correspond-

ing latencies and minimum requirements for the pro-

posed framework are discussed.

2.1 Minimum Requirements on the

Vehicle under Test (VuT) and

Operating Area

In order to obtain driving strategy advice from the

proposed framework, the vehicle under consideration

(called VuT throughout the remainder of the paper)

needs to be connected, using either 802.11p, Cellular

V2X (C-V2X) or other means of connection, e.g., us-

ing Long Term Evolution (LTE) or 5G. Any other traf-

ﬁc participant (called target hereafter) needs either to

be able to use the same communication means as the

VuT to broadcast its position or needs to be detected

by the VuT or by infrastructure sensors. This limits

the approach mainly to restricted areas, like industrial

yards or parking lots, since it is much easier to mon-

itor such areas. Furthermore, the maximum number

of participants is also much more limited. For driv-

ing strategy advice, the vehicle must be able to carry

out at least one of longitudinal (e.g., Adaptive Cruise

418

Klöppel-Gersdorf, M. and Otto, T.

A Framework for Robust Remote Driving Strategy Selection.

DOI: 10.5220/0011088900003191

In Proceedings of the 8th International Conference on Vehicle Technology and Intelligent Transpor t Systems (VEHITS 2022), pages 418-424

ISBN: 978-989-758-573-9; ISSN: 2184-495X

Control (ACC)) or lateral (e.g., lane keeping) control

or both (e.g., parking assistant). Of course, an ex-

ternal interface to these functions must exist, at least

temporarily (based, e.g., on location). One way of

realizing this access is the usage of openpilot

. In ad-

dition, the VuT should have sufﬁcient sensors to de-

tect situations of imminent danger (e.g., front crash

assistant) as the framework might be too slow to react

under such circumstances due to message latency.

2.2 Vehicle-to-Everything (V2X)

Communication

The main source of position information is posi-

tion data broadcasted via V2X using the Coopera-

tive Awareness Message (CAM) (ETSI EN 302 637-

2 V1.3.2 (2014-11), 2014) or alternatively the Basic

Safety Message (BSM). The following discussion is

based on ETSI ITS-G5 communication, but similar

values also hold true for other standards. Depending

on the dynamics of the vehicle, the CAM will be gen-

erated every 0.1 − 1 s. According to the speciﬁcation,

the position given in the message cannot be older than

50ms. Transferring the message using our implemen-

tation of the V2X stack (Jacob et al., 2020) takes an

additional 1−13ms, with an average of 9.1ms (Strobl

et al., 2019). One additional method of gaining posi-

tion information is via the newly proposed Collective

Perception Message (CPM) (ETSI TR 103 562 V2.1.1

(2019-12), 2019), which can be used to transmit lists

of detected objects. It is important to keep in mind

that measurements sent via CPM are relative to the

sending station, i.e., besides the accuracy of the sen-

sors, also the position accuracy of the sending station

has to be taken into account.

2.3 Video Detection

The main approach to detect non-connected partici-

pants in the proposed framework relies on RGB and

thermal video data (Kl

oppel-Gersdorf et al., 2021).

Based on YoloV3 (Redmon and Farhadi, 2018), pro-

cessing times between 0.3 − 2.5s for the whole chain

from taking the image to the calculated position are

achieved on a constrained computation device, the

NVIDIA Jetson AGX Xavier. The former num-

ber corresponds to a simple projection of one sin-

gle image of the detected object to the ground plane,

whereas the latter corresponds to the fusion of multi-

ple images and a 3D reconstruction. Other authors

report similar numbers, e.g., (Ortiz Castell

o et al.,

2020), where the detection process for a single im-

https://github.com/commaai/openpilot

ages takes a little less than 0.1s. Depending on the

scenario, more accurate processing methods can be

applied, e.g., the algorithm presented in (Ihrke, 2018).

2.4 Additional Means of Object

Detection

Although not considered here, several other informa-

tion sources could be included in the framework, e.g.,

Lidar detection (Barea et al., 2018) or the usage of lo-

cation tags based on, e.g., Zigbee (Kuo et al., 2010).

In this case, objection fusion as described in (Barea

et al., 2018; Liang et al., 2019) might be necessary.

3 FRAMEWORK

The framework introduced here shares the ideas of

(Stahl and Hauth, 2011) and (Blackmore, 2006), us-

ing Model predictive control (MPC) and the parti-

cle ﬁlters, not only to determine the current state but

also to predict future states. But instead of calculat-

ing different optimal control values depending on the

evolution of the underlying process only one control

variable per time step is determined, which satisﬁes

the given constraints for all sampled realizations of

the given process, which is an application of the sce-

nario approach to robust optimization (Calaﬁore and

Campi, 2006). On the other hand, the problem solved

at every step of the MPC scheme can also be consid-

ered a special case of (Blackmore, 2006), where the

probability of violating the constraints is required to

be zero.

3.1 Particle Filter

A particle ﬁlter (Gordon et al., 1993) with system-

atic resampling (Douc and Capp

e, 2005) is used to

estimate the current location of the VuT as well as

the target vehicles. A separate particle ﬁlter is em-

ployed for each tracked entity. The ﬁrst time an entity

is detected, an initial distribution to sample from has

to be chosen. As this choice depends on the internal

state used within the particle ﬁlter, only few details

can be given here. The minimum information tracked

by the particle ﬁlter is the current position of the ve-

hicle, therefore, it is useful to initialize the position

information part of the particles with the ﬁrst mea-

sured position plus some Gaussian noise with zero

mean and variance according to the accuracy of the

sensor. Particles are then propagated using a prede-

ﬁned movement model with some additional random

noise. In the case of the VuT, this propagating func-

tion also considers control actions determined before,

A Framework for Robust Remote Driving Strategy Selection

419

i.e., for a single particle x

VuT

n+1

= f (x

VuT

,ξ

,∆t

track,VuT

), (1)

where u

∈ U ⊂ R

are the control variables, x

VUT

∈

are the state variables of the VuT, ξ

are stochas-

tic components with known distribution, ∆t

track,VuT

the time step since the last update and the function

f describes the movement. Note, that there are no

smoothness assumptions on this function. The prop-

agation function for particles belonging to the addi-

tional targets t ∈ T

, where T is an index set of the

currently existing target vehicles at time step n, is sim-

ilar to the deﬁnition above but does not include con-

trols

n+1

= g(y

n+1

,η

,∆t

track,t

), (2)

where η

are stochastic components with known dis-

tribution. The particle ﬁlter employed follows the

usual steps of the particle ﬁltering algorithm, i.e.,

sampling the new population of particles using the

previous sampled particles and the movement model,

adapting the weights given new position measure-

ments and a possible resampling. The number of

particles used per ﬁlter and time step is denoted by

particles

and typically ranges between 100 –1000, de-

pending on the underlying model. If only a restricted

driving area is given (as in the case study below, with

large non-drivable areas), this information can also

be included when adapting the weights. This is even

possible when using the particle ﬁlter for propagation

into the future. As mentioned above, the process of

tracking the single participants is completely asyn-

chronous. Therefore, as starting point for the opti-

mization process, the particles are propagated to one

single future time point, which is deﬁned by the min-

imum amount of time required to generate the solu-

tion and transmit it to the VuT. Here, particles are

only reweighed by the drivable area criterion as no

measurements exist. As mentioned before, different

detectors need different computation times to gener-

ate a position information for a given object, e.g.,

GPS measurements are faster than information gained

via video detection. This can lead to asynchronous

and non-sequential data acquisition. Especially if the

slower sensor gives a very accurate position informa-

tion, it might be beneﬁcial to recalculate the particle

ﬁlter chain including the newly obtained information.

Therefore, older states of the ﬁlter as well as the al-

ready obtained measurements have to be saved.

3.2 Robust Optimization

Borrowing the notation from (Stahl and Hauth, 2011),

the following stochastic optimization problem is to be

solved:

min

,...,u

k+T

J(x

,.. .,u

k+T

), (3)

s.t. X

VuT

n+1

= f (X

VuT

,ξ

), (4)

n+1

= g(Y

n+1

,η

), (5)

OS(x

VuT

) ∩ OS(y

) =

VuT

∈ X

VuT

, y

∈ Y

(6)

t ∈ T , (7)

∈ U, (8)

n = k,. .., k + T

, (9)

where the variables are deﬁned as above in the parti-

cle ﬁlter deﬁnition and X

VuT

and Y

describe the sets

of all particles belonging to either the VuT or the tar-

gets t ∈ T , respectively. The function OS(·) describes

the space occupied by a vehicle with a given state, i.e.,

equation (6) describes a no crash condition. The func-

tions f and g, representing the dynamics of the VuT

as well as the target vehicles, are the same as in the

description of the particle ﬁlter above, with the only

difference that the time step ∆t

prop

is now the same

for all vehicles as we are propagating into the future.

Finally, the objective function J has the form

J(x

,.. .,u

k+T

) =

k+T

∑

n=k

− u

n−1

k+T

∑

n=k+1

− x

,(10)

where the norms are weighted Euclidian norms with

weighting matrices R and Q, and s

∈ R

are desired

set points. Evaluating the constraints (6) requires

|T |n

particles

computations, which might be computa-

tionally challenging. For an easier computation with

only |T | checks,

∀t ∈ T : conv(OS(X

VuT

)) ∩ conv(OS(Y

)) =

0 (11)

can be used instead of (6). Here, conv(·) describes

the convex hull. Although this reduces the number of

constraints to be checked signiﬁcantly, this might lead

to a more conservative approach.

4 CASE STUDY

This use case is inspired by a real-world example.

Therefore, we want to mimic these circumstances

as much as possible, i.e., choosing the same venue,

adapting noise parameters to real-world sensor data

and reﬂecting the existing control actions. In this

special case, this means that we can only inﬂuence

the velocity of the VuT via Maneuver Coordination

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

420

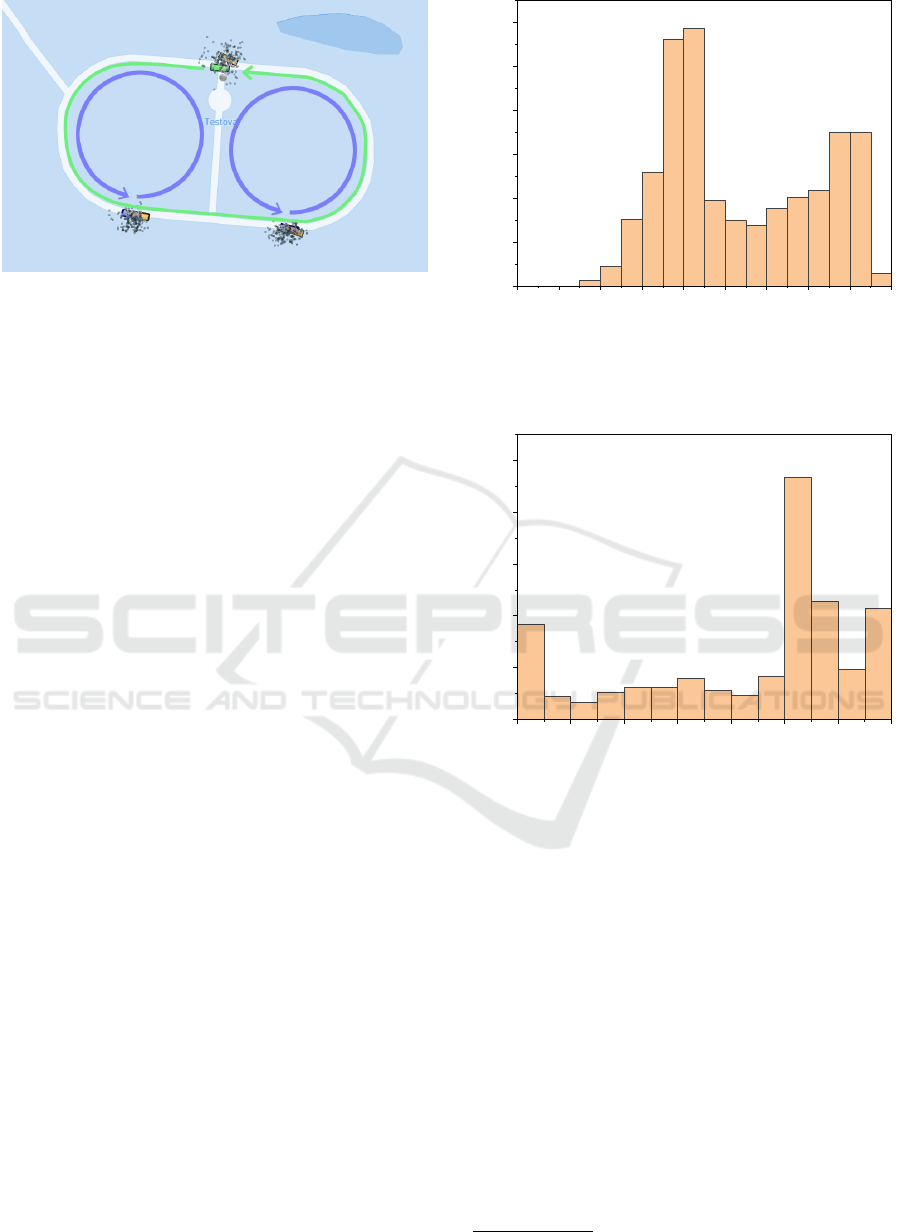
Figure 1: Simulation setup of the case study extracted from

Streetscape.gl (Uber ATG and VIS.GL, 2020) visualization.

Shown are the VuT in green and the two target vehicles in

purple as well as their corresponding driving trajectories.

Additionally, in orange are the position as given by the sim-

ulated GPS sensor. The point clouds represent position hy-

potheses generated by the particle ﬁlter.

Message (MCM) (Auerswald et al., 2019) but can-

not change the trajectory. The whole simulation sce-

nario is shown in Fig. 1 and consists of the VuT and

two other target vehicles. The VuT initially moves

at 50km/h, whereas the target vehicles move with

18km/h. Trajectories as used in the scenario are also

shown in Fig. 1. These trajectories are derived us-

ing a bicycle model (Althoff et al., 2017), but are not

known to the optimization algorithm.

For all three vehicles the states of the particle ﬁl-

ter consist of ¯x = (x,y, v,θ), where x, y are coordinates

in a local Cartesian coordinate system measured in

meters, v is the velocity measured in meters per sec-

ond and θ is the heading measured in radians. For

the initialization of the particle ﬁlter, x and y are sam-

pled from a Gaussian distribution with the ﬁrst mea-

surement received used as mean and Σ = 4.5 m × I

2x2

which corresponds to the Circular Error Probable

(CEP) of the GPS chip used (u blox, 2019). The ve-

locity is sampled from a normal distribution with zero

mean and standard deviation σ = 15 m/s. Finally,

the heading θ is sampled from a uniform distribution

from 0 to 2π, i.e., no information about the initial di-

rection of the vehicles is known. Similar to (Scheffe

et al., 2021), quantized control values are employed,

i.e., the acceleration of the VuT is controlled with

∈



−6m/s

,−3 m/s

,0 m/s

,3 m/s

,6 m/s



. In

addition, constraints on the maximum and minimum

speed of the VuT were considered, i.e., 0 m/s ≤ v ≤

13.88m/s. To propagate the particles, a simple linear

movement model is used, i.e.,

f ( ¯x,u,ξ) = ¯x + ∆t (v cos(θ),v sin(θ), u, 0) + ξ (12)

and

g( ¯y,η) = ¯y + ∆t (v cos(θ),v sin(θ),0, 0) + η, (13)

0 1 0 2 0 3 0 4 0 5 0 6 0 7 0 8 0 9 0

1 0 0

2 0 0

3 0 0

4 0 0

5 0 0

6 0 0

C o u n t

D i s t a n c e o f V u T t o o t h e r m o v i n g p a r t i c i p a n t s [ m ]

Figure 2: Histogram showing the distribution of distances

of the VuT to the other participants over a simulation time

of 171.4s, with a 0.1 s resolution, i.e., 1714 total time steps.

At no time, the distance is less than 15m.

0 2 4 6 8 1 0 1 2 1 4

1 0 0

2 0 0

3 0 0

4 0 0

5 0 0

C o u n t

V e l o c i t y [ m / s ]

Figure 3: Histogram showing the velocity of the VuT over a

simulation time of 171.4s, with a 0.1s resolution, i.e., 1714

total time steps. At several time steps the velocity drops to

0m/s. Average velocity is 8.7m/s.

where ξ, η ∼ N (0, diag(0.02,0.02, 1,0.2)). As

the vehicles follow circular motions, their heading

changes constantly. Therefore, CAM are generated

at a frequency of 10 Hz. Correspondingly, ∆t

track

≈

0.1s.

A prediction horizon of T

= 3 with ∆t

prop

1s is used. In (10), we choose R = 1 and Q =

diag(0,0,1,0), i.e., only a set point for the target

velocity of s

= s = (0,0,13.88 m/s, 0) (correspond-

ing to 50 km/h) is given. The simulation and opti-

mization uses a proof-of-concept implementation in

Python using pﬁlter

with n

particles

= 200 for each en-

tity and time step, without any optimization like par-

allelization. To still achieve real-time performance,

an aggressive branch-and-bound scheme (Frese et al.,

https://github.com/johnhw/pﬁlter

A Framework for Robust Remote Driving Strategy Selection

421

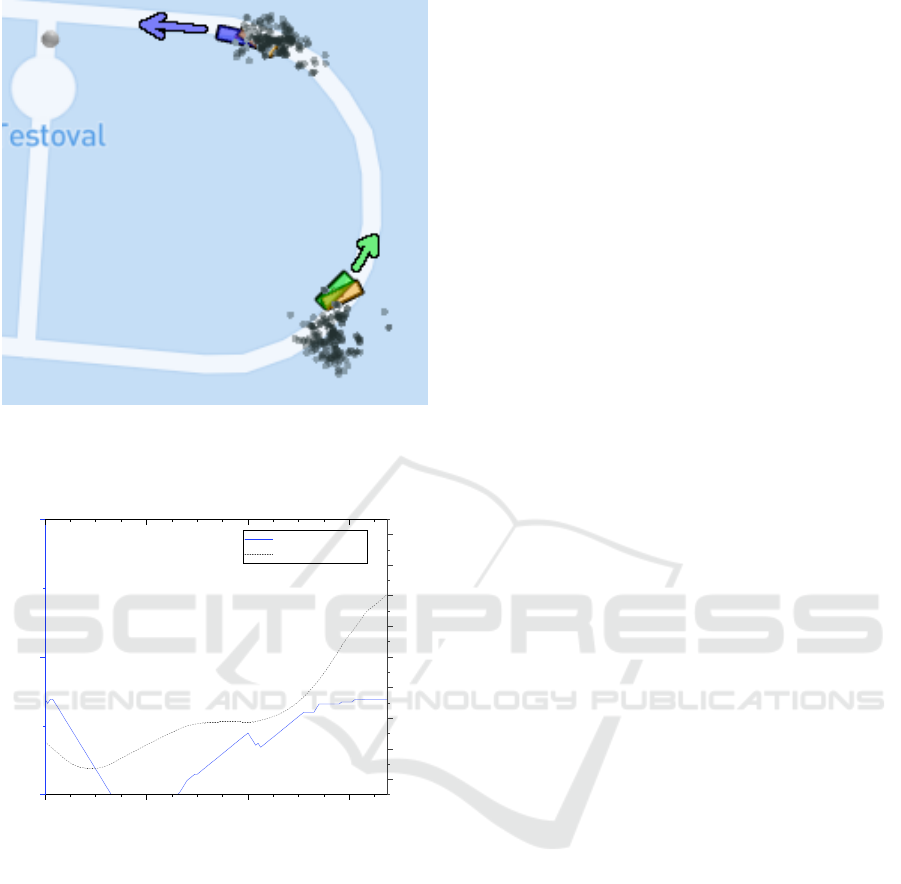
Figure 4: Vehicle conﬁguration at t = 20s. Both vehicles

are moving anti-clockwise as shown. At this time instance,

the green VuT moves with 50 km/h whereas the violet par-

ticipant moves at 18 km/h.

2 1 2 2 2 3 2 5 2 6 2 7 2 9 3 0 3 1 3 32 0 2 4 2 8 3 2

2 0

4 0

V e l o c i t y V u T

T a r g e t D i s t a n c e

T i m e t [ s ]

V e l o c i t y V u T [ m / s ]

1 0

2 0

3 0

4 0

5 0

6 0

7 0

8 0

9 0

D i s t a n c e t o V u T [ m ]

Figure 5: Distance to one of the targets and resulting veloc-

ity of the VuT after optimization. The initial conﬁguration

corresponding to t = 20 s is shown in Fig. 4.

2010) is used. Additionally, variant (11) is used to

ease the computational burden. Simulation results for

a time horizon of 171.4s can be found in Fig. 2–

5. In Fig. 2, a histogram of the Euclidian distance

of the VuT’s center to the target vehicles centers is

shown. Given the chosen vehicle dimensions, any dis-

tance less than 6 m could be considered hazardous and

would possibly lead to a collision. As can be seen, the

distances do not fall under the critical value, i.e., the

algorithm was able to provide feasible driving strate-

gies. As the histogram in Fig. 3 shows, the algorithm

leads to lower VuT velocities over large parts of the

scenario and even stopped the vehicle for a total of

nearly 20 seconds. One instance of this happening is

shown in Fig. 4 and 5. Here, Fig. 4 shows the ve-

hicle conﬁguration at t = 20 s and Fig. 5 shows the

VuT’s velocity as well as the distance to one of the

two participants. As the VuT gets closer to the other

participant, the optimization framework advises sharp

deceleration to avoid a collision, bringing the VuT to

a full stop at t = 22.6 s. As the distance to the tar-

get grows larger again, the algorithm responds with

accelerating the VuT at t = 25.2s.

Overall, it can be found that the derived acceler-

ations lead to a rather conservative behavior. Even

in the worst case, occurring at t = 21.4s (compare

Fig. 5), the distance to the target is 13.71 m, which

is more than double of the critical distance. Further-

more, the VuT came to a halt at several instances. This

is partly caused by the rather large CEP of the GPS

chip when used without real-time kinematics, which

leads to large variations when propagating the par-

ticles and is partly also a result of the chosen opti-

mization scheme. An approach based on chance con-

straints (Blackmore, 2006) would possibly lead to a

less conservative result. Nonetheless, one should keep

in mind that no trajectory information was available

to the algorithm, allowing for rather large deviations

in the propagation algorithm. If these were available,

e.g., via a future version of the MCM, and would be

incorporated in the algorithm, better optimization re-

sults could be expected as the particle ﬁlter penalizes

hypotheses deviating from the given trajectory and

not only penalize hypotheses outside the drivable area

as in the given case.

4.1 Scaling the Scenario

As mentioned above, the presented show case ran in

real-time, i.e., every computation step took strictly

less than 0.1 s on an Intel i7-10850H with 32 GiByte

RAM using only one of the existing six processor

cores (ignoring hyperthreading). In the following, we

will discuss how enlarging the scenario (more targets

and/or more VuTs) would inﬂuence computation time

and how real-time performance could be achieved in

these cases.

When increasing the number of targets, the com-

putational load increases linearly, i.e., using parallel

computing on the CPU would allow to handle up to

12 targets using the given hardware. Higher number

of targets could be dealt with employing more capa-

ble hardware. In such cases it might be also beneﬁcial

to detect relevant targets, e.g., based on Euclidian dis-

tance or road geometry, and only include these into

the optimization algorithm. While non-relevant tar-

gets still have to be tracked (as they could become

relevant later on), no collision checks have to be car-

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

422

ried out in the optimization step. Generally, the prop-

agation of particles is very suited for processing on

graphic cards, since the same transformations is ap-

plied to a large number of different particles. De-

pending on the hardware employed, up to several hun-

dred targets could be tracked in the same time it now

takes to track the participants in the scenario pre-

sented above.

When increasing the number of VuTs, computa-

tional load very much depends on the speciﬁc sce-

nario. In the best case, there is no interaction be-

tween VuTs, e.g., because of distance, and the opti-

mization can be carried out for each VuT separately,

leading only to a linear increase in computational de-

mand. If there are interactions, two approaches come

to mind. First, one could still optimize the VuTs sep-

arately and treat the other VuTs as targets. This leads

to a super-linear increase in computational demand,

since there are still n

VuT

optimization problems to be

solved, where n

VuT

is the number of VuTs, but the

number of targets is also increased by n

VuT

−1. While

this could still be handled by parallelization, some

situations might require joint optimization, i.e., co-

operation between the vehicles, e.g., if two VuTs are

approaching each other head on. In joint optimiza-

tion, computation time very much depends on the op-

timization algorithm and the speciﬁc problem formu-

lation. Above, a discrete optimization problem is for-

mulated. Naively scaling this to several VuTs, would

lead to an exponential increase in possible control val-

ues. While parallelization might allow to deal with

up to three VuTs in joint optimization, more aggres-

sive optimization routines would have to be employed

(Tang, 1998), at the cost of ﬁnding only a reasonable

but not the optimal solution.

The current implementation is in Python, further

speed ups could be expected from switching to C++,

although it is hard to quantify which speed ups can

be achieved as some of the Python libraries already

employ C/C++ code themselves.

5 CONCLUSIONS AND FUTURE

WORK

In this paper, a framework for assisting CV with at

least on driving function, e.g., ACC, was proposed.

The approach only relies on position information de-

rived via V2X messages or through external sensors

like cameras and, therefore, can incorporate even a

certain number of conventional vehicles or persons.

Use case are mainly in yard automation or on other

restricted zones, e.g., automatically moving freshly

build vehicles from the conveyor belt to a parking

area without the need for a human driver. A simu-

lation based on a real-live scenario showed the fea-

sibility of the framework. While the scenario ran in

real-time without much need for optimization, larger

scale problems could beneﬁt from parallelization.

Applications in live trafﬁc are also possible, but

given the conservativeness of the presented approach,

it would possibly take a long time to cross, for exam-

ple, a non-signalized intersection. Approaches based

on chance-constraints (Blackmore, 2006) could be a

better choice in this case. One additional drawback

of using the method in live trafﬁc is the requirement

to detect every trafﬁc participant, which could require

a large number of detectors. Finally, some situations

could also be difﬁcult to track with the particle ﬁlter,

e.g., a person entering a vehicle or a passenger vehicle

being loaded on a truck. Such scenarios would require

additional information from the sensor system.

The simulations, so far, considered only sparsely

populated scenarios. While the conservativeness of

the algorithm would lead to longer driving times in

comparison to a human driver, this is not a problem in

such cases. Future work includes simulations of more

densely populated uses cases to allow a measurement

how performance is impacted by using the algorithm

instead of a human driver.

ACKNOWLEDGEMENTS

This research is ﬁnancially supported by the German

Federal Ministry of Transport and Digital Infrastruc-

ture (BMVI) under grant numbers FKZ 45FGU141 B

(DiSpoGo) and co-ﬁnanced by the Connecting Eu-

rope, Facility of the European Union (C-ROADS Ur-

ban Nodes). We would like to thank Ina Partzsch for

her valuable comments and suggestions.

REFERENCES

Althoff, M., Koschi, M., and Manzinger, S. (2017). Com-

monroad: Composable benchmarks for motion plan-

ning on roads. In 2017 IEEE Intelligent Vehicles Sym-

posium (IV), pages 719–726. IEEE.

Auerswald, R., Dod, M., Franke, L., Fritzsche, R., Haber-

jahn, M., Jungmann, A., Kl

oppel-Gersdorf, M.,

Krems, J. F., Lorenz, S., Kreißig, I., et al. (2019).

Heterogeneous infrastructure for cooperative driving

of automated and non-automated connected vehicles.

In Smart Cities, Green Technologies and Intelligent

Transport Systems, pages 270–296. Springer.

Barea, R., P

erez, C., Bergasa, L. M., L

opez-Guill

en, E.,

Romera, E., Molinos, E., Ocana, M., and L

opez, J.

(2018). Vehicle detection and localization using 3d

A Framework for Robust Remote Driving Strategy Selection

423

lidar point cloud and image semantic segmentation.

In 2018 21st International Conference on Intelligent

Transportation Systems (ITSC), pages 3481–3486.

Belov, N., Barbosa, C. E. V., Keppler, F., Kolb, J., Nitzsche,

G., and Wagner, S. (2021). Trucktrix

 path-planning

in the helyos operating system for yard automation.

In 2021 IEEE 19th International Conference on In-

dustrial Informatics (INDIN), pages 1–6. IEEE.

Blackmore, L. (2006). A probabilistic particle control ap-

proach to optimal, robust predictive control. In AIAA

Guidance, Navigation, and Control Conference and

Exhibit, page 6240.

Calaﬁore, G. and Campi, M. (2006). The scenario approach

to robust control design. IEEE Transactions on Auto-

matic Control, 51(5):742–753.

Douc, R. and Capp

e, O. (2005). Comparison of resampling

schemes for particle ﬁltering. In ISPA 2005. Proceed-

ings of the 4th International Symposium on Image and

Signal Processing and Analysis, 2005., pages 64–69.

IEEE.

ETSI EN 302 637-2 V1.3.2 (2014-11) (2014). ETSI EN

302 637-2 V1.3.2 (2014-11) Intelligent Transport Sys-

tems (ITS); Vehicular Communications; Basic Set of

Applications; Part 2: Speciﬁcation of Cooperative

Awareness Basic Service. Standard, ETSI.

ETSI TR 103 562 V2.1.1 (2019-12) (2019). ETSI TR 103

562 V2.1.1 (2019-12) Intelligent Transport Systems

(ITS); Vehicular Communications; Basic Set of Ap-

plications; Analysis of the Collective Perception Ser-

vice (CPS); Release 2. Standard, ETSI.

Frese, C., Beyerer, J., and Huber, M. (2010). Cooperative

motion planning using branch and bound methods. In

Proc. of the 2009 Joint Workshop of Fraunhofer IOSB

and Institute for Anthropomatics, Vision and Fusion

Laboratory (J. Beyerer and M. Huber, eds.), no. IES-

2009-13, pages 187–201.

Gordon, N. J., Salmond, D. J., and Smith, A. F. (1993).

Novel approach to nonlinear/non-gaussian bayesian

state estimation. In IEE Proceedings F-radar and sig-

nal processing, volume 140, pages 107–113. IET.

Ihrke, S. (2018). Precise edge tracking of vehicles using a

static camera setup. In 2018 International Symposium

on Intelligent Signal Processing and Communication

Systems (ISPACS), pages 12–17.

Jacob, R., Anwar, W., Schwarzenberg, N., Franchi, N., and

Fettweis, G. (2020). System-level performance com-

parison of ieee 802.11p and 802.11bd draft in highway

scenarios. In 2020 27th International Conference on

Telecommunications (ICT), pages 1–6.

oppel-Gersdorf, M., Trauzettel, F., Koslowski, K., Pe-

ter, M., and Otto, T. (2021). The fraunhofer ccit

smart intersection. In 2021 IEEE International In-

telligent Transportation Systems Conference (ITSC),

pages 1797–1802. IEEE.

Kuo, W.-H., Chen, Y.-S., Jen, G.-T., and Lu, T.-W. (2010).

An intelligent positioning approach: Rssi-based in-

door and outdoor localization scheme in zigbee net-

works. In 2010 International Conference on Machine

Learning and Cybernetics, volume 6, pages 2754–

2759.

Liang, M., Yang, B., Chen, Y., Hu, R., and Urtasun, R.

(2019). Multi-task multi-sensor fusion for 3d ob-

ject detection. In Proceedings of the IEEE/CVF Con-

ference on Computer Vision and Pattern Recognition

(CVPR).

Manzinger, S., Leibold, M., and Althoff, M. (2017). Driv-

ing strategy selection for cooperative vehicles using

maneuver templates. In 2017 IEEE Intelligent Vehi-

cles Symposium (IV), pages 647–654.

Ortiz Castell

o, V., Salvador Igual, I., del Tejo Catal

O., and Perez-Cortes, J.-C. (2020). High-proﬁle

vru detection on resource-constrained hardware using

yolov3/v4 on bdd100k. Journal of Imaging, 6(12).

Redmon, J. and Farhadi, A. (2018). Yolov3: An incremental

improvement. arXiv preprint arXiv:1804.02767.

Scheffe, P., Pedrosa, M. V., Flaßkamp, K., and Alrifaee, B.

(2021). Receding horizon control using graph search

for multi-agent trajectory planning.

Stahl, D. and Hauth, J. (2011). Pf-mpc: Particle ﬁlter-

model predictive control. Systems & Control Letters,

60(8):632–643.

Strobl, S., Kl

oppel-Gersdorf, M., Otto, T., and Grimm, J.

(2019). C-its pilot in dresden – designing a modu-

lar c-its architecture. In 2019 6th International Con-

ference on Models and Technologies for Intelligent

Transportation Systems (MT-ITS), pages 1–8.

Tang, Z. (1998). Time constrained optimization. In Pro-

ceedings of the 37th IEEE Conference on Decision

and Control (Cat. No.98CH36171), volume 4, pages

3899–3906 vol.4.

Tsukada, M., Oi, T., Kitazawa, M., and Esaki, H. (2020).

Networked roadside perception units for autonomous

driving. Sensors, 20(18).

u blox (2019). Product summary NEO-M8P series u-blox

M8 high precision GNSS modules. https://www.u-

blox.com/en/docs/UBX-15015836. Accessed: 2022-

01-14.

Uber ATG and VIS.GL (2020). AVS project page.

https://avs.auto. Accessed: 2020-12-15.

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

424