A Bayesian Network for the Analysis of Trafﬁc Accidents in Peru

Willy Ugarte

, Manuel Alcantara-Zapata, Leibnihtz Ayamamani-Choque, Renzo Bances-Morales

and Cristian Cabrera-Sanchez

Universidad Peruana de Ciencias Aplicadas (UPC), Lima, Peru

Keywords:

Probabilistic Graphical Model, Bayesian Network, Graph Learning, Trafﬁc, Accidents.

Abstract:

Trafﬁc accidents are a problem that affects the State and society, because they cause material damage, injuries

and even the death of a person. This has led countries such as China, Switzerland and Australia to carry out

studies using Bayesian networks to determine the main causes and, based on them, propose measures to reduce

the number of trafﬁc accidents. Following this trend, we, without having any expert knowledge on the subject,

decided to analyze the data of trafﬁc accidents on the Pan-American Highway in Lima, Peru. This analysis

was done by means of directed graph learning with the Hill Climbing Search, Chow-Liu, K2, BIC and BDEU.

In addition, we used a Bayesian estimator to calculate the conditional probability distribution for our dataset.

This dataset contains observations from the years 2017 to 2019 and approximately 16 km of this highway.

Our results show that it is possible to identify the possible causes of excess accidents in speciﬁc areas of the

Pan-American Highway in certain shifts i.e., 32% of fatal accidents occur between 12 am and 7 pm in the

Rimac district and of these 20% are due to pedestrians on the highway.

1 INTRODUCTION

Trafﬁc accidents are a problem that affects people and

societies. This is because it does not allow the Peru-

vian State to guarantee the life and physical integrity

of its people as indicated in the Peruvian constitution.

Furthermore, it causes material damages, injuries and

can even prematurely end a person’s life. The Na-

tional Institute of Statistics and Informatics (INEI)

indicates that the number of fatal vehicle accidents

throughout Peru reported from 2012 to 2019, is on

average 3,000. Additionally, according to the Min-

istry of Health (MINSA), the World Health Organiza-

tion (WHO), places Peru as the third country with the

highest mortality from vehicular accidents

Due to all the above, a method is required to an-

alyze this problem based on the dependence of prob-

abilities between variables that these accidents occur

in detail, considering variables and their speciﬁc val-

ues, in order to allow us make inferences and based on

the results of these, the citizens and the corresponding

authorities adopt the corresponding measures to pre-

vent these unfortunate events. Currently there are ma-

chine learning algorithms that allow predicting events

https://orcid.org/0000-0002-7510-618X

“8’929 accidentes de tr

ansito registra nuestro pa

ıs a

causa de la ebriedad del conductor” - MINSA - 2012

based on a set of data, which could contribute to this

problem, however these only provide a numerical or

nominal value as a result, other methods are required

to understand how the algorithm arrived to that con-

clusion and do not provide sufﬁcient information to

adopt the corresponding measures to prevent these ac-

cidents (for example, knowing at what time the most

accidents are likely to occur in order to deploy more

trafﬁc police ofﬁcers).

A Bayesian Network (BN) is a probabilistic

graphical model (PGM) that is represented by a di-

rected acyclic graph (DAG) that depicts a set of vari-

ables and their conditional relationships. Bayesian

networks are perfect for forecasting the likelihood

that any one of numerous possible known causes con-

tributed to an event that occurred. A BN, for example,

could be used to illustrate the probability correlations

between weather and climate conditions. The net-

work may be used to calculate the chances of certain

weather being present based on cLimate conditions.

In Bayesian networks, efﬁcient algorithms can do in-

ference and learning. The repercussions of highway

accidents can be characterized and assessed in terms

of accident severity, which can range from catas-

trophic events with fatalities to minor fender bender

damage. In most nations, ofﬁcial accident data exist

that categorize accidents according to severity using

the following simple scale: fatal accident, accident

308

Ugarte, W., Alcantara-Zapata, M., Ayamamani-Choque, L., Bances-Morales, R. and Cabrera-Sanchez, C.

A Bayesian Network for the Analysis of Trafﬁc Accidents in Peru.

DOI: 10.5220/0011045900003191

In Proceedings of the 8th International Conference on Vehicle Technology and Intelligent Transport Systems (VEHITS 2022), pages 308-315

ISBN: 978-989-758-573-9; ISSN: 2184-495X

resulting in serious injury, accident resulting in mi-

nor injury, and accident resulting in merely property

damage. The severity level is ﬁrst deﬁned when the

incidents are documented, and these basic classiﬁca-

tions are not consistent between countries.

Our contributions are as follows:

• We develop a Bayesian Network obtain with the

Hill Climbing Search with Bdeu score and Chow-

Liu Algorithm with K2 score.

• We carry out experiments to demonstrate that it is

possible to identify that very serious accidents are

generated with greater probability in the sections

of the Pan-American Highway at a belonging to

different districts, in speciﬁc shifts, due to differ-

ent reasons and in different types.

Our work is structured as: in Section 2 presents

the related works. Then, Section 3 presents the

background of our approach and the structure of our

model. Afterwards, Section 4 presents the experimen-

tation and ﬁnally in Section 5, our conclusions.

2 RELATED WORKS

In (Deublein et al., 2015), the authors seek to predict

the rates of minor, serious and fatal accidents that will

occur on the road segments in Switzerland. They per-

form a multivariate regression analysis on the origi-

nal data to obtain a base model. To this model they

applied an algorithm called ”expectation - maximiza-

tion” to train the base model. And with this later

model they calculate the conditional probabilities of

the number of accidents per road segment. The pur-

pose of this Bayesian model is to identify the road

segments with the highest probability of accident oc-

currence for risk reduction.

In (Hongguo et al., 2010), the authors explain that

the vehicular trafﬁc system is complex, since it has as

actors: people, vehicles, roads and the environment.

And a trafﬁc accident is caused by alteration of one

of these components. The purpose of this paper is to

ﬁnd, through a Bayesian network, the causality in ve-

hicular trafﬁc accidents. The authors indicate that in

previous studies only a unitary analysis is made and

this can only reveal the inherent laws of trafﬁc ac-

cident in a certain aspect, but does not contemplate

that the causality of trafﬁc accidents is multidimen-

sional and there are correlations and logical relation-

ships between causality factors. To learn the Bayesian

graph, they used the K2 algorithm and the tool tool

that Matalab offers for working with BN.

In (Zou and Yue, 2017), the authors give a gen-

eral consideration of the factors affecting road safety

assessments, Bayesian network theory based on prob-

ability risk analysis is applied in the causality analy-

sis of road accidents. Taking as a case the Adelaide

Central Business District (CBD) in South Australia,

the structure of the Bayesian network was established

by integrating the K2 algorithm with the knowledge

of experts, and the Expectation-Maximization algo-

rithm was adopted that could process the missing

data to perform parameter learning, thus establishing

the Bayesian network model for the analysis of the

causality of trafﬁc accidents. The results showed that

the Bayesian network model could effectively explore

the complex logical relationship in trafﬁc accidents

and express the uncertain relationship between the re-

lated variables. Not only was the model able to quan-

titatively predict the probability of an accident under

certain trafﬁc conditions, it can also ﬁnd the key rea-

sons and worst-case combination that leads to the oc-

currence of an accident. Their results can provide the-

oretical support for urban road management author-

ities to thoroughly analyze the drivers of road acci-

dents and then lay the basis for improving the safety

performance of the urban road trafﬁc system.

In (Makaba et al., 2021), the authors investigate

the cost-implications of road trafﬁc collision factors

for the economy, and transport policies. They de-

velop a Bayesian network framework using real-life

road trafﬁc collision data and expert knowledge to as-

sess the cost of road trafﬁc collisions.

In the ﬁrst work, an analysis focused on a speciﬁc

zone and evaluate where the most trafﬁc accidents oc-

cur and provide improvement actions. The second

work motivate us to map the different actors we had in

the dataset to ﬁnd causal relationships. In addition, it

motivate us to explore and test with more Bayesian

Network generation algorithms, not only K2. The

third work help us to emphasize ﬁnding the proba-

bilistic dependency relationships from the variables

to improve urban road safety management.

3 MATERIAL

In this section we present and explain the main con-

cepts that are used as the foundation of our work.

3.1 Preliminary Concepts

A Bayesian network is a probabilistic graphical model

that consists of a set of random variables and their

conditional dependencies represented by a directed

acyclic graph (cause-effect relationships). If a vari-

able has a parent node then it will have a table of con-

ditional probability. These graphs have as main appli-

A Bayesian Network for the Analysis of Trafﬁc Accidents in Peru

309

cations: classiﬁcation, diagnosis, among others. An-

other advantage is that we can generate the Bayesian

graphs without the complete dependence on ﬁeld ex-

perts. This thanks to algorithms such as exhaustive

search, the K2 algorithm and Hill-climbing. The ba-

sis of the Bayesian network is Bayes’ formula (see

Equation (1)) for conditional probability:

P(H | D) =

P(H) × P(D | H)

P(D)

(1)

3.2 Methods

Now, we present some methods used to generate

Bayesian Networks from the data.

3.2.1 Hill Climbing Search

It is a mathematical optimization algorithm, whose

purpose is to ﬁnd the best solution to a problem that

has a large number of possible solutions in a short

time, which is probably not the global optimal. Fig 1

depicts an elevation related to the goal function in a

one-dimensional state-space landscape. The objective

is to locate the global maximum. As indicated by the

arrow, hill-climbing search adjusts the existing condi-

tion in an attempt to enhance it. For our case, we are

seeking to maximize the score obtained for the graphs

generated during graph learning.

3.2.2 Chow-Liu Algorithm

It is a method that learns a Bayesian network with

a tree structure that maximizes the probability of the

training data. This algorithm uses the mutual infor-

mation, compute weight, between the events of the

variables by the Equation (2).

I(X, Y ) =

∑

x∈values(X)

∑

y∈values(Y )

P(x, y)log

P(x, y)

P(x)P(y)

(2)

Then it ﬁnds the maximum weight spanning tree,

which connects all vertices of a graph. And ﬁnally,

Figure 1: An overview of a one dimension function (Russell

and Norvig, 2020).

Figure 2: A ﬁrst-order dependency tree representing the

product on the left (Chow and Liu, 1968).

Figure 3: Accidents that occur on the Pan-American High-

way at Lima.

it assigns the directions. Fig 2 depicts a ﬁrst-order

dependency tree representing the product on the left.

3.3 Model

The data was obtained from the governmental open

data portals (see Section 4) which consists of trafﬁc

accidents records that occurred at the Pan-American

Highway in Lima (i.e., material damage, injured vic-

tims and fatalities). Fig. 3 depicts these accidents with

blue dots. Table 1 shows the trafﬁc accident variables.

Table 1: Variables related to car accidents in Peru.

Variable Description

Day Day of accident occurrence

Shift Shift corresponding to the time

Sense Direction in which a vehicle is traveling

Vehicles Involved Vehicles involved in the accident

Reason Cause of the accident generation

District District of the Lima region where it occurred

Type Type of accident that occurred

Severity Importance of an accident according to its effects

• Material Accidents: Fig. 4a depicts the count of

material accidents by their types. For instance,

the most common type of material accidents are

rear collision. Fig. 4b depicts the count of material

accidents by district.

• Accidents with Injuries: Fig. 5a depicts the

count of accidents with injuries by their types. For

instance, the most common type of material acci-

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

310

(a) Accident types. (b) Count of Accidents for Districts.

Figure 4: Material Accident Data related to car accidents in Peru.

(a) Accident types. (b) Count of Accidents for Districts.

Figure 5: Accidents with Injuries Data related to car accidents in Peru.

(a) Accident types. (b) Count of Accidents for Districts.

Figure 6: Deathly Accident Data related to car accidents in Peru.

dents are rear collisions or motorcycle collisions.

Fig. 5b depicts the count of accidents with injuries

by district.

• Deathly Accidents: Fig. 6a depicts the count of

deathly accidents by their types. For instance, the

most common type of deathly accidents are runs

over or rear collisions. Fig. 6b depicts the count

of deathly accidents by district.

3.3.1 Scores

Bayesian Information Criterion (BIC) (Schwarz,

1978) is a criterion for model selection among a ﬁnite

set of models; models with lower BIC are generally

preferred. It is based, in part, on the likelihood func-

tion. When ﬁtting models, it is possible to increase

the likelihood by adding parameters, but it may result

in overﬁtting. BIC is formally deﬁned as:

BIC = k ln(n) − 2 ln(

L). (3)

where :

L = the maximized value of the

likelihood function of the model M

x = the observed data

n = the sample size

k = the number of parameters

estimated by the model

K2 (Cooper and Herskovits, 1992) ﬁnds the struc-

ture that maximizes each factor of a BN. It is derived

by assuming uniform prior distributions on the values

of an attribute foreach possible instantiation of its par-

ent attributes. This assumption introduces a tendency

A Bayesian Network for the Analysis of Trafﬁc Accidents in Peru

311

to select simpler network structures. The K2 metric is

formally deﬁned as:

K2(B, T ) = log(P(B))+

∑

i=1

∑

j=1



log



−1)!

i j

−1)!



∑

k=1

log(N

i jk



where

B : a network

P(B) : represents the prior probability of the network B

T : data

: number of states of the ﬁnite random variable X

i jk

: number of instances in the data T where

the variable X

takes its k-th value x

and

the variables in Π

take their j-th conﬁguration w

i j

BDeu (Heckerman et al., 1995) is a special case of

BDe, where BDe means Bayesian Dirichlet scoring,

and, thanks to likelihood equivalence, yields the same

score for any two Markov equivalent structures given

D and a prior network from which the priors are de-

rived. For BDeu, they use uniform priors.

BDeu(B, T ) = log(P(B))+

∑

i=1

∑

j=1

log







i j



∑

k=1

log

Γ(N

i jk

)

Γ(

)

where

B : a network

P(B) : represents the prior probability of the network B

Γ : theGamma f unction

T : data

: number of states of the ﬁnite random variable X

i jk

: number of instances in the data T where

the variable X

takes its k-th value x

and

the variables in Π

take their j-th conﬁguration w

i j

According to (Liu et al., 2012), BIC score can still

work well for large sample sizes, however it can per-

form arbitrarily worse than other functions for small

data sets. Additionally, according to (Riggelsen,

2008) the methodology for calculating the K2 score

is analogous to that of BDEu, however it differs in

that K2 makes use of a priori parameters equal to one.

4 EXPERIMENTATION

In this section we present our experimental study to

show the results of our study.

4.1 Experimental Protocol

For the development of our approach, we used the fol-

lowing resources:

1. Software: We develop our proposal with Python

3.7 with Google Colab Pro

2. Hardware: We use Google Colab Pro service

with SSD 125GB for storage, 24GB of RAM, a

GPU Nvidia

Tesla V100-SXM2 16 GB and a

CPU Intel

Xeon

CPU @ 2.20GHz

3. Dataset: We used the public dataset

from Municipality of Lima: https:

//aplicativos.munlima.gob.pe/extranet/

datos-abiertos/.

Our code is publicly available at: https:

//colab.research.google.com/drive/

1rpSPGnCQsWmUlYGZCnonOI20_7mPAiny?usp=

sharing

4.2 Results

The algorithms (see Section 3.2) and the scores (see

Section 3.3.1) are evaluated in order to determine the

best possible model for a BN.

4.2.1 BN Model

Hill Climbing Search: When applying the Hill

Climbing Search method (see Section 3.2.1), the fol-

lowing Bayesian networks were obtained with their

respective scores. Fig. 7a depicts the best BN ob-

tained with hill climbing algorithm for BIC score, as

we can see, it only considers three variables letting

aside the other ones. Hence it is not useful in prac-

tice, since the queries cannot be made over the vari-

ables that are not taken into account.

Fig. 7b (resp. Fig. 7c) depicts the best BN ob-

tained with hill climbing algorithm for K2 score (resp.

BDeu score), as we can see, it considers all ﬁve vari-

ables. Furthermore, Fig. 7b and Fig. 7c show that with

K2 score and BDeu scores obtain the same BN.

Chow-Liu Algorithm. When applying the Chow-

Liu algorithm (see Section 3.2.2), the following

Bayesian networks were obtained with their respec-

tive scores. Fig. 8a, Fig. 8b and Fig. 8c show that

all three scores (i.e., BIC score, K2 score and BDeu

score) obtain the same BN as a tree centered on “Ve-

hicles

Involved” variable.

4.2.2 Queries

Thanks to the Variable Elimination method (Zhang

and Poole, 1994), we can use the obtained BN models

to make inference queries.

Hill Climbing Search: We use the BN obtained by

hill climbing method with BDeu score (see Fig. 7c).

For instance, Table 2 shows the distribution for dis-

tricts knowing that the reason of an accident is an

animal on the road (i.e., Q

: P(District | Reason =

animal on the road)).

Now, we are going to make some queries with the

BN model according to the data:

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

312

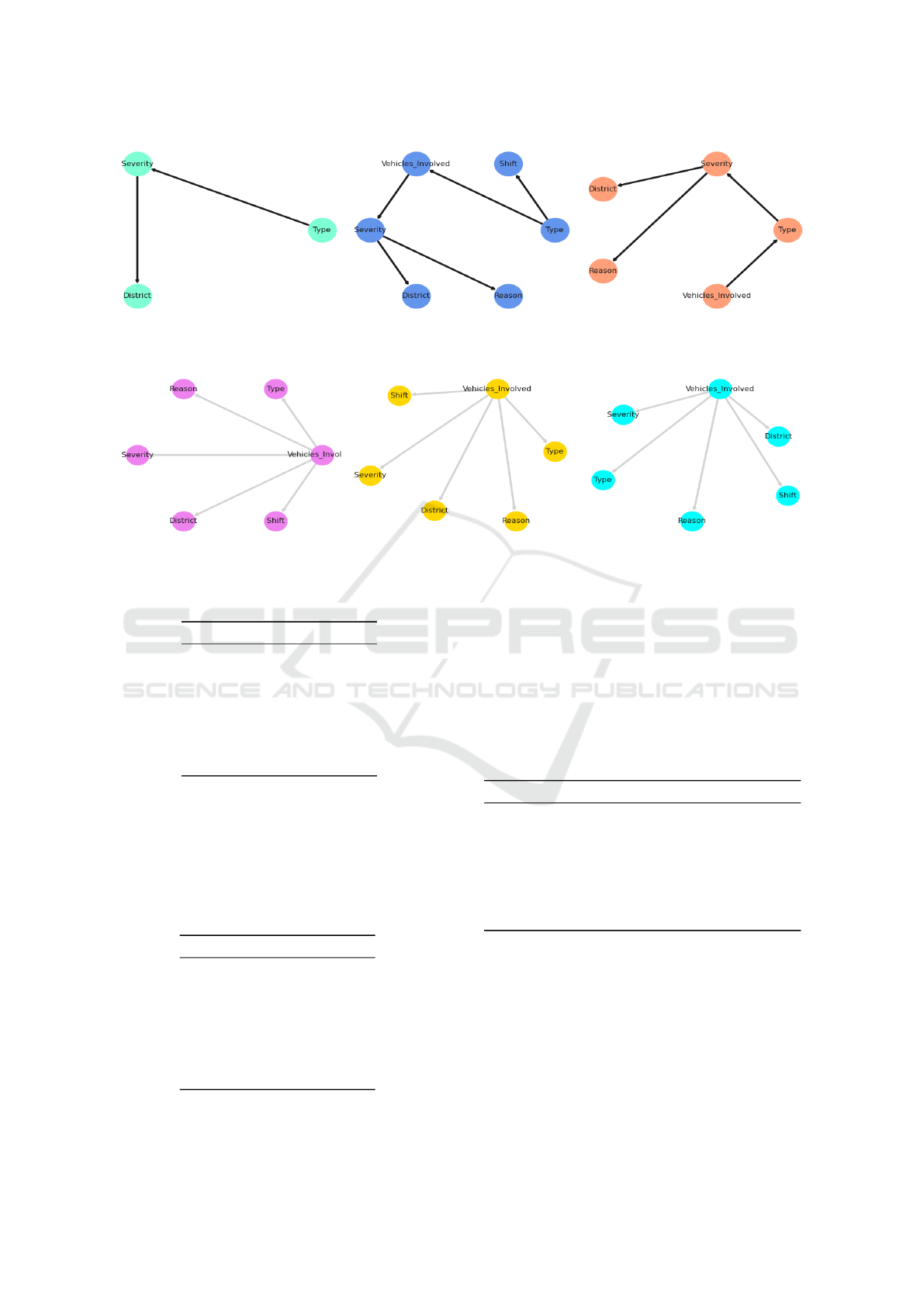
(a) BIC (-6007.599403466215). (b) K2 (-13910.791490413974) (c) BDEU (-11844.857478769678)

Figure 7: BN obtained with Hill Climbing for various scores.

(a) BIC (-28690.35418960265). (b) K2 (-14663.279955755112) (c) BDEU (-14703.524814010063)

Figure 8: BN obtained with Chow Liu Algorithm for various scores.

Table 2: Percentage values for query Q

District Percentage (%)

Rimac 32.2897

Ate 20.4259

El Agustino 14.9067

San Martin de Porres 12.7724

Santa Anita 7.0057

Lima 6.0446

La Molina 4.4526

Santiago de Surco 2.1024

: P(District | Severity = deathly) , this query

helps to obtain the distribution of Districts knowing

that a deathly accident has happened. Table 3 shows

the distribution for this query, where we can pick the

ﬁrst four districts according to their percentage (i.e.,

Rimac, El Agustino, ate and San Martin de Porres).

Table 3: Percentage values for query Q

District Percentage (%)

Rimac 31.2005

El Agustino 25.3065

ate 13.0754

San Martin de Porres 10.4243

Santa Anita 8.2161

Lima 5.6259

La Molina 4.8440

Santiago de Surco 1.3074

: P



Reason, Type



Severity = deathly,

District = Rimac



, this

query helps to obtain the distribution of Reasons and

Types of accidents knowing that a deathly accident at

Rimac District has happened. Table 4 shows the dis-

tribution for this query, the main reasons and types

are pedestrian on the road, reckless driver with rear

collision and side collision.

Table 4: Percentage values for query Q

Reason Type Percentage (%)

pedestrian on the

road

hit a pedestrian on

the road

19.8853

reckless driver rear collision 18.5141

reckless driver side collision 8.3092

reckless driver hit a pedestrian on

the road

7.7709

pedestrian on the

road

run over 5.6028

: P



Reason, Type



Severity = deathly,

District = El Agustino



this query helps to obtain the distribution of Reasons

and Types of accidents knowing that a deathly acci-

dent at El Agustino District has happened. Table 5

shows the distribution for this query, the main reasons

and types are pedestrian on the road, homeless on the

road that are runned over and reckless drivers.

A Bayesian Network for the Analysis of Trafﬁc Accidents in Peru

313

Table 5: Percentage values for query Q

Reason Type Percentage (%)

pedestrian on the

road

hit a pedestrian on

the road

24.8418

homeless on the road run over 15.2892

reckless driver hit a pedestrian on

the road

10.1552

reckless driver rear collision 6.1704

reckless driver side collision 5.1654

: P



Reason, Type



Severity = deathly,

District = ate



, this

query helps to obtain the distribution of Reasons and

Types of accidents knowing that a deathly accident at

ate District has happened. Table 6 shows the distri-

bution for this query, the main reasons and types are

pedestrian on the road, homeless on the road that are

runned over and reckless drivers.

Table 6: Percentage values for query Q

Reason Type Percentage (%)

pedestrian on the

road

hit a pedestrian on

the road

24.8418

homeless on the road run over 15.2892

reckless driver hit a pedestrian on

the road

10.1552

reckless driver rear collision 6.1704

reckless driver side collision 5.1654

: P



Reason, Type



Severity = deathly,

District = San Martin de Porres



this query helps to obtain the distribution of Reasons

and Types of accidents knowing that a deathly

accident at ate District has happened. Table 7 shows

the distribution for this query, the main reasons and

types are pedestrian on the road, reckless drivers and

collisions.

Table 7: Percentage values for query Q

Reason Type Percentage (%)

pedestrian on the

road

hit a pedestrian on

the road

28.6446

reckless driver hit a pedestrian on

the road

10.4051

reckless driver rear collision 7.5471

pedestrian on the

road

run over 4.9270

reckless driver side collision 4.1947

Chow-Liu Algorithm: We use the BN obtained by

Chow-Liu Algorithm with K2 score (see Fig. 8b). For

instance, Table 8 shows the distribution for districts

and severity knowing that the reason of an accident is

a drunk driver.

Now, we are going to make some queries with the

Table 8: Percentage values for query P(District | Reason =

animal on the road).

Severity District Percentage (%)

mild Rimac 20.4145

serious Rimac 15.2064

mild Ate 9.1750

serious Ate 7.6141

mild San Martin de Porres 7.4299

mild El Agustino 7.0407

serious El Agustino 6.6580

serious San Martin de Porres 4.5564

serious La Molina 3.7086

mild Lima 3.5557

BN model according to the data:

: P



Shi f t



Severity = deathly,

District = Rimac



, this

query helps to obtain the distribution of Shift know-

ing that a deathly accident at Rimac District has

happened. Table 9 shows the distribution for this

query, the main shift for accident is the afternoon.

Table 9: Percentage values for query Q

Shift Percentage (%)

afternoon 38.0837

morning 31.2627

night 21.8436

early morning 8.8099

: P





Reason



Severity = deathly,

District = Rimac,

Shi f t = a f ternoon





this query helps to obtain the distribution of Reason

knowing that a deathly accident at Rimac District

at afternoon has happened. Table 10 shows the

distribution for this query, the main reasons are

reckless driver, pedestrian on the road and speeding.

Table 10: Percentage values for query Q

Reason Percentage (%)

reckless driver 44.7673

pedestrian on the road 21.2712

speeding 6.2850

mechanical / electrical problems 5.6429

previous accident 5.4414

: P





Reason, Type



Severity = deathly,

District = Rimac,

Shi f t = a f ternoon





this query helps to obtain the distribution of Reason

and Type knowing that a deathly accident at Rimac

District at afternoon has happened. Table 11 shows

the distribution for this query, the main reasons are

reckless driver, pedestrian on the road and speeding.

VEHITS 2022 - 8th International Conference on Vehicle Technology and Intelligent Transport Systems

314

Table 11: Percentage values for query Q

Reason Type Percentage (%)

reckless driver rear collision 22.0395

pedestrian on the

road

hit a pedestrian on

the road

14.0416

reckless driver side collision 8.4765

reckless driver hit a pedestrian on

the road

5.9364

pedestrian on the

road

run over 4.3538

4.3 Discussion

The Q

query allowed us to identify the four districts

in which road sections have a higher probability of fa-

tal vehicle accidents. Based on these results, we carry

out queries Q

, Q

and Q

to infer the probabil-

ities for the reasons and types of accidents that these

fatal accidents occur in these four districts.

The results of the Q

query also helped us to de-

velop the last 3 queries, since it allowed us to detect

the section of the Pan-American highway belonging

to the Rimac district as the one with the greatest prob-

ability for fatal vehicle accidents, based on this, we

carry out query Q

, to infer the probabilities of the

shifts when these fatal accidents occur in the Rimac

district, resulting in the afternoon.

Based on the result of query Q

, we carry out

queries Q

and Q

that consider vehicular accidents

whose severities are fatal in the Rimac district that

occur in the afternoon, these queries let us identify

the reasons and types of accidents respectively. We

believe that these results will be of great relevance to

carry out preventive actions and thus reduce the num-

ber of these unfortunate accidents.

5 CONCLUSIONS

A Bayesian network was obtained with one of the

highest scores, using the Hill Climbing Search and

Chow Liu algorithm with K2 score- After carrying

out the experiments, it was possible to identify that

very serious accidents occur with a high probability

in the part of the Pan-American Highway belonging

to the Rimac district at the afternoon shift and due to

pedestrian on the road, a reckless driver or speeding.

It is recommended to place a greater police guard

in the part of the Pan-American Highway, belonging

to the Rimac district between 12 and 18 hours and to

carry out awareness campaigns in this area, in order to

reduce the speed of cars and thus reduce the number

of accidents with fatalities. Due to the fact that one of

the factors is speeding, a photo ballot systems with the

respective notice to drivers should be implemented.

Further works can be done with similar analysis of

other critical points in the country, for instance, ﬁnd

other trafﬁc problems by applying Markov chains,

for example variations in driving patterns, pose esti-

mation for road pedestrians (Fernandez-Ramos et al.,

2021) and looking if car sharing may help to decrease

the trafﬁc accident rate (V

asquez-Garaya et al., 2021).

REFERENCES

Chow, C. and Liu, C. (1968). Approximating discrete

probability distributions with dependence trees. IEEE

Transactions on Information Theory, 14(3).

Cooper, G. F. and Herskovits, E. (1992). A bayesian method

for the induction of probabilistic networks from data.

Mach. Learn., 9:309–347.

Deublein, M., Schubert, M., Adey, B. T., and Garc

ıa de

Soto, B. (2015). A bayesian network model to pre-

dict accidents on swiss highways. Infrastructure Asset

Management, 2(4).

Fernandez-Ramos, O., Johnson-Ya

nez, D., and Ugarte, W.

(2021). Reproducing arm movements based on pose

estimation with robot programming by demonstration.

In IEEE ICTAI.

Heckerman, D., Geiger, D., and Chickering, D. M.

(1995). Learning bayesian networks: The combina-

tion of knowledge and statistical data. Mach. Learn.,

20(3):197–243.

Hongguo, X., Huiyong, Z., and Fang, Z. (2010). Bayesian

network-based road trafﬁc accident causality analysis.

In WASE ICIE.

Liu, Z., Malone, B. M., and Yuan, C. (2012). Empirical

evaluation of scoring functions for bayesian network

model selection. BMC Bioinform., 13(S-15):S14.

Makaba, T., Doorsamy, W., and Paul, B. S. (2021).

Bayesian network-based framework for cost-

implication assessment of road trafﬁc collisions. Int.

J. Intell. Transp. Syst. Res., 19(1):240–253.

Riggelsen, C. (2008). Approximation Methods for Efﬁcient

Learning of Bayesian Networks, volume 168 of Fron-

tiers in Artiﬁcial Intelligence and Applications. IOS

Press.

Russell, S. J. and Norvig, P. (2020). Artiﬁcial Intelligence:

A Modern Approach (4th Edition). Pearson.

Schwarz, G. (1978). Estimating the Dimension of a Model.

The Annals of Statistics, 6(2):461 – 464.

asquez-Garaya, J. P., Munayco-Apolaya, E., and Ugarte,

W. (2021). Carsharing system for urban transport in

lima using internet of things. In WEBIST.

Zhang, N. L. and Poole, D. L. (1994). A simple approach

to bayesian network computations. In Canadian AI.

Zou, X. and Yue, W. (2017). A bayesian network approach

to causation analysis of road accidents using netica.

Journal of Advanced Transportation, 2017.

A Bayesian Network for the Analysis of Trafﬁc Accidents in Peru

315